A Many-objective Optimization Framework for Virtualized Datacenters

Fabio L

opez Pires

1,2

and Benjam

ın Bar

2,3

Itaipu Technological Park (PTI), Hernandarias, Paraguay

National University of Asunci

on (UNA), San Lorenzo, Paraguay

National University of the East (UNE), Ciudad del Este, Paraguay

Keywords:

Virtual Machine Placement, Many-objective Optimization, Datacenter, Virtualization, Cloud Computing.

Abstract:

The process of selecting which virtual machines should be located (i.e. executed) at each physical machine of

a datacenter is commonly known as Virtual Machine Placement (VMP). This work presents a general many-

objective optimization framework that is able to consider as many objective functions as needed when solving

the VMP problem in a pure multi-objective context. As an example of utilization of the proposed framework,

for the ﬁrst time a formulation of the many-objective VMP problem (MaVMP) is proposed, considering the

simultaneous optimization of the following ﬁve objective functions: (1) power consumption, (2) network traf-

ﬁc, (3) economical revenue, (4) quality of service and (5) network load balancing. To solve the formulated

many-objective VMP problem, an interactive memetic algorithm is proposed. Simulations prove the correct-

ness of the proposed algorithm and its effectiveness converging to a treatable number of solutions in different

experimental scenarios.

1 INTRODUCTION

One of the key challenges in modern datacenters is

to efﬁciently manage power consumption, conside-

ring electricity costs and the carbon dioxide foot-

prints (Beloglazov et al., 2011). Most of the time,

servers operate in a very low energy-efﬁciency re-

gion (i.e. between 10 and 50% of resource utiliza-

tion), even considering that workload peaks rarely

occur in practice (Barroso and H

olzle, 2007). Conse-

quently, applying techniques for higher resource uti-

lization can result in more energy-efﬁcient server ope-

ration. Virtualization of computational resources is a

technology that dynamically improves the utilization

of available resources in a datacenter according to the

existing demand, improving efﬁciency. Correctly lo-

cating virtual machines (VMs) into physical machines

(PMs) reduces the amount of hardware in use, let-

ting unused PMs to be in standby mode or even to

shut down. This way, average resource utilization as

well as energy efﬁciency may be improved, resulting

in better economical revenue and greener datacenters.

Virtualization in modern datacenters introduces

management decisions related to the placement of

VMs. In this context, Virtual Machine Placement

(VMP) is the process of selecting which VMs should

be executed in a given set of PMs of a datacenter.

1.1 Background and Motivation

In datacenters with a considerable amount of PMs

and VMs, there is a large number of possible criteria

that can be considered when selecting a placement,

depending on the priorities and optimization objec-

tives. These criteria can even change from one period

of time to another, which implies a variety of possi-

ble formulations of the VMP problem and objective

functions to be optimized for virtualized datacenters.

According to (L

opez Pires and Bar

an, 2015), the

optimization of the energy consumption is the most

studied objective function in VMP literature (Sun

et al., 2013; Beloglazov et al., 2012). On the other

hand, network trafﬁc (Anand et al., 2013), economi-

cal revenue (Shi et al., 2013; Sato et al., 2013), per-

formance (Bin et al., 2011) and resource utilization

(Mishra and Sahoo, 2011) optimization are also very

studied. For each objective function, several possible

formulations can be proposed.

In the VMP context, objective functions can be

studied according to the following identiﬁed opti-

mization approaches: (1) mono-objective (MOP), (2)

multi-objective solved as mono-objective (MAM) and

(3) multi-objective (PMO) (L

opez Pires and Bar

an,

2015). The mono-objective approach considers the

optimization of only one objective or the individual

439

López Pires F. and Barán B..

A Many-objective Optimization Framework for Virtualized Datacenters.

DOI: 10.5220/0005434604390450

In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 439-450

ISBN: 978-989-758-104-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

optimization of more than one objective, one at a

time. On the other hand, multi-objective solved as

mono-objective approach considers the optimization

of multiple objectives combined into one objective

(usually as a weighted sum of different normalized

objectives), while a pure multi-objective approach

considers the simultaneous optimization of different

(possible contradictory) objectives. To the best of

the authors’ knowledge, there is no many-objective

optimization formulation proposed for the VMP pro-

blem in the specialized literature (L

opez Pires and

Bar

an, 2015), i.e a multi-objective optimization pro-

blem with at least four conﬂicting objective functions

(von L

ucken et al., 2014).

Considering the large number of existing objective

functions for the VMP problem, this work presents a

many-objective optimization framework to be able to

consider as many objective functions as needed when

solving the VMP problem. As an example of uti-

lization of the proposed framework, for the ﬁrst time

a formulation of the many-objective VMP problem

(MaVMP) is proposed, considering the following ﬁve

objective functions: (1) power consumption minimi-

zation, (2) network trafﬁc minimization, (3) economi-

cal revenue maximization, (4) QoS maximization and

(5) network load balancing optimization. In the pre-

sented formulation, a multi-level priority is associa-

ted to each VM, representing a Service Level Agree-

ment (SLA) considered in the placement process. To

solve the formulated MaVMP problem, an interactive

memetic algorithm is proposed considering the is-

sues that give place the formulated problem of many-

objective optimization for Pareto-based algorithms.

This paper is structured in the following way: Sec-

tion 2 presents a multi-objective optimization pro-

blem formulation, considering the issues that give

place the problem of many-objective optimization.

Section 3 details the proposed general many-objective

optimization framework, while Section 4 summarizes

a many-objective formulation of the VMP problem

considering the simultaneous optimization of ﬁve ob-

jective functions and a multi-level priority of SLA.

Section 5 presents a novel interactive memetic al-

gorithm proposed for solving the formulated many-

objective problem, while Section 6 presents ﬁrst expe-

rimental results. Finally, conclusions and future work

are left to Section 7.

2 MULTI-OBJECTIVE

OPTIMIZATION

A general pure multi-objective optimization problem

(PMO) includes a set of p decision variables, q objec-

tive functions, and r constraints. Objective functions

and constraints are functions of decision variables. In

a PMO formulation, x represents the decision vector,

while y represents the objective vector. The decision

space is denoted by X and the objective space as Y .

These can be expressed as (Coello et al., 2007):

Optimize:

y = f (x) = [ f

(x), f

(x),..., f

(x)] (1)

subject to:

e(x) = [e

(x),e

(x),...,e

(x)] ≥ 0 (2)

where:

x = [x

,...,x

] ∈ X (3)

y = [y

,...,y

] ∈ Y (4)

It is important to remark that optimizing, in a parti-

cular problem context, can mean maximizing or mi-

nimizing. The set of constrains e(x) ≥ 0 deﬁnes the

set of feasible solutions X

⊂ X and its corresponding

set of feasible objective vectors Y

⊂ Y . The feasible

decision space X

is the set of all decision vectors x in

the decision space X that satisﬁes the constraints e(x),

and it is deﬁned as:

= {x | x ∈ X ∧ e(x) ≥ 0} (5)

The feasible objective space Y

is the set of the ob-

jective vectors y that represents the image of X

onto

Y and it is denoted by:

= {y | y = f (x) ∀x ∈ X

} (6)

To compare two solutions in a multi-objective

context, the concept of Pareto dominance is used.

Given two feasible solutions u, v ∈ X, u dominates v,

denoted as u  v, if f (u) is better or equal to f (v) in

every objective function and strictly better in at least

one objective function. If neither u dominates v, nor

v dominates u, u and v are said to be non-comparable

(denoted as u ∼ v).

A decision vector x is non-dominated with respect

to a set U, if there is no member of U that dominates x.

The set of non-dominated solutions of the whole set of

feasible solutions X

, is known as optimal Pareto set

∗

. The corresponding set of objective vectors consti-

tutes the optimal Pareto front PF

∗

PMOs with more than three objective functions

are known as Many-Objective Optimization Problems

(MaOPs), as deﬁned in (Cheng et al., 2014). MaOPs

differ signiﬁcantly from PMOs because several issues

should be considered when solving problems with

more than three objective functions (Farina and Am-

ato, 2002). In case of Pareto-based algorithms, these

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

440

issues are intrinsically related to the fact that as the

number of objective increases, the proportion of non-

dominated elements in the population grows, being

increasingly difﬁcult to discriminate among solutions

using only the Pareto dominance relation (Deb et al.,

2006). Additionally, determining which solution to

keep and which to discard in order to converge toward

the Pareto set is still a relevant issue to be addressed

(Farina and Amato, 2002). Pareto-based algorithms

are still not able to provide the required selection pres-

sure towards better solutions in order to conduct an

efﬁcient evolutionary search and, even elitism may be

difﬁcult. As the number of objectives grows, the pro-

portion of non-comparable solutions to the total num-

ber of solutions tends to one (von L

ucken et al., 2014),

making more difﬁcult to solve a MaOP. Clearly, difﬁ-

culties in solving MaOPs explain why it has not yet

been studied in the VMP literature.

3 MANY-OBJECTIVE

OPTIMIZATION FRAMEWORK

The general many-objective optimization framework

for the VMP problem proposed in this work consi-

ders that as the number of conﬂicting objectives of

a MaVMP problem formulation increases, the total

number of non-dominated solutions increases (even

exponentially in some cases), being increasingly dif-

ﬁcult to discriminate among solutions using only the

dominance relation (Farina and Amato, 2002). For

this reason, this work proposes the utilization of lower

and upper bounds associated to each objective func-

tion z ∈ {1,...,q} (L

≤ f

(x) ≤ U

) to be able to

reduce iteratively the number of possible compro-

mise solutions of the Pareto set approximation, when

needed by the decision maker.

A VMP formulation, based on many objective

functions and constraints to be detailed in Section 4,

may be written as:

Optimize:

y = f (x) = [ f

(x), f

(x),..., f

(x)] (7)

where:

(x) = power consumption minimization

(x) = network trafﬁc minimization

(x) = economical revenue maximization

(x) = QoS maximization

(x) = network load balancing optimization

(x) = any other considered function

(8)

subject to:

(x) : unique placement of VMs;

(x) : assure provisioning of highest SLA;

(x) : processing resource capacity of PMs;

(x) : memory resource capacity of PMs;

(x) : storage resource capacity of PMs;

(x) : f

(x) ∈ [L

];

(x) : f

(x) ∈ [L

];

(x) : f

(x) ∈ [L

];

(x) : f

(x) ∈ [L

];

(x) : f

(x) ∈ [L

];

(x) : any other considered constraint.

(9)

4 MANY-OBJECTIVE VIRTUAL

MACHINE PLACEMENT

A few articles proposed formulations of a pure

multi-objective VMP problem (MVMP) (Gao et al.,

2013; L

opez Pires and Bar

an, 2013), considering the

simultaneous optimization of at most three objective

functions. To the best of the authors’ knowledge,

this work proposes for the ﬁrst time the formulation

of a MaVMP problem considering the following ﬁve

objective functions to be simultaneously optimized:

(1) power consumption, (2) network trafﬁc, (3)

economical revenue, (4) quality of service and (5)

network load balancing. In this many-objective for-

mulation, a multi-level priority is associated to each

VM, representing a SLA. Formally, the proposed

ofﬂine many-objective optimization VMP problem

can be enunciated as:

Given a set of PMs, H = {H

,...,H

}, a

network topology G (as illustrated in Figure 1) and a

set of VMs, V = {V

,...,V

}, it is sought a correct

placement of the set of VMs V in the set of PMs

H satisfying the r constraints of the problem and

simultaneously optimizing all q objective functions

deﬁned in this formulation (as energy consumption,

network trafﬁc, economical revenue, QoS and load

balancing in the network), in a pure many-objective

context.

4.1 Input Data

The proposed formulation of the VMP problem mo-

dels a virtualized datacenter infrastructure, composed

by PMs and a network topology. The set of PMs

AMany-objectiveOptimizationFrameworkforVirtualizedDatacenters

441

is represented as a matrix H of dimension (n x 4).

Each H

is represented by processing resources CPU

(as ECU)

, RAM memory [GB], storage [GB] and a

maximum power consumption [W] as:

= [Hcpu

,Hram

,Hhdd

, pmax

]

∀i ∈ {1,...,n}

(10)

where:

Hcpu

: Processing resources of H

;

Hram

: Memory resources of H

;

Hhdd

: Storage resources of H

;

pmax

: Maximum power consumption of H

;

n: Number of PMs.

As shown in Figure 1, the network topology of

the virtualized datacenter is represented as:

G: Network topology;

L: Set of links l

in G. For simplicity, we

assume that all links are semi-duplex;

M: Set of paths for all-to-all PM interconnec-

tions;

K: Capacity set of the communication cha-

nnel, typically in [Mbps].

The set of VMs requested by customers is repre-

sented as a matrix V of dimension (m x 5). Each V

requires processing resources CPU (as ECU)

, RAM

memory [GB] and storage [GB], providing for them

an economical revenue R

[$] for the provider. A SLA

is also assigned to each VM to indicate its level of

priority. Consequently, a V

is represented as:

= [V cpu

,V ram

,V hdd

,SLA

]

∀ j ∈ {1,...,m}

(11)

where:

V cpu

: Processing requirements of V

;

V ram

: Memory requirements of V

;

V hdd

: Storage requirements of V

;

: Economical revenue for locating V

;

SLA

: Service Level Agreement SLA

of a V

. If

the highest priority level is s, then SLA

∈

{1,. . . , s};

m: Number of VMs.

The trafﬁc between VMs is represented as a ma-

trix T of dimension (m x m). Each V

requires net-

work communication resources [Mbps] to communi-

cate with other VMs. These communication resources

http://aws.amazon.com/ec2/faqs

are represented as:

= [T

,..., T

]

∀ j ∈ {1,...,m}

(12)

where:

: Average network trafﬁc between V

and

[Mbps]. Note that we can consider

j j

= 0.

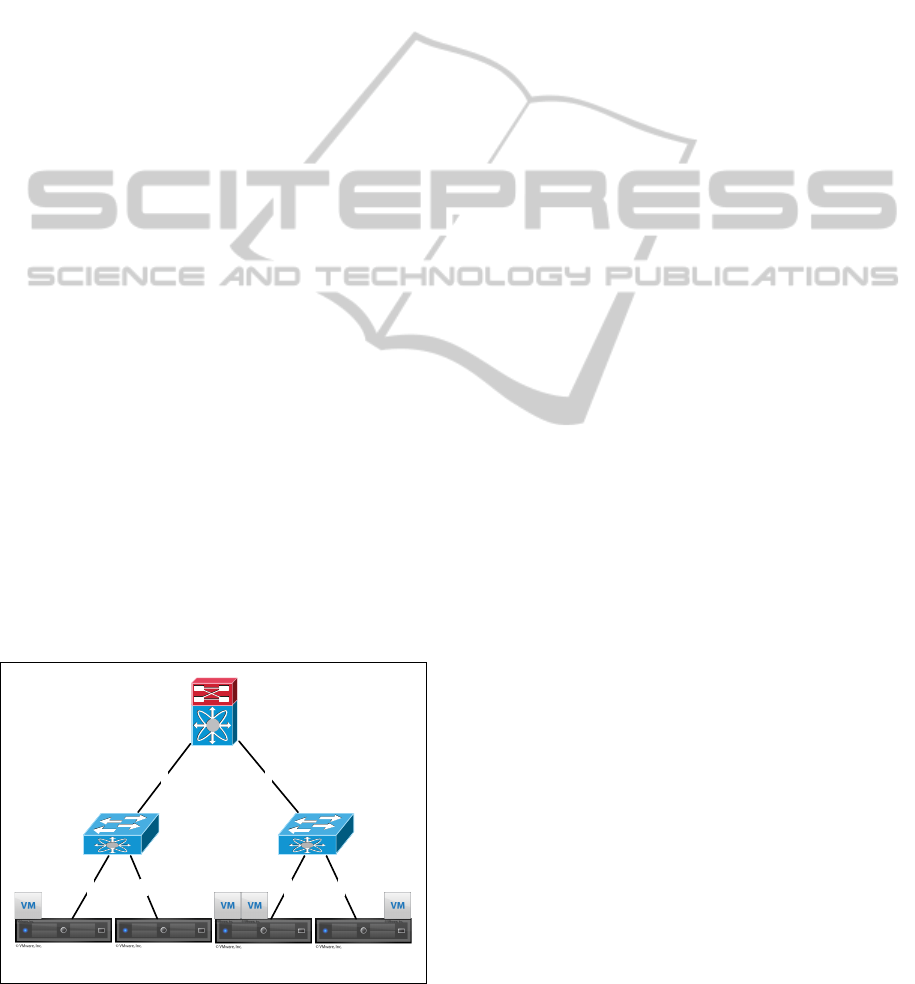
Figure 1 presents a basic example of a virtualized

datacenter infrastructure, composed by 4 PMs H =

} and a network topology considering

6 physical network links L = {l

}. In

this example, the set of capacity for each communica-

tion channel is K = {100,100,100,100,1000, 1000}

[Mbps] respectively. Using shortest path, a path m

between H

and H

uses links {l

}, i.e. m

}. Analogously, m

= {l

} and m

}, as shown in Figure 1.

4.2 Output Data

A calculated solution should indicate the exact place-

ment of each VM V

on the necessary PMs H

considering the many-objective optimization criteria

applied. A placement (or possible solution to the

formulated problem) is represented in what follows

as a matrix P = {P

} of dimension (m x n), where

∈ {0,1} indicates if V

is located (P

= 1) or not

= 0) for execution on a PM H

(i.e., P

: V

→ H

4.3 Constraints

4.3.1 Constraint 1: Unique Placement of VMs

A VM V

should be located to run on a single PM H

or alternatively, it could be not located in any PM if

the associated SLA

is not the highest level of priority

s. Consequently, this constraint is expressed as:

∑

i=1

≤ 1 ∀ j ∈ {1,...,m}

(13)

where:

: Binary variable equals 1 if V

is located to

run on H

; otherwise, it is 0.

4.3.2 Constraint 2: Assure SLA Provisioning

A VM V

with the highest level of SLA (i.e. SLA

= s)

must necessarily be located to run on a PM H

. Con-

sequently, this constraint is expressed as:

∑

i=1

= 1 ∀ j such that SLA

= s

(14)

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

442

4.3.3 Constraints 3-5: Physical Resource

Capacity of PMs

A PM H

must have sufﬁcient available resources

to meet the requirements of all VMs V

that are lo-

cated to run on H

. In this work, it is not considered

the overbooking of resources (Tom

as and Tordsson,

2013). Consequently, this set of constraints can be

mathematically formulated as:

∑

j=1

V cpu

× P

≤ Hcpu

(15)

∑

j=1

V ram

× P

≤ Hram

(16)

∑

j=1

V hdd

× P

≤ Hhdd

(17)

∀i ∈ {1,...,n},i.e. for all physical machine H

4.3.4 Adjustable Constraints

This work proposes the utilization of lower and upper

bounds associated to each objective function to re-

duce the number of possible solutions of the Pareto set

approximation P

known

, when needed by the decision

maker. Consequently, this set of adjustable bounds

can be mathematically formulated as the following

constraints:

(x) ∈ [L

] ∀z ∈ {1,...,q}

(18)

4.4 Objective Functions

A VMP problem can be deﬁned as a many-objective

optimization problem, considering the simultaneous

optimization of more than three objective functions.

Active paths of M

= {l

}

= {l

}

= {l

}

100 Mbps 100 Mbps 100 Mbps 100 Mbps

1000 Mbps 1000 Mbps

Total traffic per path

= 4 Mbps

= 2 Mbps

= 4 Mbps

Figure 1: Example of placement in a virtualized datacenter

infrastructure, composed by PMs and a network topology.

As a concrete example, this work proposes for the ﬁrst

time the optimization of the following ﬁve objective

functions:

4.4.1 Power Consumption Minimization

Based on (Beloglazov et al., 2012) formulation, this

work also proposes the minimization of power con-

sumption, represented by the sum of the power con-

sumption of each PM H

(x) =

∑

i=1

((pmax

− pmin

) ×Ucpu

+ pmin

) ×Y

(19)

where:

(x): Total power consumption of the PMs;

pmin

: Minimum power consumption of H

. In

what follows, pmin

= pmax

∗ 0.6 (Belo-

glazov et al., 2012);

Ucpu

: Utilization ratio of processing resources

used by H

;

: Binary variable equals 1 if H

is turned

on; otherwise, it is 0.

4.4.2 Network Trafﬁc Minimization

(Shrivastava et al., 2011) proposed the minimization

of network trafﬁc among VMs by maximizing local-

ity. Based on this approach, this work proposes equa-

tion (20) to estimate network trafﬁc represented by the

sum of average network trafﬁc generated by each VM

, that is located to run on any PM, with other VMs

that are located to run on different PMs.

(x) =

∑

j=1

∑

k=1

× D

) (20)

where:

(x): Total network trafﬁc among VMs;

: Binary variable that equals 1 if V

and V

are located in different PMs; otherwise, it

is 0.

The trafﬁc between two VMs V

and V

which are

located on the same PM H

do not contribute to in-

crease the total network trafﬁc given by equation (20);

therefore, D

= 0 if P

= P

= 1.

4.4.3 Economical Revenue Minimization

Based on (L

opez Pires and Bar

an, 2013), this work

presents equation (21) to estimate the total economi-

cal revenue that a datacenter receives for meeting the

requirements of its customers, represented by the sum

AMany-objectiveOptimizationFrameworkforVirtualizedDatacenters

443

of the economical revenue obtainable by each VM V

placement that is effectively located for execution on

any PM.

(x) =

∑

j=1

× X

) (21)

where:

(x): Total economical revenue for placing

VMs;

: Binary variable that equals 1 if V

is lo-

cated for execution on any PM; other-

wise, it is 0.

4.4.4 QoS Maximization

In this work, the QoS maximization proposes to lo-

cate the maximum number of VMs with the highest

level of priority associated to the SLA. This objective

function is proposed in equation (22).

(x) =

∑

j=1

(

SLA

× SLA

× X

) (22)

where:

(x): Total QoS ﬁgure for a given placement;

C: Constant, large enough to prioritize ser-

vices with larger SLA over the ones with

lower SLA (see example in Section 4.4.6).

4.4.5 Network Load Balancing Optimization

This work calculates the total amount of trafﬁc going

through a semi-duplex link l

as:

∑

i=1

∑

aii

∑

j=1

∑

× P

× D

j j

× T

j j

(23)

where:

T l

: Total amount of trafﬁc going through link

[Mbps];

aii

: Binary variable that equals 1 if l

∈ m

;

otherwise, it is 0.

Inspired in (Donoso et al., 2005) formulation,

this work calculates the Maximum Link Utilization

(MLU) as:

MLU = max

∀l

∈L



T l



(24)

where:

MLU: Maximum Link Utilization;

: Channel capacity of link l

[Mbps].

In this paper, the load balancing optimization of

the network is formulated as the minimization of the

MLU, i.e.,

(x) = MLU (25)

4.4.6 Example

The following example details how the values of f

(x)

and f

(x) are calculated, considering the datacenter

infrastructure presented in Figure 1. For the other

three objective functions, see (L

opez Pires and Bar

an,

2013).

Consider the following placement matrix P where,

VMs V

and V

are executed in H

, while V

is exe-

cuted in H

and V

in H

P =







0 0 1 0

1 0 0 0

0 0 0 1







(26)

Additionally, consider

C = 100 and the values of SLA

and X

presented in Table 1, f

(x) is calculated as:

(x) =

SLA

× SLA

× X

+ ··· +

SLA

× SLA

× X

= 100

× 2 × 1 + ··· + 100

× 3 × 1

= 3.06X10

(27)

It is important to remark that if

C is not sufﬁciently

large, f

(x) could prefer a large number of VMs with

lower priority. As an example, if

C = 1, 2 VMs with

SLA

= 2 result in a better ﬁgure of f

(x) than 1 VM

with SLA

= 3, what is not correct according to what

was presented in Section 4.4.4.

On the other hand, considering that each VM V

communicates at 1 [Mbps] with any other V

(k 6= j),

the placement P results in the values of T l

and Cl

presented in Table 2. So f

(x) is calculated as:

(x) = max



T l



= max



100

1000



100

(28)

5 INTERACTIVE MEMETIC

ALGORITHM

A Memetic Algorithm (MA) could be understood as

an Evolutionary Algorithm (EA) that in addition to

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

444

Table 1: Data for requested VMs used in basic example (see

Section 4.4.6).

SLA

2 1

3 1

Table 2: Data of network links used in basic example (see

Section 4.4.6).

T l

[Mbps] Cl

[Mbps] T l

/Cl

6 100 6/100

0 100 0/100

8 100 8/100

6 100 6/100

6 1000 6/1000

MLU 8/100

the standard selection, crossover and mutation opera-

tors of most Genetic Algorithms (GA) includes a local

optimization operator to obtain good solutions even at

early generations of an EA (B

aez et al., 2007).

This work proposes an interactive memetic al-

gorithm for solving the VMP problem in a many-

objective context, considering the proposed formu-

lation presented in Section 4 to simultaneously opti-

mize the ﬁve objective functions presented in the pre-

vious section. The proposed algorithm is extensible to

consider as many objective functions as needed while

only minor modiﬁcations may be needed if the num-

ber of objective functions changes.

It was shown in (von L

ucken et al., 2014) that

many-objective optimization using Multi-Objective

Evolutionary Algorithms (MOEAs) is an active re-

search area, having multiple challenges that need to

be addressed regarding scalability analysis, visualiza-

tion of the results, algorithm design and experimen-

tal algorithm evaluation. The interactive memetic al-

gorithm presented in this section as a viable way to

solve a many-objective VMP problem, proposes the

inclusion of desirable ranges of values for the objec-

tive functions costs in order to interactively control

the possible huge number of feasible non-dominated

solution, as described in Section 2. The proposed in-

teractive memetic algorithm is based on the one pro-

posed in (L

opez Pires and Bar

an, 2013) and works as

follows:

In step 1, it is veriﬁed if the problem has at least

one solution (considering only VMs with SLA

= s)

to continue with next steps. If there is no possible so-

lution to the problem, the algorithm returns an appro-

priate error message. If the problem has at least one

solution, the algorithm proceeds to step 2, which ge-

nerates a set of random candidates P

, whose solu-

tions are repaired at step 3 to ensure that P

con-

tains only feasible solutions. Then, the algorithm tries

to improve candidates at step 4 using local search.

With the obtained non-dominated solutions, the ﬁrst

set P

known

(Pareto set approximation) is generated at

step 5. After initialization in step 6, evolution begins

(iterations between steps 7 and 18).

The evolutionary process basically follows the

same behavior: solutions are selected from the union

of P

known

with the evoluationary set of solutions (or

population) also known as P

(step 8), crossover and

mutation operators are applied as usual (step 9), and

eventually solutions are repaired, as there may be in-

feasible solutions (step 10). Improvements of solu-

tions of the evolutionary population P

may be gen-

erated at step 11 using local search (local optimiza-

tion operators). At step 12, the Pareto set approxi-

mation P

known

is updated (if applicable); while at step

13 the generation (or iteration) counter is updated. At

step 15 the decision maker adjust the lower and upper

bounds if it is necessary, while at step 17 a new evo-

lutionary population P

is selected. The evolutionary

process is repeated until the algorithm meets a stop-

ping criterion (such as a maximum number of gen-

erations), ﬁnally returning the set of non-dominated

solutions P

known

in step 19.

Algorithm 1: Interactive Memetic Algorithm.

Data: datacenter infrastructure (see Section 4.1)

Result: Pareto set approximation P

known

1 check if the problem has a solution

2 initialize set of solutions P

3 P

= repair infeasible solutions of P

4 P

= apply local search to solutions of P

5 update set of solutions P

known

from P

6 t = 0; P

= P

7 while is not stopping criterion do

8 Q

= selection of solutions from P

∪ P

known

9 Q

= crossover and mutation of solutions of Q

10 Q

= repair infeasible solutions of Q

11 Q

000

= apply local search to solutions of Q

12 update set of solutions P

known

from Q

000

13 increment t

14 if interaction is needed then

15 ask for decision maker action (L

and U

)

16 end

17 P

= non-dominated sorting from P

∪ Q

000

18 end

19 return Pareto set approximation P

known

5.1 Population Initialization

Initially, a set of solutions (or population P

) is ran-

donmly generated. Each solution (or individual) is

represented as C = [C

,. . . ,C

]. The possible val-

AMany-objectiveOptimizationFrameworkforVirtualizedDatacenters

445

ues that can take each C

for VMs with the highest

value of SLA

(SLA

= s) are in the range [1, n]. For

VMs V

with SLA

< s, the possible values are in the

range [0, n]. Within these ranges deﬁned by the SLA

of each V

, the algorithm ensures at the initialization

stage that all VMs V

with the highest level of prio-

rity will be located for execution on a PM H

, while

for VMs V

with lower levels of priority SLA

, there

is always a probability larger than 0 that they may not

be located for execution in any PM.

5.2 Infeasible Solution Reparation

With a random generation at the initialization phase

(step 2 of Algorithm 1) and/or solutions generated by

standard genetic operators (step 9 of Algorithm 1), in-

feasible solutions may appear, i.e. the resources re-

quired by the VMs located for execution on certain

PMs could exceed the available resources (see Section

4.3.3), or one or more objectives functions may not

meet the adjustable constraints (see Section 4.3.4).

Repairing these infeasible solutions (steps 3 and

10 of Algorithm 1) may be done in two stages: ﬁrst,

in the feasibility veriﬁcation process, the population is

classiﬁed in two classes: feasible and infeasible (Al-

gorithm 2). Later, in the process of repairing infea-

sible solutions (Algorithm 3), the solutions which do

not meet the feasibility criteria are repaired in three

ways: (1) migrating some VMs to an available hard-

ware, (2) turning on some PMs and then migrating

VMs to them, or (3) turning off some VMs. Note that

at step 3 of Algorithm 3, V

migration to H

can be

done to other PMs, even if they are shut down.

Algorithm 2: Feasibility Veriﬁcation

Data: set of solutions P

Result: set of feasible solutions P

1 while there are solutions not veriﬁed do

2 feasible = true ; i = 1

3 while i ≤ n and feasible = true do

4 if solution does not satisfy constraints (3-5)

then

5 feasible = false ; break

6 else

7 increment i

8 end

9 end

10 if feasible = false then

11 call Algorithm 3 (repair solution)

12 end

13 end

14 return set of feasible solutions P

Algorithm 3: Infeasible Solutions Reparation.

Data: infeasible solution

Result: feasible solution

1 feasible = false ; j = 1

2 while j ≤ m and feasible = false do

3 if it is possible then

4 migrate V

to H

6= i)

5 else

6 if SLA

6= s then

7 turn off V

on H

8 else

9 replace solution with another solution

from P

known

10 end

11 end

12 end

13 return feasible solution

5.3 Local Search

Once a population contains only feasible solutions, a

local search is performed (steps 4 and 11 of Algorithm

1) for improving the solutions found so far in the evo-

lutionary population P

. The local search pseudo-code

is presented in Algorithm 4.

Algorithm 4: Local Search.

Data: set of feasible solutions P

Result: set of feasible optimized solutions P

1 probability = random number between 0 and 1

2 while there are solutions not veriﬁed do

3 if probability < 0.5 then

4 Try to turn off all the possible H

migrating all the V

assigned to H

with

available resources (i

6= i) and then try to

turn on all the possible V

(using SLA

priority order) assigning them to a H

with

available resources

5 else

6 Try to turn on all the possible V

(using

SLA

priority order) assigning them to a H

with available resources and then try to turn

off all the possible H

by migrating all the V

assigned to H

with available resources

6= i)

7 end

8 end

9 return set of feasible optimized solutions P

For each individual in the population P

, the pro-

posed algorithm attempts to optimize a solution with a

local search (step 2 of Algorithm 4). For this purpose,

with probability

, the algorithm tries to maximize

the number of located VMs with higher level of prio-

rity, locating all possible VMs that were not located

so far, directly increasing f

(x) (total QoS) and f

(x)

(total economical revenue) (steps 3 to 5 of Algorithm

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

446

4). On the other hand, also with probability

, the al-

gorithm tries to minimize the number of PMs turned

on, directly reducing f

(x) (total power consumption)

(steps 6 to 8 of Algorithm 4). With the proposed prob-

abilistic local search method, a balanced exploitation

of objective functions (QoS, economical revenue and

power consumption) is achieved, as experimentally

veriﬁed with results presented in next section.

5.4 Fitness Function

The ﬁtness function used in the proposed algorithm

is the one presented in (Deb et al., 2002). This ﬁt-

ness value deﬁnes a non-domination rank in which

a value equal to its Pareto dominance level (1 is the

highest level of dominance, 2 is the next, and so on)

is assigned to each individual of the population. Bet-

ween two individuals with different non-domination

rank, the individual with lower value (higher level of

dominance) is considered better. To compare indivi-

duals with the same non-domination rank, a crowding

distance is used. The basic idea is to ﬁnd the Eu-

clidean distance (properly normalized when the ob-

jectives have different measure units) between each

pair of individuals, based on the q objectives, in a

hyper-dimensional space (Deb et al., 2002). The in-

dividual with larger crowding distance is considered

better.

5.5 Variation Operators

The proposed interactive memetic algorithm uses a

Binary Tournament approach for selecting individuals

for crossover and mutation (Coello et al., 2007). The

crossover operator used in the presented work is the

single point cross-cut (Coello et al., 2007). The se-

lected individuals in the ascending population are re-

placed by descendants individuals.

This work uses a mutation method in which each

gene is mutated with a probability

, where m rep-

resents the number of VMs. This method offers the

possibility of full uniform gene mutation, with a very

low probability (but larger than zero), which is bene-

ﬁcial to the exploration of the search space, reducing

the probability of stagnation in a local optimum.

The population evolution in the proposed inter-

active memetic algorithm is based on the population

evolution proposed in (Deb et al., 2002). A population

t+1

is formed from the union of the best known pop-

ulation P

and offspring population Q

, applying non-

domination rank and crowding distance operators.

5.6 Many-objective Considerations

Given that the number of non-dominated solutions

may rapidly increase, an interactive approach is re-

commended. That way, a decision maker can intro-

duce new constraints or adjust existing ones, while

the execution continues learning about the shape of

the Pareto front in the process. For simplicity, the

present work considers lower and upper bounds asso-

ciated to each objective function in order to help the

decision maker to reduce interactively the huge num-

ber of potencial solutions in the Pareto set approxi-

mation P

known

, while observing the evolution of its

corresponding Pareto front PF

known

6 EXPERIMENTAL RESULTS

To validate the proper operation of the proposed in-

teractive memetic algorithm for solving the MaVMP

on a purely many-objective context, different exper-

iments were proposed for problem instances consi-

dering both homogeneous as well as heterogeneous

hardware conﬁgurations of PMs, considering VMs

instance types offered by Amazon Elastic Compute

Cloud (EC2)

. Experiment 1 considered 2 problem

instances with homogeneous hardware conﬁgurations

of PMs (Hcpu = 4 [ECU], Hram = 16 [GB], Hhdd =

150 [GB], pmax = 1740 [W]), while Experiment 2

considered heterogeneous hardware conﬁgurations of

PMs according to Table 6.

A detailed description of the hardware of the VMs

instance types considered for the experiments is pre-

sented in Table 3. A general description of the con-

sidered problem instances is presented in Table 4,

while the complete set of datacenter infrastructure in-

put ﬁles used for the experiments with the correspon-

ding experimental results are available online

6.1 Experiment 1: Quality of Solutions

To compare the results obtained by the proposed in-

teractive memetic algorithm and to validate its proper

operation, an exhaustive search algorithm was also

implemented for ﬁnding all (n + 1)

possible solu-

tions of a given instance of the VMP problem, when

this alternative is computationally possible for the au-

thors. These results were compared to the results ob-

tained by the proposed interactive memetic algorithm

after evolving populations with 100 individuals for

100 generations. Both algorithms were implemented

http://aws.amazon.com/ec2/instance-types

https://sites.google.com/site/ﬂopezpires/

AMany-objectiveOptimizationFrameworkforVirtualizedDatacenters

447

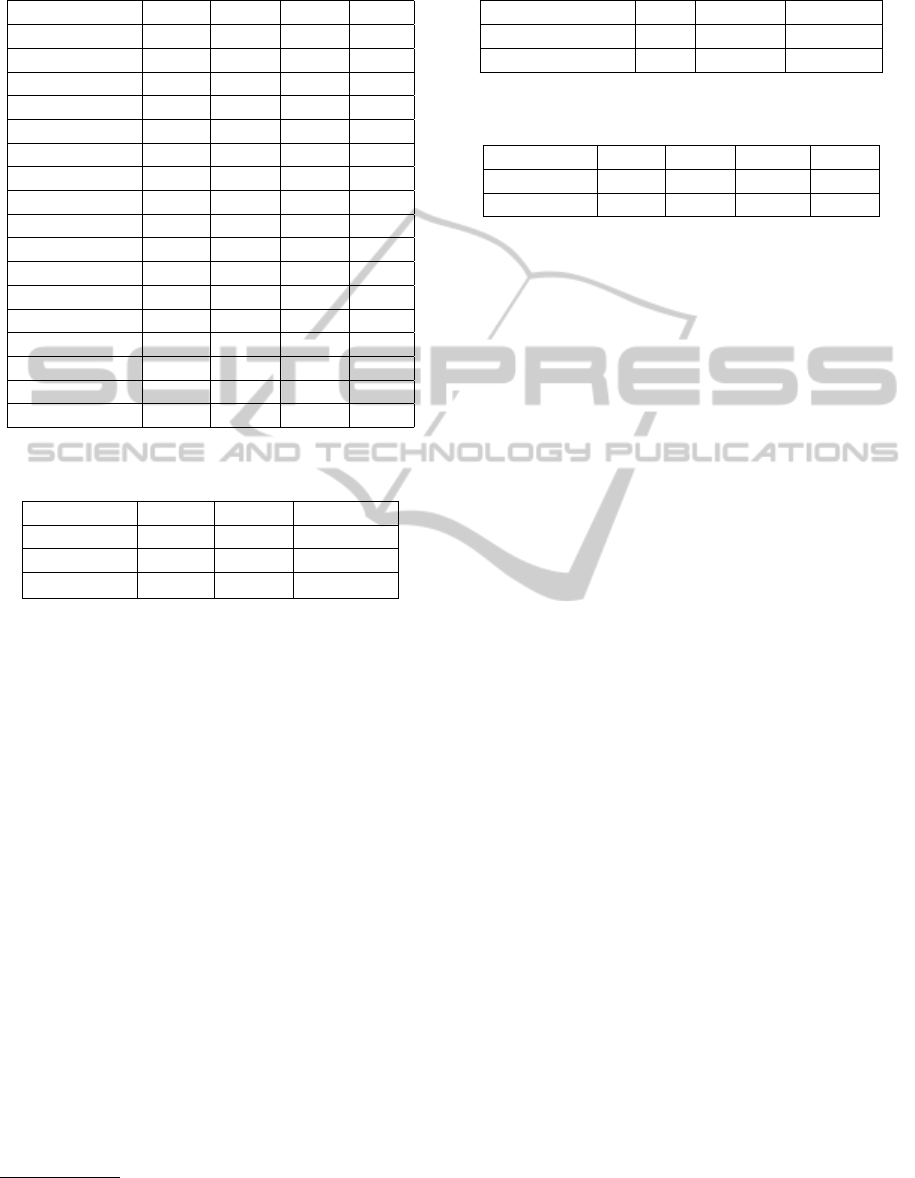
Table 3: Instance types of VMs considered in experiments.

For notation see equation (11).

Instance Type Vcpu Vram Vhdd R

t2.micro 1 1 0 9

t2.small 1 2 0 18

t2.medium 2 4 0 37

m3.medium 1 4 4 50

m3.large 2 8 32 100

m3.xlarge 4 15 80 201

m3.2xlarge 8 30 160 403

c3.large 2 4 32 75

c3.xlarge 4 8 80 151

c3.2xlarge 8 15 160 302

c3.4xlarge 16 30 320 604

c3.8xlarge 32 60 640 1209

r3.large 2 15 32 126

r3.xlarge 4 30 80 252

r3.2xlarge 8 61 160 504

r3.4xlarge 16 122 0 320

r3.8xlarge 32 244 0 320

Table 4: Problem instances considered in experiments, all

with 50% of VMs with the highest SLA s = 2.

Input File # PMs # VMs (n + 1)

3x5.vmp 3 5 1024

4x8.vmp 4 8 390625

12x50.vmp 12 50 ∼ 5X10

using ANSI C programming language (gcc)

and the

source code is also available online

Considering that this particular experiment aims

to validate the good level of exploration in the set of

feasible solutions X

, the local search of the algorithm

was disabled, strengthening its capability of explo-

ration rather than the rapid convergence to good so-

lutions even in early generations of the population.

For each problem instance considered in this ex-

periment (3x5.vmp and 4x12.vmp), one run of the ex-

haustive search algorithm was completed, obtaining

the optimal Pareto front PF∗ and its corresponding

Pareto set P∗. Furthermore, ten runs of the proposed

algorithm were completed, after evolving populations

of 100 individuals for 100 generations at each run.

The results obtained by the proposed algorithm for

each run were combined to obtain the Pareto front

known

and its corresponding Pareto set P

known

. For

the 3x5.vmp and 4x8.vmp problem instances, the pro-

posed algorithm obtained every solution of the opti-

mal Pareto set and its corresponding Pareto front. A

summary of the number of elements in the correspon-

ding Pareto sets obtained are presented in Table 5.

http://gcc.gnu.org

Table 5: Summary of results obtained in Experiment 1 using

the proposed memetic algorithm (see Section 5).

Input File Name # P

∗

# P

known

% Found

3x5.vmp 51 51 100%

4x8.vmp 30 30 100%

Table 6: Types of PMs considered in Experiment 2. For

notation see equation (10).

PM Type Hcpu Hram Hhdd pmax

h1.medium 180 512 10000 1000

h1.large 350 1024 10000 1300

6.2 Experiment 2: Interactive Bounds

As mentioned in Section 3, this work proposes the

utilization of lower and upper bounds for each ob-

jective function f (z) (L

≤ f

(x) ≤ U

) to be able to

reduce iteratively the number of possible solutions of

the Pareto set approximation P

known

, when needed.

For the problem instance considered in this experi-

ment (12x50.vmp), one run of the proposed algorithm

was completed, after evolving populations of 100 in-

dividuals for 300 generations. The number of gener-

ations was incremented for this experiment from 100

to 300 considering the large number of possible solu-

tions for the particular problem considered (see Table

4). An interactive adjustment of the lower or upper

bounds associated to each objective function was per-

formed after every 100 generations in order to con-

verge to a treatable number of solutions.

It is important to remark that the interactive ad-

justment used in this experiment is only one of seve-

ral possible ones. As an example, we may consider:

(1) automatically adjusting 10% of the lower bounds

associated to maximization objective functions when

the Pareto front has more than 200 elements or (2)

manually adjusting upper bounds associated to mi-

nimization objective functions until the Pareto front

does not have more than 20 elements, just to cite a

pair of alternatives.

The Pareto front approximation PF

known

repre-

sents the complete set of Pareto solutions considering

unrestricted bounds (L

= −∞ and U

= ∞). On the

other hand, Pareto front approximation PF

reduced

rep-

resents the reduced set of Pareto solutions obtained by

interactively adjusting bounds L

and U

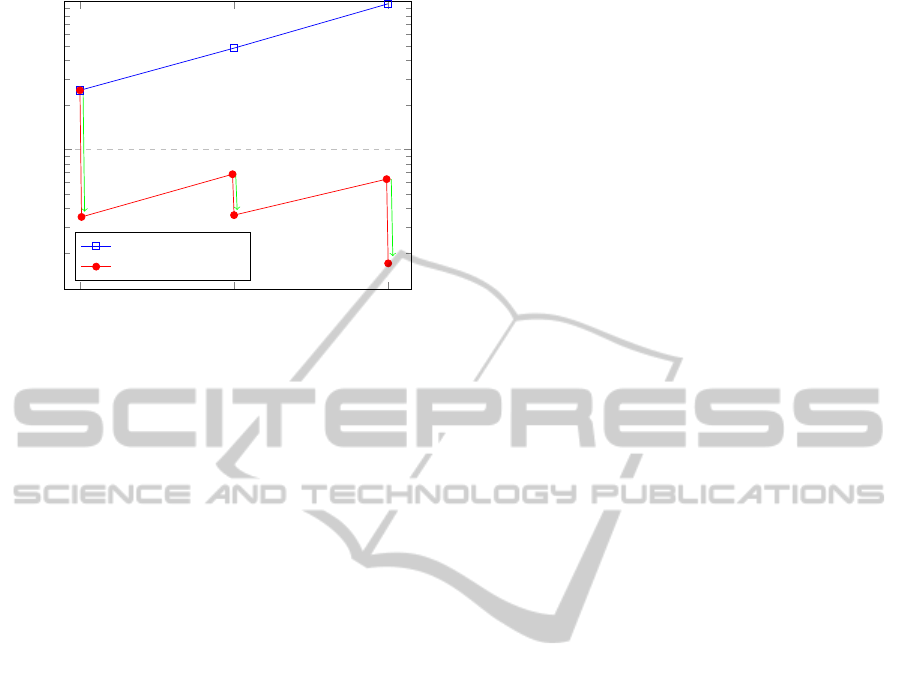
In the ﬁrst 100 generations, the proposed al-

gorithm obtained 251 solutions with unrestricted

bounds. A decision maker evaluated the bounds asso-

ciated to power consumption and adjusted the upper

bound U

to U

= 9000 [W], selecting only 35 of the

251 solutions (not considering 216 otherwise feasible

solutions) for the PF

reduced

as shown in Figure 2.

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

448

100 200 300

251

484

965

35 36

Number of generations

Number of solutions

unrestricted bounds

adjustable bounds

Figure 2: Summary of results obtained in Experiment 2.

After 200 generations, the algorithm obtained a

total of 484 solutions with unrestricted bounds. Con-

sidering instead U

= 9000 [W], the algorithm only

found 68 solutions. The decision maker evaluated the

bounds associated to network trafﬁc and adjusted the

upper bound U

to U

= 115 [Mbps], selecting only

36 of the 68 solutions (not considering 32 otherwise

feasible solutions) for the PF

reduced

Finally, after 300 generations, the algorithm ob-

tained a total of 965 solutions with unrestricted

bounds. Considering U

= 9000 [W] and U

= 115

[Mbps], the algorithm found 63 solutions. The de-

cision maker evaluated the bounds associated to eco-

nomical revenue and adjusted the lower bound L

= 13500 [$], selecting only 17 of the 63 solutions

(not considering 46 feasible solutions) for the ﬁnal

reduced

as shown in Figure 2. Clearly, at the end

of the iterative process, the decision maker found 17

solutions according to his preferences instead of the

untreatable number of 965 candidate solutions.

7 CONCLUSIONS AND FUTURE

WORK

This work proposed a general many-objective opti-

mization framework that is able to consider as many

objective functions as needed when solving the VMP

problem. As an example of utilization of the pro-

posed framework, for the ﬁrst time a formulation of

the many-objective VMP problem (MaVMP) is pro-

posed, considering the simultaneous optimization of

the following ﬁve objective functions: (1) power con-

sumption, (2) network trafﬁc, (3) economical revenue,

(4) quality of service and (5) network load balanc-

ing. In addition, a generalized multi-level of priori-

ties for the SLA associated to each VM is presented.

At the same time, constraints on upper and lower lim-

its of each objective function are also recommended

as a way to interactively control a potential explo-

sion in the number of non-dominated solutions, a well

known problem of many-objective optimization pro-

blems (von L

ucken et al., 2014).

A short review of the most studied objective func-

tions was also presented to demonstrate that the num-

ber of objective functions may rapidly increase once

a complete understanding of the VMP problem is ac-

complished for practical problems were many diffe-

rent parameters should be ideally considered. Based

on the number of possible objective functions for

the VMP, this problem can clearly be addressed as a

many-objective optimization problem (MaOP).

Multiple challenges need to be considered for sol-

ving a many-objective optimization problem; there-

fore, an interactive memetic algorithm was proposed

to solve the proposed many-objective formulation,

validating the presented formulation and proving that

it is solvable. By no means, the authors claim that

the proposed interactive memetic algorithm is the best

way to solve this problem. This proposal only illus-

trates that it is possible to solve the problem although

the VMP problem becomes harder when increasing

the number of conﬂicting objective functions.

To validate the proposed algorithm, it was run

with different problem instances and experimental re-

sults were compared to the exact solution obtained

using an exhaustive search algorithm when possible.

In fact, the proposed algorithm found the complete

Pareto front and Pareto set (100%) for the 2 instan-

ces of Experiment 1. To validate the effectiveness

of the proposed algorithm reducing the increasing

number of non-dominated solutions obtained by the

Pareto dominance comparison, several problem ins-

tances were executed. In fact, considering the pro-

posed technique of interactively adjusting lower and

upper bounds associated to the values of each ob-

jective functions, the Pareto front could be reduced

from 965 original candidates to a treatable 17 non-

dominated solutions that satisfy the decision maker

preferences, as illustrated in Experiment 2.

At the time of this writing, the authors are working

on VMP formulations considering more complex net-

work topologies with full-duplex links. Considering

that this is the ﬁrst formulation of the VMP problem

in a many-objective context, several future works can

be proposed considering all the already presented ob-

jective functions, studied so far in mono-objective as

well as multi-objective contexts.

Considering that this work proposed an ofﬂine

(static) formulation of the VMP problem in a many-

AMany-objectiveOptimizationFrameworkforVirtualizedDatacenters

449

objective optimization context, several challenges

need to be addressed for online (dynamic) formula-

tions of the problem, considering multi-objective and

many-objective approaches. At the same time, diffe-

rent meta-heuristics, methods and algorithms should

be still tested before a real good tool is ready for mas-

sive use in commercial cloud computing datacenters.

REFERENCES

Anand, A., Lakshmi, J., and Nandy, S. (2013). Virtual ma-

chine placement optimization supporting performance

slas. In Cloud Computing Technology and Science

(CloudCom), 2013 IEEE 5th International Confer-

ence on, volume 1, pages 298–305. IEEE.

aez, M., Z

arate, D., and Bar

an, B. (2007). Algorit-

mos mem

eticos adaptativos para optimizaci

on multi-

objetivo. In XXXIII Conferencia Latinoamericana de

Inform

atica–CLEI, volume 2007.

Barroso, L. A. and H

olzle, U. (2007). The case for energy-

proportional computing. IEEE computer, 40(12):33–

37.

Beloglazov, A., Abawajy, J., and Buyya, R. (2012). Energy-

aware resource allocation heuristics for efﬁcient man-

agement of data centers for cloud computing. Future

Generation Computer Systems, 28(5):755–768.

Beloglazov, A., Buyya, R., Lee, Y. C., Zomaya, A., et al.

(2011). A taxonomy and survey of energy-efﬁcient

data centers and cloud computing systems. Advances

in Computers, 82(2):47–111.

Bin, E., Biran, O., Boni, O., Hadad, E., Kolodner, E. K.,

Moatti, Y., and Lorenz, D. H. (2011). Guarantee-

ing high availability goals for virtual machine place-

ment. In Distributed Computing Systems (ICDCS),

2011 31st International Conference on, pages 700–

709. IEEE.

Cheng, J., Yen, G. G., and Zhang, G. (2014). A many-

objective evolutionary algorithm based on directional

diversity and favorable convergence. In Systems,

Man and Cybernetics (SMC), 2014 IEEE Interna-

tional Conference on, pages 2415–2420.

Coello, C. C., Lamont, G. B., and Van Veldhuizen, D. A.

(2007). Evolutionary algorithms for solving multi-

objective problems. Springer.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

Nsga-ii. Evolutionary Computation, IEEE Transac-

tions on, 6(2):182–197.

Deb, K., Sinha, A., and Kukkonen, S. (2006). Multi-

objective test problems, linkages, and evolutionary

methodologies. In Proceedings of the 8th annual

conference on Genetic and evolutionary computation,

pages 1141–1148. ACM.

Donoso, Y., Fabregat, R., Solano, F., Marzo, J.-L., and

Bar

an, B. (2005). Generalized multiobjective multi-

tree model for dynamic multicast groups. In Commu-

nications, 2005. ICC 2005. 2005 IEEE International

Conference on, volume 1, pages 148–152. IEEE.

Farina, M. and Amato, P. (2002). On the optimal solution

deﬁnition for many-criteria optimization problems. In

Proceedings of the NAFIPS-FLINT international con-

ference, pages 233–238.

Gao, Y., Guan, H., Qi, Z., Hou, Y., and Liu, L. (2013). A

multi-objective ant colony system algorithm for vir-

tual machine placement in cloud computing. Journal

of Computer and System Sciences, 79(8):1230–1242.

opez Pires, F. and Bar

an, B. (2013). Multi-objective vir-

tual machine placement with service level agreement.

In Proceedings of the 2013 IEEE/ACM 6th Interna-

tional Conference on Utility and Cloud Computing,

pages 203–210. IEEE Computer Society.

opez Pires, F. and Bar

an, B. (2015). A virtual machine

placement taxonomy. In Proceedings of the 2015

IEEE/ACM 15th International Symposium on Cluster,

Cloud and Grid Computing. IEEE Computer Society.

Mishra, M. and Sahoo, A. (2011). On theory of vm

placement: Anomalies in existing methodologies and

their mitigation using a novel vector based approach.

In Cloud Computing (CLOUD), 2011 IEEE Interna-

tional Conference on, pages 275–282. IEEE.

Sato, K., Samejima, M., and Komoda, N. (2013). Dy-

namic optimization of virtual machine placement by

resource usage prediction. In Industrial Informatics

(INDIN), 2013 11th IEEE International Conference

on, pages 86–91. IEEE.

Shi, L., Butler, B., Botvich, D., and Jennings, B. (2013).

Provisioning of requests for virtual machine sets with

placement constraints in iaas clouds. In Integrated

Network Management (IM 2013), 2013 IFIP/IEEE In-

ternational Symposium on, pages 499–505. IEEE.

Shrivastava, V., Zerfos, P., Lee, K.-W., Jamjoom, H., Liu,

Y.-H., and Banerjee, S. (2011). Application-aware vir-

tual machine migration in data centers. In INFOCOM,

2011 Proceedings IEEE, pages 66–70. IEEE.

Sun, M., Gu, W., Zhang, X., Shi, H., and Zhang, W. (2013).

A matrix transformation algorithm for virtual machine

placement in cloud. In Trust, Security and Privacy

in Computing and Communications (TrustCom), 2013

12th IEEE International Conference on, pages 1778–

1783. IEEE.

Tom

as, L. and Tordsson, J. (2013). Improving cloud infras-

tructure utilization through overbooking. In Proceed-

ings of the 2013 ACM Cloud and Autonomic Comput-

ing Conference, CAC ’13, pages 5:1–5:10, New York,

NY, USA. ACM.

von L

ucken, C., Bar

an, B., and Brizuela, C. (2014). A

survey on multi-objective evolutionary algorithms for

many-objective problems. Computational Optimiza-

tion and Applications, pages 1–50.

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

450