Student Ratings, Class Size, Written Comments, Rank and Gender Bias

Bradford P. Sobakowitz

and Jacob Kogan

AT Center for Applied Research, Columbia, MD 21045, U.S.A.

Department of Mathematics and Statistics, UMBC, Baltimore, MD 21250, U.S.A.

Keywords:

World Wide Web, Student Course Evaluation Questionnaire, Numerical Student Ratings, Student Written

Comments, Rank and Gender Bias.

Abstract:

The preliminary analysis presented is based on examination of two publicly available data sets. The ﬁrst

one consists of approximately 30,000 Student Course Evaluation Questionnaires (SCEQ) available at the

University of Maryland, Baltimore County’s (UMBC) website (http://www.umbc.edu/oir/sceq/index.html.

This dataset is used to analyze the effect of class size, faculty rank and gender on student rat-

ings. The second data set is available at the University of Maryland College Park’s (UMCP) website

(http://www.ourumd.com/viewreviews/?all). The website contains over 10,000 students’ rating (both numer-

ical and written comments). This data set is used to examine correlation between the ratings and size of

students’ written comments. The results presented are compared with those already reported in the literature.

1 INTRODUCTION

The paper examines two sets of student ratings

available from Maryland public universities.

The ﬁrst one consists of 29, 681 student rat-

ings covering 19 semesters (from Spring 2005

through Spring 2014) available at the Univer-

sity of Maryland, Baltimore County’s website

(http://www.umbc.edu/oir/sceq/index.htm). The sec-

ond one is 10, 584 University of Mary-

land College Park student ratings cover-

ing years 2007–2014 and available from

(http://www.ourumd.com/viewreviews/?all).

We analyze the datasets in order to address the fol-

lowing topics:

1. Student ratings and class size.

2. Ratings of tenured/tenure track faculty vs. ratings

of untenured full time faculty.

3. Ratings of male instructors vs. ratings of female

instructors.

4. Student ratings vs. size of student written com-

ments.

These topics (except, perhaps, the last one) have been

extensively discussed in literature. We address the

ﬁrst three items above using the UMBC data set. The

We follow terminology suggested in (Cashin, 1995)

last item is analyzed through the UMCP data that con-

tains both numerical ratings and written comments.

Colleges advertise student–teacher ratio to attract

parents willing to pay high tuition for small class

sizes. “Large, highly signiﬁcant, and nonlinear neg-

ative impact of class size on student evaluations of

instructor effectiveness” is reported by (Bedard and

Kuhn, 2008). We examine the impact of class size

on student ratings by focusing on two math classes

with size doubled (sometimes almost tripled) over the

last ten years. The numerical results presented in this

paper contradict conclusions of (Bedard and Kuhn,

2008).

The rank of the instructor and student ratings are

discussed already in (Aleamoni, 1999). While mixed

results are reported, a “negative relationship” is in-

dicated. Our examination of UMBC student ratings

shows that for the last ten years ratings of full time

untenured faculty are signiﬁcantly higher than those

of tenured and tenure track faculty.

For general discussion of gender bias in student

ratings of university instructors see (Young et al.,

2009). In a study conducted at the Hong Kong Poly-

technic University (Kwan, 1999) reached the conclu-

sion that students base their answers on factors ex-

ternal to the course. In a similar line, (Karlsson and

Lundberg, 2012) analyzed ninety-eight assessments

of faculty from across Swedish universities and con-

cluded that the ratings involve a clear gender bias.

218

P. Sobakowitz B. and Kogan J..

Student Ratings, Class Size, Written Comments, Rank and Gender Bias.

DOI: 10.5220/0005435002180223

In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 218-223

ISBN: 978-989-758-108-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Women teachers consistently receive poorer ratings

in comparison with their male counterparts. Gen-

der effect on teaching evaluations is also addressed

by (Sprague and Massoni, 2005) with similar conclu-

sions. The results provided by UMBC data lead to

the opposite conclusion (a milder conclusion can be

found in (Feldman, 1992), for a claim coinciding with

our ﬁndings see e.g. (Feldman, 1993)).

Written comments have been analyzed in the lit-

erature (see e.g. (Hodges and Stanton, 2007), (Alhija

and Fresko, 2009) and references therein). Little re-

search has been done to examine possible correlation

between the written comments and numerical ratings,

for a notable exception see (Sliusarenko et al., 2013).

The paper attempts to make a small step in this direc-

tion.

2 UMBC STUDENT RATINGS

The UMBC questionnaire consists of seven sets of

items. One set contains general questions that should

be applicable to almost all courses. The remaining

sets are designed for lectures, discussion, mathemat-

ics and science laboratories, seminars, ﬁeld experi-

ence, and self-paced courses. Six questions permit

separate evaluation of as many as four instructors.

The instructor has the option of administering

whichever sets of questions are applicable. This study

focuses on general question 9 (G9) “How would you

grade the overall teaching effectiveness.” In addition

to numerical responses provided on a 5 point Likert

scale (Likert, 1932) from 5 (one of the best instruc-

tors I’ve had) to 1 (one of the worst instructors I’ve

had) each questionnaire contains enrollment informa-

tion, and instructor’s name.

The ratings per question are averaged out, i.e.,

the ratings per question are added up and the sum is

divided by the number of students responded to the

question (see e.g. (Hardy et al., 1934) where mean

evaluations are discussed). This average is named

“Instructor Mean.”

Along with individual instructor statistics per

class/question, SCEQ provides additional statistical

indicators, among them “Org Mean” representing a

discipline. UMBC computed org means are actually

mean averages of the instructor’s means. The aver-

age scores for a class with one response are weighted

equally to a class with numerous responses when “av-

eraging the averages.” Instructor Means for classes

of different size contribute equally to the Org Mean,

hence the input of large student groups (students in

large classes) to the computation of Org Mean is iden-

tical to that of small student groups (students in small

classes). For detailed discussion of UMBC means we

refer an interested reader to (Kogan, 2014).

The results reported in this paper provide means

computed in accordance with standard mathematical

deﬁnition of the arithmetic mean (see e.g. (Hardy

et al., 1934), (Hodges Jr. and Lehmann, 1964)). The

same way means are computed by the University of

Maryland College Park (UMCP). Each reference to

means computed by UMBC is speciﬁcally indicated

in the text below.

3 CLASS SIZE AND STUDENTS’

RATING

We focus on two math classes, a part of a three course

calculus chain mandatory for many undergraduate

students. The ﬁrst class, MATH 151, with the total

enrollment of 10, 514 over the last 19 semesters (the

second one is MATH 152, total enrollment of 6, 932

for the same time period).

0 2 4 6 8 10 12 14 16 18 20

100

120

140

160

180

Spring 2005−Spring 2014, MATH 151 AVERAGE CLASS SIZE

semester

average class size

Fall 09

Figure 1: MATH 151 average class size.

Fall 2009 witnessed an unusual spike in MATH

151 enrollment (1, 182 students enrolled as opposed

to 405 students enrolled in Spring 2009, and 562

students enrolled in Fall 2008). At the same time

the average class size more than doubled (Figure 1),

yet the average student rating for the class responded

robustly–one needs a magnifying glass to see the dif-

ference between “before” and “after” Fall 2009 rat-

ings (see Figure 2). In fact the highest average rating,

4.48, was obtained in Spring 2013, with the average

class size much higher then the pre Fall 2009 average

sizes.

The other class, MATH 152, is the second one in

the three classes undergraduate calculus chain offered

by the Department. As Figure 3 shows the average

StudentRatings,ClassSize,WrittenComments,RankandGenderBias

219

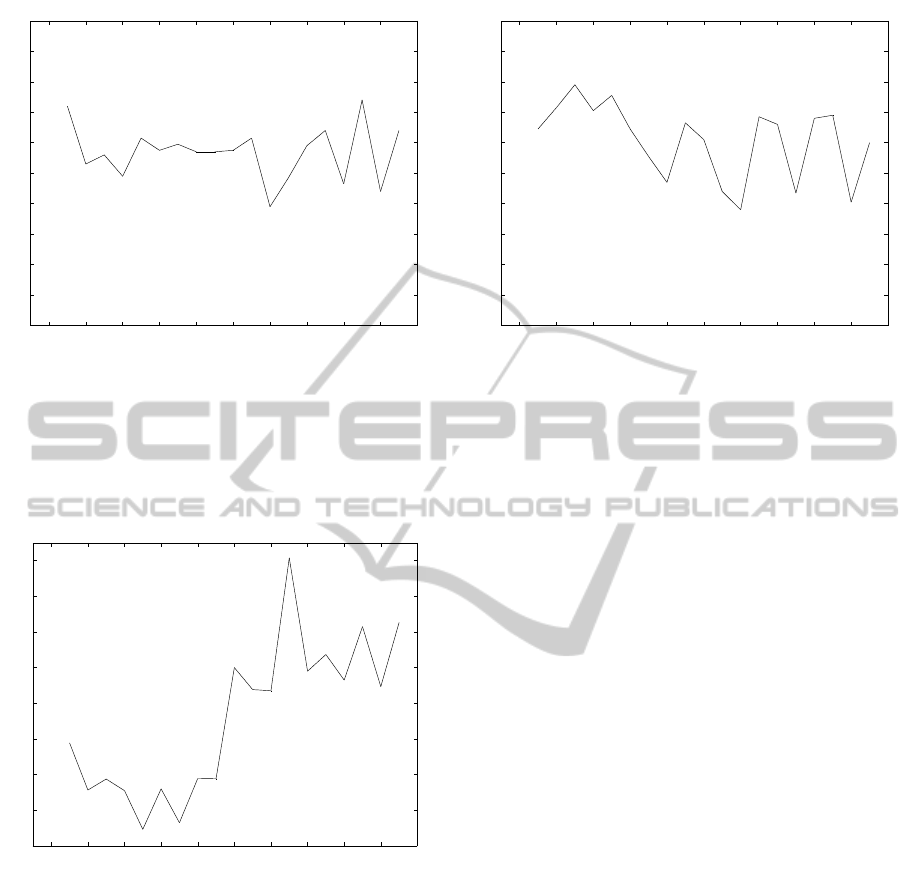
0 2 4 6 8 10 12 14 16 18 20

3.2

3.4

3.6

3.8

4.2

4.4

4.6

4.8

Spring 2005−Spring 2014, MATH 151 RATING

semester

rate

Fall 09

Figure 2: MATH 151 average Q9 rating.

class size more that doubled in Fall 2009. The av-

erage student response rate graph (Figure 4) indicates

no signiﬁcant difference between “before” and “after”

Fall 2009 ratings.

0 2 4 6 8 10 12 14 16 18 20

100

120

140

160

180

Spring 2005−Spring 2014, MATH 152 AVERAGE CLASS SIZE

semester

average class size

Fall 09

Figure 3: MATH 152 average class size.

4 MATH AT UMBC: RANK AND

GENDER

In this section we focus on a single org, “MATH”, and

provide information extracted from student ratings

and pertaining to ratings received by tenured/tenure

track faculty and full time lecturers teaching

“MATH”.

As of Fall 2014 the Department faculty is made up

of:

• 1 post doc,

• 5 lecturers (with no research responsibilities),

0 2 4 6 8 10 12 14 16 18 20

3.2

3.4

3.6

3.8

4.2

4.4

4.6

4.8

Spring 2005−Spring 2014, MATH 152 RATING

semester

rate

Fall 09

Figure 4: MATH 152 average Q9 rating.

• 28 tenured or tenure track faculty (to make the

title shorter we shall refer to those also as “Re-

search Faculty”).

Of the 33 research faculty and lecturers (we leave

out the post doc), 23 are Mathematicians, and 10 are

Statisticians.

Typically (but not always) Mathematicians teach

only MATH classes, and Statisticians are involved in

STAT instruction only. The results presented below

mainly cover the 23 Mathematicians (a female Statis-

tics Lecturer often also teaches MATH classes, and

this is the reason for fractional number of female fac-

ulty members and lecturers that will appear in the text

later).

The group of the 23 Mathematicians consists of 4

lecturers and 19 research faculty. Although 4.5 lec-

turers are about only 20% of the math group they

teach from 30% to over 50% of the MATH classes

per semester. While the typical teaching work load

for a research faculty member is deﬁned in writing

as 2 classes per semester, the teaching workload for

Lecturers appears to vary from semester to semester.

Of the 23.5 instructors involved in teaching

MATH 4.5 are female and 19 are male faculty mem-

bers. The female faculty membersteach between 30%

to over 50% of the MATH classes per semester.

The distribution of the teaching load between re-

search faculty and lecturers is very similar to that

between male and female faculty members. These

distributions allow us to compare student ratings for

these groups inspite of the relatively small size of lec-

turers and female professors.

4.1 Rank Bias

The average of student ranking for lecturers and re-

search faculty is shown on Figure 5. As the graph

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

220

shows lecturers consistently receive better student rat-

ings. Although the issue of teaching load is beyond

the scope of this paper we note that lecturers mainly

teach low level large math classes (such as MATH 151

and MATH 152 discussed earlier), while research fac-

ulty often teach small graduate classes.

−2 0 2 4 6 8 10 12 14 16 18 20

3.2

3.4

3.6

3.8

4.2

4.4

4.6

4.8

Spring 2005−Spring 2014, MATH, LECTURERS VS TENURED/TENURE TRACK

semester

rating

lecturers

tenured/tenure track

Figure 5: Lecturers vs. Tenured/Tenure Track faculty aver-

age Q9 rating.

4.2 Gender Bias

Finally we move to student ratings of male and fe-

male instructors. The average rating for both groups

is shown on Figure 6, and the graph speaks for itself.

So far ratings of female faculty supersede those of

male faculty. Reasons for convergence of two graphs

is beyond the scope of this paper and will be analyzed

elsewhere.

−2 0 2 4 6 8 10 12 14 16 18 20

3.2

3.4

3.6

3.8

4.2

4.4

4.6

4.8

Spring 2005−Spring 2014, MATH MALE VS FEMALE RATING

semester

rating

female instructors

male instructors

Figure 6: Male faculty vs. Female faculty average Q9 rat-

ing.

5 NUMERICAL RATINGS AND

WRITTEN COMMENTS

In addition to considering quantitativeresponses there

is an attractive option of gaining an insight into teach-

ing ratings through students’ written comments. The

open ended free text allows students to focus on mat-

ters they perceive as important, the lack of formal

structure makes analysis of written comments difﬁ-

cult.

Manual analysis of large amount of text requires

considerable resources and is time consuming. Re-

cent advances in Text Mining-research area devoted

to computerized text processing (Berry and Kogan,

2010) opens the door for computer aided analysis of

large text collections (Sliusarenko et al., 2013).

The University of Maryland

College Park (UMCP] website

http://www.ourumd.com/viewreviews/?all pro-

vides 10, 584 student ratings for 2, 122 instructors

covering years 2007–2014. The course numbers

are ranging from 003 to 899, with 267 courses

assigned no course number. As it was mentioned in

the literature students tend to provide more written

comments when “the course invoked relatively strong

reaction” (Alhija and Fresko, 2009).

In this section we attempt to provide a simple

numerical description of students’ “strong reaction.”

The entire collection of 10, 584 written comments is

divided into ﬁve groups. Texts corresponding to the

same numerical rating are grouped together, the num-

ber of written comments in each group is reported in

column “size” of Table 1, the entries of this column

add up to 10, 584.

The size of written comments (in characters) in

the same group is averaged out and reported in col-

umn “mean” of Table 1. As rating decreases the mean

of written comments grows longer. When, for exam-

ple, the numerical rating is 5 an average written com-

ment contains about 540 characters. For the numeri-

cal rating 4 an average written comment is about 610

character long, an increase of almost 13%. Hence, if

the average size of written comments corresponding

to the numerical rating 5 is used as a benchmark (i.e.

540.89 is considered as 100%), then the average size

of written comments corresponding to the numerical

rating 4 (610.37) is 112.85% of the benchmark.

Similarly to the column “size” the last column of

Table 1 shows the “percentage-wise size” of an aver-

age written comment as rating goes down from 5 to

StudentRatings,ClassSize,WrittenComments,RankandGenderBias

221

Table 1: Ratings vs. Average Size of Written Comments.

rating mean size percentage

5 540.89 3855 100.00%

4 610.37 2250 112.85%

3 654.41 1518 120.99%

2 689.43 1159 127.46%

1 719.57 1802 133.04%

6 CONCLUSIONS AND FUTURE

STUDY

This paper presents a preliminary analysis of Stu-

dent Course Evaluations at the University of Mary-

land Baltimore County (UMBC) and the University

of Maryland College Park (UMCP).

A relevant part of the UMBC data is selected and

analyzed to investigate a single discipline. We would

like to investigate data pertaining to additional disci-

plines. An interesting research direction is to clus-

ter together disciplines using similarity measures pro-

vided by student ratings (see e.g. (Kogan, 2007),

(Mirkin, 2005) for general description of clustering

techniques). A step in this direction (based on man-

ual clustering) is reported in (Kogan, 2014).

Teaching effectiveness and involvement in re-

search is a topic of current public interest in the USA.

The claim “the relationship between teaching and re-

search is zero” is attributed to education experts who

analyzed data on “more than half a million profes-

sors” (Grant, 2014). While the claim might surprise

some it is endorsed by speciﬁc evidence provided by

UMBC SCEQs covering instruction in statistics. For

example, SCEQ for Fall 2010 STAT 350 01 (instruc-

tor Deneen Blair) reports class average rating of 4 for

question 9

. While Ms. Blair is lacking research ex-

perience in statistics (she is a secretary in the Depart-

ment) her ratings are much better than those of many

statistics research faculty.

The secretary’s rating makes one wonder how stu-

dents’ ratings reﬂect on instructor’s qualiﬁcations,

knowledge of the subject, and professional compe-

tence. Additional Maryland colleges, and, perhaps,

nationwide data should be analyzed to provide accu-

rate account of the relationship between teaching and

research as well as other relevant topics.

The UMCP data provides written comments along

with numerical ratings. Analysis of written comments

may accurately reveal students’ reason for satisfac-

tion or discontent. The problem of processing large

amounts of text naturally lends itself to Text Mining,

http://oir.umbc.edu/ﬁles/2013/02/STAT

−

F10.pdf

a powerful approach to efﬁciently handle text collec-

tions.

Computer aided examination of texts (as opposed

to numbers) is a nontrivial exercise. Free text lacks

structure, and often is contaminated. Expressions

such as “you c” instead of “you see”, or “on ur own”

instead of “on your own” should be automatically de-

ciphered (these examples are coming from the UMCP

collection analyzed in this paper). Applications of

Text Mining, an interdisciplinary ﬁeld that combines

statistics and computational linguistics, might be a

right way to proceed (Manning and Sch¨utze, 1999).

Reliability of the data is an issue of fundamental

importance for any meaningful analysis. A UMBC

SCEQ form provides information concerning enroll-

ment and the number of questionnaires ﬁlled out by

students in the class. The ratio of these two numbers

has been currently deﬁned as “response rate.” If, for

example, 35 questionnaires has been ﬁlled out in a

class with total enrollment of 100 students, then the

response rate is 35% (Bell, 2014).

Some believe a low response rate is correlated

with poor teaching. Inspection of SCEQ forms shows

that while sometimes the response rate can reach the

perfect 100% (see e.g. Fall 2005 ART 210 0101, “Vi-

sual Concepts”

, the forms also reports higher than

100% response rate (see Fall 2005 BIOL 100 0101,

“Concepts in Biology”

, and even much higher than

that response rate (see e.g., Spring 2005, phil 399,

“philosophy of humor”

) with course title perhaps re-

ﬂecting on the form’s content.

Consistency of the data under scrutiny is of

paramount importance for success of any computer

aided analysis. The inconsistency as, for example, il-

lustrated above (see also (Kogan, 2014) for additional

examples) should be detected. This requires develop-

ment and implementation of appropriate tests the data

should be subjected to before it is analyzed. With no

reliable data any analysis of student ratings is worth-

less.

ACKNOWLEDGEMENTS

The authors thank anonymous reviewers whose con-

structive comments improved exposition of the re-

sults.

http://oir.umbc.edu/ﬁles/2013/02/ART-F05.pdf

http://oir.umbc.edu/ﬁles/2013/07/EDUC

−

S13.pdf

http://oir.umbc.edu/ﬁles/2013/02/PHIL

−

Spring-2005.pdf

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

222

REFERENCES

Aleamoni, L. M. (1999). Student rating myth versus re-

search facts from 1924 to 1998. Journal of Personnel

Evaluation in Education, 13:2.

Alhija, F. N. A. and Fresko, B. (2009). Student evaluation of

instruction: What can be learned from students written

comments? Studies in Educational Evaluation, 35:1.

Bedard, K. and Kuhn, P. (2008). Where class size mat-

ters: class size and student rating of instructor effec-

tiveness. Economics of Education Review, 27:3.

Bell, J. (2014). Private communication. February 26, 2014.

Berry, M. and Kogan, J. (2010). Text Mining: Applications

and Theory. Wiley.

Cashin, W. (1995). Student ratings of teaching: the research

revisited. Center for Faculty Evaluation & Develop-

ment, Division of Continuing Education, (32).

Feldman, K. (1992). College students’ view on male and

female college teachers: Part I–evidence from the so-

cial laboratory and experiments. Research in Higher

Education, 33(3).

Feldman, K. (1993). College students’ view on male and fe-

male college teachers: Part II–evidence from students’

evaluations of their classroom teachers. Research in

Higher Education, 34(2).

Grant, A. (2014). A solution for bad teaching. NY Times,

February 5, 2014.

Hardy, G., Littlewood, J. E., and Polya, G. (1934). Inequal-

ities. Cambridge University Press, Cambridge.

Hodges, L. C. and Stanton, K. (2007). Translating com-

ments on student evaluations into the language of

learning. Innovative Higher Education, 31:5.

Hodges Jr., J. L. and Lehmann, E. L. (1964). Basic Con-

cepts of Probability and Statistics. Holden-Day, San

Francisco.

Karlsson, M. and Lundberg, E. (2012). I betraktarens

¨ogon betydelsen av k¨on och ˚alder f¨or studenters

l¨araromd¨omen. H¨ogre utbildning, 2:1.

Kogan, J. (2007). Introduction to Clustering Large

and High–Dimensional Data. Cambridge University

Press, New York.

Kogan, J. (2014). Student course evaluation: Class size,

class level, discipline, and gender bias. In Interna-

tional Conference on Computer Supported Education.

INSTICC Press.

Kwan, K.-p. (1999). How fair are student ratings in assess-

ing the teaching performance of university teachers?

Assessment & Evaluation in Higher Education, 24:2.

Likert, R. (1932). A technique for measurement of attitudes.

Arhives of Psychology, 140:1.

Manning, C. and Sch¨utze, H. (1999). Foundations of Statis-

tical Natural Language Processing. MIT Press, Cam-

bridge, MA.

Mirkin, B. (2005). Clustering for Data Mining: A Data Re-

covery Approach. Chapman & Hall/CRC, Boca Ra-

ton.

Sliusarenko, T., Clemmensen, L. H., and Ersball, B. K.

(2013). Text mining in students’ course evaluations.

In International Conference on Computer Supported

Education. INSTICC Press.

Sprague, J. and Massoni, K. (2005). Student evaluations

and gendered expectations: What we cant count can

hurt us. Sex Roles: A Journal of Research, 53, 11-

12:779–793.

Young, S., Rush, L., and Shaw, D. (2009). Evaluating gen-

der bias in rating of university instructors’ teaching

effectiveness. International Journal of Teaching and

Learning, 3(2).

StudentRatings,ClassSize,WrittenComments,RankandGenderBias

223