DeLi2P

A User Centric, Scalable Demand Side Management Strategy for Smart Grids

Syed Muhammad Ali

, Mohammad Naveed

, Fahad Javed

, Naveed Arshad

and Jahangir Ikram

Department of Electrical Engineering, University of British Columbia, Okanagan BC, Canada

Syed Babar Ali School of Science and Engineering, Lahore University of Management Sciences, Lahore, Pakistan

Department of Computer Science GIFT University, Gujranwala, Pakistan

Keywords:

Smart Grids, Demand Side Management, Peak Reduction, Demand Elasticity.

Abstract:

Smart grids coulpled with efﬁicient demand side management (DSM) is an important step for greener cities

of the future. DSM has the potential to signiﬁcantly improve smart grid operations by reducing the peak to

average ratio. Current DSM schemes are able to reduce peak load by as much as 30% which can translate to

signiﬁcant cost savings and reduction in green house emissions. But for realistic deployment of DSM systems

in the grid there are two very important aspects which need to be considered: scalability and user acceptability.

Since the current DSM algorithms are required to control potentially hundreds of thousands of devices, they

have to be scalable and tractable for such myriad numbers. On the other hand DSM affects the life style of

the consumer and this should be as less disruptive as possible. The various DSM techniques proposed in the

literature attempt to ﬁrst reduce the cost and then attempt to resolve one of the two aforementioned aspects.

The result is that the techniques are either scalable or are only considerate of the deadlines of the consumers.

An ideal system should cater to both of these aspects. Our system Deli2P is user centric and scalable thus

catering to both of these aspects. Essentially we provide to the consumer a deadline centric interface. The

deadlines solutions are generally not scalable. But instead of solving this problem as a scheduling for deadline

problem we transform the problem to a priority-based problem thus making it scalable for large number of

devices. Our results show that with this scheme we can reduce peak power by upto 30% but without violating

consumers‘ deadlines.

1 INTRODUCTION

The continuous increase in electricity demand and

the shrinking resources of energy has resulted in a

scarcity of electricity. In such a scenario conserv-

ing and optimally consuming the existing resources

has gained paramount importance. In fact energy

efﬁciency is being called as ‘the most important’

fuel for the future. One of the major ways for ef-

ﬁcient energy management is demand side manage-

ment (DSM) (Gellings, 1985). Coupling DSM with

the future smart grids technologies therefore is being

seen as the major resource for the future smart grids

(Rahimi and Ipakchi, 2010). The goal of these future

DSM systems is to manage the domestic consumer’s

load for a more environmental and economically ef-

ﬁcient energy generation scheduling. This is usually

achieved by ofﬂoading the electric consumption from

high cost timings to other timings when the electric-

ity price is low (Liu et al., 2014). This phenomenon

is commonly known as peak shaving.

However, for a DSM strategy to be viable for do-

mestic consumer it is imperative that this load move-

ment is acceptable to the consumers‘ schedules and

practical constraints. Historically it has been ob-

served that strategies which do not consider con-

sumers preferences as ﬁrst class requirement fail to

deliver due to stiff resistance or non-cooperation from

the consumers. As Kim and Shcherbakova report on

the reasons for DSM failures, the consumer needs

to be involved in the DSM activities and her re-

quirements need to be understood and catered for

(Kim and Shcherbakova, 2011). To cater to the con-

sumers‘ needs there are two strategies used by the

DSM planners and researchers: Either consumer’s ex-

act requirements are captured by eliciting the deadline

within which the task must be achieved (Arif et al.,

2013), or the devices are assigned priorities and these

priorities are used for planning (Beal et al., 2012).

The difference in the two strategies on operational

148

Muhammad Ali S., Naveed M., Javed F., Arshad N. and Ikram J..

DeLi2P - A User Centric, Scalable Demand Side Management Strategy for Smart Grids.

DOI: 10.5220/0005437301480156

In Proceedings of the 4th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS-2015), pages 148-156

ISBN: 978-989-758-105-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

level may seem insigniﬁcant initially but from a com-

putational perspective the two strategies have signiﬁ-

cant implication in the scalability of the system. The

preference based scheduling problem is a very com-

mon problem in operations research and computer

science. Various job scheduling tasks exist in real

world and researchers have analyzed this problem in

detail. Scheduling of loads constrained by prefer-

ences is very similar to job scheduling problem. How-

ever, this problem is classiﬁed as NP-complete prob-

lem and to-date no scalable algorithm has been pro-

posed to solve this problem. The implication of this

NP-complete classiﬁcation is that a problem without

necessary transformations will be intractable for large

number of devices thus making it not suitable for large

number of devices. As the number of devices increase

the algorithm will take an exponentially more time for

computation.

On the other hand priority-based systems are able

to aggregate the devices into priority classes and the

planning decision is reduced from controlling hun-

dreds of devices under constraints to just control-

ling each priority class. Since the number of priority

classes is much smaller than number of devices, plan-

ning for this system is tractable. ColorPower is an ex-

ample of such a technique (Ranade and Beal, 2010).

This reduction in size makes the problem tractable for

a micro-grid or even city level scheduling.

However, priority classes are limiting in that dead-

lines for individual devices are not part of the schedul-

ing. This is problematic as this results in lower con-

sumer satisfaction as the needs of the consumer can

be violated. From the experience of Power7 of UK

we know that the consumers‘ life styles are dynamic

and such ﬁxed measures are not very useful. To this

end, in this paper we propose a novel transformation

of deadlines to priority-based DeLi2P model.

Deli2P collects user deadlines from devices. The

modern electronic devices are ﬁtted with timers to

stop or start a device at a speciﬁc time. Similar to

these timers in Deli2P consumer can select the time

at which she requires the device’s process to be com-

plete by putting in the“putoff” time on the device or

device plug interface. For example, if a consumer is

putting in dishes for washing then the consumer can

feed in 6 hours for the dishes to be washed and ready.

Deli2P transforms this deadline into a priority in

the following way. The controller gathers three im-

portant parameters of a particular device. These pa-

rameters include operational time of a device, dead-

line of the operation and the time available before

deadline, the “putoff”. Based on these parameters it

assigns priority to a device, which changes as time

available approaches the deadline of operation. For

example, a device with operational time of 2 hours has

a deadline of operation 6 hours from the time the re-

quest was made. Using this information our controller

computes the time available after every decision cycle

in our algorithm as will be explained later. Priority as-

signment will be done using a mathematical function

described in section 3 of the paper. With each de-

vice assigned a priority, based on the time available

for execution we can aggregate the priority demands

and schedule the device operation in the same way as

done by Ranade and Beal (Ranade and Beal, 2010). If

the device is not activated for operation in the current

level of priority then it moves to a higher level. With

higher priority level, the device has a higher chance of

getting the activation signal. Priority level transition

is done at equal time intervals based on time available

which in this case is six hours divided into time pe-

riods of three hours (where 6 is the deadline and 3 is

the number of ﬂexible (Rehman et al., ) priority lev-

els). This process is continued till the device is either

operated or it is at the highest level where it is guar-

anteed execution.

When sufﬁcient supply is available the system al-

lows all the devices to execute as soon as they submit

a demand to consume. As the demand grows above

the supply, the devices with the least priority are in-

structed to ”wait” for servicing based on a probabilis-

tic model. This ensures that the demand never sur-

passes the supply. For example, in the early hours of

the day when the demand is much less than supply

and all devices are given go ahead for execution. But

as the demand is about to cross the supply our algo-

rithm puts each device in one of the ﬂexible priority

levels and let them change their state only when the

demand-supply situation gets better or the deadline is

close enough. Deli2P in this way is able to reduce

the peak demand of the day while satisfying the con-

sumer’s preferences.

The rest of the paper discusses the related work

in this area, our proposed solution, its model and ﬁ-

nally a discussion on evaluation, conclusion and fu-

ture work.

1.1 Related Work

Demand side management (DSM) techniques usually

have one of the two goals: the ﬁrst one is to reduce

the electricity cost and the second is to reduce the

peak load (Chai et al., 2014). A range of algorithms

attempt to reduce the cost of electricity for the con-

sumers. These include algorithms which incorporate

the time of use pricing in reducing the cost of electric-

ity of the consumer (Fan, 2011)(Lee and Lee, 2011),

and DSM systems which maximizes the beneﬁt of

DeLi2P-AUserCentric,ScalableDemandSideManagementStrategyforSmartGrids

149

renewable energy sources for home consumer (Arif

et al., 2013)(Daoxin et al., 2012). For these systems

the goal is not overall supply-demand management

but rather it is to minimize the cost of electricity to

the consumer. However, this does not guarantee that

the demand is shaped according to the global or util-

ity’s goals. To achieve this speciﬁc goals direct con-

trol systems are proposed which aim at reducing the

peak load. The difference is that in the ﬁrst category

the goal is cost reduction and peak load reduction is

implicit whereas in the second the peak load reduction

is the goal and cost savings due to better load proﬁles

are implicit.

The direct control algorithms thus control the con-

sumer devices remotely. However, shutting down end

user device is usually not very acceptable to the end

users. This has been studied and expounded by many

researchers (Kim and Shcherbakova, 2011). To cap-

ture the needs of the consumers there are two main

processes proposed in the literature.

One stream of research for such DSMs is to gather

the preferences or constraints of the consumers. That

is, for each device the system predicts or collects from

user the range within which the device can be sched-

uled. These constraint elicitation can be implicit as is

the case Du and Lu (Du and Lu, 2011) and Molderink

(Molderink et al., 2010) where forecasting and con-

sumer proﬁling using sensors in the user premises are

used to determine the constraints of the consumers. In

other cases such as those proposed by Kim and Poor

(Kim and Poor, 2011) and Arif and colleagues (Arif

et al., 2013), the constraints are explicitly provided by

the consumers through some interface. The authors

of the systems argue that since we have knowledge of

the consumer’s constraints and schedule the devices

accordingly, the DSM load management will be ac-

ceptable to the consumers.

However, as has been discussed by Molderink

(Molderink et al., 2010), Arif (Arif et al., 2013)

and Javed in AdOpt (Javed and Arshad, 2009), such

scheduling is NP-complete (Ullman, 1975). To date

there has been no polynomial time algorithm to solve

the NP-complete problems. The only way to solve

such problems is to enumerate all the possible com-

binations. But all combinations are exponential and

thus planning for hundreds of thousands of devices is

not possible. Use of artiﬁcial intelligence techniques

such as genetic algorithms and ant colony optimiza-

tion decrease the computation time but still take too

long for large scale system scheduling and are known

to be inaccurate.

The other stream is to allow the users to stipulate

priority classes to devices or join the device to a con-

tractual obligation group. ColorPower1 and Color-

Power 2 allow the consumers to assign priorities to

devices (Ranade and Beal, 2010; Beal et al., 2012).

The system then manages the probability of execution

for each priority class such that the demand shaping

goals are reached while maintaining that the distri-

bution is fair and according to consumer’s priorities.

Kim and Poor also proposed similar system however

their grading of the devices was not as versatile(Kim

and Poor, 2011). Pennywise on the other hand allow

users to sign contracts with the utility. Since these

contracts are standardized the utility can bunch to-

gether devices under similar contracts for computa-

tion. Escriva and colleagues also used such contracts

for their proposed DSM strategy (Escriv-Escriv et al.,

2010).

Since in these systems there is a natural way to

combine the devices into consumption classes, the

number of decision variable reduces to the number

of consumption classes. For few hundred classes the

existing algorithms are able to solve within a reason-

able time as is shown by Javed and Arshad in AdOpt

(Javed and Arshad, 2009).

However, since the priority systems observed by

the authors are somewhat rigid. ColorPower, and

Pennywise do not allow the consumers to change

the priorities. Colorpower allows consumers to press

an emergency button to explicitly demand electricity.

However if priority of a device changes then this up-

dation will take 24 hours to come into effect. Simi-

larly re-negotiating contracts for Pennywise or in Es-

criva’s system is a cumbersome task. As has been

shown in UK’s Power7 package, the consumers do

not like to be bounded to certain priorities and con-

tracts. As a biological being, the priorities and needs

for the human consumer changes rapidly and regu-

larly. The priorities for consumers are rarely consis-

tent and ﬁxed contracts do not do justice either.

To this end, in this paper we propose a transforma-

tion to convert a simple deadline based user feedback

into a priority based system. Since we collect explicit

preference and bound the system by it, we can reap

the beneﬁts of better user acceptability. Since we con-

vert these preferences into priorities very similar to

the ColorPower scheme, we can compute the solution

in reasonably small time as well getting use the bene-

ﬁt of both the systems.

1.2 Proposed Solution

In this section we will ﬁrst describe how our strategy

consider consumers deadlines. Then we discuss how

we have incorporated and improved existing Color-

Power algorithm for our planning.

The goal of DSM is to control consumer devices to

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

150

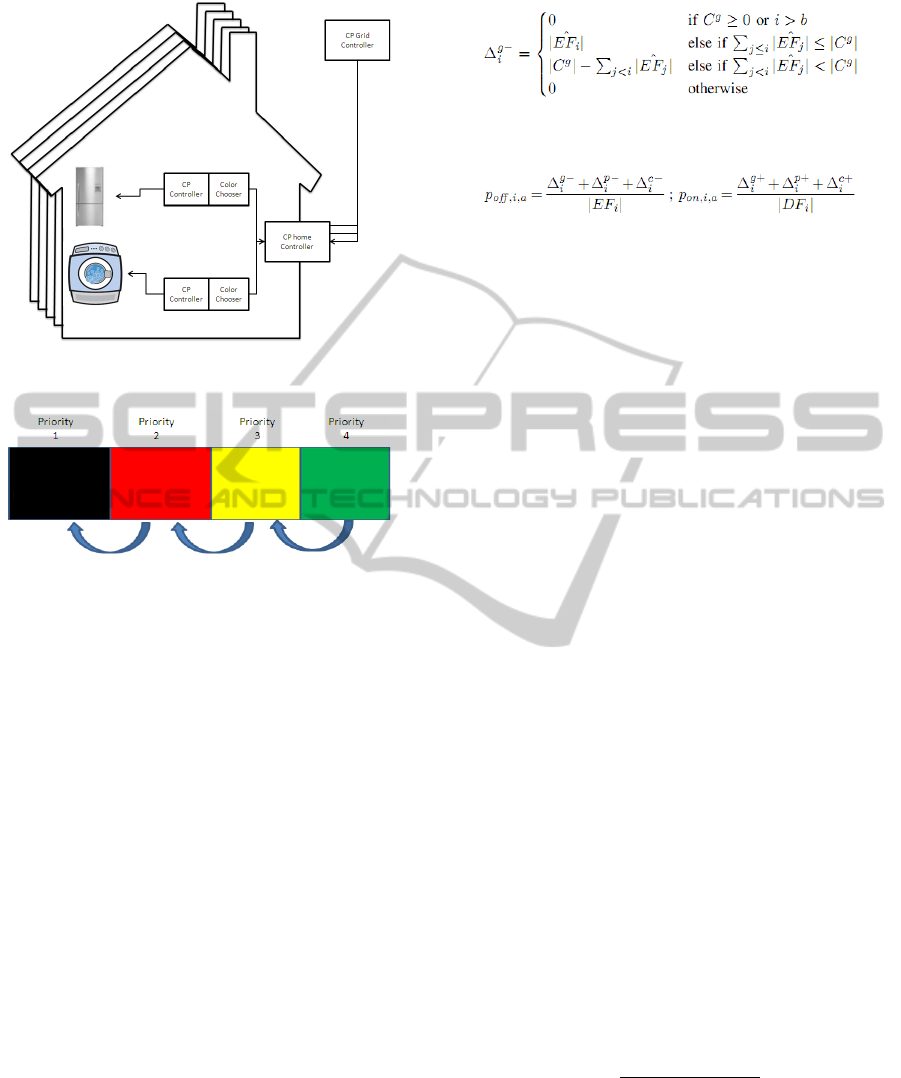
Figure 1: The architecture of the home system working with

Deli2p and its interaction with the grid controller.

Figure 2: Priority scale for DeLi2P. As the deadline time ap-

proaches the priority color transitions from green to yellow

to red and then black, the highest priority level.

reduce the electricity demand to speciﬁc thresholds.

As previously discussed, there are two non-functional

requirements of the DSM system, ﬁrst is that it should

be scalable and second it should be bound by the

needs of the consumers. In this regard the priority

based algorithms provide adequate solution for the

ﬁrst requirement. For instance, ColorPower is scal-

able, provides privacy preserving aggregation method

and is fair in its distribution of electricity.

This algorithm operates in the following way. The

controller assigns each device a color specifying its

priority as shown in ﬁgure 2. At every heartbeat the

home controller collects its demand from devices of

each color. If two devices are yellow then it will

add the demand of both devices as yellow. The al-

gorithm provides for a grid wise aggregation mecha-

nism whereby the grid controller has the aggregated

demands for each of the four priority colors. The grid

controller then assigns a probability to each priority

color based on the supply demand equation. The pol-

icy is that the highest priority gets to use the supply

till its demand is met. If supply is left then the lower

priority is provided the supply. If for a priority level

the supply is partial then each device in the priority is

given a probability based on the amount of electricity

available and the demand of that color. This way the

Figure 3: ColorPower (Beal et al., 2012) controller for de-

vice.

Figure 4: ColorPower (Beal et al., 2012) controller for the

grid.

lower priority devices run on a probabilistic basis.

However, this scheme does not provide provisions

for the consumer to constraint the load movement ac-

cording to consumer’s operations. If a consumer pur-

chases a washing machine then she would wish to

have the clothes washed within a speciﬁc period of

time and if the algorithm does not provide this guar-

antee then the consumer will be tempted to bump up

the device’s priority to get the required service. This

may result in spiraling up of priorities thereby leaving

no space for optimization. Essentially the CP does

not guarantee running a device even if the electricity

is available.

DeLi2P uses the same efﬁcient, scalable and fair

ColorPower (CP) controllers to provide control of the

device to the utility planner. One of the contributions

and indeed an important contribution of our work is

that instead of consumer assigning priorities we make

these priorities adaptable in that the device controller

adapts the devices’ color according to the amount of

time it has available to complete the task.

The difference is that when a consumer attempts

to use a device, the consumer is provided with a

timer to set the time of task completion. This can

be achieved by installing a timer on the device. This

maybe an external timer for legacy machine or it

maybe an internal timer in the future smart devices

however, discussion of its deployment is beyond the

scope of this work. The consumer sets the time when

she requires the task to be completed. Based on the

time to deadline DeLi2P calculates the color of the

device at runtime using the following formula:

d(d

− o

) − curre

len(k)

Where d

is the deadline set by the user, o

is the op-

erational execution time or the maximum time it will

take the device to complete the task and curr is the

current time. C

is the priority color of the device at

time curr. len(k) is the length of interval that we give

to each color.

DeLi2P-AUserCentric,ScalableDemandSideManagementStrategyforSmartGrids

151

As the time moves forward, that is the difference

between (d

− o

) − curr reduces, the priority of the

device increase thereby increasing its chance to com-

plete the task. The operational ﬂow is similar to Col-

orPower except for the color assignment after each

two minute period the color for the device is ascer-

tained. If the consumer has asked for the device to

operate and the operation has not yet started then the

color is propagated to the CP home controller along

with historical consumption value. The CP home con-

troller aggregates the demand for each color, adds it

to the data passed by previous house and passes it

forward to next house so that it is transmitted to the

CP Grid controller as shown in ﬁgure 1 and discussed

in (Ranade and Beal, 2010). The CP grid controller

based on its algorithm shown in ﬁgure 4 calculate the

fractional part for each color. This value is passed to

the CP Device controller and the device controller se-

lects the state of the device using formula in ﬁgure

To illustrate the process, let us assume that a con-

sumer attempts to use washing machine. The con-

sumer wants the operation to be completed in 8 hours

time and the operational execution time for the ma-

chine is 1 hour. Thus we have (8 - 1) hours to com-

plete the task. This puts the device in yellow or cat-

egory 3. Based on the global demand the CP grid

controller assign probabilities to the colors and these

probabilities are propagated to the CP device con-

trollers. If at this time the supply is sufﬁcient to sup-

ply yellow priority then this device will run immedi-

ately. But if yellow is partially supplied or not sup-

plied at all then this device will use the CP controller

using formula in ﬁgure 3. If the device gets a chance

to run then it will execute otherwise it will wait till C

is red. With an updated color the device’s probabil-

ity of execution will chance. If the supply is so short

that even the red does not execute then 1 hour before

the deadline device will turn black. Since black is

emergency color the device will be provided with sup-

ply and the task will be achieved within the stipulated

time. Figure 5 describes the aforementioned process

as a ﬂow chart.

1.3 Solution Model

In this section we model the demand of electricity ac-

cording to its priorities. The time in our algorithm is

divided into t time slices and we have j priorities. De-

mand of electricity for j priority class generated in a

time slice t is given as:

∀

= Demand for j

priority at t time

For ColorPower, this will also be net demand or

Figure 5: Flow chart describing the algorithm opertion on a

single device.

of the respective time slice and the priority class

since there is no concept of carrying over load which

has not been provided supply. But for DeLi2P, load

which is not provided supply is considered is carried

over thus net demand at time t for j priority class is:

∀

= d

+ (D

t−1

× p

t−1

+ ∆

j−1

) − ∆

Here ∆

j−1

is the demand for the lower priority

level which has expired and needs to elevated to the

next level and ∆

is the expired demand from j

level

which needs to be elevated to the j + 1

level.

is the probability of selection for the j

prior-

ity at time t. DeLi2P and ColorPower use the same

formulation for calculating p

gieven as:

= 1 if

max( j)

∑

i= j

≤ S

= 0 if

max( j)

∑

i= j+1

≥ S

S −

∑

max( j)

i= j+1

otherwise

Where S is the total supply to the system.

The graphs in ﬁgure 6 show this transformation

of priority level induced by the transfer of ∆ load

from load priority levels to higher levels. Initial pri-

ority levels in form of colors are shown in ﬁgure

7. Though the probability assignment in ColorPower

and DeLi2P is same, the underlying total demand D

varies in DeLi2P to incorporate the concept of dead-

line but in ColorPower, the deadline is not accommo-

dated. With this strategy a peak reduction of up to

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

152

a b

c d

e f

Figure 6: Graphs showing demand and DSM through DeLi2P results. On the left the graphs show the demand for the day and

on the right the demand after application of DeLi2P. The peak demand ranges from 26MW on day 3 to 23MW on day 2. on

all these days DeLi2P has restricted the peak demand to 18MW without violating consumer deadlines. x-axis shows time in

minutes while y-axis shows power consumption in watts.

30% is achieved with minimum missed deadlines thus

ensuring user satisfaction.

2 EVALUATION

Our evaluation comprise of three steps: In the ﬁrst

step we show the working of Deli2p as a case study

for one house consisting of four devices. The main

objective of this demonstration is to show the color

transition feature of Deli2p. In the second step we

show the evaluation of Deli2p for one hundred de-

vices under various deadline constraints and user pri-

orities. In the third step we compare Deli2p with Col-

orPower algorithm and show their comparative effec-

tiveness and peak shaving ability.

2.1 Experimental Setup

To carry out analysis, simulations for the proposed al-

gorithm and related work were developed in C# pro-

gramming language. These simulations were con-

ducted on Intel i5 Processor with 4GB of physical

memory having 2.4GHz of clock speed. Power con-

sumption data for 100 different devices was used in

simulations for extensive testing of algorithms. The

data is generated at the rate of 2 samples / minute by

the conﬁgurable simulator presented in (Arshad et al.,

2013). The aggregated consumption of each device

at a articular time window was used to compute av-

erage power for that speciﬁc appliance. The average

powers were then put to use in demand response al-

gorithms corresponding to the time window for which

they were computed to obtain results close to the ac-

tual environment.

DeLi2P-AUserCentric,ScalableDemandSideManagementStrategyforSmartGrids

153

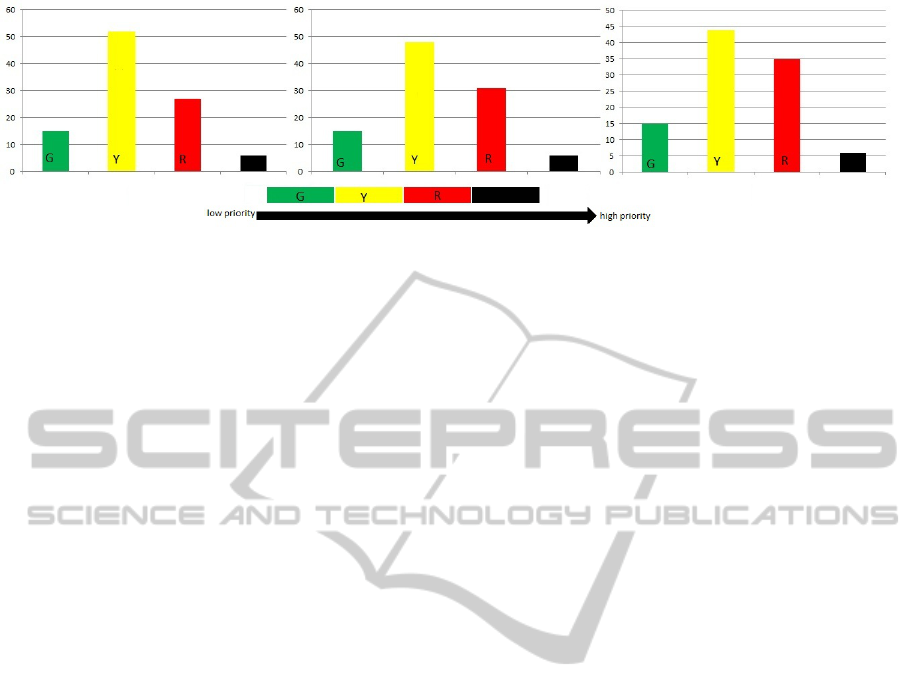
Figure 7: Initial priority levels assigned to devices on Days 1, 2 and 3 respectively from ﬁgure 6. These priority levels change

over the course of 24 hrs based on the supply demand situation.

2.2 Case Study of DeLi2P for One

House

In this case study we show the operation of 4 devices

for a single household. All four devices’ requirements

are fed to the system at the same time. As shown in

ﬁgure 8 when the device operational request is fed in

our system, the controller assigns priority based on

deadline and duration. The probabilistic model then

sends it turn ON or OFF signal. If the device turns ON

it completes its operation in a single time period, as

seen for device 4 in this case. However, failing to do

so causes device transition to a higher priority level.

As it can be seen from this table that device 1 is ﬁrst

in a least prior GREEN mode. Since it does not get

activated it moves to higher priority until eventually at

time t = d

− o

is the deadline of ith device and o

is the operational time of ith device) it enters BLACK

mode where it is applied turn ON signal to ensure ex-

ecution of operation for that particular device before

the deadline. After it has completed its operation the

device turns white indicating the operation has been

accomplished.

2.3 Applying DeLi2P to One Hundred

Devices

In our evaluation above, we expand our algorithm

on a pool of 100 devices which are assigned opera-

tional duration and putoff time. The ﬁgure 9 shows

one case in which devices are activated by scheduling

their deadlines into priority levels. Based on Power

demand-supply equations explained earlier our prob-

abilistic model turn on the devices without exceed-

ing total supply. The devices which are not oper-

ated eventually move into higher level of priority i.e

from Green to Yellow to Red. However, if a device

fails to activate within ﬂexible priority levels it enters

BLACK category in which each device is given turn

on signal to make sure no device goes non-operated

in order to achieve consumers‘ satisfaction

In this section we show the results of applying

DeLi2P for one hundred devices. As described ear-

lier, when a consumer attempts to use a machine the

system asks the consumer to provide a deadline by

which time she requires the task done. Based on the

available time the algorithm assigns an initial priority

level to the device. Considering the overall supply-

demand equation, the device is run when its deadline

is near or earlier if there is enough electricity avail-

able.

The results of application of DeLi2P are shown

in ﬁgure 6. The graphs on the left show the demand

of the system without DeLi2P and on the right the

results are with DeLi2P with 18000 KW (18MW) as

the target maximum load. As can be seen, DeLi2P is

able to maintain this target even though the demand

ranged from 25 MW on day 3 to 23 MW on day 2

while satisfying the deadlines set by the consumers.

2.4 Comparison of DeLi2P with

ColorPower

To illustrate on grid let us consider the demand in

ﬁgure 10(a). This is a hypothetical but realistic de-

mand where each of the priority level is equally di-

vided. This is the demand that was assumed by Color-

Power algorithm authors for their validation (Ranade

and Beal, 2010). The second ﬁgure 10(b) shows the

response of ColorPower and similar algorithms. As

can be seen the demand is ﬂat lined at demand of

140 units. This may result in a yellow device to be

unavailable for as much as 20 hours. To ameliorate

this situation in ﬁgure 10(c) the response of DeLi2P

is shown. As the time moves forward DeLi2P ele-

vates the priority of yellow, green and red. This el-

evation of priority means that the device has the op-

portunity to run within the deadline constrain set by

the consumer. the deadline will fail only when a part

of black is above the threshold line. This in essence

is the breaking point of the algorithm, that is, if we

require to shut down devices in black then the dead-

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

154

Figure 8: . This ﬁgure shows how colors are changed for a 24 hours period for four devices in a house depending on their

priority and how close they are to their deadline.

Figure 9: This ﬁgure shows the working of Deli2p with one hundred devices over a 24 hours period. The algorithm starts of

by putting the devices in one of the priority and changes the priority as the deadline is close.

a b c

Figure 10: Graphs showing net demand, demand shaping through ColorPower and through DeLi2P.

lines for those consumers will be violated. In com-

parison ColorPower does not cater for this situation

hence evaluating it for deadline failure is not possi-

ble.

3 CONCLUSION AND FUTURE

WORK

The need to incorporate consumer’s priorities and re-

quirements in to demand side management system is

critical to its acceptance and thereby its use. In this

paper we have considered two key requirements for

increasing the acceptability of the consumer. First

we have provided a way for the consumer to be an

active part of the DSM. This provides satisfaction to

the consumer as proposed by Breukers and colleagues

(Breukers et al., 2001). Secondly, we have provided

a way for the consumer’s deadlines to be catered for

in a scalable manner by converting those deadlines to

priority levels and thereby making the algorithm scal-

able, secure and fair as well.

We see this as a viable solution for future DSM

DeLi2P-AUserCentric,ScalableDemandSideManagementStrategyforSmartGrids

155

systems. The future of this work is to apply it to a

residential area and observe the consumer’s response

to this strategy. A second path of research is to incor-

porate machine learning to learn consumer behavior

in order to automate the timer task in order to aid the

consumer. Yet another possibility is to incorporate

time of use pricing in this system such that the con-

sumer is informed of the price savings that she can

achieve by setting the timer to a later time.

ACKNOWLEDGEMENT

This work is in part supported by grants from the De-

partment of Computer Science at LUMS, and ICT Re-

search and Development Fund of Pakistan.

REFERENCES

Arif, A., Javed, F., and Arshad, N. (2013). Integrating re-

newables economic dispatch with demand side man-

agement in micro-grids: a genetic algorithm-based ap-

proach. Energy Efﬁciency, pages 1–14.

Arshad, N., Ali, U., and Javed, F. (2013). A highly conﬁg-

urable simulator for assessing energy usage. Energy

Procedia, 42:308–317.

Beal, J., Berliner, J., and Hunter, K. (2012). Fast precise

distributed control for energy demand management.

In Self-Adaptive and Self-Organizing Systems (SASO),

2012 IEEE Sixth International Conference on, pages

187–192. IEEE.

Breukers, S., Keiskanen, E., Brohmann, B., Mourik, R., and

Feenstra, C. (2001). connecting research to practice

to improve energy demand-side management (dsm).

Energy, 36(4):2176–2185.

Chai, B., Costa, A., Ahipasaoglu, S., Huang, S., Yuen, C.,

and Yang, Z. (2014). Minimizing commercial build-

ing cost in smart grid: An optimal meeting schedul-

ing approach. In Smart Grid Communications (Smart-

GridComm), 2014 IEEE International Conference on,

pages 764–769.

Daoxin, L., Lingyun, L., Yingjie, C., and Ming, Z. (2012).

Market equilibrium based on renewable energy re-

sources and demand response in energy engineering.

Systems Engineering Procedia, 4(0):87 – 98. Infor-

mation Engineering and Complexity Science - Part II.

Du, P. and Lu, N. (2011). Appliance commitment for house-

hold load scheduling. Smart Grid, IEEE Transactions

on, 2(2):411 –419.

Escriv-Escriv, G., Segura-Heras, I., and Alczar-Ortega, M.

(2010). Application of an energy management and

control system to assess the potential of different con-

trol strategies in hvac systems. Energy and Buildings,

42(11):2258 – 2267.

Fan, Z. (2011). Distributed demand response and user adap-

tation in smart grids. In Integrated Network Manage-

ment (IM), 2011 IFIP/IEEE International Symposium

on, pages 726 –729. Internet trafﬁc method for DR.

Modeling user preference as willingness to pay. Sim-

ulation based. no rebound calculations.

Gellings, C. (1985). The concept of demand-side manage-

ment for electric utilities. Proceedings of the IEEE,

73(10):1468 – 1470.

Javed, F. and Arshad, N. (2009). Adopt: An adaptive

optimization framework for large-scale power distri-

bution systems. In Proceedings of the 2009 Third

IEEE International Conference on Self-Adaptive and

Self-Organizing Systems, SASO ’09, pages 254–264,

Washington, DC, USA. IEEE Computer Society.

Kim, J.-H. and Shcherbakova, A. (2011). Common failures

of demand response. Energy, 36(2):873 – 880.

Kim, T. and Poor, H. (2011). Scheduling power consump-

tion with price uncertainty. Smart Grid, IEEE Trans-

actions on, 2(3):519 –527.

Lee, J.-W. and Lee, D.-H. (2011). Residential electricity

load scheduling for multi-class appliances with time-

of-use pricing. In GLOBECOM Workshops (GC Wk-

shps), 2011 IEEE, pages 1194 –1198. Scheduling al-

gorithm using time of use to reduce cost. No rebound

in simulation.

Liu, Y., Yuen, C., Huang, S., Ul Hassan, N., Wang,

X., and Xie, S. (2014). Peak-to-average ratio con-

strained demand-side management with consumer’s

preference in residential smart grid. Selected Topics in

Signal Processing, IEEE Journal of, 8(6):1084–1097.

Molderink, A., Bakker, V., Bosman, M., Hurink, J., and

Smit, G. (2010). Management and control of domes-

tic smart grid technology. Smart Grid, IEEE Transac-

tions on, 1(2):109 –119.

Rahimi, F. and Ipakchi, A. (2010). Demand response as a

market resource under the smart grid paradigm. Smart

Grid, IEEE Transactions on, 1(1):82 –88. Introduc-

tory case building paper.

Ranade, V. V. and Beal, J. (2010). Distributed control

for small customer energy demand management. In

SASO’10, pages 11–20.

Rehman, M. M. U., Javed, F., Arshad, N., Ikram, M. J.,

Babri, A. H., and Masood, U. A cooperative de-

mand response system for small scale commercial

consumers.

Ullman, J. D. (1975). Np-complete scheduling problems.

Journal of Computer and System sciences, 10(3):384–

393.

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

156