Novel Progress in the High-sensitivity Heterolithic Ring Laser Gyroscope

Technology

R. Santagata

1,2

, J. Belﬁ

, N. Beverini

2,3

, G. Carelli

2,3

, A. Di Virgilio

, E. Maccioni

2,3

and A. Simonelli

2,3,4

Department of Physics, University of Siena, Via Roma 56, Siena, Italy

INFN Section of Pisa, Largo Bruno Pontecorvo 3, Pisa, Italy

Department of Physics, University of Pisa, Largo Bruno Pontecorvo 3, Pisa, Italy

Department of Earth Sciences, University of Pisa, Via Santa Maria 53, Pisa, Italy

1 ABSTRACT

The sensitivity achieved by large ring laser gyro-

scopes opens the perspective to observe in an Earth-

located laboratory extremely small effects expected

from fundamental theories of physics. The next-

generation sensor that could provide the required ac-

curacy is a multiaxial heterolithic ring laser actively

stabilized via a precise external diagnostic of circu-

lating laser beams path.

Here we report about the research activities and

recent progress toward the development of a large

frame He-Ne triaxial sensor with an ultimate accu-

racy of 10

−11

, in order to detect the relativistic Lense-

Thirring effect related to the Earth rotating mass. The

actual activity is focused on the control of the sys-

tematic errors related to the ﬂuctuation of the cavity

geometry and the laser active medium parameters. In

this work we will discuss in details only the ﬁrst issue,

to which my PhD studies are mainly dedicated.

2 RESEARCH PROBLEM AND

OUTLINE OF OBJECTIVES

Ring lasers gyroscopes (RL) are inertial sensors

able to measure absolute rotations (Stedman G.E.,

1997); if they are placed at rest in a ground-located

laboratory, the measured rotation is that of our planet

Ω

⊕

Lense-Thirring effect, predicted by Einstein’s Theory

of General Relativity, consists in a dragging of

the local inertial frame of reference caused by the

perturbation of the local metrics in the proximity

of a spinning massive body like Earth (Lense J.

and Thirring H., 1918). This implies that the Earth

rotation rate measured against the ”ﬁxed-stars”

inertial frame differs from the rotation rate measured

in the laboratory frame. In the low ﬁeld approxi-

mation, the dominant correction terms are given by

a geodetic term (or gravito-electric effect) due to

the gravitational red-shift, and by a dragging term

proportional to the angular momentum, known as

Lense-Thirring effect or gravito-magnetic effect. On

the Earth surface both corrective effects are of the

order of 1 part in 10

Ω

⊕

, but while the geodetic

term is radially directed, the dragging one has a

dipolar shape.

This has been already observed as global effect on

orbiting satellites, as GRAVITY-B experiment and

LAGEOS orbital data analysis (Everitt C.W.F. et al.,

2011) (Ciufolini I., 1986). The experiment named

GINGER (Gyroscopes IN GEneral Relativity) (Bosi

F. et al., 2011) (Di Virgilio A. et al., 2014) aims

at measuring, for the ﬁrst time in a ground-based

laboratory, the Lense-Thirring effect locally, by

using an array of large RLs placed in a Earth-based

laboratory.

The requirements needed to make this possible

can be clearly understood examining the sensor re-

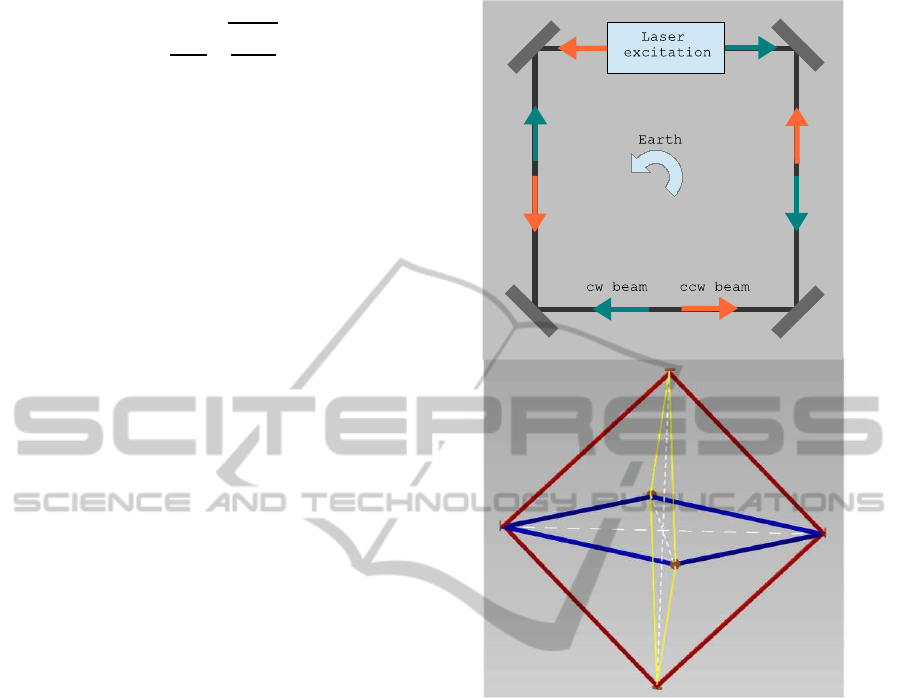
sponse. The basic setup of a RL is made up of a sta-

ble ring optical cavity along which an active medium,

typically a He-Ne mixture, is placed (ﬁgure 1); two

laser beams are generated and propagate in opposite

directions along the loop. A Sagnac beat frequency of

the circulating beams is measured (Sagnac G., 1913):

A·

Ω

λP

, (1)

where

Ω =

Ω

⊕

Ω

′

is the rotation relative to the local

Lorentz inertial frame (being Ω

′

any correction term),

A is the area vector enclosed by the ring optical path

P and λ is the wavelength of the laser.

The sensitivity limit of a RL is given by the shot-

noise:

Santagata R., Jacopo J., Beverini N., Carelli G., Di Virgilio A., Maccioni E. and Simonelli A..

Novel Progress in the High-sensitivity Heterolithic Ring Laser Gyroscope Technology.

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Ω

4AQ

out

, (2)

where v is the velocity of the laser beam along the

cavity, Q is the quality factor of the resonator, h the

Planck constant, P

out

the detected optical power and

T the measuring time.

From equation 1 two important features follow:

the dependence of Sagnac frequency f

on the laser

path geometry via the scale factor k

= 4A/λP, and

the scalar nature of the sensor output, being measured

only the projection of the velocity vector

Ω on the

enclosed area

The development of a high sensitivity RL requires:

• a large frame structure. To increase the size of the

ring cavity, in fact, implies to increase the signal

to noise ratio (SNR), being the signal proportional

to the ratio A/P via the scale factor, and the shot

noise of the sensor proportional to P via the qual-

ity factor Q.

• a high-Q resonator (> 10

and higher). Low-loss

’ﬁve-9s quality’ supermirrors must be used.

• a multi-axial system of RL, in order to recon-

struct the modulus of the Earth rotational vec-

tor and compare the Earth rotation rate measured

locally with the one provided by IERS (Interna-

tional Earth Rotation and Reference Systems Ser-

vice). Otherwise, an absolute calibration of the

RL orientation at a level of 0.1 nrad would be

needed.

• to reduce the instrumental drift in the measure-

ment of rotation rate to less than Ω

′

/Ω

⊕

. This

needs a long-term strict control on the ﬂuctuation

of laser active medium, cavity geometry and, in a

RLs array, of relative dihedral angles.

• to reduce all the sources of Earth-surface and en-

vironmental noise, installing the detector in a very

stable geological environment, well coupled to the

solid rock, in a low environmental noise labora-

tory, possibly located underground.

3 STATE OF THE ART

To this day, the best RL is the Grossring ’G’, lo-

cated at the Geodatisches Observatorium in Wettzell,

Bavaria (Schreiber K.U. et al., 2009) (Schreiber K.U.

et al., 2011). It has achieved a resolution better than

5× 10

−13

rad/s with an integration time of few hours,

becoming of geodetic interest for measuring short-

term ﬂuctuation, with periods of hours to days, in

Earth rotation.

Figure 1: Ring laser gyroscope. Above: setup of a square

RL. Below: triaxial sensor made of 6 mirrors. Each couple

of opposite mirrors is shared between two rings.

This stability record is mainly due to its building

material that allows a strong passive stabilization of

the optical cavity. G, in fact, is a semi-monolithic de-

vice made in Zerodur, a glass ceramic with an espe-

cially small thermal expansion, high mechanical sta-

bility and consistency of shape and length. Four bars

are rigidly connectedto a base plate forming the edges

of a square 4 m length in side; spherical supermirrors

are attached to the face sides of the bars by molecu-

lar adhesion, ensuring a stable vacuum seal. It is kept

in an underground controlled room and equipped with

an active control of the cavity perimeter that stabilizes

the circulating laser beams frequency against an opti-

cal frequency reference.

Albeit G resolution is very close to that required

to detect the relativistic effects on rotation, its design

can’t be used to develope a large frame RLs array,

since larger monolithic blocks of Zerodur are not

available. The next-generation RL able to detect tiny

effects, as Lense-Thirring effect, has a heterolitic

NovelProgressintheHigh-sensitivityHeterolithicRingLaserGyroscopeTechnology

multi-axial design equipped with a precise diagnostic

system of laser beam path deformation, in order to

stabilize the scale factor k

better than 10

−10

Recent studies and experimental activities made in

this context on the middle-size heterolitic RL ’G-Pisa’

(Belﬁ J. et al., 2012), have motivate the design of the

GINGER device. It consists in a triaxial system of

large square heterolitic RLs arranged in a octahedral

structure (ﬁgure 1). A suitable location for this device

could be the underground facility of LNGS (Labora-

tori Nazionali del Gran Sasso - Italy).

To accomplish GINGER’s goal needs a control of the

systematic errors related to the ﬂuctuation of the cav-

ity geometry and the laser active medium parameters.

As regards the last issue, a set of spectroscopic di-

agnostic of the active medium parameters and an off-

line denoising method that, based on the Kalman ﬁlter

approach, subtracts from the raw Sagnac data the sys-

tematic effects induced by the non-linearity of the RL

dynamics, has been developed (Beghi A. et al., 2012)

(Cuccato D. et al., 2014). In the following, we’ll dis-

cuss mainly about the ﬁrst research ﬁeld.

4 RING CAVITY GEOMETRY

CONTROL

The measure of Lense-Thirring effect in a ground-

based laboratory requires a stabilization of the scale

factor k

better than 10

−10

. This implies an accuracy

on mirror positions better than 1 nm and on the ring

cavities relative orientation better than 1 nrad.

In a square RL, a so strict control on mirror posi-

tions can be reduced if the absolute length of the diag-

onal cavities is stabilized in addition to the perimeter

one, so that the closed optical path shape is that of a

regular square. Our theoretical and numerical stud-

ies are reported in detail in Ref.(Santagata R. et al.,

2014). We showed that if the length of the two diago-

nals are locked to the same value, the perturbations to

the mirror positions affect only quadratically the ring

laser scale factor. This constraint reduces the mirror

position ﬂuctuation at a level of 1 part in 10

, even if

the two lengths are stabilized to values that differs at

a micrometric scale.

These results motivated the design of GP2 (Di

Virgilio A. et al., 2014), an intermediate prototype

of GINGER speciﬁcally devoted to test the active

control strategies and, in particular, to implement

the length stabilization of the diagonal resonators by

means of optical interferometry. In addition to it, the

GINGERino prototype has also been developed last

year (Di Virgilio A. et al., 2014); it is especially birth

to analyze the seismic noise at LNGS location, but

also to tryout the SNR improvement of a larger cav-

ity.

The optical setup of both devices consists in four

supermirrors each one contained in a steel holder

placed at the corner of a granite support ﬁxed on a

concrete base. Steel pipes connected by the mirror

holders deﬁne the vacuum chamber that encloses the

optical path of the circulating beams along a square

loop. The vacuum chamber is ﬁlled with a mixture of

He-Ne and the capacitive discharge for laser excita-

tion, consisting in a pyrex capillary, is located in the

middle of a side of the cavity. The laser frequency is

stabilized with respect an optical frequency reference

in order to actively control the ring cavity perimeter.

In section 5 GP2 and GINGERino prototype are

described. To stabilize the absolute length of di-

agonal resonators we worked out an interferometric

metrology technique and we tested it on two Fabry-

Perot cavities simulating the ring diagonals on an op-

tical bench. We report some details about this work,

whose results has been published in Ref.(Belﬁ J. et

al., 2014), in section 6. Finally, in section 7 expected

outcome and future perspectives are discussed.

5 METHODOLOGY

5.1 GP2

5.1.1 Optical Setup

GP2 is the seed device for the next generation het-

erolitic active-stabilized RLs. It has been designed in

order to gain a long term stability and accuracy of the

scale factor, via a precise control of the systematic er-

rors related to the ﬂuctuation of the cavity geometry

and the active medium parameters. In particular, it is

dedicated to implement a length stabilization of the

diagonal cavities using optical interferometric tech-

niques.

Figure 2 shows a drawing of GP2 (above) and its

installation in a clean room at INFN Pisa laboratories

in March 2014 (below). The granite slab whereon the

cavity is placed is oriented along the local latitude in

order to maximize the Sagnac signal and minimize

the orientation errors on scale factor. The four mir-

rors holders are placed at the corner of a square gran-

ite slab and the vacuum chamber encloses the beam

optical path along a square loop 1.60 m length in

side. Figure 3 shows a preliminary Sagnac spectrum;

a Sagnac frequency of 184 Hz has been observed, as

expected.

To check the quality factor Q = 2π fτ of the laser

PHOTOPTICS2015-DoctoralConsortium

Figure 2: GP2 ring laser gyroscope. Above: drawing of the

design. Below: The sensor installed at the clean room of

INFN Pisa section laboratory (March 2014).

150 160 170 180 190 200 210

−8

−6

−4

−2

Frequency (Hz)

PSD

√

H z

Figure 3: Power spectral density of GP2 data. The Sagnac

response peak at 184 Hz is observed.

cavity we made a ring-down time τ measurement

of the laser by short-circuiting the discharge capac-

itor. In ﬁgure 4 we report the laser intensity decay

trace acquired by the oscilloscope. Fitting to data

the exponential function I = I

+ Ce

−t/τ

, where I

is the initial intensity and C a numerical constant,

we have obtained a measure for the ring-down time

τ = 154.4± 0.5 µs. This corresponds to a quality cav-

ity factor Q = 4.6 × 10

Figure 4: Ring-down time measurement of GP2 laser cavity.

Black line: trace of laser intensity decay acquired by the

oscilloscope. Red line: exponential ﬁt of data points. Fit

results: τ = 154.4 ± 0.5 µs; I

= −3.35 ± 0.10 mV; C =

114.63± 0.14 mV.

5.1.2 Mechanical Expedients for Diagonal

Cavities Stabilization

The slab whereon the holders are mounted is made of

precise black granite, a rock well suited for metrology

application for his long term thermal and dimensional

stability, high ﬂatness accuracy, high bending strength

and insensitivity to mechanical overloading. It has

been machined with a precision better than 10 µm to

guarantee a preliminary well positioning of the corner

mirrors.

To implement the diagonal absolute length sta-

bilization, by using the experimental technique de-

scribed in section 6, the GP2 vacuum chamber has

been designed in order to give access to the diagonal

resonators by enclosing the path of two external laser

beams along these, as well as the perimeter path of

the counter-propagating beams. These two additional

chamber parts, schematically indicated in the above

of ﬁgure 2, will be installed in the near future.

A high ﬁnesse of the Fabry-Perot cavities is guar-

anteed by a special mirror coating that ensures a re-

ﬂectivity of about 99.9% at normal incidence, in ad-

dition to a reﬂectivity > 99.999% at 45 deg angle of

incidence.

The design of mirror holders, whose most impor-

tant features are showed in ﬁgure 5, is of key impor-

tance in view of the diagonal cavities use.

The mirrors are accessible through big optical

transparent windows installed parallel to them on

the holders. The window allows the circulating

monobeams to exit the cavity and to be monitored;

an external optical setup detects the beat frequency. In

addition, it consents to an external He-Ne laser source

hitting it at normal incidence to enters into the diago-

nal resonators, as showed in the below of ﬁgure 5.

NovelProgressintheHigh-sensitivityHeterolithicRingLaserGyroscopeTechnology

Figure 5: GP2 Mirror holders. Above: drawing of the

holder design; the piezo system is shown. Middle: picture

of the holders installed on the granite slab. The big optical

transparent window allowing the optical access to corner

mirror is shown. Below: detail of holder. The optical setup

needed to combine the circulating beams is also shown. The

combiner is mounted on a small breadboard and consists in

two high-reﬂection dielectric mirrors 0.5 inch in size. For

the detection of the beat frequency, a photodiode integrated

with an interference ﬁlter is used. The three allowed di-

rections (monobeams exiting the cavity and external laser

source entering in the diagonal resonator) are pointed out.

To get a regular square cavity by a dynamic con-

trol, the mirror holders are equipped with a piezo

nano-positioning system. Since each mirror displace-

ment can be described as a variation in the space of the

position of its curvature center, the geometry of the

optical path along the square loop is completely de-

termined by the 12 centres coordinates (12 degree of

freedom). In Ref.(Santagata R. et al., 2014) we have

deﬁned the eigenvectors basis of the cavity deforma-

tions, identiﬁed the rigid body motion of the cavity,

and then classiﬁed the residual 6 optical cavity defor-

mations once the diagonal lengths are stabilized. For

this reason, in GP2 a total of 6 piezo-electric trans-

ducers (PZT) is used. One holder is provided with a

3-axial PZT, while the other three with a 1-axial PZT

along the diagonal.

The piezo system has a dynamic range of 80 µm.

To have an estimate of the displacement response, we

made a calibration of the 1-axial translators by mea-

suring the displacement induced by an applied volt-

age. The PZT calibration data are plotted in ﬁgure

6; a second order polynomial ﬁt provide a displace-

ment constant mean value of (7.4 ± 0.6) µmV

−1

for

the mirrors mounted on the north side of the RL, and

(9.2 ± 0.4) µmV

−1

for the mirrors mounted on the

south side.

Figure 6: PZT calibration data. The displacement data

induced by an applied voltage are plotted for each 1-

axial piezo moving the mirror holder along the ring cav-

ity diagonal. Positive variation means displacement to-

ward the center of the ring. A second order polynomial

∆x = AV

PZT

+ BV

PZT

is ﬁtted to data. From top to bot-

tom: corner 4 (green line), A

= (−9.3 ± 0.2) µmV

−1

= (0.271 ± 0.013) µmV

−2

; corner 3 (blue line), A

(−9.0± 0.3) µmV

−1

, B

= (0.269 ± 0.018) µmV

−2

; cor-

ner 1 (black line), A

= (−7.2±0.3) µmV

−1

, B

= (0.132±

0.017) µmV

−2

; corner 2 (magenta line), A

= (−7.5 ±

0.5) µmV

−1

, B

= (0.10± 0.04) µmV

−2

Figure 7: Pyrex tube for the excitation of the He-Ne plasma.

PHOTOPTICS2015-DoctoralConsortium

A ﬁne control of the laser beam path requires also

a well positioning of the discharge system. To this

aim, the pyrex capillary is linked to the steel pipes by

means of a cage system equipped with a micrometric

regulation of its position and tilt. A detail of the cage

system is reported in ﬁgure 7.

5.2 GINGERino

GINGERino is an evolution of G-Pisa RL. While the

fundamental purpose of G-Pisa was to acquire the ex-

pertise on the operation of a large frame RL, GIN-

GERino is its upgrading that has been placed in the

LNGS underground laboratory in order to test the ad-

equacy of the site to guest the GINGER apparatus.

The 1400 m thick rock of the central massif of

Gran Sasso constitutes a natural shielding against all

the sources of noise coming from the surface activi-

ties. The underground environment guarantees in ad-

dition a high stability of the local environmental pa-

rameter such as pressure, temperature and humidity.

At the same time, the operation of GINGERino in

a low local noise laboratory could give the possibil-

ity to detect geodetic signals (Polar motion, Chan-

dler wobble, tidal effects,...) and seismic signals (S-

wave phase velocity,...) for which a sensitivity of

−9

− 10

−13

rad/s is sufﬁcient. The analysis of the

rotational seismic noise and its correlation with clas-

sical seismometer signals will be carried out by re-

searchers of INGV (Italian National Institute of Geo-

physics and Vulcanology). A comparison with G

measurements would be very interesting in the case

of non-local effects, such as tele-seismic events.

Figure 8 shows a drawing of GINGERino (above)

and its installation in the Node A of the so-called ”in-

terferometric tunnel” at LNGS in October 2014 (be-

low). This gallery is in the northern part of the labo-

ratories, away from the 3 large Halls hosting the main

experiments and so away from the principle sources

of daily human activity noise. As in GP2, the square

optical cavity consists in supermirrors placed inside

corner holders connected by steel pipes. Holders

and pipes are those of the ﬁrst prototype, G-Pisa, in-

creased in size to get a length of side of 3.60 m. A

Sagnac frequency of 280 Hz has been observed, as

shown in ﬁgure 9.

The cavity is mounted on a granite slab installed

on a concrete monument well connected to the rock

ﬂoor. To reduce the weight of the apparatus and sim-

plify its installation in the cave, the slab consists in

four arms that has been inserted in loco into a central

square granite block. To improve the mechanical sta-

bility of the discharge system, the capillary holder is

ﬁxed on a breadboard sustained by four concrete pil-

Figure 8: GINGERino ring laser gyroscope. Above: draw-

ing of the design. Middle: detail of the lever system con-

trolled by micrometric screws used to align the ring cavity.

Below: installation at LNGS underground facility (October

2014). The thermal-acustic shielding enclosing it is shown.

lar; two of these sustain each cavity side also. The

mirrors, rigidly connected to the holders, can be tilted

to align the cavity by means of levers controlled by

micrometric screws (ﬁgure 8). Only two of the four

mirrors are equipped with a monodimensional micro-

metric PZT that, mounted under the holders, movethe

mirror along one diagonal of the square cavity. This

makes possible only a dynamic control of the beam

path perimeter, that is keep constant against an opti-

cal frequency standard.

The apparatus is enclosed by a thermal-acustic

shielding and the laboratory is warm up making

use of heat lamps simmetrically arranged around the

device. To give an assessment about the room-

temperature stability and homogeneity, we attached a

NovelProgressintheHigh-sensitivityHeterolithicRingLaserGyroscopeTechnology

240 260 280 300 320 340

−13

−12

−11

−10

−9

PSD

√

H z

Frequency (Hz)

Figure 9: Power spectral density of GINGERino data. The

Sagnac response peak at 280.05 Hz is observed.

platinum RTD (Resistance Temperature Device) sen-

sor attached to each corner of the steel cavity struc-

ture. Throughout 5 days, a maximum gradient of

0.5

◦

C between the mean values of temperature in two

different corners is observed; the ﬂuctuation around

each mean value, measured using standard deviation,

is of 0.04

◦

6 STAGE OF THE RESEARCH.

ABSOLUTE LENGTH

STABILIZATION OF THE

SQUARE RL DIAGONAL

CAVITIES

6.1 Measurement Principle

To stabilize the absolute length of a square RL di-

agonal resonators with respect to an interrogating

high-stability laser we worked out an interferometric

metrology technique and we tested it on two Fabry-

Perot cavities simulating the ring diagonals on an op-

tical bench. The technique we used is based on an

accurate frequency measurement of the resonant lon-

gitudinal mode and an univocal determination of the

interference order (Belﬁ J. et al., 2014). For a TEM00

laser mode of order n resonating in a cavity formed

by two concave spherical mirrors of radius R, the res-

onance frequency f

is given by:



2π

(Ψ

+ Φ

)



(3)

where v is the speed of light inside the cavity and L

is the distance between the mirrors. Ψ

and Φ

are

two phase corrections due respectively to the phase

accumulation along the direction of laser beam prop-

agation (Guoy phase) and the dielectric mirror phase

shift upon reﬂection; these two terms can be evaluated

from the knowledge of R and the mirror reﬂectivity

curve.

To measure L with a 10

−10

accuracy needs to mea-

sure f

with the same accuracy and deﬁne univocally

the integer n. This can be done locking the cavity

resonance to the laser carrier frequency (carrier lock)

and the phase modulation frequency to a harmonic m

of the free spectral range (sideband lock). We get the

two error signals required to implement the double-

lock modulating the laser source with a electro-optic

modulator (EOM) driven by three independent mod-

ulation frequencies: the ﬁrst modulation at frequency

provides the Pound-Drever-Hall signal for carrier

lock; the second modulation at frequency ω

provides

the lock-in ampliﬁer error signal; the latter is referred

to a third modulation at ω

for shifting the the FSR

detection down to few tens kHz.

6.2 Apparatus and Experimental

Procedure

The apparatus we developed is shown in ﬁgure 10.

The laser source is a 10mW diode laser emitting at

633 nm. A high spectral purity is gained referring

it to an optical reference frequency provided by a

100 µW He-Ne laser frequency stabilized on the sat-

urated absorption line R-127 11-5 of Iodine. This

is achieved implementing a light ampliﬁer based on

injection-locking. The features of the laser source are

summarized in table 1.

The Fabry-Perot resonators simulate the ring cav-

ity diagonals on an optical bench. They are formed

by curved mirrors mounted on holders connected by

Invar spacers; the output mirror is equipped with

a piezoelectric translator to implement the feedback

correction to the cavity length. The parameters of the

two resonators are reported in table 2.

The injection-locked laser beam, after being

triple-phase-modulated by a single ﬁber-coupled

EOM, enters into the two Fabry-Perot cavities. The

reﬂected beam, detected by a photodiode and splitted

by a two way power divider, is demodulated accord-

ing to a standard Pound-Drever-Hall scheme (ﬁrst one

way) and by a digital lock-in ampliﬁer (second one

way) in order to recover the carrier error signal ε

and

sideband error signal ε

S(1,2)

. These are used to apply

corrections to the cavity PZTs and to a Voltage Con-

trolled Oscillator (VCO) generating the sidebands at

m· FSR.

Table 1: Injection-locked laser source features.

Wavelength 633 nm

Output power 10 nW

Allan deviation 10

−11

(at100s)

The carrier feedback loop locks the two cavities

PHOTOPTICS2015-DoctoralConsortium

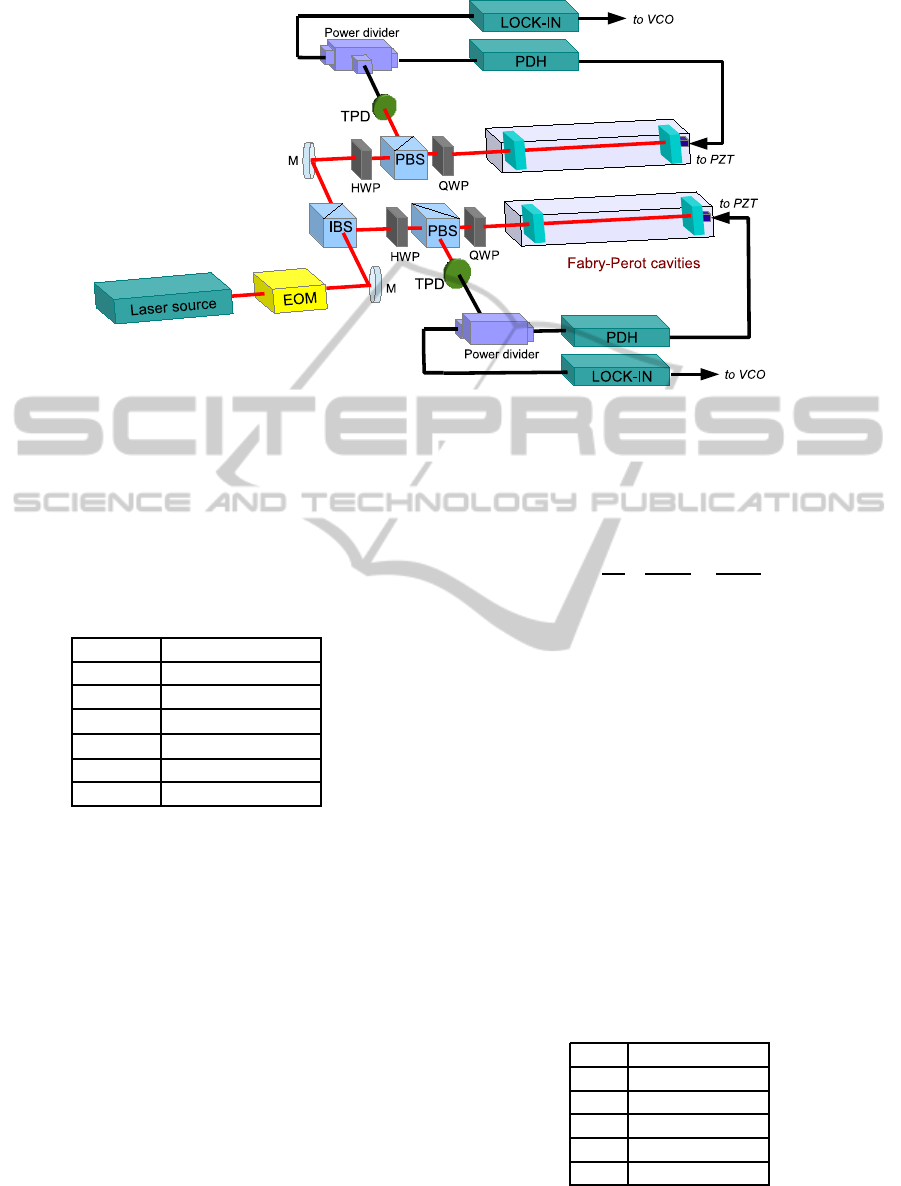
Figure 10: Conceptual scheme of experimental apparatus. A more detailed scheme is reported in (Belﬁ J. et al., 2014). The

laser source block represents the injection locking setup. The PDH stage represents the module for locking with Pound-Drever-

Hall scheme, while the Lock-in one includes the circuit for the digital lock-in ampliﬁer phase-detection. EOM: Electro-Optic

Modulator. IBS: Intensity Beam Splitter. PBS: Polarizing Beam Splitter. HWP: Half Wave Plate. QWP: Quarter Wave Plate.

TPD: Transimpedance Photodiode. PZT: Piezoelectric Transducer. VCO: Voltage Controlled Oscillator.

Table 2: Optical parameters of cavities test-bench. They

have an identical mechanical setup, but the reﬂectivity of

the input mirror are different leading to different Full Width

at Half Maximum (FWHM) width of the resonator reso-

nances. Left: Cavity 1. Right: Cavity 2.

L 1.32 m

R 4 m

FSR 113 MHz

0.988; 0.997

out

0.999; 0.999

Finesse 480; 1570

FWHM 225 kHz; 54 kHz

resonance frequencies to the same laser carrier fre-

quency. The sideband feedback loop processes the

error signals ε

S(1,2)

by a LabView program running

on a PC and locks by turns the VCO frequency alter-

natively to m · FSR

or m · FSR

until the two inter-

ference orders n

1,2

= ω

/2π · FSR

1,2

are determined

with the required precision. A microwave frequency

counter connected to the auxiliary output of the VCO

acquires with a gate-time of 1 s the FSR

1,2

data.

6.3 Results

A gaussian ﬁt of the FSR data provides an esti-

mate for the central frequency of the two cavities

, f

and the standard deviation about these

, σ

. The frequency data are then used to cal-

culate the distribution of the mode number difference:

2π



FSR

−

FSR



, (4)

whose standard deviation σn

is ﬁnally used to es-

timate the length difference δD = (λ/2) · σn

. The

mode difference n

should be an integer univocally

determined; in this case the error on the length differ-

ence between the two diagonals is ultimately limited

by the uncertainty on the laser wavelength.

Since the optical frequency is stabilized at the

level of 1 part in 10

, the uncertainty on the mode

number difference σn

is given by the uncertainty

∆FSR

/FSR

, i = 1,2. In table 1 we report the results

of the analysis of the frequency data acquired modu-

lating at ω

= 6 × FSR. The FSR mean values are

determined to few parts in 10

, and the correspond-

ing mode number difference with an uncertainty of

1.6. This is ﬁnally used to estimate the length differ-

ence δD = (λ/2) · σn

, that with our set-up is 500 nm

(Belﬁ J. et al., 2014). Note that the FSR uncertainty

Table 3: Experimental results of cavities test bench.

681211560 Hz

230 Hz

680000798 Hz

140 Hz

7427

σn

1.6

decreases as cavity ﬁnesse increases. We have studied

also the dependence of σ

on harmonic m, and our ex-

NovelProgressintheHigh-sensitivityHeterolithicRingLaserGyroscopeTechnology

perimental results suggest an improvementin FSR de-

termination as m

−1

. These considerations are of rele-

vance in view of the implementation of the technique

in GP2.

7 EXPECTED OUTCOME

The primary expected outcome of the future work is

to make the most of the developed expertise to run

GP2 with the target geometrical stability of 1 part in

. We intend to implement the length stabilization

of the GP2 diagonal cavities by using the experimen-

tal setup described in section 6 with some adaptions.

First, in the test bench experiment the laser source

was modulated by a single EOM and a single VCO

was alternatively locked to the resonances of the two

cavities. To ensures a long-term run of the RL with

the diagonal stabilization constraint, we plan to divide

the laser beam with a bifurcated ﬁber and to modulate

the resulting two beams by using two identical EOMs.

Moreover, we have to take into account that an un-

avoidable uncertainty on the measurement of the in-

stantaneous length of a cavity is the acoustic. Since

in a RL the mirror position actuators have a limited

bandwidth (< 100 Hz) due to mirror holders inertia,

a possible solution is to lock the laser to the diagonal

cavities using an acousto-optic modulator (AOM) that

compensatesthis noise by shifting the laser frequency.

The GP2 diagonal resonators have a FSR of

66 MHz and a ﬁnesse of ≃ 3000. In this case, operat-

ing with a modulation frequency ω

= 1 GHz (EOM

bandwidth cut-off) we expect to be able to determine

the mode number difference univocally, i.e. with an

uncertainty less than 1.

Furthermore, the full startup of GINGERino pro-

totype will test the adequacy of LNGS location in

terms of rotational noise and environmental stabil-

ity. From its operation we foresee an improvement

of SNR respect to G-Pisa of about a factor 7, be-

ing the increase in SNR more than quadratic with the

ring side size, as explained in section 2. In this case,

geodetic and microseismic signals will be detected,

and we plan to compare the acquired data with those

provided by G ring laser and by different rotational

seismology observatories.

If we achieve these results, the potentialities of an

heterolitic large RL for the detection of tiny effects, as

Lense-Thirring effect, will be experimentally demon-

strated, and a ﬁrst important step toward GINGER

will be taken.

REFERENCES

Beghi A. et al. (2012). Compensation of the laser parameter

ﬂuctuations in large ring-laser gyros: a Kalman ﬁlter

approach. Appl. Opt. 51, 7518-7528.

Belﬁ J. et al. (2012). A 1.82 m2 ring laser gyroscope for

nano-rotational motion sensing. Appl. Phys. B 106,

271-281.

Belﬁ J. et al. (2014). Interferometric length metrology for

the dimensional control of ultra-stable ring laser gyro-

scopes. Class. Quant. Grav. 31, 225003.

Bosi F. et al. (2011). Measuring Gravito-Magnetic Effects

by Multi Ring-Laser Gyroscope. Phys. Rev. D 84,

1220022.

Ciufolini I. (1986). Measurement of the Lense-Thirring

drag effect on LAGEOS and another high altitude

laser ranging satellite. Phys. Rev. Lett. 56, 278-281.

Cuccato D. et al. (2014). Controlling the non-linear in-

tracavity dynamics of large He-Ne laser gyroscopes.

Metrologia, 51, 97-107.

Di Virgilio A. et al. (2014). A ring lasers array for funda-

mental physics. Compt. rend. Phys. 15, 866-874.

Everitt C.W.F. et al. (2011). Gravity Probe B: Final Re-

sults of a Space Experiment to test General Relativity.

Phys. Rev. Lett. 106, 221101.

Lense J. and Thirring H. (1918). Uber den Einﬂuss der

Eigenrotation der Zentralkorper auf die Bewegung der

Planeten und Monde nach der Einsteinschen Gravita-

tions theorie. Phys. Z. 19, 156-163.

Sagnac G. (1913). L’ether lumineux demontre par l’effet du

vent relatif d’ether dans un interferometre en rotation

uniforme. Comp. Rend. 157, 708.

Santagata R. et al. (2014). Optimization of the geo-

metrical stability in square ring laser gyroscopes.

arXiv:1411.2585.

Schreiber K.U. et al. (2009). The Large Ring Laser G for

Continuous Earth Rotation Monitoring. Journal of

Pure and Applied Geophysics, 166 1485.

Schreiber K.U. et al. (2011). How to Detect the Chandler

and the Annual Wobble of the Earthwith a Large Ring

Laser Gyroscope. Phys. Rev. Lett. 107, 173904.

Stedman G.E. (1997). Ring-laser tests of fundamental

physics and geophysics. Rep. Prog. Phys. 60, 615-

688.

PHOTOPTICS2015-DoctoralConsortium