
CSP Formulation for Scheduling Independent Jobs in Cloud Computing
M’hamed Mataoui
1
, Faouzi Sebbak
2
, Kada Beghdad Bey
2
and Farid Benhammadi
2
1
IS & DB Laboratory, Ecole Militaire Polytechnique, Algiers, Algeria
2
AI Laboratory, Ecole Militaire Polytechnique, Algiers, Algeria
Keywords:
Scheduling Algorithms, Cloud Computing, Job Scheduling, Resource Allocation, CSP Formulation.
Abstract:
This paper investigates the use of Constraint Satisfaction Problem formulation to schedule independent jobs in
heterogeneous cloud environment. Our formulation provides abasis for computing an optimal Makespan using
job and machine reordering heuristics based on Min-min algorithm result. The combination of these heuristics
with the weighted constraints allows improving the efficiency of the tree search algorithm to schedule jobs with
considerable space search reduction. The proposed CSP model is validated through simulation experiments
against clusters of 10 virtual machines. The results demonstrate that our model is able to efficiently allocate
resources for jobs with significant performance gains between 18% - 40% compared to the Min-Min heuristic
results to optimize the Makespan.
1 INTRODUCTION
Nowadays heterogeneous cloud computing is expand-
ing its services to data-intensive computing on cloud
platforms because each job (application) of users runs
on a separate virtual machine. In these platforms,
the jobs are independent and different from one an-
other and it needs an optimal maximal completion
time (Makespan). Hence the Scheduling process in
cloud computing systems is useful for several dif-
ferent user needs. Static or dynamic heuristics are
proposed for cloud to find an optimal solution to the
scheduling. Static heuristics define a schedule at com-
piled time based on the knowledge of the processors
availability and tasks to be executed. Dynamic heuris-
tics, on the other hand, are applied when the tasks ar-
rival time is not beforehand known and therefore the
system needs to schedule tasks as they arrive (Bar-
bosa and Moreira, 2009). The scheduling strategy
defines the instants when the scheduling algorithm
is called to produce a schedule based on forecasting
resources performances and independent tasks to be
executed. The aim of task scheduler in cloud com-
puting environment is to determine a proper assign-
ment of resources to the tasks of jobs to complete
all the jobs received from clients. Large numbers
of jobs scheduling heuristics are available for maxi-
mizing profit via resources allocation in cloud com-
puting systems (Kuribayashi, 2011; Abirami and Ra-
manathan, 2012; Gouda et al., 2013; Irugurala and
Chatrapati, 2013).
The challenge that needs to be addressed is how
efficiently schedule jobs in cloud computing based on
the job completion time’s optimization to increase re-
source utilization. In this paper, we consider the prob-
lem of resource allocation in heterogeneous cloud
environment. The proposed solution in this work
is based on the computing power parameter for re-
sources allocation in cloud environment. Clients
in our case are jobs decomposed into various tasks
where each task should be assigned to one of the
resources, which is best suited for its execution to
maximize the profit. The proposed approach uses
constraint satisfaction problem formulation to sched-
ule independent jobs in heterogeneous cloud environ-
ment. Our formulation provides a basis for comput-
ing an optimal Makespan using job and machine re-
ordering heuristics based on Min-min algorithm re-
sult. The combination of these heuristics with the
weighted constraints allows improving the efficiency
of the tree search algorithm to schedule jobs with
considerable space search reduction. The proposed
CSP model is validated through simulation experi-
ments. Our evaluation shows that the proposed ap-
proach can improve efficiency and effectiveness of
heterogeneous cloud computing systems with signif-
icant performance gains between 18% - 40% com-
pared to the Min-Min heuristic results to optimize the
Makespan.
This paper is organized as follows. Related works
105
Mataoui M., Sebbak F., Beghdad Bey K. and Benhammadi F..
CSP Formulation for Scheduling Independent Jobs in Cloud Computing.
DOI: 10.5220/0005438801050112
In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 105-112
ISBN: 978-989-758-104-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

about resources allocation strategies in cloud comput-
ing environment are introduced in Section 2. Section
3 presents the makespan optimization problem defini-
tion. Section 4 describes the proposed solution in re-
source allocation in heterogeneous cloud computing
environments, assuming both task arrive simultane-
ously and machine available time updated. The simu-
lation results are presented in Section 5 and Section 6
concludes this paper.
2 RELATED WORK
There has been a large amount of work focusing
on static scheduling approaches on cloud computing
platforms and are currently prevalent in clouds. These
approaches use static heuristics which are suitable for
known prior time execution of jobs. Yuan et al. (Yuan
et al., 2011) propose an intelligent scheduler which
can handle heterogeneous resources. , and be able
to allocate resources according to user needs. The
proposed intelligent scheduler shows an improved
scheduling algorithm for making efficient resources
allocation in cloud. Zhang et al. (Xie et al., 2012) uses
the a dynamic constraint programming to solve the
problem of virtual cloud resource allocation model.
This approach takes into account both users’ QoS re-
quirements and the cost of virtual cloud resources.
The simulation results show that the proposed ap-
proach can efficiently allocate and manage the virtual
resources of the cloud platform, and are in agreements
with those of (Zhang et al., 2013). Goudarzi and Pe-
dram (Goudarzi and Pedram, 2011), address the Ser-
vice Level Agreements (SLA)-based resource alloca-
tion problem for cloud and a distributed solution for
this problem is proposed. The response time of the
request based on the different allocation of resources
for different servers and the cluster is modeled and
used in the profit optimization problem.
In (Santos et al., 2002), the authors propose a
mathematical formulation for the resource allocation
problem in clusters. The authors describe a method
to find the best resource assignment in a cluster in
the case that the application has certain resource re-
quirements. Experimental results proved that the pro-
posed method was able to realize best load balanc-
ing and reasonable resources utilization. In (Li et al.,
2010), an adaptive resource allocation algorithm for
the cloud system with preemptable tasks is consid-
ered. The proposed algorithms adjust the resource al-
location adaptively based on the updated of the actual
task executions. A. Kundu et al (Kundu et al., 2010)
proposed the memory utilization method in cloud
computing environment based on transparency. The
proposed mechanism enables users to access mem-
ories depending on the predefined criteria. The re-
source allocation is made based on the selection crite-
ria which will improve the efficiency of the cloud en-
vironment. The memory manager is responsible for
allocating memory resources to the clients. The au-
thors introduced a cloud service based memory uti-
lization which is an effective mechanism for allocat-
ing memories in cloud computing environment. A
scheduling algorithm named as Linear Scheduling for
Tasks and Resources (LSTR) is designed in (Abi-
rami and Ramanathan, 2012). This algorithm per-
forms tasks and resources scheduling respectively.
The combination of Nimbus and Cumulus services
are imported to a server node to establish the IaaS
cloud environment. The virtualization technique used
with the scheduling algorithm will yield higher re-
source utilization, and improvethe performance of the
cloud resources.
Chen et al. (Chen and Tseng, 2012) intro-
duced an Improved Load Balanced algorithm on the
groundof Min-Min algorithm to reduce the Makespan
and increase resource utilization. Another optimal
joint multiple resource allocation method based on
the above resource allocation model is presented in
(Kuribayashi, 2011). The Author develops a resource
allocation model for cloud computing environments,
assuming both processing ability and bandwidth are
allocated simultaneously to each service request and
rented out on an hourly basis. Gouda et al. (Gouda
et al., 2013) proposed a new approach that allocates
resource with minimum wastage and provides max-
imum profit. This approach used priority algorithm
which decides the allocation sequence for different
jobs requested among the different users after consid-
ering the priority based on some optimum threshold
decided by the cloud owner. An innovative admis-
sion control and scheduling algorithms for efficient
resource allocation to maximize profit by minimizing
cost and improving customer level is introduced in
(Irugurala and Chatrapati, 2013). The authors showed
that the algorithms work well in a number of scenar-
ios and give the maximum profit among all proposed
algorithms by varying all types of QoS parameters.
Silva et al. (Silva et al., 2008) presented a heuris-
tic for optimizing the number of machines that should
be allocated for processing an analytical task so that
maximum speedup can be achieved within a limited
budget. The traffic of web applications is dynamic
and random; hence predicting the optimal number
of machines for the completion of the client appli-
cations in real time and within budget is not a triv-
ial task. Gomathi and Karthikeyan (Krishnasamy and
Gomathi, 2013) proposed Hybrid Particle Swarm Op-
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
106

timization (HPSO) based scheduling heuristic to bal-
ance the load across the entire system while trying to
minimize the makespan as well as to utilize the re-
sources in an efficient way in cloud environment. In
addition, the results are in agreement with those of
(Guo et al., 2012).
In (Katyal and Mishra, 2014), authors have dis-
cussed a selective algorithm for resources alloca-
tion in cloud environment to end-users on-demand
basis. The proposed algorithm is based on min-
min and max-min conventional task scheduling algo-
rithms. The selective algorithm uses certain heuristics
to select between the two algorithms so that overall
makespan of tasks on the machines is minimized. In
(Han et al., 2013), the authors presented a QoS guided
task scheduling model based on Sufferage-Min-Min
heuristic algorithm. An efficiency improvement has
been obtained by dividing the tasks and resources into
two groups of high QoS level.
3 RESOURCES ALLOCATION
STRATEGY
To meet the increasing computational requirements
of scientist needs, cloud computing environments are
promising platforms which ensure the resources al-
location with high quality of service. Therefore the
essential challenge of cloud computing scheduler is
to provide an optimal scheduling of the jobs based on
Makespan optimization to allocate jobs on suitable re-
sources.
The scheduling problem of finding the optimal
Makespan is a known NP-complete problem. The
scheduling problem that we consider can be stated as
follows. Let J = { j
1
, j
2
, ··· , j
n
} denote the set of jobs
which are independent and let M = {m
1
, m
2
, ··· , m
n
}
be the set of machines in the cloud computing envi-
ronment. We assume that each machine can estimate
how much time is required to perform each job. In
(Minarolli and Freisleben, 2011), Expected Time to
Compute (ETC) is an m× n matrix, used to estimate
the expected execution time of the job J
j
on the ma-
chine m
i
. In ETC matrix, n is the number of jobs
and m is the number of machines. One column of
the ETC matrix contains the estimated execution time
for a given job on each machine. Similarly one row
of the ETC matrix contains the estimated execution
time of a given machine for each job. Hence, for a
given job J
j
and a given machine m
i
, ETC
ij
is the es-
timated execution time of job J
j
on machine m
i
. For
this problem, we assume take the hypothesis that the
computing capacity of each resource and the running
time of each job are known.
The Makespan is equal to maximum completion
time of all jobs and can be estimated using the fol-
lowing equation (Eq.1):
makespan = max
i∈{1,···,m}
{
∑
j∈J
m
i
ETC
ij
} (1)
where J
m
i
is the set of the jobs mapped on the machine
m
i
.
4 OUR STATIC SCHEDULING AS
CSP FORMULATION
In this study we start with a presentation to the prac-
tical part of our Constraint Satisfaction problem mod-
elling for independenttasks scheduling to improvethe
Min-Min algorithm result. Thereafter we show that
this problem can be described using this formalism
using the Min-Min developed job and machine order-
ing heuristics. These heuristics aim to minimize the
total completion time (Makespan).
4.1 SCSP Problem Formulation
The Constraint Satisfaction Problem model is widely
used to represent and solve various AI related prob-
lems such as Scheduling or Optimization. A SCSP
(Scheduling CSP) is defined by a set of jobs, a set
of allowed estimated execution time of machines
(the domain) is associated to each job and a Global
Completion Time constraint (GCT). Solving a SCSP
means finding an assignment for each job on one ma-
chine that satisfies a GCT constraint.
Based on the Min-min scheduling results, we
present a formal model for minimizing the completion
time obtained by this algorithm. Using this model, we
formulate the static scheduling problem for indepen-
dent job scheduling in heterogeneous environment as
a constraint satisfaction problem (CSP). Our formula-
tion provides a basis for computing an optimal com-
pletion time based on several CSP search strategies to
refine the Makespan obtained by Min-min algorithm.
The SCSP consists of:
• N jobs J
1
, J
2
, ··· , J
n
, and M machines
M
1
, M
2
, ··· , M
m
.
• D = {D
1
, ··· , D
n
} is a set of n domains where
each D
n
= {ETCn
1
, ETCn
2
, ··· , ETCn
m
} is asso-
ciated with J
n
.
• GCT
m
=
∑
j
ETC
jm
< (1− α) ×C
max
for all m ∈
{1, ··· ,M}. GCT is the global completion time
constraint on the machine m. The parameter α ∈
[0, 1[ represents the improvement of the C
max
ob-
tained by the Min-Min algorithm. The search
CSPFormulationforSchedulingIndependentJobsinCloudComputing
107

Table 1: An ETC matrix example.
Jobs Completion Time
Machines j
1
j
2
j
3
j
4
j
5
j
6
m
1
129 109 42 218 113 168 779
m
2
89 73 33 178 83 106 562
m
3
164 141 45 305 148 221 1024
Table 2: Execution results of Min-Min algorithm.
Jobs Total
Machines j
1
j
2
j
3
j
4
j
5
j
6
m
1
0 0 0 218 113 0 331
m
2
0 73 33 0 0 106 212
m
3
164 0 0 0 0 0 164
space can be reduced by applying this parameter
as mentioned in experimental section. If α = 0 we
use the C
max
of the Min-Min algorithm to avoid
the systematic search assignation which explores
systematically the whole search space. So using
this GCT constraint, we minimize the maximum
completion time for all machines. Note that the
C
max
value is modified in the search process ac-
cording to the obtained maximal completion time.
As example, consider a simple SCSP of 3 ma-
chines m
1
, m
2
and m
3
and 6 jobs J
1
, J
2
, ···, J
6
.
A scenario of ETC (durations) is given in Table 1.
First, Min-Min algorithm determines that the mini-
mum completion time for J
3
will be achieved on m
2
,
and makes this assignment. After the first assign-
ment, Min-Min algorithm continues to schedule the
jobs J
2
, J
5
, J
1
, J
6
and J
4
as well on m
2
, m
1
, m
3
, m
2
,
m
1
machines respectively. Consequently, this algo-
rithm finds that the maximum completion time is 331
seconds on m
1
as reported on Table 2. The schedul-
ing, like the following can be expressed as SCSP:
• (06) Jobs J
1
, J
2
, J
3
, J
4
, J
5
and J
6
as variables
• (06) Domains D
1
= {89, 129, 164}, D
2
=
{73, 109, 141}, ···, and D
6
= {106, 168, 221}.
• GCT < (1 − α) × 331
Most algorithms for solving CSP
s
search system-
atically through the possible assignments of values to
variables. These algorithms seek any solution or all
solutions of a CSP. Or they try to prove that no solu-
tion exists. In the present work, we have adapted the
Forward Checking (FC) algorithm to find all SCSP
solutions because the original algorithm aimed simply
at finding a feasible solution. So we use FC algorithm
with an incremental and modified maximal comple-
tion time process. However, the order in which jobs
are considered for allocation on machines (instantia-
tion) has a dramatic effect on the time taken to solve
our SCSP, relatively to the order in which each job’s
ETC
s
are considered. There are general principles
which are commonly used in selecting the jobs and
their ETC values on the machines ordering. The job
and machine ordering may be either a static or dy-
namic ordering according to the current state of the
search. In our approach, we use both job and ma-
chine ordering heuristics. The job ordering uses the
inverse job order obtained by the Min-Min algorithm.
The machine ordering heuristic is based on the global
completion time of each machine under hypothesis
that all jobs are affected to the same machine.
The SCSP formalism allows defining the space of
a combinatorial search as a tree. To cut branches in
the search tree based on our adapted FC algorithm,
we add job and machine ordering heuristics with the
incremental maximal completion time as follow:
• The job ordering heuristic uses the order J
4
≪
J
6
≪ J
1
≪ J
5
≪ J
2
≪ J
3
which is the inverse order
obtained by Min-Min algorithm. (see Fig.1)
• The value (machine) ordering heuristic uses the
completion time reported in Table 1. So we ob-
tained m
2
≪ m
1
≪ m
3
for J
4
. (see Fig.1)
• Modification of the maximal completion time
C
max
in the GCT constraint in the search tree pro-
cess.
Applying our search algorithm, more work per
node but, presumably, the extra effort will be com-
pensated by the reduction on the number of visited
nodes. Fig. 2 shows an example of search space re-
duction obtained by our FC algorithm. As can be seen
the use of the C
max
modification in the search pro-
cess offers more reduction of the visited nodes to skip
the instantiations with no possibleC
max
improvement.
For instance, the new obtained C
max
= 260 allows to
cut practically the whole branches in the rest of the
search tree. So for this example, our algorithm visited
only 117 nodes instead of 1093. For example, our
algorithm FC has detected that the partial assignment
with GCT
m
3
= 305 is inconsistent with the global con-
straint (GCT
m
3
> C
max
= 260), and the algorithm will
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
108
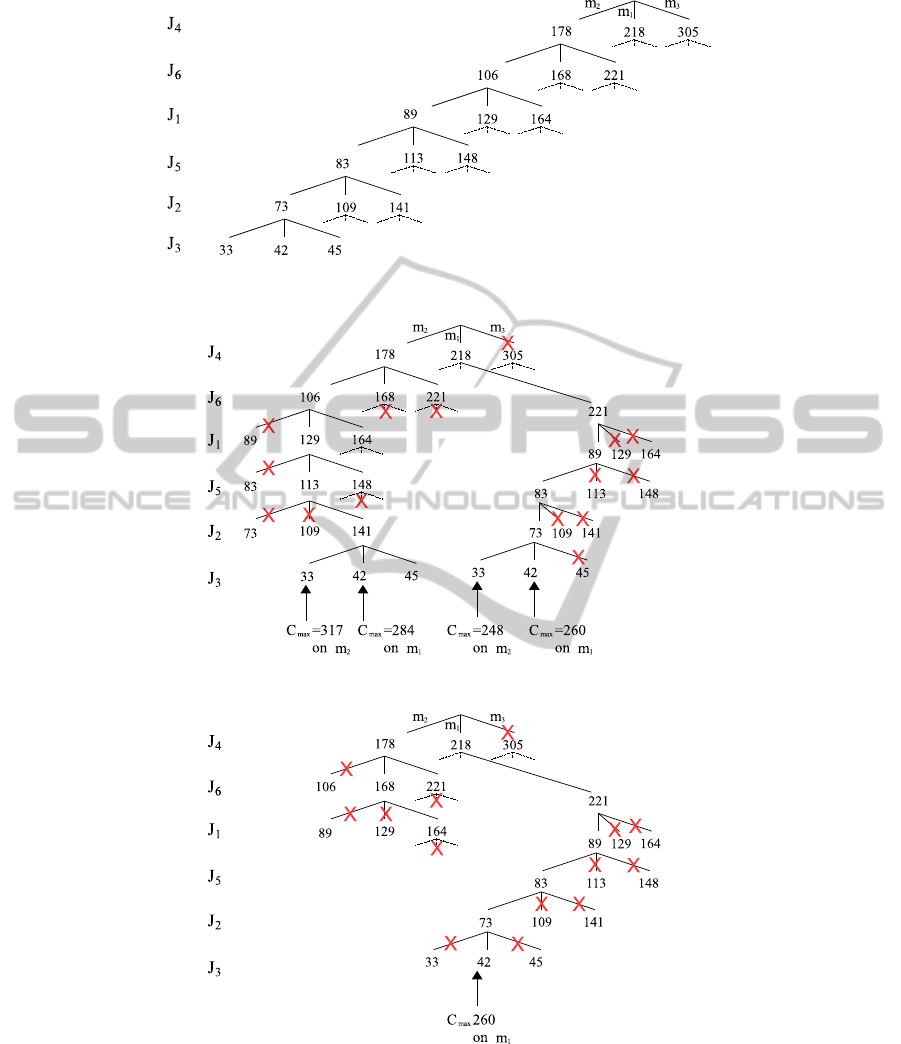
Figure 1: Search tree for the instance: 6 jobs and 3 machines (data from Table 1).
Figure 2: The search tree generated by our algorithm (with α = 0).
Figure 3: The search of tree generated by our algorithm (α = 0.2).
therefore backtrack immediately.
In order to make our search algorithm more effi-
cient, another preprocessing treatment can be added
that initially introduces the α parameter value for the
global completion time constraint. Hence, if we fix
α = 0.2, the space of a combinatorial search tree will
be reduced to only 66 visited nodes (Fig. 3).
5 SIMULATION RESULTS
Simulation evaluations of our formalism have been
CSPFormulationforSchedulingIndependentJobsinCloudComputing
109

Table 3: The resulting Makespans compared to Min-Min algorithms for 20 jobs ( α = 0).
C
max
Machines Time Total nodes Explored nodes Min-Min Proposed Makespan
Algorithm approach Improvement
2 2.00 2097151 33794 1074 973 9%
3 18.22 5.23E+09 434382 744 692 7%
4 58.73 1.47E+12 1718228 684 562 18%
5 80.73 1.19E+14 2747020 571 480 16%
performed. The SCSP resolution uses the inverse of
the obtained total order from the Min-Min algorithm
to optimize the maximum completion time. The de-
tails of the simulation setting are presented in the
following. In the literature, many heuristic-based
techniques have been proposed for independent job
scheduling in heterogeneous environment. The Min-
Min heuristic algorithm is the most efficient and used
one.
The proposed scheduling algorithm has been ap-
plied on simulated data, with 3 different types of ETC
matrices up to 3 heterogeneous machines, and up to
20 randomly generated heterogeneous jobs used in
(Ibarra and Kim, 1977). These different types of ETC
matrices are generated based on the following proper-
ties (Inomata et al., 2011):
• Job Heterogeneity – represents the amount of
variance among the jobs execution times for a
given machine. The job heterogeneity is defined
as: J(l): Job low and J(h): Job high.
• Machine Heterogeneity – represents the varia-
tion among the execution times for a given job
across all machines. The machine heterogeneity
is defined as: M(l): Host low and M(h): Host
high.
• Consistency – an ETC matrix is said to be con-
sistent (c) whenever a machine m executes all
jobs faster than another machine and the incon-
sistency (i) if the machine m may be faster than
another machine for some jobs and slower for
others. Partially-consistent (s) matrices are in-
consistent matrices that include a consistent sub-
matrix of a predefined size and are a combination
of consistent and inconsistent matrices (Minarolli
and Freisleben, 2011). Instances are labeled as
J(x)M(y)C(z) as follows: x indicates the job het-
erogeneity, y represents the machine heterogene-
ity and z shows the type of consistency.
Table 3 shows the results of the maximum com-
pletion times compared to the Min-Min algorithm for
scheduling 20 jobs (J(l)M(l)c(c)) based on theC
max
of
this algorithm (α = 0). The results are based on the
computation of job completion times across explored
nodes. As can be seen the search space can be reduced
by applying our heuristics where the total explored
nodes are widely lower compared to the total nodes of
the search space. Moreover, we obtain minimal com-
pletion times with the improvements 9%, 7%, 18%
and 16% for 2, 3, 4 and 5 machines respectively.
Table 4 reports the speed-ups for the same in-
stance with different values of α parameter. The ef-
ficiency observed is very good where the computa-
tion time’s decrease for all instances compared to the
above results from 1 to 5 machines. Also, it is ob-
served that for 6, 7, 8, 9 and 10 machine instances,
the execution times are considerably reduced. For ex-
ample, for the last instance (20 jobs on 10 machines)
the execution time 2748 seconds and is reduced to
3.79 seconds with α = 40.45. It is interesting to note
that the execution time is reduced by 99.85% for 10
machines and we note that the resulting Makespan of
Min-Min heuristic is constant starting from 571 be-
cause the Min-Min algorithm does not maximize the
use of resources. Overall, our results demonstrate that
where there is a consistency for low jobs, and having
large number of machines, we obtains an efficiency
superior to 95% with α >= 30%.
Finally, Table 5 presents the results of the com-
pletion times compared to Min-Min heuristic using
maximal values of the parameter α. It is interesting to
note that our heuristic outperforms the Min-Min al-
gorithm in all cases (job heterogeneity, machine het-
erogeneity and consistency) by obtaining the minimal
Makespan. Clearly, with the use of an adequate α
value, our algorithm performs well in all cases and
reduces the tree space search and the execution time
to schedule these instances from many hours to a few
minutes. A remark has to be made on the computation
time irregularity observed for the inconsistent cases
for high jobs and low machines. So a major drawback
of α values determined by our simulations is that the
execution times for the same scheduling problem can
be very different from an execution to another for dif-
ferent types of ETC matrix up to 10 heterogeneous
machines, and up to 20 randomly generated heteroge-
neous jobs of the same instance category. An impor-
tant point to notice is that our approach cannot consid-
ered as very effective for large scheduling problems.
To be efficient we remedied the poor performance of
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
110
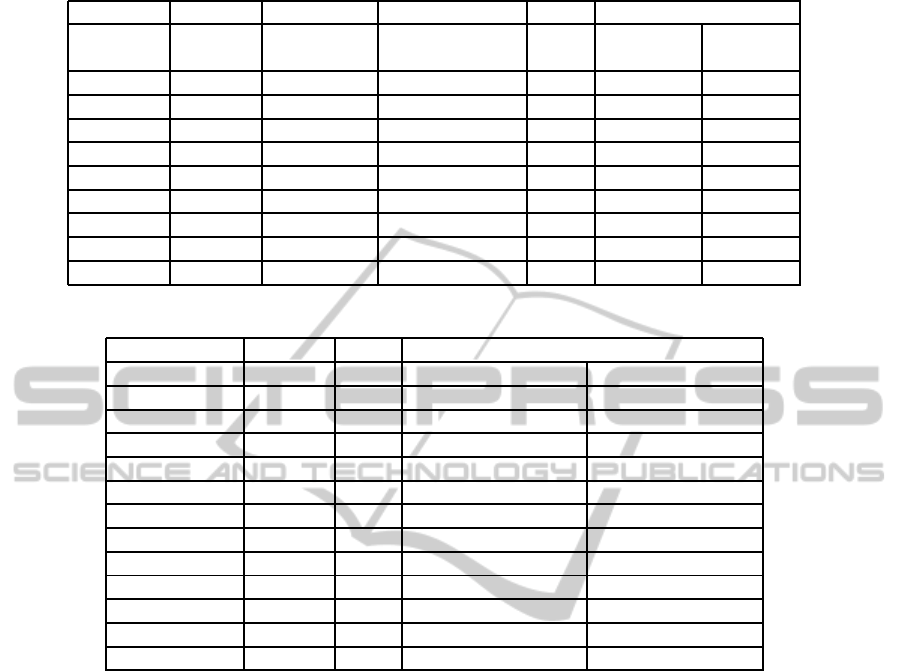
Table 4: The computation time reduction using different values of α parameter for 20 jobs.
C
max
Machines Time Total nodes Explored nodes α(%) Min-Min Proposed
(second) Algorithm approach
2 01.53 2097151 24990 10 1074 973
3 11.50 5.23E+09 266832 8 744 692
4 39.75 1.47E+12 1167804 18 684 562
5 49.73 1.19E+14 1683660 15 571 480
6 51.92 4.39E+15 1945518 23.5 571 434
7 89.72 9.31E+16 3690876 30.29 571 398
8 27.67 1.32E+18 1215384 33.97 571 377
9 10.09 1.37E+19 469152 38.01 571 353
10 03.79 1.11E+20 185420 40.45 571 340
Table 5: Makespan results for all heterogeneity and consistency cases.
C
max
Instance Time (s) α(%) Min-Min Algorithm Proposed approach
J(l)M(l)C(c) 03.79 40 571 340
J(l)M(h)C(c) 35.1 32 17271 11627
J(h)M(l)C(c) 1029.4 13 10640 8167
J(h)M(h)C(c) 36.3 37 685303 427236
J(l)M(l)C(i) 1290.4 10 442 397
J(l)M(h)C(i) 62.7 35 22947 14734
J(h)M(l)C(i) 1304.2 38 11495 7109
J(h)M(h)C(i) 1265.9 38 1068180 654517
J(l)M(l)C(s) 7.3 18 341 278
J(l)M(h)C(s) 6.37 16 20025 14734
J(h)M(l)C(s) 3.86 22 10286 6992
J(h)M(h)C(s) 8.82 22 969294 654517
our FC search algorithm by avoiding the recursivetree
traversal based on a parallel computation for global
completion time constraint. This parallelization uses
decomposition methods which distribute the search
tree at a particular depth level (Habbas et al., 2005).
6 CONCLUSION
In this work, a static scheduling problem in cloud en-
vironment based on a combination of a CSP formu-
lation and Min-Min job ordering heuristic. To im-
prove the Min-Min algorithm result a refinement pro-
cess uses the incremental maximal completion time
as weighted global constraint.
We used various ETC matrixes to investigate ef-
ficiency of our approach based on different degrees
of job and machine heterogeneities and consistencies.
The results indicated that our CSP solver provides to
reach an optimal completion time in very short time
for small instances compared to Min-Min algorithm.
However, our approach cannot considered as very ef-
fective for large instances.
For future work, there are still some aspects for
further investigation in our CSP job scheduling al-
gorithm especially for parallel CSP solver using de-
composition strategy of the search tree in cloud en-
vironment and prediction model for the job comple-
tion time distribution that is applicable to making de-
cisions in scheduling.
REFERENCES
Abirami, S. and Ramanathan, S. (2012). Linear scheduling
strategy for resource allocation in cloud environment.
International Journal on Cloud Computing: Services
and Architecture (IJCCSA), 2(1):9–17.
Barbosa, J. and Moreira, B. (2009). Dynamic job schedul-
ing on heterogeneous clusters. In Eighth International
Symposium on Parallel and Distributed Computing,
2009. ISPDC’09., pages 3–10. IEEE.
Chen, C.-Y. and Tseng, H.-Y. (2012). An exploration of
the optimization of excutive scheduling in the cloud
computing. In Advanced Information Networking and
CSPFormulationforSchedulingIndependentJobsinCloudComputing
111

Applications Workshops (WAINA), 2012 26th Interna-
tional Conference on, pages 1316–1319. IEEE.
Gouda, K., Radhika, T., and Akshatha, M. (2013). Prior-
ity based resource allocation model for cloud com-
puting. International Journal of Science, Engineering
and Technology Research (IJSETR), ISSN, 2(1):2278–
7798.
Goudarzi, H. and Pedram, M. (2011). Maximizing profit
in cloud computing system via resource allocation.
In 31st International Conference on Distributed Com-
puting Systems Workshops (ICDCSW), 2011, pages 1–
6. IEEE.
Guo, L., Zhao, S., Shen, S., and Jiang, C. (2012). Task
scheduling optimization in cloud computing based on
heuristic algorithm. Journal of Networks, 7(3):547–
553.
Habbas, Z., Krajecki, M., and Singer, D. (2005). Decompo-
sition techniques for parallel resolution of constraint
satisfaction problems in shared memory: a compar-
ative study. International Journal of Computational
Science and Engineering, 1(2):192–206.
Han, H., Deyui, Q., Zheng, W., and Bin, F. (2013). A
qos guided task scheduling model in cloud comput-
ing environment. In Fourth International Conference
on Emerging Intelligent Data and Web Technologies
(EIDWT), 2013, pages 72–76. IEEE.
Ibarra, O. H. and Kim, C. E. (1977). Heuristic algorithms
for scheduling independent tasks on nonidentical pro-
cessors. Journal of the ACM (JACM), 24(2):280–289.
Inomata, A., Morikawa, T., Ikebe, M., Okamoto, Y.,
Noguchi, S., Fujikawa, K., Sunahara, H., and Rah-
man, M. (2011). Proposal and evaluation of a dy-
namic resource allocation method based on the load
of vms on iaas. In 4th IFIP International Conference
on New Technologies, Mobility and Security (NTMS),
2011, pages 1–6. IEEE.
Irugurala, S. and Chatrapati, K. S. (2013). Various schedul-
ing algorithms for resource allocation in cloud com-
puting. The International Journal Of Engineering And
Science (IJES), 2(5):16–24.
Katyal, M. and Mishra, A. (2014). Application of selec-
tive algorithm for effective resource provisioning in
cloud computing environment. International Jour-
nal on Cloud Computing: Services and Architecture
(IJCCSA),, 4(1):1–10.
Krishnasamy, K. and Gomathi, B. (2013). Task scheduling
algorithm based on hybrid particle swarm optimiza-
tion in cloud computing environment. Journal of The-
oretical & Applied Information Technology, 55(1):33–
38.
Kundu, A., Banerjee, C., Guha, S. K., Mitra, A.,
Chakraborty, S., Pal, C., and Roy, R. (2010). Mem-
ory utilization in cloud computing using transparency.
In 5th International Conference on Computer Sci-
ences and Convergence Information Technology (IC-
CIT), 2010, pages 22–27. IEEE.
Kuribayashi, S.-i. (2011). Optimal joint multiple resource
allocation method for cloud computing environments.
International Journal of Research & Reviews in Com-
puter Science, 2(1).
Li, J., Qiu, M., Niu, J.-W., Chen, Y., and Ming, Z. (2010).
Adaptive resource allocation for preemptable jobs in
cloud systems. In 10th International Conference on
Intelligent Systems Design and Applications (ISDA),
2010, pages 31–36. IEEE.
Minarolli, D. and Freisleben, B. (2011). Utility-based re-
source allocation for virtual machines in cloud com-
puting. In IEEE Symposium on Computers and Com-
munications (ISCC), 2011, pages 410–417. IEEE.
Santos, C., Zhu, X., and Crowder, H. (2002). A mathemat-
ical optimization approach for resource allocation in
large scale data centers. Technical Report HPL-2002-
64, HP Labs, March 2002.
Silva, J. N., Veiga, L., and Ferreira, P. (2008). Heuristic for
resources allocation on utility computing infrastruc-
tures. In Proceedings of the 6th international work-
shop on Middleware for grid computing , MGC ’08,
pages 1–6. ACM.
Xie, W.-j., Tang, Z., Yang, L., and LI, R.-f. (2012). Re-
search on the virtual machine placement algorithm in
cloud computing based on stochastic programming.
Computer Engineering & Science, 5(5):95–100.
Yuan, J.-B., Lee, Y.-C., Wu, W., Young, H.-C., and Liang,
K.-H. (2011). Building an intelligent provisioning en-
gine for iaas cloud computing services. In 13th Asia-
Pacific Network Operations and Management Sympo-
sium (APNOMS), 2011, pages 1–6. IEEE.
Zhang, L., Zhuang, Y., and Zhu, W. (2013). Constraint
programming based virtual cloud resources allocation
model. International Journal of Hybrid Information
Technology, 6(6):333–344.
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
112
