
Model of a Neuron Network in Human Brains for Learning Assistance in
E-Learning Environments
Harald R. Kisch
1,2
and Claudia L. R. Motta
1
1
Instituto de Matem
´
atica, Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil
2
Department of Computer Sciences, University of Applied Sciences, Augsburg, Germany
Keywords:
E-Learning, E-Learning Environments, E-Learning Assistance, Cognition Simulation, Recommender Sys-
tems, Brain Neuron Model, UFO.
Abstract:
It is typically known that brain neurons are responsible for a significant part of our knowledge adaption process.
However, it is not yet fully understood how knowledge adaption works or what conscious intelligence is.
The aim of this research is to investigate how an E-learning environment can automatically identify learning
sequences to dynamically map them to specific learning types for suggesting course material, which makes
learning more individual, flexible and faster. For the purpose of this research, a neural ontology is created.
In this ontology, the characterization of one neural brain cell is meant to represent every neuron cell in our
brain as a specific part of a neural network to get closer to the answer how a simulation of brain functions
could be accomplished. This paper describes a neural network theory and how the conceptual model of a
neural brain cell could be interpreted through the concept of cognitive pattern match in relation to intelligence.
In conclusion, two fundamental hypotheses for effective knowledge adaption in E-learning environments are
derived.
1 INTRODUCTION
Modeling reality is a common approach in the com-
puter sciences. First of all, building models is not
only a means of reducing costs; it also helps in un-
derstanding what is of yet currently unknown about
the conception of ideas. Unified Foundation Ontolo-
gies (UFO) (Poli et al., 2010, pp.175), demonstrates
how ontologies can be used as technology in build-
ing models which approximate reality. Many differ-
ent brain models have been described by scientists in
various fields. This paper diverges significantly from
these other approaches, however, in that it offers an
ontological focus on the functionalities and properties
which a single neuron cell can have, and thus holds
for all the different specializations of all types of neu-
rons in the body. With this in mind, it is possible to
acquire each type of neuron cell from a generalized
neural axon entity, which all neurons possess. The
focus lies on the creation of a neural network for con-
scious cognition through computer simulation. Onto-
logical perspectives are used to create this brain neu-
ron model which results in conceptual models that are
closer to reality and applicable in E-Learning environ-
ments.
1.1 Related Work
The ontological simulation of neural brain func-
tions has already been carried out. An example
for bee swarm intelligence research can be found at
(Mosteghanemi and Drias, 2012), however it was not
focused on educational learning environments until
now. Simulation research began investigating the use
of ontology from the year 2000 onwards. In Pro-
ceedings of the 2004 Winter Simulation Conference
(Fishwick and Miller, 2004, pp. 259) the authors de-
scribe both the RUBE project by providing an XML-
based simulation modeling framework, as well as the
DeMo project by supporting an ontology-driven dis-
crete event simulation (Silver et al., 2009). Through
high-level simulation language, the DeMo project
supports the paradigms of ‘state-oriented’, ‘event-
oriented’, ‘activity-oriented’ and ‘process-oriented’
simulation, although it was not based on a foun-
dational ontology (Guizzardi and Wagner, 2010, p.
653).
1.2 Justification for the Research
The ontological model of a single neuron cell devel-
407
R. Kisch H. and L. R. Motta C..
Model of a Neuron Network in Human Brains for Learning Assistance in E-Learning Environments.
DOI: 10.5220/0005439904070415
In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 407-415
ISBN: 978-989-758-108-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
oped in this research describes what a neuron is able
to do, its relevant components from a computational
point of view, and the events which a neuron is able to
fire. These previous aspects were combined in order
to build a neuron cell database with entities and rela-
tions. Keeping this in mind, the developed ontology
in this research enables the creation of a neural net-
work of databases up from a single neuron cell node.
Therefore, each database in the neural network can
store information, within the entity of a single neu-
ron, all information concerning connections to other
neurons, the definition of products, and the opera-
tions which were made in the neuron’s connection
states. This event-based approach can be viewed as
the starting point for the simulation of the thinking
processes. With this conceptual model, we could be
able to map thinking and learning activities from their
base (buttom up) instead of tracking behaviors and
map them back to neural activities captured before-
hand (top-down). An example of the complexity of
the top-down approach in mapping and tracing the
neurons in the brain of a bee into a common 3D ref-
erence system is illustrated by (Rybak et al., 2010).
With tracking and mapping the expected thinking be-
havior in a E-learning environment, the learner can
be supported with learning-suggestions based on pre-
dicted learning-paths of other learners whose learning
maps has already been created.
2 MODEL EVOLUTION
This section will explain the evolution of the neu-
ron cell model. The figures are meant to clarify how
the syntax of UFO leads to models which become
increasingly closer to reality. Each model’s itera-
tion was built in three steps. First, the iteration was
checked for syntax using the Ontouml Lightweight
Editor OLED (https://code.google.com/p/ontouml-
lightweight-editor/), a case tool for ontological con-
cept modeling. Second, the semantic relations be-
tween the entities were widely discussed for ex-
tension with many neural and biological scientists.
Third, conceptual description was widely borrowed
from the Systematic Approach for Building Ontolo-
gies (SABiO) (Falbo, 2004), which explains precisely
how an ontology can be built step-by-step.
2.1 Identification of Ontological
Objectives
During the first iteration, the focus was on compe-
tence questions, such as: ”What is the central unit of
a single neuron?”. Based on different articles pub-
lished in the scientific journal Nature e.g. (Grubb and
Burrone, 2010), it was recognized that the axon of a
brain neuron cell is the best starting point by which
to begin modeling a neuron. Therefore, the axon en-
tity was used as the main entry point for developing
the model in each model iteration. The axon entity
should also be used as the starting point for the inter-
pretation of all models.
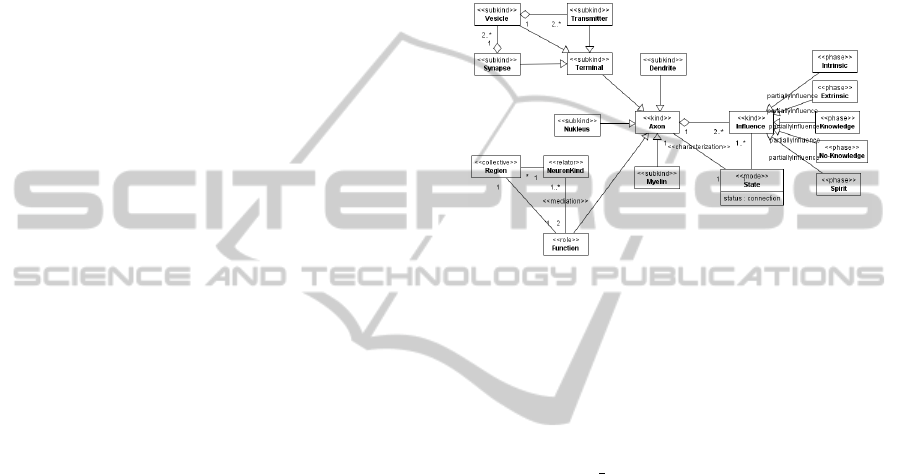
Figure 1: Neuron Node.
The model represented in figure 1 is the easiest to
understand. The axon entity is located at the center
and many other entities are specialized around it. A
dendrite is a subkind of the axon, because it comes
out of the axon and connects the axons, bodycells
and dendrites of other neurons (http://www.human-
memory.net/brain neurons.html, 01/07/2014). In the
top left corner of the model, the entities responsible
for information retrieval between the axons can be
seen. A terminal emerges from the axon on the op-
posite side of the dendrites. It has transmitters and
synapses. Synapses contain many vesicles which are
released by one or many transmitters. Properties and
abilities such as the transmission ability of synapses,
vesicles and transmitters are acquired from the ter-
minal. At the bottom left, specialized functions that
take place in specific types of neurons in particular
brain regions can be seen. A function refers to the
functional role which a neuron can have. The neu-
ron is represented by its axon entity and so the func-
tional role inherits all its abilities. A region is de-
fined as a collection of particular neurons which are
related to a specific function by mediation. There-
fore, functions operate on the specific types of neu-
rons in a region. On the right side of the model, many
of the possible influences on the connection state of
the axon can be seen. Axons can have three different
states (connected, semi-connected and unconnected)
(Sporns, 2011, p. 128). The given state of an axon
is characterized through the many conditional influ-
ences which are part of other axon states. The myelin
CSEDU2015-7thInternationalConferenceonComputerSupportedEducation
408

entity is an axon subkind which controls the velocity
of the signals between neurons (Sanders, 1946). Fol-
lowing sections will refine this conceptual model by
elaborating on many more aspects such as the storage
function of the nucleus.
2.2 Capturing Ontology along Entities
and Their Relations
The second iteration focused on the force-feedback
ability of neuron cells. According to the Hebb-Rule
(Hebb, 1949), the ”fired together - wired together”
principal, one of the most important facts about neu-
ron cells is that they influence one another. Hebb
(1949) discovered that every neuron receives a feed-
back response after it has fired. Accordingly, for feed-
back about an actual axon state to be given, all of
the neurons involved must be wired together. The
axon state in this conception is considered to be of
high importance in reconnecting neurons in the same
constellation as they were before firing. Therefore,
axon connection states for any specific moment need
to be saved somewhere. As of yet, it still remains
unknown to science where exactly information such
as axon states is saved within the neuron. In a gen-
eral manner, it appears that storage takes place in the
nucleus of the neuron. The ”lastThought” entity is re-
sponsible for mediating the knowledge which is pro-
cessed in one or many regions. The ”lastThought” en-
tity is also responsible for the transformation of axon
states according to the next conscious product from
one thought to the next.
2.3 Knowledge Processing - Pattern
Match
The entity rolemixin ”lastThought” can be special-
ized as additional information, the production of new
knowledge, or the declination of previous cognitive
definitions. These three entities represent the con-
cept of the specific influences by which the axon
states can be modified. Created knowledge mediates a
neurotropic influence on the frequency which in turn
creates the collective ”Motif” entities (cf.) (Sporns,
2011). These operations take place to create new
knowledge. The mixin ”Neurotropic” consists of en-
tities which are not relevant for the conceptual model
illustrated here and therefore requires no further ex-
planation. These specialized entities were excluded
from the model in the last iteration for complexity rea-
sons. Based on the neuron’s feedback process, three
mayor abilities were discovered in the following con-
ceptual model iteration, as illustrated in figure 3:
• Collection. On the upper left area of the model,
collection is refined by a material derivation
where chemical information is retrieved from the
vesicle entities and transfered to the synapses.
The collection itself is understood as the be-
ginning of the thinking process where relevant
knowledge fragments are collected from memory.
• Association. On the left side, the model illus-
trates how the collected knowledge fragments
are chemically retrieved from the soma entity,
and are then electrically combined in a frequency
which allows the axon state of neurons to create
a collective association between themselves.
This association, called collective ”Motif”, has a
specific function and operates on specific neuron
types which have specialized themselves in visual
movement calculation for example.
• Definition. A motif is created by connections
between neurons. These connections are estab-
lished over the axon states of associated neurons.
The connected neurons operate on information.
Each operation generates knowledge which can
be either stored or transformed further. The def-
inition of further transformation is mediated by
the rolemixin ”lastThought” entity and can be
specialized into three further role entities. The
transformation which takes place through the role
”Transformation”, however, leads to a new collec-
tion by which the circle is closed.
2.4 Motif Refinement
The next important iteration (figure 4) takes a closer
look on part-whole relations. Part-whole relations are
especially important for the motifs because each mo-
tif is controlled by a higher instance collective, called
collective ”Controller”. The exact manner in which
this controlling occurs is not well-known (Nan-Jie Xu
et al., 2011), but fortunately, this does not make a dif-
ference for the conceptual model. What is important
for a computational model is the relationship between
thought and states of connection. In this model, we
go further by describing the relationship between the
controller and the motif as being transitive and exten-
sional in nature. This is done because each thought
is seen as a whole in its own right which can be re-
fined into more specific thoughts, and each of these
thoughts can in turn be extended with further infor-
mation. A thought is non-shareable in that it has a
particular relation to a context. A conclusion based on
a thought is always reached according to the environ-
ment in which the thought was processed. The same
ModelofaNeuronNetworkinHumanBrainsforLearningAssistanceinE-LearningEnvironments
409
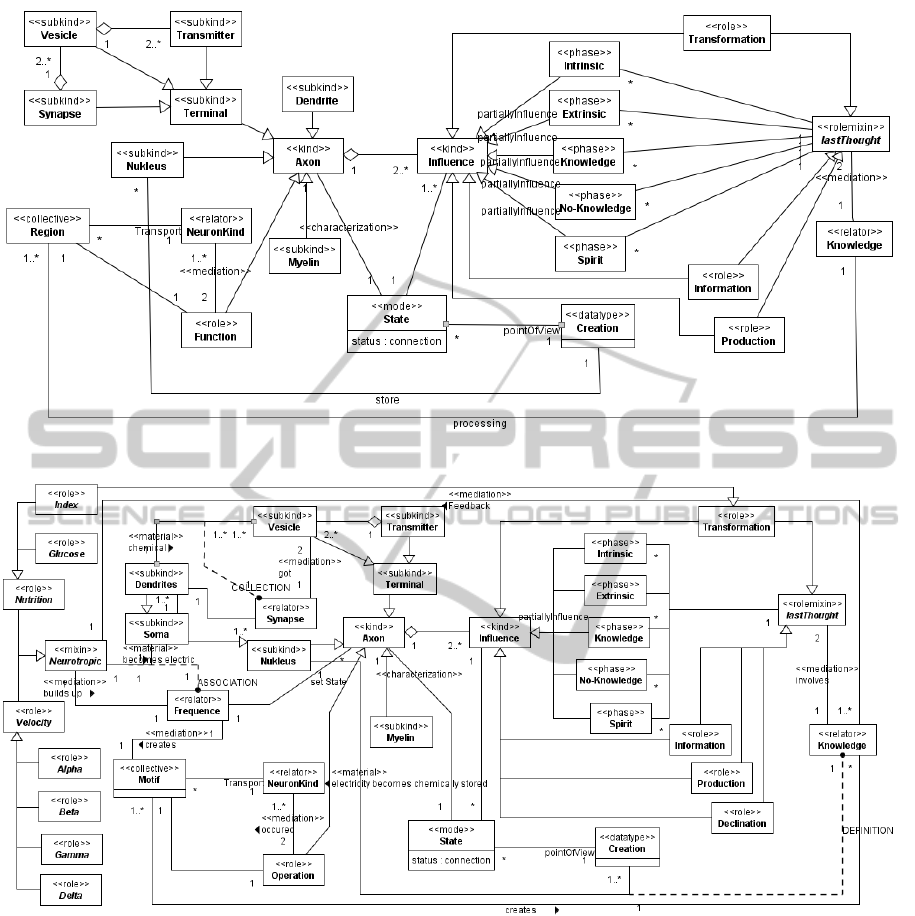
Figure 2: Force-Feedback.
Figure 3: Knowledge Processing.
thought, while correct in the environment in which the
thought was processed, could be wrong in a different
environment. The environment is always essential for
a conclusion, otherwise the conclusion (cognitive def-
inition) would cease to be reliable. All thought relies
on the axon state of the wired neurons. Therefore we
can say that all thoughts are homeomerous to each
other.
Furthermore, a motif is understood as a functionally
separate part of the whole brain, while a neuron cell
is seen as a functionally seperate but substantially re-
lated individual of the whole sub-motif. The neuron
does not lose its function if the whole (sub-motif)
ceases to exist. Instead, the specialized abilities of
neurons are used by another motif, which is most
probably the motif which surrounded the sub-motif,
thus automatically becoming related to a new whole.
All the functions of one neuron cell are applied to a
brain impact-function, and thus a brain operation will
only have the expected (better procedural promised)
impact on the motif to which the neuron cell applies.
2.5 Dynamification using UFO-B
In general UFO-B is an UFO-A increment related to
perdurants (Guizzardi, 2005, p. 382). UFO-B is very
CSEDU2015-7thInternationalConferenceonComputerSupportedEducation
410
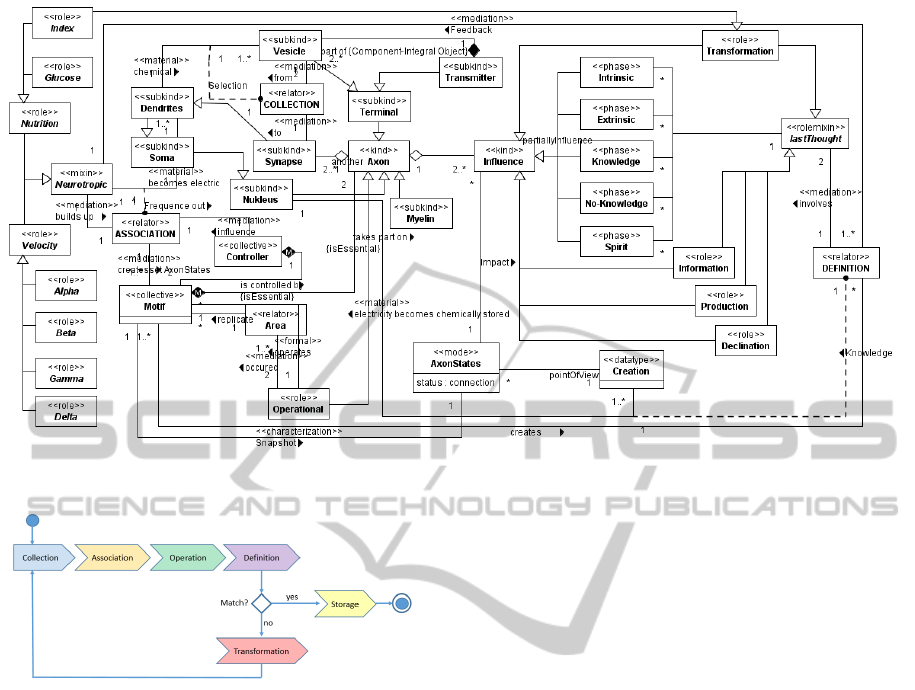
Figure 4: Wholes and parts.
Figure 5: Event execution process.
useful for modeling events which have dynamical as-
pects and which occur in quantifiable time-space or
in a defined situation. A situation is mostly construed
as being changed by an event to fit a specific prepo-
sition. In figure 6, it can be seen that each event is
marked with a specific color. There are six different
colors which stand for six different events. Each event
in turn has four related entities which define the situ-
ation. One of the entities is marked with three differ-
ent colors which means that this entity is shared by
three different events. This also indicates that these
three different events are fired in an uninterrupted se-
quence. Figure 5 illustrates the execution of the col-
ored events for a single though process.
Figure 7, derived from (Guizzardi and Wagner, 2010,
p. 657), generally illustrates the higher level ontol-
ogy concept of each event. The whole event exe-
cution process, which can be seen in figure 5, is an
instance of the entity ‘Complex Event’. The ‘UFO-
A::Object’ entity is defined through its near represen-
tation of the complete neuron cell model as shown in
figure 6. Each ‘Object Participation Event’ will be de-
fined in the following subsections. The ‘Agent’ entity,
which every illustration represents, generalizes all the
participation entities that a single event has (the pre-
situation and post-situation being excluded).
Collection - Event (blue). The soma situation (sub-
kind ”Soma-Situation”) satisfies the influence prepo-
sition (subkind ”Infl-Preposition”). The influence
preposition can either be changed by a previous
definition-event and/or a transformation-event. In
the case of a transformation-event, the role ”Index-
Collector” inherits most of the information which
should be collected by the role ”Transformation”.
In case of a definition, the index inherits most of
the information from the mixin ”Neurotropic”. In
both cases, these information entities (Transforma-
tion, Neurotropic) are used to create an information
index for the role ”Index-Controller” which collects
the indexed axon states stored in the nucleus of all
neuron cells involved. When all of the chemically
stored axon states have been collected, the index con-
troller allows the mode ”Collected” condition, simpli-
fied in figure 8, which then enables the association-
event.
Association - Event (orange). The ”Neurotropic-
Situation” created by collection from the previous
event serves to satisfy the last thought preposi-
tion (”lT-Preposition”) which is the rolemixin ”last-
Thought” specialization. The role ”Associator” ac-
quires all the information needed from the previous
collective ”Motif”, and then formally uses the infor-
mation from the collective ”Controller” to prepare the
ModelofaNeuronNetworkinHumanBrainsforLearningAssistanceinE-LearningEnvironments
411
Figure 6: Parallel processing events.
Figure 7: Event ontology.
Figure 8: Collection Agent.
axon states of the needed motifs. In order to cre-
ate new motifs and to establish novel connections be-
tween them, newly collected chemical material is de-
rived from the subkind ”Soma” (body cell) and con-
verted to an electric impulse which travels at a specific
frequency and sets the new axon states. When all the
Figure 9: Association Agent.
motifs needed have been prepared, the accociation is
then complete and the role ”Accociator” enables the
condition of the mode ”Associated” (simplified in fig-
ure 9) which in turn enables the operation-event.
Operation - Event (green). The present ”Axon-
Situation” created by the role ”Associator” serves to
satisfy a previous snapshot mode ”AxonStates”, as
prepositioned by the role ”Operationial” beforehead.
The role ”Operational” entity, which is created as a
specialization from the ”Axon-Situation”, mediates
one or more ”Operation-Area” relations by replicat-
ing considerable information into the associated col-
lective ”Motif”. With this information, the role ”Op-
erational” formally operates on different motifs, en-
abling the condition of mode ”Operated”, and it is at
CSEDU2015-7thInternationalConferenceonComputerSupportedEducation
412
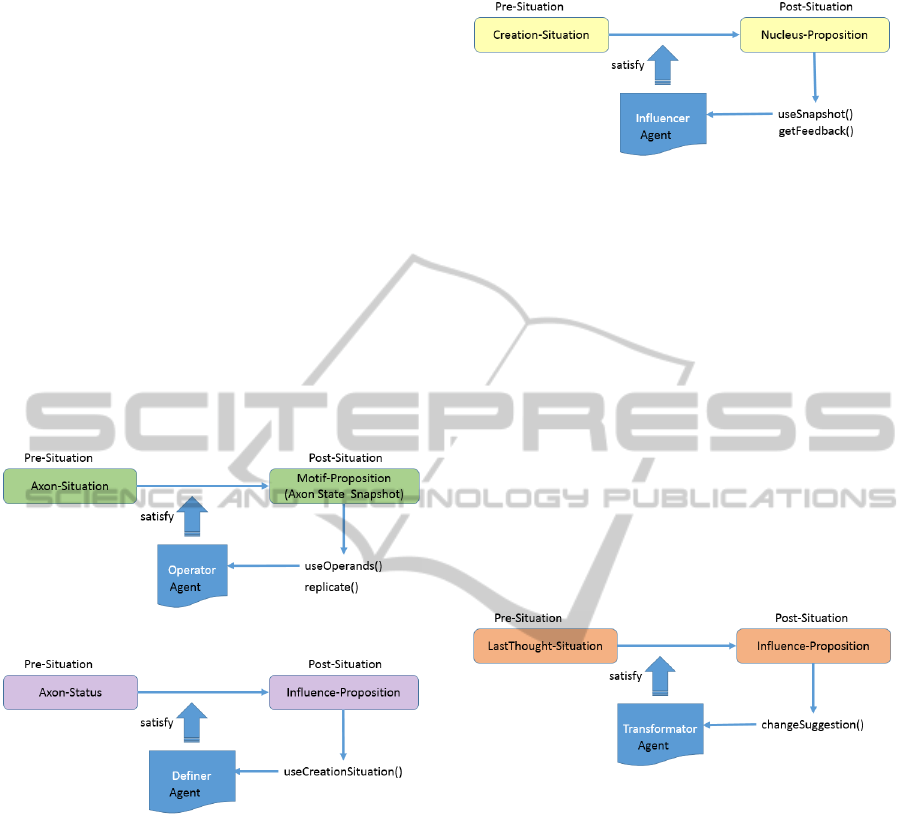
this moment that all the operations needed are com-
pleted. It is at this time that the mode ”Operated”,
simplified in figure 10, enables the definition event.
Definition - Event (purple). The mode ”Axon-
Status”, which was operated upon earlier, is the sit-
uation which satisfies the subkind ”Infl-Preposition”
(influence preposition) of the previous thought. The
role ”Definer”, specialized from the current collec-
tive ”Motif”, formally uses the specialized ”Axon-
States” to define whether or not something should
be stored (role ”Production”) or transformed again
(role ”Declination” and/or role ”Information”). The
roles ”Production”, ”Declination” and ”Information”
are specializations of rolemixin ”lastThought”. They
are used as specification components for the defini-
tion event. In case of the definition that current axon
states should be stored, the mode ”Defined”, simpli-
fied in figure 11, enables the storage event.
Figure 10: Operation Agent.
Figure 11: Definition Agent.
Storage - Event (yellow). The datatype ”Creation-
Situation” acquires the datatype ”Creation” and
presents a situation which needs to satisfy the
subkind ”Nucleus-Preposition”. The ”Nucleus-
Preposition” is a specialization of the subkind
”Nukleus” which indicates whether storage is per-
formed or not. At this time, the point of view (the
data type extracted from the axon states) is stored by
the role ”Influencer”. This mediated role is acquired
from the kind ”Influence” and enables the mode
”stored” condition. It is the mode ”stored” condition,
simplified in figure 12, which in turn enables the
transformation event.
Figure 12: Storage Agent.
Transformation - Event (red). The relator
”Transform” builds the subkind ”Infl-Preposition”
(influence preposition) through mediation which
satisfies the rolemixin ”lT-Situation” (last thought
situation). The ”lT-Situation” is a rolemixin ”last-
Thought” specialization and represents the actual
state of the last thought. The role ”Transformation” is
also a rolemixin ”lastThought” specialization which
enables the mode ”Transformed” condition. The
mode ”Transformed” condition represents the time
at which all definitions are performed, and the role
”Index-Collector” (the collection of transformation
information) is mediated by the relator ”Definition”.
Then the mode ”Transformed”, simplified in figure
13, enables the collection event where a new iteration
of the thinking process begins.
Figure 13: Transformation Agent.
2.6 Formalization of the Captured
Ontologies
In the following subsections, the entities and their se-
mantical objectives will be formalized.
Quantity of Thoughts. If a thought is a container
categorized by its environment, then there are a quan-
tity (q) of particular thoughts (A, B, C) about how a
neural network in the brain could look (quantity A,
short qA). There exists a quantity of thoughts in qA
concerning one specific motif M of neuron cells (qB),
and within these thoughts about a particular thought,
there are a quantity of thoughts about the manner in
which the components of a neuron cell (qC) could op-
erate (O) recursively together in their environment E
of neural axon states (S) within a collective (C). It
could be said for example:
ModelofaNeuronNetworkinHumanBrainsforLearningAssistanceinE-LearningEnvironments
413

∀C(M) → O(E
S
) = M(qA) ⊂ (M(qB) ∪M(qC)) (1)
From this perspective of thoughts concerning a neural
network in the human brain, each neuron has the exact
same functions, attributes and components for reach-
ing mathematical and mereonymic operability. Addi-
tionally, the life-span (essential and separable cogni-
tive products of a thought as the result of operatios
on neural axon states of created motifs) of the rela-
tionship between first-thought, next-thought (thought
and SubQuantity of thoughts as individual wholes),
and a single motif (neural axon states which turn a
substantial neuron into a particular thought) all corre-
spond to Guizzardi’s description of inseparable parts.
Axon-states and thoughts are essential and seperable;
they are highly dependent on one another other due
to the fact that life-span of individual sub-quantities
of thoughts are wholes in their own right, and thus do
not loose their existence when they loose their whole.
A quantity of thoughts must be as infinitely diversible
(homeomerous) as the neural axon-states (motif) for
the creation of sub-quantities of further though (think-
ing fractals). This is exactly what could be key in the
production of the infinitely diverse intuitive cognitive
products of creativity, which could in turn be the most
important factor in measuring consciousness.
Transitivity Problem. All compositions need to be
transitive as to assure that the operations of the whole
have the correct impact on each of its parts. Transi-
tivity holds true between component functional com-
plexes when the parts share a similar essential part-
hood relationship which also applies to the whole
(cf.) (Guizzardi, 2005, pp. 187). If the relation-
ship between the parts is not the same as that be-
tween the wholes, the applicability of operations to
the whole needs to be validated in order to assure that
the operations between the parts of the whole have
the correct impact. A formalized solution to isolate
the scope of transitivity of functional part-whole re-
lations can be found in (Guizzardi, 2009). However,
all neurons must have the same kind of relationship
within their sub-collections, and all sub-collections
should also share the same type of relation as the
neuron cells share with one another. The ideal situa-
tion would be that of a subQuantityOf and subCollec-
tionOf relationships (corresponding to node-weight
which equals the quantity of connections in neural
networks) (Sporns, 2011, p. 8).
3 CONCLUSION
This paper describes the development of an ontology
with the aim to answer many questions for conscious-
ness in an automated way. This ontology has identi-
fied the most important factor in consciousness as be-
ing the creation of infinitely diversible cognitive prod-
ucts of creativity based on cognitive pattern-matching
between particular collections of thoughts. Further-
more, three mayor neural brain cell abilities (de-
scribed in section 6) were discovered as being of high
importance for further researches in the field of cog-
nitive product generation. Transitivity was introduced
to be essential in the correct application of function
impacts within particular thoughts. In conclusion to
the created theory, two hypothesis can be derived:
Hypothesis 1. With the simulation of pattern
matches between mapped thought collectives a learn-
ing environment is able to construct cognition au-
tomatically by observing learning behavior during
course accomplishment.
Hypothesis 2. By observing learning behavior, a
learning environment is able to adapt, create and
differ learning fractals individually to support the
learner with suggestions in order to understand
materials better and faster.
Further research is needed to sequentially map
and process patterns for cognition detection in
E-learning environments. This knowledge answer the
question how cognition relates to consciousness on a
fundamental ontological basis.
REFERENCES
Falbo, R. A. (2004). Experiences in using a method for
building domain ontologies. Proc. of International
Workshop on Ontology In Action, Banff, Alberta,
Canada.
Fishwick, P. and Miller, J. (Jan. 2004). Winter SImulation
Conference, Proceedings of The 2004. IEEE, Piscat-
away.
Grubb, M. S. and Burrone, J. (2010). Activity-dependent
relocation of the axon initial segment fine-tunes neu-
ronal excitability. 465(7301), pages 1070–1074. Na-
ture.
Guizzardi and Wagner (op. 2010). Towards an ontological
foundation of discrete event simulation. In Proceed-
ings of the 2010 Winter Simulation Conference, eds. B.
Johansson, S. Jain, J. Montoya-Torres, J. Hugan, and
E. Ycesan, 652-664. Piscataway, New Jersey: Institute
of Electrical and Electronics Engineers, Inc. IEEE,
Piscataway.
Guizzardi, G. (2005). Ontological foundations for struc-
tural conceptual models, volume no. 015 of Telemat-
ica Instituut fundamental research series. Centre for
CSEDU2015-7thInternationalConferenceonComputerSupportedEducation
414

Telematics and Information Technology and Telemat-
ica Instituut, Enschede and Enschede.
Guizzardi, G. (2009). The problem of transitivity of part-
whole relations in conceptual modeling revisited. Fed-
eral University of Espirito Santo (UFES).
Hebb, D. O. (1949). The organization of behavior: A neu-
ropsychological theory. A Wiley book in clinical psy-
chology. Wiley [u.a.], New York u.a.
Mosteghanemi, H. and Drias, H. (2012). Bees swarm opti-
mization for real time ontology based information re-
trieval. In Web Intelligence and Intelligent Agent Tech-
nology (WI-IAT), 2012 IEEE/WIC/ACM International
Conferences on, volume 3, pages 154–158.
Nan-Jie Xu, S. S. et al. (2011). A dual shaping mechanism
for postsynaptic ephrin-b3 as a receptor that sculpts
dendrites and synapses. Nature Neuroscience.
Poli, R., Healy, M., and Kameas, A. (2010],
c
2010). The-
ory and applications of ontology. Springer, Dordrecht
and London and New York.
Rybak, J. et al. (2010). The Digital Bee Brain: Integrating
and Managing Neurons in a Common 3D Reference
System. Frontiers Research Foundation.
Sanders, W. (1946). Conduction velocity and myelin thick-
ness in regenerating nerve fibres. Department of Phys-
iology and Zoology and Comparative Anatomy.
Silver et al. (op. 2009). Supporting Interoperability Us-
ing the Discrete-Event Modeling Ontology (DeMo).
In Proceedings of the 2009 Winter Simulation Con-
ference, eds. M. D. Rosetti, R. R. Hill, B. Johansson,
A. Dunkin and R. G. Ingalls, 1399-1410. Piscataway,
New Jersey: Institute of Electrical and Electronics En-
gineers, Inc. IEEE, Piscataway.
Sporns, O. (2011). Networks of the brain. MIT Press, Cam-
bridge and Mass.
ModelofaNeuronNetworkinHumanBrainsforLearningAssistanceinE-LearningEnvironments
415
