
Silicon Kerr Effect Electro-optic Switch
Deepak V. Simili and Michael Cada
Department of Electrical and Computer Engineering, Dalhousie University, 1459 Oxford Street, Halifax, Canada
1 RESEARCH PROBLEM
The research problem that we are investigating deals
with designing and testing an ultrafast silicon
electro-optic switch for integrated-optic applications
that employs the Kerr effect. Silicon photonics for
optical interconnects offers a possibility to provide a
low cost, mass manufacturable solution for data
communication applications such as data centers,
high performance computing, mobile devices (cell
phones or tablets) to server interconnects, and
desktop computers (Reed G.T et. al., 2010). A
switch or a modulator is one of the building blocks
in an integrated-optic data transmitter connected to a
fiber-optic channel. In order to better utilize the THz
bandwidth capabilities of fiber optic channels and to
meet increasing bandwidth demands of future
communication networks, it is highly desired to
develop optical switches with modulation
bandwidths in the range of 100 GHz and higher.
In this paper we address the problem of
optimizing the ring resonator structure for the Kerr
effect switch considered in previous work (Cada,
2011, Simili et. al., 2013) in order to achieve
bandwidth performance in the range of 100 GHz or
higher. An analysis of the key performance
indicators of the switch is also presented.
2 OUTLINE OF OBJECTIVES
The desired characteristics for the electro-optic
switch are as follows:
• Modulation bandwidth in the range of 100 GHz
or higher.
• Low switching voltage on the order of a few
volts.
• A Silicon-based device as silicon is widely
used in the electronics industry and is
compatible with the CMOS fabrication
technique.
• Operating at the telecommunication wavelength
of 1.55 micrometers.
• Compact size with a device footprint in the
range of 10
or lower.
• Average switching energy lower than 10 pJ/bit
with a target of 10 fJ/bit.
• Overcome coupling losses due to polarization
dependence.
The above mentioned objectives are based on a
review of silicon-based electro-optic modulators
present in the literature, which are discussed in the
next section.
3 STATE OF THE ART
The most commonly used electro-optic effect to
achieve modulation in silicon devices has been the
plasma dispersion effect. This is because electric
field effects based on electro-refraction such as the
Pockels effect do not exist in silicon while the Kerr
effect induces a small refractive index change
∆ = 10
, for an applied electric field of 10
V/m
(Soref et. al., 1987) at 1.55 micrometer wavelength
to be useful for integrated-optic applications.
Electric field effects in silicon, based on electro-
absorption such as the Franz-Keldysh effect also
induce a low refractive index change (∆ = 1.5×
10
,=10
/) at 1.55 micrometers (Soref et.
al., 1987) to be useful. For device applications a ∆
of the order of 10
or greater is desired also to
avoid a danger of an electrical breakdown of the
medium. For intrinsic silicon at room temperature,
the dielectric breakdown field is of the order of 3 ×
10
V/m (Kim, 2010).
The plasma dispersion effect is based on a
change in the free carrier concentration of silicon to
induce a change in the absorption spectrum and
therefore a change in the refractive index. The
change in the refractive index of silicon was
computed through experimentally obtained
absorption spectrum in (Soref et. al., 1987). A
refractive index change of the order of 10
was
obtained for free carrier (electrons) concentration
change of 10
/
at 1.55 micrometer
wavelength. The different mechanisms used to
achieve the plasma dispersion effect in the medium
74
V. Simili D. and Cada M..
Silicon Kerr Effect Electro-optic Switch.
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

through which light is propagating are carrier
accumulation, carrier injection and carrier depletion.
In the carrier injection technique, electrons and
holes are injected into an intrinsic waveguide region.
The structure used is a p-i-n junction diode. The
injection of electrons and holes into the waveguide
region is controlled by changing the voltage applied
to the highly doped p and n regions of the structure.
The charge transport mechanism is based on carrier
diffusion. The switch off time for the device would
depend on the electron-hole recombination lifetime
for silicon which is 100 ns for n-type silicon at
temperature of 300 K (Saleh et. al., 2007). An
example of a top performing modulator employing
this technique uses a micro ring resonator structure
to achieve speeds of 12.5 Gbps with a high
extinction ratio greater than 9 dB at a modulation
voltage of approximately 4 V (Xu et. al., 2007).
In the carrier accumulation technique, mobile
carriers are diffused into the intrinsic waveguide
region. The concentration of mobile carriers in the
waveguide region is controlled by adjusting the
potential of the doped regions. The intrinsic
waveguide region is split into two halves separated
by an insulator region so the mobile carriers begin to
accumulate on both sides of the insulator to form a
capacitor structure. This type of structure would
avoid the slow recombination process of the diffused
mobile carriers. The first implementation of this
technique reported a bandwidth in the neighborhood
of 1-2 GHz with an extinction ratio greater than 16
dB and a device phase efficiency (
) of
approximately 8 V.cm (Liu et. al., 2004).
Subsequent optimizations to this technique reported
10 GHz bandwidth with 3.8 dB extinction ratio and
a better
of 3.3 V.cm (Liao et. al., 2005).
In the carrier depletion technique, the silicon
waveguide is a lightly doped p-n junction. The width
of this depletion layer is controlled by reverse
biasing the structure and therefore carrier
concentration experienced by the propagating light
in the waveguide is changed. This technique
reported the highest bandwidth of 30 GHz, with an
extinction ratio of 1.1 dB and a
of 4 V.cm (Liao
et. al., 2007). The carrier transport mechanism in
this case is carrier drift which is faster than the
carrier diffusion used in previous techniques.
The main drawback of the plasma dispersion effect
is that it relies on carrier transport phenomena of
carrier drift or carrier diffusion for which the
response times are at best in the range of
picoseconds. Therefore this effect is not suitable for
the design of electro-optic modulators with desired
modulation speeds over 100 GHz.
4 METHODOLOGY
The general methodology in the design and
development of a silicon-based electro-optic switch
is selecting a silicon-based material with useful
material properties for use with an ultrafast electro-
optic effect. This is followed by using the material
and the effect in a suitable structure to obtain a
measure of performance parameters for the switch.
The material chosen as an optical medium for the
silicon-based electro-optic switch is silicon
nanocrystals in silica ( − /
). It has a third-
order nonlinear susceptibility (
()
) of 2×
10
/
and 3.8×10
/
at a
wavelength of 1.55 micrometers for LPCVD and
PECVD deposition methods, respectively (Cada,
2008). These values are at least one order of
magnitude greater than that of bulk silicon and silica
glass (Cada, 2008). − /
fabricated through
the PECVD technique has a better material nonlinear
figure of merit (
(
)
) of 0.649 compared to that
of silicon’s 0.495 at the wavelength of 1.55
micrometers (Cada, 2008). This makes −
/
more suitable than silicon to be used with
nonlinear effects such as the Kerr effect. −
/
can be mass manufactured through LPCVD
and PECVD techniques, so the device would be
CMOS compatible.
The physical effect chosen for the design
analysis of a silicon-based electro-optic switch is the
Kerr effect, which exists in all materials. It is a pure
electric field-effect that depends on
()
of the
material, where the refractive index of the medium
changes with a square of an applied electric field. It
is inherently ultrafast as it depends on displacement
of the electron cloud due to an applied electric field
with response times on the order of 10
s for non-
resonant conditions (Boyd, 2008). The induced
refractive index change due to the Kerr effect (Δn)
for a fully applied electric field is (Cada et. al.,
2008)
Δn =
3
()
2
(1)
For an applied electric field E of 1V/100nm, a useful
Δn of 1.76 × 10
is obtained for − /
,
which can be considered as the dominant factor for
the induced refractive index change in the medium.
The induced refractive index change due to the
optical Kerr effect (Δ =
) is at least 2 orders of
magnitude smaller than the electric Kerr effect for
low optical powers (1mW or less) with a waveguide
SiliconKerrEffectElectro-opticSwitch
75
cross section of 0.1
. It has been experimentally
observed that the ultrafast optical Kerr effect which
is also based on
()
, dominates slow free carrier
effects such as the two photon absorption at telecom
wavelengths of 1550 nm in silicon nanocrystals
(Martinez et. al., 2010). Therefore one can consider
the pure electric field Kerr effect as the dominant
effect compared to optical Kerr effect and slow free
carrier effects in determining the refractive index
changes of the medium.
5 EXPECTED OUTCOME
In this section we describe the optimization
performed on a ring resonator structure for a Kerr
switch and the analysis of key performance
parameters of the Kerr switch. A ring resonator’s
transmission output is highly sensitive to the
resonant wavelength of the ring structure. It is
compact and has a size in the range of micrometers,
which is suitable for integrated optic applications.
The criteria for choosing the ring resonator
structure are that it should have a low cavity photon
lifetime (around 1 ps or lower) to ensure a high
maximum modulation bandwidth (100 GHz or
higher) and there should be experimental data
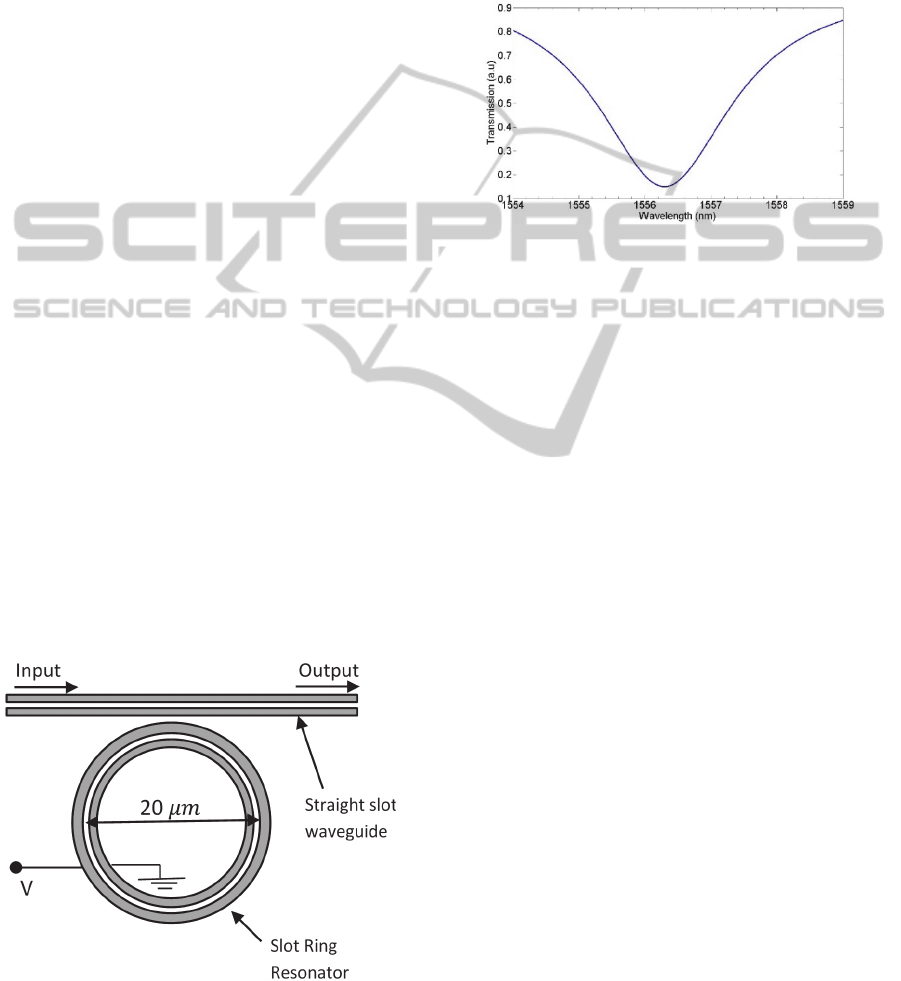
available on a ring resonator structure. One such ring
resonator structure is the slot waveguide ring
resonator described in (Xu et. al., 2004). This ring
resonator has a diameter of 20 micrometers and the
separation distance between the slot regions of the
straight slot waveguide and the slot ring resonator is
1 micrometer. The Q-factor of the ring resonator is
around 1000 at a wavelength of 1.55 micrometers in
the experimentally obtained transmission spectrum
Figure 1: Schematic of the ring resonator structure for the
Kerr switch.
(Xu et. al., 2004). This yields the structure’s cavity
photon lifetime of 0.822 ps. The layout of the
considered ring resonator structure for the Kerr
switch is shown in Figure 1.
We simulated the transmission resonance dip in
the 1.55 micrometer regime of the measured
transmission spectrum in the considered ring
resonator.
Figure 2: Transmission spectrum for the coupled slot ring
resonator.
Figure 2 shows the simulated transmission spectrum
for the slot waveguide ring resonator in the 1550 nm
regime with air as the slot medium. Here it is was
assumed that the effective index of the medium does
not vary significantly over the wavelength range
considered and can be taken constant. The design
parameters for the simulated ring resonator were a Q
factor of 1000 around a wavelength of 1550 nm and
a free spectral range of 15 nm.
Next we simulated the same slot waveguide ring
resonator structure with a diameter of 20
micrometers but with a − /
material as the
slot medium instead of air. Due to a change in the
slot medium, the effective index of the mode in the
slot waveguide would be changed and therefore the
transmission resonant wavelength as well. We
consider an optimized version of the slot waveguide
so that the optical mode is strongly confined in the
slot region. The optimized slot waveguide in a
vertical configuration was obtained from (Sanchis et.
al., 2007). The slot waveguide has two silicon slabs
(
=3.48) and a narrow slot region filled with a
low index medium which is − /
(
=
1.78), and silica (
=1.46) material as cladding.
The optimized slot waveguide dimensions are: the
slab thickness (h) of 400 nm, the silicon waveguide
width (w) of 220 nm, and the slot width of 100 nm
(Sanchis et. al., 2007). The calculated effective
index in the slot region for the waveguide
dimensions considered is 2.06 (Sanchis et. al.,
2007). The polarization which gives the strongest
field confinement in the slot region is the x-
PHOTOPTICS2015-DoctoralConsortium
76
polarized mode or TE polarization for the considered
vertical configuration of the slot waveguide (i.e. a
waveguide TM mode).
The transmission spectra for the slot waveguide
ring resonator with − /
as the slot medium
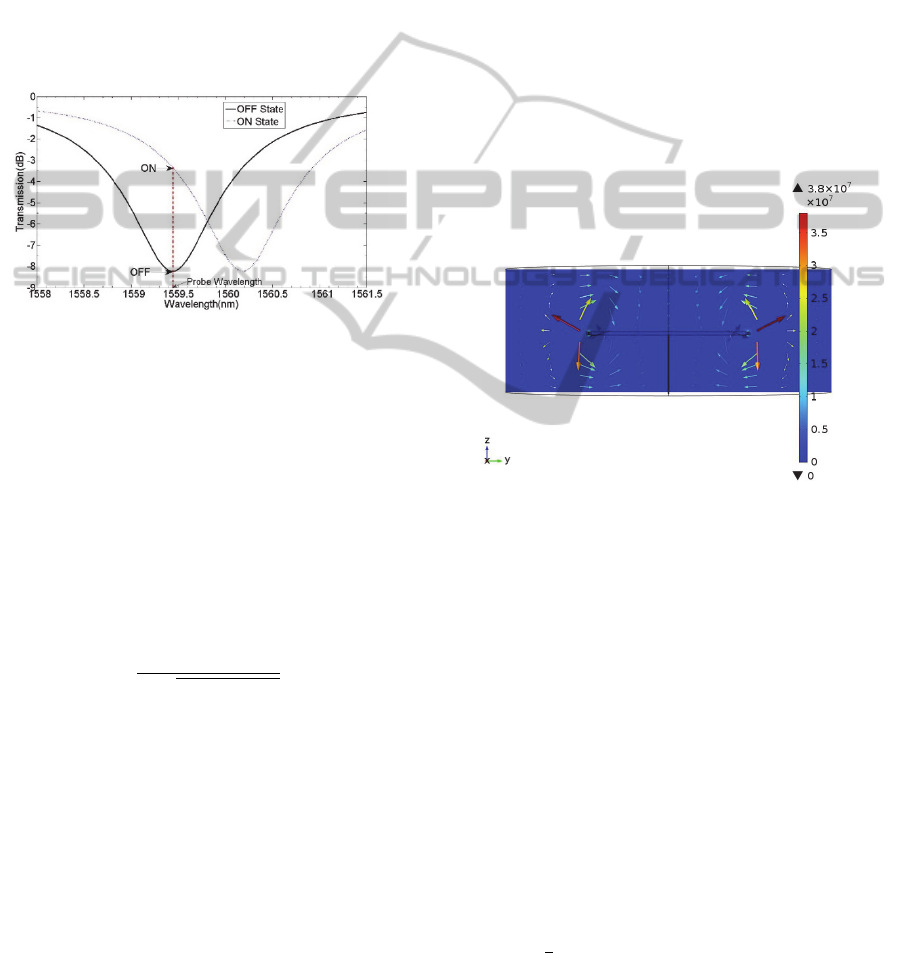
is shown in figure 3. The resonant wavelength
obtained is 1.55945 micrometers. To achieve a
useful extinction ratio of around 5 dB between off
and on states for the switch, an effective index
change (∆
) of 9.8 × 10
is required. For slot
waveguides this means a material index change in
the slot region of the order of 2.33 × 10
(Barrios,
2004).
Figure 3: Kerr switch transmission spectra.
5.1 Key Performance Indicator
Analysis
Here we analyse the performance of the Kerr switch
in terms of key parameters for the device.
(1) Maximum modulation frequency (
): The
3dB modulation bandwidth for the Kerr switch
is determined by the RC time constant (
)
and the cavity photon lifetime (
) for the
resonator structure. It can be calculated via the
equation (Dong et. al., 2009)
=
1
2
(2)
Estimation of the capacitance of the ring
waveguide structure is an electrostatic problem.
Using a parallel plate capacitor formula would
not account for the electrostatic energy in the
fringe electric field for the structure. So we
used Finite Element Methods in COMSOL as it
determines the total electrostatic energy around
the volume of the ring waveguide structure. The
capacitance from the simulation was
determined to be 16.32 fF. As expected this
value is greater than the parallel plate
capacitance approximation of 13.796 fF. This is
due to the fringe electric field for the structure
which is shown by arrows in figure 4. The
relative permittivity for − /
was
taken as 6.2 considering a filling factor of 29 %
silicon (Cada, 2011) in the simulation. For a
contact resistance of 50 ohms and considering
highly doped silicon slabs (carrier
concentration on the order of 10
/
) to
ensure good ohmic contact between metal and
silicon, the RC time constant is 0.816 ps. With
a
of 0.822 ps for the ring resonator, the 3
dB modulation bandwidth for the Kerr switch is
calculated to be 137.409 GHz. Such high
modulation speeds have not been achieved in
silicon-based electro-optic modulators. Due to
the presence of high free carrier concentrations
in the silicon slabs, one would have to consider
associated optical losses.
Figure 4: Electric field strength (V/m) around the ring
resonator capacitor structure (YZ plane). The arrow
volume indicates the electric field and the peak electric
field strength is 3.718× 10
V/m inside the slot region.
(2) Energy/bit (fJ/bit): The modulation power
consumption for a ring resonator structure of
the Kerr switch would be due to charging the
ring resonator which acts as a capacitor in
addition to parasitic and stray capacitances.
The average switching energy-per-bit (E/bit)
for a lumped modulator acting as a capacitor is
(Li et. al., 2013),
/ = ×
(3)
Here C is the device capacitance; V is the
applied voltage and is the activity factor
associated with the modulation encoding.
Considering a pseudorandom bit sequence with
=
, as the probability of a “0” to “1”
transition is ¼ (Li et. al., 2013), the average
switching energy-per-bit for the Kerr switch is
SiliconKerrEffectElectro-opticSwitch
77

56.413 fJ/bit.
(3) Switching Voltage (
): The switching
voltage is determined by the required electric
field to achieve the resonance shift for a useful
extinction ratio. For a 5-dB extinction ratio, the
material index change required in the slot
region is 2.33 × 10
. This index change can
be achieved in − /
through the Kerr
effect for an applied voltage of 3.718 V for a
100 nm slot width.
(4) Resonance shift efficiency (pm/V): One of the
figures of merit for the ring resonator structure
is the resonance shift efficiency which is the
ratio of the resonant wavelength shift achieved
to the applied input voltage. As discussed
previously, a resonance shift of 0.75 nm is
required for a 5-dB extinction ratio, and this
requires a voltage of 3.718 V across the slot
region. So the resonance shift efficiency in our
case is 201.72 pm/V.
(5) Device footprint (
): As the diameter of our
chosen ring resonator structures is 20
micrometers, a substrate of 25 microns by 25
microns would be reasonable to fabricate the
device. This would give the device a footprint
of the order of 6.25 × 10
.
(6) Working Spectrum (nm): This refers to the
required operating wavelength precision for the
structure. For the ring resonator considered, it
is of the order of 0.1 nm. This places high
demands on the fabrication accuracy for the
ring resonator structure due to its narrow
wavelength operating range. One would also
have to consider thermal effects for the
structure, which is a topic that requires further
research.
The ring resonator structure considered for the Kerr
switch gives excellent theoretical results for the
modulation speed and resonance efficiency but with
trade-offs on the extinction ratio and the Q- factor
of the resonator.
6 STAGE OF RESEARCH
The different stages for the design, development,
and characterization of the silicon-based Kerr switch
are as follows:
1. Understanding of physical concepts involved
and preliminary evaluation of performance
parameters for the switch.
2. Computer aided design modeling of switch
structures and simulation of the switch using
numerical methods such as FDTD.
3. After useful results are obtained in stage 2,
fabrication of the optimum structure for the
Kerr switch.
4. Electrical characterization of the Kerr switch
and comparison of experimental results and
simulated results.
ACKNOWLEDGEMENTS
I would like to thank my supervisor Dr. Michael
Cada for the expert guidance and the opportunity to
work on this project. I also thank the ASPIRE
(Advanced Science in Photonics and Innovative
Research in Engineering) NSERC (Natural Science
and Engineering Research Council) Program of
Canada for providing financial support.
REFERENCES
Reed, G. T, Mashanovich, G., Gardes, F. Y., Thomson, D.
J, 2010, Silicon Optical Modulators, vol. 4, Nature
Photonics.
Cada, M., 2011, Electro-Optic functionalities with Kerr
Optical media, International Symposium on
Microwave and Optical Technology, 445- 453.
Simili, D. V., Cada, M., 2013, Nanophotonic Silicon
Electro-Optic Switch, Photonics North Conference,
Proc. Of SPIE vol. 8915 89151S1-8.
Soref, R. A., Bennett, B. R., 1987, Electrooptical
effects in Silicon, vol. QE-23, no. 1, pp. 123-129,
IEEE Journal of Quantum Electronics.
Kim, D.M., 2010, Introductory Quantum Mechanics for
Semiconductor Nanotechnology, Wiley-VCH, Great
Britain.
Saleh, B. E. A, Teich, M. C, 2007, Fundamentals of
Photonics, John Wiley & sons, Inc., Singapore.
Xu, Q., Manipatruni, S., Scmidt, B., Shakya, J., Lipson,
M., 2007, 12.5 Gbit/s carrier-injection-based silicon
micro-ring silicon modulators, vol. 15, No. 2, pp. 430-
436, Optics Express.
Liu, A., Jones, R., Liao, L., Samara-Rubio, D., Rubin, D.,
Cohen, O., Nicolaescu, R., Paniccia, M., 2004, A high-
speed silicon optical modulator based on a metal-
oxide-semiconductor capacitor, vol. 427, Nature.
Liao, L., Samara-Rubio, D., Morse, M., Liu, A., Hodge,
D., Rubin, D., Keil, U. D, Franck, T., 2005, High
Speed silicon Mach-Zehnder modulator, vol. 13, no. 8,
pp. 3129-3135, Optics Express.
Liao, L., Liu, A., Rubin, D., Basak, J., Chetrit, Y., Nguyen
H., Cohen, R., Izakhy, N., Paniccia, M., 2007, 40
Gbit/s silicon optical modulator for high speed
applications, vol. 43, no. 22, Electronics Letters.
Cada, M., 2008, Research Report on Electro-Optic
Materials, Nanophotonic Technology Center,
Polytechnic University of Valencia, Spain.
PHOTOPTICS2015-DoctoralConsortium
78

R. W. Boyd, 2008, Nonlinear Optics, Elsevier,
Amsterdam, 3rd edition.
Cada, M., Qasymeh, M., and Pistora, J., 2008, Electrically
and optically controlled cross-polarized wave
conversion, vol. 16, no. 5, pp. 3083-3100, Optics
Express.
Martinez, A., Blasco, J., Sanchis, P., Galan, J.,V., Garcia-
Ruperez, J., Jordana, E., Gautier, P., Lebour,
Y.,Hernanadez, S., Daldosso, N., Garrido, B., Fedili,
J.,M., Pavesi, L. and Marti, J., 2010, Ultrafast All-
Optical Switching in a Silicon-Nanocrystal-Based
Silicon Slot Waveguide at Telecom Wavelengths, 10,
pp.1506-1511, Nano Letters.
Xu, Q., Almeida, V., R., Panepucci, R., R. and Lipson,
M., 2004, Experimental demonstration of guiding and
confining light in nanometer-size low-refractive-index
material, vol. 29, no. 14, pp. 1626-1628 Optics
Letters.
Sanchis, P., Martinez, A., 2007, Design of Silicon-Based
Slot Waveguide Configurations for Optimum
Nonlinear Performance, vol. 25, no. 5, Journal of
Lightwave Technology.
Barrios, C. A., 2004, High-performance all-optical silicon
microswitch, vol. 40, no. 14, Electronics Letters.
Dong, P., Liao, S., Feng, D., Liang, H., Zheng, D.,
Shafiiha, R., Kung, C., Quian W., Li, G., Zheng, X.,
Krishnamoorthy, A. V., Asghari, M., 2009, Low
,
ultralow-energy, compact, high-speed silicon electro-
optic modulator, vol. 17, no. 25, Optics Express.
Li, G., Krishnamoorthy, A. V, Shubin, I., Yao, J., Luo, Y.,
Thacker, H., Zheng, X., Raj, K., Cunningham, J. E.,
2013, Ring Resonator Modulators in Silicon for
Interchip Photonic Links, vol. 19, no. 6, IEEE journal
of selected topics in Quantum Electronics.
SiliconKerrEffectElectro-opticSwitch
79
