New Approach to Partitioning Conﬁdential Resources in Hybrid Clouds

Kaouther Samet

, Samir Moalla

and Mahdi Khemakhem

Department of Computer Science, Faculty of Sciences, University Tunis El Manar, Tunis, Tunisia

Department of Telecommunications, National School of Electronics and Telecommunications,

University of Sfax, Sfax, Tunisia

Keywords:

Partitioning Resources, Hybrid Clouds, Conﬁdentiality.

Abstract:

Today, companies use more cloud environments such as hybrid clouds. Indeed, hybrid clouds give the op-

portunity to better manage resources mostly when companies have no space to store more resources in their

private clouds. The best solution here is to allocate the required space in public cloud at a low cost. But

how can resources be partitioned in hybrid clouds while assuring conﬁdentiality of resources moved to public

cloud. Many works have been done in this context. They suppose that conﬁdentiality is assured by using

encryption methods. But with this solution the cloud provider can access the resources stored on the cloud,

which weakens the conﬁdentiality of these. This work proposes an approach to the Conﬁdential Resources

Partitioning Problem in Hybrid Clouds (CRPHC) which aims at ensuring the conﬁdentiality of resources by

grouping as much as possible the most conﬁdential resources in private cloud and resources with low degrees

of conﬁdentiality in public cloud while minimizing the size of resources to host in public cloud and conse-

quently reducing the storage cost. This solution allows the possibility of using non-performing encryption

methods which have a reduced treatement cost compared to efﬁcient methods. Experimentally, our solution

will be evaluated and compared to optimal solution given by CPLEX.

1 INTRODUCTION

Cloud computing has become a major concept re-

ferring to the use of memory, computing capabili-

ties computers and servers around the world, all of

them linked by a network such as the Internet. Today,

companies use more cloud environments for deploy-

ment and execution of their applications. Usually, the

most used type of clouds in the cloud environment

is the hybrid cloud. The infrastructure of this type of

cloud is composed of two or several public and private

clouds. It is obvious for a company that applications

must be deployed in the private cloud as resources can

be provided by their cloud.

However, when the physical limit of the private

cloud is reached, the company may need to use other

resources (data, services or applications) from a pub-

lic cloud. This occurs when applications and plat-

forms of companies need to be enlarged and request

additional resources that the private cloud is not able

to provide. In this case, obtaining new resources from

public cloud can solve this problem. Consequently,

resources will be partitioned between private and pub-

lic clouds. Among the obstacles, mentioned by au-

thors of (Stoica and Zaharia, 2009), in cloud environ-

ment is conﬁdentiality and the study of secure data

in this environment is fairly new and has become in-

creasingly important (Nepal and Calvo, 2014). In-

deed, they consider that it is the most important obsta-

cle in this environment. So, how can conﬁdentiality of

resources be ensured in the hybrid cloud? To ensure

conﬁdentiality in the clouds, encryption methods have

been used. But to have better results, it is necessary

to use performing encryption methods which are very

expensive in terms of execution time and complexity

(Chokhani, 2013). However these works fail to raise

the problem that the public cloud providers theoreti-

cally have access to the received resources.

In this context, we propose an approach to solve

the Conﬁdential Resources Partitioning Problem in

Hybrid Cloud (CRPHC) which aims at ensuring the

conﬁdentiality of resources by grouping as much as

possible the most conﬁdential resources in private

cloud and resources with low degrees of conﬁden-

tiality in public cloud while minimizing the size of

resources to host in public cloud and cosequently re-

ducing the cost of storage.This solution allows to use

a non-performing encryption methods which have a

reduced treatment cost compared to efﬁcient meth-

ods. Experimentally, our solution will be evaluated

506

Samet K., Moalla S. and Khemakhem M..

New Approach to Partitioning Conﬁdential Resources in Hybrid Clouds.

DOI: 10.5220/0005444505060513

In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 506-513

ISBN: 978-989-758-104-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

and compared to optimal solution given by the com-

mercial software IBM-ILOG-CPLEX 12.5 applied to

an integer linear programming formulation of the CR-

PHC.

The rest of the paper is organized as follows: in

section 2, we present an overview of works study-

ing the partitioning problem. In section 3, we list

in details the integer linear programming formulation

of the CRPHC, while in section 4 we clarify our ap-

proach to partitioning conﬁdential resources in hybrid

clouds. In section 5, we evaluate and compare our so-

lution to optimal solution given by CPLEX. Finally,

we end up giving our conclusion and future works in

section 6.

2 STATE OF ARTS

The problem of partitioning resources in cloud en-

vironments has been seen from different viewpoints,

while considering different types of criteria such as

conﬁdentiality, access frequency of query execution,

communication, etc.

In the following, we present some studies for con-

ﬁdentiality management in clouds.

2.1 Conﬁdentiality Management

Assured by the Public Cloud

Provider

We present below approaches Schism and Birch

(Zhang; and Madden, 2010) and (Ramakrishnan and

Livny, 1996) treating the problem of partitioning data

in databases. They try to produce the best quality

clustering with the available memory and time con-

straints.

Authors of (Tata and Moalla, 2012) propose a new

algorithm that approximates the optimal placement of

services based on communication and hosting costs

induced by the shifting of components towards the

public cloud. This research is interested in deciding

which services will be deployed to the public clouds

based on communications between services within

the public cloud, and communications between ser-

vices of the private cloud and services of the public

cloud.

In (Wang and C.Jiang, 2012) and (Wang and

Guo, 2013), authors propose a model for the multi-

objective data placement and use a particle swarm op-

timization algorithm to optimize the time and cost in

cloud computing.

In works already mentioned, the authors are not

interested in the conﬁdentiality of resources moved to

the public clouds. In fact, they suppose that conﬁ-

dentiality is guaranteed by the public cloud provider

using encryption methods applied on all the resources

moved to the public cloud regardless of their degree of

conﬁdentiality (Mehrotra and Thuraisingham, 2012)

and (Kantarcioglu and Thuraisingham, 2011). But, in

this case, the cloud provider can consult and access to

conﬁdential resources in public cloud.

2.2 Conﬁdentiality Management in

Hybrid Clouds

In (Pilli and Joshi, 2013), authors present a solution

approach to the data partitioning problem. They cre-

ate different partitions and estimate the execution cost

of the query workload for each of these partitions and

check whether any monetary and conﬁdentiality risk

constraints were violated. Authors assume that all

predicates have the same level of conﬁdentiality.

Authors of (Mehrotra and Thuraisingham, 2012),

(Kantarcioglu and Thuraisingham, 2011), (Marwaha

and Bedi, 2013) and (Lamba and Kumar, 2014) pro-

pose approaches to ensure conﬁdentiality in clouds

based on encryption. Indeed, they suppose that re-

sources conﬁdentiality is assured by encryption meth-

ods. But in (Nepal and Calvo, 2014) authors con-

sider that this solution is computationally inefﬁcient

and locates a large workload on the data owner when

considering factors such as updating encryption keys.

Likewise, according to (Chokhani, 2013) encryption

methods have additional complexity in cloud environ-

ments which makes this operation very expensive and

complex.

To solve this problem, we propose an approach

to the Conﬁdential Resources Partitioning Problem

in Hybrid Clouds (CRPHC) which aims at ensuring

the conﬁdentiality of resources by keeping the most

conﬁdential resources in private cloud and moving

resources with lower degrees of conﬁdentiality into

public cloud; while minimizing the size of resources

to host in the public cloud.

3 INTEGER LINEAR

PROGRAMMING

FORMULATION FOR THE

CRPHC

In this section we present an integer linear program-

ming formulation for the Conﬁdential Resources Par-

titioning Problem in Hybrid Cloud (CRPHC). Our

aim is to:

NewApproachtoPartitioningConfidentialResourcesinHybridClouds

507

• Ensure conﬁdentiality by storing resources with

low conﬁdentiality in public cloud,

• Minimize resources storage cost in the public

cloud while respecting a minimal size of resources

to host in public cloud.

3.1 Problem Statement

Generally, the CRPHC can be deﬁned on an undi-

rected graph G(X,A) where X = {1,2,. .., n} is the

set of vertices and A = {[i, j], i, j ∈ X,i 6= j} is the set

of edges representing the existence of communication

between two vertices i and j.

A vertex presents data, service or application.

Each vertex is characterized by a conﬁdentiality de-

gree d

and size s

. Each edge is characterized by a

communication frequency f

i j

if the two vertices i and

j are accessed by the same query and need some com-

munication.

Initially, we consider that all vertices are hosted

in the private cloud and the public one is empty as

illustrated in ﬁgure 1. Because the incapacity of the

private cloud to host all vertices, the decision maker

must specify which vertices to move to the public

cloud. After the partitioning vertices (resources) pro-

cess, we will obtain a private cloud which contains the

resources with high conﬁdentiality and a public cloud

which contains resources with low conﬁdentiality as

illustrated in ﬁgure 2.

Figure 1: Hybrid cloud before partitioning process.

Figure 2: Hybrid cloud after partitioning process.

Usually, except conﬁdentiality minimization, the

partitioning process must also take into account the

minimization of the total size of vertices affected to

the public cloud and the minimization of the total

communication frequency outside the private cloud

(i.e. the public-public and private-public communi-

cation). In this work, we not interested to the mini-

mization of the communication cost and thereafter we

assume that f

i j

= 0, ∀i, j ∈ X.

3.2 Mathematical Model

To formulate the mathematical model for CRPHC, we

consider the following data and variables:

• n: number of vertices in the graph,

• X: set of vertices formed the graph,

• d

: degree of conﬁdentiality of each vertex i ∈ X.

The affectation of values of degree of conﬁden-

tiality is performed using the opinion of an expert

based on transaction historic.

• s

: size of each vertex i ∈ X,

• MS: the Minimal Size of ressources to host in

public cloud. Indeed, the use of the public cloud is

motivated by the insufﬁciency of the private cloud

to host all vertices.

• x

∈ {0,1}: a binary decision variables. ∀i ∈ X ,

= 1 if the vertex i is affected to the public cloud

and x

= 0 if it’s affected to the private one.

Initially, the CRPHC can be formulated by a 0-1

linear program:

Min Z = max

i∈X

{

}

∑

i∈X

(1)

subject to

∑

i∈X

≥ MS (2)

∈ {0, 1},∀i ∈ X (3)

Equation (1) represents the objective function of

the CRPHC. It consists to minimize: (i) the maximum

conﬁdentiality degree between the vertices affected to

the public cloud and (ii) the total size of resources

to host in the public cloud. Inequality (2) represents

the size constraint of the public cloud. Equation (3)

represents the constraints of the decision variables.

We note that the objective function is composed

by two inhomogeneous terms in term of their metrics.

Indeed, the sizes and the conﬁdentiality degrees are

not belonging in the same values intervals. Hence-

forth, to eliminate this inconvenience, we use the nor-

malized data s

and d

instead of s

and d

, ∀i ∈ X

where:

max

k∈X

: s

∈ [0, 1]∀i ∈ X

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

508

max

k∈X

: d

∈ [0, 1]∀i ∈ X

We also note that the proposed objective function

is not linear. So, to linearize the model, in order to

simplify its resolution by any mathematical models

solver, we consider a new integer decision variable

λ ∈ N to be the maximal conﬁdentiality degree be-

tween verticies affected to the public cloud.

λ = max

i∈X





: λ ∈ [0, 1]

In the improvement model, λ must be minimized

and each conﬁdentiality degree of the vertices af-

fected to the public cloud can not exceed λ. The mod-

iﬁed model can be formulated as follows:

Min Z = λ +

∑

i∈X

: Z ∈ [0, 2] (4)

subject to

∑

i∈X

≥ MS (5)

≤ λ, ∀i ∈ X (6)

∈ {0, 1},∀i ∈ X (7)

λ ∈ N (8)

4 THEORETICAL BASIS OF

CRPHC’S APPROACH

In this section, we describe our proposed approach to

solve the CRPHC. To classify the resources, we are

looking for grouping resources which have the clos-

est degrees of conﬁdentiality and to minimize size of

resources which will be hosted in the public cloud.

Resources classiﬁcation must take into account to the

already mentioned criteria such as:

• Minimizing degrees of conﬁdentiality of re-

sources (vertices) moved to the public cloud C

• The size of resources affected to C

must exceed

slightly a ﬁxed values MS. This constraint allows

minimizing the storage cost of resources moved to

the public cloud C

4.1 Principle

Our approach aims at partitionning n vertices to two

clusters (Private Cloud C

and Public Cloud C

)

with respecting certain number of criteria ( already

mentionned in the previous paragraph).

Step 1: The initial set of vertices will be pati-

tioned into two clusters: The ﬁrst cluster C

will con-

tain conﬁdential resources and the second cluster C

will contain non-conﬁdential resources.

Step 2: The constraint of the MS of resources to

host in public cloud MS must be veriﬁed. So two

cases are possibles:

Case 1: the Total Size of resources affected to C

(T S

) is greater than MS, C

will be partitioned into

two clusters CL

(Private CLoud) and CL

(Public

CLoud). Then we have: C

= CL

and C

= C

∪

Case 2: the Total Size of resources affected to C

(T S

) is smaller than MS, C

will be partitioned into

two clusters CL

and CL

. Then we have: C

and C

= C

∪ CL

Step 3: Repeat Step 2 until MS is reached or ex-

ceeded.

Figure 3 illustrate the already described steps of

the proposed approach.

Figure 3: Illustration of approach process.

4.2 The CRPHC Algorithm

In this part, we present our solution to classifying re-

sources into two clusters: private and public clusters.

NewApproachtoPartitioningConfidentialResourcesinHybridClouds

509

So we implement CRPHC Algorithm to classify re-

sources into two clusters.

First, we suppose that all vertices (resources) are

hosted in the private cloud, then each vertex is af-

fected in the right cloud taking into account the pre-

vious criteria already mentioned. However to apply

CRPHC Algorithm, a metric must be deﬁned to clas-

sify a set of vertices.

In our case, the distance must take into account the

degree of conﬁdentiality d

and the size s

of each ver-

tex i ∈ X. As a result, the private cloud C

will con-

tain vertices which have the highest degree of conﬁ-

dentiality while minimizing the costs of storage in the

public cloud. So, the public cloud C

will contain

resources having lower conﬁdentiality degree which

will minimize the costs of storage in the public cloud.

4.2.1 Deﬁnition 1: (Distance)

We consider that each vertex is characterized by coor-

dinates (s

). So, the distance δ

i j

between two ver-

tices i and j will be deﬁned as following:

i j

− s

)

+ (d

− d

)

4.2.2 Deﬁnition 2: (Centroid)

A centroid is characterized by coordinates (s

These coordinates are calculated as following:

∑

i∈C

, ∀k ∈ {1,2}

∑

i∈C

, ∀k ∈ {1,2}

4.2.3 Algorithm

Our solution is based on a main algorithm (CRPHC

Algorithm) which uses each time Affect Algorithm to

classify different vertices of the graph into two clus-

ters. The input of the CRPHC Algorithm is the graph

to be partitioned. As is already mentioned, each ver-

tex of the graph is characterized by a degree of con-

ﬁdentiality d

and a size s

. Then, the output is two

clusters: private cloud C

and public cloud C

. For

Affect Algorithm, the output is also a private cloud

and a public cloud CL

. Algorithm 1 describes

the proposed approach to solve the CRPHC.

Initially, we assume that all vertices are hosted in

the private cloud and the public cloud is empty. The

Affect Algorithm will be applied to all the graph to

give ﬁrstly two clusters: private cloud CL

and public

cloud CL

. If the Total Size T S

of resources hosted

in public cloud is greater than MS (see line 6), Affect

Algorithm will be applied to public cloud CL

. This

Algorithm 1: CRPHC Algorithm.

input : G(X,A)/|X| = n.

output: C

and C

where C

∪C

= X and

∩C

1 C

← X ;

2 C

←

3 Affect(X) /* Apply Affect (see

Algorithm 2) */;

4 C

←

{

}

;

5 C

←

{

}

;

6 if T S

≥ MS /* (TS: Total Size of

resources affected to public cloud)

*/ then

7 repeat

8 X ← CL

;

9 Affect(X);

10 C

← C

∪CL

;

11 C

← CL

;

12 until T S

> MS;

13 else

14 repeat

15 X ← CL

;

16 Affect(X);

17 C

← C

∪CL

;

18 C

← CL

;

19 until T S

< MS;

20 end

allows to decrease the Total Size of resources hosted

in C

, indeed, vertices of CL

will be moved from

the public cloud C

to the private cloud C

(see lines

7-12). So the Affect Algorithm will be applied to pub-

lic cloud CL

until the MS is reached.

Likewise, if T S

is lower than MS (see lines 13-

19), the Affect Algorithm will be applied to CL

. In-

deed, the vertices of CL

will be moved from private

cloud C

to public cloud C

until the MS is reached

or exceeded.

Affect Algorithm consists in a ﬁrst step to choose

two vertices ω

and ω

from the graph (see lines 1-

2). The choice of these vertices is performed using

two functions max() and min().The function max()

choose the vertex with the maximal degree of conﬁ-

dentiality in the graph and the function min() choose

the vertex with the minimal degree of conﬁdentiality

in the graph. In this case, Affect Algorithm regroup

vertices with higher conﬁdentiality in one cluster (pri-

vate cloud) and vertices with lower conﬁdentiality in

another cluster (public cloud).

To affect vertices to the right cluster (see lines 7-

11), the idea is to compute the distance δ

(i,ω

)

, with

k =

{

pr, pu

}

, between each vertex in the graph and

each centroid. If the vertex is closest to ω

, it will be

hosted to the private cloud CL

and if the vertex

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

510

Algorithm 2: Affect Algorithm.

input : A set of vertices X to be partitioned.

output: Tow clusters CL

and CL

for the

vertices hosted (respectively) in private

and public clouds.

1 ω

← max(X);

2 ω

← min(X );

3 repeat

4 CL

← X ;

5 CL

←

6 for each i ∈ X do

7 if δ

iω

≤ δ

iω

then

8 CL

← CL

∪ {i};

9 else

10 CL

← CL

∪ {i};

11 end

12 end

13 old ω

← ω

;

14 old ω

← ω

;

15 new ω

← centroid(CL

);

16 new ω

← centroid(CL

);

17 until old ω

== new ω

AND

old ω

== new ω

;

is closest to ω

, it will be hosted to the public cloud

. Then, we compute centroids of the new clusters

(see lines 15-16) and we repeat this process (see lines

4-16) until we have the stability of the two clusters

i.e. we reach the same centroids in two successive

iterations (see line 17).

5 EXPERIMENTAL EVALUATION

To apply and assess our approach, we need instances

for CRPHC algorithm. Then we need to vary the fol-

lowing parameters:

• n: number of vertices of the graph,

• d: degrees of conﬁdentiality of vertices of the

graph,

• T S: Total Size of vertices of the graph,

• MS: Minimal Size of resources to host in public

cloud.

But, it is not possible to ﬁnd real cases or bench-

marks based on previous parameters and able to vary-

ing them. This is why we need to create several

graphs according to our need. For this reason we have

developed a generator of graphs. Each graph is com-

posed by six elements: number of vertices, vector of

size of each vertex, a vector of conﬁdentiality degree

of each vertex, MS, matrix of execution frequency be-

tween two vertices and minimal degree of conﬁden-

tiality in public cloud. In our work we just interest

to the four ﬁrst elements. The generated graphs are

available on http://goo.gl/uvO8B8.

In this section, we will evaluate our solution with

an optimal solution CPLEX. CPLEX is a computing

tool of optimization (Aitha, 2014) which gives opti-

mal solutions applied to a integer programming for-

mulation.

So, to assess our solution we applied CPLEX to

the same graphs that we used to test CRPHC Algo-

rithm. Then we compare the results obtained with our

solution and those obtained by CPLEX.

To better analyze and interpret results, we calcu-

late the Gap between results given by CRPHC and

those given by CPLEX. This Gap is given by:

Gap = (CRPHC OF −CPLEX OF)/cplex OF

Then, we recognize that a solution is called:

• Optimal: if the Gap associated is 0%,

• Excellent: if the Gap associated it does not exceed

15%,

• Incorrect: if the Gap associated exceeds 50%.

5.1 Varying Number of Vertices

These tests consist in varying the number of vertices

of graphs (500, 1000, 1500, 2000, 2500 and 3000)

and ﬁxing the MS = 20%, Total Size of the graph T S =

10000 and degree of conﬁdentiality d

∈ [0% - 100%].

Figure 4: Gap for varying number of vertices.

Figure 4 shows that the Gap values are betwwen

3,4% et 5% so they are so close.

We remark that the Gap between our solution and

optimal solution does not exceed 5%. So, in this case,

our solution can be considered excellent.

5.2 Varying Degree of Conﬁdentiality

For these tests, we ﬁxed the number of vertices n =

2000,MS = 20% and Total Size of the graph T S =

NewApproachtoPartitioningConfidentialResourcesinHybridClouds

511

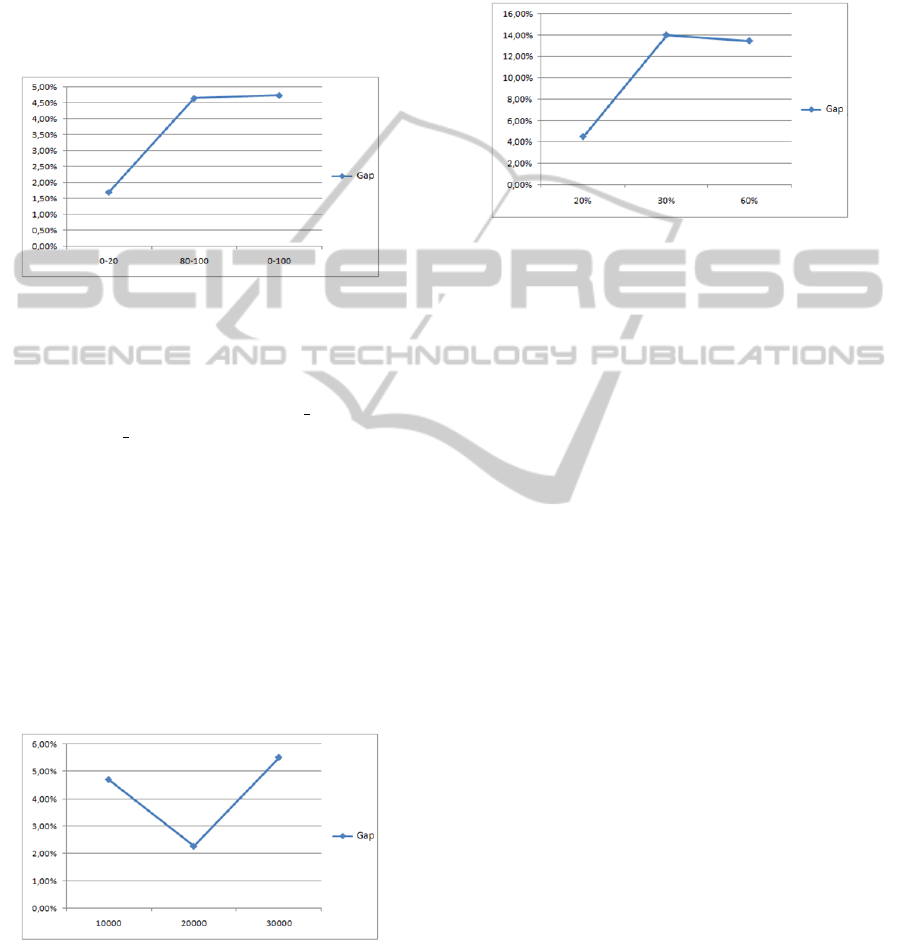
10000. Then we varied the range of degree of conﬁ-

dentiality. To do this, we have chosen three ranges:

• [0% − 20%] this range represents resources with

low conﬁdentiality,

• [80% − 100%] this range represents resources

with high conﬁdentiality,

• [0% − 100%] this range represents resources with

low and high conﬁdentiality.

Figure 5: Gap for varying degree of conﬁdentiality.

Figure 5 shows that the Gap for [0% − 20%] is

1,6%. This value is low compared to values of

other range of conﬁdentiality. So, for resources

with low conﬁdentiality, the CRPHC OF value is

close to CPLEX OF. Then the graph is almost sta-

ble in the order of 4,7% between [0% − 100%] and

[80% − 100%].

The Gap between our solution and optimal solu-

tion does not exceed 4, 7%. So, we can consider that

our solution is excellent in this case.

5.3 Varying Total Size

For these tests, we ﬁxed number of vertices n =

2000,MS = 20% and the degree of conﬁdentiality d

∈ [0% - 100%]. Then we varied the Total Size of the

graph (10000, 20000 and 30000).

Figure 6: Gap for varying size.

Figure 6 shows that the best Gap value is given for

T S = 20000.

Then we have the Gap between our solution and

optimal solution does not exceed 6%. So, we can con-

sider that our solution is excellent in this case.

5.4 Varying MS

For these tests, we ﬁxed number of vertices n = 2000,

degree of conﬁdentiality d

∈ [0% - 100%] and Total

Size of the graph T S = 10000. Then we varied MS

(20%,30% and 60%) in the public cloud.

Figure 7: Gap for varying MS.

Figure 7 shows that the Gap for MS = 20% is

4,3%. This value is the best result given by our so-

lution compared to MS = 30% and MS = 60%.

Then we remark that the graph is almost stable in

the order of 14% between MS = 30% and MS = 60%.

The Gap between our solution and optimal solu-

tion does not exceed 14%. So, in this case, our solu-

tion can be considered excellent.

6 CONCLUSION AND FUTURE

WORK

In this paper, we tackled a new approach for partition-

ing conﬁdential resources between private and public

components in hybrid cloud. Our objective is to en-

sure conﬁdentiality by moving conﬁdential resources

to private cloud and resources with low conﬁdential-

ity to public cloud. And also, minimizing the size of

resources to host in public cloud. Then we have com-

pared the results given by our proposed solution with

optimum results given by CPLEX, and we have found

that our results are acceptable.

In this work, we have supposed that hybrid cloud

is composed by one private cloud and one public

cloud. So to enlarge our work, we hope to propose an

approach to partitioning conﬁdential resources in hy-

brid clouds based on multitude of criteria which man-

aging the allocation decision of each resource to one

of the classes: private clouds and public clouds. Thus

we place ourselves in a melting problem of sources of

information (conﬁdentiality, capacity, degree of de-

pendence between resource, etc.). Then we focus on

the notion of dynamicity such as conﬁdentiality and

sizes of resources that will be partitioned in hybrid

clouds.

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

512

REFERENCES

Aitha, P. (2014). Cplex tutorial handout.

http://fr.scribd.com/doc/63956075/CPLEX-Tutorial-

Handout.

Chokhani, R. C. M. I. S. (2013). Cryptographic key man-

agement issues and challenges in cloud services. Na-

tional Institute of standards and Technology.

Kantarcioglu, V. K. M. and Thuraisingham, B. (2011). Se-

cure data processing in a hybrid cloud. Paciﬁc Asia

conference on Intelligence and Security Informatics.

Lamba, S. and Kumar, A. (2014). An approach for ensuring

security in cloud environment. International Journal

of Computer Applications.

Marwaha, M. and Bedi, R. (2013). Applying encryption al-

gorithm for data security and privacy in cloud comput-

ing. IJCSI International Journal of Computer Science

Issues.

Mehrotra, V. K. K. O. B. H. M. K. S. and Thuraisingham, B.

(2012). Risk- aware data processing in hybrid clouds.

IEEE 5th International Conference on cloud Comput-

ing.

Nepal, D. T. S. C. S. and Calvo, R. (2014). Secure data

sharing in the cloud. Security; Privacy and Trust in

cloud Systems.

Pilli, P. R. P. M. R. S. E. and Joshi, R. (2013). Improved

technique for data conﬁdentiality in cloud environ-

ment. Networks and Communications.

Ramakrishnan, T. Z. R. and Livny, M. (1996). Birch : An ef-

ﬁcient data clustering method for very large database.

SIGMOD.

Stoica, M. A. A. F. R. G. A. J. R. A. K. G. L. A. P. A.

R. I. and Zaharia, M. (2009). Above the clouds : A

berkeley view of cloud computing. In a.

Tata, F. B. N. T. S. and Moalla, S. (2012). Approxi-

mate placement of service based applications in hy-

brid clouds. 21st International conference IEEE WET-

ICE.

Wang, L. G. Z. H. S. Z. N. Z. J. and C.Jiang (2012). Multi-

objective optimization for data placement strategy in

cloud computing. Springer.

Wang, X. and Guo, W. (2013). A data placement strategy

based on genetic algorithm in cloud computing plat-

form. 10th Web Information System and Application

Conference (WISA).

Zhang;, C. C. E. J. Y. and Madden, S. (2010). Schism : a

workload-driven approach to database replication and

partitioning. VLDB; 36th International Conference on

Very Large Data Bases.

NewApproachtoPartitioningConfidentialResourcesinHybridClouds

513