
Power Capping of CPU-GPU Heterogeneous Systems using Power and
Performance Models
Kazuki Tsuzuku and Toshio Endo
Tokyo Institute of Technology, Tokyo, Japan
Keywords:
GPGPU, Power Capping, DVFS, Power Model, Performance Model.
Abstract:
Recent high performance computing (HPC) systems and supercomputers are built under strict power budgets
and the limitation will be even severer. Thus power control is becoming more important, especially on the
systems with accelerators such as GPUs, whose power consumption changes largely according to the charac-
teristics of application programs. In this paper, we propose an efficient power capping technique for compute
nodes with accelerators that supports dynamic voltage frequency scaling (DVFS). We adopt a hybrid approach
that consists of a static method and a dynamic method. By using a static method based on our power and per-
formance model, we obtain optimal frequencies of GPUs and CPUs for the given application. Additionally,
while the application is running, we adjust GPU frequency dynamically based on real-time power consump-
tion. Through the performance evaluation on a compute node with a NVIDIA GPU, we demonstrate that our
hybrid method successfully control the power consumption under a given power constraint better than simple
methods, without aggravating energy-to-solution.
1 INTRODUCTION
The issue of power/energy consumption of HPC sys-
tems and supercomputers has been and will be an im-
portant research topic. For example, Tianhe-2
1
, the
current fastest supercomputer with performance of
33.86 PFLOPS consumes the power of 17.6 MW dur-
ing Linpack benchmark. A realistic power budget for
an exascale system is considered as 20 MW, which re-
quires an energy efficiency of 50 GFLOPS/W(Lucas,
2014). Therefore, exascale systems, which are ex-
pected to appear around 2020, require 25 times higher
energy efficiency than the current fastest supercom-
puter.
Recently, in order to improve energy efficiency
of HPC systems, accelerators including GPUs or
Xeon Phi have been attracted attention. For ex-
ample, Tianhe-2 and TSUBAME supercomputer in
Tokyo Institute of Technology(Matsuoka, 2011) are
equipped with accelerators, in addition to general pur-
pose CPUs. In spite of better efficiency, however, the
fluctuation of power consumption tend to be larger
with accelerators. While keeping better efficiency,
the peak power consumption of the system should be
capped by the power budget determined by the build-
1
http://www.top500.org
ing or organization.
This paper describes an efficient power capping
method for computing nodes with accelerators, as-
suming the existence of dynamic voltage frequency
scaling (DVFS) mechanism of modern CPUs and ac-
celerators. Here we should note that a naive usage of
DVFS may degrade the application performance and
sometimes harmful for energy optimization. Instead,
our goal is to minimize energy consumption during
the application run, while conforming a given power
constraint. Towards this goal, there are several issues:
• Most of modern PCs and servers already use
DVFS for power saving by controlling the fre-
quency according to the node load. Also some
advanced servers support power capping by com-
paring the realtime power consumption and the
cap value (Gandhi et al., 2009). However, it is un-
clear whether this method can optimize energy ef-
ficiency of HPC systems, where the average load
is much higher than client PCs.
• For energy optimization, we need to take the
application characteristics into account, such as
GPU/CPU usage, arithmetic intensity and mem-
ory access frequency.
• Recent Intel CPUs are equipped with Running
Average Power Limit (RAPL) technique, which
226
Tsuzuku K. and Endo T..
Power Capping of CPU-GPU Heterogeneous Systems using Power and Performance Models.
DOI: 10.5220/0005445102260233
In Proceedings of the 4th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS-2015), pages 226-233
ISBN: 978-989-758-105-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

supports not only DVFS but power capping of
CPUs. However, RAPL itself does not cap the
power consumption of the entire node.
Towards the above-mentioned goal, this paper
proposes a hybrid power capping method of a static
method and a dynamic method. When the application
starts, we determine the initial frequency statically
based on our power and performance model. Then
during the application is running, we dynamically
change the frequencies based on monitored power
consumption. This dynamic phase is introduced to
recover the excess of power, which may be caused by
model errors. Through the experiments using a com-
pute node with a NVIDIA GPU, we demonstrate that
neither the static approach nor the dynamic approach
can satisfy the goal solely, and combining the two is
essential.
2 BACKGROUND
The control of power consumption of supercomput-
ers, which may reach the order of megawatts, is be-
coming an important issue towards the protection of
the environment and cost reduction for energy.
Power capping technique is even more important,
especially for the systems with accelerators, whose
power fluctuation is larger. Towards power cap-
ping for systems, this paper focus on power capping
and energy saving on a compute node equipped with
CPUs and GPUs.
In previous HPC systems, it was more difficult
to obtain power consumption of each node due to
lack of smart power sensors or meters. Thus in or-
der to estimate power consumption of applications on
such nodes, statistical power models based on per-
formance counters have been constructed(Nagasaka
et al., 2010).
More recently, detailed monitoring of node power
consumption is much easier due to spread of power
sensors in computer systems. The real time power
consumption can be obtained with interfaces such as
RAPL for Intel CPUs and NVIDIA Management Li-
brary (NVML) for NVIDIA GPUs. Such interfaces
are used both for power monitoring and control; the
GPU clock speed can be configured by using the
NVML library.
Not only for power in processor level, with the
spread of inexpensive smart meters, HPC commu-
nity has started to develop the specification of power
monitor/control API of HPC systems(Laros, 2014).
As an example of a working system, TSUBAME-
KFC(Endo et al., 2014), ranked as No.1 in the world
in the GREEN500 List
2
, has a detailed monitoring
system, which can monitor not only CPUs and GPUs
power but also AC power of each node by intervals of
a second.
In response to the spread of monitoring systems,
we design our power capping method that uses real
time monitoring as described in the next section.
3 PROPOSED POWER CAPPING
METHODS
In this section, we discuss two simple power-capping
methods, a dynamic method and a static method. And
then we combine them into a hybrid method. Our
goal is to keep power consumption lower than a given
power budget during the execution of user applica-
tions. Generally it is hard to avoid instantaneous
excess of power; instead, we minimize the duration
when the power consumption is exceeding the limit
(hereafter, excess duration). Our goal also includes
the optimization of energy consumption, while keep-
ing the excess duration minimum.
We currently focus on power capping of a sin-
gle node equipped with an NVIDIA GPU accelerator.
Our power capping method is designed to support ap-
plications that have various characteristics, however,
we assume that a single application is running on a
node at a time. Also currently we have the following
assumptions on the application; the application uses
mainly GPUs for its computation, and a single CPU
core is mainly used for initialization of the applica-
tion, controlling the GPU. The application uses GPU
kernel functions that have similar characteristics to
each other; thus GPU power consumptions when ker-
nel functions are running do not change drastically.
3.1 Dynamic Power Capping Method
Here we describe the power capping technique using
dynamic changing of clock speeds of GPUs. With this
method, we continuously monitor power consump-
tion of the node, and if power consumption reaches
or exceeds the power limit, we decrease GPU clock
speeds. If the power consumption is much lower than
the limit contrarily, we increase the speed.
While this dynamic method is simple, we still
have to take care of control amount and control in-
terval. As for the control amount, we adopt a simple
method to change the clock by only a single step once.
As for the interval of control, there is a tradeoff; if the
interval is too long, we may miss the sudden increase
2
http://www.green500.org
PowerCappingofCPU-GPUHeterogeneousSystemsusingPowerandPerformanceModels
227

600#
620#
640#
660#
680#
700#
720#
740#
760#
780#
800#
0#
50#
100#
150#
200#
250#
300#
0.019662#
5.326117#
10.803902#
16.178947#
21.600619#
27.04757#
32.459628#
37.862695#
43.246856#
48.669975#
54.352138#
59.769908#
65.16012#
70.720196#
76.139882#
81.684174#
87.040461#
92.387222#
97.754481#
103.075815#
108.425398#
114.034187#
119.418912#
GPU$frequency(MHz)
Power$consump5on(W)
Time(second)
GPU#frequency# Power#constraint# Node#power#consumpBon#
Figure 1: Change of the power consumption when the con-
trol interval is 0.2 seconds.
of power consumption and extend the excess duration.
On the other hand, too short interval may lead vibra-
tion of clock speeds as follows.
For the experiments, we have implemented a dae-
mon program that continuously monitors the node
power and changes the GPU clock speed as described.
Figure1 shows the results when the control interval is
0.2 seconds. The graph shows changes of the GPU
clock speed and power consumption of the node. We
observe a fast and large (the clock varies from min-
imum speed to maximum speed) fluctuation of the
clock speed, which leads a frequent excess of the
power consumption. The reason of this phenomena
is as follows; due to the delay of power sensor, the
control daemon observes old power values. If the
clock interval is shorter than the delay, the daemon
changes the clock speed before the previous change
affects power consumption. As a result, excess dura-
tion gets larger.
During preliminary experiments, we adopted 5.0
seconds as the control frequency. However, this is
fairly long, and may incur slow adaptation to an ap-
propriate clock. Thus initial setting of clock speed is
important for our objectives.
3.2 Static Power Capping Method
This section explains a model-based power capping
method, which determines appropriate CPUs and
GPUs clock speeds based on a power and perfor-
mance model. We model relationship of clock speeds
and the power consumption and execution time for
given applications. Using the model, we can deter-
mine the clock speeds that achieve our goals as fol-
lows. We compute the power consumption and energy
consumption during the execution of the given appli-
cation execution for all combinations of GPU clocks
and CPU clocks. Among the results of all combina-
tions, we select the best clocks, which does not cause
sta$c
CPU
1
Time (sec)
Power consumption (W)
CPU-GPU
Communication
GPU*Kernel
Figure 2: Our model of power consumption during GPU
application execution.
exceeding the power limit, while minimizing the en-
ergy consumption.
3.2.1 Modeling Execution of GPU Applications
In our model, the execution of a GPU application is
divided into the following categories as shown in Fig-
ure 2: the duration when GPU kernels are running,
the duration when CPU are running, the duration for
communication between CPU and GPU, and the du-
ration when both CPU and GPU are idle. Thus E,
the energy consumption of a node during application
execution is represented by the following equation.
E = P
static
∗ T
all
+ P
Comm
∗ T
Comm
+ P
CPU
∗ T
CPU
+ P
GPU
∗ T
GPU
(1)
where variables are explained in Table 1.
For simplicity, our current model depends on the
following assumptions. First, the GPU kernels in an
application are uniform and the power consumption
P
GPU
is constant if the clock speed is constant. Simi-
larly, P
CPU
is constant. Secondly, GPU kernels, CPU
computation and communication between CPU and
GPU do not overlap with each other.
Table 1: variables of equation.
P
static
Static node power consumption
P
Comm
Increased node power consumption
for communication between CPU and GPU
P
CPU
Increased node power consumption
for CPUs
P
GPU
Increased node power consumption
for GPU kernels
T
all
Overall execution time
T
Comm
Total execution time of communication
T
CPU
Total execution time of CPU
T
GPU
Total execution time of GPU kernels
The values of variables in Table 1 are affected by
characteristics of applications, characteristics of ar-
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
228

chitecture, and CPU/GPU clock speeds. Thus we con-
struct a model equation for each variable including
these factors. In the following explanation, we pick
up several variables.
3.2.2 Power Model
Here we mainly pick up P
GPU
, GPU power consump-
tion while GPU kernels are running, which accounts
for a large percentage of overall power consumption.
We model P
GPU
as follows.
P
GPU
( f ) = α
kernel
∗ A
GPU
∗V ( f )
2
∗ f (2)
+ β
kernel
∗ B
GPU
+C
GPU
∗V ( f )
The model of P
GPU
consists of three terms. The
first corresponds to the power consumed by the GPU
cores for computation. It is proportional to the GPU
clock frequency f and to the square of the voltage
V ( f ). Since the voltage is automatically determined
by NVML according to f
3
, we let V ( f ) be a func-
tion of f . The power consumption of cores is also
affected both by characteristics of GPU architecture
and those of kernel functions of the application. In
order to express them, we introduce an architecture
parameter A
GPU
and an application parameter α
kernel
,
where 0 ≤ α
kernel
≤ 1. Intuitively, A
GPU
corresponds
to capacitance of GPU cores and α
kernel
corresponds
to compute intensity of the kernel.
The second term of the equation corresponds to
the power consumed by the GPU device memory, and
is derived from an architecture parameter B
GPU
and
an application parameter β
kernel
, where 0 ≤ β
kernel
≤
1. Although it would be more precise if it included
the frequency and the voltage of device memory, the
current GPUs do not provide good control ways for
them. Thus we assume they are fixed and already re-
flected into B
GPU
. β
kernel
corresponds to the memory
access frequency, and larger β
kernel
represents mem-
ory intensive kernels.
The third term corresponds the static power con-
sumption, and we currently assume it is proportional
to the core voltage V ( f ).
This model is used as follows. As the
first step, when the target GPU architecture for
modeling is fixed, the architecture parameters,
V ( f ),A
GPU
,B
GPU
,C
GPU
should be obtained. In order
to determine V ( f ), we execute a simple and extremely
memory intensive benchmark (we assume it has pa-
rameters of α
kernel
= 0,β
kernel
= 1), and measure GPU
power consumption P
GPU
for every supported clock.
3
The relationship between f and voltage on NVIDIA
GPUs is not open information
Since we assume the first term is zero and the sec-
ond term is constant, we can obtain C
GPU
and V ( f )
for every f
4
. Also by observing the constant factor of
the power, we can obtain B
GPU
. Similarly, by measur-
ing GPU power with a highly compute intensive ker-
nel, with α
kernel
= 1,β
kernel
= 0, we can derive A
GPU
.
Now we have obtained architecture parameters for the
given GPU architecture.
The second step is to obtain application param-
eters. In order to support various types of applica-
tions, this step should use simpler methods than in
the first step; we execute test-runs and power mea-
surements twice per application as follows. For a
given application, we execute the first test-run at the
maximum GPU clock to obtain GPU power consump-
tion P
GPU
( f
max
). Also the second test-run is done
at the minimum GPU clock to obtain P
GPU
( f
min
).
With these values and architecture parameters ob-
tained above, we can calculate α and β by solving
simple simultaneous equations.
Using architecture parameters and application pa-
rameters, now we can estimate the GPU power con-
sumption at arbitrary GPU clock speeds.
With similar discussion, we estimate P
CPU
at arbi-
trary CPU clock speeds. As for other power param-
eters P
static
and P
Comm
, we assume that they depend
only on architecture, and are independent from ap-
plication characteristics and clock speeds. Thus we
obtain them by preliminary power measurement.
3.2.3 Performance Model
Here we pick up T
GPU
( f ), the total execution time
of GPU kernels during the application execution. Our
estimation is based on the measured values in prelimi-
nary measurements; we obtain T
GPU
( f
min
) at the min-
imum clock, and T
GPU
( f
max
) at the maximum clock.
From these two values, we estimate T
GPU
( f ) for arbi-
trary f as follows
5
.
T
GPU
( f ) = max(T
GPU
( f
min
) ∗ f
min
/ f ,T
GPU
( f
max
)) (3)
Similarly, we estimate T
CPU
at arbitrary CPU
clock speeds. T
Comm
, which is roughly independent
from clock speeds, is obtained during the preliminary
measurement of the application.
3.3 Hybrid Power Capping Methods
For the dynamic method in Section 3.1, we observed
that a longer control frequency is better for stable con-
trol. With this choice, however, it may take a long
4
Here we assume that V( f
min
) = 1 without loss of gen-
erality.
5
we omit the detail for this for want of space
PowerCappingofCPU-GPUHeterogeneousSystemsusingPowerandPerformanceModels
229

time to settle at the appropriate clock after applica-
tion execution starts. On the other hand, the static
method can find the appropriate clocks before execu-
tion, however, it may suffer from errors in the model
or fluctuation of power consumption.
Based on this discussion, we propose to combine
the two. Before the application execution, we de-
termine the initial GPU/CPU clock speeds based on
the static method. During the execution, we continu-
ously controls the clock speeds by using the dynamic
method.
We describe two variants of the hybrid method,
whose difference appears in the usage of the dynamic
method.
Hybrid1. During the execution, we simply use the
dynamic method.
Hybrid2. During the execution, we also control the
clock speed dynamically, however, it does not ex-
ceed the initial clock obtained using the model.
The performance of this hybrid method is dis-
cussed in the following section in detail.
4 Evaluation
4.1 Methodology
In the experiment, we apply the proposed power cap-
ping methods while a GPU application is running un-
der a given power constraint. We evaluate average
power consumption of the node, excess duration and
the energy consumption among the execution. We use
a computing node with two CPUs and two GPUs (Ta-
ble 2), though each application uses a single CPU core
and a GPU.
Our power capping method has been implemented
in a daemon process, which continuously monitors
power consumption and configures GPU/CPU clock
speeds. We measure the real time power consump-
tion of the node with ”OMRON RC3008”, which
is a portable power distribution unit equipped with
smart power meters. While we measure the power
consumption at every 15 miliseconds, we control the
clock speeds per 5.0 seconds.
We evaluate three application benchmarks shown
in Table 3. We compare power capping methods
shown in Table 4. The hybrid method includes two
variants described in the previous section. In some
experiments, we also show the cases without power
control, ”static max” and ”static min”.
Table 2: CPUs and GPUs in the compute node for evalua-
tion.
CPU
Intel(R) Xeon(R)
CPU E5-2660
GPU NVIDIA K20Xm
CPU Frequencies(MHz)
1200,1300,1400,1500
1600,1700,1800,1900
2000,2100,2200,2201
GPU Frequencies(MHz)
614,640,666,705
732,758,784
Table 3: GPU application benchmarks.
diffusion thermal diffusion simulation
matmul matrix multiplication
gpustream
stream benchmark,
measuring memory
bandwidth for GPU
4.2 Evaluation of Power Consumption
and Excess Duration
Figure 3 shows average power consumption during
execution of each application. We observe the aver-
age power consumption is under the constraint in all
cases.
Not only capping average consumption, also re-
stricting power fluctuation is important. Figure 4
shows excess durations, the durations when the power
consumption is exceeding the given constraint. In the
graphs, the durations are normalized to the applica-
tion execution time. We observe that excess durations
tend to be larger with the static method and the dy-
namic max, especially in the case of gpustream with
the constraint of 260W.
In order to analyze this case, we show the dynamic
change of power and clock speeds in figure 5. In
the graph of ”dynamic max”, we see that the appli-
cation starts with the maximum clock, which leads
the excess of power, and it takes about 30 seconds un-
til the clock becomes optimal setting (the minimum
clock in this case). Thus the excess duration gets
larger. With ”static”, the model suggested 640MHz
as the appropriate clock. However, we see that the ac-
tual power consumption sometimes exceeds the con-
straint, and the excess duration reaches about 30%
due to the lack of feedback. On the other hand, with
”hybrid” method, we can reduce the excess duration.
Compared with ”dynamic max”, the excess duration
is even shorter, since the initial clock, which has been
determined with the model, is closer to the appropri-
ate clock than the maximum clock is.
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
230

!"#$
!%#$
!&#$
!'#$
!(#$
!)#$
*##$
!'#$ !(#$ !)#$
Power&consump-on(W)
Power&constraint(W)
+,-./012/0-$ +,-./012/.3$ 45.61$
7,890+:$ 7,890+!$ 45.61$/.3$
45.61$/0-$
[1]diffusion
!"#$
!%#$
!&#$
!'#$
!(#$
!)#$
*##$
*+#$
!(#$ !)#$ *##$
Power&consump-on(W)
Power&constraint(W)
,-./012301.$ ,-./01230/4$ 56/72$
8-9:1,+$ 8-9:1,!$ 56/72$0/4$
56/72$01.$
[2]matmul
!"#$
!%#$
!&#$
!'#$
!(#$
!&#$ !&%$ !'#$ !'%$
Power&consump-on(W)
Power&constraint(W)
)*+,-./0-.+$ )*+,-./0-,1$ 23,4/$
5*67.)8$ 5*67.)!$ 23,4/$-,1$
23,4/$-.+$
[3]gpustream
Figure 3: Average power consumption for each power constraint.
!"
!#$"
!#%"
!#&"
!#'"
("
$)!" $'!" $*!"
Ra#o%of%the%#me%of%excess%
power%constraint%in%
execu#on%#me
Power%constraint(W)
+,-./012/0-" +,-./012/.3" 45.61"
7,890+(" 7,890+$"
[1]diffusion
!"
!#$"
!#%"
!#&"
!#'"
("
$'!" $)!" *!!"
Ra#o%of%the%#me%of%excess%
power%constraint%in%
execu#on%#me
Power%constraint(W)
+,-./012/0-" +,-./012/.3" 45.61"
7,890+(" 7,890+$"
[2]matmul
!"
!#$"
!#%"
!#&"
!#'"
("
$&!" $&)" $*!" $*)"
Ra#o%of%the%#me%of%excess%
power%constraint%in%
execu#on%#me
Power%constraint(W)
+,-./012/0-" +,-./012/.3" 45.61"
7,890+(" 7,890+$"
[3]gpustream
Figure 4: Time of excess power constraint.
600#
650#
700#
750#
800#
0#
100#
200#
300#
0.0##
7.0##
14.1##
21.2##
28.3##
35.4##
42.6##
49.9##
57.0##
64.1##
71.2##
78.4##
85.6##
92.6##
99.6##
GPU$frequency(MHz)
Power$consump7on(W)
Time(sec)
GPU#frequency# Power#constraint#
Node#power#consumpBon#
[1]dynamic max
600#
650#
700#
750#
800#
0#
100#
200#
300#
0.0##
7.6##
15.2##
22.8##
30.5##
38.4##
46.0##
53.6##
61.3##
69.0##
76.7##
84.3##
91.9##
99.7##
GPU$frequency(MHz)
Power$consump7on(W)
Time(sec)
GPU#frequency# Power#constraint#
Node#power#consumpBon#
[2]static
600#
650#
700#
750#
800#
0#
100#
200#
300#
0.0##
7.0##
14.1##
21.3##
28.4##
35.7##
42.8##
49.9##
57.1##
64.2##
71.3##
78.5##
85.5##
92.5##
99.8##
GPU$frequency(MHz)
Power$consump7on(W)
Time(sec)
GPU#frequency# Power#constraint#
Node#power#consumpBon#
[3]hybrid1
Figure 5: Change of the power consumption on gpustream with each power capping technique.
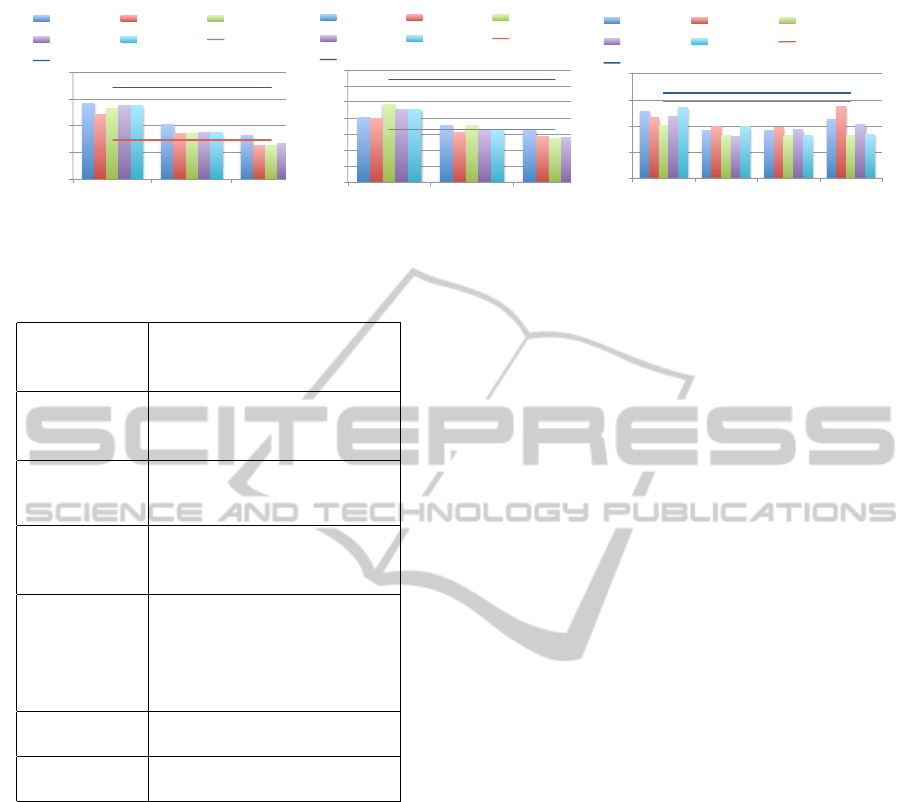
4.3 Evaluation of Energy Consumption
When power capping is achieved well, it is also de-
sirable to restrict the energy consumption during the
application execution. Figure 6 compares energy con-
sumption of GPU applications.
With diffusion and matmul applications, which
are compute-intensive, we observe that energy con-
sumption tends to be smaller with the power con-
straint gets larger (relaxed). This indicates that the
improvement of speed performance outweighs the in-
crease of power consumption. The selection of the
power capping method affects the energy for less than
3%.
On the other hand, the memory intensive appli-
cation, gpustream, demonstrates a different tendency.
Changing the power constraint from 270W to 275W
increases the energy consumption, if we adopt dy-
namic or hybrid1 methods. This is due to the fol-
lowing reason. The speed performance of memory
intensive programs is hardly affected by the clock
speed. Thus using lower clock is not harmful for
such programs. However, when dynamic and hybrid1
methods notice that the current power consumption is
much lower than power constraint, they continuously
raise the clock, which does not improve performance.
On the other hand, the hybrid2 method successfully
avoids this useless rise of clock by introducing the up-
per bound of the clock.
5 RELATED WORK
DVFS has been the most popular method for power
control not only for CPUs but GPUs. The effects
of DVFS on power consumption and performance of
PowerCappingofCPU-GPUHeterogeneousSystemsusingPowerandPerformanceModels
231
18000$
19000$
20000$
21000$
22000$
270$ 280$ 290$
Energy'consump.on(J)
Power'constraint(W)
dynamic_min$ dynamic_max$ sta3c$
hybrid1$ hybrid2$ sta3c$max$
sta3c$min$
[1]diffusion
!"###$
!%###$
!&###$
!'###$
!(###$
!)###$
!*###$
"####$
!)#$ !*#$ "##$
Energy'consump.on(J)
Power'constraint(W)
+,-./012/0-$ +,-./012/.3$ 45.61$
7,890+:$ 7,890+!$ 45.61$/.3$
45.61$/0-$
[2]matmul
16000$
16500$
17000$
17500$
18000$
260$ 265$ 270$ 275$
Energy'consump.on(J)
Power'constraint(W)
dynamic_min$ dynamic_max$ sta4c$
hybrid1$ hybrid2$ sta4c$max$
sta4c$min$
[3]gpustream
Figure 6: Energy consumption.
Table 4: Compared power capping methods.
dynamic min
The dynamic method.
Initial frequency is
the minimum one
dynamic max
The dynamic method.
Initial frequency is
the maximum one
static
The static method.
The frequency is determined
by the model
hybrid1
The hybrid method.
Initial frequency is
determined by the model
hybrid2
The hybrid method.
Initial frequency and
configurable maximum
frequency are determined
by model
static max
The frequency is fixed
at the maximum one
static min
The frequency is fixed
at the minimum one
GPUs have been studied (Jiao et al., 2010; Mei et al.,
2013). Recently Burschen et al (Burtscher et al.,
2014) have investigated one of issues in controlling
current GPUs, the time lag of NVML, and proposed
a technique to recreate power consumption correctly.
While these efforts do not include algorithms to con-
trol power consumption directly, we will improve our
models by harnessing their knowledge.
There are several projects for estimating power
consumption of computer nodes. Some of them have
proposed power model of GPU kernels, which give
the relation between power consumption and perfor-
mance counters(Nagasaka et al., 2010; Song et al.,
2013). On the other hand, our hybrid method assumes
that real time power monitoring is commodity; we can
feedback the measured values.
Komoda et al. (Komoda et al., 2013) have pro-
posed a power capping technique using both DVFS
and task mapping to cap the power consumption of
the systems with GPUs. Unlike our approach, they
assume that users describe applications to enable to
change their load balance between CPU and GPU. In
contrast, our focus is to control power consumption
during execution of arbitrary GPU applications.
Shr
¨
one et al. have discussed measurement and
analysis methods for the energy efficiency of HPC
systems(Sch
¨
one et al., 2014). Their discussion in-
cludes using power model in order to find a CPU
clock frequency that is optimal for better energy ef-
ficiency. Our static method has a similar purpose,
however, we combine a dynamic method and a static
method in order to alleviate the effect of errors in the
model. Our future plan includes an extension to the
whole system, by combining our method with power
aware job scheduling, as they suggest.
6 CONCLUSION AND FUTURE
WORK
We have proposed an efficient power capping method
for compute nodes equipped with accelerators. To
avoid the increase of energy consumption under a
given power constraint, we adopt a hybrid approach
of a model-based static method and a dynamic con-
trolling method. We have shown that the proposed
technique successfully reduces the excess of power
consumption.
Our future work includes extension of our method
for more CPU intensive applications, or applications
that consist of several phases, each of which shows
different characteristics in power and performance.
Also we will extend the methods to the whole HPC
system towards the next-gen energy efficient exascale
systems.
ACKNOWLEDGEMENTS
This research is mainly supported by Japanese
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
232

MEXT, ”Ultra Green Supercomputing and Cloud
Infrastructure Technology Advancement” and JST-
CREST, ”Software Technology that Deals with
Deeper Memory Hierarchy in Post-petascale Era”.
REFERENCES
Burtscher, M., Zecena, I., and Zong, Z. (2014). Measuring
gpu power with the k20 built-in sensor. In Proceed-
ings of Workshop on General Purpose Processing Us-
ing GPUs, pages 28:28–28:;36. ACM.
Endo, T., Nukada, A., and Matsuoka, S. (2014). Tsubame-
kfc : a modern liquid submersion cooling prototype
towards exascale becoming the greenest supercom-
puter in the world. In ICPADS2014, editor, The 20th
IEEE International Conference on Parallel and Dis-
tributed Systems.
Gandhi, A., Harchol-Balter, M., Das, R., and Lefurgy, C.
(2009). Optimal power allocation in server farms. In
Proceedings of the Eleventh International Joint Con-
ference on Measurement and Modeling of Computer
Systems, pages 157–168. ACM.
Jiao, Y., Lin, H., Balaji, P., and W., F. (2010). Power
and performance characterization of computational
kernels on the gpu. In Proceedings of the 2010
IEEE/ACM Int’L Conference on Green Computing
and Communications & Int’L Conference on Cy-
ber, Physical and Social Computing, pages 221–228.
IEEE.
Komoda, T., Hayashi, S., Nakada, T., Miwa, S., and Naka-
mura, H. (2013). Power capping of cpu-gpu hetero-
geneous systems through coordinating dvfs and task
mapping. In Computer Design (ICCD), IEEE 31st In-
ternational Conference, pages 349–356. IEEE.
Laros, J., e. a. (2014). High performance computing - power
aoolication programming interface specification ver-
sion 1.0. In SANDIA REPORT, volume SAND2014-
17061.
Lucas, R. e. a. (2014). Top ten exascale research challenges.
In DOE ASCAC Subcommitte Report.
Matsuoka, S. (2011). Tsubame 2.0 begins - the long road
from tsubame1.0 to 2.0(part two). In e Science Jour-
nal, editor, Global Scientific Information and Comput-
ing Center, volume 3, pages 2–8. Tokyo Institute of
Technology.
Mei, X., Yung, L. S., Zhao, K., and Chu, X. (2013). A
measurement study of gpu dvfs on energy conserva-
tion. In Proceedings of the Workshop on Power-Aware
Computing and Systems, pages 10:1–10:5. ACM.
Nagasaka, H., Maruyama, N., Nukada, A., Endo, T., and
Matsuoka, S. (2010). Statistical power modeling of
gpu kernels using performance counters. In Green
Computing Conference, 2010 International, pages
115–122. IEEE.
Patki, T., Lowenthal, D. K., Rountree, B., Schulz, M., and
de Supinski, B. R. (2013). Exploring hardware over-
provisioning in power-constrained, high performance
computing. In Proceedings of the 27th International
ACM Conference on International Conference on Su-
percomputing, ICS’13, pages 173–182. ACM.
Sch
¨
one, R., Treibig, J., Dolz, M. F., Guillen, C., Navarrete,
C., Knobloch, M., and Rountree, B. (2014). Tools
and methods for measuring and tuning the energy ef-
ficiency of hpc systems. In Scientific Programming,
pages 273–283. IOS Press.
Song, S., Su, C., Rountree, B., and Cameron, K. (2013). A
simplified and accurate model of power-performance
efficiency on emergent gpu architectures. In Parallel
& Distributed Processing (IPDPS), pages 673–686.
IEEE.
PowerCappingofCPU-GPUHeterogeneousSystemsusingPowerandPerformanceModels
233
