A Sensitivity Study of PMU-based Fault Detection on Smart Grid

Richard Barella

, Duc Nguyen

, Ryan Winter

, Kuei-Ti Lu

, Scott Wallace

, Xinghui Zhao

and Eduardo Cotilla-Sanchez

School of Engineering and Computer Science, Washington State University,

14204 NE Salmon Creek Ave., Vancouver, WA 98686, U.S.A.

School of Electrical Engineering and Computer Science, Oregon State University,

3023 Kelley Engineering Center, Corvallis, OR 97331, U.S.A.

Keywords:

Smart Grid, Sensitivity, Fault Detection, Accuracy, PMU Deployment.

Abstract:

Phasor measurement units (PMUs) are widely used in power transmission systems to provide synchronized

measurements for the purpose of fault detection. However, how to efﬁciently deploy those devices across a

power grid – so that a comprehensive coverage can be provided at a relatively low cost – remains a challenge.

In this paper, we present a sensitivity study of a PMU-based fault detection method using three different dis-

tance metrics. This study can serve as a guideline for efﬁcient PMU deployment. To illustrate the effectiveness

of this approach, we have derived an alternative PMU placement plan for a power grid. Experimental results

show that our PMU placement reduces the required PMU deployment by more than 80% as compared to the

original placement, yet still provides similar level of accuracy in fault detection.

1 INTRODUCTION

Phasor measurement units (PMUs), or synchropha-

sors, are devices that are deployed in power systems

to measure phase angles and magnitudes of the elec-

trical waves in real time, for monitoring the health of

the power grid. A signiﬁcant amount of work has

been done in analyzing real-time PMU data for de-

tecting faults (Jiang et al., 2000) (Liang et al., 2014),

oscillations (Liu and Venkatasubramanian, 2008), as

well as tracking fault locations (Chang et al., 2008).

However, these approches assume a comprehensive

coverage of PMUs on the power grid. Due to the in-

stallation cost, instrumenting every bus with PMUs

is not always practical. Therefore, it is critical to efﬁ-

ciently deploy a limited number of PMUs so that com-

prehensive coverage in terms of fault detection can be

provided. Instead of developing fault detection meth-

ods based on a known topology of PMUs on a power

grid, we take a different approach in which we use

an existing fault detection algorithm as a guideline to

derive more efﬁcient PMU placement plans.

As the ﬁrst step toward better deployment of

PMUs, it is essential to quantitively analyze how the

distance between a fault and the PMU(s) used to de-

tect that fault impact the detection process itself. To

this end, we have carried out a sensitivity study of dis-

tances in PMU-based fault detection. Speciﬁcally, we

use a PMU-based fault detection method that we pre-

viously developed as a baseline, and investigate the

accuracy of this method with respect to the distance

between the fault location and the PMUs being uti-

lized Here, three distance metrics are studied: topo-

logical distance, logical distance, and electrical dis-

tance. Topological distance is derived from the sys-

tem schema of the grid, i.e., number of hops between

two sites. Logical distance is the Pearson correla-

tion coefﬁcient which is derived from two PMU data

streams. Electrical distance is derived from the Ybus

of the power grid, representing another way to elu-

cidate the electrical structure of a power grid (Hines

et al., 2010).

The results of the sensitivity study indicate that

there is a potential to accurately detect faults even

when no PMU is placed on a bus immediately adja-

cent to the fault. Rather, fault detection remains accu-

rate within a small neighborhood near the fault, and

then accuracy falls off as distance from the fault in-

creases. This relationship creates an opportunity for

efﬁcient PMU deployment. Speciﬁcally, we use the

results of the sensitivity study as a guideline and de-

velop a PMU placement algorithm which derives de-

ployment solutions based on distance constraints. We

veriﬁed our algorithm using PMU data collected from

a power grid; experimental results show that our PMU

placement plan uses 80% fewer PMUs compared to

185

Barella R., Nguyen D., Winter R., Lu K., Wallace S., Zhao X. and Cotilla-Sanchez E..

A Sensitivity Study of PMU-based Fault Detection on Smart Grid.

DOI: 10.5220/0005453801850192

In Proceedings of the 4th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS-2015), pages 185-192

ISBN: 978-989-758-105-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

the original placement; however, it provides similar

level of accuracy in detecting faults.

The remainder of the paper is organized as fol-

lows. Section 2 reviews related work in both PMU-

based fault detection and PMU placement in a smart

grid. Section 3 introduces the background of this

work, including the fault detection method we use

in this study, as well as a description of the dataset

we use. The experimental results from the sensitivity

study we carried out on three different distances are

presented in Section 4. In Section 5, we develop a

new PMU deployment algorithm which derives pos-

sible PMU placement solutions based on the results

from the sensitivity study. Section 6 concludes the

paper and proposes future directions for this work.

2 RELATED WORK

With the growing popularity of using phasor measure-

ment units (PMUs) to monitor power systems and

enhance their reliability, there is increasing interest

in analyzing real-time PMU data to detect and lo-

cate faults in the power grid. A signiﬁcant amount

of work has been done to detect or monitor certain

conditions of a power grid by leveraging informa-

tion extracted from PMU data. Jiang et al. propose

an online approach for fault detection and localiza-

tion using SDFT (smart DFT) (Jiang et al., 2000).

Liu et al. use Frequency Domain Decomposition for

detecting oscillations (Liu and Venkatasubramanian,

2008). Kazemi et al. propose a multivariable re-

gression model to track fault locations using PMU

data (Chang et al., 2008). A more comprehensive sur-

vey can be found in (Glavic and Van Cutsem, 2011).

These approaches assume a comprehensive PMU de-

ployment across the smart grid. Most recently, with

the emergence of big data analytics, a variety of ma-

chine learning techniques have been applied to an-

alyze PMU data in power grid systems, including

classiﬁcation (Alsafasfeh, 2010), clustering (Antoine

and Maun, 2012), artiﬁcial neural networks (Mishra

et al., 2008), Support Vector Machines (Gomez et al.,

2011), and regression trees (Zheng et al., 2013).

Along with the work of monitoring the power grid

using PMUs, the challenge of optimizing PMU place-

ment has also attracted much attention. This is be-

cause deploying PMUs is expensive and a per-bus

coverage of PMU deployment is not always practi-

cal (Mili et al., 1990). Traditional approaches formu-

late PMU deployment as an optimization problem, in

which the power grid is modeled as a graph, and the

objective is to deploy PMUs at a minimum number of

nodes so that the state of the whole power grid is ob-

servable (Anderson and Chakrabortty, 2012a) (Ander-

son and Chakrabortty, 2012b) (Brueni, 1993) (Haynes

et al., 2002). This problem has been proven to be

NP-complete. It has also been proven that no more

than 1/3 of the nodes in a connected graph of at least

3 nodes are requirement to be equipped with PMUs

in order to provide coverage for the whole power

grid (Brueni and Heath, 2005).

Besides these graph-theoretic approaches, simu-

lation based methods have also been used in devel-

oping optimal placement for PMUs. For instance,

in (Liu et al., 2012), a generic algorithm is proposed to

ﬁnd optimal deployment for heterogeneous measure-

ment devices, including both PMUs and Smart Meter-

ing systems. The results are tested using simulation.

Similar simulation approaches are used in (Zhu et al.,

2009) to evaluate a PMU placement method which

aims for improving the accuracy of state estimation

of the grid. In (Lien et al., 2006), a concept of fault-

location observability is proposed. PMUs are placed

on buses based on the one-bus spaced deployment

strategy, and then the results are tested using simu-

lation. In (Pegoraro et al., 2012), generatation from

renewable sources are considered in the deployment

of PMU and smart metering.

In this paper we propose a novel approach to de-

rive an anytime-optimal PMU placement plan guided

by a sensitivity study of a PMU-based fault detection

method. Our work differs from the previous work in

the following aspects. First, instead of proposing a

theoretical deployment algorithm, we take a practical

approach by developing a fault detection algorithm

ﬁrst, and then carrying out a sensitivity study which

serves as the guideline for PMU deployment. Sec-

ond, instead of using simulation, we used real PMU

data collected over one-year period on a smart grid

in Paciﬁc NorthWest region of the United States of

America.

3 BACKGROUND

In order to derive efﬁcient PMU deployment plans for

a smart grid, we ﬁrst develop a simple fault detection

method, and verify this method using a year worth of

real PMU data collected from a smart grid in the Pa-

ciﬁc NorthWest of the United States of America. The

dataset we used in this study, as well as the fault detec-

tion method are presented in the following sections.

3.1 Dataset

The dataset we use in this research is from Bonneville

Power Administration, the ﬁrst utility agency that im-

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

186

plements a comprehensive adoption of synchropha-

sors in their wide-area monitoring system. The smart

grid is located in paciﬁc northwest area in the United

States, and it contains both 500KV and 230KV buses.

In this grid, there are 31 sites which are equipped

with PMUs to measure voltage, current, and fre-

quency data. The dataset we use in this paper is col-

lected from October 17, 2012 to September 16, 2013.

During this time period, there are 107 documented

faults, including single-line-to-ground faults, line-to-

line faults, and three-phase faults.

3.2 Fault Detection Method

The fault detection method used in this study was de-

veloped based on a theoretical analysis on the charac-

teristics of faults, as well as the BPA datasets (Liang

et al., 2014). The algorithm is a threshold based

decision tree, which classiﬁes faults into the three

fault types – single-line-to-ground, line-to-line, and

three-phase – using the voltage sag values on all three

phases. This fault detection method classiﬁes faults

based on a set of pre-deﬁned threshold values on

voltage sags, which are calculated by surveying the

dataset for the voltage sag values during the same

type of faults. The voltage sag values are in p.u., nor-

malized with respect to the voltage level at the steady

state of that phase.The steady state voltage magnitude

is calculated as follows: 1) use a sliding window to

scan a period before the fault occurs; 2) calculate the

median of voltage magnitude within the window; 3)

if the ﬂuctuation of the voltage magnitude in the win-

dow is within a small range, we consider the median

of voltage steady state; otherwise we keep searching

by moving the sliding window forward, until we ﬁnd

a steady state.

It has been shown that the accuracy of this method

is more than 96% (Liang et al., 2014). Further, it is

worth noting that we develop this simple fault detec-

tion technique to serve as a baseline for our sensitivity

study, but the approach presented in this paper is not

limited to this fault detection method. Any other ap-

proaches for fault detection could also be used for this

purpose.

4 SENSITIVITY STUDY

When a fault occurs on a power grid, the signature is

typically visible at nearby locations although the sig-

nature is typically reduced in magnitude. This fact

makes it possible to optimize the PMU placement by

removing PMUs which provide redundant coverage.

To fully understand the impact of distances on smart

grid fault detection, we have carried out a sensitivity

study on the fault detection method described in Sec-

tion 3. Speciﬁcally, we have investigated the accuracy

of the method when fault signatures are observed by

PMUs at different locations on the power grid.

Site1 (Faulted Site)

Site2

Site3

Site4

dis(1,3)

dis(1,2)

dis(1,4)

FD(t) = SLG

FD(t) = F

Site5

FD(t) = F

dis(2,5)

Figure 1: Impact of a Fault on Smart Grid.

4.1 Distance Metrics

A smart grid consists of a large number of intercon-

nected sites. In order to efﬁciently deploy PMUs

across the grid, we must ﬁrst analyze the impact of

various types of faults on the entire grid. Figure 1

shows an example grid which includes 5 sites. Sup-

pose at certain point in time, a single-line-to-ground

fault (SLG) occurs at Site 1, the impact of this fault

is usually observable from other locations of the grid.

As shown in Figure 1, this impact can be captured

by our fault detection method FD which is executed

on various sites. Here in this example, the fault type

(SLG) is successfully detected at sites 1, 2, and 3.

However, as indicated in Figure1, Site 4 and 5 have

failed to detect the fault, simply because they are fur-

ther away. In this speciﬁc example, if a PMU is de-

ployed on any of the sites 1, 2, or 3, this particular

single-line-to-ground fault can be detected.

As the ﬁrst step toward efﬁcient deployment of

PMUs across a power grid, we have carried out a sen-

sitivity study of our fault detection method with re-

spect to the distances to the faulted locations (sites)

using real PMU data gathered from BPA’s smart grid.

Note that the distance between two sites can be repre-

sented in different ways. In our work, we have inves-

tigated three different distance metrics: topological

distance, logical distance, and electrical distance.

Topological distance, or hop distance, is a dis-

tance metric for estimating geographical distances.

To calculate the topological distance between two

ASensitivityStudyofPMU-basedFaultDetectiononSmartGrid

187

sites, we represent the grid as a graph with intercon-

nected nodes. Each node is a site with a functioning

PMU and edges between nodes are transmission lines

that are also monitored by one or more PMUs

. We

then use Dijkstra’s algorithm (Dijkstra, 1959) to de-

rive the shortest path between any two sites, and con-

struct a distance matrix for the grid. Note that the

topological distance matrix is static for a given smart

grid, because it is derived from the topology of the

grid.

Logical distance is a dynamic distance metric

representing the linear correlation between two data

streams. In this work, we use Pearson correlation

coefﬁcient (PCC) as the metric for logical distance.

The PCC of two data streams X(x

, x

, ..., x

) and

Y (y

, y

, ..., y

) can be calculated as follows:

PCC =

∑

i=1

− X)(y

−Y )

∑

i=1

− X)

∑

i=1

−Y )

(1)

The value of PCC ranges from −1 to 1, represent-

ing the linear relationship between the two PMU data

streams: 0 indicates no linear relationship, 1 and −1

indicate linear relationships, in positive or negative di-

rection.

Electrical distance is an electrical cohesiveness

metric, as proposed in (Cotilla-Sanchez et al., 2012).

The electrical distance between buses i and j is ob-

tained from the quadrant of the ac power ﬂow Jaco-

bian that measures the incremental change in voltage

phase angle difference between i and j for an incre-

mental active power transaction between i and j. This

power ﬂow Jacobian is itself computed from a combi-

nation of the Y

bus

(nodal admittance matrix), and gen-

eration and load information. In this particular set

of experiments we build a ‘nominal’ power ﬂow Ja-

cobian by assuming that power injections are small

increments, whereby the Jacobian is basically inher-

ited from the Y

bus

structure (this is analogous to a ‘ﬂat

start’ before solving the power ﬂow problem).

The above three metrics represent distances be-

tween sites in different ways. However, they are also

related. For example, the topological distance, i.e.,

hop distance, has been shown to be a good indica-

tor for electrical distance. Figure 2 shows a box-

plot which depicts the relationship between these two

types of distances derived from our dataset. As shown

in Figure 2, the electrical distance increases when the

topological distance increases. Note that a topological

Note that this method of deriving the connectivity

graph means ensures that our representation is a subset of

the underlying power grid’s full connectivity (other paths

between sites may exist)

Figure 2: Topological Distance vs. Electrical Distance.

distance of −1 indicates that the two sites are not con-

nected by a path that is monitored by PMUs. Those

sites generally have higher electrical distances too, as

shown in the ﬁgure.

4.2 Fault Detection Sensitivity

With the three distance matrices being calculated, we

can then analyze the accuracy of our fault detection

algorithm presented in Section 3 across the whole

smart grid, with respect to the distance to the faulted

site.

4.2.1 Topological Distance

For each documented fault in our dataset, we ﬁrst

execute our fault detection algorithm on every PMU

site, using the data being recorded during the time

of the fault, then we compare the results with the

ground truth (the recorded fault type), to determine

whether the fault is correctly detected on each site.

We then associate each result with the topological dis-

tance between the site where the data is collected and

the faulted site. After all the faults have been ana-

lyzed, we calculate the accuracy of our fault detection

method on a certain topological distance.

Figure 3 shows the histogram of the accuracy of

the the fault detection method at various of distances

away from the location of the fault. There is a clear

correlation between the accuracy of the fault detec-

tion method and the topological distance from the

fault location to the PMU where the data is collected.

Speciﬁcally, if the PMU is located within 2 hops from

the fault location, the accuracy of our fault detection

method is above 80% for all 107 recorded faults in the

dataset. The accuracy decreases as topological dis-

tance increases.

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

188

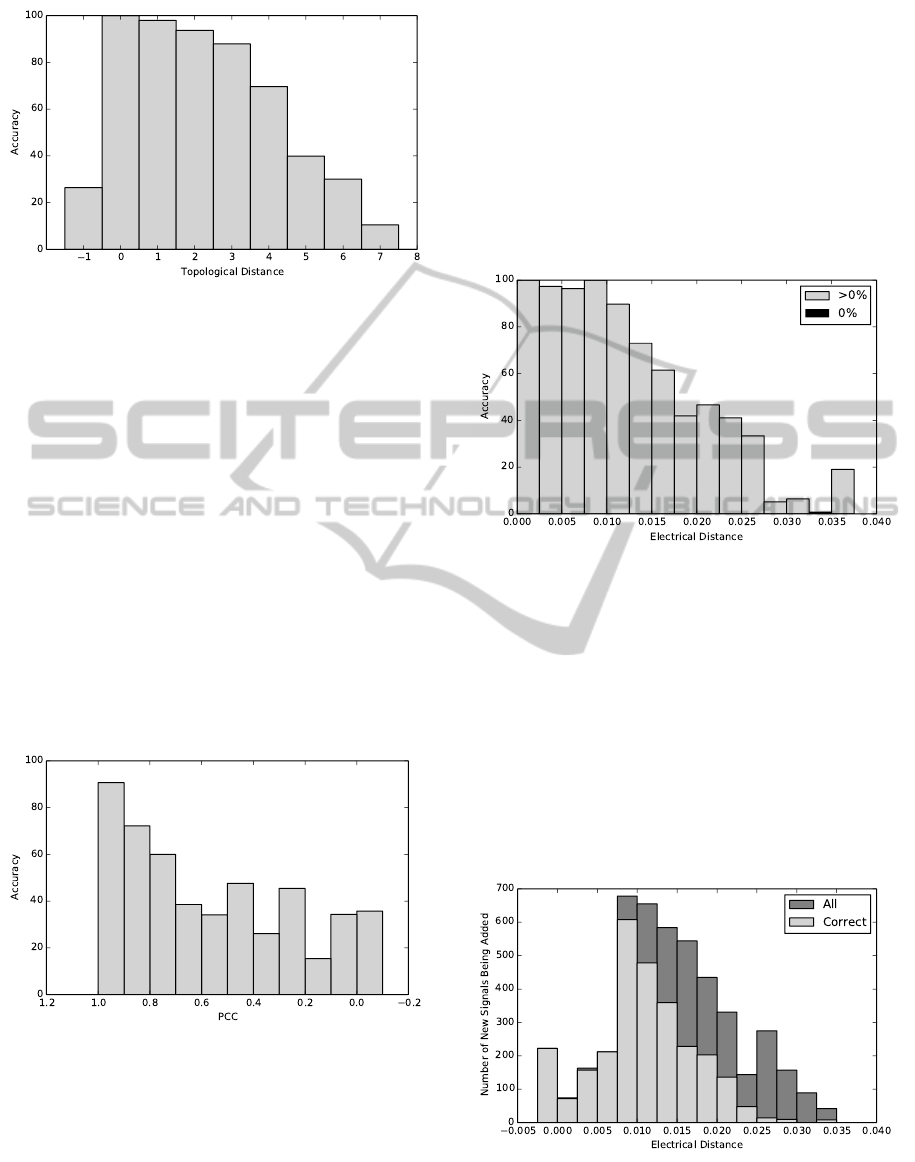
Figure 3: Accuracy vs. Topological Distance.

4.2.2 Logical Distance

We represent logical distance between two sites us-

ing Pearson correlation coefﬁcient (PCC) as shown in

Equation 1. This distance metric models the similar-

ity of two data streams within a certain period of time,

therefore it is a dynamic metric which changes over

time. In our study, we calculate logical distance using

a 15-second time window preceding a fault, and ana-

lyze the accuracy of the fault detection method with

respect to this distance metric. Speciﬁcally, for each

fault, we ﬁrst calculate the logical distance between

the fault location and any other PMU site using the

15-second time window before the fault, then we ex-

ecute the fault detection method using the data col-

lected at each of the non-fault site, and associate the

accuracy with the logical distance.

Figure 4: Accuracy vs. Logical Distance.

The results of the sensitivity analysis with respect

to the logical distance are shown in Figure 4. In gen-

eral, the fault detection methods has higher accuracy

when it is executed on a PMU site which has higher

correlation with the fault location.

4.2.3 Electrical Distance

Similarly, we have carried out a sensitivity study on

electrical distance, which is a static distance metric

derived from the schema of the smart grid, as de-

scribed in Section 4.1. The results are shown in Fig-

ure 5. As expected, the accuracy of our fault detec-

tion method decreases when the electrical distance to

the fault location increases. However, the accuracy is

close to 100% when the electrical distance is within

0.010.

Figure 5: Accuracy vs. Electrical Distance.

To further investigate the electrical distance, we

have calculated the number of added signals when

we gradually increase the electrical distance bound-

ary. Figure 6 shows the results. Green indicates the

signals on which the fault detection method can accu-

rately detect faults, while blue bars indicate the total

set of signals for within a speciﬁc electrical distance

from the fault’s source. When the electrical distance

is within 0.010, the fault detection method is accurate

for most of the signals. When the boundary increases,

more signals result in incorrect detection results.

Figure 6: Electrical Distance vs. Sites.

The sensitivity study presented in this section indi-

cates that it is not necessary to deploy PMUs at every

ASensitivityStudyofPMU-basedFaultDetectiononSmartGrid

189

site in a smart grid. This is simply because most of

the faults can be detected from a site which is within

a certain distance from the fault location.

5 PMU DEPLOYMENT

Based on the sensitivity study, we can derive an im-

proved PMU deployment plan for the smart grid.

Here we use the topological distance as an example

to illustrate this approach.

The sensitivity study suggests that the accuracy of

our fault detection method is reasonably good when

the PMU is located within two hops from the fault.

Based on this observation, we have developed a PMU

placement algorithm which deploys PMUs in the way

that each site in the smart grid is less than or equal to

n hops away from a PMU. Algorithm 1 shows how a

PMU placement plan is derived.

Algorithm 1: PMU Placement.

randomly pick a site S

;

place PMU at S

;

.distance = 0;

Queue.push(S

);

while Queue is not empty do

nextSite = Queue.pop();

currentDistance = nextSite.distance;

if nextSite.distance ≤ 2 then

Visited.append(nextSite);

for neighbor in nextSite’s neighborset

if neighbor is not visited then

neighbor.distance =

nextSite.distance+1;

Queue.push(neighbor);

end

else

place PMU at nextSite;

nextSite.distance = 0;

Queue.push(nextSite);

end

if Queue is empty && not all sites are

visited then

randomly pick an unvisited site;

Place PMU at newSite;

newSite.distance = 0;

Queue.push(newSite);

end

The algorithm randomly picks a starting site to

place a PMU, then traverses the grid while iteratively

placing PMUs on the sites as needed. Depending on

the staring site, and choices made during the course

of execution, the algorithm may return different solu-

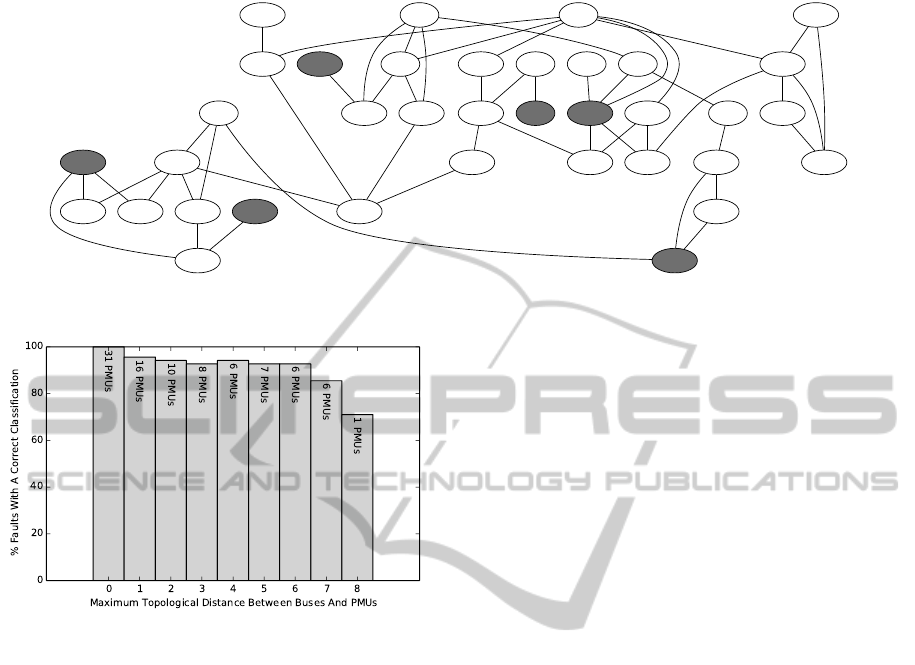
tions. Figure 7 shows an example placement solution

which uses only 6 PMUs (highlighted in gray in the

ﬁgure), as opposed to 31 in the original smart grid

schema.

The placement is derived with a topologi-

cal distance constraint of 3, which means that any site

on the smart grid is less than or equal to 3 hops away

from a site with a PMU.

To evaluate the PMU placement plan shown in

Figure 7, we have simulated a smart grid with these

6 PMUs, and execute our fault detection method us-

ing data from these 6 PMUs. For the 107 recorded

faults, the accuracy of the fault detection on the 6-

PMU smart grid is 93.9%, only 2.1% less than the

accuracy of the original smart grid with 31 PMU-

equipped sites (96%). These results illustrate that it is

possible to accurately detect faults using signiﬁcantly

less PMUs, creating the opportunities of cost savings

for PMU deployment.

Since our PMU placement approach shown in Al-

gorithm 1 can generate a number of different solutions

for one distance constraint, to illustrate the accuracy

of the new PMU placement plans generated by this

algorithm, we randomly picked some placement so-

lutions generated by our PMU deployment algorithm

using various of distance constrants, and calculated

their accuracy. Figure 8 shows a comparison of the

accuracy of these solutions with respect to their dis-

tance constraints. The number of PMUs of each solu-

tion is also noted in the ﬁgure. As shown in the ﬁgure,

it is possible to achieve more than 90% of accuracy

in fault detection with only 6 PMUs. As expected,

when the distance constraint increases, the accuracy

descreases, so does the number of required PMUs.

Based on a recent cost analysis report by Department

of Energy (Department Of Energy, 2014), the average

cost per PMU ranges from $40k to $180k, which in-

cludes cost for procurement, installation and commis-

sioning. Therefore, our work can potentially result in

signiﬁcant cost savings for a smart grid.

The actual site names are not displayed in Figure 7

due to security reasons. Figure 7 shows 36 sites because

we included 5 sites which do not have PMUs installed in

the original grid, in order to maintain the original topol-

ogy. Note that the new PMU deployment plan we generated

only places PMUs on the sites that are PMU-equipped in

the original power grid.

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

190

Site33

Site18

Site28 Site27Site14

Site29 Site31

Site35

Site12

Site5

Site34

Site36

Site1

Site2

Site10

Site11 Site32

Site3

Site22

Site23

Site4

Site17

Site9 Site6

Site7

Site21

Site25

Site8

Site15Site20

Site19

Site24

Site30

Site26

Site13Site16

Figure 7: An Example PMU Placement Plan (PMU sites are highligthed in gray).

Figure 8: Comparison of PMU Placement Plans.

6 CONCLUSION

Synchrophasors are widely used in power grids to en-

hance situation awareness, and robustness of power

delivery. A signiﬁcant amount of work has been done

in fault detection using PMU data. However, these

approaches assume a predeﬁned PMU deployment

scheme across the smart grid. Since deploying PMUs

is costly, it is not necessarily practical or scalable to

equip every bus with a PMU. A more cost-effective

solution for PMU deployment is needed.

While traditional approaches usually simulate the

power grid and derive efﬁcient PMU deployment

plans, in this paper, we take a novel approach to in-

vestigate ways to efﬁciently deploy PMUs across a

power grid based on the accuracy of detecting faults.

The goal of this work is to deploy the fewest PMUs

while still providing comprehensive coverage in terms

of fault detection. Speciﬁcally, we ﬁrst developed a

fault detection method based on voltage sags of three

phases, and then carried out a sensitivity study on the

accuracy of this method, with respect to the distance

from the fault location. To this end, we have investi-

gated three different types of distances, namely topo-

logical distance, logical distance, and electrical dis-

tance. The sensitivity study shows that our fault de-

tection method can achieve high accuracy when it is

executed using data collected within certain distance

to the fault location. This creates opportunities to de-

tect faults using less PMUs. We then developed a

PMU deployment algorithm which derives valid so-

lutions for PMU deployment based on a pre-deﬁned

distance constraint. The evaluation results show that

our new PMU deployment plan can achieve high ac-

curacy with less than one-ﬁfth of PMUs originally de-

ployed in the smart grid.

Our work is ongoing in several directions. First,

we will develop new fault detection approaches us-

ing machine learning techniques, such as classiﬁca-

tion and clustering. Second, we will create visualiza-

tion tools based on our study, for enhancing the real-

time situation awareness of a smart grid. Third, we

will investigate the possibilities to repurpose our fault

detection techniques for solving other problems on a

smart grid, such as data cleansing, and cyber security

challenges.

ACKNOWLEDGEMENT

The generous support from Bonneville Power Admin-

istration and OregonBest through the NW Energy XP

Award is gratefully acknowledged. The authors also

would like to thank Bonneville Power Administration

for providing PMU data used in this research.

REFERENCES

Alsafasfeh, Q. H. (2010). Pattern Recognition for Fault De-

tection, Classiﬁcation, and Localization in Electrical

Power Systems. PhD thesis, Kalamazoo, MI, USA.

ASensitivityStudyofPMU-basedFaultDetectiononSmartGrid

191

Anderson, J. and Chakrabortty, A. (2012a). A Minimum

Cover Algorithm for PMU Placement in Power Sys-

tem Networks Under Line Observability Constraints.

In IEEE Power and Energy Society General Meeting,

pages 1–7.

Anderson, J. and Chakrabortty, A. (2012b). Graph-

Theoretic Algorithms for PMU Placement in Power

Systems Under Measurement Observability Con-

straints. In the 3rd IEEE International Conference

on Smart Grid Communications (SmartGridComm),

pages 617–622.

Antoine, O. and Maun, J.-C. (2012). Inter-Area Oscilla-

tions: Identifying Causes of Poor Damping using Pha-

sor Measurement Units. In IEEE Power and Energy

Society General Meeting, pages 1–6.

Brueni, D. J. (1993). Minimal PMU Placement for Graph

Observability: A Decomposition Approach.

Brueni, D. J. and Heath, L. S. (2005). The PMU Placement

Problem. SIAM J. Discret. Math., 19(3):744–761.

Chang, G., Chao, J.-P., Huang, H.-M., Chen, C.-I., and

Chu, S.-Y. (2008). On tracking the source location

of voltage sags and utility shunt capacitor switching

transients. IEEE Transactions on Power Delivery,

23(4):2124–2131.

Cotilla-Sanchez, E., Hines, P., Barrows, C., and Blumsack,

S. (2012). Comparing the Topological and Electrical

Structure of the North American Electric Power In-

frastructure. IEEE Systems Journal, 6(4):616–626.

Department Of Energy (2014). Factors Affecting PMU

Installation Costs. https:// www.smartgrid.gov/

sites/ default/ ﬁles/ doc/ ﬁles/ PMU-cost-study-ﬁnal-

10162014.pdf. Accessed: 2015-03-24.

Dijkstra, E. (1959). A Note on Two Problems in Connexion

with Graphs. Numerische Mathematik, 1(1):269–271.

Glavic, M. and Van Cutsem, T. (2011). A short survey

of methods for voltage instability detection. In IEEE

Power and Energy Society General Meeting, pages 1–

Gomez, F., Rajapakse, A., Annakkage, U., and Fernando,

I. (2011). Support vector machine-based algorithm

for post-fault transient stability status prediction using

synchronized measurements. Power Systems, IEEE

Transactions on, 26(3):1474–1483.

Haynes, T. W., Hedetniemi, S. M., Hedetniemi, S. T., and

Henning, M. A. (2002). Domination in Graphs Ap-

plied to Electric Power Networks. SIAM J. Discret.

Math., 15(4):519–529.

Hines, P., Blumsack, S., Cotilla Sanchez, E., and Barrows,

C. (2010). The topological and electrical structure of

power grids. In Proceedings of the 43rd Hawaii In-

ternational Conference on System Sciences (HICSS),

pages 1–10.

Jiang, J.-A., Yang, J.-Z., Lin, Y.-H., Liu, C.-W., and Ma,

J.-C. (2000). An adaptive pmu based fault detec-

tion/location technique for transmission lines. i. the-

ory and algorithms. IEEE Transactions on Power De-

livery, 15(2):486–493.

Liang, X., Wallace, S., and Zhao, X. (2014). A technique

for detecting wide-area single-line-to-ground faults.

In Proceedings of the 2nd IEEE Conference on Tech-

nologies for Sustainability (SusTech 2014), SusTech

’14, pages 1–4. IEEE.

Lien, K.-P., Liu, C.-W., Yu, C.-S., and Jiang, J.-A. (2006).

Transmission Network Fault Location Observability

with Minimal PMU Placement. IEEE Transactions

on Power Delivery, 21(3):1128–1136.

Liu, G. and Venkatasubramanian, V. (2008). Oscillation

monitoring from ambient pmu measurements by fre-

quency domain decomposition. In IEEE International

Symposium on Circuits and Systems (ISCAS 2008),

pages 2821–2824.

Liu, J., Tang, J., Ponci, F., Monti, A., Muscas, C., and Pe-

goraro, P. (2012). Trade-Offs in PMU Deployment for

State Estimation in Active Distribution Grids. Smart

Grid, IEEE Transactions on, 3(2):915–924.

Mili, L., Baldwin, T., and Adapa, R. (1990). Phasor Mea-

surement Placement for Voltage Stability Analysis of

Power Systems. In Proceedings of the 29th IEEE Con-

ference on Decision and Control, pages 3033–3038.

Mishra, S., Bhende, C., and Panigrahi, K. (2008). Detec-

tion and Classiﬁcation of Power Quality Disturbances

Using S-Transform and Probabilistic Neural Network.

IEEE Transactions on Power Delivery, 23(1):280–

287.

Pegoraro, P., Tang, J., Liu, J., Ponci, F., Monti, A., and

Muscas, C. (2012). Pmu and smart metering deploy-

ment for state estimation in active distribution grids.

In IEEE International on Energy Conference and Ex-

hibition (ENERGYCON), pages 873–878.

Zheng, C., Malbasa, V., and Kezunovic, M. (2013). Re-

gression Tree for Stability Margin Prediction Using

Synchrophasor Measurements. Power Systems, IEEE

Transactions on, 28(2):1978–1987.

Zhu, K., Nordstrom, L., and Ekstam, L. (2009). Applica-

tion and Analysis of Optimum PMU Placement Meth-

ods with Application to State Estimation Accuracy. In

IEEE Power Energy Society General Meeting, pages

1–7.

SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems

192