Accurate Detection and Visualization of 3D Shape Deformation

by using Multiple Projectors

Masayasu Yoshigi, Fumihiko Sakaue and Jun Sato

Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Japan

Keywords:

Shape Deformation Detection, Projector-projector Systems, Object Deformation Visualization, Super-

resolution.

Abstract:

In this paper, we propose a method for detecting the deformation of object shape by using multiple projectors.

In this method, a set of specially coded patterns are projected onto a target object from multiple projectors.

Then, if the target object is not deformed, the object is illuminated by plain white color, and if the object is

deformed, it is illuminated by radical colors. Thus, we can visualize and detect the deformation of object just

by projecting lights from multiple projectors. The proposed method uses the disparities of multiple projectors,

and thus, we do not any complicated method for detecting object shape deformation. In addition, we utilize

image super-resolution technique for object deformation visualization, so that we can visualize extremely

small deformation easily.

1 INTRODUCTION

Object shape measurement is very important in many

ﬁelds such as industry, 3D event detection and so on.

In particular, 3D shape reconstruction is the most im-

portant challenge in the ﬁeld of computer vision. In

ordinary cases, stereo camera systems composed of

multiple cameras are used for 3D object measure-

ment. In this method, several images are taken by

multiple cameras, and 3D shape are estimated from

the set of images (Hartley and Zisserman, 2000). By

using this reconstructed 3D information, many kinds

of applications such as event detection are done.

For this purpose, the projector-camera (active

camera) systems are also used for 3D shape mea-

surement in recent years. For example, the Mi-

crosoft Kinect is used for various kinds of applica-

tions. In these method, a speciﬁc pattern is projected

from the projector to the scene, and is observed by

a camera. Then, we can reconstruct 3D shape from

the relationship between projected patterns and ob-

served images. In many cases, 3D reconstruction

from projector-camera systems is more stable and ac-

curate than that from ordinary multiple camera sys-

tems, since the projector-camera systems can project

corresponding points explicitly and extraction of cor-

responding points is much easier and denser than the

ordinary stereo camera systems.

In recent years, a projector-projector system was

also proposed for visualizing 3D information of ob-

jects (Sakaue and Sato, 2011). In this method, mul-

tiple patterns projected from multiple projectors are

combined physically on the surface of object, and

the combined lights on the object surface represent

the 3D information of the object. This method uses

the disparity of multiple projector images efﬁciently

for visualizing the 3D information just by project-

ing coded lights from projectors. For example, it

can visualize 3D information such as the distance

from the projector to the object and the height of ob-

ject by using color as shown in Fig.1. This method

does not require 3D measurements from sensing sys-

tems, and thus it does not need any sensing devices

such as cameras and sensing costs of computer. The

projector-projector system also enables us to avoid

system delays caused by sensing and computation,

since it does not need any sensing and computation

for obtaining 3D information and visualizing it. This

is a very big advantage for industrial applications, and

hence several methods have been proposed based on

this framework(R. Nakamura, 2010; S. Takada, 2014;

K. Suzuki, 2013). In addition, we can obtain 3D infor-

mation easily just taking the scene by using the cam-

era devices and just simple image processing such as

color detection.

However, unfortunately these methods cannot vi-

sualize detail structure of the scene because of the

limit of projector resolution. Thus, we in this pa-

577

Yoshigi M., Sakaue F. and Sato J..

Accurate Detection and Visualization of 3D Shape Deformation by using Multiple Projectors.

DOI: 10.5220/0005455405770582

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (MMS-ER3D-2015), pages 577-582

ISBN: 978-989-758-090-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

(a) Distance visualization (b) Height visualization

Figure 1: Distance visualization by projector-projector sys-

tem. In ﬁgure(a), objects are colored by red, yellow and

green when objects are arranged near, middle and far from

projectors, respectively. In ﬁgure(b), height from ﬂoor is

visualized by green, yellow and red.

Figure 2: 3D structure visualization by using projection

from multiple projectors.

per propose a new projector-projector coordination

method, which enables us to visualize very tiny de-

formation of object shape just by projecting images

from multiple projectors. For this objective, we use

more than 3 projectors, and realize super-resolution

visualization of object deformation.

2 OBJECT EMPHASIS BY USING

MULTIPLE PROJECTORS

2.1 Object Shape Emphasis

We ﬁrst introduce the detail of object shape emphasis

using multiple projectors. Nakamura et al.(R. Naka-

mura, 2010) proposed 3D structure visualization us-

ing multiple projectors. By using their method, we

(a) Target surface

(b) Projection result

Figure 3: Visualization of surface deformation from 2 pro-

jectors.

(a) without deformation

(b) with deformation

Figure 4: Visualization of surface deformation from 2 pro-

jectors.

can visualize arbitrary 3D structure just by projecting

speciﬁc images from multiple projectors. We summa-

rize their method in this section.

Let us consider the case where we visualize the

3D space as shown in Fig.2. In this case, an object

situated at the center of the region is colored by red,

and an object situated at the other regions is colored

by white. In this case, the object position is visualized

by colors, and thus we can catch the 3D position of the

object intuitively. Figure 2 shows the result of visu-

alized position by their method. As shown in Fig. 2,

the object is colored by red when it exists at the center

region, and it is colored by white when it exists at the

other region.

2.2 Object Deformation Visualization

The 3D structure visualization described in the previ-

ous section can be extended to visualization of arbi-

trary 3D structures if we can use inﬁnite number of

projectors. However, we can use limited number of

projectors in reality, and thus, we cannot visualize ar-

bitrary 3D structure. This is because projected images

from projectors are 2-dimensional images, while the

object has 3-dimensional structure in general.

In order to avoid this problem, Takada et

al.(S. Takada, 2014) proposed a method for empha-

sizing 3D surface just by using 2 projectors. In their

method, they focused not on 3D structure but on 3D

surface. In this case, we only need to consider pro-

jected pattern on a 2-dimensional curved surface, and

thus we can emphasize object surface by using only 2

projectors. Figure 3 shows the basic principle of this

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

578

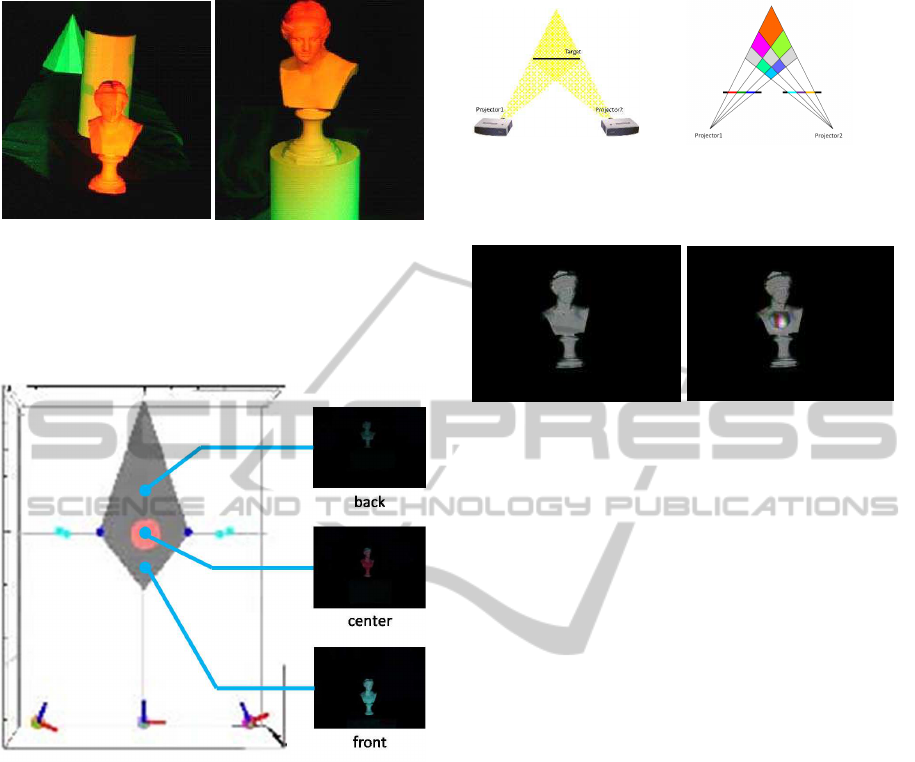
Figure 5: Image super-resolution by superimposed images.

method. The object shown in Fig. 3 (a) is illuminated

by a set of projectors. Then, 2 images projected from

2 projectors are combined on the object surface. The

projected images has complementary colors, e.g. red

and cyan, at a pair of corresponding pixels. Then, the

combined color at the object surface becomes white

when the target object is at the calibrated position. If

the object surface is deformed or moved from the cal-

ibrated position, the pair of corresponding pixels of 2

projectors changes, and thus the observed color also

changes as shown in Fig.3 (b). Thus, we can visual-

ize the changes in object shape by using the changes

in projected colors on the object surface.

The method can visualize object deformation just

by projecting speciﬁc patterns from multiple projec-

tors. However, the accuracy of visualization strongly

depends on the resolution of projected images. There-

fore, we need high resolution projectors if we want

to visualize small deformation of object shape. How-

ever, the resolution of projectors is determined by dis-

play devices such as DLP and LCD, and thus their

resolution is physically limited.

3 SUPER-RESOLUTION OF

PROJECTED IMAGES

In order to improve the resolution of projected im-

ages, image super-resolution using multiple projec-

tors were invented in recent years (Venkata and

Chang, 2007). In this method, multiple images are

projected from multiple projectors to the same area of

the screen simultaneously as shown in Fig.5. The pro-

jected images have sub-pixel shift as shown in this ﬁg-

ure. Thus, we can represent higher resolution images

by controlling the sub-pixel information efﬁciently.

Let us consider image projection for image super-

resolution. The image projection from each projector

is described by a linear equation as follows:

y = A

(1)

where y indicates a vector which consists of the com-

ponents of an M

′

× N

′

high resolution image, x

indi-

cates a vector which consists of the components of an

M × N low resolution image projected from i-th pro-

jector and A

indicates a projection matrix from the

i-th projector. The j-th column of A

represents the

PSF (Point Spread Function) of j-th pixel of the i-th

projector. Thus, the projected image y consists of a

weighted sum of the PSF.

From Eq.(1), the evaluation function for image su-

per resolution can be described as follows:

E = ||y−

∑

(0 ≤ x

≤ I

max

) (2)

where I

max

is the maximum intensity which can

be projected from the projector. By estimating x

which minimize E in Eq.(2) and projecting them from

the multiple projectors, we can generate a super-

resolution image from superimposed images.

By using the above method, we can utilize higher

resolution projectors virtually, even if we use only

low resolution projectors. Furthermore, the projec-

tion surface is not limited to a planar surface. If

we compute the PSF matrix A

on a curved surface,

the super-resolution images can be generated even

on the curved surface. This means the image super-

resolution can be achieved in the visualization of ob-

ject surface deformation, and we can visualize the

change in shape more precisely, even if we use low

resolution projectors.

4 SUPER-RESOLUTION OF

SHAPE DEFORMATION

VISUALIZATION

4.1 Visualization of Shape Deformation

with Image Super-resolution

Let us consider a method for achieving accurate vi-

sualization of object surface deformation by using a

set of low resolution projectors. The simplest way

to achieve high resolution visualization of surface de-

formation is to compose 2 sets of virtual high reso-

lution projectors, each of which is composed of a set

of low resolution projectors. However, this is not the

most efﬁcient way to improve the accuracy of surface

deformation visualization, since we can only utilize

sub-pixel information of each virtual projector. If we

use sub-pixel information generated by all projectors,

we may be able to visualize object surface deforma-

tion more accurately. Thus, instead of considering the

relationship among a set of projectors in a single vir-

tual projector, we consider the relationship among all

AccurateDetectionandVisualizationof3DShapeDeformationbyusingMultipleProjectors

579

projectors used for visualizing object surface defor-

mation, and derive the most efﬁcient projection pat-

terns of these projectors for improving the accuracy

of surface deformation visualization.

4.2 Efﬁcient Super-resolution

Visualization

In order to realize accurate surface deformation visu-

alization, we deﬁne an evaluation function of projec-

tion patterns.

In the surface deformation visualization, we gen-

erate projection patterns, so that the object is colored

by white if there is no deformation, and is colored by

the other colors if there exist surface deformations.

Thus, for evaluating the whiteness of object surface

with original shape, we deﬁne the following evalua-

tion function:

= ||w−

∑

(0 ≤ x

≤ I

max

) (3)

where w is a super-resolution white color pattern on

the object surface. By minimizing E

, we can observe

white color on the original object surface. Note that

the white color on the object surface is not necessar-

ily composed of the projection of white color, and it

can be composed of the projection of various colors

from multiple projectors. Also, basis white color on

the original object shape can be changed to arbitrary

colors if we want. For example, we can add shad-

ing information to the basis white color such that the

surface is illuminated by a single light source, which

is useful for visualizing 3D information of original

surface shape. If we use truly white color in Eq.(3),

shading information of object surface disappears.

We next consider the evaluation function for visu-

alizing the deformation of object surface. For accu-

rate surface deformation visualization, the object sur-

face color should be changed drastically when object

shape is changed. The change in color can be rep-

resented by the derivative of the observed color, and

then the derivative should be as large as possible for

efﬁcient deformation visualization. Since the deriva-

tive of the observed color depends on the color of

projected images, the derivative of projected images

should be as large as possible for efﬁcient surface de-

formation visualization. Thus, we deﬁne the second

evaluation function as follows:

= ||

∑

+ ||

∑

(0 ≤ x

≤ I

max

) (4)

where D

and D

indicate the derivative operators in

horizontal and vertical directions. By maximizing

, the image derivatives become large. Note that,

corresponding points among projector images are on

epipolar lines deﬁned by arbitrary two projectors, and

the change in corresponding points caused by the

deformation of object shape occurs on the epipolar

lines. Therefore, the derivatives along the epipolar

lines are important for visualizing the shape deforma-

tion. For example, if the epipolar lines are parallel

to the horizontal axis, we only need to consider hor-

izontal derivatives. Thus, the horizontal and vertical

derivatives in Eq.(4) can be replaced by directional

derivatives along with the epipolar lines.

Since we want to derive projection images so that

they minimize E

and maximize E

, we deﬁne the

evaluation function for visualizing object shape de-

formation as follows:

= wE

− (1− w)E

(5)

where w is a weight. By minimizing E

, we can ob-

tain optimized projection images of multiple projec-

tors for visualizing object surface deformation.

5 EXPERIMENTS

5.1 Environment

We evaluated the proposed method by using multi-

ple projectors. We used 3 projectors as shown in

Fig.6. The resolution of these projected images are

50 × 50. The projector images are projected onto a

target object shown in Fig.7. The object was situ-

ated in front of the projectors. The PSF in projection

matrices A

were measured at each pixel on this ob-

ject. Figure 8 shows examples of the measured PSF.

In this experiment, color images were used, and thus,

PSF for red, green and blue were measured respec-

tively. In these ﬁgures, the bottom left region shows

resized PSF. Note, the resolution of a camera image is

much higher than the resolution of projector images.

Thus, the measured PSF is spread over some pixels in

these images. By using the PSF, the projection images

for visualizing object surface deformation were com-

puted. The computed images for each projector are

shown in Fig.9. For comparison, projection images

for not only 3 projectors, but also 2 projectors were

computed. These images were projected onto the tar-

get object simultaneously from multiple projectors.

5.2 Results

Figure10 shows illuminated results when the target

object was situated at the original position. As shown

in this ﬁgure, although the target object was slightly

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

580

Figure 6: Experimental Environment.

Figure 7: Target object.

(a) PSF (Red) (b) PSF (Green) (c) PSF (Blue)

Figure 8: Examples of measured PSF.

(a) Projected images for 3 projectors.

(b) Projected images for 2 projectors.

Figure 9: Images projected by 3 projectors and 2 projectors.

colored, the object was observed as it is illuminated

by an ordinary single white light source. In particu-

lar, the result projected by 3 projectors is more close

to white and better, since the projected images can ap-

proach to ideal result by using larger number of pro-

jectors.

We next translated the object with 3 mm. This ob-

ject translation indicates whole shape deformation of

(a) by 3 projectors (b) by 2 projectors

Figure 10: Observed results when the object was situated at

the original position.

(a) by 3 projectors (b) by 2 projectors

Figure 11: Observed results when the object was moved

from the original position.

the target object. The observation result is shown in

Fig.11. As shown in this ﬁgure, the appearance of the

target object was drastically changed, and the object

was colored by various colors. These results show

that the proposed method can visualize the change in

object surface accurately. In addition, we can detect

object shape deformation by using simple image pro-

cessing method such as color detection.

From the comparison of results of 2 projectors and

3 projectors in Fig.11 (a) and (b), we ﬁnd that larger

change in appearance occurs in 3 projectors than in 2

projectors. The result indicates that we can visualize

the deformation of object shape more efﬁciently and

accurately by using larger number of projectors.

5.3 Evaluations

We next evaluate the accuracy of the proposed

method. In this experiment, target object was moved

step by step, and the change of appearance was eval-

uated at each distance. An object shown in Fig 7 was

used as a target object. For comparison, the target ob-

ject was illuminated by 2 different projector systems,

that is 2 projector system and the proposed 3 projec-

tor system.

Figure 12 shows the changes in appearance in the

2 projector system and the 3 projector system re-

AccurateDetectionandVisualizationof3DShapeDeformationbyusingMultipleProjectors

581

spectively. In this ﬁgure, the horizontal axis shows

the magnitude of object motion and the vertical axis

shows the RMS difference of intensity from that at the

original position. As shown in this ﬁgure, when we

use the 3 projector system, the change in appearance

is larger than that of the 2 projector system. From

these results, we ﬁnd that the proposed method can

visualize object surface deformation more efﬁciently

and accurately.

Figure 12: Relationship between object motion and change

in appearance.

6 CONCLUSIONS

In this paper, we proposed a method for visualiz-

ing/detecting the deformation of object surface by

using the disparity in multiple projector images, in

which the deformation of object surface is visualized

by color information. In order to visualize the small

shape deformation accurately, we utilized the image

super-resolution technique. By using the proposed

method, we can use the sub-pixel information of pro-

jected images efﬁciently, and can visualize extremely

small object deformation accurately. The experimen-

tal results show that our method can visualize small

shape deformation more accurately than the existing

method. The proposed method does not require com-

puters nor cameras for visualizing the deformation

of object surface once the projector system was cal-

ibrated. Thus, the proposed method is very useful for

many industrial applications such as defect inspection

in factory automation and 3D event detection.

REFERENCES

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-

etry in Computer Vision. Cambridge University Press.

K. Suzuki, F. Sakaue, J. S. (2013). 3d invariants from coded

projection without explicit correspondences. In Proc.

International Conference on Computer Vision and Ap-

plications(VISAPP2013), pages 286–293.

R. Nakamura, F. Sakaue, J. S. (2010). Emphasinzing 3d

structure visually using projection from multiple pro-

jectors. In Proc. Asian Conference on Computer Vi-

sion, pages 619–632.

S. Takada, F. Sakaue, J. S. (2014). 3d object empha-

sis using multiple projectors. In International Con-

ference on Computer Vision Theory and Applica-

tions(VISAPP2014).

Sakaue, F. and Sato, J. (2011). Surface depth computa-

tion and representation from multiple coded projector

light. In Proc. International Workshop on Projector-

Camera Systems(PROCAMS2011), pages 75–80.

Venkata, N. and Chang, N. (2007). Realizing super-

resolution with superimposed projections. In Proc.

International Workshop on Projector-Camera sys-

tems(Procams), pages 1–8.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

582