Maritime Targets Detection from Ground Cameras Exploiting

Semi-supervised Machine Learning

Eftychios Protopapadakis

, Konstantinos Makantasis

and Nikolaos Doulamis

Technical University of Crete, Chania, Greece

National Technical University of Athens, Athens, Greece

Keywords:

Vision-based System, Maritime Surveillance, Semi-supervised Learning, Visual Attention Maps, Vehicle

Tracking.

Abstract:

This paper presents a vision-based system for maritime surveillance, using moving PTZ cameras. The pro-

posed methodology fuses a visual attention method that exploits low-level image features appropriately se-

lected for maritime environment, with appropriate tracker. Such features require no assumptions about envi-

ronmental nor visual conditions. The ofﬂine initialization is based on large graph semi-supervised technique in

order to minimize user’s effort. System’s performance was evaluated with videos from cameras placed at Li-

massol port and Venetian port of Chania. Results suggest high detection ability, despite dynamically changing

visual conditions and different kinds of vessels, all in real time.

1 INTRODUCTION

Management of emergency situations, known to the

maritime domain, can be supported by advanced

surveillance systems suitable for complex environ-

ments. Such systems vary from radar-based to video-

based. The former, however, has two major draw-

backs (Zemmari et al., 2013); it is quite expensive

and its performance is affected by various factors (e.g.

echoes from targets out of interest). The latter, con-

sists of various techniques, each one with speciﬁc ad-

vantages and drawbacks. The majority of such sys-

tems are are controlled by humans, who are respon-

sible for monitoring and evaluating numerous video

feeds simultaneously.

Advanced surveillance systems should process

and present collected sensor data, in an intelligent and

meaningful way, to give a sufﬁcient information sup-

port to human decision makers (Fischer and Bauer,

2010). The detection and tracking of vessels is inher-

ently depended on dynamically varying visual con-

ditions (e.g. varying lighting and reﬂections of sea).

So, to successfully design a vision-based surveillance

system, we have to carefully deﬁne both its operation

requirements and vessels’ characteristics.

On the one hand there are minimum stan-

dards concerning operation requirements (Szpak and

Tapamo, 2011). At ﬁrst, it must determine possible

targets within a scene containing a complex, mov-

ing background. Additionally, the system must not

produce false negatives and keep as low as possible

the number of false positives. Since we are talking

about surveillance system, it must be fast and highly

efﬁcient, operating at a reasonable frame rate and for

long time periods using a minimal number of scene-

related assumptions.

On the other hand, regardless of vessel types vari-

ation, there are four major descriptive categories.

First comes the size, which ranges from jet-skis to

large cruise ships. Secondly, we have the moving

speed. Thirdly, vessels move to any direction, accord-

ing to the camera position, and thus their angle varies

from 0

◦

to 360

◦

. Finally, there is vehicles’ visibility.

Some vessels have a good contrast to the sea water

while others are intentionally camouﬂaged. A robust

maritime surveillance system must be able to detect

vessels having any of the above properties.

1.1 Related Work

This paper focuses on detection and tracking of tar-

gets within camera’s range, rather than their trajec-

tory patterns’ investigation (Lei, 2013; Vandecasteele

et al., 2013) or their classiﬁcation in categories of in-

terest (Maresca et al., 2010). The system’s main pur-

pose is to support end-user in monitoring coastlines,

regardless of existing conditions.

Object detection is a common approach with

583

Protopapadakis E., Makantasis K. and Doulamis N..

Maritime Targets Detection from Ground Cameras Exploiting Semi-supervised Machine Learning.

DOI: 10.5220/0005456205830594

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (MMS-ER3D-2015), pages 583-594

ISBN: 978-989-758-090-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

mayny variations; i.e. an-isotropic diffusion (Voles,

1999), which has high computational cost and per-

forms well only for horizontal and vertical edges,

foreground object detection /image color segmenta-

tion fusion (Socek et al., 2005). In (Albrecht et al.,

2011a; Albrecht et al., 2010) a maritime surveillance

system mainly focuses on ﬁnding regions in images,

where is a high likelihood of a vessel being present,

is proposed. Such system was expanded by adding a

sea/sky classiﬁcation approach using HOG (Albrecht

et al., 2011b). Vessel classes detection, using a trained

set of MACH ﬁlters was proposed by (Rodriguez Sul-

livan and Shah, 2008).

All of the above approaches adopt ofﬂine learn-

ing methods that are sensitive to accumulation errors

and difﬁcult to generalize for various operational con-

ditions. (Wijnhoven et al., 2010) utilized an online

trained classiﬁer, based on HOG. However, retrain-

ing takes place when a human user manually anno-

tates the new training set. In (Szpak and Tapamo,

2011) an adaptive background subtraction technique

is proposed for vessels extraction. Unfortunately,

when a target is almost homogeneous is difﬁcult, for

the background model, to learn such environmental

changes without misclassifying the target.

More recent approaches, using monocular video

data, are the works (Makantasis et al., 2013) and

(Kaimakis and Tsapatsoulis, 2013). The former, uti-

lizes a fusion of Visual Attention Map (VAM) and

background subtraction algorithm, based on Mixture

Of Gaussians (MOG), to produce a reﬁned VAM.

These features are fed to a neural network tracker,

which is capable of online adaptation. The lat-

ter, utilized statistical modelling of the scene’s non-

stationary background to detect targets implicitly.

The work of (Auslander et al., 2011) emphasize

on algorithms that automatically learn anomaly de-

tection models for maritime vessels, where the tracks

are derived from ground-based optical video, and no

domain-speciﬁc knowledge is employed. Some mod-

els can be created manually, by eliciting anomaly

models in the form of rules from experts (Nilsson

et al., 2008), but this may be impractical if experts

are not available, cannot easily provide these models,

or the elicitation cost may be high.

1.2 Our Contribution

A careful examination of the proposed methodolo-

gies suggest that speciﬁc points have to be addressed.

Firstly, a system needs to combine both supervised

and unsupervised tracking techniques, in order to ex-

ploit all the possible advantages. Secondly, since we

deal with vast amount of available data, we need to re-

duce, as much as possible, the required effort for the

initialization of the system.

The innovation of this paper lies in the creation of

a visual detection system, able to overcome the afore-

mentioned difﬁculties by combining various, well

tested techniques and, at the same time, minimizes

effort during the ofﬂine initialization using a Semi-

Supervised Learning (SSL) technique, appropriate for

large data sets.

In contrast to the approach of (Makantasis et al.,

2013), the user has to roughly segment few images,

i.e. use minimal effort, in order to create an initial

training set. Such procedure is easily implemented

using the suggested areas according to the unsuper-

vised techniques’ results. Collaboration of visual at-

tention maps, that represents the probability of a ves-

sel being present in the scene, and background sub-

traction algorithms provides to the user initially seg-

mented parts, over which user further actuates.

Then, SVMs are used as the additional super-

vised technique, in order to handle new video frames.

The signiﬁcant amount of labelled data for the train-

ing process originates from the previously generated

roughly segmented data sets. In order to facilitate

the creation of such training set and further reﬁne it

(i.e. correct some user errors), SSL graph-based algo-

rithms need to be involved.

Unfortunately, SSL techniques scale badly as the

available data rises. To make matters worse, (Nadler

et al., 2009) have shown that graph laplacian methods

(and more speciﬁc the regularization approach (Zhu,

2003) and the spectral approach (Belkin and Niyogi,

2002)) are not well posed in spaces R

, d ≥ 2, and

as the number of unlabelled points increases the solu-

tion degenerates to a non-informative function. Con-

sequently, a semi-supervised procedure, suitable for

large data sets is exploited for the ofﬂine initializa-

tion, signiﬁcantly reducing the effort required.

The rest of the paper is organized as follows: Sec-

tion 2 presents the system’s structure, suitable for the

maritime surveillance problem. Section 3 describes

the procedure followed for the construction of feature

vectors, capable to characterize the pixels of a frame.

Section 4 explains how target detection is performed

using pixel-wise binary classiﬁcation technique. Fi-

nally, in section 5, an excessive study on system’s re-

sults is presented.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

584

2 THE PROPOSED SYSTEM

2.1 System Architecture

The goal of the presented system is the real-time de-

tection and tracking of maritime targets. Towards this

direction, an appearance-based approach is adopted

to create visual attention maps that represent the prob-

ability of a target being present in the scene. High

probability implies high conﬁdence for a maritime

target’s presence.

Visual attention maps creation is based exclu-

sively on each frame’s visual content, in relation to

their surrounding regions or the entire image. Due

to this limitation, high probability is assigned, fre-

quently, to image regions that depict non-maritime

targets (e.g. stationary land parts). In order to over-

come such drawback, our system exploits the tem-

poral relationship between subsequent frames. Con-

cretely, video blocks, containing a predeﬁned number,

h, of frames and covering a time span, T , are used to

model the pixels’ intensities.

Thus, the temporal evolution of pixels intensities

is utilized to estimate a pixel-wise background model,

capable to denote each one of the pixels of the scene

as background or foreground. By using a background

modelling algorithm, system can efﬁciently discrimi-

nate moving from stationary objects in the scene. In

order to model pixels’ intensities, we use the back-

ground modelling algorithm presented in (Zivkovic,

2004). This choice is justiﬁed by the fact that this al-

gorithm can automatically fully adapt to dynamically

changing visual conditions and cluttered background.

Let us denote as p

(i)

the pixel of a frame i at loca-

tion (x, y) on image plane. Having constructed the vi-

sual attention maps and applied background modeling

algorithm, the pixel p

(i)

is described by a feature vec-

tor f

(i)

: f

(i)

= [ f

(i)

1,xy

... f

(i)

k,xy

]

, where f

(i)

1,xy

, ... , f

(i)

k−1,xy

stand for scalar features that correspond to the proba-

bilities assigned to the pixel p

(i)

by different visual at-

tention maps, while f

(i)

k,xy

is the binary output of back-

ground modeling algorithm, associated with the same

pixel. In order to detect maritime targets, these fea-

tures are fed to a binary classiﬁer which classiﬁes pix-

els into two disjoint classes, C

and C

If we denote as Z

(i)

= C

(i)

∪C

(i)

the set that con-

tains all pixels of frame i, then the ﬁrst class, C

(i)

, con-

tains all pixels that depict a part of a maritime target,

while the second class, C

(i)

, equals to Z

(i)

−C

(i)

. We

used SVMs to transact the classiﬁcation task for the

proposed maritime surveillance system. Selection of

the SVM, over other supervised classiﬁcation meth-

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

Figure 1: System’s architecture illustration. Image in (i),

corresponds to the original captured frame. In (ii), the out-

put of visual attention maps is presented. High probabil-

ity is represented with red color, while low probability with

deep blue. The output of background modeling algorithm

is shown in (iii). The column in (iv) represents a feature

vector for a speciﬁc pixel, which is fed to a binary classiﬁer

(v). The output of the classiﬁer in pixel level is presented in

(vi) and in frame level in (vii).

ods, is justiﬁed by its robustness, when handling un-

balanced classes.

The overall architecture of the proposed maritime

surveillance system is presented in Fig.1. Initially, the

original captured frame, Fig.1(i), is processed to ex-

tract pixel-wise features using visual attention maps,

Fig.1(ii), and background modelling, Fig.1(iii). Then

the feature vector of each one pixel, Fig.1(iv), is pro-

cessed by a binary classiﬁer, Fig.1(v), who decides

if the pixel corresponds to a part of a maritime tar-

get, Fig.1(vi). The classiﬁer’s output in frame-level is

shown in Fig.1(vii).

2.2 Problem Formulation

Maritime target detection can be seen as an image

classiﬁcation problem. Thus, we classify each one of

the frame’s pixels in one of two classes, C

and C

If we denote as l

(i)

the label of pixel p

(i)

, then, for a

frame i, the classiﬁcation task can be formulated as:

(i)

(

1 if p

(i)

∈ C

−1 if p

(i)

∈ C

(1)

where x = 1, ..., w, y = 1, ..., h and h,w stand for

frame’s height and width.

The SVM classiﬁer will be formed through a

training process, which requires the formation of a

robust training set composed of pixels, along with

their associated labels. Such a set can be formed by

the user, through a rough segmentation of a frame t

into two regions, that contain positive and negative

samples, i.e. C

(t)

class labelled with 1 and C

(t)

class

labelled with -1. The union of C

(t)

and C

(t)

consists

the initial training set S.

MaritimeTargetsDetectionfromGroundCamerasExploitingSemi-supervisedMachineLearning

585

At this point in the training set S, each pixel is de-

scribed only by its intensity, which does not provide

sufﬁcient information for separating pixels into two

disjoint classes. Taking into consideration the appli-

cation domain, which indicates that the largest part

of a frame will depict sea and sky, we exploit low

level features to emphasize man-made structures in

the scene.

Then, visual attention maps are created, which in-

dicate the probability a pixel to depict a part of a mar-

itime target. In addition, based on the observation that

a vessel must be depicted as a moving object, we im-

plicitly capture the presence of motion by exploiting a

background modeling algorithm. Using the output of

visual attention maps and the background modeling

algorithm, each pixel is described by the feature vec-

tor of sec.2.1 and the training set S can be transformed

to: S = {( f

(t)

, l

(t)

)} for x = 1, ..., w and y = 1, ..., h.

Although the elements of S are labelled by a hu-

man user, the labelling procedure may contain incon-

sistencies. This is mainly caused by the fact that hu-

man centric labelling, especially of image data, is an

arduous and inconsistent task, due to the complexity

of the visual content and the huge manual effort re-

quired.

In order to overcome this drawback, we reﬁne the

initial training set by i) selecting the most represen-

tative samples from each class and ii) labelling the

rest of the samples using a semi-supervised algorithm.

Selection of the most representative samples is taken

place py applying simplex volume expansion on the

samples of each class separately. Then representative

samples are used by the semi-supervised algorithm as

landmarks, in order to label the rest of the samples.

Using the reﬁned training set, the binary classiﬁer can

be successfully trained to classify the pixels of subse-

quent frames, addressing this way the initial classiﬁ-

cation problem of Eq.1.

3 PIXEL-WISE VISUAL

DESCRIPTION

In this section we describe the procedure for con-

structing feature vectors, capable to characterize the

pixels of a frame. The whole process is tuned for

maritime imagery and is guided by the operational

requirements that an accurate and robust maritime

surveillance system must fulﬁl. Feature vectors are

created for each pixel.

3.1 Scale Invariance

Potential targets in maritime environment vary in

sizes, either due to their physical size or due to the

distance between them and the camera. Despite that,

most of the feature detectors operate as kernel based

method and thus they prefer objects of a certain size.

As presented in (Alexe et al., 2010) and (Liu et al.,

2011) images must be represented in different scales

in order to overcome this limitation. In our approach,

a Gaussian image pyramid is exploited in order to pro-

vide scale invariance and to take into consideration

the relationship between adjacent pixels.

The Gaussian image pyramid is created by succes-

sively low-pass ﬁltering and sub-sampling an image.

During the stage of low-pass ﬁltering the Gaussian

function can be approximated by a discretized con-

volution kernel as follows:

256







1 4 6 4 1

4 16 24 16 4

6 24 36 24 6

4 16 24 16 4

1 4 6 4 1







(2)

During sub-sampling every even-numbered row

and column is removed. If we denote as I

the orig-

inal captured image and as I

the image at pyramid

level φ then image at pyramid level φ+ 1 is computed

as: I

φ+1

(x, y) = [G

∗ I

](2x, 2y)

One must combine the various scales together into

a single uniﬁed and scale-independent feature map,

to provide scale-independent feature analysis. To do

so, image at level φ + 1, ﬁrstly, is upsized twice in

each dimension, with the new even rows and columns

ﬁlled with zeros. Secondly, a convolution is per-

formed with the kernel G

to approximate the values

of the ”missing pixels”. Because each new pixel has

four non new-created adjacent pixels, G

is deﬁned

as: G

= 4 · G

Then, a pixel-wise weighted summation is per-

formed to adjacent images in pyramid so as the uni-

ﬁed image at level φ, J

is deﬁned as:

· [I

+ [G

∗U(I

φ+1

)]] (3)

where U stands for the upsize operation. The ﬁnal

uniﬁed image is computed by repeating the above op-

eration, from coarser to ﬁner pyramid image levels.

3.2 Low-level Features Analysis

As described in (Albrecht et al., 2011b) different low-

level image features respond to different attributes of

potential maritime targets. A combination of features

should be exploited in order to reveal targets’ pres-

ence. The selected features do not require a speciﬁc

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

586

format for the input image. These are edges, horizon-

tal and vertical lines, frequency, color and entropy.

Each one of these features are calculated for all

image’s pyramid levels, independently. Then, image’s

pyramid is combined to form a single uniﬁed feature

map by using Eq.(3). In Fig.2 the original captured

frame along with the features responses are presented.

All of the features emphasize the stationary land part

and the white boat, which is the actual maritime tar-

get.

3.2.1 Edges

Edges in the form of horizontal and vertical lines are

able to denote man-made structures, making the sys-

tem able to suppress large image regions, depicting

sea and sky. Canny operator (McIlhagga, 2011) is a

very accurate image edge detector, which outputs ze-

ros and ones for image edges absence and presence

respectively. Sobel operator (Yasri et al., 2008), al-

though being less accurate, measures the strength of

detected edges by approximating the derivatives of in-

tensity changes along image rows and columns.

So, by multiplying pixel-wise the output of two

operators the system is able to detect edges in a very

accurate way, while at the same time it preserves their

magnitude. If we denote as C

and S

the Canny and

Sobel operators for image I, then the edges E

are de-

ﬁned as: E

= C

· S

. Matrix E

has the same dimen-

sions with image I; its elements E

(x, y) correspond

to the magnitude of an image edge at location (x, y)

on image plane.

3.2.2 Frequency

The high frequency components of the input frame,

I, are computed as: F

= ∇

· I. The matrix F

has

the same dimensions with image I and its elements

(x, y) correspond to the frequency’s magnitude at

location (x, y) on image plane.

While exploitation of frequency features may em-

phasize (highly) wavy sea regions, they will suppress

image regions that depict sky parts, since such image

parts are dominated by low frequencies. Furthermore,

image frequencies are complementary to image edges

emphasizing highly structured regions within an ob-

ject and thus improving detection accuracy.

3.2.3 Horizontal and Vertical Lines

The detection of horizontal and vertical lines in an im-

age require an appropriate kernel K. Kernel K is tuned

to strengthen the response of a pixel if this consists a

part of a horizontal or vertical line and suppress pix-

els’ responses in all other cases. Kernel will be con-

volved with each image’s pyramid level. In order to

emphasize this kind of lines the kernel K is designed

as:

K =







0 0 1 0 0

0 0 2 0 0

1 2 4 2 1

0 0 2 0 0

0 0 1 0 0







(4)

and vertical and horizontal lines in a frame I can

be computed as: L

= K

K ∗ I. Again, the matrix L

has the same dimensions with image I and its ele-

ments L

(x, y) indicates the magnitude of an hori-

zontal and/or vertical line at location (x, y) on image

plane.

Line detector works like an edge detector. In

coastal regions, captured frames are likely to contains

land parts that will respond to the edge detector, af-

fecting detection accuracy of actual maritime targets.

Since vertical and horizontal lines are more dominant

in man-made structures the line detector supports ac-

curacy of actual targets by suppressing the regions of

the image that depict natural land parts, such as rocks.

3.2.4 Color

In maritime environment, no assumptions about the

color of vessels can be made. For this reason differ-

ences in color are more likely to indicate the presence

of a potential target. Furthermore, maritime scenes

usually contain large regions with similar colors (sea

and sky). This observation as described in (Achanta

et al., 2009) and (Achanta and Susstrunk, 2010) can

be exploited to increase the performance of visual at-

tention map by identifying potential targets.

In order to compute the color difference, the cap-

tured frame’s colorspace is converted to CIELab. The

computation of color differences takes place by cal-

culating the Euclidean distances between individual

pixels color vectors and the mean color vector of the

whole frame. For a frame I this procedure results

in a matrix C

of the same dimensions, whose ele-

ment, C

(x, y), at location (x, y) on image plane, in-

dicates the difference in color between this pixel and

the mean color of the rest pixels of the frame.

3.2.5 Entropy

Images that depict large homogeneous regions, such

as sky or sea regions, present low entropy, while

highly textured images will present high entropy. Im-

age entropy can be interpreted as a statistical measure

of randomness, which can be used to characterize the

texture of the input image. Thus, entropy can be uti-

lized to suppress homogeneous regions of sea and sky

MaritimeTargetsDetectionfromGroundCamerasExploitingSemi-supervisedMachineLearning

587

and highlight potential maritime targets. Entropy, H

of a region r of an image is deﬁned as:

∑

j=1

(r)

· logP

(r)

(5)

where P

(r)

is the frequency of intensity j in image

region r. For a grayscale image, variable k is equal to

256.

In order to compute entropy for a pixel located at

(x, y) on image plane, we apply the relation of Eq.5

on a square window centered at (x, y). In our case, the

size of the window is 5 × 5 pixels. The application of

Eq.5 on (x, y) of a frame I, for x = 1, ..., w and y =

1, ..., h, where w and h correspond to frame’s width

and height, results in a matrix H

that has the same

dimensions with the frame I. The matrix H

can be

interpreted as a pixel-wise entropy indicator of I.

(a) (b) (c)

(d) (e) (f)

Figure 2: Original captured frame (a) and feature responses

(b)-(f); (b) edges, (c) frequencies, (d) vertical and horizontal

lines, (e) color and (f) entropy. All feature responded to the

land part and the boat (maritime target).

3.3 Visual Descriptors

Visual descriptors are computed to encode visual in-

formation of captured images, using the extracted

low-level features described in subsection 3.2. These

descriptors are utilized for constructing the visual at-

tention maps. Their computation, instead of pixel-

wise, takes place block-wise, in order to reduce the

effect of noisy pixels during low-level features extrac-

tion. In this paper, three different descriptors are com-

puted:

a) Local Descriptors that take into consideration

each one of the image pixels separately. Local de-

scriptors indicate the magnitude of local features

for each one of image pixels.

b) Global Descriptors that are capable to emphasize

pixels with high uniqueness compared to the rest

of the image. To achieve this they indicate how

different local features for a speciﬁc pixel are, in

relation with the same features of all other image

pixels.

c) Window Descriptors that compare local features

of a pixel with the same features of its neighboring

pixels.

3.3.1 Local Descriptor

One local descriptor is computed for each one of the

extracted low-level features. Let us denote as F the

feature in question, which can correspond to image

edges, frequency, horizontal and vertical lines, color

or entropy. For the feature F, the computation of lo-

cal descriptor is derived by feature’s response image.

Firstly the feature’s response image is divided into B

blocks of size 8 × 8 pixels. Then, the local descriptor

for a speciﬁc block j is deﬁned as the average mag-

nitude of the feature F in the same block. More for-

mally, for a block j, with b

height and b

width, the

local descriptor of feature F is computed as follows:

· b

∑

(x,y)∈ j

F(x, y) (6)

where F(x, y) is the response of feature in question

at pixel (x, y). This kind of descriptor is capable to

highlight image bocks with high feature responses.

3.3.2 Global Descriptor

The local descriptors handle each image block sep-

arately and, thus, are insufﬁcient to provide useful

information when features’ responses are quite sim-

ilar along all image blocks (e.g. a wavy sea). The

proposed system can overcome this problem by using

global descriptors. Uniqueness of a block j can be

evaluated by the absolute difference of the feature re-

sponse between this block and the rest blocks of the

image. The global descriptor for a feature F and im-

age block j is deﬁned as:

∑

i=1

|lF

− lF

| (7)

As mentioned before a global descriptor is able to

emphasize blocks presenting high uniqueness, in term

of features’ responses, compared to the rest blocks of

the image.

3.3.3 Window Descriptor

Unfortunately, if potential targets are presented in

more than one block, the local and global descriptors

will emphasize the most dominant target and will sup-

press the others. In order to overcome this problem,

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

588

Edges Frequency Lines Color

Entropy

Local

Global

Window

Figure 3: Visual attention maps for each local, global and

window descriptors. Using give low level features and three

descriptor, each one of the frames pixels is described by a

15-dimensional vector. The presented visual attention maps

correspond to the original frame of Fig.2.

system exploits a window descriptor, that compares

each image block with its neighbouring blocks.

Window descriptor for an image with N × M

blocks uses an image window W , which is spanned

by the maximum symmetric distance, d

and d

along

horizontal and vertical axes respectively. Symmetric

distances are deﬁned as d

= min(l, k

, N − k

) and

= min(l, k

, M −k

), where l is the default symmet-

ric distance, 3 blocks in our case, and k

and k

stands

for block coordinates on image plane along horizontal

and vertical axes respectively. The window descriptor

for a feature F and image block j with coordinates

( j

, j

) is deﬁned as:

· 2d

∑

k=−d

∑

l=−d

|lF

− lF

+k, j

| (8)

By using three descriptors and ﬁve low-level im-

age features, each image block is described by a

1 × 15 feature vector. Each feature of this vector

corresponds to a different visual attention map. For

blocks of size 8 × 8 pixels the visual attention maps

are sixty four times smaller than the original captured

frame. In order to create a pixel-wise feature vector,

visual attention maps must have the same dimensions

with the original captured frame. For this reason they

are up-sampled, by using Eq.3.

Visual attention maps that correspond to the orig-

inal frame of Fig.2, for each one of the descriptors

and each one of the low level features, are presented

in Fig.3. All visual attention maps emphasize the sta-

tionary land part and the boat, while at the same time

they suppress the background.

3.4 Background Subtraction

In maritime surveillance, most state-of-the-art back-

ground modeling algorithms, like (Doulamis and

Doulamis, 2012), (Makantasis et al., 2012), fail ei-

ther due to their high computational cost or due to the

continuously moving background, and moving cam-

eras. However, if the background modeling algorithm

output is fused in a uniﬁed feature vector with the pre-

viously constructed visual attention maps, our system

will be able to emphasize potential threats and at the

same time to suppress land parts that may be appeared

in the scene by implicitly capture motion presence.

The proposed system uses the Mixtures of Gaus-

sians (MOG) background modeling technique, pre-

sented in (Zivkovic, 2004). This choice is justiﬁed

by the fact that MOG is fast, robust to small peri-

odic movements of background, and easy to param-

eterize algorithm. By fusing together the outputs of

visual attention maps and the output of a background

modeling algorithm, camera motion temporarily in-

creases false positives detections, but false negatives,

that comprises the most important characteristic of a

maritime surveillance system, are not affected.

(a) (b)

Figure 4: Original frame (a) and the output of background

modeling algorithm (b).

4 TARGET DETECTION

The maritime target detection can be seen as an image

segmentation problem. In our case target detection, is

further reduced to a binary classiﬁcation problem. For

any pixel at location (x, y) of a frame i, the feature ex-

traction process (see Sec.3) constructs an 1 × 16 fea-

ture vector, f

(i)

. Given f

(i)

as input, the classiﬁer will

decide if the corresponding pixel depicts some part of

a maritime target or not.

4.1 Initial Training Set Formation

In order to be able to exploit a binary classiﬁer, a pro-

cess of classiﬁer training should be preceded. Train-

ing process requires the formation of a robust training

set which contains pixels along with their associated

labels. Let us denote as Z

(t)

the set that contains all

the pixels of frame t, C

(t)

the set that contains pixels

that depict some part of a maritime target and as C

(t)

the set Z

(t)

−C

(t)

The creation of a training set S requires from the

user to roughly segment the frame t into two regions,

which contain positive and negative samples (i.e. pix-

els that belong to C

(t)

and C

(t)

class respectively).

MaritimeTargetsDetectionfromGroundCamerasExploitingSemi-supervisedMachineLearning

589

This segmentation results in a set S = {(p

(t)

, l

(t)

)},

and labels are deﬁned as:

(

1 if p

∈ C

−1 if p

∈ C

(9)

where p

is a pixel at location (x,y). By utilizing the

feature vector f

(t)

the set S takes the form described

in Sec.2.2.

However, human centric labeling, especially of

image data, is an arduous and inconsistent task,

mainly due to the complexity of the visual content and

the huge manual effort required. To overcome this

drawback, we reﬁne the initial training set through a

semi-supervised approach.

4.2 Training Set Reﬁnement

In order to reﬁne the initial user-deﬁned training set,

we partition the set S into two disjoint classes, R and

U. The class R contains the most representative sam-

ples of S, i.e. the samples that can best describe the

classes C

and C

, while class U is equal to S − R.

Samples of class R are considered as labeled, while

samples belonging to U are considered as unlabeled.

Then, via a semi-supervised approach the samples of

R are used for label propagation through the ambigu-

ously labeled data of U. In the following we describe

in detail the aforementioned process.

For selecting the most representative samples for

each one of the classes C

and C

, we consider each

sample as a point into an µ-dimensional space. Then,

simplex volume expansion is utilized. In our case µ

is equal to 16, because the dimension of the space is

equal to the dimension of the feature vectors that de-

scribe the pixels. The process for representatives se-

lection is conducted twice, once for class C

and once

for C

4.3 Graph-based Label Propagation

The aforementioned procedure results to two sets of

representative samples, C

T,R

and C

B,R

, one for each

class. The samples of C

T,R

and C

B,R

are considered

as labeled, while the rest samples of the classes C

and C

are considered as ambiguously labeled. More

formally, we have: i) R = C

T,R

∪C

B,R

and ii) U = S −

T,R

−C

B,R

. At this point, we need to reﬁne the initial

training set, S, using a suitable approach for the label

propagation, through the ambiguously labeled data.

Thus, we need to estimate a labeling prediction

function g : R

7→ R deﬁned on the samples of S, by

using the labeled data R. Let us denote as r

the sam-

ples of set R such as R = {r

}

i=1

, where m is the car-

dinality of the set R. Then, according to (Liu et al.,

2010), the label prediction function can be expressed

as a convex combination of the labels of a subset of

representative samples:

g( f

) =

∑

k=1

· g(l

) (10)

where Z

denotes sample-adaptive weights, which

must satisfy the constraints

∑

k=1

= 1 and Z

≥ 0

(convex combination constraints). By deﬁning vec-

tors g

g and α

α respectively as g

g = [g( f

), ..., g( f

)]

and α

α = [g(r

), ..., g(r

)]

. Eq.10 can be rewritten as

g = Zα

α where Z ∈ R

n×m

The design of matrix Z, which measures the un-

derlying relationship between the samples of U and

representative samples R (were R ⊂ U), is based on

weights optimization; actually non-parametric regres-

sion is being performed by means of data reconstruc-

tion with representative samples. Thus, the recon-

struction for any data point f

, i = 1, ..., n is a con-

vex combination of its closest representative samples.

In order to optimize these coefﬁcients the following

quadratic programming problem needs to be solved:

min

∈R

h(z

) =

|| f

− R

· z

s.t. 1

= 1, z

≥ 0

(11)

where, R

∈ R

µ×s

is a matrix containing as elements a

subset of R = {r

, ..., r

} composed of s < m nearest

representative samples of f

and z

stands for the i

row of Z matrix.

Nevertheless, the creation of matrix Z is not suf-

ﬁcient for labeling the entire data set, as it does not

assure a smooth function g. As mentioned before, a

large portion of data are considered as ambiguously

labeled. Despite the small labeled set, there is always

the possibility of inconsistencies in segmentation; in

speciﬁc frames the user may miss some pixels that

depict targets. In order to deal with such cases the

following SSL framework is employed:

min

A=[α

,...,α

]

Q (A) =

||Z · A − Y||

trace(A

LA) (12)

where

L = Z

· L · Z is an memory-wise and com-

putationally tractable alternative of the Laplacian ma-

trix L. The matrix A = [a

, ..., a

] ∈ R

m×c

is the soft

label matrix for the representative samples, in which

each column vector accounts for a class. The matrix

Y = [y

, ..., y

] ∈ R

n×c

a class indicator matrix on am-

biguously labeled samples with Y

i j

= 1 if the label l

of sample i is equal to j and Y

i j

= 0 otherwise.

In order to calculate the Laplacian matrix L, the

adjacency matrix W needs to be calculated, since

L = D − W, where D ∈ R

n×n

is a diagonal degree

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

590

matrix such that D

∑

j=1

i j

. In this case W is ap-

proximated as W = Z · Λ

−1

· Z

, where Λ

Λ ∈ R

m×m

deﬁned as: Λ

∑

i=1

. The solution of the Eq.12

has the form of: A

∗

= (Z

·Z + γ

Y. Each sam-

ple label is, then, given by:

= arg max

j∈{1,...,c}

· α

(13)

where Z

. ∈ R

1×m

denotes the i-th row of Z, and

the normalization factorλ

= 1

Zα

balances skewed

class distributions.

4.4 Maritime Target Detection

Having constructed a training set, S = { f

, l

}

i=1

, a

binary classiﬁer, capable to discriminate pixels that

depict some part of a maritime target from pixels that

depict the background, can be trained. In this paper

we choose to utilize Support Vectors Machine (SVM)

to transact the classiﬁcation task. The optimization

problem is described as (Cortes and Vapnik, 1995):

min

w,b,ξ

||w

w|| + c

∑

i=1

s.t. l

w · f

− b) ≥ 1 − ξ

(14)

for i = 1, ..., n, ξ

≥ 0. Where ξ

≥ 1 are variables that

allow a sample to be in the margin or to be misclassi-

ﬁed and c is a constant that weights these errors.

In the framework of maritime detection, SVM

must be able to handle unbalanced classiﬁcation prob-

lems, due to the fact that maritime target usually oc-

cupy the minority of captured frames’ pixels let alone

their total absence from the scene for large time peri-

ods. To address this problem, the misclassiﬁcation er-

ror for each class is weighted separately. This means

that the total misclassiﬁcation error of Eq.14 is re-

placed with two terms:

∑

i=1

→ c

∑

{i|l

=1}

+ c

∑

{i|l

=−1}

(15)

where c

and c

are constant variables that weight

separately the misclassiﬁcation errors for positive and

negative examples. The solution of Eq.14 with the

classiﬁcation error of Eq.15 results to a trained SVM,

which is capable to classify the pixels of new captured

frames.

5 EXPERIMENTAL RESULTS

There is code in Python, concerning visual atten-

tion maps construction, available to download

. The

https://github.com/konstmakantasis/Poseidon

performance of each system’s component have been

checked separately; extracted features were evalu-

ated in terms of discriminative ability and importance,

semi-supervised labeling for the predicting outcome

and, ﬁnally, the binary classiﬁer for its performance.

5.1 Data Set Description

Data consists of recorded videos from cameras

mounted at the Limassol port, Cyprus and Chania old

port, Crete, Greece. The data sets describe real life

scenarios, in various weather conditions. As long as

the camera is able to capture a vessel (i.e. spans an

area of more than 40 pixels in the frame) the system

will likely detect it, regardless the weather conditions

(e.g. rain, fog, waves etc.).

Unfortunately, for the vast majority of the video

frames, maritime targets are absent from the scene. In

order to deal with such cases, we manually edited the

videos and kept only the tracks that depict intrusion of

one or more targets in the scene. Then, we manually

labeled the pixels of key video frames, keyframes, to

create a ground truth dataset for evaluating our sys-

tem.

Keyframes originate from raw video frames that

correspond to time instances t, 2t, 3t, ··· The time

span is selected to be 6 seconds, which means that one

frame out of 150 is denoted as keyframe. We followed

this approach for practical reasons. Firstly, it would

be impossible to manually label all video frames at

a framerate of 25 fps. Also, the time interval of 6

seconds is small enough to allow the detection of the

intrusion of a maritime target in the scene. At this

point it has to be clariﬁed that feature extraction task,

as well as the binary classiﬁcation are performed for

all frames of a video track. Keyframes are used only

for system’s performance evaluation.

5.2 Evaluation of Extracted Features

In this section, we examine if extracted features fulﬁl

speciﬁc requirements, i.e. be informative and sepa-

rable, in order to assure good classiﬁcation accuracy

and smooth training set reﬁnement, through the graph

based SSL technique.

To evaluate features information, we utilized the

keyframes’ ground truth data. The feature extrac-

tion task results in a 16-dimensional feature vector

for each pixel in a frame. The quality of features’ in-

formation is evaluated through dimensionality reduc-

tion and samples plotting, in order to visually examine

their distribution in space, see Fig.5. The two classes,

as shown in Fig.5, are linearly separable, which sug-

gests high quality features. The small amount of pos-

MaritimeTargetsDetectionfromGroundCamerasExploitingSemi-supervisedMachineLearning

591

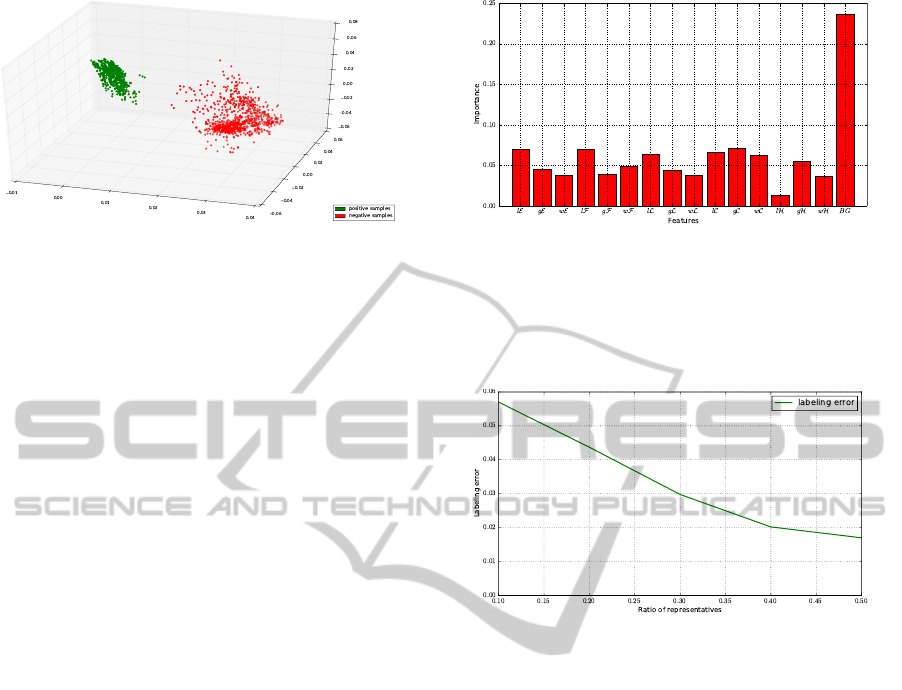
Figure 5: Positive and negative samples plotted in 3-

dimensional space. Randomized PCA was used to extract

the three dominant components of the dataset. The class

containing positive samples can be linearly separated from

the class containing negative samples. The small amount

of positive samples that lie inside the region of the negative

class, correspond to maritime targets’ contours.

itive samples, that lie inside the region of the negative

class, correspond to maritime targets’ contours and

probably occurred due to segmentation errors during

manual labeling.

The importance of each one of the extracted fea-

tures is examined separately, in order to deﬁne how

much each one of the features affects the classiﬁca-

tion task. The importance of features is speciﬁed via

Forest of Randomized Trees. The relative rank (i.e.

depth) of a feature used as a decision node in a tree

can be used to assess the relative importance of that

feature with respect to the predictability of the target

variable. Features used at the top of the tree contribute

to the ﬁnal prediction decision of a larger fraction of

the input samples. The expected fraction of the sam-

ples they contribute to can thus be used as an estimate

of the relative importance of the features.

In Fig.6 the relative importance of each one of the

extracted features is presented (features labeling fol-

lows the notation of Section 3). The dominant fea-

ture is the one that corresponds to the output of back-

ground modeling algorithm, which, in practice, cap-

tures the presence of motion in the scene. The rest of

the features contribute almost the same, except from

the feature that corresponds to the local descriptor of

image entropy.

5.3 Evaluation of Semi-supervised

Labeling

In order to evaluate semi-supervised labeling, we as-

sume that manual labeling of keyframes contains no

segmentation errors. The ratio of the representa-

tives samples in relation with the ambiguously labeled

samples is the only factor that affect the performance

of labeling algorithm.

As shown in Fig.7, the labeling error is lower than

Figure 6: Features importances. The feature that corre-

sponds to output of background modeling algorithm, which

implicitly captures the presence of motion in the scene, is

presented to be he most important.The rest of the features

contribute almost the same to the classiﬁcation task, except

from the feature that corresponds to the local descriptor of

image entropy, which presents the lowest importance.

Figure 7: Semi-supervised labeling performance. When ra-

tio of representative samples is over 40% the labeling error

is lower than 2%. When the ratio of representatives is lower

than 40% the error is linearly increasing till the value of

5.7% for 10% of representatives.

2% when the ratio of the representatives samples in

relation with the ambiguously labeled samples is over

40%. When the ratio is smaller than 40% the labeling

error is linearly increasing and it reaches the value of

5.7% when the ratio of representative samples is 10%.

The choice for an appropriate value for the ratio of

representatives is inherently dependent on the quality

of human based labeling. If labeling is the result of a

rough image segmentation, a lot of the labeled pixel

will carry the wrong label. In such cases the afore-

mentioned ratio must be set to a small value. The

most representative samples from each class is as-

sumed that carry the right label, while the labels of

the rest of the samples must be reconsidered.

In our case, we ask the user to segment the frame

in a very careful way, which implies that the vast

majority of the pixels will carry the right label. For

this reason we set the ratio value to 40%. The semi-

supervised labeling algorithm with 40% of represen-

tatives is expected to re-label 1.7% of the samples.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

592

5.4 Binary Classiﬁer Evaluation

The performance of the binary classiﬁer is dependent

on the values of the parameters c

and c

of Eq.15.

Let us denote as n

and n

the number of samples in

positive and negative class respectively. To examine

the inﬂuence of parameters c

and c

on classiﬁcation

accuracy we deﬁne the parameter k as:

k =

· n

(16)

In practice, parameter k assigns different weights to

misclassiﬁcation errors, which correspond to posi-

tive and negative examples. When the value of k is

equal to one, the weights that penalize misclassiﬁca-

tion sample for each class are inversely proportional

to the cardinalities of the classes. When k < 1 a big-

ger penalty is assigned to false negatives, while for

k > 1 false positives are considered more important.

False negatives correspond to pixels that actually de-

pict some part of a maritime target, but are denoted as

background by the classiﬁer.

However, a maritime surveillance system must

emphasize on minimizing the false negative rate. In

other words, it is more important, the system to de-

tect all potential maritime targets, even if it will raise

a small amount of false alarms, than minimizing false

positives at the cost of missing target intrusions.

Fig.8 presents the performance of classiﬁer for

different values of parameter k. The green line rep-

resents classiﬁcation accuracy, while the blue line the

recall of the system. If we denote as p

the set of pixel

that denoted by the classiﬁer as positive samples and

as p

the set of pixels that actually belong to the posi-

tive class, then recall ρ is deﬁned as:

ρ =

∩ p

(17)

When ρ is equal to one, all true positive samples have

been correctly classiﬁed by the binary classiﬁer. Ac-

curacy is the proportion of correctly classiﬁed sam-

ples of the whole dataset. As shown by the green line

in Fig.8 the accuracy of the classiﬁer reaches its max-

imum value, when k is equal to one. On the other

hand, the recall of the system is monotonically de-

creasing as the value of k is increasing. In our case

we set k = 0.7 to balance between maximizing classi-

ﬁcation accuracy and minimizing false negative rate.

For k = 0.7 the accuracy of the classiﬁer is equal to

96.4%, while recall is equal to 97.1%.

6 CONCLUSIONS

A vision based system, using monocular camera data,

is presented in this paper. The system provides ro-

Figure 8: Classiﬁer performance. The recall of the system

is monotonically decreasing as the value of k is increas-

ing (blue line). The accuracy presents the maximum value

when k = 1, which means that the penalties for misclassify-

ing positive and negative samples are inversely proportional

to the cardinalities of positive and negative classes.

bust results by combining supervised and unsuper-

vised methods, appropriate for maritime surveillance,

utilizing an innovative initialization procedure. The

system ofﬂine initialization is achieved through graph

based SSL algorithm, suitable for large data sets, sup-

porting users during segmentation process.

Extensive performance analysis suggest that the

proposed system performs well, in real time, for long

periods without any special hardware requirements

and the without any assumptions related to scene, en-

vironment and/or visual conditions. Such system is

expected to be easily expanded to other surveillance

cases, using minor modiﬁcations depending on the

case.

ACKNOWLEDGEMENTS

The research leading to these results has been sup-

ported by European Union funds and National funds

(GSRT) from Greece and EU under the project JA-

SON: Joint synergistic and integrated use of eArth ob-

Servation, navigatiOn and commuNication technolo-

gies for enhanced border security funded under the

cooperation framework. The work has been partially

supported by IKY Fellowships of excellence for post-

graduate studies in Greece−Siemens program.

REFERENCES

Achanta, R., Hemami, S., Estrada, F., and Susstrunk, S.

(2009). Frequency-tuned salient region detection. In

IEEE Conf. on Comp. Vis. and Pat. Rec., 2009. CVPR

2009, pages 1597–1604.

Achanta, R. and Susstrunk, S. (2010). Saliency detection

using maximum symmetric surround. In 2010 17th

MaritimeTargetsDetectionfromGroundCamerasExploitingSemi-supervisedMachineLearning

593

IEEE Int. Conf. on Image Processing (ICIP), pages

2653–2656.

Albrecht, T., Tan, T., West, G., Ly, T., and Moncrieff, S.

(2011a). Vision-based attention in maritime environ-

ments. In Communications and Signal Processing

(ICICS) 2011 8th Int. Conf. on Information,pages 1–5.

Albrecht, T., West, G., Tan, T., and Ly, T. (2010). Multi-

ple views tracking of maritime targets. In 2010 Int.

Conf. on Digital Image Computing: Techniques and

Applications (DICTA), pages 302–307.

Albrecht, T., West, G., Tan, T., and Ly, T. (2011b). Vi-

sual maritime attention using multiple low-level fea-

tures and na #x0ef;ve bayes classiﬁcation. In 2011 Int.

Conf. on Digital Image Computing Techniques and

Applications (DICTA), pages 243–249.

Alexe, B., Deselaers, T., and Ferrari, V. (2010). What is an

object? In 2010 IEEE Conf. on Comp. Vis. and Pat.

Rec. (CVPR), pages 73–80.

Auslander, B., Gupta, K. M., and Aha, D. W. (2011). A

comparative evaluation of anomaly detection algo-

rithms for maritime video surveillance. volume 8019,

pages 801907–801907–14.

Belkin, M. and Niyogi, P. (2002). Using manifold structure

for partially labelled classiﬁcation. page 929.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning, 20(3):273–297.

Doulamis, N. and Doulamis, A. (2012). Fast and adaptive

deep fusion learning for detecting visual objects. In

Fusiello, A., Murino, V., and Cucchiara, R., editors,

Comp. Vis. ECCV 2012. Workshops and Demonstra-

tions, number 7585 in Lecture Notes in Computer Sci-

ence, pages 345–354. Springer Berlin Heidelberg.

Fischer, Y. and Bauer, A. (2010). Object-oriented sensor

data fusion for wide maritime surveillance. In Water-

side Security Conf. (WSS), 2010 Int., pages 1–6.

Kaimakis, P. and Tsapatsoulis, N. (2013). Background

modeling methods for visual detection of maritime

targets. In Proceedings of the 4th ACM/IEEE Int.

Workshop on Anal. and Retrieval of Tracked Events

and Motion in Imagery Stream, ARTEMIS ’13, pages

67–76, New York, NY, USA. ACM.

Lei, P.-R. (2013). Exploring trajectory behavior model for

anomaly detection in maritime moving objects. In

2013 IEEE Int. Conf. on Intelligence and Security In-

formatics (ISI), pages 271–271.

Liu, T., Yuan, Z., Sun, J., Wang, J., Zheng, N., Tang, X.,

and Shum, H.-Y. (2011). Learning to detect a salient

object. IEEE Trans. on Pat. Anal. and Machine Intel-

ligence, 33(2):353–367.

Liu, W., He, J., and Chang, S.-F. (2010). Large graph

construction for scalable semi-supervised learning. In

Proceedings of the 27th Int. Conf. on Machine Learn-

ing (ICML-10), pages 679–686.

Makantasis, K., Doulamis, A., and Doulamis, N. (2013).

Vision-based maritime surveillance system using

fused visual attention maps and online adaptable

tracker. In 2013 14

Int. Workshop on Image Anal. for

Multimedia Interactive Services (WIAMIS),pages 1–4.

Makantasis, K., Doulamis, A., and Matsatsinis, N. (2012).

Student-t background modeling for persons’ fall de-

tection through visual cues. In 2012 13th Int. Work-

shop on Image Anal. for Multimedia Interactive Ser-

vices (WIAMIS), pages 1–4.

Maresca, S., Greco, M., Gini, F., Grasso, R., Coraluppi, S.,

and Horstmann, J. (2010). Vessel detection and clas-

siﬁcation: An integrated maritime surveillance system

in the tyrrhenian sea. In 2010 2

Int. Workshop on

Cognitive Information Processing (CIP),pages 40–45.

McIlhagga, W. (2011). The canny edge detector revisited.

Int. Journal of Comp. Vis., 91(3):251–261.

Nadler, B., Srebro, N., and Zhou, X. (2009). Statistical anal-

ysis of semi-supervised learning: The limit of inﬁnite

unlabelled data. In Bengio, Y., Schuurmans, D., Laf-

ferty, J. D., Williams, C. K. I., and Culotta, A., editors,

Advances in Neural Information Processing Systems

22, pages 1330–1338. Curran Associates, Inc.

Nilsson, M., van Laere, J., Ziemke, T., and Edlund, J.

(2008). Extracting rules from expert operators to sup-

port situation awareness in maritime surveillance. In

2008 11

Int. Conf. on Information Fusion,pages 1–8.

Rodriguez Sullivan, M. D. and Shah, M. (2008). Visual

surveillance in maritime port facilities. volume 6978,

pages 697811–697811–8.

Socek, D., Culibrk, D., Marques, O., Kalva, H., and Furht,

B. (2005). A hybrid color-based foreground object de-

tection method for automated marine surveillance. In

Blanc-Talon, J., Philips, W., Popescu, D., and Scheun-

ders, P., editors, Advanced Concepts for Intelligent Vi-

sion Systems, number 3708 in Lecture Notes in Com-

puter Science, pages 340–347. Springer Berlin Hei-

delberg.

Szpak, Z. L. and Tapamo, J. R. (2011). Maritime surveil-

lance: Tracking ships inside a dynamic background

using a fast level-set. Expert Systems with Applica-

tions, 38(6):6669–6680.

Vandecasteele, A., Devillers, R., and Napoli, A. (2013). A

semi-supervised learning framework based on spatio-

temporal semantic events for maritime anomaly detec-

tion and behavior analysis. In Proceedings CoastGIS

2013 Conf.: Monitoring and Adapting to Change on

the Coast.

Voles, P. (1999). Target identiﬁcation in a complex maritime

scene. volume 1999, pages 15–15. IEE.

Wijnhoven, R., van Rens, K., Jaspers, E., and de With, P.

(2010). Online learning for ship detection in maritime

surveillance. pages 73–80.

Yasri, I., Hamid, N., and Yap, V. (2008). Performance anal-

ysis of FPGA based sobel edge detection operator. In

Int. Conf. on Electronic Design, 2008. ICED 2008,

pages 1–4.

Zemmari, R., Daun, M., Feldmann, M., and Nickel, U.

(2013). Maritime surveillance with GSM passive

radar: Detection and tracking of small agile targets.

In Radar Symposium (IRS), 2013 14th Int., volume 1,

pages 245–251.

Zhu, X. (2003). Semi-supervised learning using gaussian

ﬁelds and harmonic functions. In Proceedings of the

20th Int. Conf. on Machine learning (ICML-2003),

volume 20, page 912.

Zivkovic, Z. (2004). Improved adaptive gaussian mixture

model for background subtraction. In Proceedings of

the 17th Int. Conf. on Pat. Rec., 2004. ICPR 2004, vol-

ume 2, pages 28–31 Vol.2.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

594