
Prior Knowledge About Camera Motion for Outlier Removal in
Feature Matching
Elisavet K. Stathopoulou, Ronny H
¨
ansch and Olaf Hellwich
Computer Vision and Remote Sensing, Technische Universit
¨
at Berlin, Marchstr. 23, MAR6-5, 10623 Berlin, Germany
Keywords:
Point Correspondences, Point Matching, Guided Matching, Path Estimation, 3D Reconstruction.
Abstract:
The search of corresponding points in between images of the same scene is a well known problem in many
computer vision applications. In particular most structure from motion techniques depend heavily on the
correct estimation of corresponding image points. Most commonly used approaches make neither assumptions
about the 3D scene nor about the relative positions of the cameras and model both as completely unknown.
This general model results in a brute force comparison of all keypoints in one image to all points in all other
images. In reality this model is often far too general because coarse prior knowledge about the cameras is often
available. For example, several imaging systems are equipped with positioning devices which deliver pose
information of the camera. Such information can be used to constrain the subsequent point matching not only
to reduce the computational load, but also to increase the accuracy of path estimation and 3D reconstruction.
This study presents Guided Matching as a new matching algorithm towards this direction. The proposed
algorithm outperforms brute force matching in speed as well as number and accuracy of correspondences,
given well estimated priors.
1 INTRODUCTION
Many computer vision algorithms depend on a suc-
cessful estimation of point correspondences between
several images. One example, which is of particu-
lar interest for the work discussed here, are Structure
from Motion (SfM) techniques that estimate camera
positions as well as a 3D model of the scene from a
given set of input images. The estimation of point
correspondences is a crucial part of such methods, as
they rely on them to estimate the underlying geometry
of the image set. Although modern approaches suc-
cessfully showed their potential on many datasets, the
point matching procedure still faces many challenges
such as ambiguities (e.g. due to repetitive scene pat-
terns), memory consumption, as well as a high com-
putational load.
A commonly used point matching technique is the
so-called brute force matching (BFM), which com-
pares every keypoint of an (source) image with ev-
ery keypoint within a second (target) image. This in-
volves the comparison of every keypoint descriptor of
the first image to all keypoint descriptors of the sec-
ond one. The point-pairs with the smallest difference
are kept as matching candidates, which are further
processed by several filtering steps. There are many
attempts to lift the computational burden of BFM, e.g.
by using suitable data structures (e.g. trees (Muja and
Lowe, 2012)) or special hardware (e.g. multi-core
systems or GPUs (Garcia et al., 2008)). BFM only
assumes that the images have a certain pairwise over-
lap, but makes no further assumptions about the pose
of the cameras or point distribution. These basic as-
sumptions make BFM on the one hand easy to imple-
ment and generally applicable, but are on the other
hand also the main factor for its limitations with re-
spect to speed and accuracy.
(a) One keypoint of the
source image
(b) Respective search
region in target image
Figure 1: Keypoint and its corresponding search area.
603
Stathopoulou E., Hänsch R. and Hellwich O..
Prior Knowledge About Camera Motion for Outlier Removal in Feature Matching.
DOI: 10.5220/0005456406030610
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (MMS-ER3D-2015), pages 603-610
ISBN: 978-989-758-090-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

The basic insight of the proposed method is to
use available prior knowledge of camera position and
orientation to guide the matching procedure by re-
stricting the correspondence search to a specific area
within the target image. The right side of Figure 1
shows an example of such a search area that was com-
puted by the Guided Matching (GM) method as pro-
posed by this paper. Only keypoints within this area
are used for comparisons while the rest of the points
are not taken into consideration. Consequently, fewer
comparisons have to be performed and the risk of
matching two non-homologous keypoints decreases.
Thus, post-processing techniques like point filtering
can be avoided. Guided Matcher is especially appli-
cable in cases where texture ambiguities are present.
Geometric constraints in image matching can be
imposed in various ways like object scene informa-
tion, point distribution or camera path constraints etc.
This study focuses on the use of easy to acquire path-
based constraints, such as noisy location and orienta-
tion data in order to achieve efficient outlier removal.
Camera positions and orientations are seldom known
accurately enough for an automatic 3D reconstruc-
tion and thus need to be estimated from the image
sequence. However, modelling this sequence as a
completely unordered set of images is far too general
in a variety of practical scenarios. Nowadays, sev-
eral camera setups are equipped with systems such
as Global Positioning System (GPS) and/or Inertial
Navigation System (INS). Unmanned Aerial Vehicles
(UAVs), rovers, or even mobile phone cameras (e.g.
geotagging) are just a few examples of imaging sys-
tems which attach basic location information to their
image data. Even in cases where this information is
not directly delivered by the imaging system itself, the
user might be able to provide a coarse description of
the camera setup, e.g. a rough estimation of the path
followed during capturing the images.
Although such prior information is often avail-
able, it is mostly ignored by current systems. This
paper proposes a simple, yet efficient, robust, and ac-
curate method to exploit any prior knowledge about
camera location and orientation in a probabilistic
manner. If no prior knowledge is available or the
uncertainty of the provided information is too large,
the system behaviour saturates to that of the standard
BFM. In all other cases it leads to superior results with
respect to computation time, number of matches, as
well as accuracy of the finally estimated epipolar ge-
ometry. An overview of the related work is presented
in the next section (Section 2). Section 3 describes in
detail the proposed method (Guided Matcher, GM),
followed by experimental results (Section 4) and con-
clusions (Section 5).
2 RELATED WORK
During the last years various works have been pub-
lished towards accurate and efficient keypoint match-
ing with the application to path estimation and 3D re-
construction. State of the art algorithms not only esti-
mate the camera path but also create textured 3D point
clouds. Most of them completely exclude any kind
of prior information and model the image sequences
as a an unordered set of images. In 2006 Photo Ex-
plorer, a 3D photo browsing interface, was presented
(Snavely et al., 2006). Their approach uses random
pictures of the same object collected from the inter-
net. SIFT (Lowe, 2004) is used for keypoint extrac-
tion and description. Camera parameters are recov-
ered through standard SfM techniques. A 3D scene
is rendered in order to enable navigation and explo-
ration. A few years later the authors of (Agarwal
et al., 2011) made a significant improvement towards
handling very large datasets by using parallel com-
puting. Following the typical procedure, coarse SIFT
features are extracted, described, and matched. SfM
is solved with bundle adjustment. The final output is
a sparse 3D model. (Furukawa and Ponce, 2010) fur-
ther extend the existing multi-view methods and use
them to create dense point clouds through a new im-
age clustering algorithm. Their system is able to deal
efficiently with very large unorganized photo collec-
tions. Other studies use content-based filtering algo-
rithms for unstructured data stored in the Web in order
to reconstruct objects of interest (Makantasis et al.,
2014).
On the other hand, there are studies that restrict
the correspondence search area by using geometric
or algebraic constraints. The work of (Baltsavias,
1991) assumes that the cameras are calibrated and
have known exterior orientation. Collinearity con-
ditions are used to restrict the search area to a 1D
space. In (Hess-Flores et al., 2012) the camera path
is projected onto a plane to track image features for
aerial video sequences. They use consensus infor-
mation about the camera parallax to avoid outliers.
The approach of (Strelow, 2004) models inertial mea-
surements of the robots motion. In (Wendel, 2013)
the geometric prior knowledge about the 3D structure
of the scene is modelled for navigation purposes. In
(Szeliski and Torr, 1998) keypoint coplanarity is as-
sumed for accurate SfM. In (Lopez, 2013) algebraic
epipolar constraints are used to minimize the alge-
braic epipolar cost between each stereo pair.
In practice it is unlikely that the true epipolar geom-
etry of two images is estimated. Inaccurate keypoint
locations, mismatches, and critical keypoint config-
urations lead to small errors within the final estima-
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
604

tion. Consequently, many approaches model the fun-
damental matrix F as stochastic variable. The uncer-
tainty of F is represented by a covariance matrix C
F
.
The so-called probabilistic epipolar geometry exploits
the knowledge of C
F
to improve image matching, pro-
jective reconstruction, and self calibration. One ex-
ample is (Brandt, 2008), which calculates a probabil-
ity density function of the location of feasible key-
points in the target image. The corresponding point
lies in the neighbourhood of the narrowest point of the
epipolar envelope, e.g. the region defined by all pos-
sible epipolar lines. In (Unger and Stojanovic, 2010)
point correspondences are evaluated by taking the un-
certainty of the epipolar geometry into account.
The above mentioned studies are related to the
proposed approach as all of them aim to eliminate
false matches during point correspondence search.
GM, however, uses more general probabilistic models
to describe available prior knowledge and provides a
simpler and more efficient scheme to exploit this in-
formation for keypoint matching. In cases where no
prior knowledge is available, the proposed method is
still applicable and simply degenerates to the standard
BFM.
3 GUIDED MATCHER
This article studies the potential of using prior knowl-
edge about the location and orientation of the cam-
eras during the search for corresponding keypoints.
In practice this prior information is available in
many forms, ranging from GPS/INS measurements of
UAVs, to GPS tags of modern consumer cameras, to a
coarse path description by the user. The only require-
ment of the proposed method is, that this prior knowl-
edge can be expressed as probability density function
of location p
c
(t) and pose p
c
(R) for each camera c.
A simple example is that both quantities are Gaus-
sian distributed p
c
(R) ∼ N(µ
R
c
,Σ
R
c
), p
c
(t) ∼ N(µ
t
c
,Σ
t
c
),
where the mean values µ
c
R
,µ
c
t
, as well as the variance-
covariance matrices Σ
R
c
,Σ
t
c
represent the given prior
knowledge.
The proposed framework can be applied to the
matching of any kind of image quantities, including
points, lines, and planes. For the sake of simplicity the
following discussion is restricted to the standard case
of matching keypoints. These have to be detected and
described before the matching procedure by any of the
available keypoint detectors/descriptors such as SIFT,
SURF, FAST, etc. (see for example (Mikolajczyk and
Schmid, 2004; Mikolajczyk and Schmid, 2005) for
more details on keypoint detection/description).
Given a pair of cameras c
1
,c
2
as well as their re-
spective calibration matrices K
1
,K
2
, their correspond-
ing lists of keypoints, and the probability densities
p
c
1
(R), p
c
2
(R), p
c
1
(t), p
c
2
(t) describing the prior
distribution of location and orientation, the proposed
method (as summarized by Algorithm 1) restricts the
search area for each point of the source image instead
of comparing it to all possible points in the target im-
age. The following explanation only briefly mentions
established concepts of epipolar geometry. More ex-
tensive as well as more detailed information about
stereo vision can be found in (Hartley and Zisserman,
2003).
Algorithm 1: Guided Matching.
Require: Set of keypoints KP
i
, Calibration K
i
, Prior
knowledge p
i
(R), p
i
(t) (i ∈ {1,2})
Sample N different R
i
and t
i
from p
i
(R) and p
i
(t)
Compute F
j
from (t
j
1
,R
j
1
,K
1
) and (t
j
2
,R
j
2
,K
2
)
for every keypoint kp
1
∈ KP
1
do
define search area based on set of fundamental
matrices F
j
for every keypoint kp
2
∈ KP
2
do
if kp
2
is inside search area then
compute distance between kp
1
and kp
2
end if
end for
keep kp
2
with minimal distance as correspond-
ing point to kp
1
end for
Several rotation matrices R
j
i
and location vectors t
j
i
(i ∈ {1, 2}, j = 1,..., N) are sampled for each camera
c
i
from the provided probability densities and com-
bined to a roto-translation matrix Q
j
i
by Equation 1.
Q
j
i
=
R
j
i
t
j
i
0 1
(1)
The relative roto-translation matrix Q
j
12
from camera
c
1
to camera c
2
is then given by Equation 2.
Q
j
12
= (Q
j
2
)
−1
· Q
j
1
=
R
j
12
t
j
12
0 1
(2)
where R
j
12
and t
j
12
are the relative rotation and transla-
tion from camera c
1
and c
2
.
The fundamental matrix describing this geometric
setup can then be calculated by Equation 3.
F
j
= K
−T
2
R
j
12
h
t
j
12
i
x
K
1
(3)
where K
i
are the calibration matrices of the cam-
eras and
h
t
j
12
i
x
is the skew-symmetric matrix-
representation of vector t
j
12
.
PriorKnowledgeAboutCameraMotionforOutlierRemovalinFeatureMatching
605

(a) Potential epipolar lines (b) Potential matches
(c) Best match obtained by GM
(d) Best match obtained by BFM
Figure 2: Matching procedure for a single keypoint in the
source image.
The search region of each of the keypoints of the
source image is constructed as follows: For a given
point x
1
in the source image each of the N differ-
ent fundamental matrices leads to one epipolar line
l
2
= F
j
· x
1
in the target image (Figure 2(a)). The
convex envelope of all these lines is approximated by
the extreme intersections of these lines with the image
borders as well as a vertical line in the image center.
Potential correspondences of a point are assumed
to lie only inside this area. Every keypoint of the
target image is tested whether it is inside the esti-
mated polygon (Figure 2(b)). Only if this is the case
the far more expensive calculation of the (Euclidean)
distance between both keypoint descriptors is carried
out. The point with the smallest distance is kept as
corresponding point (Figure 2(c)).
Thus, instead of doing an exhaustive search, i.e.
comparing each keypoint of the source image with ev-
ery keypoint of the target image, it is compared with a
significantly smaller subset of keypoints. On the one
hand, the number of necessary comparisons is lim-
ited which leads to a substantial decrease of the com-
putational load. On the other hand, it increases the
probability of finding a correct match. BFM defines
the global best match as corresponding point. GM
excludes huge portions of an image, that might con-
tain similar areas in terms of geometry or radiometry.
These areas lead to wrong correspondences if BFM
methods are used (Figure 2(d)). It should be noted
that GM is not able to resolve all ambiguities. If the
best global (but wrong) match lies outside the search
area, GM is more likely to give the correct point cor-
respondence. However, if the best global (but wrong)
match lies inside the borders of the area it will be de-
fined as corresponding point by both methods.
(a) σ
R
= σ
t
= 0.01 (
◦
/m)
(b) σ
R
= σ
t
= 0.1 (
◦
/m)
(c) σ
R
= σ
t
= 0.3 (
◦
/m)
Figure 3: Influence of uncertain prior knowledge on search
regions Σ
R
= diag(σ
R
),Σ
t
= diag(σ
t
); Keypoints excluded
(included) into detailed comparisons are marked in red
(blue), epipolar lines are marked in green.
The distribution of the epipolar lines and conse-
quently the shape of the computed envelope depends
on the accuracy of the prior knowledge. The more ac-
curate the priors are, the narrower the envelope is as
shown exemplary in Figure 3. In the extreme case that
the prior knowledge exactly models the true position
and orientation of the cameras, the envelope reduces
to the true epipolar line. In the other extreme case the
uncertainty of the prior information is too large, the
search area approaches the area of the whole image,
and GM behaves almost identically to BFM.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
606
4 EXPERIMENTS
The following experiments are designed to evalu-
ate the performance of the proposed matching algo-
rithm (GM) and compare it to the standard brute force
matching (BFM) approach. Both methods are applied
to all adjacent image pairs of the Castle-P19, Castle-
P30, Entry-P10, Fountain-P11, Herz-Jesu-P8, and
Herz-Jesu-P25 image data sets (Strecha et al., 2008),
which provide reference data of the absolute camera
poses additionally to the images. In total nearly 100
image pairs were processed. The results presented be-
low are averaged over all these image pairs and depict
the performance of GM relative to BFM. That means
in particular, that the absolute performances of GM
(P
GM
) and BFM (P
BMF
) are combined to the relative
performance P by Equation 4, where P stands for any
of the following measurements which are displayed in
Figures 4-7.
P =
P
GM
P
BMF
(4)
(a) Ratio of number of
matches
(b) Ratio of mean Samp-
son error with respect to
true fundamental matrix (all
matches)
Figure 4: Relative performance of GM and BFM (see
Eq. 4).
SURF, used as keypoint detector/descriptor for
its computational speed and robustness, detected be-
tween 3200 and 9200 keypoints (around 5500 on av-
erage). The prior knowledge is modelled as Gaussian
distributions p
c
(R) ∼ N(µ
R
c
,Σ
R
c
), p
c
(t) ∼ N(µ
t
c
,Σ
t
c
),
where the mean values µ
R
,µ
t
are based on the pro-
vided reference data. The variance-covariance ma-
trices Σ
R
c
, Σ
t
c
are modelled as diagonal matrices with
identical entries σ
R
c
= σ
R
,σ
t
c
= σ
t
on the main diago-
nal. This model is seldom true in practice since often
at least one of the directions is known with higher cer-
tainty than the others (e.g. in the case of planar move-
ment). However, it restricts the amount of variables
and allows an easy visualization while still capturing
the main properties of the proposed algorithm. From
the given probability density function 100 different
locations and orientations are sampled for each cam-
era, which are subsequently combined to 100 funda-
mental matrices as described above (see Equation 3).
All the figures below have common logarithmic axes
depicting σ
R
in degree and σ
t
in meter.
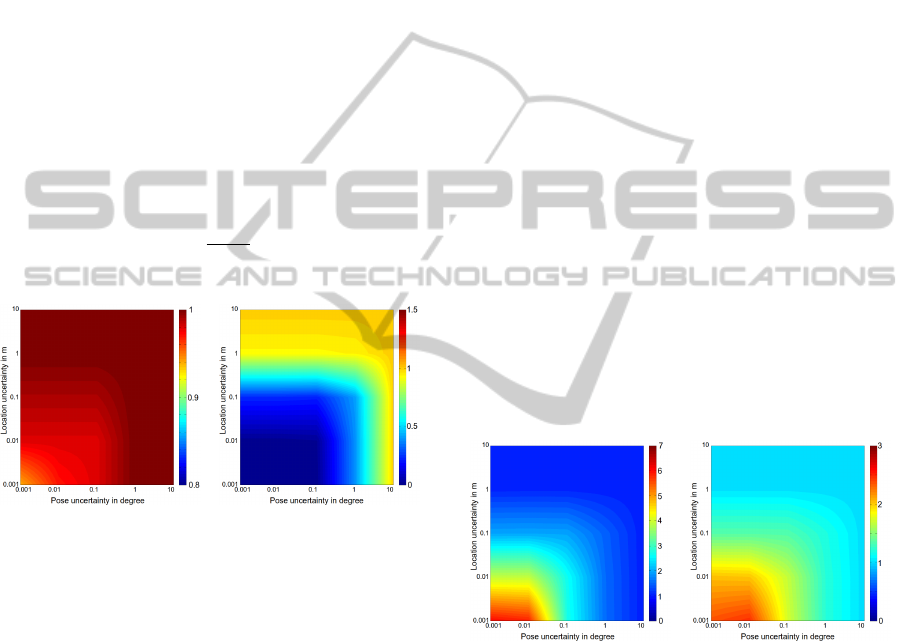
Figure 4(a) shows the ratio of the number of
matches found by both methods. While BFM al-
ways returns a match, GM might not if the established
search area of a keypoint does not contain any points.
The probability of this case increases with lower un-
certainty values, which leads to a ratio smaller than
one. However, even for very narrow search regions
more than 90% of the number of matches of BFM
are found. It should be noted, that even if both meth-
ods return the same number of matches, they probably
will not be the same matches (see discussion below).
Usually the established set of corresponding
points is filtered before it is used to estimate the fun-
damental matrix. However, it is interesting to see
that even the unfiltered set of matches can already
lead to reasonable results for GM. Figure 4(b) depicts
the ratio of the mean Sampson error of both methods
if the matched keypoints are compared to the funda-
mental matrix which is computed from the provided
reference data. For a small amount of uncertainty
the Sampson error of the GM matches approaches
zero, while it it is still reasonable small for a medium
amount of uncertainty.
(a) Ratio of RANSAC in-
liers
(b) Ratio of numbers of fil-
tered matches
Figure 5: Relative performance of GM and BFM (see
Eq. 4).
If RANSAC is used to estimate the fundamental
matrix based on the found matches, the number of in-
liers gives a good cue about the correctness of the cor-
respondence of the point sets. Figure 5(a) shows the
ratio of inliers of both methods. It should be noted,
that the absolute number of inliers is used. GM re-
sults always in a greater or equal number of inliers
(up to a factor of six more), even if less matches (e.g.
only 95%) are available.
Although beyond the scope of this paper, a sim-
ple and well known filtering method is applied to the
found matches: A match is kept iff the ratio of the
PriorKnowledgeAboutCameraMotionforOutlierRemovalinFeatureMatching
607

distances between the best and the second best match
exceeds a certain threshold. Figure 5(b) shows the ra-
tio of the number of matches that remained after this
ratio filter. Similar to the discussion above the abso-
lute numbers are used to compute the ratio. Neverthe-
less, GM results always in a larger or equal number of
filtered matches than BFM.
Figure 6 shows the ratio of RANSAC inliers and
the mean Sampson error with respect to the true fun-
damental matrix if the filtered matches are used in-
stead of all matches. Again GM outperforms BFM
if the uncertainty of the prior knowledge is small
enough and leads to identical results otherwise. The
absolute mean Sampson error of both methods is sig-
nificantly reduced by using filtered matches.
It should be noted that, although the mean Samp-
son error of GM is always smaller or equal to the error
of GM (Figure 6(b)), this does not necessarily hold
for the maximal Sampson error as Figure 7(a) shows.
Lets assume the search area as a horizontal band. Any
keypoint in the image which is similar with respect to
its descriptor will be found by BFM. If this best (but
wrong) match shows a vertical displacement, it will
not be considered by GM, because it is outside of the
search area. GM searches for the best match inside the
search area, which might be located at the other side
of the image and thus showing a much larger spatial
distance allowing for a larger Sampson error.
(a) Ratio of RANSAC in-
liers
(b) Ratio of mean Sampson
errors with respect to
true fundamental matrix
(filtered matches)
Figure 6: Relative performance of GM and BFM (see
Eq. 4).
All of the above discussion is concerned with the
relative accuracy of GM and BFM with respect to
quantitative as well as qualitative measurements. Fig-
ure 7(b) depicts the ratio of computation time, that
was needed on average in order to compute the point
correspondences. As long as the prior knowledge is
given with a sufficient amount of certainty GM is sig-
nificantly faster than BFM. But for too high uncer-
tainty the search regions span the most part of the im-
age, which results in a saturation of the accuracy of
GM to the performance of BFM. In this case the same
comparisons are carried out by both methods, lead-
ing to identical results. The overhead to compute the
search regions, however, leads to a further increase of
computational time.
(a) Ratio of max. Sampson
errors with respect to
true fundamental matrix
(filtered matches)
(b) Ratio of computation
times
Figure 7: Relative performance of GM and BFM (see
Eq. 4).
The range of uncertainty of the prior knowledge
where GM shows its full potential occurs to be rather
small within the above experiments. However, it
should be noted, that the uncertainty is given with
respect to the absolute camera position and orienta-
tion. The fundamental matrix depicts the relative ori-
entation of the two cameras and consequently is ba-
sically given with twice the amount of uncertainty as
the absolute positions. In applications where the rel-
ative position is given as prior knowledge (e.g. by
motion models or inertial measurements) the range
of values where GM leads to reasonable increase of
performance can be doubled. Furthermore, often at
least one of the possible moving or looking directions
is given with much higher accuracy, e.g. in the case
of planar motion where the height component of the
translation as well as the variation of the pitch angles
are negligible.
5 CONCLUSIONS
Prior knowledge about the position and orientation of
the cameras is available in many practical scenarios:
UAVs often fly a path given by predefined GPS loca-
tions, modern consumer cameras attach GPS tags to
their image data, mobile phones have access to GPS
data as well and can provide additional measurements
of the relative movement, and last but not least, the
user, who acquired the image data, might be able to
give a coarse description of the path he took during
data acquisition. Nevertheless, most modern methods
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
608

of keypoint matching disregard this knowledge com-
pletely and assume the most general case in which no
prior knowledge is available whatsoever.
The goal of this paper is to propose a simple,
efficient, and accurate method to include this prior
knowledge into the task of keypoint matching. Cam-
era positions and orientations are modelled as prob-
ability density distributions from which several fixed
poses are sampled. These are combined to a set of
possible fundamental matrices. For each keypoint
of the first image each of these matrices defines one
epipolar line in the other image. An approxima-
tion of the convex envelope of these epipolar lines
defines the area in which the matching keypoint is
searched. Keypoints outside this area are not consid-
ered and do not need to be compared to the source
keypoint. If the search areas are sufficiently small
(i.e. the prior knowledge sufficiently accurate) this
approach saves computation time since considerably
less comparisons have to be carried out. Addition-
ally, the correspondence set will be much more accu-
rate since problems due to repetitive image structures
can be resolved more easily leading to less ambiguous
matches.
The results of the experimental section show that
these theoretical considerations are valid. GM leads
to superior performance with respect to quantitative
(e.g. number of valid matches) as well as qualitative
(e.g. mean Sampson error) measurements, while be-
ing also significantly faster than BFM. If the uncer-
tainty of the prior knowledge is too large, the perfor-
mance of GM saturates to BFM leading to identical
but never inferior results.
It should be noted that all optimization techniques
that are usually applied to enhance BFM methods can
equally be applied to GM. All keypoints are handled
independently which allows for parallel processing.
Since one keypoint within the first image is compared
to all keypoints within the respective search region
within the second image, ideas like tree-based data
structures etc. are equally possible.
Future work will focus on a more efficient def-
inition of search regions to reduce the overhead on
calculations. Also an easy to use but general graphi-
cal user interface will be developed to allow the user
to provide the available prior knowledge in any given
form. Last but not least the method presented in this
paper should be extended by including other types of
prior knowledge, e.g. about the 3D scene structure, to
further enhance results.
ACKNOWLEDGEMENTS
This project has been co-financed through the action
”State Scholarships Foundation’s Grants Programme
following a procedure of individualized evaluation for
the academic year 2012-2013”, from resources of the
operational program ”Education and Lifelong Learn-
ing” of the European Social Fund and the National
Strategic Reference Framework 2007-2013.
REFERENCES
Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Curless,
B., Seitz, S., and Szeliski, R. (2011). Building Rome
in a Day. Commun. ACM, 54(10):105–112.
Baltsavias, E. (1991). Multiphoto Geometrically Con-
strained Matching. PhD thesis, ETH Z
¨
urich.
Brandt, S. (2008). On the Probabilistic Epipolar Geometry.
Image Vision Computing, 26(3):405–414.
Furukawa, Y. and Ponce, J. (2010). Accurate, Dense,
and Robust Multiview Stereopsis. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
32(8):1362–1376.
Garcia, V., Debreuve, E., and Barlaud, M. (2008). Fast
k nearest neighbor search using gpu. In Computer
Vision and Pattern Recognition Workshops, 2008.
CVPRW ’08., pages 1–6.
Hartley, R. and Zisserman, A. (2003). Multiple View Geom-
etry in Computer Vision. Cambridge University Press.
Hess-Flores, M., Duchaineau, M., and Joy, K. (2012). Path-
based Constraints for Accurate Scene Reconstruction
from Aerial Video. In AIPR, pages 1–8. IEEE Com-
puter Society.
Lopez, A. L. R. (2013). Algebraic Epipolar Constraints
for Efficient Structrureless Multiview Estimation. PhD
thesis, Universidad de Murcia.
Lowe, D. (2004). Distinctive Image Features from Scale-
Invariant Keypoints. International Journals of Com-
puter Vision, 60(2):91–110.
Makantasis, K., Doulamis, A., Doulamis, N., and Ioan-
nides, M. (2014). In the wild image retrieval and clus-
tering for 3d cultural heritage landmarks reconstruc-
tion. Multimedia Tools and Applications, pages 1–37.
Mikolajczyk, K. and Schmid, C. (2004). Scale and affine in-
variant interest point detectors. Int. J. Comput. Vision,
60(1):63–86.
Mikolajczyk, K. and Schmid, C. (2005). A perfor-
mance evaluation of local descriptors. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
27(10):1615–1630.
Muja, M. and Lowe, D. G. (2012). Fast matching of binary
features. In Computer and Robot Vision (CRV), pages
404–410.
Snavely, N., Seitz, S., and Szeliski, R. (2006). Photo
Tourism: Exploring Photo Collections in 3D. ACM
Trans. Graph., 25(3):835–846.
PriorKnowledgeAboutCameraMotionforOutlierRemovalinFeatureMatching
609

Strecha, C., Von Hansen, W., Van Gool, L., Fua, P., and
Thoennessen, U. (2008). On benchmarking camera
calibration and multi-view stereo for high resolution
imagery. In Computer Vision and Pattern Recognition,
2008. CVPR 2008. IEEE Conference on, pages 1–8.
Strelow, D. (2004). Motion Estimation from Image and In-
ertial Measurements. PhD thesis, Robotics Institute,
Carnegie Mellon University, Pittsburgh, PA.
Szeliski, R. and Torr, P. (1998). Geometrically Constrained
Structure from Motion: Points on Planes. In European
Workshop on 3D Structure from Multiple Images of
Large-Scale Environments (SMILE), pages 171–186.
Unger, M. and Stojanovic, A. (2010). A New Evaluation
Criterion for Point Correspondences in Stereo Images.
In WIAMIS, pages 1–4. IEEE.
Wendel, A. (2013). Scalable Visual Navigation for Micro
Aerial Vehicles using Geometric Prior Knowledge.
PhD thesis, Graz University of Technology.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
610
