Fault Detection Architecture for Proprioceptive Sensors based on a

Multi Model Approach and Fuzzy Logic Decisions

Nicolas Pous

, Dominique Gruyer

and Denis Gingras

LIV (Laboratory of Intelligent Vehicles), in the Electrical and

Computer Engineering Department of Sherbrooke University, Sherbrooke, Qc J1K 2R1, Canada

IFSTTAR- IM - LIVIC, 14 route de la minière, bat. 824, 78000 Versailles-Satory, France

Keywords: Failure Detection, Intelligent Vehicle, Localization, Data Fusion.

Abstract: In this paper a new fault detection architecture will be presented. Inspired by multi-model data fusion

algorithms and fuzzy logic decisions, it consists in the comparison between the estimation of a dynamic mode

using each sensor independently. This method is used to deal with important non-linearity and strong

interaction with the environment usually encountered in the domain of the intelligent vehicles localization.

The concept of analytic redundancy is also used to ignore model uncertainties.

1 INTRODUCTION

More and more, our society is evolving to be partially

automatized. In this context, the automotive industry

is contributing by focusing on autonomous vehicles.

As a step between this technology and the previous

one, vehicular companies are developing a large

series of tools helping drivers and improving both

safety and comfort. These tools, when used to

improve driving safety, are generally named ADAS

(Advance Driver Assistance System) (Andreas

Riener, 2009). ADAS are generally composed of a

large amount of tools permitting, for example, to

reduce stopping distance, or improve the car position

determination. In that case precisely, a large set of

exteroceptive and proprioceptive sensors are used to

obtain a better knowledge of the vehicle environment

and attitude, in order to reduce the localization

uncertainties via data fusion algorithms. Some of

them are using only proprioceptive sensors (Cai Bai-

gen et al., 2009), others are using both (Kim, S.-B et

al., 2011 and Adrien Bak et al., 2012).

Communication and map matching can also be used

to reinforce the precision of the measurement (Rohani

et al., 2013 and Rohani et al., 2014).

In both cases, a faulty data source can lead to a

catastrophic error in the position determination.

That’s why, in order to properly improve safety, we

need to detect faults and identify the associated

sources before using faulty data in the fusion

algorithm. One of the most used detection method is

based on the comparison between the normal

behavior model and the recording of the real behavior

from the sensors. This method supposed that the

system behavior is perfectly known and can be

modeled (Patton, R. J. et al., 1989).

But, the important non-linearity of our system (The

vehicle) behavior and the strong impact of

environmental perturbation will improve the

complexity of our task. Others methods based on

analytical redundancy are also used to avoid the

model issues, as described in (Sun and Cannon,

1998), where a Kalman filter is used to obtain

estimations of a same metric in order to compare the

values obtained from different sensors.

In this paper an alternative approach based on the

determination of the dynamic comportment of the

vehicle using analytical redundancy is developed in

order to treat with the non-linearity of the system. The

nominal comportment was divided in 4 sub-systems

defined by the direction changes and longitudinal

accelerations as describe in table 1.

Table 1: Dynamic modes definition.

Straight line H1 H3

Speed change H2 H4

Based on the sensors information, we will use fuzzy

logic and calculate the weight corresponding to the

membership degree of each dynamic mode in every

time, and use these values from each sensor to

determine the presence of a faulty data source.

Pous N., Gruyer D. and Gingras D..

Fault Detection Architecture for Proprioceptive Sensors based on a Multi Model Approach and Fuzzy Logic Decisions.

DOI: 10.5220/0005459700250032

In Proceedings of the 1st International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS-2015), pages 25-32

ISBN: 978-989-758-109-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

In part 2 a traditional approach for the fault detection

will be studied and our context will be presented.

Then, in part 3, the proposed method based on the

dynamic mode determination will be presented.

Section four will then present some simulation results

and a performance analysis before treating in the fifth

section of the ongoing developments and conclude in

section six.

2 CONTEXT AND TRADITIONAL

APPROACH

2.1 Context

As we focused on the ego-localization of an

intelligent vehicle, we decided to focus on

proprioceptive sensors related to the vehicle

comportment determination.

2.1.1 Odometer

The odometer is based on an electric sensor detecting

marks equally disposed on a wheel. As the odometer

is a counting device, the output will be a discrete

value representing both the integrated travelled

distance and the speed during a sampling time.

2.1.2 INS

The INS is usually composed with 3 accelerometers

and 3 gyroscopes which respectively provide

information about linear accelerations and angular

speed on the 3 axes.

2.1.3 Compass

The compass, usually integrated on the INS chip, will

inform us about the absolute orientation of our

mobile.

2.1.4 GNSS

This device provide the absolute position of the

vehicle on the earth.

2.2 Traditional Approach

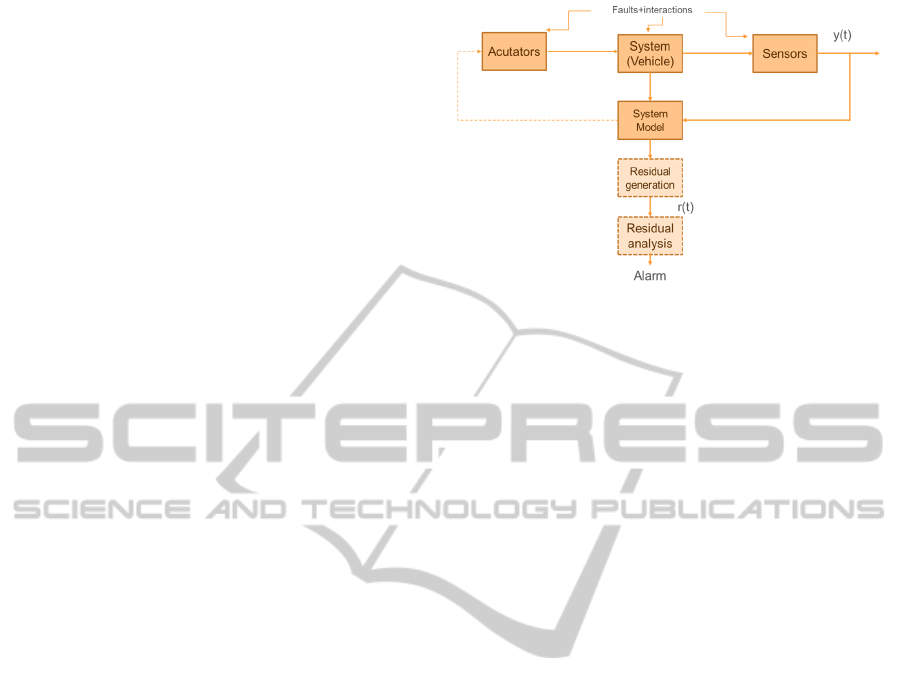
Traditionally, a system and the associated FDI (Fault

Detector and Identification) are represented as

followed. In this representation, we can distinguish

three parts which can present faults. The actuators,

the system itself and the sensors which give

information about the system comportment.

Figure 1: Classical structure of an FDI model based.

(Qi et al., 2013) present a description of the different

eligible faults on the actuators, the system and the

sensors. According to these description, we can

elaborate tests to detect every kind of fault, for every

part of the complete data flow (Actuators, System, in

our case, the vehicle and Sensors) as describe in

figure 1. Here, as we focus in this publication on the

sensors faults, actuators and system failures and

uncertainties will not described.

Four types of faults are depicted by Qi et al. for the

sensors.

- Total failure

- Constant bias failure

- Constant gain failure

- Outlier failure

Knowing these failures nature, we can elaborate tests

to detect the presence of each kind of failure. Usually,

model-based fault detector assume that at least one

part of the global system (representing the system

with its actuators and sensors) is working efficiently.

In this paper we will discuss about new techniques to

detect and identify faults without any assumptions on

any part of the global system. In that purpose, we

developed a detection method based on the

information redundancy and determination of the

system comportment.

3 DYNAMIC MODE

DETERMINATION

Inspired by the IMM fusion algorithm presented in

(Gruyer et al., 2010), we developed a multi-model

approach to detect faulty behavior on sensors used in

the determination of a mobile position. The multi-

model implementation consists in separating the

operating space into linear sub-spaces where we can

identify some simple maneuvers. This sub-space, also

called dynamic mode, has then to be determined only

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

using the sensors data. The determinations from

different sensors will so diverges if one of them

present a faulty comportment.

The global structure of our fault detection and

identification architecture is depicted in figure 2.

Figure 2: Proposed FDI structure.

The dynamic modes are defined by the longitudinal

acceleration and the angular velocity of the mobile

(representing the two possible maneuvers for the

user), and we so can separate the operating space into

four principle dynamic modes as seen in Table 1.

Figure 3: Acceleration and angular speed distribution for

the four dynamic modes.

According to the dynamic mode description, the two

needed metrics are the acceleration and the angular

speed of the vehicle.

3.1 Metrics Determination

So we need to determine these two characteristics

using each sensor independently. Concerning the

INS, these two values will be directly given by the

sensor. Concerning the odometer, it is necessary to

recalculate the value according to the nature of the

information given by the sensor. As we have the

speed of each wheel from the odometer, we can

approximate the speed of the vehicle (VE_S) by

computing the mean value of the right and left wheels

speed.

(1)

Where RW_S and LW_S are the right and left

wheel speeds respectively. It is now possible to

determine the acceleration by deriving the speed

value.

(2)

Having the acceleration, we need now to

determine the angular speed of the vehicle. In order

to determine if we are in a straight line or in a curve,

we analyze the differential speed between the 2

wheels given by (3).

(3)

Concerning the compass, it can only inform us

about the angular speed, by derivation of the

orientation θ(t).

(4)

3.2 Weight and Residual

Determination

Knowing acceleration and angular speed values, it is

now possible to determine the dynamic mode. Let’s

call Acc the presence of an acceleration, and Vθ the

presence of a rotation, so the 4 dynamic modes will

be defined as follow.

(5)

Instead of a classic determination using a simple

threshold, a fuzzy logic decisions permit to determine

a weight corresponding to the presence of an

acceleration/rotation, as represented in figure 4 for an

acceleration. The event probability is currently

determine using a Gaussian threshold as depicted in

equation 6 for the presence of an acceleration, where

the σ coefficient value permit adjust the sensitivity if

the detector.

(6)

(7)

() _ ()

_()

WSt LWSt

Ve S t





(_()) _() _(1)

()

Odo

DVESt VESt VESt

Acc t

Dt T





_() _() _()

Odo

DifS t RWSt LWSt





()

_()

Compass

An Sp t









HAccV









0.5*( / )

0.5

(0.4 * (2 * )

INS

Acc

expP



























(1 ) * (1 )

*(1 )

(1 ) *

HAccV

HAcc V

HAccV

PP P

PPP











FaultDetectionArchitectureforProprioceptiveSensorsbasedonaMultiModelApproachandFuzzyLogicDecisions

Then, the dynamic mode membership degree can

be determined as followed, where Px is the weight

corresponding to the event x.

Figure 4: Acc Weight’s determination according to the

acceleration value.

Using these weights from each sensor, it is

possible to determine an instantaneous mean value of

the corresponding metric weight by using equation

(8) taking into account every sensors independently.

Instead of calculating dynamic mode weights, we

dissociate the 2 metrics weights (Po(Acc) and

Po(Vθ)) which will be more useful.

(8)

Where is the mean value

taking all the sensors, is

the acceleration weight for the sensor

i, and C

corresponding to the decision of the fault

detection device.

Using both the mean weight value and individual

ones, we can calculate a residual value for each sensor

equal to the difference between the two of them (9).

A residual variable will then be calculated for each

sensor and each metric used (acceleration and angular

speed).

(9)

The calculated residual has to be stationary to

make the detection easier. In our case, for a normal

behavior, the residual variable will have a zero mean

value. In order to illustrate it, we simulate the drive of

a vehicle with the appearance of the 4 dynamic

modes, with only the use of four odometers (one on

each wheel, simulated by the recording of the wheel

speed), and an inertial system with accelerometers

and gyroscopes on the three axes. The figure 5

represents the mean weight calculated with

information of all the sensors, and figure 6 is the

residual variable for both acceleration and angular

speed for the inertial sensor.

Figure 5: Dynamic modes weights evolution in time.

These results were obtained by calculating the

differential weight between the mean weight values

and the INS ones. As the sensors information was

noisy, we decided in a first time to apply a

Butterworth low pass filter to eliminate the high

frequencies component of signals.

The residual value is still not perfect, and some

adjustment are still needed, but it remains possible to

use these results for the detection algorithm. Actually,

what is primordial is to observe modification of the

residual values, so, it’s possible to imagine calibration

procedure to determinate a standard residual profile

before beginning the analysis.

Figure 6: Acceleration and angular speed residual for the

INS sensor.

( , ... ) ( )

o Acc S S S C Po Acc S





( , ) ( , ... ) ( )

iNi

RAccS PoAccS S S PoAccS

( , ... )

Po Acc S S S

()

oAccS

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

3.3 Fault Detection

In this section, faulty data will be introduce in sensors

information, according with what was described in

section 2-c, regarding the sensors faults. We so

simulated each kind of fault and analyzed the residual

values in order to establish some detection rules. Just

as we did previously in this section, we will focus on

two kind of sensors, odometers (one on each wheel)

and inertial system.

As depicted in the previous section, the residual

will be calculated by computing the difference

between the mean weight value and the weight from

the sensor under watching. But as a failure will induce

some perturbation on the mean value calculation, it’s

important to determinate how this perturbation will

impact the failure detection. Considering a

perturbation ΔPo on one sensor noted S

, the mean

weight value, before the decision can be represented

by equation 10.

(10)

The residual of a non-faulty sensor will so be

impacted by a failure, and this impact will depend on

the number N of sensors used in the detection

algorithm. Residuals for both faulty and non-faulty

sensors can so be calculated by (11) and (12), and the

related perturbations can so be depicted by (13) and

(14), where N is the number of sensors used in the

mean value calculation.

(11)

(12)

(13)

(14)

The more sensors we use, the more important the

difference between a non-faulty and a faulty residual

will be. This also mean that it is important to

distinguish by comparison, a perturbation on the

residual due to another sensor fault.

4 SIMULATIONS AND

PERFORMANCE ANALYSIS

All the simulation were realized with the help of the

ProSivic simulator, which permit to simulate the

dynamic behavior of a vehicle, and the real reaction

registered by the sensors. This simulator allow us to

determine the trajectory and the speed of a vehicle

and will return us all the others component of the

mobile state, like position, acceleration, angular

speed…

In order to illustrate the response to a faulty

comportment, a gain on the speed measurement of the

left front wheel has been injected to simulate a failure,

100 seconds after the beginning of the simulation.

Figure 7: Comportment of residuals with the introduction

of a faulty comportment on one of the sensors.

Figure 7 presents the residuals for respectively the

INS, the front and the back odometers for the angular

speed determination. As predicted, the amplitude of

the residual value is increasing after the injection of a

failure, and the most important raise coming from the

affected sensor. It also appears that the residual of the

faulty sensor is the opposite of the others sensors as

prove equations (11) and (12). As the appearance of a

failure will create an event different for each type

(Detecting a rotation in a straight line mode, an

acceleration in a constant speed mode) but will

remain undetectable during some dynamic mode. It’s

so important to go through every dynamic mode to be

sure to detect failures. For example, a failure on an

odometer as presented previously will introduce a

rotation even if the real dynamic mode is descripting

a straight line. But if the vehicle remains in a rotation,

the detection cannot be done. A better way is to

analyze the mean values of all the residual on a long

(,...) ()

Po Acc S S S C Po Acc S Po





















( ) ( ) ( , ... )

()( ) (,...)

() ( ) ()

FF N

FNF N

FNFi

R Acc S Po Acc S Po Acc S S S

R Acc S Po Acc S Po Po Acc S S S

Acc S Po Po Acc S Po Acc S











 







() () ()

NF NF i

Acc S Po Po Acc S Po Acc S







 







RPo



 

RPo





FaultDetectionArchitectureforProprioceptiveSensorsbasedonaMultiModelApproachandFuzzyLogicDecisions

time period with the occurrence of all the dynamic

mode in order to realize the detection.

We can observe in figure 8 that the mean value of

each residual is varying according to equation (13)

and (14), but it’s necessary now to determine decision

laws to minimize the false alarms and missed

detections rate. The optimization will be part of the

future work. For now, we assume that the detection is

decided by a threshold determined analytically at 0.4.

In that case, after the detection the faulty data source

will not be taken into account in the mean value

computation, just as described in equation (9) where

the corresponding decision coefficient C will be equal

to 0. The residual of a non-faulty and a faulty sensor

will so be as described respectively in equation (15)

and (16).

( ) ( ) ( , ... )

NF NF N

R Acc S Po Acc S Po Acc S S S

(15)

( ) ( ) ( , ... )

FNF N

R Acc S Po Acc S Po Po Acc S S S

(16)

Figure 8: Residual mean value calculated every 10 seconds

for each sensor.

Figure 9: Residual mean value taking into account the

decision procedure.

The perturbation for a non-faulty sensor will so be

zero centered while the perturbation for a faulty one

will correspond to the perturbation on the weight

ΔPo.

As predicted, incorporating the decision process

will keep the non-faulty residuals around zero and

increase the faulty residual value.

A second set of simulations has been run in order

to illustrate the detection of a failure corresponding to

an offset appearing on the acceleration given by the

INS. In these simulations we varied both the offset

values and the threshold sensitivity σ to study their

impact on the fault detection. Figure 10 present the

results of the fault detection according to σ and the

offset value.

Figure 10: Fault detection according to sigma and offset

value.

The red zone correspond to a good fault detection,

and the blue correspond to a missed detection. It’s so

possible to see that reducing the σ value permit the

detection of smaller faults. But, reducing this value

will also mean that the fault detector will be more

sensitive to noise. A simulation with different noise

levels has also been realized in order to study this

sensitivity. A white noise was so injected on the INS

measurement only, with an RMS value varying from

0.01 to 0.2 m/s2. A new set of simulation was run,

keeping an offset of 0.5 m/s2 (100 seconds after the

beginning of the simulation) and varying the sigma

value from 0.1 to 1 (just like the previous simulation

set).

During the first part of the simulation, when the

fault has still not appeared, the presence of noise can

create some false alarm when the sigma value is too

low.

After the appearance of the offset, the algorithm

is working efficiently. As the injected offset is set at

0.5 m/s2, the minimum sigma value needed for the

detection will be around 0.5 (as shown by the

previous study, figure 10). It seems logical to expect

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

a detection for the sigma values below 0.5 while there

will be no detection for the upper values. This is

verified in this simulation (figure 12) where the

detection is realized for the lower sigma values.

Figure 11: false alarm due to noise when sigma value is too

low.

Figure 12: Offset detection with different sigma values

varying noise level.

These results verify what has been said earlier, the

detection is well done for a sigma value lower than

0.5, for every noise level injected.

For now, the residuals generated permit the

distinction of most of the default presented in the

section 2, but not all of them. It is still necessary to

work on the residual analysis and on others residuals

to be able to detect and identify all kind of faults.

5 FUTURE WORK

As it was said in the previous section, the analysis of

residuals will lead to the failure detection, and the

distinction of which sensor is faulty. But, in our

problematic, it’s also important to distinguish faults

generated by sensors to other ones due to

environment interferences or a system perturbation

(flat wheel…). So, we need to develop strategies to

establish the distinction between each kind of fault.

To bring out this strategy, let’s discuss about a

concrete case, and compare the results obtained for

three different faults.

We imagined a scenario where a fault on one of

the odometers appears. This fault is traduced by a

gain on the distance measured as described in (17).

(17)

Dist

is the measures distance, Dist

Real

is the real

distance and x is the number of marks originally

presented on the encoded wheel. This kind of fault is

generally caused by a missing mark on the coded

wheel. It’s corresponding to a contact gain failure, as

depicted in the second section concerning sensors

failures. But, a flat tire could also have an equivalent

impact, as the wheel diameter will be reduced, with a

same angular speed, the travelled distance will be

smaller.

(18)

Where

and D

are respectively the flat tire

and the normal wheel diameter. Mathematically these

two errors lead to the same result, but it remains

important to be able to distinguish the two of them. In

the future work we will focus on this distinction by

using a three dimensional model of our system.

6 CONCLUSIONS

This first paper is a presentation of the architecture

and preliminary results on the fault detection method

proposed.

In this paper a new fault detection architecture was

presented, based on a multi-model approach. In a first

time, our context was presented before introducing

the developed method using both a multi –model

approach and a fuzzy logic decision to generate

residual variables allowing to distinguish faulty data.

As explained in the section 3, the residual will permit

to detect perturbation by computing the difference

between weights of each sensor independently and a

mean value computed with all the sensors. It also has

been demonstrated that adding the decision result to

the mean value computation will increase the

difference between a faulty and a non-faulty residual,

which permit a better discrimination between the two

of them.

(1 1 / )

Me al

Dist Dist x





Me al

Dist Dist









FaultDetectionArchitectureforProprioceptiveSensorsbasedonaMultiModelApproachandFuzzyLogicDecisions

In the simulation results presented in the section

four, two study cases have been presented. The first

one corresponding to a gain on the odometer speed

allowed us to illustrate the calculation proposed on

the previous section, and so to verify the efficiency of

the proposed FDI. Finally, a study on the sensitivity

and robustness has been effected on the second case,

presenting an offset on the INS acceleration. This

study also permit to determine the importance of the

detector parameters configuration according to the

noise and the needed sensitivity.

ACKNOWLEDGEMENTS

This work is part of CooPerCom, a 3-year

international research project (Canada-France). The

authors would like to thank the National Science and

Engineering Research Council (NSERC) of Canada

and the Agence nationale de la recherche (ANR) in

France for supporting the project STP 397739-10.

REFERENCES

Andreas Riener; 2009; Sensor-Actuator Supported Implicit

Interaction in Driver Assistance Systems; Chapter 9;

vieweg-teubner.

Cai Bai-gen; Wang Jian ; Yin Qin ; Liu Jiang, 2009, A

GNSS Based Slide and Slip Detection Method for Train

Positioning, Asia-Pacific Conference on Information

Processing, APCIP 2009.

Kim, S.-B.; Bazin, J.-C.; Lee, H.-K.; Choi, K.-H.; Park, S.-

Y.; 2011; Ground vehicle navigation in harsh urban

conditions by integrating inertial navigation system,

global positioning system, odometer and vision data;

Radar, Sonar & Navigation; Vol.5; pp 814 – 823.

Adrien Bak; Dominique Gruyer; Samia Bouchafa; Didier

Aubert; 2012; Multi-Sensor Localization – Visual

Odometry as a Low Cost Proprioceptive Sensor; ITSC.

Rohani, M.; Gingras, D.; Vigneron, V.; Gruyer, D., 2013;

A New Decentralized Bayesian Approach for

Cooperative Vehicle Localization based on fusion of

GPS and Inter-vehicle Distance Measurements;

ICCVE.

M. Rohani; D. Gingras; D. Gruyer, 2014; Vehicular

Cooperative Map Matching; International Conference

on Connected Vehicles and Expo (ICCVE).

Patton, R.J; Frank, P.; Clark, R.; 1989; Fault Diagnosis in

Dynamic Systems, Theory and Application; prentice

hall.

Xin Qi; Didier Theilliol; Juntong Qi; Youmin Zhang;

Jianda Han, 2013; A Literature Review on Fault

Diagnosis Methods for Manned and Unmanned

Helicopters; International Conference on Unmanned

Aircraft Systems; May 28-31.

Gruyer, D.; Pechberti, S.; Gingras, D.; Dupin, F.; 2010,

Robust positioning in safety applications for the CVIS

project; IEEE Intelligent Vehicles Symposium; pp 262 -

268.

Mr. Huangqi Sun; Dr. M. Elizabeth Cannon, 1998;

Relibaility analysis of an ITS navigation system;

Department of Geomatics Engineering; The University

of Calgary; Calgary, Alberta, Canada.

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems