PRIAR using a Graph Segmentation Method

M. Righi

1,3

, M. D’Acunto

1,2,3

and O. Salvetti

1,3

ISTI-CNR, via Moruzzi 1, 56124, Pisa, Italy

ISM-CNR, via Fosso del Cavaliere, 100, 0133, Roma, Italy

NanoICT Laboratory, Area della Ricerca CNR Pisa, Pisa, Italy

Keywords:

Pattern Recognition, Image Analysis, Image Segmentation, Boundary Detection, Graph Partitioning Algo-

rithm.

Abstract:

Recently, we have suggested a simple and general-purpose method able to combine high-resolution analysis

with the classiﬁcation and identiﬁcation of components of microscopy imaging. The method named PRIAR

(Pattern Recognition Image Augumented Resolution) is a tool developed by the authors that gives the possi-

bility to enhance spatial and photometric resolution of low-res images. The implemented algorithm follows

the scheme: 1) image classiﬁcation; 2) blind super-resolution on single frame; 3) pattern-analysis; 4) recon-

struction of the discovered pattern.

In this paper, we suggest some improvements of the PRIAR algorithm, in particular, the deﬁnition of a seg-

mentation method which is based on homomorphism between a processed image and a graph describing the

image itself, able to identify object of interest in complex patterns. The case study is the identiﬁcation of

organs inside biological cells acquired with Atomic Force Microscopy Technique.

1 INTRODUCTION

Microscope image analysis is used in many ﬁelds of

technology, science and medicine. In all these appli-

cations, a common problem is represented by the low

resolution of objects of interest, so that detection and

classiﬁcation are difﬁcult and, because of correspon-

dent poor resolution, analysis of such objects can be

lead to misunderstanding. As a consequence, pattern

recognition (PR) and identiﬁcation of objects of in-

terest is a ﬁrst necessary step in order to improve the

quality of image analysis, the second step is to im-

prove the resolution from low level to high level, or

equivalently, multiple scale resolution.

PR applied to the imaging techniques is a term de-

noting supervision methods developed by the combi-

nation of machine learning, artiﬁcial intelligence and

data mining. PR methods can be categorized accord-

ing to the type of learning procedure used to generate

output value from input images. For example, super-

vised learning procedure assumes that a set of train-

ing data has been previously provided (Gonzalez and

Woods, 2008). Then, a further learning processing

generates a model that attempts to meet two general

requests: i), perform as well as possible on the train-

ing data, and, ii) generalize as well as possible to new

data or other input images. The other one category

is represented by the unsupervised learning methods.

This class of pattern recognition methods assumes

training data that has not been previously labelled,

and try to ﬁnd inherent patterns in the data that can

be used to identify a correct output value for new data

instances (Theodoridis et al., 2008). A combination

of the two categories is also possible, mixing labelled

and unlabeled data in suitable ways, depending by the

data in input, and where the data to be labelled is the

training data (Bishop, 2006). Most common pattern

recognition algorithms are probabilistic in nature, in

that they use statistical inference to ﬁnd label for a

given instance. In many applications, many proba-

bilistic algorithms output a list of n-best labels with

associated probabilities, instead of simply best label.

For example, PR can be used for classiﬁcation, which

attempts to assign each input value to one of a given

set of classes, in this case, the n-best labels should be

fairly small (a binary choice for n is the best, yes or

not, 1 or 0, etc). All the microscopic techniques re-

quire highly sophisticated pattern recognition super-

vised methods, for example PR is crucial for the seg-

mentation procedure of components to be identiﬁed

and classiﬁed in a large image. Since PR strategies

are strongly dependent by the application, we focused

Righi M., D’Acunto M. and Salvetti O..

PRIAR using a Graph Segmentation Method.

DOI: 10.5220/0005461600460052

In Proceedings of the 5th International Workshop on Image Mining. Theory and Applications (IMTA-5-2015), pages 46-52

ISBN: 978-989-758-094-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

the attention on methods connected to the identiﬁca-

tion or organs and components inside biological sys-

tems like animal cells. For example, systemic analy-

sis of subcellular protein localization provides a key

for understanding gene functions and physiological

condition of the cells. However, recognition of cell

images of subcellular structures highly depends on

experience and becomes the rate-limiting step when

classifying subcellular protein localization. Several

research groups have extracted speciﬁc numerical fea-

tures for the recognition of subcellular protein local-

ization, but these recognition systems are restricted to

images of single particular cell line acquired by one

speciﬁc imaging system and not applied to recognize

a range of cell image sources.

Our imaging technique is based on the scanning

probe microscope (DAcunto, 2011), a technique that

measures the cells touching them with a probe ap-

proaching a resolution on the nanometer scale. On

the contrary, with respect to other microscope tech-

nique, like for example, the confocal microscopy, the

interaction between the microscopic tip probe and the

sample is limited to the cell cytoskeleton, i.e., the cell

surface, so pattern recognition methods must be ad-

dressed to identify skeleton components, like micro-

tubules, microﬁlaments, intermediate ﬁlaments, etc.

Once a skeleton components is identiﬁed, a proce-

dure of super-resolution (enhanced resolution) could

improve the data analysis and mining. The problem

of enhancing resolution of a single image refers to the

task of obtaining a high-resolution enlargement of a

single low resolution image, commonly recognised as

single-frame super-resolution problem. This problem

is intrinsically ill-posed because are generally multi-

ple frame images that can be combined to obtain ﬁnal

high-resolution images. Accordingly to enhancing

resolution for a single image, strong prior information

must be realized. This information is available either

in the explicit form of a distribution deﬁned on an im-

age class, or an implicit form of an example image

which leads to example-based super-resolution image

(Kim and Kwon, 2010). One diffuse approach for

the super-resolution of low-resolution image has been

characterized by algorithms including nearest neigh-

bour (NN)-based estimation. In such approach, there

are two distinct steps, in the ﬁrst one, pairs of low-

resolution and corresponding high-resolution image

patches are collected. Then in the second one, the

super-resolution step, each patch of the given low-

resolution is contrasted to the stored low-resolution

patches, and the high-resolution patch corresponding

to the nearest low-resolution patch and satisfying a

certain spatial neighbourhood similarity can be evi-

denced so that can be considered as the ﬁnal output of

the super-resolution image.

2 PRIAR 1.0: BASIC

FUNCTIONALITIES

The PRIAR (Pattern Recognition Image Augumented

Resolution) is a tool we have developed that gives the

possibility to enhance the resolution of low resolu-

tion images. It enhances the spatial resolution and

the depth of the image. The implemented algorithm

follows the scheme: 1) image classiﬁcation; 2) blind

super-resolution on single frame; 3) pattern-analysis;

4) reconstruction of the discovered pattern. PRIAR

runs on Matlab 2013b, and the main features of the

computer used to test the program follows:CPU In-

tel(R) Core(TM) i5-2400 CPU @ 3.10GHz (4 cores)

with a L2 cache of 6144 KB with 16GB of RAM. The

program has been developed as mono-task, the idea

is to have a pipe-ﬂow where each piece calculates a

subproblem sequentially. PRIAR works with in in-

put a low-resolution image and produces in output a

high-resolved computed image where the objects to

be identiﬁed are recognized and substituted with their

correspondent models. The execution time depends

on the size of the input data. A typical execution time

for patch images of 128 ×128 pixels, 8 bit per pixel,

is of about 70 seconds. The occupied memory de-

pends on the image size, the presented typical exam-

ple need of about 256 MB of RAM. The Matlab code

that describes algorithm implementation is detailed

elsewhere (Righi, 2014), here, we resume the basic

functions included inside with the following pseudo-

code:

01 Function [path enhanced_image]=PRIAR(input_image)

02 class=classification(input_image)

03 switch class

04 case:grating

segmentation_type=otsu

05 case:cell

segmentation_type=edge_discover

06 end

07 sr_image=blind_sr(input_image)

08 initial_path=

PRIAR-S(seed,super_resolved_image)

09 edge_discovered=

edge_discover(sr_image,segmentation_type)

10 path=

explore_extend(initial_path,segmented_image);

11 enhanced_image =build_model(sr_image,class)

12 end

The algorithm models a general purpose method to

analyse the images, in fact it uses a modular solu-

tion that permits to extend the class of the recog-

nized images and the image enhancement. The line

02 of the pseudo-code calls a data-mining function

PRIARusingaGraphSegmentationMethod

that classify the input image. In this particular imple-

mentation the function distinguish only two classes

of images: images representing a grating and im-

ages representing cells. The classiﬁcation is impor-

tant during the next stages to choose the better seg-

mentation to adopt. The line 07 reports the function

call that super-resolve the image. During this step

the analysed image (that is a low resolution image)

is improved by increasing the colorimetric and spa-

tial resolution. The PRIAR implements the following

SR algorithms: Kim-Kwon (Kim and Kwon, 2010),

spline interpolation (Sonka et al., 2007), nearest-

neighbor interpolation (Ikonen and Toivanen, 2005),

bilinear interpolation (Bourke, 2001), bicubic inter-

polation (Getreuer, 2011), box-shaped kernel interpo-

lation (Ardizzone, 2009), Lanczos-2 kernel interpola-

tion (Getreuer, 2011) and Lanczos-3 kernel interpo-

lation (Ardizzone, 2009). The line 08 describes the

ﬁrst step to map the object of interest (microtubule).

In each case, it needs a seed. The seed can be simply

a point of the object we are going to map or a poly-

line that follows a part of the object we are going to

discover. This is the algorithm we are going to de-

scribe in detail in the next sections. The main idea

of the explore algorithm is to crawl the surface until

certain parameters are respected. The role of the pa-

rameters can be summarized in the fact that the gap

between two next pixel must be enough small. At the

end of this exploration we have an initial path that

is a subset of the object we are going to trace. The

hypothesis that the initial path is a subset of the ﬁ-

nal path is guarantee by the strong constraint that are

applied by the explore algorithm. The complexity of

this algorithm is linear with the number of the pixel

that composed the matrix. The explore algorithm per-

forms a local exploration so it is a local search al-

gorithm. Line 09 shows the edge discover function

call. The function used with grating images is differ-

ent by the one adopted with cell images in order to

avoid unwanted shadows. In fact, in order to edging

the grating super-resolved image, we combine the So-

bel method (Gonzalez and Woods, 2008; Gonzalez et

al., 2010), the Prewitt method (Gonzalez and Woods,

2008; Gonzalez et al., 2010), the Roberts method and

the Laplacian of Gauss method (Gonzalez and Woods,

2008; Gonzalez et al., 2010). If the we are analyzing a

cell image, we combine the Canny method (Gonzalez

and Woods, 2008; Gonzalez et al., 2010), the Zero-

Cross method (Gonzalez and Woods, 2008; Gonzalez

et al., 2010) and the previous listed methods.

3 PRIAR 1.1: IMPROVEMENTS

OF PRIAR WITH GRAPH

SEGMENTATION METHOD

In this section, we put in evidence the procedure un-

derlining the line 08 of PRIAR algorithm: i.e., the

identiﬁcation of tyhe object of interest trough the seg-

mentation based on graph approach. Image segmen-

tation represents a challenge in image analysis. The

kind of segmentation that is required depends on user

objectives so different deﬁnitions and criteria have

been developed for image segmentation. Here, we

put in evidence a new method to segment a particu-

lar area of a gray-scale image,as previously identiﬁed

inside PRIAR procedure.

We represent the image with a proximity graph

where each node is associated to one image pixel. The

edges are labelled and reﬂects the neighbour relation

between pixels. Weights of edges is computed by a

function based on properties of corresponding pixel

such as the color intensity and the position. Accord-

ing to this representation the graph is used to deter-

mining the image segments. Let us consider a non-

oriented weighted graph G = (V, E,W) where V is the

set of the vertex that represents the image pixels, E the

edges that connect the vertex and the weighted edges

W represent the relationships between neighbour pix-

els. The weight matrix w

i j

, where i, j ∈ I where I

is the image, is a symmetric matrix. The use of the

image segmentation reduces the problem to a graph

clustering problem, in fact an image segment corre-

sponds to partition of the graph: the nodes of a par-

tition are strongly connected while the nodes that be-

longs to different partitions are weakly connected.

The application of a graph clustering algorithm to

a proximity graph will partition it into sub-graphs, the

objective of this research is to identify a single object

in an image so the PRIAR 1.1 algorithm will take in

account only a sub-graph. This paper extends the al-

gorithm described in (Righi et al., 2014; DAcunto et

al., 2015).

3.1 Image Representation

The graph G = (V, E,W ) represents the input image

where each node V represents a pixel of the source

image and the weight w

i j

is the distance between two

nodes. The distance between two nodes corresponds

to the distance between the the pixel i and the pixel j.

Since we want to recognize pixels that are in the same

segment, the weight of the graph represent the color

similarity and it is calculated by a likelihood func-

tion based on the local intensity of neighboring pixels.

IMTA-52015-5thInternationalWorkshoponImageMining.TheoryandApplications

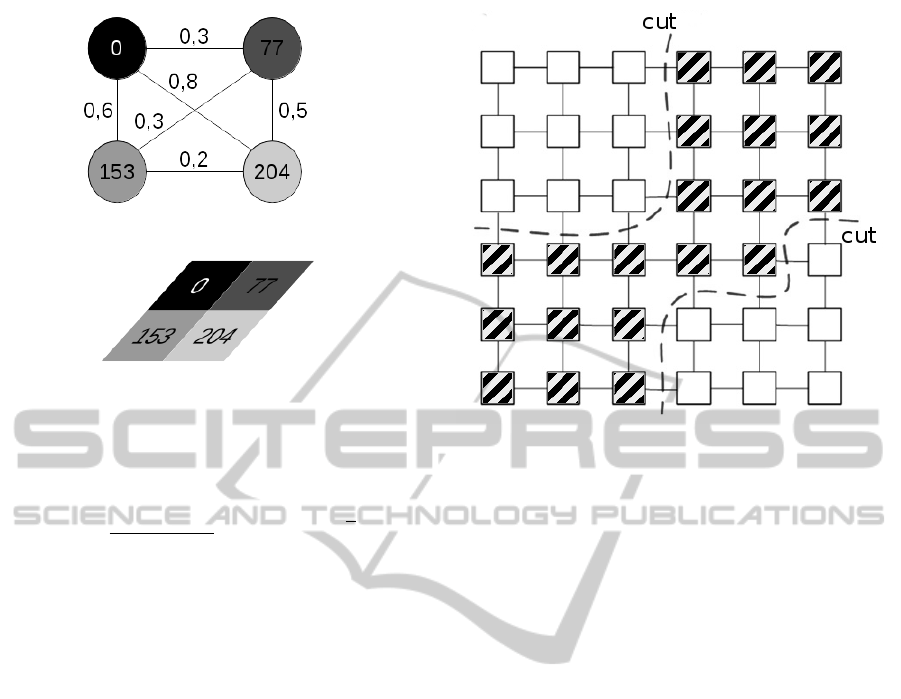
Figure 1: a portion of a 8-bit grayscale image and its asso-

ciated graph.

The weight are calculated as described in function 1.

i j







1 −



−c



max (c)

if d (i, j) ≤

√

0 otherwise

(1)

where d (i, j) is the Euclidean distance between pix-

els. There is an edge linking between two nodes only

if the nodes are close together. By using the weight of

function 1 next edges that have a close color belong

to the same structure: in this method of segmenting

a segment is determined by the homogeneity of the

color of pixels that constitute it. Figure 1 shows the

association between a portion of a 8-bit grayscale im-

age and its associated graph.

Note that by using this formulation the result can

be easily veriﬁed by a visual inspection of the image

searching homogeneous area of pixels.

A good result for a graph-based segmentation

methods depends on the translation of the color in-

formation of the source image into the graph: in order

to have an easily clusterization, the colour of a seg-

ment must be well separated from the color of other

segments. In order of improve the segmentation pro-

cedure, the image separation algorithm must use a

weighted function that is function of the input image.

This function is part of the image segmentation algo-

rithm and it is described into the next section.

3.2 Image Segmentation Algorithm

As described in section 3.1 an image can be repre-

sented by a proximity graph that can be crawled in

order to calculates a segment of interest. This method

implements the well-accepted criteria (Wertheimer,

Figure 2: an example of graph cuts and the corresponding

vertex weight.

1938) to recognize a segment. The segment of inter-

est is composed of strong bonds between the vertexes

that is surrounded by a set of weak bonds between

the vertexes. To ﬁnd a segment in proximity graphs

of image, we use the graph as described in section

3.1. The key idea is that a segment is recognizable by

analysing neighbourhood relationships between ob-

jects in a particular space which reﬂects object sim-

ilarities. In most practical problems direct analysis is

unrealistic due to the high dimensionality of the space

(Peng et al., 2013) and it is necessary use an heuristic

approach to reduce the space where to search the goal

(Russell and Norvig, 2010). Our solution linearises

the search problem by reducing the algorithm com-

plexity to O(n) where n is the number of the pixel.

In this method the search problem is expressed by the

following relation:

cut (A, B) =

(

min

∑

i, j∈A

i j

max

∑

i∈A,i∈B

i j

(2)

where A is the segment we want recognize and B the

background. In ﬁgure 2, we show an example of such

graph cut. In order to segment the image it is used

min

∑

i, j∈A

as primary objective and max

∑

i∈A,i∈B

secondary objective. The idea to threat the segmen-

tation as an exploring game placing a crawler (the

player) on a vertex that is part of the interesting seg-

ment. The crawler can move from a vertex to another

one if there exists the condition to execute this move-

ment, the condition is a function of the input image.

Considering that the weights are constant, the crawler

can be implemented using a net surfer and a pixel

harvester. Both net surfer and pixel harvester pro-

PRIARusingaGraphSegmentationMethod

cedures are implemented using a deterministic ﬁnite

automaton. The net surfer is modelled by a IFA (It-

erated Finited Automa) (Zhang, 2008) and the pixel

harvester is modelled by a DFA (Deterministic Finite

Automaton) (Hopcroft and Ullman, 1969).

3.3 Net Surfer

The net surfer must navigate the graph in order to

have an exhaustive search over the graph. This task

is particularly important because it determines the al-

gorithm complexity: in fact the other function have a

linear complexity according to the size of the data in-

put. In order to maintain his algorithmic complexity

it is necessary that this task has an O(n) complexity

(Parinya et al., 2014; Zhang, 2008). The solution we

illustrate respect this constraint permitting us to have

a algorithm with linear complexity. The IFA is de-

ﬁned by I = (S

, S

, S, I, A) where S

is the initial state,

is the ﬁnal state, S are the non-terminal states and

A is the set of the actions. The nodes of I are homo-

morphic to G nodes, the operation performed by IFA

are used to calculated the next node that must be ex-

amined by the pixel harvester.

The input of the net surfer is a labelled graph G0=

(V, E) where each edge has a label from 1 to 8.

The IFA we use has a number of states that is

equivalent to the number of the vertex V of the G

graph. Each state stores two information: the last

edge that was visited and the belonging state value.

The belonging state value can be U,B or B:

• U means that it is a state that is not yet examined;

• B means that it is a state that corresponds to a ver-

tex that belongs to the segment;

• B means that it is a state that does not correspond

to a vertex that belongs to the segment.

We show in ﬁgure 3 the node label of the G0 graph.

The net surfer gets in input the ﬁrst node and mark

its state as B, initializes the local variable of the node

edge counter with the value 1 and initialize the vari-

able history list of the nodes with the name of the ﬁrst

node. The next step consists of the examination of

the variable value node edge to locate the next note

to analyse (the node at the end of the edge). If the

node has value U the net surfer calls the pixel har-

vester function (describe in sub-section 3.4) and ac-

cording to the pixel harvester answer change the state

of the node in B or B. If the state of the node is B

it will never analysed again. Otherwise the search of

the nodes that are in the segment continues from this

node assigning the state. Each time that a node is call

back it is increased its node edge by 1 and the search

Figure 3: the labelled graph G0 used by IFA.

A B

Figure 4: (a) the box emphatize the area where it is per-

formed the search (b) the ﬁlament tracked by PRIAR 1.1

algorithm.

starts again following the new edge. The search ﬁn-

ishes when the variable node edge has reached the

value 9 and the history list contains only one node.

The returned value is a list of the pixels that are in the

segment.

3.4 Pixel Harvester

The pixel harvester evaluates the distance between

two pixels. Considering that ref(init) is the correspon-

dent value of the colour intensity between the ﬁrst

node selected and its pixel, the adopted model con-

sider that the distance between two adjacent nodes i

and j are in the set B (the set of the nodes that are in

the segment) only if the equation 3 is satisﬁed.

i ∈B∧



ref (init) −w

i j



< v

∧w

i j

< v

⇒ j ∈B (3)

The constraints v

and v

depends on input data and

are inserted by the user.

3.5 Additional Results

PRIAR 1.1 algorithm gives has provided interesting

result during cell analysis. Here we show only two

samples where we put in evidence the features of the

algorithm (ﬁgures 4 and 5).

Moreover we tested our method by applying it

to synthetic images containing a set of cylindrical

IMTA-52015-5thInternationalWorkshoponImageMining.TheoryandApplications

A B

Figure 5: (a) the box emphatize the area where it is per-

formed the search, (b) the ﬁlament tracked by using the

PRIAR 1.1 algorithm.

shapes. We found that these shapes could be recog-

nized after both reduction of resolution and addition

of noise. We found that the percentage error (num-

ber of pixels either wrongly assigned or non-assigned

to the pattern to identify) was 0.8 when the signal-to-

noise ratio was 11.6 dB and was 7.4 when the signal-

to-noise ratio was 8.7 dB.

4 CONCLUSIONS AND FUTURE

WORKS

In this paper, we have presented the PRIAR 1.1, a new

improved version of the code PRIAR (Pattern Recog-

nition Image Augmented Resolution)1.0. Essentially,

the new improvement regards the identiﬁcation of ob-

ject of interest inside an image showing complex pat-

terns. The application is on stem cell cytoskeleton

recorded with an atomic force microscope. The key

idea is that the object of interest, (for example, a seg-

ment, that in the reality represents a cytoskeleton ﬁl-

ament) is recognizable by analysing neighbourhood

relationships between objects in a particular space

which reﬂects objects similarities. Since, in most

practical problems, direct analysis is unrealistic due

to the high dimensionality of the space, we improved

the procedure linearizing the search problem by re-

ducing the algorithm complexity to O(n), where n is

the number of the pixel.

This method shows how the use of graphs to per-

form pattern-recognition is a powerful tool for the

recognition of objects in an image. Considering that

the same object can be isomorphic with more uncon-

nected subgraphs, we will study how to relate these

subgraphs and recognize when they refer to a single

object image.

ACKNOWLEDGEMENTS

The authors like to thank Serena Danti, Department

of Medicine, University of Pisa.

REFERENCES

Ardizzone, E. et al. (2009). Fuzzy-based kernel regression

approaches for free form deformation and elastic reg-

istration of medical images. In de Mello, C. A. B., ed-

itor, Biomedical Engineering. nTech.

Bishop, C. M. (2006). Pattern Recognition and Machine

Learning. Springer-Verlag New York, Inc.

Bourke, P. (2001). Bicubic Interpolation for Image Scaling.

DAcunto, M. (2011). Nanotribology and Biomaterials:

New Challenges for Atomic Force Microsopy. In Ad-

vances in Nanotechnology, Advances in Nanotechnol-

ogy, pages 105142. Nova Science.

DAcunto, M. et al. (2015). A new method combining En-

hanced Resolution and Pattern Identiﬁcation. submit-

ted to The Open Medical Informatics Journal.

Getreuer, P. (2011). Linear Methods for Image Interpola-

tion. Image Processing On Line, 18.

Gonzalez, R. C. et al. (2010). Digital Image Processing

Using MATLAB. Prentice Hall, 2nd edition.

Gonzalez, R. C. and Woods, R. E. (2008). Digital image

processing. Prentice Hall, Upper Saddle River, N.J.

Hopcroft, J. E. and Ullman, J. D. (1969). Formal Lan-

guages and Their Relation to Automata. Addison-

Wesley Longman Publishing Co., Inc., Boston, MA,

USA.

Ikonen, L. and Toivanen, P. J. (2005). Distance and Nearest

Neighbor Transforms of Gray-Level Surfaces Using

Priority Pixel Queue Algorithm. In Blanc-Talon, J. et

al., editors, ACIVS, volume 3708 of Lecture Notes in

Computer Science, pages 308315. Springer.

Kim, K. I. and Kwon, Y. (2010). Single-Image Super-

Resolution Using Sparse Regression and Natural Im-

age Prior. IEEE Trans. Pattern Anal. Mach. Intell.,

32(6):11271133.

Parinya, C. et al. (2014). Pre-Reduction Graph Products:

Hardnesses of Properly Learning DFAs and Approx-

imating EDP on DAGs. In Foundations of Computer

Science (FOCS), 2014 IEEE 55th Annual Symposium

on, pages 444453. IEEE.

Peng, B. et al. (2013). A Survey of Graph Theoretical Ap-

proaches to Image Segmentation. Pattern Recogn.,

46(3):10201038.

Righi, M. (2014). Pattern Recognition Image Augmented

Resolution: a tool for image analysis. Technical Re-

port.

Righi, M. et al. (2014). PRIAR (Pattern Recognition Image

Augmented Resolution) a tool to combine pattern-

recognition with superresolution. In 9th International

Conference on Open German Russian Workshop on

Pattern Recognition and Image Understanding.

Russell, S. and Norvig, P. (2010). Artiﬁcial Intelligence: A

Modern Approach. Prentice Hall, 3 edition.

PRIARusingaGraphSegmentationMethod

Sonka, M. et al. (2007). Image Processing, Analysis, and

Machine Vision. Thomson-Engineering.

Theodoridis, S. et al. (2008). Pattern Recognition. Aca-

demic Press, 4th edition.

Wertheimer, M. (1938). Laws of organization in perceptual

forms. In Ellis, W., editor, A Source Book of Gestalt

Psychology, pages 7188. Routledge and Kegan Paul,

London.

Zhang, J. (2008). Complexity and Universality of Iterated

Finite Automata. Complex Systems, 18.

IMTA-52015-5thInternationalWorkshoponImageMining.TheoryandApplications