A Case Study for Evaluating Bidirectional Transformations in QVT

Relations

Bernhard Westfechtel

Applied Computer Science I, University of Bayreuth, D-95440 Bayreuth, Germany

Keywords:

Model-driven Software Engineering, Bidirectional Model Transformations, QVT Relational.

Abstract:

In model-driven software engineering, high-level models of a software system are eventually transformed into

executable code. Model transformations constitute a key technology for model-driven software engineering.

QVT Relations (QVT-R) is a language for the declarative speciﬁcation of model transformations which was

deﬁned in an OMG (Object Management Group) standard. In addition to unidirectional transformations, QVT-

R supports bidirectional transformations: Rather than writing two unidirectional transformations separately,

the user may provide a single relational speciﬁcation which may be executed in both directions. In this way,

the speciﬁcation of a bidirectional transformation may be simpliﬁed considerably — which is crucial e.g. for

round-trip engineering. This paper investigates a case study for evaluating QVT-R’s capabilities for specifying

bidirectional transformations. Even in this rather simple case study, development of a bidirectional transfor-

mation turns out to be more complex than expected. Motivated by the case study, we propose extensions to

QVT-R which facilitate the speciﬁcation of bidirectional transformations considerably.

1 INTRODUCTION

In model-driven software engineering (Schmidt,

2006), software development is driven by the con-

struction of high-level models which are transformed

over multiple stages into executable code. For model-

driven software engineering, key enabling technolo-

gies are required for deﬁning modeling languages as

well as deﬁning and executing model transformations.

In object-oriented modeling, the abstract syntax

of a modeling language is deﬁned by a metamodel

(a structural class model). To this end, the Object

Management Group (OMG) provides the Meta Object

Facility standard (MOF (Object Management Group,

2013)), whose subset EMOF (Essential MOF) has

been implemented in the Eclipse Modeling Frame-

work (EMF) (Steinberg et al., 2009). (E)MOF is used

widely for metamodeling.

In contrast, a wide variety of languages and

tools for model transformations has been devel-

oped (Jakumeit et al., 2014). Model transforma-

tion languages are based on different computational

paradigms (procedural, functional, rule-based, object-

oriented), application and scheduling strategies, di-

rectionality (unidirectional vs. bidirectional), support

for in-place or out-place, batch or incremental trans-

formations, etc. (Czarnecki and Helsen, 2006).

In the light of this diversity, the OMG issued the

QVT standard (Queries, Views, and Transformations),

which deﬁnes a family of model transformation lan-

guages at different levels of abstraction (Object Man-

agement Group, 2014). The most high-level language

is QVT Relations (QVT-R), which supports the declar-

ative speciﬁcation of transformations between MOF-

based models. Furthermore, QVT-R reuses the Object

Constraint Language (OCL), an expression language

for MOF models (Object Management Group, 2012).

QVT-R addresses a wide spectrum of model transfor-

mation scenarios, including enforcing and checking,

unidirectional and bidirectional, batch and incremen-

tal, and n:1 transformations.

While QVT-R provides many interesting and

promising features, the language has not been adopted

widely. This stands in sharp contrast to OMG stan-

dards for deﬁning modeling languages such as MOF

and OCL. Thus, on the one hand, model transforma-

tions constitute a key enabling technology for model-

driven software engineering. On the other hand, the

QVT-R language, which is promoted as an OMG

standard, has not gained signiﬁcant acceptance so far.

These observations motivated our research into

the evaluation of the QVT-R language. In particular,

we investigate the following features of QVT-R: (1)

expressiveness (what kinds of transformation prob-

141

Westfechtel B..

A Case Study for Evaluating Bidirectional Transformations in QVT Relations.

DOI: 10.5220/0005466801410155

In Proceedings of the 10th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE-2015), pages 141-155

ISBN: 978-989-758-100-7

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

lems may be solved?), (2) conciseness (may transfor-

mations be written concisely, at a high level of ab-

straction?), (3) readability (how easy is it to under-

stand a transformation written in QVT-R?), and (4)

semantic soundness (are the semantics of transforma-

tions deﬁned clearly and in a unique way?).

This paper focuses on a particularly interesting

feature of QVT-R: the declarative speciﬁcation of

bidirectional transformations. Rather than writing

two unidirectional transformations separately, a trans-

formation developer may provide a single relational

speciﬁcation which may be executed in both direc-

tions. This approach does not only save speciﬁcation

effort. In addition, it ensures the consistency of for-

ward and backward transformations.

Bidirectional transformations are required in a va-

riety of use cases of industrial relevance. For exam-

ple, round-trip engineering integrates forward and re-

verse engineering into a coherent process which needs

to be supported by bidirectional transformation tools.

Furthermore, integration of heterogeneous tools calls

for data converters which ideally perform lossless

transformations in all directions.

The property of bidirectionality merely states that

a given transformation deﬁnition may be executed in

both directions. In addition, it is highly desirable that

forward and backward transformations behave consis-

tently. The strongest form of mutual consistency is

mutual invertibility: By transforming back and forth

in either direction, the original model is always re-

produced. Unfortunately, mutual invertibility may

not be achievable in the case of heterogeneous meta-

models due to loss of information. Even then, how-

ever, bidirectional transformations with weaker con-

sistency properties may still be achievable.

In this paper, we evaluate QVT-R’s support for

bidirectional transformations through a case study

from the domain of project management (Kerzner,

1998). The case study deals with transformations be-

tween different kinds of activity networks for project

planning: While Gantt diagrams are composed of

activities related by dependencies of different types

(end-start, start-start, etc.), CPM networks consist of

events which are connected by activities. Their under-

lying metamodels are similar, yet heterogeneous. Any

Gantt diagram may be transformed into an equivalent

CPM network. The corresponding backward transfor-

mation may reconstruct the original Gantt diagram,

but it works only for those kinds of CPM networks

which may be generated by the forward transforma-

tion. This restriction is inherent to the transformation

problem at hand and applies no matter which trans-

formation language is used. Full mutual invertibility

cannot be achieved here. The backward transforma-

tion inverts the forward transformation, but this state-

ment does not always hold for the opposite direction:

If the backward transformation is applied to some “in-

appropriate” CPM network, the forward transforma-

tion may not reconstruct the original network.

The case study is small enough to be presented in

a single, self-contained paper. Though being small, it

does provide some important insights into potentials

and limitations of QVT-R with respect to the speciﬁca-

tion of bidirectional transformations. While we suc-

ceeded in solving the transformation problem at hand

with a concise speciﬁcation, development of the bidi-

rectional transformation turned out to be more com-

plex than expected. In particular, the QVT-R user has

to consider the execution semantics of QVT-R in de-

tail to ensure that the transformation is actually exe-

cutable in both directions. Furthermore, the resulting

speciﬁcation is hard to read and understand. Finally,

the case study reveals several issues concerning the

deﬁnition of the dynamic semantics.

Motivated by the case study, we propose exten-

sions to QVT-R which facilitate the speciﬁcation of

bidirectional transformations considerably. These ex-

tensions make speciﬁcations of bidirectional transfor-

mations easier to construct and understand. Further-

more, they remove some problems regarding the se-

mantics deﬁnition of QVT-R. The proposed exten-

sions may contribute to a wider adoption of QVT-R.

The rest of this paper is structured as follows: Sec-

tion 2 introduces basic notions from the domain of

model transformations. Section 3 brieﬂy describes

QVT-R. Section 4, the core part of this paper, presents

the case study, including an evaluation and a proposal

for revising QVT-R. Section 5 compares related work.

Section 6 concludes the paper by summarizing and

discussing our ﬁndings.

2 MODEL TRANSFORMATIONS

A model is an abstraction of a system allowing pre-

dictions or inferences to be made (K

uhne, 2006). A

model is expressed in a modeling language. A meta-

model deﬁnes the abstract syntax of a modeling lan-

guage, usually with the help of class diagrams and

additional constraints (written e.g. in OCL). A model

obeying the rules deﬁned in a metamodel is called an

instance of that metamodel.

A model transformation operates on a set of mod-

els, each of which may be either read, created, or up-

dated. A single-source-single-target transformation

takes a single source model as input and produces a

single target model as output. A transformation is

called exogenous (endogenous) if the source and tar-

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

142

get metamodels are different (the same). The case

study presented in this paper deals with an exogenous

single-source-single-target transformation.

A transformation may be modeled as a function

from a source model to a target model. A transfor-

mation is total if it may be applied to any instance

of the source metamodel, deterministic if it returns a

unique target model for a given source model, injec-

tive if it returns different target models for different

source models, surjective if it can generate any in-

stance of the target metamodel, and bijective if it is

both injective and surjective.

As deﬁned so far, a transformation is unidirec-

tional: It can generate an instance of the target meta-

model from an instance of the source metamodel, but

not vice versa. A bidirectional transformation is a

pair of opposite unidirectional transformations (called

forward and backward transformation).

In the context of round-trip engineering and bidi-

rectional data converters, it is highly desirable that

both forward and backward transformation are total

and mutually inverse. Totality ensures that the trans-

formations may be applied to all instances of the re-

spective metamodels. Mutual inversion ensures con-

sistent behavior: Applying the backward transforma-

tion after the forward transformation returns the orig-

inal model; likewise for the opposite direction.

However, in practical applications these require-

ments may at best be approximated. If the for-

ward and the backward transformation are both to-

tal and mutually inverse, there is a bijective (1:1)

mapping between source models and target models.

Such a mapping does not exist in the case of het-

erogeneous metamodels. This is illustrated in Fig-

ure 1, where c

i j

denote concepts deﬁned in meta-

models (in terms of classes, attributes, or references):

cannot be mapped at all, c

and c

are mapped

to the same concept c

, c

may be mapped non-

deterministically to c

or c

, and c

has to be sim-

ulated by the set of concepts {c

, c

Thus, total and mutually inverse forward and

backward transformations may be provided only in

degenerate cases such as e.g. an endogenous copy

transformation. In the case of exogenous transfor-

mations, neither the metamodels nor their instances

may be mapped 1:1 onto each other; if the metamod-

els were equivalent, one of them could be simply dis-

carded. However, weaker notions of mutual consis-

tency may still be achieved. For example, the bidi-

rectional transformation may be forward invertible:

The forward transformation is total, and the back-

ward transformation inverts the forward transforma-

tion. But applying the transformations in the oppo-

site direction does not guarantee the reconstruction of

MetamodelM

Figure 1: Mappings between heterogeneous metamodels.

the original model; rather, this property holds only for

models generated by the forward transformation. The

property of forward invertibility will be demonstrated

by the case study presented in Section 4.

3 QVT RELATIONS (QVT-R)

QVT-R is a declarative language for specifying both

uni- and bidirectional model transformations as well

as consistency checks. This section gives a brief

overview of the concepts underlying QVT-R; see (Ob-

ject Management Group, 2014) for a comprehensive

description and (Reddy et al., 2006) for a tutorial.

In QVT-R, a transformation may be deﬁned on

n ≥ 2 models; here, we assume n = 2. In this case, a

transformation deﬁnes a relation T ⊆ M

×M

, where

and M

denote sets of models.

A transformation is speciﬁed in terms of rules,

each of which deﬁnes a relation between source and

target patterns. A relation consists of domains, each

of which deﬁnes a pattern in one model. A domain

has a unique root object and is marked by a domain

qualiﬁer (checkonly or enforce) which controls how the

domain may be used in a transformation (see below).

Furthermore, a relation may have a when clause which

serves as a precondition for applying the relation. A

relation may also comprise a where clause which es-

sentially acts as a postcondition. Finally, variables

may be declared in a relation which are used in do-

mains, the when and the where clause.

QVT-R offers two modes of execution. In the

checking mode, the transformation is executed on two

models m

∈ M

and m

∈ M

. For each relation

and each instance of a source pattern in m

, a corre-

sponding target pattern instance is searched in m

and

vice versa. If all of these checks succeed, T (m

, m

)

holds. Domain qualiﬁers are immaterial in the check-

ing mode.

In the enforcing mode, the transformation is exe-

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

143

3 4

5 6

7 8

A1(2)

A2(3)

A3(4)

A1A2(2)

A1A3(0)

A2A4(0)

A3A4(4)

A4(2)

A2(3)

A3(4)

A1(2)

A4(2)

A1

A2 (2)

A1A3(0)

A2A4(0)

A3A4 (4)

A2(3)

A3(4)

A1(2)

A4(2)

A1

A2 (2)

A3A4 (4)

Figure 2: Gantt diagrams and CPM networks.

cuted either in forward or backward direction. If the

transformation is executed on a given pair of models

and m

in forward direction, m

is updated to es-

tablish consistency (and m

remains unchanged); like-

wise for the opposite direction. A batch transforma-

tion is treated as a special case (m

is empty).

To establish consistency, it is checked for each re-

lation and each source pattern instance whether a cor-

responding instance of the target pattern already ex-

ists. If there is no such instance, it is created if the

target pattern is qualiﬁed by enforce; otherwise, an

inconsistency is reported. Furthermore, the check is

performed also in the opposite direction. If there is

no matching source pattern instance, the target pat-

tern instance is deleted if its domain is qualiﬁed by

enforce; otherwise, an inconsistency is reported.

Ideally, a transformation may be executed both in

the checking mode and the enforcing mode in either

direction. Thus, a bidirectional transformation may

be deﬁned by a single speciﬁcation. In this case, all

domains should be qualiﬁed by enforce. For a unidi-

rectional transformation, source and target domains

should be qualiﬁed by checkonly and enforce, respec-

tively. Transformations which are run only in check-

ing mode should mark all domains by checkonly.

4 CASE STUDY

To evaluate QVT-R’s capabilities for specifying bidi-

rectional transformations, we performed a case study

in the project management domain (Kerzner, 1998).

The case study is kept deliberately small so that it may

be presented in a self-contained paper. It deals with

bidirectional data conversion between different kinds

of activity networks for project scheduling, namely

Gantt diagrams and CPM networks.

The bidirectional transformation is developed in

multiple steps. First, we develop a forward transfor-

mation from Gantt diagrams to CPM networks. Sec-

ond, we construct a corresponding backward trans-

formation. In the third step, we synthesize the uni-

directional transformations into a single bidirectional

transformation. After that, we evaluate the case study

with respect to the criteria mentioned in the introduc-

tion and conclude with some proposals for revising

QVT-R.

4.1 Activity Networks

A Gantt diagram is an acyclic graph whose nodes and

edges represent activities and dependencies, respec-

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

144

Ganttdiagrams

<<enumeration>>

DependencyType

‐ StartStart

‐ StartEnd

‐ EndStart

‐ EndEnd

diagram

elements

GanttDiagram

name :String

1..*

Activity

name :String

duration :Integer

dependencyType :

DependencyType

offset :Integer

Dependency

successor

0..*

predecessor

incomingDependencies

outgoingDependencies

CPMnetworks

network

elements

CPMNetwork

name :String

1..*

incomingActivities

0..*

outgoingActivities

targetEvent

sourceEvent

Event

number :Integer

Activity

name :String

duration :Integer

0..*

Element

Figure 3: Metamodels for Gantt diagrams and CPM networks.

tively (Figure 2a,c,d). For each activity (time-scaled

bar), a name and a duration is speciﬁed. An activ-

ity with duration 0 is a milestone (black diamond). A

dependency from activity a

to a

deﬁnes an order-

ing constraint: a

can be started/ﬁnished only after

has been started/ﬁnished. Dependencies are clas-

siﬁed into four types: start-start, start-end, end-start,

and end-end. Each dependency has an offset

, which

describes the delay between the start/end of the pre-

decessor and the successor activity, respectively.

In contrast to a Gantt diagram, a CPM network

(Critical Path Method) is not time-scaled (Figure 2b).

CPM networks differ from PERT charts only in the

treatment of durations (which are deterministic in a

CPM network and stochastic in a PERT chart); this

difference is immaterial in the context of this paper.

A CPM network is an acyclic graph whose nodes

and edges represent events and activities, respectively.

An event may occur after its incoming activities have

been ﬁnished. Conversely, an activity may start after

its source event has occurred. Events do not consume

time. An activity has a name and a duration. Events

are illustrated as circles which are labeled with unique

numbers. An activity is shown as an arrow labeled

with its name and duration. A dashed arrow indicates

a pseudo activity with duration 0.

Both kinds of activity networks may be employed

for scheduling. From the data provided in a Gantt dia-

gram, earliest/latest start/ﬁnish times of activities may

be calculated automatically. Activities whose earliest

and latest start times coincide are located on a critical

path. Similar calculations may be performed in CPM

networks (e.g., earliest/latest times of events).

Figure 3 displays the metamodels for Gantt dia-

grams and CPM networks on which our QVT-R trans-

formations are based. The metamodels are deﬁned

as class diagrams in Ecore, EMF’s implementation of

EMOF. In a Gantt diagram, both activities and depen-

To simplify matters, we assume non-negative offsets.

dencies are represented as objects; likewise for events

and activities of CPM networks. Our Ecore models

do not include derived attributes for calculated times

because the model transformations deal only with in-

trinsic data.

The metamodels are closely related since Gantt di-

agrams and CPM networks are essentially used for

the same purpose. However, the metamodels are still

heterogeneous; concepts may not be mapped 1:1 to

each other. First, a Gantt activity is mapped not only

to a CPM activity, but also to a source and a target

event. Second, the different types of Gantt dependen-

cies have to be simulated by CPM activities connect-

ing appropriate events. Third, event numbers have no

correspondence in Gantt diagrams.

4.2 Forward Transformation

A Gantt diagram is transformed into an equivalent

CPM network as follows: Each Gantt activity is

mapped to a source event, a target event, and a con-

necting CPM activity with the same name and dura-

tion. The events are numbered in a unique way. Each

Gantt dependency is mapped to a CPM activity, as

well. The type of the Gantt dependency determines

the source and target events; for example, in the case

of a start-start dependency the source event of the pre-

decessor activity is connected to the source event of

the successor activity. The name of the CPM activ-

ity is composed from the predecessor and successor

names, and the duration is copied from the depen-

dency’s offset. With these rules, the diagram of Fig-

ure 2a is transformed into the network of Figure 2b.

Figure 4 shows the QVT-R speciﬁcation of the for-

ward transformation. The transformation operates on

a diagram and a network (line 1). The direction of the

transformation is not speciﬁed explicitly, but can be

inferred from the domain qualiﬁers of the relations.

The relation Diagram2Network (lines 2–6) maps a

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

145

1 transformation f orwar d ( diagram : g a n tt , network : cpm ) {

2 top r e l a t i o n Diagram2Network {

3 name : S t r i n g ;

4 checkonly domain diagram gd diagram : g a n t t : : GanttDiagram {name = name};

5 enforce domain network cn net w ork : cpm : : CPMNetwork {name = name};

6 }

7 top r e l a t i o n A c t i v i t y 2 A c t i v i t y {

8 name : S t r i n g ; d u r a t i o n : I n t e g e r ;

9 sourceEventNumber , targetEventNumber : I n t e g e r ;

10 checkonly domain diagram g d a c t i v i t y : g a n t t : : A c t i v i t y {

11 name = name , d u r a t i o n = du r a t i o n ,

12 diagram = gd diagram : g a n t t : : GanttDiagram {}

13 };

14 enforce domain network c n a c t i v i t y : cpm : : A c t i v i t y {

15 name = name , d u r a t i o n = du r a t i o n ,

16 network = cn n e twork : cpm : : CPMNetwork {} ,

17 sourceEvent = cn sourc eEve nt : cpm : : Event {

18 network = cn network , number = sourceEventNumber

19 } ,

20 t a r g e t E v e n t = c n t a r g e t E v e n t : cpm : : Event {

21 network = cn network , number = targetEventNumber

22 }

23 };

24 when {

25 Diagram2Network ( gd diagram , cn networ k ) ;

26 }

27 where {

28 sourceEventNumber = 2∗ n o O f A c t i v i t y ( g d a c t i v i t y ) − 1 ;

29 targetEventNumber = 2∗ n o O f A c t i v i t y ( g d a c t i v i t y ) ;

30 }

31 }

32 top r e l a t i o n D e p e n d e n c y 2 A c t i v i t y {

33 c n p r e d A c t i v i t y , c n s u c c A c t i v i t y : cpm : : A c t i v i t y ;

34 gd dependencyType : g a n t t : : DependencyType ;

35 o f f s e t : I n t e g e r ; name : S t r i n g ;

36 checkonly domain diagram gd dependency : g a n t t : : Dependency {

37 o f f s e t = o f f s e t ,

38 diagram = gd diagram : g a n t t : : GanttDiagram {} ,

39 predecessor = g d p r e d A c t i v i t y : g a n t t : : A c t i v i t y {} ,

40 successor = g d s u c c A c t i v i t y : g a n t t : : A c t i v i t y {} ,

41 dependencyType = gd dependencyType

42 };

43 enforce domain network c n a c t i v i t y : cpm : : A c t i v i t y {

44 d u r a t i o n = o f f s e t , name = name,

45 network = cn n e twork : cpm : : CPMNetwork {} ,

46 sourceEvent = cn sourc eEve nt : cpm : : Event {} ,

47 t a r g e t E v e n t = c n t a r g e t E v e n t : cpm : : Event {}

48 };

49 when {

50 Diagram2Network ( gd diagram , cn networ k ) ;

51 A c t i v i t y 2 A c t i v i t y ( g d p r e d A c t i v i t y , c n p r e d A c t i v i t y ) ;

52 A c t i v i t y 2 A c t i v i t y ( g d s u c c A c t i v i t y , c n s u c c A c t i v i t y ) ;

53 }

54 where {

55 cn sour ceEv ent = sourceEvent ( c n p r e d A c t i v i t y , gd dependencyType ) ;

56 c n t a r g e t E v e n t = t a r g e t E v e n t ( c n s u c c A c t i v i t y , gd dependencyType ) ;

57 name = g d p r e d A c t i v i t y . name + ’−>’ + g d s u c c A c t i v i t y . name ;

58 }

59 }

60 }

Figure 4: Forward transformation.

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

146

diagram to a network of the same name. The rela-

tion Activity2Activity (7–31) transforms a Gantt activ-

ity to a CPM activity. Its source pattern consists of

a Gantt activity; pattern matching binds variables for

the name, the duration, and the enclosing diagram. Its

when clause ensures that the relation is applied only

after the diagram has been transformed into a net-

work. Furthermore, the relation call is used to retrieve

the corresponding network object. The target pattern

consists of a CPM activity whose name and duration

are copied from the Gantt activity. Furthermore, the

activity is inserted into the network which has been re-

trieved via the relation call in the when clause. Source

and target events are created along with the activity;

their numbers are calculated in the where clause. To

this end, the number of the Gantt activity — say n —

is determined from the source model (its index in the

list for the containment reference from the diagram).

Source and target event are assigned the unique num-

bers 2n − 1 and 2n.

noOfActivity (lines 28–29) is a query, i.e., a func-

tion whose body is speciﬁed by an OCL expression.

Queries may be deﬁned as part of a QVT-R speciﬁca-

tion; due to the lack of space, all query deﬁnitions are

omitted in this paper.

The relation Dependency2Activity (32–59) maps a

Gantt dependency to a CPM activity. The source pat-

tern is composed of a dependency as well as its pre-

decessor and successor activities. The when clause

ensures that the enclosing diagram and the predeces-

sor and successor activities have already been trans-

formed. The target pattern consists of the activity to

be created and the (already existing) events to which it

is to be connected. The variables for the source event

and the target event are bound in the where clause, tak-

ing the dependency type into account. Furthermore,

the where clause composes the name of the activity

for the dependency from the names of the predecessor

and successor activities. Finally, the duration of the

activity is copied from the offset of the dependency.

The forward transformation performs a straight-

forward syntax-based translation of a Gantt diagram

into a CPM network: The source model is trans-

formed in terms of syntactic elements — the diagram

and its composed activities and dependencies — into

the target model. The transformation is total, deter-

ministic and injective, but it is not surjective: For ex-

ample, the CPM network 1 → A1 → 2 → A2 → 3 can-

not be generated by the forward transformation be-

cause A1 and A2 share the common event 2.

4.3 Backward Transformation

The backward transformation may be performed in

different ways, meeting different requirements. A

syntax-based transformation which may be applied to

any network (including e.g. 1 → A

→ 2 → A

→ 3)

maps each event to a milestone, each real activity to

an activity, and each pseudo activity to a dependency.

Figure 2d demonstrates that this backward transfor-

mation does not invert the forward transformation. In

general, the resulting Gantt diagram contains at least

twice as many activities as the original Gantt diagram.

Thus, an iterative application would generate a se-

quence of monotonically growing Gantt diagrams.

Instead, we develop a pattern-based backward

transformation which inverts the forward transforma-

tion (but is partial rather than total). In the backward

transformation, it has to be decided whether a network

activity is transformed to an activity or a dependency

in the diagram. This decision cannot be performed

uniquely using only structural information. For ex-

ample, we may attempt to calculate a maximal match-

ing, i.e., a maximal set of edges such that no node is

incident to more than one edge in the set, and trans-

form the edges in the matching back to activities. For

this purpose, the algorithm of Edmonds may be used

(see (Jungnickel, 2008), Section 13.4). However, the

maximal matching is not unique, as demonstrated in

Figure 2b,c.

To avoid non-deterministic behavior, the back-

ward transformation relies on coding conventions ap-

plied in the forward transformation. For example, a

CPM activity which was generated from a Gantt ac-

tivity may be recognized with the help of event num-

bers: The number n of its source event is odd, and the

number of its target event is n + 1.

In the speciﬁcation of the backward transforma-

tion (Figure 5), the relation Activity2Activity maps a

CPM activity to a Gantt activity of the same name and

duration when the query MapToActivity, which exploits

the coding convention explained above, returns true

(line 15). Similarly, the relation Activity2Dependency is

applicable only when the complementary query Map-

ToDependency evaluates to true (line 37). From the

source and the target event, the respective owning ac-

tivities are retrieved, again relying on coding conven-

tions (38–39). From these CPM activities, the corre-

sponding activities in the Gantt diagram are retrieved

by relation calls (40–41). The type of the dependency

is determined in the where clause (44).

4.4 Bidirectional Transformation

The bidirectional transformation is synthesized from

the unidirectional transformations by merging corre-

sponding relations. All domains are qualiﬁed by en-

force. Domains, when and where clauses are merged

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

147

1 trans formation backward ( network : cpm , diagram : g a n t t ) {

2 top r e l a t i o n Network2Diagram { . . . }

3 top r e l a t i o n A c t i v i t y 2 A c t i v i t y {

4 name : S t r i n g ; d u r a t i o n : I n t e g e r ;

5 checkonly domain network c n a c t i v i t y : cpm : : A c t i v i t y {

6 name = name , d u r a t i o n = du r a t i o n ,

7 network = cn n e twork : cpm : : CPMNetwork {}

8 };

9 enforce domain diagram g d a c t i v i t y : g a n t t : : A c t i v i t y {

10 name = name , d u r a t i o n = du r a t i o n ,

11 diagram = gd diagram : g a n t t : : GanttDiagram {}

12 };

13 when {

14 Network2Diagram ( cn network , gd diagram ) ;

15 ma p ToA c t i vity ( c n a c t i v i t y ) ;

16 }

17 }

18 top r e l a t i o n A c t i v i t y 2 D e p e n d e n c y {

19 c n p r e d A c t i v i t y , c n s u c c A c t i v i t y : cpm : : A c t i v i t y ;

20 gd dependencyType : g a n t t : : DependencyType ;

21 o f f s e t : I n t e g e r ;

22 checkonly domain network c n a c t i v i t y : cpm : : A c t i v i t y {

23 d u r a t i o n = o f f s e t ,

24 network = cn n e twork : cpm : : CPMNetwork {} ,

25 sourceEvent = cn sourc eEve nt : cpm : : Event {} ,

26 t a r g e t E v e n t = c n t a r g e t E v e n t : cpm : : Event {}

27 };

28 enforce domain diagram gd dependency : g a n t t : : Dependency {

29 o f f s e t = o f f s e t ,

30 diagram = gd diagram : g a n t t : : GanttDiagram {} ,

31 predecessor = g d p r e d A c t i v i t y : g a n t t : : A c t i v i t y {} ,

32 successor = g d s u c c A c t i v i t y : g a n t t : : A c t i v i t y {} ,

33 dependencyType = gd dependencyType

34 };

35 when {

36 Network2Diagram ( cn network , gd diagram ) ;

37 mapToDependency ( c n a c t i v i t y ) ;

38 c n p r e d A c t i v i t y = o w n i n g A c t i v i t y ( cn sourceEven t ) ;

39 c n s u c c A c t i v i t y = o w n i n g A c t i v i t y ( cn ta r g e t E v e n t ) ;

40 A c t i v i t y 2 A c t i v i t y ( c n p r e d A c t i v i t y , g d p r e d A c t i v i t y ) ;

41 A c t i v i t y 2 A c t i v i t y ( c n s u c c A c t i v i t y , g d s u c c A c t i v i t y ) ;

42 }

43 where {

44 gd dependencyType = dependencyType ( c n a c t i v i t y ) ;

45 }

46 }

47 }

Figure 5: Backward transformation.

component-wise. Merging is straightforward for do-

mains: The respective domain patterns coincide in

common parts and contain only elementary expres-

sions (variables and constants). Thus, the union of

patterns is well-deﬁned, and matching may be per-

formed in both directions. In contrast, manual adjust-

ments may be required after a union of the when and

where clauses to ensure bidirectional executability.

Execution of a relation involves the following

kinds of steps: match an object in the source do-

main, bind a variable, call a relation, check a con-

straint, create a target domain object, or assign an ob-

ject property. The order in which these steps are exe-

cuted must satisfy data ﬂow constraints which are de-

scribed in the QVT-R standard ((Object Management

Group, 2014), Section 7.5), and does not necessarily

match the textual order in the speciﬁcation. Depend-

ing on the binding states of the variables, equations

may play a dual role: If all variables are bound, an

equation acts as a check; otherwise, it is used to bind

an object property or assign a value to a variable. In

the case of a bidirectional transformation, it has to be

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

148

1 top r e l a t i o n A c t i v i t y 2 A c t i v i t y {

2 name : S t r i n g ; d u r a t i o n : I n t e g e r ;

3 sourceEventNumber , targetEventNumber : I n t e g e r ;

4 enforce domain diagram g d a c t i v i t y : g a n t t : : A c t i v i t y {

5 name = name , d u r a t i o n = du r a t i o n ,

6 diagram = gd diagram : g a n t t : : GanttDiagram {}

7 };

8 enforce domain network c n a c t i v i t y : cpm : : A c t i v i t y {

9 name = name , d u r a t i o n = du r a t i o n ,

10 network = cn n e twork : cpm : : CPMNetwork {} ,

11 sourceEvent = cn sourc eEve nt : cpm : : Event {

12 network = cn network , number = sourceEventNumber

13 } , −− F orward t r a n s f o r m a t i o n

14 t a r g e t E v e n t = c n t a r g e t E v e n t : cpm : : Event {

15 network = cn network , number = targetEventNumber

16 } −− For ward t r a n s f o r m a t i o n

17 };

18 when {

19 Diagram2Network ( gd diagram , cn networ k ) ;

20 i f g d a c t i v i t y . o c l I s U n de fi n e d ( ) then

21 m a pToA c t ivit y ( c n a c t i v i t y )

22 else

23 true

24 e n d i f ; −− Backward t r a n s f o r m a t i o n

25 sourceEventNumber =

26 i f c n a c t i v i t y . o c l I s U n de fi n e d ( ) then

27 2∗ n o O f A c t i v i t y ( g d a c t i v i t y ) − 1

28 else

29 c n a c t i v i t y . sourceEvent . number

30 endif ; −− Forward t r a n s f o r m a t i o n

31 targetEventNumber =

32 i f c n a c t i v i t y . o c l I s U n de fi n e d ( ) then

33 2∗ n o O f A c t i v i t y ( g d a c t i v i t y )

34 else

35 c n a c t i v i t y . t a r g e t E v e n t . number

36 endif ; −− Forward t r a n s f o r m a t i o n

37 }

38 }

Figure 6: Bidirectional transformation: Activities.

ensured that the data ﬂow constraints are satisﬁed for

both directions.

A bidirectional relation may contain unidirec-

tional elements, i.e., elements which are relevant for

only one transformation direction. QVT-R does not

provide language constructs for designating elements

as unidirectional. The QVT-R user has to ensure that

conceptually unidirectional elements do not prevent

execution of the relation in the opposite direction.

Figure 6 displays the bidirectional relation be-

tween Gantt and CPM activities. Unidirectional

elements are annotated with comments. While

sourceEvent and targetEvent are relevant only for the

forward direction, they do no harm in the backward

direction. However, the unidirectional expressions in

the when and the where clause cannot be copied liter-

ally from the forward and the backward relation.

In the backward relation, the call of the query

mapToActivity (line 15 in Figure 5) checks that the

CPM activity actually represents a Gantt activity. If

this call is copied literally to the when clause of the

bidirectional relation, execution in the forward direc-

tion aborts with a runtime error because the variable

cn activity is still unbound. Thus, the evaluation of

the query is performed in a conditional expression

(lines 20–24 in Figure 6): The transformation direc-

tion is queried by accessing the binding state of the

variable gd activity. If the variable is unbound, the rela-

tion is executed in backward direction, and the query

mapToActivity is evaluated. Otherwise, the constraint is

ignored by evaluating the constant true.

A similar problem occurs in the calculation of the

event numbers. In the forward relation, the numbers

are calculated in the where clause from the number of

the Gantt activity in the opposite domain (lines 28–29

in Figure 4). Therefore, we rewrite these expressions

into conditional expressions (lines 25–36 in Figure 6).

If these expressions are evaluated in backward direc-

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

149

1 top r e l a t i o n D e p e n d e n c y 2 A c t i v i t y {

2 c n p r e d A c t i v i t y , c n s u c c A c t i v i t y : cpm : : A c t i v i t y ;

3 gd dependencyType : g a n t t : : DependencyType ;

4 o f f s e t : I n t e g e r ;

5 name : S t r i n g ;

6 enforce domain diagram gd dependency : g a n t t : : Dependency {

7 o f f s e t = o f f s e t ,

8 diagram = gd diagram : g a n t t : : GanttDiagram {} ,

9 predecessor = g d p r e d A c t i v i t y : g a n t t : : A c t i v i t y {} ,

10 successor = g d s u c c A c t i v i t y : g a n t t : : A c t i v i t y {} ,

11 dependencyType = gd dependencyType

12 };

13 enforce domain network c n a c t i v i t y : cpm : : A c t i v i t y {

14 d u r a t i o n = o f f s e t ,

15 network = cn n e twork : cpm : : CPMNetwork {} ,

16 name = name ,

17 sourceEvent = cn sourc eEve nt : cpm : : Event {} ,

18 t a r g e t E v e n t = c n t a r g e t E v e n t : cpm : : Event {}

19 };

20 when {

21 Diagram2Network ( gd diagram , cn networ k ) ;

22 i f gd dependency . o c l I s U n d e f i ne d ( ) then

23 mapToDependency ( c n a c t i v i t y )

24 else

25 true

26 e n d i f ; −− Backward t r a n s f o r m a t i o n

27 c n p r e d A c t i v i t y = o w n i n g A c t i v i t y ( cn sourceEven t ) ; −− Backward t r a n s f o r m a t i o n

28 c n s u c c A c t i v i t y = o w n i n g A c t i v i t y ( cn ta r g e t E v e n t ) ; −− Backward t r a n s f o r m a t i o n

29 A c t i v i t y 2 A c t i v i t y ( g d p r e d A c t i v i t y , c n p r e d A c t i v i t y ) ;

30 A c t i v i t y 2 A c t i v i t y ( g d s u c c A c t i v i t y , c n s u c c A c t i v i t y ) ;

31 gd dependencyType =

32 i f gd dependency . o c l I s U n d e f i ne d ( ) then

33 dependencyType ( c n a c t i v i t y )

34 else

35 gd dependency . dependencyType

36 endif ; −− Backward t r a n s f o r m a t i o n

37 }

38 where {

39 cn sour ceEv ent = sourceEvent ( c n p r e d A c t i v i t y , gd dependencyType ) ;

40 −− F orward t r a n s f o r m a t i o n

41 c n t a r g e t E v e n t = t a r g e t E v e n t ( c n s u c c A c t i v i t y , gd dependencyType ) ;

42 −− F orward t r a n s f o r m a t i o n

43 name = g d p r e d A c t i v i t y . name + ’−>’ + g d s u c c A c t i v i t y . name ;

44 −− F orward t r a n s f o r m a t i o n

45 }

46 }

Figure 7: Bidirectional transformation: Dependencies.

tion, they return the value to which the variable has

been bound in pattern matching. Please notice that

these expressions were moved from the where clause

to the when clause. In the where clause, the expres-

sions would not work because the variable cn activity is

already bound (by instantiation of the target pattern).

The bidirectional relation Dependency2Activity is

constructed similarly (Figure 7). Again, all unidi-

rectional expressions are annotated by comments. In

lines 22–26 and 31–36, we constructed conditional

expressions querying the binding state, as demon-

strated above. Since this approach does not work in

the where clause, the expression for the dependency

type was moved to the when clause.

For each transformation direction, we have to

check whether the data ﬂow constraints described in

the QVT-R standard (see Section 7.5, p. 18) are satis-

ﬁed. Figure 8 demonstrates this for the forward di-

rection. To this end, a graph is constructed which

contains a node for each expression occurring in the

relation. Each node is partitioned into three com-

partments. The ﬁrst compartment references the line

number of the expression. The second compartment

speciﬁes the action to be performed. If the action re-

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

150

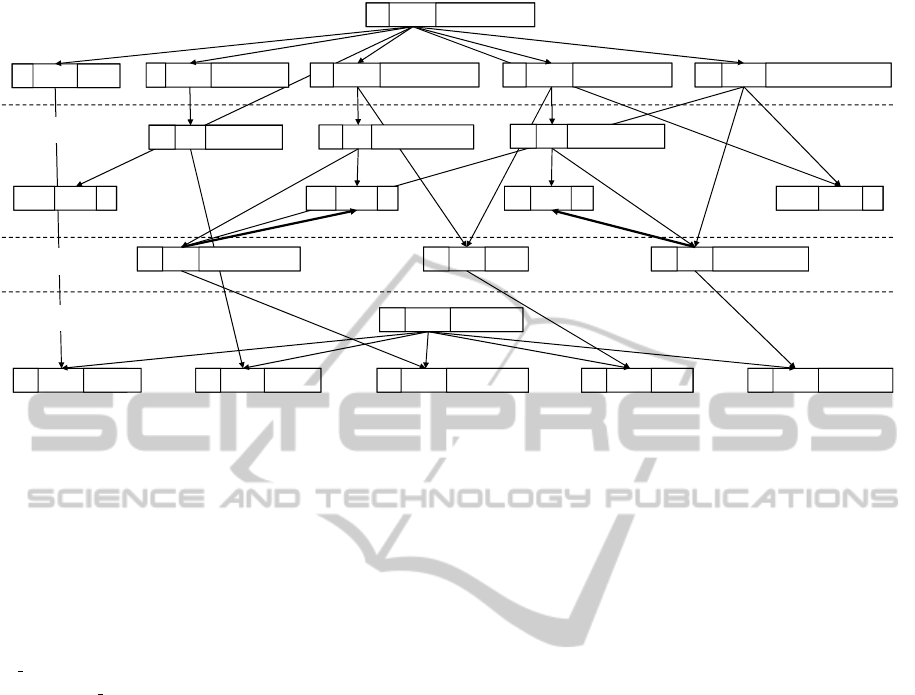
8matchgd_diagram

9 match gd_predActivity 10 match gd_succActivity

11 match gd_dependencyType

call

cn_network

29 call cn_predActivity

30 call

cn_succActivity

22‐26 check … 27 check … 31..36 check …28 check …

39 bind cn_sourceEvent 41 bind cn_targetEvent43 bind name

13 create cn_activity

14 assign duration 15 assign network 16 assign name

assign

sourceEvent 18

assign

targetEvent

source domain

when clause

target domain

where clause

7 match offset

6 match gd_dependency







Figure 8: Dependency graph for the forward execution of Dependency2Activity.

sults in the binding of some variable, the name of this

variable is shown in the third compartment. Arrows

represent data ﬂow dependencies. An arrow from

node s to node t implies that s binds a value to some

variable which is used in t.

The graph is acyclic, but contains an anomaly:

Two arrows point upwards from nodes in where

clauses to nodes in when clauses. For example,

we obtain the following chain of actions: (1) Bind

cn predActivity by a relation call (when clause, line 29).

(2) Bind cn sourceEvent by navigation in the target

model (where clause, line 39). (3) (Redundantly)

check the equation in line 27 of the when clause.

Dependencies of the when clause on the where

clause are allowed in QVT-R. Section 7.5 of the stan-

dard demands only that the expressions of a relation

may be arranged into a consistent order of evaluation

satisfying the data ﬂow constraints.

While the bidirectional transformation behaves as

required in enforcing mode in both directions, it does

not work correctly in checking mode. The simulation

of unidirectional expressions by conditional expres-

sions querying the binding state implies that these ex-

pressions are effectively ignored. In checking mode,

all variables in domain patterns have already been

bound when an expression in a when or where clause

is evaluated. For example, the conditional expres-

sion for checking in backward direction whether a

CPM activity should be mapped onto a Gantt activ-

ity (lines 20–24 in Figure 6) always evaluates to true.

However, for CPM activities to be mapped onto Gantt

dependencies there is no corresponding Gantt activ-

ity. This results in an error even if the diagram and

the network are mutually consistent.

4.5 Evaluation

In the following, we summarize the lessons learned

from the case study. The presentation is structured

according to the criteria introduced in Section 1.

Expressiveness. Construction of bidirectional

transformations is inherently difﬁcult due to hetero-

geneity of the underlying metamodels (Figure 1).

Thus, there is a problem-inherent limitation concern-

ing the functionality of bidirectional transformations.

In our case study, Gantt diagrams and CPM networks

are closely related, but the concepts of activity and

dependency in Gantt diagrams cannot be mapped

1:1 to the concepts of activity and event in CPM

networks. While the forward transformation is total,

the backward transformation may reconstruct the

original Gantt diagram, but can be applied only to

CPM networks generated by the forward transfor-

mation. This problem-inherent limitation would also

hold if we had used any other model transformation

language.

An important added value of QVT-R consists in its

language support for relational speciﬁcations of bidi-

rectional transformations. In this respect, expressive-

ness of QVT-R is concerned with the following is-

sue: Suppose that we constructed two unidirectional

transformations that exhibit the desired behavior (as

in our case study). Is it possible to synthesize a single,

equivalent bidirectional transformation? The more of-

ten the answer to this question is positive, the more

expressive is QVT-R compared to languages support-

ing only unidirectional transformations.

In our case study, the synthesis succeeded to a

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

151

large extent. The resulting bidirectional transfor-

mation works correctly in enforcing mode and ex-

hibits the same behavior as the unidirectional trans-

formations from which it was synthesized. Unfortu-

nately, the transformation does not behave correctly in

checking mode. This is due to the fact that our simu-

lation of unidirectional expressions does not work in

checking mode (see previous subsection).

Conciseness. Since QVT-R is a declarative rather

than procedural language, speciﬁcations written in

QVT-R are concise inasmuch as they just describe

the patterns to be searched and instantiated, without

specifying algorithmic details to be taken care of by a

QVT-R execution engine.

Furthermore, as far as bidirectional transforma-

tions are concerned, conciseness results from the fact

that both transformation directions can be expressed

by a single relational speciﬁcation. In other lan-

guages, separate transformations have to be deﬁned

for each direction.

Readability. Another relevant issue is cognitive

complexity: How easy is it to understand a QVT-R

speciﬁcation of a transformation? In our case study,

the unidirectional transformations are relatively easy

to understand. The relations have a straightforward

semantics: Search an instance of the source pattern,

check the when clause, and instantiate the target pat-

tern using the where clause. The when clause and the

where clause have clearly separated responsibilities:

They act as pre- and postconditions. The order in

which relations are executed may be constrained by

relation calls in the when clauses.

However, if we specify separate forward and back-

ward transformations, we have to ensure manually

that the opposite transformations are mutually consis-

tent. The full power of QVT-R is exploited only when

we construct a bidirectional transformation which is

executable in both the enforcing mode (in both direc-

tions) and the checking mode. The term relational

speciﬁcation suggests that such a relation may be de-

ﬁned declaratively at a high level of abstraction.

Unfortunately, the bidirectional transformation

constructed in the case study does not meet these ex-

pectations. The author of the transformation has to

consider in detail the execution semantics of the spec-

iﬁcation. For each mode and each direction, it has to

be veriﬁed that the relations work correctly and ex-

ecution satisﬁes all data ﬂow constraints. To make

the transformation executable in both directions, it

may be necessary to simulate unidirectional expres-

sions. However, this simulation impedes readability

and does not work in checking mode. Furthermore,

the separation of responsibilities is blurred: Condi-

tional expressions have to be moved to the when clause

because they do not work in the where clause. Finally,

execution of the when clause and the where clause may

be intertwined, resulting in further confusion. Alto-

gether, we conclude that the bidirectional transforma-

tion which we constructed in this paper is very hard

to understand (although it was constructed systemati-

cally from two unidirectional transformations).

Semantic Soundness. To a large extent, cognitive

complexity results from ﬂaws in the semantics deﬁ-

nition. In unidirectional transformations, source pat-

tern, target pattern, when and where clause have clearly

separated responsibilities. But for bidirectional trans-

formations, the responsibilities are blurred. An ex-

pression acting as a precondition in the forward di-

rection may play the role of a postcondition in the

backward direction. Thus, it is by no means straight-

forward to decide whether an expression should go

the when clause or the where clause.

The unclear separation of responsibilities even

goes as far as allowing dependencies of expressions

in the when clause on expressions in the where clause.

This liberty results from the fact that a relation is es-

sentially considered as a set of expressions which are

evaluated in an order conforming to data ﬂow con-

straints (before a variable may be accessed, it must

be bound). Unfortunately, this declarative approach

to deﬁning the execution semantics does not guaran-

tee conﬂuence in general: If the data ﬂow constraints

permit different orders of evaluation, the results of ex-

ecution may differ (inadvertent non-determinism).

4.6 Proposals for Revising QVT-R

Based on the experiences gained through the case

study, we propose several revisions to QVT-R and il-

lustrate these revisions with an example.

Model Qualiﬁers. In QVT-R, domain qualiﬁers de-

termine in which way a domain of a relation may be

used in a transformation. These qualiﬁers may dif-

fer from relation to relation. Since we did not en-

counter any use cases requiring this degree of free-

dom, we suggest to replace local domain qualiﬁers by

global model qualiﬁers specifying the roles of models

in transformations. The model qualiﬁers are inherited

by all relations, i.e., the qualiﬁer of a model consis-

tently applies to the domains of all relations.

Unidirectional Expressions. Frequently, expres-

sions speciﬁed in a relation are relevant in only one

direction. The “solution” presented in this paper —

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

152

1 trans formation b i d i r e c t i o n a l R e v i s e d ( enforce diagram : g a ntt , enforce network : cpm) {

2 . . .

3 top r e l a t i o n D e p e n d e n c y 2 A c t i v i t y {

4 c n p r e d A c t i v i t y , c n s u c c A c t i v i t y : cpm : : A c t i v i t y ;

5 gd dependencyType : g a n t t : : DependencyType ;

6 o f f s e t : I n t e g e r ; name : S t r i n g ;

7 domain diagram gd dependency : g a n t t : : Dependency {

8 o f f s e t = o f f s e t ,

9 diagram = gd diagram : g a n t t : : GanttDiagram {} ,

10 predecessor = g d p r e d A c t i v i t y : g a n t t : : A c t i v i t y {} ,

11 successor = g d s u c c A c t i v i t y : g a n t t : : A c t i v i t y {} ,

12 dependencyType = gd dependencyType

13 };

14 domain network c n a c t i v i t y : cpm : : A c t i v i t y {

15 d u r a t i o n = o f f s e t , name = name,

16 network = cn n e twork : cpm : : CPMNetwork {} ,

17 sourceEvent = cn sourc eEve nt : cpm : : Event {} ,

18 t a r g e t E v e n t = c n t a r g e t E v e n t : cpm : : Event {}

19 };

20 when {

21 Diagram2Network ( gd diagram , cn networ k ) ;

22 to diagram {

23 mapToDependency ( c n a c t i v i t y ) ;

24 c n p r e d A c t i v i t y = o w n i n g A c t i v i t y ( cn sour ceEv ent ) ;

25 c n s u c c A c t i v i t y = o w n i n g A c t i v i t y ( c n t a r g e t E v e n t ) ;

26 }

27 A c t i v i t y 2 A c t i v i t y ( g d p r e d A c t i v i t y , c n p r e d A c t i v i t y ) ;

28 A c t i v i t y 2 A c t i v i t y ( g d s u c c A c t i v i t y , c n s u c c A c t i v i t y ) ;

29 }

30 where {

31 to network {

32 cn sour ceEv ent = sourceEvent ( c n p r e d A c t i v i t y , gd dependencyType ) ;

33 cn t a r g e t E v e n t = t a r g e t E v e n t ( c n s u c c A c t i v i t y , gd dependencyType ) ;

34 name = g d p r e d A c t i v i t y . name + ’−>’ + g d s u c c A c t i v i t y . name ;

35 }

36 to diagram {

37 gd dependencyType = dependencyType ( c n a c t i v i t y ) ;

38 }

39 }

40 }

41 }

Figure 9: Bidirectional relation for dependencies in revised notation.

conditional expressions querying the binding state —

may be considered only a workaround which signif-

icantly increases cognitive complexity and does not

work in the checking mode. Therefore, we propose

to support unidirectional expressions directly in the

QVT-R language. To this end, we propose to place

an optional direction speciﬁcation before an expres-

sion list occurring in a relation. The direction speci-

ﬁcation is indicated by the keyword to followed by a

model name. If the direction speciﬁcation is present,

the expression list is considered only in the direction

of the speciﬁed model.

Structured Execution of Relations. To eliminate

inadvertent non-determinism and to ensure separation

of responsibilities, we propose to structure the execu-

tion of relations into clearly delineated phases: (1)

Match source domain. (2) Evaluate when clause. (3)

Evaluate where clause. (4) Instantiate target domain.

Each phase may rely only on previous phases. Since

expressions may have to be evaluated after instan-

tiation of the target domain, we propose to add an

optional post clause which is executed in phase (5)

(which, however, is not needed in our case study).

Example. Figure 9 presents the revised bidirec-

tional relation for transforming dependencies into ac-

tivities. The domain qualiﬁers were replaced with

model qualiﬁers. The relation may be synthesized

in a straightforward way from the forward and the

backward relation. The when and the where clause

are merged separately; unidirectional expressions are

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

153

marked with a direction speciﬁcation. The resulting

relation is slightly more concise and considerably eas-

ier to understand than the standard-compliant bidirec-

tional relation in Figure 7. Furthermore, it works in

checking mode, as well.

5 RELATED WORK

The vast majority of transformation languages sup-

ports only unidirectional transformations; consider

e.g. the well-known ATL language (Jouault et al.,

2008). However, bidirectionality is not a unique fea-

ture of QVT-R (Czarnecki et al., 2009). The most

prominent competitors are languages and tools based

on triple graph grammars (Sch

urr, 1995; K

onigs and

Sch

urr, 2006; Sch

urr and Klar, 2008; Kindler and

Wagner, 2007). In contrast to the grammar-based ap-

proach, QVT-R follows a relational paradigm where a

transformation is speciﬁed by a set of relations among

patterns to be instantiated in the participating models.

To the best of our knowledge, our work is unique

inasmuch as it addresses the evaluation of QVT-R

with respect to bidirectional transformations. Other

work focuses primarily on the formal deﬁnition of

QVT-R’s semantics (Stevens, 2010; Stevens, 2013;

Guerra and de Lara, 2012; de Lara and Guerra, 2009).

While support of bidirectional transformations consti-

tutes the most interesting (and challenging feature) of

QVT-R, this issue has been neglected severely from

the application point of view. The standard itself

provides only examples of unidirectional transforma-

tions. We are aware of only a single application-

oriented paper dealing with bidirectional transforma-

tions in QVT-R (Schwichtenberg et al., 2014), which

uses, but does not evaluate QVT-R’s features for spec-

ifying bidirectional transformations.

6 CONCLUSION

Bidirectional transformations are required in a num-

ber of applications of industrial relevance, includ-

ing bidirectional data converters and round-trip en-

gineering. In this paper, we presented a case study

for evaluating QVT-R, a declarative language which

was deﬁned in an OMG standard. QVT-R is distin-

guished from other model transformation languages

by providing the concept of a relational speciﬁcation

of a transformation which may be executed in differ-

ent modes and different directions. For bidirectional

transformations, this approach reduces the effort of

writing speciﬁcations and contributes to providing

mutually consistent forward and backward transfor-

mations. However, the case study revealed severe

deﬁciencies of QVT-R: The speciﬁcation of a bidi-

rectional transformation between Gantt diagrams and

CPM networks works only in enforcing mode, it is

very hard to understand since the QVT-R user has to

consider the details of the execution semantics care-

fully, and the execution semantics is deﬁned in an un-

clear way. Therefore, we proposed several revisions

of QVT-R to remove these deﬁciencies.

The work presented in this paper is embedded into

a more comprehensive investigation into bidirectional

transformations in QVT-R. In (Westfechtel, 2015),

seven case studies are explored, ranging from sim-

ple cases (e.g., migration between unweighted and

weighted Petri nets) to complex cases such as an

object-relational mapping. For each of the cases, a

QVT-R solution is provided. Furthermore, the trans-

formations are classiﬁed with respect to their formal

properties, and guidelines are given for applying the

QVT-R language as it stands. The problems occurring

the project management case study presented here

were observed also in other case studies, and most of

the proposed language revisions may already be de-

duced from the project management case.

Currently, we are using QVT-R to implement

a tool for round-trip engineering between UML

class diagrams and Java code. The tool is real-

ized as part of Valkyrie, a model-driven environment

for model-driven software engineering (Buchmann,

2012). Valkyrie is based on the EMF version of the

UML 2 metamodel; the Java model is provided by

MoDisco (Bruneli

ere et al., 2014). The round-trip en-

gineering tool will operate incrementally, propagat-

ing changes forth and back. Thus, the tool provide

us with a non-trivial case study dealing with incre-

mental transformations, which go beyond the scope

of the current paper. Furthermore, we will compare

the QVT-R-based tool against an earlier implementa-

tion based on triple graph grammars (Buchmann and

Westfechtel, 2013). In addition, we will also solve

the transformation problems presented in (Westfech-

tel, 2015) with triple graph grammars. In this way,

we will obtain a set of case studies for a comparative

evaluation of QVT-R and triple graph grammars.

ACKNOWLEDGEMENTS

The speciﬁcations presented in this paper were devel-

oped and tested with medini QVT, version 1.7.0 under

Eclipse Indigo.

ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

154

REFERENCES

Bruneli

ere, H., Cabot, J., Dup

e, G., and Madiot, F.

(2014). MoDisco: A model-driven reverse engineer-

ing framework. Information and Software Technology,

56(8):1012–1032.

Buchmann, T. (2012). Valkyrie: A UML-based model-

driven environment for model-driven software engi-

neering. In Hammoudi, S., van Sinderen, M., and

Cordeiro, J., editors, Proceedings of the 7th Interna-

tional Conference on Software Paradigm Trends (IC-

SOFT 2012), pages 147–157. ScitePress.

Buchmann, T. and Westfechtel, B. (2013). Towards in-

cremental round-trip engineering using model trans-

formations. In Demirors, O. and Turetken, O., edi-

tors, Proceedings of the 39th Euromicro Conference

on Software Engineering and Advanced Applications

(SEAA 2013), pages 130–133. IEEE Conference Pub-

lishing Service.

Czarnecki, K., Foster, J. N., Hu, Z., L

ammel, R., Sch

urr, A.,

and Terwilliger, J. F. (2009). Bidirectional transforma-

tions: A cross-discipline perspective. In Paige, R. F.,

editor, Proceedings of the Second International Con-

ference on Theory and Practice of Model Transforma-

tions (ICMT 2009), volume 5563 of Lecture Notes in

Computer Science, pages 260–283, Zurich, Switzer-

land. Springer-Verlag.

Czarnecki, K. and Helsen, S. (2006). Feature-based sur-

vey of model transformation approaches. IBM Sys-

tems Journal, 45(3):621–645.

de Lara, J. and Guerra, E. (2009). Formal support for QVT-

Relations with coloured petri nets. In Sch

urr, A. and

Selic, B., editors, Proceedings of the 12th Interna-

tional Conference on Model Driven Engineering and

Systems (MODELS 2009), volume 5795 of Lecture

Notes in Computer Science, pages 256–270, Denver,

CO. Springer-Verlag.

Guerra, E. and de Lara, J. (2012). An algebraic semantics

for QVT-Relations check-only transformations. Fun-

damentae Informaticae, 114(1):73–101.

Jakumeit, E., Buchwald, S., Wagelaar, D., Dan, L.,

Heged

us, A., Herrmannsd

orfer, M., Horn, T., Kalnina,

E., Krause, C., Lano, K., Lepper, M., Rensink, A.,

Rose, L., W

atzold, S., and Mazanek, S. (2014). A sur-

vey and comparison of transformation tools based on

the transformation tool contest. Science of Computer

Programming, 85A:41–99.

Jouault, F., Allilaire, F., B

ezivin, J., and Kurtev, I. (2008).

ATL: A model transformation tool. Science of Com-

puter Programming, 72(1–2):31–39.

Jungnickel, D. (2008). Graphs, Networks and Algorithms,

volume 5 of Algorithms and Computation in Mathe-

matics. Springer, Berlin, Germany, 3rd edition.

Kerzner, H. (1998). Project Management: A Systems

Approach to Planning, Scheduling, and Controlling.

John Wiley & Sons, New York, NY, 6th edition.

Kindler, E. and Wagner, R. (2007). Triple graph grammars:

Concepts, extensions, implementations, and applica-

tion scenarios. Technical Report tr-ri-07-284, Univer-

sity of Paderborn, Paderborn, Germany.

onigs, A. and Sch

urr, A. (2006). Tool integration with

triple graph grammars - a survey. In Heckel, R., ed-

itor, Proceedings of the School of SegraVis Research

Training Network on Foundations of Visual Modelling

Techniques (FoVMT 2004), volume 148 of Electronic

Notes in Theoretical Computer Science, pages 113–

150, Dagstuhl, Germany. Elsevier Science.

uhne, T. (2006). Matters of (meta-)modeling. Software

and Systems Modeling, 5(4):369–385.

Object Management Group (2012). Object Constraint Lan-

guage Version 2.3.1. Needham, MA, formal/2012-01-

01 edition.

Object Management Group (2013). OMG Meta Object Fa-

cility (MOF) Core Speciﬁcation Version 2.4.1. Need-

ham, MA, formal/2013-06-01 edition.

Object Management Group (2014). Meta Object Facility

(MOF) 2.0 Query/View/Transformation Speciﬁcation

Version 1.2 Beta. Needham, MA, ptc-2014-03-38 edi-

tion.

Reddy, S., Venkatesh, R., and Zahid, A. (2006). A rela-

tional approach to model transformation using QVT

Relations. Technical report, Tata Research Develop-

ment and Design Centre, Pune, India.

Schmidt, D. C. (2006). Guest editor’s introduction: Model-

driven engineering. IEEE Computer, 39(2):25–31.

Sch

urr, A. (1995). Speciﬁcation of graph translators with

triple graph grammars. In Proceedings of the 20th In-

ternational Workshop on Graph-Theoretic Concepts

in Computer Science (WG 1994), volume 903 of

Lecture Notes in Computer Science, pages 151–163,

Herrsching, Germany. Springer-Verlag.

Sch

urr, A. and Klar, F. (2008). 15 years of triple graph

grammars – research challenges, new contributions,

open problems. In Ehrig, H., Heckel, R., Rozen-

berg, G., and Taentzer, G., editors, Graph Transfor-

mations: 4th International Conference (ICGT 2008),

volume 5214 of Lecture Notes in Computer Science,

pages 411–425, Leicester, UK. Springer-Verlag.

Schwichtenberg, S., Gerth, C., Huma, Z., and Engels, G.

(2014). Normalizing heterogeneous service descrip-

tion models with generated QVT transformations. In

Cabot, J. and Rubin, J., editors, Proceedings of the

10th European Conference on Modelling Foundations

and Applications (ECMFA 2014), volume 8569 of

Lecture Notes in Computer Science, pages 180–195,

York, UK. Springer-Verlag.

Steinberg, D., Budinsky, F., Paternostro, M., and Merks,

E. (2009). EMF Eclipse Modeling Framework. The

Eclipse Series. Addison-Wesley, Upper Saddle River,

NJ, 2nd edition.

Stevens, P. (2010). Bidirectional model transformations in

QVT: Semantic issues and open questions. Software

and Systems Modeling, 9(1):7–20.

Stevens, P. (2013). A simple game-theoretic approach to

checkonly QVT Relations. Software and Systems

Modeling, 12(1):175–199.

Westfechtel, B. (2015). Bidirectional transformations in

QVT Relations: Potentials and limitations. Journal

of Object Technology. Submitted for publication.

ACaseStudyforEvaluatingBidirectionalTransformationsinQVTRelations

155