
On the Discovery of Explainable and Accurate Behavioral Models for
Complex Lowly-structured Business Processes
Francesco Folino, Massimo Guarascio and Luigi Pontieri
Institute ICAR, National Research Council (CNR), via P. Bucci 41C, 87036, Rende, CS, Italy
Keywords:
Data Mining, Business Process Intelligence, Trace Clustering, Workflow Discovery.
Abstract:
Process discovery (i.e. the automated induction of a behavioral process model from execution logs) is an
important tool for business process analysts/managers, who can exploit the extracted knowledge in key pro-
cess improvement and (re-)design tasks. Unfortunately, when directly applied to the logs of complex and/or
lowly-structured processes, such techniques tend to produce low-quality workflow schemas, featuring both
poor readability (“spaghetti-like”) and low fitness (i.e. low ability to reproduce log traces). Trace clustering
methods alleviate this problem, by helping detect different execution scenarios, for which simpler and more
fitting workflow schemas can be eventually discovered. However, most of these methods just focus on the
sequence of activities performed in each log trace, without fully exploiting all non-structural data (such as
cases’ data and environmental variables) available in many real logs, which might well help discover more
meaningful (context-related) process variants. In order to overcome these limitations, we propose a two-phase
clustering-based process discovery approach, where the clusters are inherently defined through logical deci-
sion rules over context data, ensuring a satisfactory trade-off is between the readability/explainability of the
discovered clusters, and the behavioral fitness of the workflow schemas eventually extracted from them. The
approach has been implemented in a system prototype, which supports the discovery, evaluation and reuse
of such multi-variant process models. Experimental results on a real-life log confirmed the capability of our
approach to achieve compelling performances w.r.t. state-of-the-art clustering ones, in terms of both fitness
and explainability.
1 INTRODUCTION
Process discovery (more precisely, control-flow dis-
covery) techniques (van der Aalst et al., 2003) are
a valuable tool for automatically extracting a behav-
ioral schema for a business process (out of past execu-
tion traces), which can profitably support key process
analysis, (re-)design, and optimization tasks.
Unfortunately, a direct application of such tech-
niques to the logs of lowly-structured processes
(featuring a large variety of behavioral patterns) is
likely to yield low quality (“spaghetti-like”) workflow
schemas, exhibiting both low readability and low fit-
ness (Buijs et al., 2012). By contrast, reliable work-
flow schemas would be very important for many real-
life flexible and dynamic process management set-
tings, where little a-priori knowledge is available on
what typical work schemes are followed in reality.
To alleviate such a problem, several trace clustering
approaches (De Weerdt et al., 2013; Bose and van der
Aalst, 2009a; Bose and van der Aalst, 2009b; Song
et al., 2008; Greco et al., 2006) have been proposed in
the literature, which help recognize different homoge-
nous execution scenarios (or “process variants”), each
of which can be effectively described through a sim-
pler and more fitting workflow schema.
However, most of these approaches only focus on
structural aspects of the traces (e.g., which activities
were performed, and in what an order), paying no at-
tention at all to all kinds of non-structural data (such
as qualitative/quantitative properties of process cases,
or other context factors characterizing the state of the
execution environment at the moment when the case
was performed),which are often available in most real
logs. And yet, such data may well help the analyst get
insight on the discovered execution scenarios, when-
ever the behavior of the process tends to be correlated
to non-structural context variables.
In fact, it was shown in (Folino et al., 2008; Folino
et al., 2011) that such correlations between non-
structural variables and process behaviors do exist
in some real application scenarios, and it is possi-
206
Folino F., Guarascio M. and Pontieri L..
On the Discovery of Explainable and Accurate Behavioral Models for Complex Lowly-structured Business Processes.
DOI: 10.5220/0005470602060217
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 206-217
ISBN: 978-989-758-096-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

ble to learn a classification model for discriminating
among different behavioral classes discovered with a
trace clustering procedure. However, the application
of standard classifier-induction methods, as a post-
processing step, to the results of a purely-structural
trace clustering method is not guaranteed to achieve
good accuracy performances in general — as con-
firmed by experimental findings presented in Sec-
tion 6.
To overcome the above limitations we here try
to face a new kind of clustering-oriented process
discovery problem, specifically tailored to the case
of complex and/or lowly-structured process logs.
The ultimate goal of our approach is to discover a
high-quality multi-variant process model for a given
log, consisting of different workflow schemas, one
for each of discovered trace clusters, which en-
sures an optimal trade-off between: (i) the readabil-
ity/interpretability of the discovered clusters and of
their distinguishing features (possibly linked to con-
text factors), on the one hand, and (ii) the behavioral
fitness of the discovered workflow schemas (i.e., the
capability to adequately capture the behaviors regis-
tered in the log), on the other hand. As to the for-
mer point, for a certain level of behavioral fitness,
higher readability/interpretability is ensured by mod-
els featuring a lower number of clusters, easily ex-
plainable in terms of (accurate enough) discriminat-
ing rules over non-structural context variables.
In order to obtain clusters inherently correlated to
non-structural data, we focus on a specific family of
conceptual clustering models, represented as logical
(decision) rules. Technically, the search for such a
model is carried out by adopting a predictive clus-
tering approach (Blockeel and Raedt, 1998), where
context-oriented case variables are called to play as
descriptive attributes, while the target of prediction is
a number of simple structural patterns, capturing ba-
sic intra-trace precedence relationships between pro-
cess activities. As a result, a preliminary set of clus-
ters is found, each associated with a specific decision
rule representing a specific setting of context vari-
ables (i.e. a specific “context” variant). Since there
is no guarantee that the discovered clusters really
correspond to neatly different behavioral schemes, a
greedy iterative restructuring procedure is carried out,
where redundant clusters showing similar behaviors
are merged together, as long as the average fitness of
the associated workflow schemas can be increased.
The whole approach has been implemented into
a system prototype, which fully assists the user in
discovering, inspecting and evaluating such multi-
variant process models, and helps reuse them in ad-
vanced analyses and run-time support tasks. In par-
ticular, the system is meant to both help the analyst
inspect and validate the correlations discovered be-
tween non-structural context factors and the structure
of process instances (encoded in the form of logical
clustering rules), as well as to exploit them for the
provision of advanced run-time services, which can
be very useful when enacting flexible and dynamic
processes. In particular, by applying the discovered
classification model to a partially unfolded (i.e. not
finished) process case, it is possible to show the work-
flow schema of the cluster it is estimated to belong to,
as a customized (context-adaptive) process map, de-
scribing how the case may proceed.
Experimental results confirmed its capability to
achieve compelling performances, in terms of both
fitness and explainability, with respect to several
state-of-the-art clustering approaches: algorithm
Actitrac
(De Weerdt et al., 2013); the sequence-
based and alphabet-based versions of the approach
proposed in (Bose and van der Aalst, 2009b), based
on the mapping of log traces onto a space of be-
havioral patterns (namely, tandem repeats and max-
imal repeats, respectively); the approach proposed
in (Bose and van der Aalst, 2009a), which exploits
a k-gram representation of traces; and
DWS
algo-
rithm (Greco et al., 2006), which recursively parti-
tions a log based on a sequential patterns capturing
unexpected behaviors.
The rest of the paper is organized as follows. We
first present some related research work in Section 2,
and a few basic concepts in Section 3. The core tech-
nical framework is described in Section 4, while Sec-
tion 5 illustrates our discovery approach and system
prototype. An empirical evaluation of our proposal
on a real-life log is discussed in Section 6, while a
few concluding remarks are drawn in Section 7.
2 RELATED WORK
Several clustering approaches have been proposed in
the literature, which try to exploit different kinds of
information captured in log traces, in order to help
recognize different behavioral classes of process in-
stances automatically.
Some of these solutions leverage sequence-
oriented techniques (Ferreira et al., 2007; Bose and
van der Aalst, 2009a), which compare entire traces
by way of string-oriented distance measures. For in-
stance, the context-based approach defined in (Bose
and van der Aalst, 2009a) relies on the generic edit
distance, embedded within an agglomerative cluster-
ing scheme. A probabilistic approach was proposed
instead in (Ferreira et al., 2007), where a mixture of
OntheDiscoveryofExplainableandAccurateBehavioralModelsforComplexLowly-structuredBusinessProcesses
207

first-order Markov models approximating the distri-
bution of log traces (still considered as sequences) is
computed via an EM scheme.
Unfortunately, all of these string-oriented tech-
niques require very expensive computations, which
may make them unsuitable for the analysis of massive
logs. Conversely, higher scalability can be achieved
by resorting to feature-based approaches, such as
those in (Greco et al., 2006; Song et al., 2008; Bose
and van der Aalst, 2009b), which reuse efficient clus-
tering methods defined for vectorial data, after pro-
jecting each trace onto some space of derived features.
In more detail, different kinds of features were
considered in (Song et al., 2008) to this purpose,
as a way to capture the behavior of a trace accord-
ing to different perspectives (activities, transitions,
data, performance values, etc). Each of such fea-
tures is associated with a measure that assigns a nu-
meric value to the feature over any possible trace.
After replacing each trace with a vector storing such
measures, whatever distance-based clustering method
can be reused to partition the log. In particular,
in (Song et al., 2008), the usage of three standard
distance measures (namely, the Euclidean distance,
Hamming distance and Jaccard coefficient) was in-
vestigated, in combination with four alternative clus-
tering schemes (namely, K-means, Quality Thresh-
old Clustering, Agglomerative Hierarchical Cluster-
ing and Self-Organizing Maps).
As a more expressive kind of trace features, it was
proposed in (Bose and van der Aalst, 2009b) to ex-
ploit certain sequential patterns inspired to bioinfor-
matics (including tandem arrays and tandem repeats),
which allow for capturing recurring groups of corre-
lated activities and loop structures. After extracting
a set of frequent patterns of such a form from all the
given log, each trace can be transformed into a vector
storing how many times each of them occurs in the
trace. In order to effectively deal with the presence
of concurrent behavior, a variant (named “alphabet-
based”) of this vector-like encoding was also defined
in (Bose and van der Aalst, 2009b), based on the
very idea of regarding all patterns sharing the same
set of activities (i.e. defined over the same “alpha-
bet”) as just one dimension of the target space. In this
way, two distinct sequential patterns, e.g. the repeats
abdgh and adgbh, will be viewed as a unique feature.
It is worth noticing that, in fact, (Bose and van der
Aalst, 2009b) also explored the possibility to convert
all log traces into the (abstracted) sequences of pat-
terns occurring in them (acting as a sort of typical
sub-processes), and then comparing them by way of
some edit-distance measures.
A top-down recursive clustering scheme was pro-
posed in (Greco et al., 2006), where, at each step, a
workflow model is extracted from a set of log traces,
which may be further partitioned (until a maximal
number of clusters is reached) in order to obtain a
collection of more precise models (representing dis-
tinguished execution scenarios). In order to accom-
plish each of these trace clustering tasks, algorithm
k-means is applied to an ad-hoc propositional repre-
sentation of the traces, based on sequential patterns
(named “discriminant rules”) capturing unexpected
behaviors (w.r.t. the workflow schema currently as-
sociated with the traces that are to be partitioned).
A fitness-aware trace clustering approach was fi-
nally proposed in (De Weerdt et al., 2013), which tries
to group the traces in a way that a user-specified level
of fitness for each output process model is achieved.
Differently from our work, all the above cluster-
ing approaches are not concerned with the problem
of discovering a partition of the given traces that is
strongly correlated with context-related factors. Such
a problem was partly addressed in (Folino et al., 2008;
Folino et al., 2011), where a classification model
was learnt from a set of trace clusters (discovered
by way of the structural clustering method in (Greco
et al., 2006), in order to possibly discriminate among
them, on the basis of non-structural information as-
sociated with the traces. However, the application
of standard classifier-induction methods, as a post-
processing step, to the results of a purely-structural
trace clustering method is not guaranteed to achieve
good accuracy performances. As mentioned in the
previous section, this is the reason why we prefer to
adopt a predictive clustering approach, focusing only
on partitions of the traces that can be defined in terms
of logical rules over their associated non-structural
(context-oriented) data.
Before concluding this section, let us notice that
the usage of predictive clustering techniques (Bloc-
keel and Raedt, 1998) is not completely novel in a
process mining setting. Indeed, it was originally pro-
posed in (Folino et al., 2012), but with the different
aim of supporting run-time predictions for a case-
oriented performance metrics. In fact, the basic idea
of predictive clustering is that, once discovered a suit-
able clustering, accurate predictions for new instances
can be made by first estimating the clusters they are
deemed to belong to.
3 PRELIMINARIES
Log Traces. For each process instance (a.k.a
“case”) we assume that a trace is recorded, storing
the sequence of events happened during its enact-
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
208

ment. Let T be the universe of all (possibly partial)
traces that may appear in any log of the process un-
der analysis. For any trace τ ∈ T , len(τ) is the num-
ber of events in τ, while τ[i] is the i-th event of τ, for
i = 1 .. len(τ), with task(τ[i]) and time(τ[i]) denoting
the task and timestamp of τ[i], respectively. We also
assume that the first event of each trace is always as-
sociated with a unique “initial” task (possibly added
artificially), and its timestamp registers the time when
the corresponding process instance started.
For any trace τ, let context(τ) be a tuple gathering a
series of data about the executioncontext of τ, ranging
from intrinsic data properties to environmental vari-
able characterizing the state of the BPM system when
τ was enacted.
For ease of notation, let A
T
denote the set of all the
tasks (a.k.a., activities) that may occur in some trace
of T , and context(T ) be the space of context vec-
tors — i.e., A
T
= ∪
τ∈T
tasks(τ), and context(T ) =
{context(τ) | τ ∈ T }.
Finally, a log L is a finite subset of T .
Workflow Schemas and Behavioral Profiles. Var-
ious languages have been proposed in the literature
for specifying the behavior of a business process, in
terms of its composing activities and their mutual de-
pendencies— such as Petri nets (van der Aalst, 1998),
causal nets (van Der Aalst et al., 2011), and heuris-
tics nets (Weijters and van der Aalst, 2003). For the
sake of concreteness we next focus on the language of
heuristics nets (Weijters and Ribeiro, 2011), where a
workflow schema is a directed graph where each node
represents a process activity, each edge (x,y) encodes
a dependency of y on x, while each fork (resp., join)
node can be associated with cardinality constraints
over the the edges exiting from (resp., entering) it.
The behavior modeled by a workflow schema can
be captured approximately by way of simple pair-
wise relationships between the activities featuring in
it, named (causal) behavioral profiles (Weidlich et al.,
2011), which can be computed efficiently for many
classes of models.
Let W be a workflow schema, and A(W) be its as-
sociated activities. Let ≻
W
be a “weak order” relation
inferred from W, such that, for any x,y ∈ A(W), it is
y ≻
W
x iff there is at least a trace admitted byW where
y occurs after x. Then the behavioral profile matrix
of W, denoted by B(W), is a function mapping each
pair (x,y) ∈ A(W) × A(W) to an ordering relation in
{ ,+, k}, as follows: (i) B(W)[x, y] = , iff y≻
W
x
and x⊁
W
y (strict order); (ii) B(W)[x,y] = +, iff
x⊁
W
y and y⊁
W
x (exclusiveness); (iii) B(W)[x,y] =k,
iff x≻
W
y and y≻
W
x (either interleaving or loop).
Let τ be a trace, over trace universe T , x and y be
two activities in A
T
, and B be a behavioral profile
matrix. Then we say that τ violates (resp., satisfies)
B[x, y], denoted by τ 6⊢ B[x,y] (resp., τ ⊢ B[x,y]), if
the occurrences of x and y in τ infringe (resp., fullfill)
the ordering constraint stated in B[x, y]. More specifi-
cally, it is τ 6⊢ B[x, y] iff there exist i, j ∈ {1,..., len(τ)}
such that τ[i] = y, τ[ j] = x, and either (i) B[x,y] = +,
or (ii) B[x, y] = and i < j.
Conceptual Clustering Models. The core assump-
tion under our work is that the behavior of a process
depends on context factors. Hence, in order to predict
the structure of any trace τ, we regard its associated
context properties context(τ) as descriptive attributes.
For the sake of interpretability, we seek a concep-
tual clustering model encoded in terms of decision
rules over context(T ). Let us define conceptual clus-
tering rule over a trace universe T as a disjunction
of conjunctive boolean formulas, of the form [(A
1
1
∈
V
1
1
) ∧ (A
1
2
∈ V
1
2
) ∧ ... ∧ (A
1
k
1
∈ V
1
k
1
)] ∨ [(A
2
1
∈ V
2
1
) ∧
... ∧(A
2
k
2
∈ V
2
k
2
)]∨. ..∨ [(A
n
1
∈ V
n
1
)∧. ..∧(A
n
k
n
∈ V
n
k
n
)],
where n, k
1
,.. . ,k
n
∈ N, and, for each i ∈ {1,. .., n}
and j ∈ { 1,..., k
i
}, A
i
j
is a descriptive attribute de-
fined on T ’s instances (i.e. one of the dimensions of
the space context(T )), and V
i
j
is a subset of the do-
main of attribute A
i
j
.
For any L ⊆ T and for any such a rule r, let
cov(r,L) be the set of all L’s traces that satisfy r.
A conceptualclustering for L is a pair C = hCS,R i,
such that CS = {c
1
,...,c
n
} is a partition of L into n
clusters (for some n ∈ N), and R is a function map-
ping the clusters inCS to mutually-exclusiverules like
those above —note that
S
n
i=1
c
i
= L and
T
n
i=1
c
i
=
/
0),
while cov(R (c),L) = c for any c in CS. Due to their
generality, such rules can split any subset L
′
of Z into
n clusters — {cov(R (c
1
),L
′
),.. .,cov(R (c
n
),L
′
)} is
indeed a partition of L
′
.
In this work, we propose to discover a special
kind of conceptual clustering model for a given set
of log traces, by resorting to a predictive cluster-
ing approach (Blockeel and Raedt, 1998). In gen-
eral, in a predictive clustering setting, two kinds of
attributes are assumed to be available for each el-
ement z of a given space Z = X × Y of instances:
descriptive attributes and target ones, denoted by
descr(z) ∈ X and targ(z) ∈ Y, respectively. Hence,
the goal is to find a partitioning function (similar to
the conceptual clustering models above) that min-
imizes
∑
C
i
|C
i
| ×Var({targ(z) |z ∈ C
i
}), where vari-
able C
i
ranges over current clusters, and Var(S) is the
variance of set S. In our setting, the context data as-
sociated with each trace will be used as its descriptive
features, whereas some basic behavioral patterns ex-
OntheDiscoveryofExplainableandAccurateBehavioralModelsforComplexLowly-structuredBusinessProcesses
209

tracted from its structure (i.e. from the sequence of
activities appearing in it) will be used as targets.
4 FORMAL FRAMEWORK
The kind of process model we want to eventually
find mixes a collection of workflow schemas, asso-
ciated with distinct execution clusters (regarded as
alternative execution scenarios), with a conceptual
trace clustering model (i.e. a collection of decision
rules) that allows for discriminating among the clus-
ters, based on their link to relevant context factors.
Such a model is formally defined next.
Definition 1 (MVPM Model). Given a workflow log
L, a multi-variant process model (short MVPM) for L
is triple M = hCS, W , C i such that:
• CS = {L
1
,.. .L
n
} is a set of trace clusters, for
some n ∈ N, defining a partition of L —i.e.,
T
i=1..n
L
i
=
/
0 and
S
i=1..n
L
i
= L;
• W is a function mapping each cluster c ∈ CS to a
workflow schema, denoted by W (c);
• R is function mapping each cluster c ∈ CS to a
conceptual clustering rule, denoted by R (c), such
that C
M
= hCS,{R (c)|c ∈ CS}i is a conceptual
clustering for T .
The size of M , denoted by size(M), is the number of
clusters in CS with it — i.e. size(M) = |CS|.
In this way, L’s traces are split into different (be-
haviorally homogenous) clusters, each of which is
discriminated by a specific clustering rule (boolean
formula over traces’ properties), associated with the
cluster by function R . Each of these clusters, viewed
as a distinguished process variant, is also associated
with a workflow schema (via function W ), summa-
rizing how process activities are typically executed in
that cluster.
Problem Statement and Solution Strategy. Con-
ceptually, the induction problem faced in this pa-
per may be stated as the search for a
MVPM
of min-
imum size among those maximizing some confor-
mance measure, quantifying the ability of the model
to describe the behaviors registered in the input log
(or in a different test log used for validation).
Various log conformance metrics have been pro-
posed in the literature (see, e.g., (Alves de Medeiros
et al., 2008; Rozinat and van der Aalst, 2008)) to com-
pare the behavior registered in the log to that modeled
by the schema. Since most of these metrics (usually
defined for Petri net models) rely on a log replay strat-
egy and imply expensive model states’ explorations,
they cannot be integrated in our search for an opti-
mal
MVPM
. Therefore, we next introduce an approx-
imated (but scalable) conformance measure, named
fit
BP
, which simply compares the behavioral profiles
of each schema appearing in the
MVPM
with the cor-
responding sub-log it was discovered from. Given a
MVPM
M and a log L, the fitness of M w.r.t. L, denoted
by fit
BP
(M,L), is defined as follows:
fit
BP
(M,L) =
∑
L
i
∈M.CS
|L
i
| × λ(W (L
i
),L
i
) (1)
where, for any trace cluster L
i
and workflow
schema W
i
, λ(W
i
,L
i
) =
1
|A(W
i
)|
2
× |{(x, y) ∈ A(W
i
) ×
A(W
i
) | ¬∃ τ ∈ L
i
s.t. τ 6⊢ B(W
i
)[x,y]}|. Notice that
the function λ quantifies the fraction of W
i
’s behav-
ioral profiles that are not violated by L
i
’s traces, used
here as a rough (but scalable) fitness score.
To solve such a discovery problem efficiently, we
devised a two-phase strategy, consisting of two main
computation tasks: (i) extract a (possibly fine-grain)
conceptual clustering CM for L, by using a simplified
propositional representation of the traces, where the
structure of each of them (i.e. the sequence of activ-
ities featuring in it) is encoded into a vector of basic
behavioral features; (ii) restructure CM, by merging
together as many clusters as possible, provided that
the actual fitness of the workflow schemas associated
with CM’s clusters does not decrease.
Notably, for scalability reasons, the actual quality
(measured through function fit) of the workflow as-
sociated with each trace cluster is totally disregarded
in the first phase, where the search of a clustering
solution only tries to minimize the expected infor-
mation loss over an approximated flat representation
of the traces, according to a predictive clustering ap-
proach (Blockeel and Raedt, 1998). In particular, to
accomplish the first task, we resort to an existing PCT
learning method (CLUS), providedwith an ad-hoc en-
coding of the log, named p-view and described in de-
tails in what follows.
Propositional Trace Encoding (used in Phase I).
Basically, we want to use the context data of the
traces (and possibly the activities occurring in them)
as descriptive features for partitioning the given log
into behavioral clusters, by way of suitable clustering
rules. To concisely represent major behavioralaspects
of the traces, a target variable is defined over each ac-
tivity pair, capture basic precedence relationships.
In more details, let B be the given behav-
ioral profile matrix of some preliminary workflow
schema, trying to capture all possible behaviors
of the process analyzed. Then, for each trace
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
210

τ and each pair (a
i
,a
j
) of activities, we can de-
fine a target variable v(τ,a
i
,a
j
) as follows: (i)
v(τ,a
i
,a
j
) =
f(τ,a
i
,a
j
)
2×c(τ,a
i
,a
j
)
if both a
i
and a
j
occur in
τ, where f(τ,a
i
,a
j
) =
sum
({
sgn
( j
′
− i
′
) | i
′
, j
′
∈
{1,. .. ,len(τ)}∧ task(τ[i
′
]) = a
i
∧ task(τ[ j
′
]) = a
j
})
—with
sgn
denoting the signum function— and
c(τ,a
i
,a
j
) = |{ (i
′
, j
′
) | i
′
, j
′
∈ {1,.. .,len(τ)} ∧ i
′
6=
j
′
∧ task(τ[i
′
]) = a
i
∧ task(τ[ j
′
]) = a
j
}|; and (ii)
v(τ,a
i
,a
j
) =
null
if does not contain both a
i
and a
j
.
In this way, v(τ,a
i
,a
j
) keeps trace of the mutual po-
sitions of a
i
and a
j
, if both occur in τ (case ii); other-
wise (case ii), we just set v(τ,a
i
,a
j
) =
null
.
Based on such structural target variables, we next
formally define the propositional view (p-view) of a
log, to be eventually used to extract a conceptual clus-
tering model, by way of a PCT learner.
Definition 2 (Log View). Let L be a log over trace
universe T , and A
T
= {a
1
,...,a
k
} be the associated
activity set. Then, the propositional view (short p-
view) of L, denoted by V (L), is a relation containing
a tuple z
τ
= descr(z
τ
) ⊕ targ(z
τ
) (with ⊕ denoting
tuple concatenation) for each τ ∈ L, such that: (i)
descr(z
τ
) = context(τ) ⊕ TV(τ), where TV(τ) is a
vector in {0, 1}
k
s.t., for each i ∈ {1,.., k}, TV(τ)[i]=1
iff a
i
occurs in τ; and (ii) targ(z
τ
) = hv(τ,a
1
,a
1
),
...,v(τ,a
1
,a
k
),v(τ,a
2
,a
2
),...,v(τ,a
2
,a
k
),...,v(τ,a
2
,a
k
),
...,v(τ,a
k−1
,a
k−1
),..., v(τ,a
k−1
,a
k
),..., v(τ,a
k
,a
k
)i.
Workflow Schema Similarity (used in Phase II)
Rather than exploring all possible sequences of pair-
wise merges, over the clusters found in the first phase,
we propose to adopt a greedy iterative agglomeration
procedure, where the two clusters exhibiting the most
similar behavioral models are considered for being
possibly merged, at each iteration. In order to effi-
ciently estimate how similar two workflow schemas
are to each other, we next introduce an approximated
similarity function, defined as a variant of that pro-
posed in (Kunze et al., 2011).
Definition 3 (Schema Similarity). Let W
i
and W
j
be
two workflow models, A
i
, A
j
be their respective activ-
ity sets (i.e. A
i
= A(W
i
), and A
j
= A(W
j
)), and B
i
, B
j
their respective behavioral profiles (i.e. B
i
= B(W
i
),
and B
j
= B(W
j
)). Let S
h
k
(W
i
) = {(x,y) | (x,y) ⊆
A(W
i
) ∩ A(W
j
) ∧ B
k
[x,y] = h ∧ h ∈ { , +,k} ∧ k ∈
{i, j}} be the ordering relationships of type h that W
i
and W
j
share. Then, the BP-similarity between W
i
and W
j
, denoted by sim
BP
(W
i
,W
j
) : W
i
× W
j
→ [0,1]
defined as:
sim
BP
(W
i
,W
j
) =
∑
h∈{ ,+,k}
β
h
· J (S
h
i
,S
h
j
)+β
A
·J (A
i
,A
j
)
Input: A log L over trace universe T ,
minimal clusters’ coverage minCov ∈ (N).
Output: A
MVPM
for L;
Method: Perform the following steps:
// Phase I: Build an Initial Trace Clustering Model
1. V := V (L); // compute a p-view for L (cf. Def. 2)
2. hS, Ri :=
minePC
(V, minCov); //S is an L’s partitioning
// and {R(c)|c ∈ S} is a conceptual clustering model
3. for each cluster c ∈ S
4. W (c) :=
mineWFS
(c);
5. end for
// Phase II: Bottom-up Clusters’ Merging
6. Q := {{x,y} |x, y ∈ S} // mergeable clusters’ couples
7. repeat
8. let ( ˆc
1
, ˆc
2
) = argmax
c
i
,c
j
∈Q
{sim
BP
(W (c
i
),W (c
j
))}
9. c
new
:= ˆc
1
∪ ˆc
2
; W
new
:=
mineWFS
(c
new
);
10. Q := Q − { {x,y} | {x,y} ⊆ {ˆc
1
, ˆc
2
} }
∪ { {x,c
new
} | x ∈ S− { ˆc
1
, ˆc
2
} };
11. if | ˆc
1
| · λ(W ( ˆc
1
), ˆc
1
) + | ˆc
2
| · λ(W ( ˆc
2
), ˆc
2
)
≤ |c
new
| · λ(W
new
,c
new
) then
12. S := S − { ˆc
1
, ˆc
2
} ∪ {c
new
};
13. W (c
new
) := W
new
;
14. R (c
new
) := R ( ˆc
1
) ∨ R ( ˆc
2
);
15. end if;
16. until Q =
/
0;
17. return hS,W , R i
Figure 1: Algorithm
MVPM-mine
.
where, for any sets X and Y, J (X , Y ) =
|X∩Y|
|X∪Y|
is the
Jaccard coefficient of X and Y, while β
h
,β
A
∈ [0,1]
are weights such that
∑
h∈{ ,+,k}
β
h
+ β
A
= 1.
In this way, the more two workflow models overlap
over their activities and behavioral profiles, the more
similar they are deemed. Notice that, in the experi-
ments discussed later on, the four components of the
measure above were all weighted uniformly —i.e. we
set β
= β
+
= β
k
= β
A
= 1/4.
5 DISCOVERY APPROACH
5.1 Algorithm MVPM-mine
Figure 1 illustrates an algorithm, named
MVPM-mine
,
for inducing a
MVPM
out of a given log. As mentioned
previously, the algorithm follows a two-phase ap-
proach: it first finds a preliminary conceptual cluster-
ing model (Steps 1-3) for the traces, and then restruc-
tures the discovered clusters, along with their asso-
ciated clustering rules and workflow schemas (Steps
4-18), via a bottom-up iterative aggregation scheme.
The first phase simply amounts to encoding the in-
put log traces into a propositional dataset (Step 1) —
where each trace is equipped with both descriptive
variables and summarized behavioral features, as for-
OntheDiscoveryofExplainableandAccurateBehavioralModelsforComplexLowly-structuredBusinessProcesses
211

mally defined in Def. 2— before giving it as input
to function
minePC
(Step 2). This function imple-
ments the PCT-learning method described in (Bloc-
keel and Raedt, 1998), and returns a conceptual clus-
tering model, here denoted as a set C of trace clusters
with their associated clustering rules —for each clus-
ter c, R (c) is the rule that allows for discriminating c
from all other clusters. Essentially, this function relies
on a top-down partitioning scheme, where a split (ex-
pressed in terms of descriptive attributes) that locally
minimizes clusters’ variance (over the target space)
is greedily selected at each step, provided that reduc-
tion of variance is significant enough (according to an
F-test) and that the selected cluster contains minCov
traces at least.
Each discovered trace cluster (capturing a context-
dependent process execution variant) is then equipped
with a workflow schema (Steps 3-5), by using func-
tion
mineWFS
, which implements the Flexible Heuris-
tics Miner (FHM) method described in (Weijters and
Ribeiro, 2011) —this choice was mainly due to the
scalability and robustness to noise of this method.
It is worth noticing that our approach is paramet-
ric w.r.t. the actual implementation of both functions
mineWFS
and
minePC
, so that other solutions could
be used for implementing them. In particular, a wide
range of workflow discovery algorithm exist in the lit-
erature which could be exploited to obtain more ex-
pressive process models (such as Petri nets, or Event
Process Chains). However, such an issue is beyond
the scope of this work, yet deserving deeper investi-
gation in the future.
The second part of the algorithm follows a bottom-
up merging scheme, somewhat resembling that of ag-
glomerative clustering methods. At each step of the
loop (Steps 8-16) a couple of clusters (ˆc
1
and ˆc
2
) is
greedily chosen, such that their respective workflow
schemas are the two ones sharing the more behav-
ior, among all those schemas associated with current
trace clusters —where behavioral similarity is evalu-
ated here with the approximate measure in Def. 3.
Before merging the selected clusters, however, a
check is performed(Step 11), to assess whether such a
merge really allows for improving the overall confor-
mance measure fit —evaluated on the
MVPM
gathering
all the workflow schemas induced from current trace
clusters. Only if the check turns successful, the merge
is confirmed, and all the three components of cur-
rent
MVPM
solution are updated (Steps 12-14). In any
case, the couple of clusters chosen is removed from
Q (of candidate clusters’ pairs), as to avoid consider-
ing it in subsequent iterations —this allows to prune
the search space of the restructuring phase. It is easy
to see that the following property trivially holds, as
concerns the correctness of the check in Step 11.
Property. The conformance of MVPM hCS,W ,R i,
measured as fit(hCS, W ,R i,L), never decreases
during any computation of MVPM-mine.
It is worth noticing that, in the actual implemen-
tation of the algorithm, Q is maintained in the form
of an ad-hoc collection of priority queues, one for
each cluster in CS, all implemented as heaps. Specif-
ically, for each cluster c ∈ CS, the associated queue
stores any other cluster that may still be merged with
c, using the respective similarity to c as priority value.
Moreover, a dictionary (implemented as a hash table)
is also used to support key-based searches over the
clusters. In order to ensure fast accesses to the con-
tents of each queue, the extraction of an element is
performed by simply marking the corresponding en-
try as “invalid”, without actually removing it from the
queue, unless it occupies the top position. Similarly,
an update to a priority value is carried out through a
“virtual” removal, as explained before, followed by
an insertion. Each time a cluster c is extracted from
(resp., added to) CS, the corresponding queue is de-
stroyed (resp., created), and c is virtually removed
from (resp., added to) the queue of any other clus-
ter. The search for the closest pair of clusters (Step 8)
is eventually accomplished by only accessing the top
elements of these queues, and then selecting the one
with the highest score.
Let n be the number of clusters that were obtained
in the first computation phase (Step 3). Since no more
than n − 1 additional clusters can be created in the
second phase, any priority queue may contain O(n)
(real or invalid) elements. Thus, both the initialization
of these queues, and all subsequent accesses to them
can be performed in O(n
2
× logn).
5.2 System Prototype
Algorithm
MVPM
(cf. Fig. 1) has been fully imple-
mented in a system prototype, in order to apply and
validate the approach in practical cases. The logical
architecture of the system is depicted in Figure 2.
The Learning block is responsible for supporting
the discovery of all kinds of models composing a new
MVPM
. In particular, the Context Data Derivation mod-
ule is devised to enrich the vector of each case’s data
with additional context-related fields, which may al-
low for better discriminating among the discovered
behavioral clusters. Such additional case attributes
include both statistics computed on existing attributes
– e.g., the
workload
quantifying the the number of
total cases currently assigned to each resource or to
each high-level organizational entity – as well as new
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
212

Testing &
Evaluation
Model Analysis and Reuse
Runtime
Support
Discovered Models
Classification
Models
Workflow
Models
Context
Data
Derivation
Conceptual
Clustering
Cluster
Merging
Learning
Gateway
User Interface
BPM
Platform
Workflow
Mining
Figure 2:
MVPM
plug-in architecture.
properties defined by the analyst —e.g., what re-
source/team was initially allocated to the case.
The traces, enriched with these supplementary at-
tributes, are delivered to the Conceptual Clustering
module, which groups traces sharing both similar
structure and data values, by leveraging some core
functionalities of system CLUS (CLUS), a predic-
tive clustering framework supporting the induction of
PCT models from tabular data. To this end, a propo-
sitional encoding of the traces is built by the module,
mixing both context data and structural features (cf.
Definition 2).
For each leaf cluster in the PCT, the Workflow Min-
ing module extracts a workflow schema, and com-
putes the behavioral profiles associated with it.
Clusters exhibiting similar behaviors (according to
the similarity function in Definition 3) are then itera-
tively merged. The merging procedure, performed by
the Cluster Merging module, continues until the con-
formance of the current
MVPM
is increased, in order to
find a good balance between the size of the model,
and its ability to effectively describe different behav-
ioral classes. When two clusters are merged, their re-
spective classification rules are merged accordingly,
in order to keep the clustering model updated.
For testing purposes and further analysis, both the
workflow and the classification models are stored into
ad-hoc repositories in the Discovered Models block.
As for the Model Analysis and Reuse block, the
Testing & Evaluation model is mainly meant to assess
the quality of discovered workflow schemas and asso-
ciated classification models. In particular, the module
supports the computation of different conformance
metrics (described in Section 6), based on replaying
new test traces through the workflow schema of the
cluster they are assigned to.
Finally, the Runtime Support module is devoted to
provide advanced run-time services, which can turn
very useful for supporting the enactment of flexible
and dynamic processes. In particular, each discovered
classification model can be applied to any partially
unfolded (i.e. not finished) process case, in order to
assign it to one of the discovered process variants (i.e.
trace clusters). The workflow schema associated with
the selected cluster can be then presented to the user,
as a customized (context-adaptive) process map, de-
scribing how the case could proceed (based on how
past cases belonging to the same context variant be-
haved). In addition, this module is capable to dynam-
ically evaluate the degree of compliance between any
new (just finished or still ongoing) trace and its ref-
erence workflow schema, in order to possibly detect
deviating behaviors.
6 EXPERIMENTS
The approach proposed so far has been validated on
the log of a real problem management system (named
VINST), offered by Volvo IT Belgium, as a bench-
mark dataset for the 2013 BPI Challenge (Steeman,
2013). Precisely, we used 1487 traces spanning from
January 2006 to May 2012.
Each log event stores 8 data attributes (namely,
status
,
substatus
,
resource
,
res country
,
support team
,
org line
, and
org country
, and
functional division
). Moreover, for each prob-
lem case p, two attributes are associated with p’s
trace: p’s
impact
(medium, low, or high), and the
product
affected by p.
In order to enrich each log trace τ with further con-
text data, we extended it with a series of newattributes
indicating the support team and the country hosting
the solver team appearing in τ’s first event (denoted
by
firstOrg
and
firstCountry
, respectively), and
two other “environmental” variables: a
workload
in-
dicator, storing the total number of problems open in
the system when τ started, and several time dimen-
sions (namely,
week-day
,
month
and
year
) derived
from the timestamp of τ’s first event.
6.1 Evaluation Settings
Several kinds of metrics have been proposed
in the literature to evaluate discovered workflow
schemas (Buijs et al., 2012). In particular, fitness met-
rics, quantifying the capability to replay the log, are
typically employed as the main evaluation tool, while
other kinds of metrics (e.g., precision-oriented ones)
OntheDiscoveryofExplainableandAccurateBehavioralModelsforComplexLowly-structuredBusinessProcesses
213

Table 1: Results (avg±stdDev) obtained by
MVPM-mine
and several competitors. The best value in each column is in bold.
Trace Clustering Method Fitness BehPrec #nodes #edges #edgesPerNode
MVPM-mine (with descriptive structural features)
0.865±0.010 0.635±0.009 6.2±0.0 9.3±0.2 2.8±0.1
MVPM-mine (without descriptive structural features)
0.766±0.075 0.612±0.027 8.0±0.0 13.6±0.2 3.4±0.0
ACTITRAC(De Weerdt et al., 2013)
0.317±0.057 0.667±0.017 8.2±0.1 14.1±0.4 3.4±0.1
TRMR(Bose and van der Aalst, 2009b)
0.651±0.024 0.604±0.010 7.8±0.1 13.6±0.2 3.5±0.1
A-TRMR(Bose and van der Aalst, 2009b)
0.764±0.027 0.618±0.011 7.7±0.1 13.3±0.2 3.4±0.1
KGRAM(Bose and van der Aalst, 2009a)
0.558±0.026 0.655±0.007 8.0±0.1 13.2±0.2 3.3±0.0
Table 2: Accuracy of the classification models induced from the discovered clusters. Best values per column are in bold.
With descriptive structural features Without descriptive structural features
Trace Clustering Method Generalization error Cramer’s coefficient Generalization error Cramer’s coefficient
MVPM-mine
0.924 0.849 0.823 0.732
ACTITRAC(De Weerdt et al., 2013)
0.721 0.135 0.725 0.124
TRMR(Bose and van der Aalst, 2009b)
0.843 0.575 0.693 0.387
A-TRMR(Bose and van der Aalst, 2009b)
0.883 0.534 0.699 0.297
KGRAM(Bose and van der Aalst, 2009a)
0.789 0.592 0.560 0.330
can support finer grain comparisons among schemas
with similar fitness scores.
In our tests, the fitness of each discovered
heuristics-net schema was specifically measured via
the Improved Continuous Semantics Fitness defined
in (de Medeiros, 2006). Essentially, the fitness score
of a schemaW w.r.t. a log L (denoted by Fitness(W,L))
is the fraction of L’s events that W can parse exactly,
with a special punishment factor benefitting schemas
yielding fewer replay errors in fewer traces.
The behavioral precision of schema W w.r.t. log
L, denoted by BehPrec(W, L), is the average fraction
of activities that are not enabled when replaying L
through W:
BehPrec(W, L) =
1
|A(W)| × |traces(L)|
×
∑
τ∈traces(L)
|{a ∈ A(W)|W did not enable a in τ’s replay}|
We preferred these two rough conformance metrics
to standard ones defined for Petri-net models, since
we experienced long computation times and very low
conformance scores every time we applied the latter
ones to heuristics nets – this was likely due to the
many invisible transitions that tend to be produced
when converting them into Petri nets by using the plu-
gins available in ProM.
We also considered three structural-complexity in-
dicators: the numbers of nodes (#nodes) and of edges
(#edges), and the average number of edges per node
(#edgePerNode).
As competitors, we considered five state-of-the-art
approaches: algorithm
Actitrac
(De Weerdt et al.,
2013); the sequence-based and alphabet-based ver-
sions of the approach proposed in (Bose and van der
Aalst, 2009b) (denoted by
TRMR
and
A-TRMR
, respec-
tively), which relies on a mapping of traces onto a
space of behavioral patterns (precisely, tandem re-
peats and maximal repeats); the approach proposed in
(Bose and van der Aalst, 2009a) (denoted by
KGRAM
),
which exploits a k-gram representation of traces, and
DWS
(Greco et al., 2006), which recursively parti-
tions a log based on a special kinds of (discriminat-
ing) sequential patterns capturing unexpected behav-
iors (w.r.t. current workflow schemas).
Since some of these methods (namely,
TRMR
,
KGRAM
and
A-TRMR
) need to be provided with the desired
number of clusters, we instructed them to search
for as many trace clusters as those discovered by
our approach, while letting the other methods (i.e.,
Actitrac
and
DWS
) autonomouslydetermine the right
number of clusters. When running algorithm
DWS
,
with its default parameter setting, no actual trace par-
titioning was found for the log (i.e., only one cluster
was obtained). Therefore, since our evaluation founds
on assessing the capability to recognize (and discrimi-
nate among) different behavioral clusters, we will dis-
regard
DWS
in the remainder of our analysis.
6.2 Test Results
Table 1 shows the quality results obtained by algo-
rithm
MVPM-mine
, when run according to two alter-
native settings: (i) using, for each log trace, say τ,
the whole set of descriptive features defined in Def. 2,
namely context properties (i.e. context(τ) structural
features (i.e. TV(τ)), or (ii) using only non-structural
features (i.e., context(τ)). For each method and each
evaluation measure, the average over all trace clus-
ters, performed in 10-fold cross-validation, is shown
in the table. In particular, in each clustering test, we
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
214
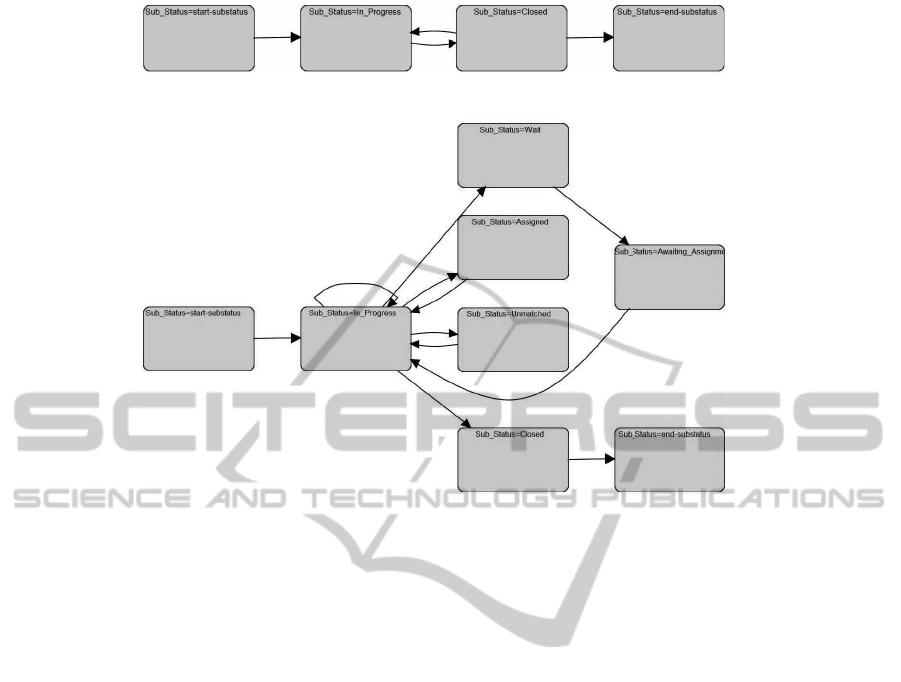
Figure 3: An execution scenario discovered by algorithm
MVPM-mine
: Workflow Schema of Cluster # 2.
Figure 4: An execution scenario discovered by algorithm
MVPM-mine
: Workflow Schema of Cluster # 4.
computed an overallFitness (resp., BehPrec) measure
for each method, as the weighted average of the Fit-
ness (resp., BehPrec) scores received by the work-
flow schemas that were induced (with FHM) from
all the trace clusters discovered in the test. Since in
all cross-validation trials
MVPM-mine
always found 6
trace clusters, the same number of clusters was given
as input to the competitors.
It is easy to see that the version of
MVPM-mine
ex-
ploiting both structural and context features neatly
outperforms all competitors in terms of average work-
flow fitness – the primary comparison metrics – with
an outstanding score of 0.865. On the other hand,the
achievementof
MVPM-mine
is quite good also in terms
of precision (0.635), if compared to other approaches.
The remaining measurements in the table show that
such achievements were obtained by way of simple
(and readable) workflow schemas:
MVPM-mine
ex-
hibits, indeed, the lowest average numbers of nodes
(6), edges (9) and edges per node (2.8).
Surprisingly good results (comparable to those
obtained by its best-performing competitors) were
achieved by
MVPM-mine
even when the descriptive
features used for the clustering do not convey any
kind of structural information. This result is quite re-
markable, as the discovered classification (i.e. con-
ceptual clustering) model can be exploited to predict
the structure of any new process case from the very
moment when it is started, by only exploiting the
knowledge of its associated context data.
This latter impression is confirmed also by the
results in Table 2, concerning the capability to ac-
curately discriminate among the discovered clusters.
Since none of the competitors directly learn any kind
of classification model, for each of these methods, we
used the cluster identifier assigned to each trace as it
were its associated class label. A logical classification
model was the induced with the PCT-learning algo-
rithm implemented in (CLUS) (provided with a single
nominal target, instead of a vector of numeric ones,
like in function
minePC
of algorithm
MVPM-mine
).
Again, two different learning settings are considered:
setting a, where both structural and context data are
used as descriptive features; and setting b, where
only context features are used as descriptive attributes
(for classification purposes). For evaluating the accu-
racy of the discovered classification models, we em-
ployed two quality metrics commonly used in classi-
fication scenarios: (i) generalization error (a.k.a. ac-
curacy), i.e. the number of correct predictions the
model performed over the total number of predic-
tions; and Cramer’s coefficient (Cramer, 1999), gaug-
ing the strength of statistical correlation between the
real and the predicted classification label.
From Table 2, it is clear that
MVPM-mine
still out-
performs all competitors, so confirming its ability to
correctly discriminate different execution scenarios
that can be, at a later stage, accurately re-discovered
when a classification model is learned over them. It
is important to notice that such an ability is kept also
OntheDiscoveryofExplainableandAccurateBehavioralModelsforComplexLowly-structuredBusinessProcesses
215

in the critical setting b, where no structural informa-
tion is exploited for separating the discovered clus-
ters. Conversely, all competitors suffers from a neat
worsening of performances in this setting.
Table 3: Classification rules describing two distinct trace
clusters discovered by
MVPM-mine
against the whole log.
Trace Cluster Clustering rule
#2
(
product
∈ {PROD278,PROD473, PROD289,.. .} ∧
firstCountry
∈ {UnitedKingdom,Thailand,...} ∧
firstOrg
∈ { G157 2nd,T8 2nd, G186 2nd,...} ∧
workload
≤ 435) ∨
(
product
∈ {PROD374,PROD729, PROD80,.. .} ∧
firstOrg
∈ { G349 3rd, J2 2nd, G67 2nd,...} ∧
workload
> 477)
#4
substatus
=assigned ∧
substatus
=wait ∧
substatus
=awaiting assignement ∧
firstOrg
∈ { T17 2nd,N14 2nd,N7 2nd, ...} ∧
workload
>423
Finally, in order to help the reader get a concrete
idea of the kind of knowledge that can be extracted
with our approach, Figures 3 and 4 show two work-
flow models induced from two of the trace trace clus-
ters found in a run of
MVPM-mine
(launched according
to setting a). It is easy to notice that the two mod-
els are quite different, so allowing to reckon that the
handling of problems tended to follow quite different
execution scenarios in the analyzed process instances.
For the sake of completeness, we also report, in Ta-
ble 3, the clustering rules associated with these trace
clusters. Notably, these easily-interpretable sets of
rules let us identify which specific settings of context
variables tended to determine the happening of each
of the execution scenarios modeled in Figures 3 and 4.
7 CONCLUSIONS
We have presented a new clustering-oriented process
discovery approach, which addresses the critical case
of lowly-structuredprocess logs through the induction
of a high-quality multi-variant model. The approach
is meant to ensure good interpretability of the clus-
ters discovered, and good levels of fitness in the rep-
resentation of each cluster’ behavior. The approach
has been implemented into a system prototype, which
supports the user in advanced analyses and monitor-
ing tasks.
Tests on a real-life log assess the ability of the ap-
proach to find both (i) readable workflow models with
high levels of behavioral fitness (w.r.t. the respec-
tive sublog); and (ii) accurate and easy-to-interpret
clustering rules, explaining the dependence of process
variants on context factors.
As future work, we plan to combine the approach
with alternative trace clustering methods (for ac-
complishing the first of algorithm
MVPM-mine
), and
more sophisticated measures for comparing work-
flow schemas and for estimating their conformance.
We will also intend to test our approach on other
real (lowly-structured) business process logs, possi-
bly featuring a richer range of non-structural data.
REFERENCES
CLUS: A predictive clustering system. http://dtai.cs.
kuleuven.be/clus/.
Alves de Medeiros, A. K., van der Aalst, W. M. P., and Wei-
jters, A. J. M. M. (2008). Quantifying process equiva-
lence based on observed behavior. Data & Knowledge
Engineering, 64(1):55–74.
Blockeel, H. and Raedt, L. D. (1998). Top-down induction
of first-order logical decision trees. Artificial Intelli-
gence, 101(1-2):285–297.
Bose, R. P. J. C. and van der Aalst, W. M. P. (2009a). Con-
text aware trace clustering: Towards improving pro-
cess mining results. In Proc. of SIAM International
Conference on Data Mining, pages 401–412.
Bose, R. P. J. C. and van der Aalst, W. M. P. (2009b).
Trace clustering based on conserved patterns: To-
wards achieving better process models. In Business
Process Management Workshops, pages 170–181.
Buijs, J., van Dongen, B., and van der Aalst, W. (2012). On
the role of fitness, precision, generalization and sim-
plicity in process discovery. In On the Move to Mean-
ingful Internet Systems: OTM 2012, volume 7565,
pages 305–322.
Cramer, H. (1999). Mathematical Methods of Statistics.
Princeton University Press.
de Medeiros, A. A. (2006). Genetic Process Mining. Phd
thesis, Eindhoven University of Technology.
De Weerdt, J., van den Broucke, S., Sand Vanthienen, J.,
and Baesens, B. (2013). Active trace clustering for
improved process discovery. IEEE Trans. on Knowl.
and Data Eng., 25(12):2708–2720.
Ferreira, D., Zacarias, M., Malheiros, M., and Ferreira,
P. (2007). Approaching process mining with se-
quence clustering: Experiments and findings. In Proc.
of 5th Int. Conf. on Business Process Management
(BPM’07), pages 360–374.
Folino, F., Greco, G., Guzzo, A., and Pontieri, L. (2008).
Discovering multi-perspective process models: The
case of loosely-structured processes. In ICEIS 2008,
Revised Selected Papers, pages 130–143.
Folino, F., Greco, G., Guzzo, A., and Pontieri, L.
(2011). Mining usage scenarios in business pro-
cesses: Outlier-aware discovery and run-time predic-
tion. Data & Knowledge Engineering, 70(12):1005–
1029.
Folino, F., Guarascio, M., and Pontieri, L. (2012). Discover-
ing context-aware models for predicting business pro-
cess performances. In Proc. of 20th Intl. Conf. on
Cooperative Information Systems (CoopIS’12), pages
287–304.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
216

Greco, G., Guzzo, A., Pontieri, L., and Sacc`a, D. (2006).
Discovering expressive process models by clustering
log traces. IEEE Trans. Knowl. and Data Eng., 18(8).
Kunze, M., Weidlich, M., and Weske, M. (2011). Behav-
ioral similarity: A proper metric. In Proc. of 9th Int.
Conf. on Business Process Management (BPM’11),
pages 166–181.
Rozinat, A. and van der Aalst, W. M. P. (2008). Confor-
mance checking of processes based on monitoring real
behavior. Information Systems, 33(1):64–95.
Song, M., G¨unther, C. W., and van der Aalst, W. (2008).
Trace clustering in process mining. In Proc. of Busi-
ness Process Management Workshops (BPI’08), pages
109–120.
Steeman, W. (2013). BPI challenge 2013, closed problems.
van der Aalst, W. (1998). The application of Petri nets to
worflow management. Journal of Circuits, Systems,
and Computers, 8(1):21–66.
van Der Aalst, W., Adriansyah, A., and van Dongen, B.
(2011). Causal nets: a modeling language tailored to-
wards process discovery. In Proc. of the 22nd Intl.
Conf. on Concurrency Theory, CONCUR’11, pages
28–42, Berlin, Heidelberg. Springer-Verlag.
van der Aalst, W. M. P., van Dongen, B. F., Herbst,
J., Maruster, L., Schimm, G., and Weijters, A. J.
M. M. (2003). Workflow mining: a survey of is-
sues and approaches. Data & Knowledge Engineer-
ing, 47(2):237–267.
Weidlich, M., Polyvyanyy, A., Desai, N., Mendling, J.,
and Weske, M. (2011). Process compliance analysis
based on behavioural profiles. Information Systems,
36(7):1009–1025.
Weijters, A. J. M. M. and Ribeiro, J. T. S. (2011). Flexi-
ble heuristics miner (FHM). In Proc. of IEEE Sympo-
sium on Computational Intelligence and Data Mining
(CIDM 2011), pages 310–317.
Weijters, A. J. M. M. and van der Aalst, W. M. P. (2003).
Rediscovering workflow models from event-based
data using Little Thumb. Integrated Computer-Aided
Engineering, 10(2):151–162.
OntheDiscoveryofExplainableandAccurateBehavioralModelsforComplexLowly-structuredBusinessProcesses
217
