
Composition of Web-services Based on Semantic Description
V. V. Klimov, A. A. Chernyshov and B. A. Shchukin
National Research Nuclear University MEPhI, Moscow Engineering Physics Institute,
Kashira Highway 31, Moscow, Russia
Keywords: Web-service, Service Composition, Ontology of Object Domain, Atomic and Composite Processes.
Abstract: The article is devoted to problems of web-services composition based on semantic descriptions in terms of
OWL-S. Mathematical model of processes is represented and the task of web-services composition is given.
Several types of web-services compositions are reviewed and their set-theoretical model is presented. The
article contains the example of web-services composition in case of searching weather conditions at the
point of aircraft arrival, which includes sequential and conditional types of composition.
1 INTRODUCTION
Web-services are program systems, which could be
unambiguously identified by their web-address with
standardized interface. Web-service does not have
user interface, i.e. it provides operations with remote
access (for example, inside the enterprise or the
Internet network). The purpose of web-services is to
provide services to other applications, as a rule, to
web-applications. Nowadays, web-services are
becoming significant elements of program systems
with service-oriented architecture (SOA) (Brogi et
al., 2008; Khobotov et al., 2012).
Widely using SOA for building information
systems, it is necessary to ensure the availability of
information about web-services proposed by a
developer. At the same time, the search for required
service or the service choreography should not
require large expenditures. Accessibility of
information could be reached by making special
repositories, comprising the web-services
description. The example of such repository is
UDDI (Universal Description Discovery &
Integration). As a standard of web-services
descriptions UDDI uses WSDL (Web Services
Description Language), recommended by
consortium W3C. The search uses keywords,
associated with this description. Obviously, this
approach has a number of disadvantages, as the
repository does not contain information about
semantics of each service. Thus, two completely
different web-services may have identical
descriptions on WSDL. This problem could be
solved by storage semantic descriptions of web-
services in repositories and using them during the
search. Web-services with the described semantics
called semantic web-services (Klimov V.V. et al,
2010; Klimov V.V. et al, 2014)
The difference between semantic web-service
and common web-service is that semantic web-
service has an additional level of semantic
description. Such a level ensures connection
between global informational resource in the form of
domain ontology and WSDL operations with their
inputs and outputs. The description of semantic web-
services could be implemented in the syntax of
OWL-S, SAWSDL, SWRL. In these languages, the
WSDL operations correspond to atomic processes
with pre-conditions and effects, and the types of
inputs and outputs are relevant to ontology classes of
domain. For example, OWL-S consists of base
ontology, process ontology, service, and service
model. This language has greater opportunities and
expressiveness than the above-listed languages, and
it also was approved by consortium W3C (Klimov
V.V. et al., 2014; Guarino N, 1998; Lee W. Lacy,
2005.).
Semantic web-services are tightly bound with
semantic web concept (Khoroshevsky V.F, 2012).
Therefore, their usage could be found in such
branches as linked open data, semantic social web
and semantic electronic libraries.
124
V. Klimov V., A. Chernyshov A. and A. Shchukin B..
Composition of Web-services Based on Semantic Description.
DOI: 10.5220/0005478601240128
In Proceedings of the 11th International Conference on Web Information Systems and Technologies (WEBIST-2015), pages 124-128
ISBN: 978-989-758-106-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
2 WEB-SERVICES
COMPOSITION
For description of web-services semantic consortium
W3C proposes to use OWL-S combined with RDF,
RDFS, OWL. OWL-S introduces the concept of
process. This concept simplifies the concept of data
streams for developers. There is also such concept as
atomic processes. They correspond to WSDL
operations, as well as composite processes, which
correspond to web-services compositions.
Atomic process is the process, which could be
executed during one interaction with the server,
where the web-service implementing this process
works on. It means that the interaction between
client and service, described by means of atomic
process, occurs by sending one message to web-
service and receiving an answer from it. Thus, the
atomic process in OWL-S corresponds to operation
of service description in WSDL (Shchukin B.A,
2013).
Composite process is the process which requires
a multistep interaction with server (servers), where
atomic services implementing this process work on.
Thus, the interaction between client and service,
described by composite process, occurs by sending
series of messages to atomic web-services in exact
order defined by the composite process description
(Khobotov, A.A. et al., 2012; Klimov V.V. et al.,
2014; Volchenkov N. G. et al., 2011).
For the composite process consisting of atomic
processes only:
I - union of I-sets of all atomic processes
included in a composite process;
O - union of O-sets of all atomic processes
included in a composite process plus outputs of
composite process, which could be calculated by
means of outputs of atomic processes;
P - union of P-sets of all atomic processes
included in a composite process;
E - union of E-sets of atomic processes included
in a composite process.
Thus, the semantic description allows refining
the search for web-services reducing it to the search
for processes. According to W3C recommendations,
the process is represented as four sets <I, O, P, E>
(Klimov V.V. et al., 2014, Volchenkov N.G. et al.,
2011)
In the semantic description, there is no algorithm
of getting outputs in terms of inputs provided by sets
<I, O, P, E>. Such connection could be
unambiguously restored from the ontology domain
description only in certain cases. The mapping of
inputs of process onto its outputs should be
explicitly given in OWL-S description by the set of
logical formulas R. As a result, each OWL-S process
will be interpreted as five sets <I, O, P, E, R>.
(
Klimov V.V. et al., 2014)
In general words the task of searching for
process is represented as comparison of the required
process description and the description of process
interpreted by real service. If such process is not
found, then it is possible to search for the required
process as composition of real ones. (
Volchenkov
N.G. et al., 2011)
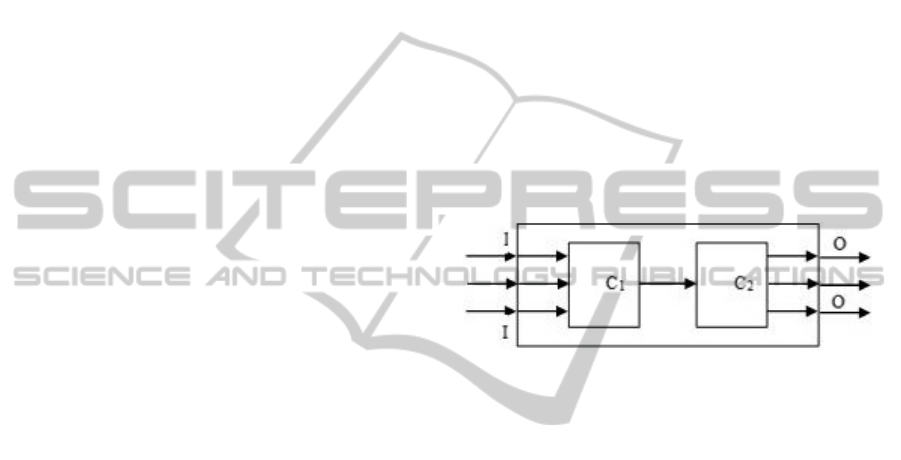
2.1 Sequential Composition (Sequence)
Sequential composition is a type of composition, in
which services are connected and may be called
sequentially. Output of the previous service must
have the same type as input of the next service (see
Fig. 1).
Figure 1: Sequential composition of two services.
The input of these processes composition is
considered to be the input of the first process and the
output – the input of the last process.
Set-theoretical model of the relevant simple
services is given below:
С1:<I1; O1; P1; R1; E1>,
С2:<I2; O2; P2; R2; E2>, I2 ⊆ O1;
Сse:<I1; O2; P1 & P2; Rse; E1 & E2>.
Let’s assume that maps R1 and R2 are services
implemented by using the schema:
R1(x1/type1,y1/type2;z1/type3,v1/type4,u1/type
7);
R2(x2/type3,y2/type5;z2/type6);
We also know that is a subtype of type4 type5,
i.e. ∀x/type4∃y/type5(x=y).
Then the mapping performed by the service
defined as sequential composition, will be performed
by Rse mapping:
Rse(x1/type1,y1/type2;z2/type6) ==
∃z1/type3∃x2/type3∃v1/type4∃y2/type5∃u1/type7
R1(x1/type1,y1/type2;z1/type3,v1/type4,u1/type7)
& (z1=x2) & (v1=y2) & R2(x2/type3, y2/type5;
z2/type6)
A part of system output С1(u1/type7) may also
be included into the output of the composition, but it
will not be clean «Sequence». In practice it is
CompositionofWeb-servicesBasedonSemanticDescription
125

necessary to solve a task when it is impossible to
find service which runs the following model
Сabs:<Iabs; Oabs; Pabs; Rabs; Eabs>.
In this case an attempt is made to run such a
model as sequential connection of two services:
С1:<I1; O1; P1; R1; E1>,
С2:<I2; O2; P2; R2; E2>.
Candidates for a serial connection are found
from the condition:
I1 = Iabs & I2 ⊆ O1 & Oabs ⊆ O2;
If such services are found, it is necessary to
prove that
Pabs → P1 & P2;
Rabs == joinOI(R1,R2);
Eabs → E1 & E2; E1 & E2 → Eabs.
2.2 Disordered Composition
(Any-Order)
This type of composition is a subtype of sequential
composition, in which processes are connected in
series, but the usage of each process occurs
randomly. In this case the condition is performed
that the types of outputs and inputs following the
previous process are the same. Additional condition
is implementation of all the processes in the
composition. There are certain constraints on both
processes for this type of composition.
The idea is that if there is no difference which of
the processes starts up first, then all the inputs and
outputs of both the processes must necessarily be
checked. I.e. the number of inputs and outputs of
both processes should be the same and the condition
of matching pairs output to input must be fulfilled.
Similarly, for the outputs (see Fig. 2).
Figure 2: Two variants of disordered composition of two
processes.
Set-theoretical model of the corresponding
simple services:
С1:<I1; O1; P1; R1; E1>,
С2:<I2; O2; P2; R2; E2>, I1 = I2 и O1 = O2
Сao:<I1; O1; P1 & P2; join(R1,R2); E1 & E2>.
Let the maps R1 and R2 be services
implemented by using the schema:
R1(x1/type1,y1/type2;z1/type1,v1/type2);
R2(x2/type1,y2/type2;z2/type1,v2/type2).
Then the service defined over "disordered"
service composition C1 and C2 will be presented by
Rao mapping:
Rao(x/type1,y/type2;z/type1,v/type2) ==
∃x1/type1∃y1/type2∃z1/type1∃v1/type2∃x2/type1∃
y2/type2∃z2/type1∃v2/type2
R1(x1/type1,y1/type2;z1/type1,v1/type2) &
z1=x2 & v1=y2 & x=x1 & y=y1 & z=z2 & v=v2
R2(x2/type1,y2/type2;z2/type1,v2/type2)
OR
R2(x2/type1,y2/type2;z2/type1,v2/type2) &
Z2=x1 & v2=y1 & x=x2 & y=y2 & z=z2 & v=v2
R1(x1/type1,y1/type2;z1/type1,v1/type2)
In this case, the task of decomposition is
formulated as for sequential connection of processes.
2.3 Conditional Composition
(if-then-else)
Conditional composition is a type of composition, in
which the execution of one of the services can only
be achieved if the following condition is fulfilled
(see Fig.3):
Figure 3: Conditional or if-then-else composition of
two processes.
Set-theoretical model of the corresponding
simple services:
С1:<I1; O1; P1; R1; E1>,
С2:<I2; O2; P2; R2; E2>.
Creating a simple service on the basis of this
design is appropriate, if the following condition is
fulfilled:
I1 = I2 and O1 = O2.
Сif:<I1; O1; P&P1 OR ¬P&P2; Rif; P&E1 OR
¬P&E2>.
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
126

Let the maps R1 and R2 are services
implemented by using the schema:
R1(x1/type1,y1/type2;z1/type3,v1/type4);
R2(x2/type1,y2/type2;z2/type3,v2/type4).
Then the service defined by conditional
composition will perform Rif mapping:
Rif(x/type1,y/type2;z/type3,v/type4) ==
∃x1/type1∃y1/type2∃z1/type3∃v1/type4∃xin/type1∃
yin/type2 P(xin/type1,yin/type2) &
R1(x1/type1,y1/type2;z1/type3,v1/type4) &x=x1 &
y=y1 & z=z1 & v=v1 & x=xin & y=yin
OR
∃x2/type1∃y2/type2∃z2/type3∃v2/type4∃xin/typ
e1∃yin/type2 ¬P(xin/type1,yin/type2) &
R2(x2/type1,y2/type2;z2/type3,v2/type4) & x=x2 &
y=y2 & z=z2 & v=v2 & x=xin & y=yin
The results of this analysis show that only two
managing structures - serial and parallel are useful
for automatic composition of processes. There must
be a process that has an input fully identical to the
input of the desired process. Other composition
types are suggested to be used to solve the tasks of
collision and invariation of proposed solutions.
3 SEARCH FOR WEATHER
CONDITIONS AT POINT OF
AIRCRAFT ARRIVAL
To describe processes we will use standard
interpretation of the first-order logic language
(Volchenkov N.G. et al., 2011).
Let the first process return destination and arrival
time by flight number:
S1(x/numFlight,y/destFlight, z/arrTimeFlight)
== ∃i/Flight Flight_fnumber(i,x) & Flight_dest(i,y)
& Flight_time(i,y)
Second process returns latitude and longitude by
city name:
S2(x/location, y/latCoordinates,
z/longCoordinates) = Location_coordinates(x,y,z)
Third and fourth processes return weather
conditions by latitude, longitude and time, but third
process works only with Northen and South America
(longitude from x to y) and the fourth one works
with Eurasia, Africa and Australia (longtitude):
S3(x/latWeather,y/longWeather,z/Time,a/Weath
erInfo)==∃i/Precipitation ∃j/Temperature
Weather_coordinates(a,x,y) & Weather_time(a,z) &
Weather_cond(a,i) & Weather_temp(a,j) & (y >= -
160) & (y <= -34)
S4(x/latWeather,y/longWeather,z/Time,a/Weath
erInfo) == ∃i/Precipitation ∃j/Temperature
Table 1: Conceptual model of knowledge domain.
Classes
Flight(x)
WeatherInfo(x)
Location(x)
FlightNumber(x) → Digital(x)
Temperature(x) → Digital(x)
Precipitation(x) → String(x)
Longitude(x) → float(x)
Latitude(x) → float(x)
Destination(x) → String(x)
ArrivalTime(x) → TimeSpan(x)
Time(x) → TimeSpan(x)
Properties
Flight_fnumber(x,y) → Flight(x) & FlightNumber(y) :
Flight_fnumber(x,y) & Flight_fnumber(x,z) → y = z
Flight_dest(x,y) → Flight(x) & Destination (y) : Flight_dest
(x,y) & Flight_dest (x,z) → y = z
Flight_time(x,y) → Flight(x) & ArrivalTime(y) : Flight_time
(x,y) & Flight_time (x,z) → y = z
Location_coordinates(x,y,z) → Location(x) & Longitude(y) &
Latitude(z) → Location_coordinates (x,y,z) &
Location_coordinates (x,a,b) → y=a & z=b
Weather_coordinates(x,y,z) → WeatherInfo(x) &
Longitude(y) & Latitude(z) → Weather_coordinates (x,y,z) &
Weather_coordinates (x,a,b) → y=a & z=b
Weather_temp(x,y) → WeatherInfo(x) & Temperature(y) →
Weather_temp (x,y) & Weather_temp (x,z) → y=z
Weather_cond(x,y) → WeatherInfo(x) & Precipitation (y) →
Weather_cond (x,y) & Weather_cond (x,z) → y=z
Weather_time(x,y) → WeatherInfo(x) & Time(y) →
Wather_time (x,y) & Weather_time (x,z) → y=z
Connections
Flight_location(x,y) = Flight(x) & Location(y)
Location_weather(x,y) = Location(x) & Weather(y)
Flight_weather(x,y,z) = Flight(x) & Weather(y) & Time(z)
Derived classes
destFlight(y) == ∃x Flight_location(x,y)
destFlight(y) → Location(y)
arrTimeFlight(y) == ∃x Flight_time(x,y)
arrTimeFlight (y) → ArrivalTime(y)
locWeather(x,y) == ∃z Weather_coordinates(z,x,y)
locWeather(x,y) → WeatherInfo(z)
numFlight(y) == ∃x Flight_fnumber(x,y)
numFlight(y) → FlightNumber(y)
longCoordinates(y) == ∃x
∀
z
Location_coordinates(x,y,z)
longCoordinates(y) → Longitude(y)
latCoordinates(z) == ∃x
∀
y
Location_coordinates(x,y,z)
latCoordinates(z) → Latitude(z)
longWeather(y) == ∃x
∀
z
Weather_coordinates(x,y,z)
longWeather(y) → Longitude(y)
latWeather(z) == ∃x
∀
y
Weather_coordinates(x,y,z)
latWeather(z) →Latitude(y)
condWeather(y) == ∃x Weather_cond(x,y)
condWeather(y) → Precipitation(y)
tempWeather(y) == ∃x Weather_temp(x,y)
tempWeather(y) → Temperature(y)
timeWeather(y) == ∃x Flight_time(x,y)
timeWeather (y) → Time(y)
Weather_coordinates(a,x,y) & Weather_time(a,z) &
Weather_cond(a,i) & Weather_temp(a,j) & (y <= -
160) & (y >= -34)
It is required to build process, which returns
information about weather conditions in the
aircraft’s destination by the flight number (see
Fig.5).
CompositionofWeb-servicesBasedonSemanticDescription
127
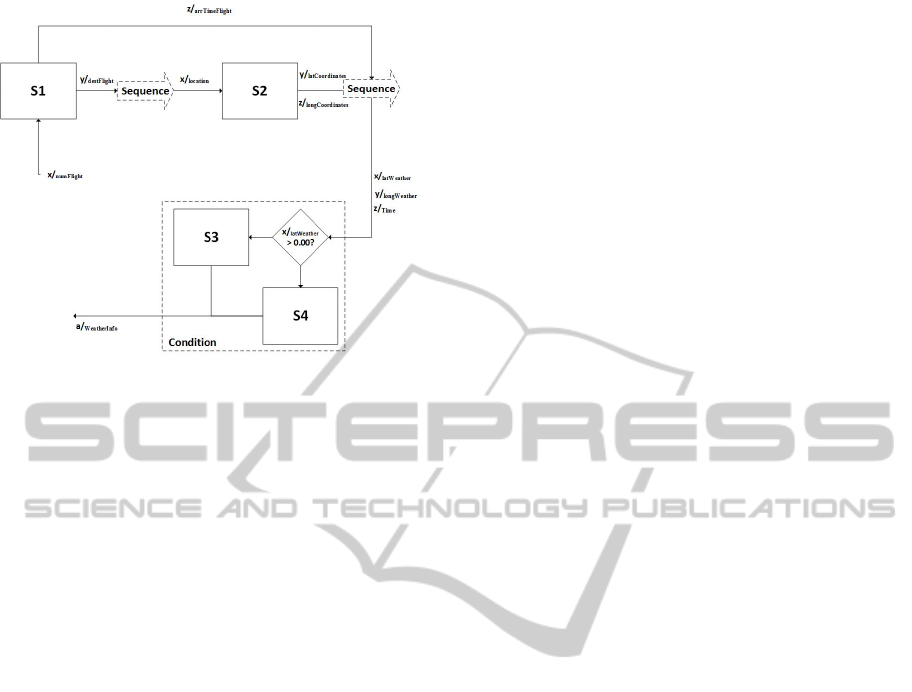
Figure 4. Process compound.
From the logical point of view, it is obvious that
sequential invocation of S1, S2 and choice between
S3 and S4 processes will solve the task. If it is
supposed that automatic search services are used for
solving the task, then it is necessary to prove that:
P(y) == (y >= -160) & (y <= -34)
S5(x/FlightNum, y/WeatherInfo) ==
(S1(x/numFlight, y/destFlight,z/arrTimeFlight) &
S2(x/location, y/latCoordinates, z/longCoordinates))
& (P(y) ? S3(x/longWeather, y/longWeather,
z/Time, a/WeatherInfo) : S4(x/longWeather,
y/longWeather, z/Time,a/WeatherInfo))
S5(x/FlightNum, y/WeatherInfo) == ∃a/Flight
∃b/Time ∃c/Location ∃d/Temperature ∃e/Longtitude
∃f/Latitude ∃g/Precipitation Flight_fnumber(a,x) &
Flight_time(a,b) & Flight_dest(a,c) &
Location_coordinates(c,e,f) &
Weather_coordinates(y,e,f) & Weather_time(y,b) &
Weather_cond(a,g) & Weather_temp(a,d)
4 CONCLUSIONS
The description of relationships between inputs and
outputs of web-services is currently not supported.
In previous paper was shown that these relationships
may not always be recovered from the description of
the domain ontology.
Have been demonstrated that search for both
atomic and composite processes is performed on
request, given in the form of
REPOI ;;;;
,
must be accompanied by the proof of statements that
can be schematically expressed as:
Pquery ⇔ Pprocess, Rquery ⇔ Rprocess and
Equery ⇔ Eprocess.
In this positional paper, several types of web-
services composition, both common and uncommon,
are presented. Shown, that using of set-theoretical
approach for describing web-services allows to
describe sophisticated web-services compositions.
Further research involves both search of
complex types of web-services composition and
applying of various semantic web-service
composition algorithms for their compound.
REFERENCES
Brogi A. et al., 2008. Semantics-Based composition-
oriented discovery of Web services // ACM Trans.
Intell. Technol. September 2008.8.4. Artice 19.
Khobotov, A. A. et al., 2012. Semantic Web-services,
their discovery and composition. In Information-
measuring and Control Systems. V.10, no.8, p. 34-39.
Klimov V. V. et al., 2010. System of description and
execution of semantic web-services compositions. In
Informational technologies in projecting and industry.
No. 4, pp. 64-70.
Klimov V. V. et al., 2014. Cloud runtime environment for
semantic web-services. In Information-measuring and
Control Systems. V.12, no.8, p. 55-59.
Guarino N, 1998. Formal, Ontology and Information
Systems. Amsterdam IOS Press.
Lee W. Lacy, 2005. Owl: Representing Information Using
the Web Ontology Language. Trafford publishing.
USA.
Khoroshevsky V. F, 2012. Semantic technologies:
expectations and trends. In Open Semantic
Technologies for Intelligent Systems (OSTIS-2012).
Proceedings of International Scientific - Technical
Conference. Section II. P. 143-158.
Shchukin B. A, 2013. Semantic Web-services. In
Information-measuring and Control Systems. V.11,
no. 6, p. 60-64.
Volchenkov N. G. et al., 2011. The composition of
semantic web-services. In Information-measuring and
Control Systems. V.9, no. 6, p. 35-42.
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
128
