Project-oriented Education as a Platform for Transfer of Math KSA

Borislav Lazarov

Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Soﬁa, Bulgaria

Keywords:

KSA Transfer, Project-oriented Education, Decontextualization.

Abstract:

Under consideration is the transfer of math knowledge, skills and attitude (KSA) built in project-oriented

education to curriculum problems using mathematical modeling. Two teaching experiments were conducted

to study the existence or lack of such kind of transfer. There were two experimental groups of regular 7th

grade students. The ﬁrst experiment (held in December 2013) aimed to clarify how students apply their KSA

developed through project-oriented activities in solving standard curriculum problems. The outcomes from

this experiment were far from satisfactory – we registered just partial and incomplete (or none) transfer of

KSA for the largest proportion of the population. The second experiment (in November 2014) was done

in more complex educational environment which included dynamic geometry software. This small change

caused an unexpectedly larger positive effect in students’ activeness and acquisition of the topic. The statistics

showed that the largest part of the students is trying to apply (more or less successfully) the knowledge in

another context. This gives us reason to believe that the project-oriented education is an appropriate platform

for decontextualization of math KSA.

1 INTRODUCTION

Different viewpoints regarding the transfer of knowl-

edge, skills and attitude (KSA) are presented in a

number of publications, e.g. a comprehensive study

on the transfer of math KSA to solving physics prob-

lems (Roorda et al., 2014) is done from actor-oriented

perspective. In fact, any application of math KSA is

a kind of transfer. For instance, the use of computers

in solving math problems requires conceptual under-

standing of mathematics and understanding how to

apply mathematics (Gravemeijer, 2014) which is, par

excellence, transfer of KSA.

Our standing point is slightly different: we con-

sider the transferability and multifunctionality of

KSA as an indicator for student’s competence of syn-

thetic type (synthetic competence). This is especially

important for the middle school math KSA because

of the higher level of abstraction, on one hand, and

on the other hand, the fact that ”mathematical be-

havior” is ... describing reality through constructs

and processes which have universal application (Eu-

ropean Commission, 2004). However, the mathemat-

ics KSA are usually developed in some clinical con-

ditions and our observations are that, when built in

such way, the KSA are rarely applicable outside the

particular educational context (Lazarov, 2014). So,

every time we speak about synthetic competence, the

next question about decontextualization stands on

agenda: are math KSA transferable and multifunc-

tional. Recently our efforts to ﬁnd a platform en-

abling the transfer of math KSA are connected mainly

with the integrated approach and project-oriented ed-

ucation (POE). Below we share our ﬁndings in two

teaching experiments with 7th grade students (mid-

dle of the secondary school). This population has

been chosen in compliance with the expectations of

the European Commission: the key competences to

be built at the end of the compulsory education (Eu-

ropean Commission, 2004) which is the 8th grade in

Bulgaria.

2 MODIFICATION OF THE

EDUCATIONAL PARADIGM

WITH RESPECT TO POE

The educational paradigm in Bulgarian traditional

school could be stated as math KSA to be formed in

classroom environment focused on reaching the ofﬁ-

cial educational standards (Bulgarian Ministry of Ed-

ucation, 2006). A nontraditional form that serves this

paradigm is the project-based education (or project-

based learning, also project-based problem solving):

it aims at forming KSA in a particular subject like

325

Lazarov B..

Project-oriented Education as a Platform for Transfer of Math KSA.

DOI: 10.5220/0005485403250330

In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 325-330

ISBN: 978-989-758-108-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

physics, biology, etc., in the frame of the classroom

activities; the indicators of progress are related to

the educational standards (Dimitrova, 2008). In one

sentence: the project-based education operates in the

same educational context as the traditional classroom

education, upgrading it with new types of activities.

The domain of the project-oriented education is ex-

tracurricular and facultative forms or interdisciplinary

activities. The educational goals of POE are con-

nected with the applications of KSA which are (ex-

pected to be) built during regular school practice in a

different educational context. The role of POE is aux-

iliary and aims to support the transition of analytical

subject knowledge into synthetic one. From this per-

spective, the following educational paradigm could be

determined:

• basic KSA to be formed in traditional classroom

practice;

• the transferability and multifunctionality of KSA

to be checked in different context;

• KSA to be turned into competence of syn-

thetic type by providing appropriate platform (like

POE).

However, sometimes new KSA are required for build-

ing bridges between school subjects that are included

in a particular project initiative and these KSA be-

come a product of POE. Then a reverse question ap-

pears: is such new knowledge applicable to some cur-

riculum topics and how does it correspond to the ed-

ucational standards. In other words are the KSA, that

are formed in auxiliary educational activity, transfer-

able to the traditional classroom context.

3 INCORPORATING POE IN

SCHOOL STRATEGY

The project-oriented education could be successfully

implemented as an upgrade of the traditional class-

room practice but there should be enough space for

it. The general mathematics schedule is overloaded

with topics closely related to the educational stan-

dards. This is why some project-oriented initiatives

should be accommodated as facultative ones. In the

years 2013/2014 and 2014/2015, we orchestrated two

teaching experiments to clarify the degree of transfer-

ability of math KSA from POE context into regular

classroom problem-solving, and as a result to evalu-

ate the achievement of the compulsory math standards

(Bulgarian Ministry of Education, 2006). Both ex-

periments took place in the frame of an elective math

course with 7th grade students.

The integrated approach was adopted as a school

strategy in a Bulgarian private secondary school

(Lazarov and Severinova, 2014). The mathematics

curriculum was split into two independent parts: the

compulsory content for the Bulgarian schools and a

complementary mathematics according to the Level

Up Maths course (Pledger, 2009). There is a poor

connection between these two parts which causes se-

rious problems for students while building even some

basic KSA in many math topics. We saw a possible

cure in organizing POE and we applied it. However,

whether POE could be such cure at all, we tried to

understand by examining the transfer of some math

KSA.

4 PARAMETERS OF THE STUDY

The experimental groups were of 16 students for the

ﬁrst experiment and 10 students for the second, all

of them 7th graders (13-14 years old). Students were

divided in teams (up to 3 members) and each team

was given a project assignment. The preparation and

project activities lasted 4 weeks.

4.1 Project Assignments

The Level Up Maths course (ibid.) contains three

lessons on solving simultaneous equations: one ded-

icated to the graphical method, another one about

some analytical methods and a special lesson called

Top Proﬁt where two optimization problems of linear

programming were given to illustrate ”the big idea”

of implementation of simultaneous equations. We

prepared project assignment for the teams which in-

cluded:

• three given problems to be solved in paper-and-

pencil (P& P) mode,

• another problem of the same type to be posed and

solved,

• dynamic-geometry-software (DGS) applets to be

composed for illustration and experimental work,

• computer presentation to be designed and per-

formed.

4.2 The Assignment Problems

The ﬁrst two problems for the project assignments

were modiﬁcations of the ones from the textbook

(Pledger, 2009); the third problem was taken (directly

or slightly modiﬁed for the different teams) from a

university math course (Jagdish and Lardner, 1989).

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

326

The fourth problem was to be stated and solved by

the teams. Here is one set of assignment problems.

Problem 1. A company manufactures two phone

models: X and Y. It takes 4 hours to produce each

item of type X and the company makes a proﬁt of 5

levs

from such an item; it takes 5 hours to produce

each item of type Y and the company makes a proﬁt of

11 levs from it. The company can produce at most 300

phones of each type and has 1600 hours to complete

the order. Find the number of phones of each type that

should be produced to make the largest proﬁt.

Problem 2. A company manufactures two bicy-

cle gears: X and Y. It takes 4 hours to produce a gear

X and the company makes a proﬁt of 7 levs from it;

it takes 2 hours to produce a gear Y which makes a

proﬁt of 3 levs. The company can produce at most 400

gears of type X and 300 Y gears; it has 2000 hours to

complete the order. Form four equations as follows:

about the maximum number of hours; about the max-

imum number of each gear type; about the proﬁt. Plot

the graph of the ﬁrst three equations (on a sheet of pa-

per and by GeoGebra). Find the point that gives the

largest proﬁt.

Problem 3. A company manufactures two prod-

ucts: X and Y. Each item of type X needs 5 units of

raw materials and 2 units of energy; each item of type

Y needs 3 units of raw materials and 4 units of energy.

The company has available 105 units of raw materials

and 70 units of energy. It can make a proﬁt of 200 levs

from each item X and 160 levs from each Y. Find the

number of items of each type that should be produced

to get the largest possible proﬁt.

Problem 4. State and solve a problem about top

proﬁt following the model of Problem 3. (Figure 1)

Figure 1: One of the 4th (students’) problems.

4.3 Data Collection and Indicator

The data to be analyzed were collected from the stu-

dents’ P& P work, from the project presentations, and

from the results of a control test. The indicator we

observed was

Lev is the Bulgarian currency

Transfer of knowledge and skills about simulta-

neous equations built in a POE context to standard

problem-solving skills, including:

I1 – introduction of relevant notations;

I2 – composition of proper equations (modeling a sit-

uation);

I3 – skills in solving linear simultaneous equations;

I4 – qualitative interpretation of the quantitative data.

The progress of this indicator we examined by

a control test of 4 standard problems, taken from a

training book (Savova et al., 2010) for the exam at

the end of the 7th grade (see the Appendix). The

ﬁrst two problems are routine ones and allow repro-

ductive approach; the third one requires transfer of

some algebraic knowledge and skills to geometrical

context. The fourth problem is also standard but at

that moment the students have not been introduced

to this particular problem-solving technique yet, so

this problem seems to be of productive (creative) type.

However, there is some common sense reasoning that

allows to solve the fourth problem without calcula-

tions.

5 KSA BUILT DURING THE POE

The outcomes of the project work in both experiments

were satisfactory in general.

Figure 2: P& P fragments from a team project.

In ﬁgures: 5 of 6 teams during the ﬁrst experiment

and 3 of 4 teams during the second one presented

their projects. Most of the teams demonstrated rea-

sonable KSA in both graphical and analytical method

(Figure 2), they prepared accurate diagrams and draw-

ings. Some students used shorthand as thick and cross

to avoid long explanations in their P& P part of the

project.

The presentation ﬁles were properly designed.

Most of the students demonstrated considerable level

of reasoning and interpretation of the solutions dur-

ing the performance (Figure 3). There were several

marginal cases in the 4th problem because the prob-

Project-orientedEducationasaPlatformforTransferofMathKSA

327

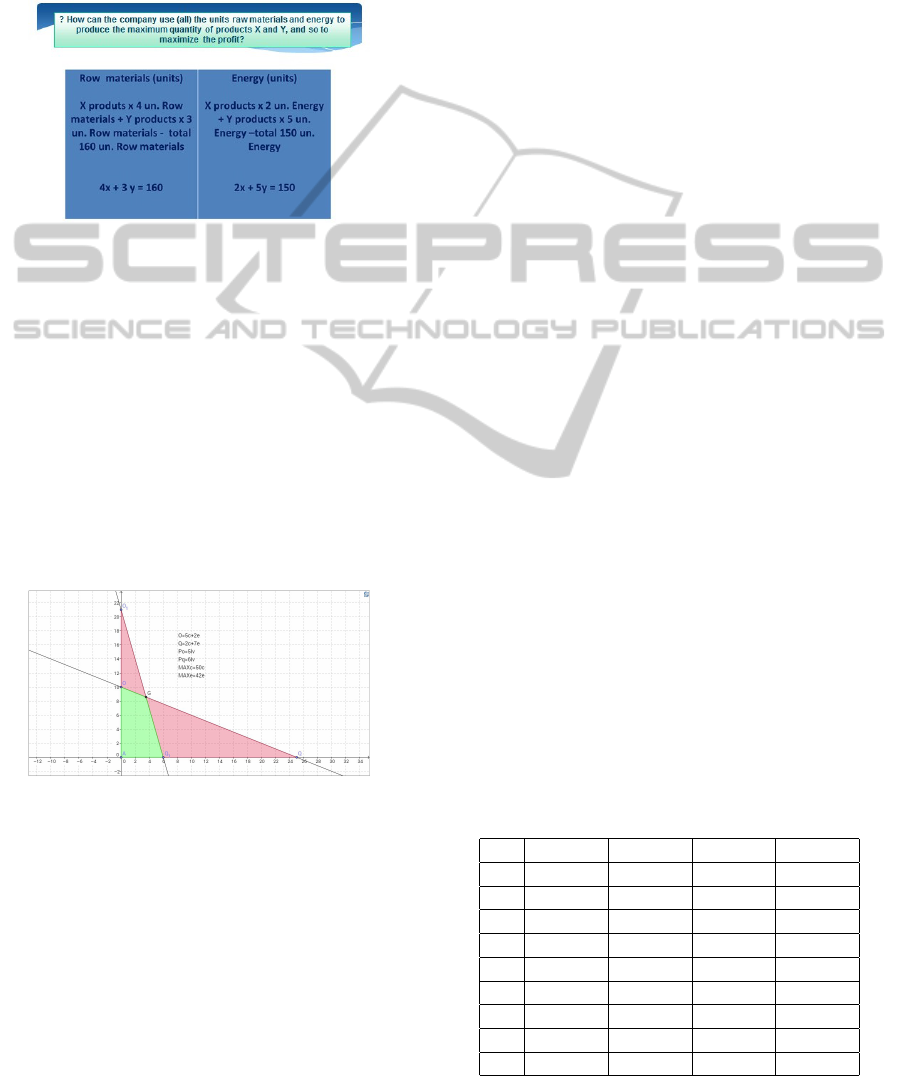
lem data were not adjusted (the students chose ﬁgures

from their common sense perspective) and even then

the teams gave sensible explanations. All these ob-

servations gave us the reason to claim that math KSA

concerning the modeling of real-life situations by si-

multaneous equations and solving them are formed in

these particular project-oriented initiatives.

Figure 3: Analyzing data to form equations (screen from a

team presentation).

We did not perform enough preparation for the

dynamic-geometry-software activities during the ﬁrst

experiment mainly because of our improper estima-

tion of the time necessary for students to learn com-

puter applications. After one introductory lesson

about GeoGebra we made just a few demonstrations

how to apply the software in solving simultaneous

equation graphically. This gap was ﬁlled up during

the second experiment by two more lessons dedicated

to DGS applets. The DGS skills built during these

two lessons were enough for the half of the students

to make appropriate applets (Figure 4).

Figure 4: Students’ graphical illustration for the 4th project

problem.

6 TEST RESULTS

We ﬁnd the students’ achievements in both experi-

ments close to the stated educational goal. But the test

results of the ﬁrst experiment are signiﬁcantly lower

than the ones of the second experiment.

6.1 The First Experiment

The test was done by 6 students. Of them: 1 stu-

dent managed to apply the method to solve 2 of the

4 problems by simultaneous equations and the rest by

common sense and basic skills; 1 student applied the

method to 1 problem and solved two more problems;

3 students tried to apply a kind of a mix of ’ideas’,

but far from satisfactory; 1 student did nothing. The

rest of the group did not do the test but showed poor

knowledge and skills in solving problems (very simi-

lar to the test ones) during the regular lessons after the

experiment.

6.2 The Second Experiment

The test was done by 9 students. One of them re-

turned blank sheet. The ﬁrst problem was solved by

the other 8 and they all applied the simultaneous equa-

tions. The second problem was solved by 4 students

completely and 1 succeeded to compose the system of

equations. The third problem was solved by 3 of the

students and 1 succeeded to compose the system of

equations. Four students composed a relevant system

for the last problem but none managed to solve it; one

of them made qualitative justiﬁcation that there is no

solution of the modeled situation.

7 SOME SPECIAL CASES FROM

THE SECOND EXPERIMENT

We are going to give more details about the second

experiment because it ﬁts better the educational goal

and the outcomes are more representative. Table 1

shows the progress made by students (S1-S9) in solv-

ing the test problems (TP1-TP4) according to the in-

dicator items (I1-I4).

Now we are going to analyze the performance of

some students whose results could be considered em-

blematic for the different stages of transfer of KSA.

Table 1: The coverage of the indicator.

TP1 TP2 TP3 TP4

S1 I1,I2,I3 I1 – I1, I2

S2 – – – –

S3 I1,I2,I3 I1,I2,I3 I1,I2 I1

S4 I1,I2,I3 I1,I2,I3 I1,I2,I3 I1,I2

S5 I1,I2,I3 – – –

S6 I1,I2,I3 – – I1,I2

S7 I1,I2,I3 I1,I2,I3 I1,I2,I3 I1,I2,I4

S8 I1,I2,I3 I1,I2,I3 I1,I2,I3 I1

S9 I1,I2,I3 – – –

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

328

7.1 Excellence

Student S7 gained the full score on the test (the only

one). She passed quickly through the ﬁrst three prob-

lems. Then she composed an equation for the fourth

problem and observed (comparing coefﬁcients) that

it cannot be solved in positive numbers. S7 demon-

strated high style of writing, proper introduction and

usage of notations, skills in algebraic transformations,

qualitative estimation of quantitative values. Accord-

ing to our indicator, we can claim that there is transfer

of KSA in full scale.

7.2 Satisfactory

Students S3, S4 and S8 managed to solve the ﬁrst two

problems completely; S4 and S5 solved problem 3

and S3 composed the system of problem 3. Let us

stress that these students applied algebraic method

to geometrical problem which requires connections

between two concepts and corresponding notations

(Figure 5). We consider this to be the desirable nor-

mal case: transfer of KSA at operational level into

new context.

Figure 5: S4’s solution of the 3rd test problem (S

and S

stand for the area, P

stands for the perimeter).

7.3 Below Average

Students S1, S5 and S9 solved completely only prob-

lem 1, applying simultaneous equations. S5 and S9

did not present their project and we will skip the dis-

cussion about transfer of their KSA. It is more likely

they have incomplete knowledge and poor skills, i.e.

there was little to be transferred. In contrast to this, S1

presented a very good project. He applied graphical

method (by DGS) to get the solutions of the problems

but made no analytical calculations. S1 also com-

posed relevant systems to problems 2 and 4 on the test

but did not solve them. It remains to clarify whether

S1 could solve these two problems if he was allowed

to use a computer.

8 CONCLUSIONS,

SPECULATIONS AND OPEN

QUESTIONS

We found that the transfer of the math KSA from the

context of their formation to another context is not to

be taken for granted for the 7th grade students. Our

conclusion is indirectly conﬁrmed by the represen-

tative statistics (CKOKUO, 2013), if we accept the

deﬁnition of synthetic competence as it is given in

(Lazarov, 2013). As a rule, on this stage the formation

of the students’ expression style and their deductive

abilities are still in progress. More able students per-

form well the reproductive tasks realizing decontex-

tualization of math KSA. But our experiments clearly

show that even advanced students (S3, S4 and S8)

meet difﬁculties when they try to apply math KSA

in productive mode and in another context. The POE

provides one more opportunity for decontextualiza-

tion of higher order math KSA. Comparing the two

experiments, we may explain the better test results in

the second experiment with the additional GeoGebra

activities. But how this factor inﬂuences the transfer

of the KSA is still not clear.

The case with S1 shows the need of rele-

vant methodology for computer-supported-problem-

solving in teaching-learning traditional math topics.

Such methodology could (and should) impact both

educational standards and examination assessment

policy. The KSA transfer is restricted by the spe-

ciﬁc subject language. This means that in a POE, stu-

dents express themselves in metalanguage which in-

cludes natural language extended with subject slang,

dynamic software and multimedia. But students are

allowed to express themselves only in narrow tradi-

tional form when doing a regular routine practice in

subject education.

The transfer of math KSA requires appropriate

media – the students’ natural language is not sufﬁ-

cient to serve this purpose. The common mathemat-

ical language is very difﬁcult to be acquired till the

end of the 7th grade. The experts in language educa-

tion introduced the concept of plurilingualism when

people communicate in a conglomerate of natural lan-

guages (Council of Europe, 2011). Spreading this

idea on the math education could be very produc-

tive in supporting the students’ creative work. The

natural language and special languages (like math-

ematical) will be only a part of a language expan-

sion. Synthetic symbols (pictures, drawings, applets,

whole screens including music and animation) are

created in a linear way but further act as multidimen-

sional semiotics terms and serve as a plurilingualis-

tic tool. Using synthetic symbols, the students get

Project-orientedEducationasaPlatformforTransferofMathKSA

329

more channels for communication, but these addi-

tional resources are available only in project-based

and project-oriented education. We prefer the sec-

ond one because it provides more opportunities and

ﬂexibility in stating goals, indicators for success, etc.

From this perspective, it is worth studying the role of

DGS in the transfer of math KSA.

ACKNOWLEDGEMENTS

The author thanks to Daniella Severinova for provid-

ing the opportunity to put into practice the experimen-

tal teaching, to Diana Semkova for the assistance in

organizing this particular POE, and to Albena Vas-

sileva for the improvement of the text. The author

also appreciates the reviewers’ notes which he takes

into account in the ﬁnal editing of the paper.

REFERENCES

Bulgarian Ministry of Education, (2006). Educational

standards. Compulsory education, Annex 3, 30-32,

http://www.minedu.government.bg (In Bulgarian, ac-

tive in Dec 2014)

Center for Control and Evaluation of the Quality of the

School Education (2013). Study of the students liter-

acy in 6th grade. 43-44 (In Bulgarian, active in March

2014)

Council of Europe (2011) Common European Framework

of Reference for Languages (Language Policy Unit,

Strasbourg, www.coe.int/lang-CEFR) 4-5

Dimitrova, N. (2008). Technological model of project-

based education in physics and astronomy. In: Prof.

Dimitar Pavlov, Raising the Spirit. Paradigma, Soﬁa,

143-151 (in Bulgarian)

European Commission (2004). Framework for key

competences in a knowledge-based society.

http://ec.europa.eu/education/policies/2010/doc/

basicframe.pdf (active in Nov 2013)

Gravemeijer, K. (2014). Competencies in and for 21st Cen-

tury. The Korean Society of Mathematical Education.

Proceedings of the 2014 Int’l Conference on Mathe-

matical Education, Cheongju National University of

Education, October 17-18, 2014

Jagdish, A., Lardner, R. (1989). Mathematical analysis.

Prentice-Hall, New Jersey. 401-404.

Lazarov, B. (2013) Developing Synthetic Competence

along Individual Educational Trajectory. The Korean

Society of Mathematical Education. Proceedings of

the International Conf. on Math. Edu. on Creativity

and Giftedness (Mokwon Univ., Seo-gu, Daejeon, Ko-

rea, August 9-10, 2013) pp 251-262.

Lazarov, B. (2014) Decontextualization. Mathematics and

Education in Mathematics. Proceedings of 43th Con-

ference of the UBM, Borovetz, April 2-6 2014, 67-77.

(in Bulgarian)

Lazarov, B. & Severinova, D. (2014). Incorporating inte-

grated approach in secondary school. MEST Journal,

15 07, 2(2).

Pledger, K. (editor) (2009). 6-8 Level Up Maths. Heine-

mann, Essex, 26-27.

Roorda, G., Vos, P. & Goedhart, M. (2014). An actor-

oriented transfer perspective on high school stu-

dents’ development of the use of procedures to

solve problems on rate of change. International

Journal of Science and Mathematics Education

(doi:10.1007/s10763-013-9501-1)

Savova, B., Todorova, M. & Zlatilov, V. (2010). Math tests

for 7th grade (Testove po matematika za 7. klas).

Prosveta, Soﬁa. (in Bulgarian)

APPENDIX

Control Test Problems

TP1. A student paid 30 levs for two books. If the ﬁrst

book was 25% cheaper and the second one was 50%

more expensive, the two books would be of the same

price. Find the price of each book.

TP2. Find the larger of two positive numbers if their

ratio is 8:5 and their difference equals 27.

TP3. The difference of the areas of two squares is 85

. The side of the ﬁrst square is 5 cm longer than

the side of the second one. Find the perimeter of the

larger square.

TP4. The copper-zinc ratio in an alloy is 1:4 and in

another alloy it is 2:3. How much of each alloy should

be taken to produce 10 kg alloy in which the copper-

zinc ratio equals 3:2?

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

330