Finding Pathways to Student Success from Data

Brendan Mumey

, Sean Yaw

, Christina Fastnow

and David J. Singel

Department of Computer Science, Montana State University, Bozeman, U.S.A.

Ofﬁce of Planning and Budget, Montana State University, Bozeman, U.S.A.

Department of Chemistry and Biochemistry, Montana State University, Bozeman, U.S.A.

Keywords:

Transcript Analysis, Pathways, Prerequisites, Course Ordering, Graduation Rates.

Abstract:

We propose some novel computational approaches to analyzing historical student transcript data to help im-

prove course sequencing and generate default pathways for students to complete a college degree. Addition-

ally, we examine whether there are “hidden prerequisites” to courses and whether there are courses which,

when taken early in a student’s career, may improve their chances of graduation. Our analysis was done on a

dataset consisting of all student-course enrollments for a period of 10 years at Montana State University.

1 INTRODUCTION

In this work, we propose some novel computational

approaches to analyzing historical student transcript

data to help improve course sequencing and generate

default pathways for students to complete a college

degree. Our analyses were done on a dataset consist-

ing of all student-course enrollments for a period of

10 years at Montana State University (MSU). We ﬁrst

introduce the concept of a centroid student for a given

major; these students can provide a prototype for de-

signing a typical course pathway for the major. We

also examined the data set to identify “hidden prereq-

uisites” to courses; these are course pairs (A,B) where

course A is not an ofﬁcial prerequisite but for which

there is statistical evidence that it helps pass course B.

Finally, we also looked at course ordering and grad-

uation using course pair statistical analysis. Our re-

sults indicate that there are courses which, when taken

early in a student’s career, tend to improve the gradu-

ation rate.

2 METHODS

We collected a data set consisting of all student-

course enrollments at MSU from Academic Year

(AY) 2004 through AY 2013. MSU’s AY consists

of two main semesters, Fall and Spring, as well as

a Summer term. We restricted attention to students

that entered their initial semester as ﬁrst-time, full-

time students. Transfer students were also not consid-

ered. There were 437,967 student-course enrollment

records in total. Additionally, the data set included

student declared majors by term as well as gradua-

tions. We used Java to implement all of the analy-

sis procedures described; all analyses could be per-

formed in a several minutes on a fast laptop computer.

3 FINDING TYPICAL STUDENTS

In this section we consider the problem of determin-

ing typical students in particular programs at our uni-

versity. We deﬁne typical as being the most similar to

all of the other students in the program. Our approach

is to ﬁrst deﬁne a similarity score S(i, j) between stu-

dents i and j based on how similar their transcripts

are. This score is based on the courses taken in the

transcript as well as which semester (relative to their

starting year) that they took them in. Let L

be the

list of courses passed by student i and for each course

c ∈ L

, let t(c,i) be the term (relative to the year that

student i ﬁrst enrolled) that i ﬁrst passed c.

To evaluate the similarity between students i and

j, we deﬁne a weighted bipartite graph G = (V, E)

where V = L

∪ L

, E ⊂ L

× L

, and the weight of an

edge (c,c

) ∈ E is deﬁned by

w(c,c

) =

M(c,c

)

κ + |t(c,i) −t(c

, j)|

, (1)

where M is a course similarity matrix and κ is a con-

stant. The course similarity matrix M was deﬁned by

457

Mumey B., Yaw S., Fastnow C. and Singel D..

Finding Pathways to Student Success from Data.

DOI: 10.5220/0005487704570460

In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 457-460

ISBN: 978-989-758-107-6

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: The centroid student computed for the Mechanical Engineering major at Montana State University.

Fall-Y1 Spring-Y1 Fall-Y2 Spring-Y2 Fall-Y3 Spring-Y3 Fall-Y4 Spring-Y4

ANTY-101 CHMY-141 EGEN-201 EELE-250 EGEN-335 EMEC-321 EMEC-405 EGEN-488

CLS-101 EGEN-117 EMAT-251 EGEN-202 EGEN-350 EMEC-326 EMEC-425 EMAT-350

EMEC-100 EGEN-118 EMAT-252 EGEN-205 EMEC-303 EMEC-342 EMEC-445 EMEC-402

M-171 M-172 M-273 ETME-215 EMEC-320 EMEC-360 EMEC-489R EMEC-403

PHSX-103 PHSX-220 ME-102 ETME-217 EMEC-341 EMEC-443 MUSI-203 EMEC-499

WRIT-101 PHSX-222 M-274 FCS-101

Table 2: The centroid student computed for the History of Religious Studies major at Montana State University.

Fall-Y1 Spring-Y1 Fall-Y2 Spring-Y2 Fall-Y3 Spring-Y3 Fall-Y4 Spring-Y4

ACT-151 ARTH-201 ART-310 ART-320 ARTH-426 ARTH-440 ARTH-451 ARTH-492

GRMN-101 EQUH-110 ARTH-200 HIST-489 ARTH-430 HONR-450 HSTA-408 HSTR-480

HIST-104 GRMN-102 HSTR-145 HSTA-311 ARTH-438 NASX-304 RELS-223 PSYX-100

HONR-201 HSTR-130 HSTR-322 HSTR-434 RLST-220 RLST-203 RLST-321 RLST-492

RLST-110 PSCI-230 RLST-202 HSTR-490 RLST-325 RLST-405 UH-400 UH-492

UH-202 RLST-204 RELS-335

RLST-410

the following simple rule: for each pair of courses

(c,c

), we let

M(c,c

) =











1.0 if c and c

: are the same course,

0.7 meet the same core requirement,

0.5 are from the same department,

0.0 otherwise.

For the constant κ, larger values deminish the rela-

tive importance of how close the terms were when the

students took the courses. After some empirical test-

ing, we choose the value κ = 3. While both M and κ

could likely be tweaked and improved, these defaults

seemed to lead to reasonable results.

Next, we deﬁne the similarity score S(i, j) be-

tween students i and j as the weight of a maximum

weight matching M

∗

in G:

S(i, j) = w(M

∗

). (2)

(A matching M is subset of the edges such that no two

edges in M share an endpoint; the weight, w(M), of

M is the sum of the weights of the edges in M.) A

maximum weight matching can be found efﬁciently

using the Hungarian algorithm (Kuhn, 2005).

3.1 Centroid Students

We deﬁne the centroid student c(m) for a particular

major as the student that maximizes the total similar-

ity score to all of other students in the major m. Let

S(m) be the set of students that graduated in major m.

Formally,

c(m) = argmax

i∈S(m)

∑

j∈S(m)

S(i, j) (3)

We can view the centroid student as the most typical

representative of the given major m.

We have computed the centroid students for all

majors at MSU. Table 1 shows the centroid student for

the Mechanical Engineering major at Montana State

University, while Table 2 shows the centroid student

for the History of Religious Studies major. By ex-

amining centroid students, departments can see what

sequencing of courses works for a typical students.

These course sequences provide an excellent starting

point to design pathways that lead to degrees for a

given major. Such pathways indicate both required

courses for the major as well as potential electives

term-by-term. There is evidence (Complete College

America, 2012) that indicates that providing incom-

ing students with pathways improves both retention

and graduation rates.

4 HIDDEN PREREQUISITES

Another type of analysis that can be useful in design-

ing student pathways is to look for so-called hidden

prerequisites among pairs of courses. We deﬁne a hid-

den prerequisite as a pair of courses (A,B) such that

students that have taken and passed course A have a

statistical advantage when it comes to passing course

B subsequently. To measure this advantage we use the

well-known Fisher exact test (Fisher, 1922), which

tests the null hypothesis that A imparts no advantage

(or disadvantage) in the ability to pass B. For a par-

Table 3: The variables a, b, c and d are the number of stu-

dents in the data set that fall in each category.

pass B fail B

with A a b

without A c d

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

458

Table 4: Top 5 hidden prerequisites for Business majors. Note CAPP-120 is computer applications course.

without A with A without A with A

A B fail B pass B fail B pass B p-value B pass rate B pass rate

CAPP-120 MUSI-203 6 78 0 309 8.3E-5 92.9% 100.0%

CAPP-120 BGEN-499 13 164 8 566 1.3E-4 92.7% 98.6%

ACTG-223 BFIN-322 47 379 12 250 1.2E-3 89.0% 95.4%

CAPP-120 STAT-216 50 111 74 308 1.3E-3 68.9% 80.6%

CAPP-120 PHL-110 12 93 4 177 1.4E-3 88.6% 97.8%

ECNS-101 BMGT-240 9 61 14 387 2.4E-3 87.1% 96.5%

M-171Q ECNS-301 42 93 0 17 2.8E-3 68.9% 100.0%

ACTG-327 BFIN-322 58 469 0 51 3.5E-3 89.0% 100.0%

WRIT-201 BGEN-499 22 555 0 165 3.6E-3 96.2% 100.0%

MUSI-211 ECNS-301 41 88 1 20 5.5E-3 68.2% 95.2%

Table 5: Most signiﬁcant course pairs where order matters. Course pairs (A,B) are listed such that is beneﬁcial to take course

A prior to course B.

A B p-value graduation (A < B) graduation (B < A)

PHSX-205 MUSI-203 5.2E-9 95.5% 77.5%

ECNS-101 MUSI-203 1.9E-6 87.0% 71.7%

WRIT-101 PHL-110 5.5E-6 73.1% 62.6%

CHMY-143 BIOM-250 7.1E-6 93.6% 66.7%

PHSX-220 PHL-110 7.7E-6 93.2% 77.2%

CHMY-141 BIOM-250 1.2E-5 88.2% 59.1%

ACTG-201 ACT-104 2.1E-5 94.7% 79.8%

ECNS-101 CHTH-205 2.2E-5 92.4% 58.1%

PHSX-220 ACT-104 3.2E-5 96.8% 71.7%

WRIT-101 ARTH-200 3.2E-5 80.3% 58.0%

ticular pair (A,B), the test is computed using Table 3.

Referring to Table 3, a p-value is computed using the

formula,

p =



a + b



c + d





a + b + c + d

a + c



. (4)

Table 4 shows the course pairs that had most striking

statistical relationships (lowest p-values). We note

that course pairs for which A is already a prerequi-

site do not show up since c and d will both be zero

and so p = 1 in (4).

Departments can use the list of hidden prerequi-

sites to improve course sequencing and potentially

make actual prerequisites. For example, in Table 4,

we see that the CAPP-120 course on computer appli-

cations is helpful for business students to take prior to

several other courses.

5 COURSE PAIR ORDERING

AND GRADUATION

Certain classes may be beneﬁcial to take early in an

undergraduate degree; conversely, other classes may

not be helpful to improving a student’s chances of

graduating. We also examined courses pairs (A,B)

to determine whether taking A before B or B before

A inﬂuenced the ﬁve-year graduation rate. For each

pair of courses in the data set, we computed the ﬁve-

year graduation rates for those students that took and

passed A prior to passing B and the opposite order-

ing. For simplicity and to avoid confounding cases,

we limited consideration to those students that passed

both courses on their ﬁrst attempt. Using a similar

equation to (4), we then computed a p-value to test

the null hypothesis that the ordering of the pair (A, B)

does not affect graduation rates. Table 5 shows the top

10 course pairs where there is signiﬁcant statistical

evidence (low p-value), taking course A before course

B (as opposed to B before A) improves the chance of

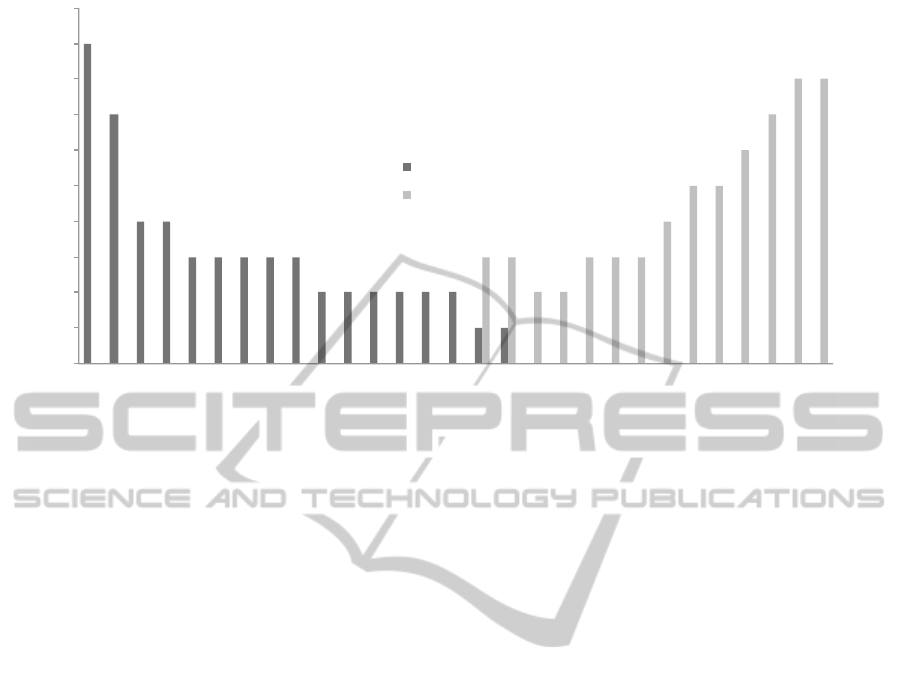
graduation. Figure 1 was generated by looking at all

signiﬁcant pairs down to a p-value of 1.0E-3 (there

were 76 such pairs). For each unique course in this

list, we then counted the number of times it appeared

as an A course (better to take early) and the number of

times it appeared as a B course (better to take later).

If the count difference was at least 2, we plotted the

A and B values in Figure 1. What the data seems to

indicate is that there are some courses, e.g. WRIT-

101, College Writing for which it is beneﬁcial to take

early in ones college career; it improves the chances

of graduation. Several other courses on the left side of

Figure 1 are also fundamental courses in mathemat-

ics and the sciences. Conversely, we see that some

FindingPathwaystoStudentSuccessfromData

459

#!"

,-./0#!#"

123/0$!'"

45670#!#"

20#(#"

897:0$!'"

897:0$$!"

;5/30$!#"

897:0$$$"

20#'#"

592<0#&%"

592<0#&#"

6=/-0$$#"

20#)$"

5>20##!"

592<0#$#"

;7/-0##!"

;5/0#'#"

;-/90$!!"

;-590%$$"

87<:0#!!"

9/90$$!"

89>/0##%"

1.>20$'!"

59/90$!'"

?570#!#"

6;7:0#!'"

89@0##!"

2=7.0$!%"

;5/0#!&"

Number'of'Occurrences'

Course'

1ABAC"ADCEF"G;H"

1ABAC"EDIAC"G1H"

Figure 1: Courses for which the order that students take the courses has an effect on graduation rate. Note that WRIT-101 is

College Writing and ACT-104 is Bowling Fundamentals.

“lighter” courses, e.g. ACT-104 Bowling Fundamen-

tals are better to delay.

6 CONCLUSIONS

In this work, we looked at several types of analy-

ses that can be performed on large historical student

course enrollment data sets. In particular we pro-

posed a method to compute centroid students for ma-

jors; these students provide a template for the course

sequence that a typical student takes on the path to

graduation. We also proposed a method for discover-

ing hidden prerequisite pairs (A,B); these are pairs of

courses where A is not an ofﬁcial prerequisite for B,

but having taken A beforehand improves the chances

of passing B. Finally, we looked at course pair or-

dering and graduation. In particular, we identiﬁed

course pairs (A, B) where there was statistical evi-

dence that taking A before taking B improved grad-

uation rates. Among the statistically signiﬁcant pairs,

certain courses stood out as being either better to take

early on (an A course) or better to take later (a B

course). This type of information is clearly useful for

student advising.

We envision using historical data to build smart

scheduling systems that better advises students. The

analogy is a GPS in your car; “What is the quick-

est and best path (highest likelihood of success) for

me to graduate in major X?” “What if I want to

change my major, how much longer would it take me,

etc.?” While there is some existing work on gener-

ating schedules (Martin, 2004; Hinkin and Thomp-

son, 2002) and using data mining for course schedul-

ing (Smith, 2005; Bala and Ojha, 2012), to date there

are no systems that we are aware of that use large-

scale historical data to help answer the hypothetical

questions posed in an automated way. Thus, intel-

ligent course scheduling based on historical student

success data seems like a ripe opportunity for future

work.

REFERENCES

Bala, M. and Ojha, D. (2012). Study of applications of data

mining techniques in education. International Journal

of Research in Science and Technology, 1:1–10.

Complete College America (2012). Guided pathways to

success. Available at http://completecollege.org.

Fisher, R. A. (1922). On the interpretation of 2 from contin-

gency tables, and the calculation of p. Journal of the

Royal Statistical Society, 85(1):87–94.

Hinkin, T. R. and Thompson, G. M. (2002). Schedulexpert:

Scheduling courses in the Cornell university school of

hotel administration. Interfaces, 32(6):45–57.

Kuhn, H. W. (2005). The Hungarian method for the as-

signment problem. Naval Research Logistics (NRL),

52(1):7–21.

Martin, C. H. (2004). Ohio university’s college of business

uses integer programming to schedule classes. Inter-

faces, 34(6):460–465.

Smith, W. (2005). Applying data mining to scheduling

courses at a university. Communications of the As-

sociation for Information Systems, 16(1):23.

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

460