Shaping the Current Waveform of an Active Filter for Optimized System

Level Harmonic Conditioning

Espen Skjong

1,3

, Marta Molinas

, Tor Arne Johansen

and Rune Volden

Center for Autonomous Marine Operations and Systems, Department of Engineering Cybernetics, Norwegian University

of Science and Technology, Trondheim, Norway

Department of Engineering Cybernetics, Norwegian University of Science and Technology, Trondheim, Norway

Ulstein Power & Control AS, Ulsteinvik, Norway

Keywords:

System Level Harmonic Conditioning, Model Predictive Control, Active Filter (AF), Multiple Shooting,

Non-linear Loads, Total Harmonic Distortion (THD).

Abstract:

Harmonic voltages and currents in electrical systems, when present to a certain degree, represent not only a

power quality problem but they are also strongly associated with the electrical system overall losses and they

are arguably a source of instability and a safety concern. Mitigating harmonics distortion across the entire

system by actively reducing harmonic currents propagation is an effective way of coping with these issues and

can be dealt with the injection of a compensating current waveform with an active ﬁlter installed at a given

bus. This paper shows how, by shaping the compensating current waveform in an optimal way, the overall

electrical system harmonic distortion can be optimally reduced in a cost effective manner with a minimum

size of the compensating device. The process of shaping this optimal compensating current is shown by how

its components are deﬁned by the optimization algorithm using the phase and amplitude of each harmonic as

degrees of freedom in the process of ﬁnding the optimal waveform. A marine vessel distribution grid is used

as representative example to prove the concept.

1 INTRODUCTION

Pure, continuous and constant frequency sinusoidal

waveforms are the ideal waveforms in most electric

power systems. A given deviation from this ideality

is deﬁned as a power quality issue and limits of toler-

ance are adopted by various standards. Harmonic dis-

tortion is one of the possible forms of deviation from

a pure sinusoidal waveform. Harmonic distortion is

a stationary form of distortion caused by the pres-

ence of additional sinusoidal components or harmon-

ics components at multiples of the fundamental fre-

quency component carrying the electrical signal un-

der consideration. Most common sources of these dis-

tortions are non-linear loads such as multi (6, 12, 18,

24)-pulse rectiﬁers, line-commutated converters, high

frequency harmonics from voltage source converters

(VSC) and switch mode power supplies, saturated

transformers and other magnetic components, and

power system background voltage distortions (Akagi

et al., 2007). These non-linear loads will generally

draw a distorted current containing several harmonic

components that are multiples of the fundamental fre-

quency component. With a sinusoidal voltage at the

source, these harmonic currents will not carry active

power to the load but will be circulating as reactive

currents in the distribution system and will represent

extra distribution losses. One way of approaching this

problem is to over-dimension the system to be able

to stand the side effects of these harmonics by de-

sign. For achieving that, generation, distribution sys-

tems and loads will need to be designed over-rated to

cope with vibration (generators, motors, transform-

ers), heating and losses originated by these harmonic

currents circulating in the system (Evans et al., 2007).

This measure however will not alleviate the inher-

ent power quality issues associated with the presence

of harmonics which will be reﬂected at the end-user

side. Stability issues in electrical networks have also

been correlated with the presence of harmonics (Bing

et al., 2007) and reduced stability margins have been

reported in association with that. The requirements

of power quality standards and safety in electrical in-

stallations demand the use of a more active approach

when coping with harmonics. Such approach should

be aimed at actively reducing the impact of harmonics

Skjong E., Molinas M., Johansen T. and Volden R..

Shaping the Current Waveform of an Active Filter for Optimized System Level Harmonic Conditioning.

DOI: 10.5220/0005488800980106

In Proceedings of the 1st International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS-2015), pages 98-106

ISBN: 978-989-758-109-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

on power quality by minimizing the total harmonics

distortion (THD) using passive or active harmonic ﬁl-

tering techniques. Actively ﬁltering or mitigating the

harmonics will have direct implications not only in

the quality of the electricity delivered but also in fuel

savings, revenues for power transactions, investments

in installed capacity of electrical system components,

efﬁcient utilization of existing installations and reduc-

tion of overall system losses.

Mitigation of harmonics in electrical systems with

dispersed generation and loads can be approached by

ﬁnding the optimum shape of the current wave form

that an active ﬁlter should inject in a given bus in or-

der to minimize the propagation of harmonics in the

entire electrical system. This paper, with references to

(Skjong et al., 2015a) and (Skjong et al., 2015b), pro-

poses such an approach based on optimization where

the objective is to search for the optimum shape of the

current waveform to be injected by an active ﬁlter to

minimize the THD of the entire electrical system. To

prove the concept, the optimization algorithm is im-

plemented in the electrical system of a marine vessel

(a discussion of harmonic mitigation using an active

ﬁlter in a marine vessel’s power distribution grid is

given in (Rygg Aardal et al., 2015)). The beneﬁts of

a system level harmonic mitigation approach is com-

pared with the classical approach of local active ﬁl-

tering. The current waveform shaping process and

components resulting from the optimization search

are shown for two different loading examples. The

component waveforms of the compensating current

clearly shows how the optimization algorithm effec-

tively exploits the amplitude and phases of each har-

monic component when searching for the optimum

waveform shape. A major ﬁnding from this research

is the possibility to minimize not only the THD of the

entire system but to achieve that with the minimum

required current rating of the active ﬁlter. This will in

turn have implications in reducing the investment in

the compensating device.

2 POWER DISTRIBUTION GRID

MODEL

Power electronics has become the most essential part

in modern electrical distribution systems as coupling

element between generation, loads and the electri-

cal network as they provide ﬂexibility and fast con-

trol capabilities. Most recently, with the emergence

of the smartgrid, and due to its inherent properties

of fast actuation capabilities and extreme ﬂexibility,

power electronics will be critical in the realization

of smart grid systems and microgrids which require

different voltage levels conversion, frequency conver-

sion capabilities, real-time supply-load match and hy-

brid AC/DC and DC/AC couplings. Representative

examples of these systems are onshore and offshore

wind farms connected to a national power distribution

network where power electronics in the form of Volt-

age Source Converters (VSC), High Voltage Direct

Current (HVDC) systems, Active Filters (AF), Solid

State Transformers (SST), etc., are critical for collect-

ing and distributing the generated power in deﬁned

voltage levels and within quality standards. Stand-

alone electrical grids are another example in which

power electronics play an essential role in enabling

the operation and control of such systems. A stand-

alone microgrid, a wave energy generation plant, an

isolated PV generation system and a marine vessel’s

power distribution grid (Patel, 2011) are typical ex-

amples with multiple and dispersed power genera-

tion units, e.g. diesel engines, gas turbines, fuel cells

and batteries, generating the power needed for dif-

ferent operation scenarios. Despite its enormous ad-

vantages, power electronics introduce new non-linear

properties and due to its switching mode of operation,

it constitutes a source of harmonic distortion in the

systems in which they are operating.

>ŽĂĚϭ



^ϭ

D

>ϭ

D

>Ϯ

,ĂƌŵŽŶŝĐ

&ŝůƚĞƌ

ϭ

^ϭ

ϭ

^ϭ

Ͳǀ

>Dн

>^ϭ



Ϯ

^Ϯ

>^Ϯ

^ŽƵƌĐĞϮ

^ϭ

D

^Ϯ

>ŽĂĚϮ

^ŽƵƌĐĞϭ

DĂŝŶƵƐ

ƵƌƌĞŶƚŵĞĂƐƵƌĞŵĞŶƚƐ

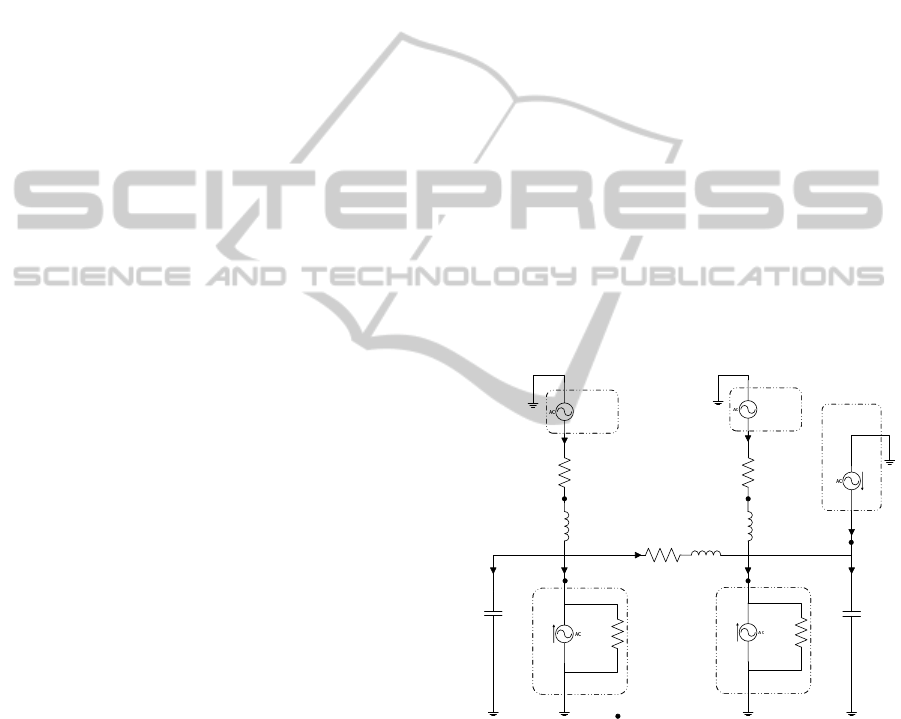
Figure 1: Simpliﬁed model of an AC power distribution

grid.

In this work a simpliﬁed stand-alone power dis-

tribution grid is assumed. The power grid, shown in

ﬁgure 1 with details given in table 1, connects two

power sources to two non-linear loads and can resem-

ble a simpliﬁed marine vessel microgrid. The loads

which can represent the propulsion system are taken

as the sources of harmonic pollution in this study. A

6-pulse diode rectiﬁer is considered to be part of the

drive system and the harmonic pollution is modelled

accordingly. An active harmonic ﬁlter based on a

ShapingtheCurrentWaveformofanActiveFilterforOptimizedSystemLevelHarmonicConditioning

Table 1: Power distribution grid parameters used in case

study.

Parameter

Value

1 mH

(0.1·L

·ω) Ω

(0.1·L

·ω) Ω

(0.1·L

·ω) Ω

0.1 µF

voltage source converter connected to one of the load

buses is considered for injecting a compensating cur-

rent which will be shaped by the optimization algo-

rithm for the purpose of system level harmonic miti-

gation.

2.1 Model Formulation

Considering ﬁgure 1 and using Kirchhoff’s laws a set

of differential equations describing the grid’s physical

behavior can be derived,

= v

−R

−v

= i

−i

= v

−v

−R

= i

+ i

−i

+ i

= v

−R

−v

(1)

The generators are modeled as ideal voltage sources

with a voltage phase shift φ

(t) =

√

rms

sin(ωt + φ

), (2)

while the non-linear loads are modeled as current

sources with harmonic components of order 5,7,11

and 13 with phase shifts φ

L,i

and peak values (am-

plitudes) I

L,i

(t) =

∑

L,i

sin



ωt + φ

L,i



∀i ∈{1, 6k±1|k = 1, 2}.

(3)

The harmonic ﬁlter is designed to suppress harmonic

pollution and can be modeled as a current source with

harmonic components of order 5, 7, 11 and 13,

(t) =

∑

F,i

sin



ωt + φ

F,i



∀i ∈{6k ±1|k = 1, 2},

(4)

where I

F,i

is the peak values (amplitudes) of the ﬁl-

ter’s harmonic current component i. The grid model

stated above is given as a single phase conﬁguration.

A single phase conﬁguration is not a realistic conﬁg-

uration in microgrids, and the equations given above

should be extended to a three-phase conﬁguration.

2.2 Three-phase Three-wire

Conﬁguration

Three-phase conﬁgurations could consist of three or

four wires. The three-phase conﬁguration is modeled

using the Clarke transform (Akagi et al., 2007), which

converts the abc phases to αβ0 phases. Assuming bal-

anced sources the neutral wire (fourth wire) is exces-

sive and the αβ0 frame is simpliﬁed to αβ, where the

β current is lagging the α current by 90

◦

. Hence, in

this work a three-phase three-wire conﬁguration is as-

sumed.

The three-phase three-wire αβ form is derived by

extending the single-phase model to three-phase abc

form. The abc form is then transformed to αβ us-

ing the Clarke transformation. As an example, the

three-phase three-wire model for the voltage sources,

assuming balanced sources, can be written in the αβ

frame as

(t) =



S,α

(t)

S,β

(t)



 √

rms

sin(ωt + φ

)

√

rms

sin(ωt + φ

)



. (5)

In the same way the load and ﬁlter models are ex-

tended to three-phase three-wire using the αβ frame,

however, the phase shifts φ

L,i

and φ

F,i

for the ﬁlter

model and the load models should be equal for the α

and β phases due to the deﬁnition of the β phase lag-

ging the α phase by 90

◦

. Also the ﬁlter amplitudes in

the αβ frame are kept equal for each harmonic com-

ponent when considering balanced loads to ensure a

balanced ﬁlter.

In the rest of this paper subscript α and β are used

to denote the α and β phases for each voltage and

current component, and the vectors (phasors) v and

i are used to represents voltages and currents, respec-

tively, given in the αβ frame. It is referred to (Ak-

agi et al., 2007) for details regarding the αβ frame in

three-phase three-wire conﬁgurations.

2.3 Active Filter (AF) Constraints

The harmonic ﬁlter model is constrained due to phys-

ical limitations of an active ﬁlter. The active ﬁlter’s

switching circuit (IGBTs) in conjunction with the rat-

ing of the voltage controlled capacitor, decides the ac-

tive ﬁlter’s power rating. The IGBT will be the crucial

component deciding the ﬁlter’s current rating, formu-

lated as current limits in the abc phases. Figure 2 il-

lustrates the active ﬁlter’s current limits in both the

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

100

lim

min

max

min

max

min

max

Current phasor

limitations

Phase current

limitations

◦

120

◦

Figure 2: Harmonic ﬁlter constraints: Three-phase three-

wire represented by the αβ and abc frames (Suul, 2012).

abc and the αβ frames. In the abc frame the phases

are restricted by

min

≤ i

≤i

max

, ∀j ∈ {a, b, c}, (6)

which forms the hexagon given in ﬁgure 2. These

restrictions can be expressed in the αβ frame by

−i

lim

≤ −i

F,β

√

F,α

≤i

lim

(7a)

−i

lim

≤ i

F,β

√

F,α

≤i

lim

(7b)

−i

≤ i

F,α

≤i

(7c)

−i

lim

≤ i

F,β

≤ i

lim

, (7d)

where the hexagon’s apothem is given by

√

lim

(8)

and i

lim

is a design variable representing the ﬁlter’s

phase current limitations. Eq. (7) gives a set of lin-

ear constraints which will be used in an optimization

scheme to conduct as much harmonic conditioning as

possible for the given power rating. For notational

simplicity we deﬁne the feasible region for the ﬁlter’s

current vector i

∈ S.

3 MODEL PREDICTIVE

CONTROL

Using the power grid model derived in the previ-

ous section an optimization procedure is developed

to minimize, by control, the total harmonic currents

in the power grid, and prevent harmonic distortions

from propagating from the loads to the sources. The

optimization procedure is stated as a non-linear model

predictive control (NMPC) (Rawlings and Mayne,

2009).

3.1 Formulating the Power Grid Model

in Standard NMPC Form

A NMPC problem for the ﬁlter current reference gen-

eration in standard form can be stated as

min

p,u

V(x, z, u, p) =

∑

n=1

l(x

, z

, u

n−1

, p)

s.t.

= f(x

, z

, u

n−1

, p) ∀n ∈ {1, . . . , N}

g(x

, z

, u

n−1

, p) = 0, ∀ n ∈ {1, . . . , N}

h(x

, z

, u

n−1

, p) ≤ 0|i

F,n

∈ S, ∀n ∈ {1, . . . , N}

given initial values x

, z

|initial value i

F,0

∈ S,

(9)

where the objective function V(·) and the stage cost

function l(·) deﬁnes the goal of the optimization. In-

dex n is the time step in the control horizon. The vec-

tors x, z, u and p deﬁnes the dynamic states, the al-

gebraic states, the controls and the parameters of the

problem formulation, respectively. g(·) represents the

problem’s equality constraints while h(·) represents

the inequality constraints. Assuming that higher or-

der harmonics (5th, 7th, 11th and 13th) generated by

a 6-pulse diode rectiﬁer are known and given by



∑

L,α,i

sin



ωt +φ

L,i



∑

L,β,i

sin



ωt + φ

L,i





∀i ∈ {6k±1|k = 1, 2},

(10)

the algebraic state vector can be stated as

z =

⊤

, v

⊤

, i

⊤

, i

⊤

, i

⊤

, (i

)

⊤

, (i

)

⊤

(11)

where the loads i

and i

are the three-phase three-

wire extension of eq. (3) given in the αβ frame, the

ﬁlter currenti

is the three-phase three-wire extension

of eq. (4) given in the αβ frame, and the harmonic

components of each load, i

and i

, are given by eq.

(10). The dynamic state vector is given by the power

grid model’s differential states,

x =

⊤

, i

⊤

, i

⊤

, v

⊤

, v

⊤

(12)

The control vector, often referred to as manipulated

variables, consists of the active ﬁlter’s amplitude and

phase components,

u =



F,α,i

, I

F,β,i

, φ

F,i



⊤

, ∀i ∈{6k ±1|k = 1, 2}

(13)

and the parameter vector is given by p = 0. The

stage cost function, which should be a convex func-

tion, addresses the goal of the optimization, which in

ShapingtheCurrentWaveformofanActiveFilterforOptimizedSystemLevelHarmonicConditioning

101

this work is to minimize the harmonic pollution in the

power grid. A suitable stage cost function is given as

l(x, z, u, p) = q



F,α

−i

L1,α



+ q



F,β

−i

L1,β



+ q



F,α

−i

L2,α



+ q



F,β

−i

L2,β



+ q



⊤



(14)

with constant weights q

, q

, where u

⊂ u that

includes the ﬁlter’s amplitudes. The last part in eq.

(14) is added to minimize the ﬁlter amplitudes, hence

minimizing the ﬁlter’s power rating, and also provid-

ing stability and robustness with regards to modeling

errors. q

< q

, q

as minimizing the power rating

is of lesser importance than decreasing the harmonic

distortion in the power grid.

4 RESULTS

The main objectiveof this work is to use the NMPC to

generate optimized active ﬁlter current references by

considering the harmonic pollution from both loads

and utilizing ﬁlter current amplitudes and phases as

control variables. Two case studies are proposed, one

with symmetric and one with asymmetric loads. In

both cases the loads introduce a high level of har-

monic pollution in form of the 5th, 7th, 11th and 13th

harmonic components, and the active ﬁlter currents

are limited to i

lim

= 0.5 [pu] (i

√

[pu]). The

load currents for both study cases are presented in ta-

ble 2. A local ﬁlter reference generation (local ﬁlter-

ing) considering only load 2 is implemented for com-

parison purposes. It is important to remark that the

local ﬁltering does not consider the ﬁlter’s physical

limits and generates ﬁlter currents exactly mimicking

the harmonic currents from load 2 with a phase shift

of 180

◦

. The fundamental frequencyis ﬁxed to f = 50

[Hz] in both study cases.

4.1 Symmetric Loads

Figure 3 and 4 represents the simulation results for

case 1 in table 2. The upper plot in ﬁgure 3(a) repre-

sents the NMPC ﬁlter current and local ﬁltering cur-

rent in the a phase. The local ﬁltering current is the

saturated load 2 harmonics phase shifted 180

◦

. By

comparing the two ﬁlter currents one clearly see that

the NMPC ﬁlter current has different amplitudes from

the local ﬁltering current, and at approximated time

instances 0.0025 and 0.0175 [s], among others, the

NMPC ﬁlter current’s phases (one phase for each har-

monic component)have been altered, which is seen as

a deviation from the local ﬁlter current’s visual repre-

sentation.

The four lower plots in ﬁgure 3(a) represent the

load voltages (a phase) and respective frequency

spectra’s with calculated THD values. Due to numer-

ical errors related to discretization, the THD values

are calculated based on a frequency spectrum in a

range of 0-650 [Hz]. With either ﬁltering technique

the THD of load 2 voltage is lower than load 1. This

is as expected since the active ﬁlter is installed near

load 2. Hence the load 1 voltage will in either case

be more distorted than the load 2 voltage due to the

inductance in the main bus preventing the ﬁlter to per-

fectly compensate for all the harmonics generated by

load 1 and 2. As can be seen, the THD values from

local ﬁltering is higher compared to the NMPC case.

First of all, the local ﬁltering does not take into con-

sideration the ﬁlter’s limitation and load 1 harmonics,

and the compensating ﬁlter current using this ﬁltering

technique would be the 180

◦

phase shifted load 2 har-

monics. However, the ﬁlter is too small to cope with

the distorted grid, which means the ﬁlter will saturate

the calculated ﬁlter current references from local ﬁl-

tering resulting in a THD value for load 1 almost as

high as without ﬁltering (19.5%). The NMPC, how-

ever, takes into account both loads and also the ﬁlter

limits in the calculation of optimal ﬁlter current refer-

ences. This way the ﬁlter current references will not

be saturated due to exceeding the active ﬁlter’s phys-

ical limits.

Figure 3(b) represents the ﬁlter current (phase a)

frequency spectra for both NMPC and local ﬁlter-

ing. As can be seen, the amplitudes for the domi-

nant frequency components are generally lower for

the NMPC ﬁlter current than for the local ﬁltering cur-

rent. The ﬁlter current were modeled by the 5th, 7th,

11th and 13th harmonic component, which represents

frequencies of 250, 350, 550 and 650 [Hz]. As evi-

dent from the plot, other frequency components are

utilized by the NMPC due to the ability to rapidly

manipulate the harmonic components’ phases. Due

to the saturation of the local ﬁltering current other

harmonic components than those modeled are also

present in the frequency spectra.

Figure 4 represents the 5th, 7th, 11th and 13th har-

monic components of the NMPC ﬁlter current and lo-

cal ﬁltering current in the a phase. From this rep-

resentation it is easy to show that the NMPC does

utilize both, the amplitudes and the phases of each

modeled harmonic component in the ﬁlter reference

current. The load 2 current, which also represents

the unsaturated reference current from local ﬁltering,

and the NMPC do share the same fundamental fre-

quency, but due to the utilization of the harmonic

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

102

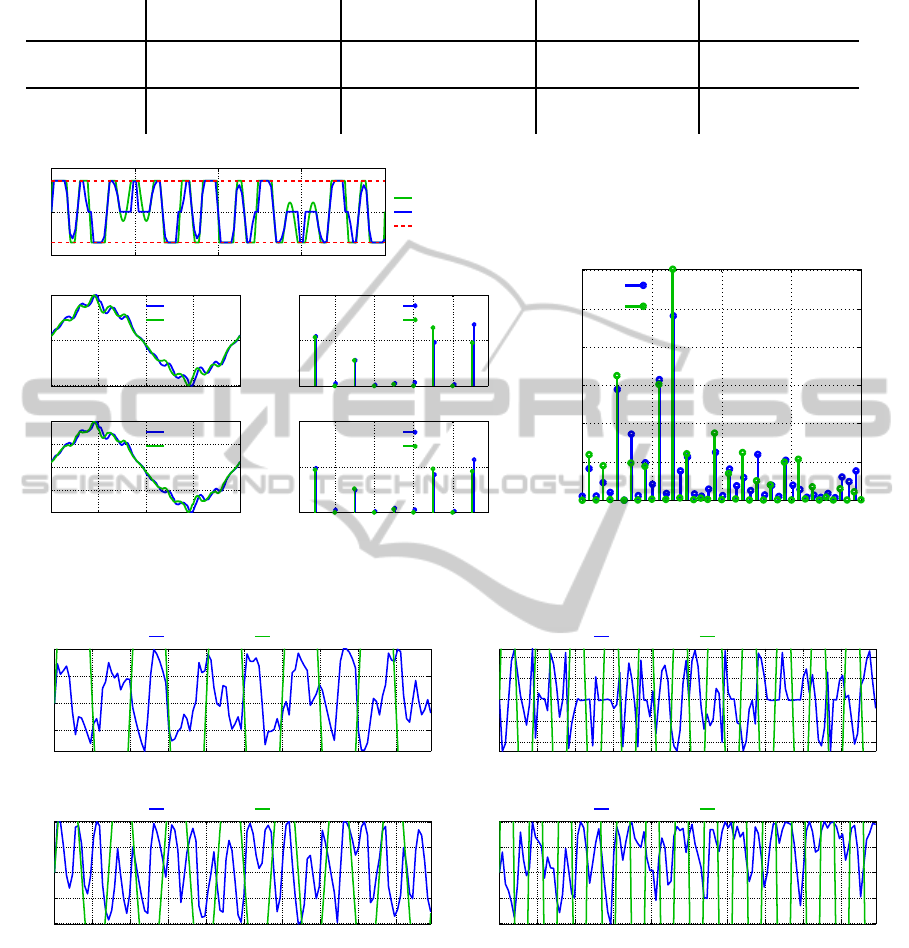
Table 2: Study case conﬁgurations.

Load 1 amplitudes Load 2 amplitudes Load 1 phases Load 2 phases

[1th, 5th, 7th, 11th, 13th] [1th, 5th, 7th, 11th, 13th] [1th, 5th, 7th, 11th, 13th] [1th, 5th, 7th,11th, 13th]

Case 1 I

= I

= [0, 0, 0, 0, 0] φ

= [0, 0, 0, 0, 0]

(symmetric)

= [0.9, 0.6, 0.3, 0.5, 0.8] = [0.9, 0.6, 0.3, 0.5, 0.8]

Case 2 I

= I

= [0, 0, 0, 0, 0] φ

= [0, 0, 0, 0, 0]

(asymmetric)

= [0.9, 0.8, 0.6, 0, 0.5] = [0.9, 0, 0.6, 0.8, 0]

0 0.005 0.01 0.015 0.02

−0.5

0.5

Time [s]

[pu]

Local filtering

NMPC

Filter limits

0 0.005 0.01 0.015 0.02

−1

Time [s]

[pu]

NMPC

Local filtering

300 400 500 600

0.05

0.1

Frequency [Hz]

THD:15.7%

THD:18.2%

0 0.005 0.01 0.015 0.02

−0.5

0.5

Time [s]

[pu]

NMPC

Local filtering

300 400 500 600

0.05

0.1

Frequency [Hz]

THD:14.4%

THD:15.6%

(a) Filter currents and load voltages.

0 500 1000 1500 2000

0.05

0.1

0.15

0.2

0.25

0.3

Frequency [Hz]

NMPC filter current

Local filtering filter current

(b) Filter current spectrum.

Figure 3: Case 1 (symmetric loads): Filter currents and ﬁltered load voltages.

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.1

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

(a) 5th and 7th ﬁlter current component.

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.1

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.1

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

(b) 11th and 13th ﬁlter current component.

Figure 4: Case 1 (symmetric loads): Filter current components.

phases the NMPC ﬁlter current components are com-

pletely changed and it is not easy to determine neither

frequency nor period from the plots. One important

ﬁnding is the total magnitude of each harmonic ﬁl-

ter current component. As can be seen, the ﬁlter cur-

rent components, in this case, do not increase beyond

0.12 [pu]. Compared to the local ﬁltering, utilization

of ﬁlter current phases would be an important degree

of freedom when coping with high harmonic pollu-

tions using a relative small active ﬁlter. Active ﬁlters

are generally quite expensive, thus increasing the ﬁl-

ter size could be a costly affair.

4.2 Asymmetric Loads

Figure 5 and 6 represents the simulation results for

case 2 in table 2. The upper plot in ﬁgure 5(a), as

in the previous case, represents the NMPC ﬁlter cur-

ShapingtheCurrentWaveformofanActiveFilterforOptimizedSystemLevelHarmonicConditioning

103

0 0.005 0.01 0.015 0.02

−0.5

0.5

Time [s]

[pu]

Local filtering

NMPC

Filter limits

0 0.005 0.01 0.015 0.02

−0.5

0.5

Time [s]

[pu]

NMPC

Local filtering

300 400 500 600

0.05

0.1

Frequency [Hz]

THD:14.6%

THD:18.6%

0 0.005 0.01 0.015 0.02

−0.5

0.5

Time [s]

[pu]

NMPC

Local filtering

300 400 500 600

0.05

0.1

Frequency [Hz]

THD:12.6%

THD:14.1%

(a) Filter currents and load voltages.

0 500 1000 1500 2000

0.05

0.1

0.15

0.2

0.25

0.3

Frequency [Hz]

NMPC filter current

Local filtering filter current

(b) Filter current spectrum.

Figure 5: Case 2 (asymmetric loads): Filter currents and ﬁltered load voltages.

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.1

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

(a) 5th and 7th ﬁlter current component.

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.4

−0.2

0.2

0.4

Time [s]

[pu]

NMPC filter current

Load 2 current

0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016 0.018

−0.1

−0.05

0.05

0.1

Time [s]

[pu]

NMPC filter current

Load 2 current

(b) 11th and 13th ﬁlter current component.

Figure 6: Case 2 (asymmetric loads): Filter current components.

rent and the local ﬁngering current in the a phase.

In this case the NMPC ﬁlter current is more phase

shifted, compared to the local ﬁltering current, than

in the synchronous loads case. This is a direct con-

sequence of the optimization trying to condition both

load currents. The phase shifting, compared to local

ﬁltering, is illustrated at, among others, approximated

time instances 0.002 and 0.008 [s].

The four lower plots in ﬁgure 5(a) shows that the

differences in THD for NMPC and local ﬁltering are

higher in the asymmetric case than in the symmet-

ric case. This is due to the NMPC’s consideration of

all loads, whereas local ﬁltering does only consider

load 2. Also, the ﬁlter limits saturate the local ﬁlter

currents, as pointed out in the previous case, prevent-

ing the ﬁlter from conducting the intended ﬁltration.

Compared with no ﬁltering for v

(21.1%) the lo-

cal ﬁltering approach performs poorly. The NMPC

avoids ﬁlter current saturation by considering the ﬁl-

ter limits and by utilizing the ﬁlter current amplitudes

and phases to make the best possible harmonic condi-

tioning out of the ﬁlter.

Figure 5(b) showcases the ﬁlter current (phase a)

frequency spectra for both NMPC and local ﬁltering.

The discussion and analysis from the symmetric case

is also applicable for the asymmetric case. In general,

dominant current amplitudes are smaller in the case of

NMPC than for local ﬁltering. However, the NMPC

utilizes the ﬁlter current phases to utilize un-modeled

frequency components with its cause of lowering the

ﬁlter current amplitude. This is seen in the ﬁgure

where amplitudes of the frequency components, apart

from the 5th, 7th, 11th and 13th, are generally higher

for the NMPC case than for local ﬁltering. Due to the

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

104

conﬁguration of the asymmetric loads, which for the

loads combined includes all modeled frequency com-

ponents, the NMPC will represent harmonic compo-

nents present in both loads. This can be seen in the

5th component (250 [Hz]), whereas the NMPC has

a non-zero amplitude compared with the local ﬁlter-

ing’s zero amplitude.

The 5th, 7th, 11th and 13th harmonic components

of the NMPC’s ﬁlter current in phase a are showcased

in ﬁgure 6 compared with the load 2 current in the

same phase. As can be seen from the conﬁguration in

table 2 and from the ﬁgure, the 5th and 13th harmonic

component in load 2 are zero. However, due to asym-

metric loads all NMPC ﬁlter current components are

utilized. This is due to the fact that load 1 and 2 com-

bined represents all modeled harmonics polluting the

grid. As with the symmetric case, the NMPC ﬁlter

current components are non-periodic due to the rapid

utilization of the ﬁlter amplitudes and phases for each

harmonic component. As a result of rapidly altering

the phases and amplitudes for each harmonic compo-

nent, the amplitudes can be kept small, which is illus-

trated in ﬁgure 6 where none of the ﬁlter components

reach a higher amplitude than 0.1 [pu]. As a result of

the utilization of amplitudes and phases for each mod-

eled harmonic component, the NMPC could also pre-

vent un-modeled harmonics from polluting the grid.

This is a useful property specially when simple grid

models are available for a real-time implementation

of the optimization scheme.

5 CONCLUSIONS

A non-linear model predictive controller (NMPC) ap-

plied to system level harmonic conditioning in a gen-

eralized power grid has been outlined and discussed

in detail. Two different study cases were presented.

A local ﬁltering procedure was introduced to compare

with the NMPC ﬁlter reference current generation ap-

proach and to highlight the beneﬁts of system level

harmonics mitigation.

The NMPC was able to achieve better harmonic

conditioning than the local ﬁltering due to the consid-

eration of both loads and the active ﬁlter’s physical

limits. The NMPC’s ability to rapidly alter the am-

plitudes and phases of each modeled harmonic com-

ponents in the ﬁlter current gave ﬂexibility in terms

of un-modeled harmonic components present in the

loads, the ability to optimize the harmonic mitiga-

tion with limited ﬁlter’s size and distortions from both

loads. The NMPC’s ability to alter the phases and

amplitudes of each harmonic ﬁlter current component

is important when un-modeled harmonic frequency

components are present in the loads, and a simple

power grid model could be enough to obtain a real-

time implementation of the NMPC. Compared with

the local ﬁltering, the NMPC was not affected by sat-

uration of the ﬁlter current references. The saturation

of the local ﬁltering resulted in higher THDs. With

the system level harmonics mitigation approach, the

NMPC was able to optimize the active ﬁlter current

to achieve the best possible harmonic conditioning for

both load currents with a given ﬁlter’s physical limi-

tations.

ACKNOWLEDGEMENT

This work has been carried out at the Centre for Au-

tonomous Marine Operations and Systems (AMOS),

supported by Ulstein Power & Control AS and

The Norwegian Research Council, project number

241205.

REFERENCES

Akagi, H., Watanabe, E., and Aredes, M. (2007). Instanta-

neous Power Theory and Applications to Power Con-

ditioning. IEEE Press Series on Power Engineering.

Wiley.

Bing, Z., Karimi, K., and Sun, J. (2007). Input impedance

modeling and analysis of line-commutated rectiﬁers.

In IEEE Power Electronics Specialists Conference,

2007. PESC 2007, pages 1981–1987.

Evans, I., Hoevenaars, A., and Eng, P. (2007). Meeting har-

monic limits on marine vessels. In Electric Ship Tech-

nologies Symposium, 2007. ESTS ’07. IEEE, pages

115–121.

Patel, M. (2011). Shipboard Electrical Power Systems.

Shipboard Electrical Power Systems. Taylor & Fran-

cis.

Rawlings, J. and Mayne, D. (2009). Model Predictive Con-

trol: Theory and Design. Nob Hill Pub.

Rygg Aardal, A., Skjong, E., and Molinas, M. (2015). Han-

dling system harmonic propagation in a diesel-electric

ship with an active ﬁlter. In ESARS 2015 Confer-

ence on Electrical Systems for Aircraft, Raukway, Ship

Propulsion and Road Vehicles.

Skjong, E., Molinas, M., and Johansen, T. A. (2015a). Op-

timized current reference generation for system-level

harmonic mitigation in a diesel-electric ship using

non-linear model predictive control. In IEEE 2015

International Conference on Industrial Technology,

ICIT.

Skjong, E., Ochoa-Gimenez, M., Molinas, M., and Jo-

hansen, T. A. (2015b). Management of harmonic

propagation in a marine vessel by use of optimiza-

tion. In IEEE Transportation Electriﬁcation Confer-

ence and Expo 2015 (ITEC).

ShapingtheCurrentWaveformofanActiveFilterforOptimizedSystemLevelHarmonicConditioning

105

Suul, J. A. (2012). Control of Grid Integrated Volt-

age Source Converters under Unbalanced Conditions.

PhD thesis, Norwegian University of Science and

Technology, Department of Electrical Power Engi-

neering.

VEHITS2015-InternationalConferenceonVehicleTechnologyandIntelligentTransportSystems

106