
Educational Microsoft Excel Add-ins
Solving Multicriteria Decision Making Problems
Radomir Perzina and Jaroslav Ramik
Silesian University in Opava, School of Business Administration in Karvina,
University sq. 1934/3, Karvina, Czech Republic
Keywords: Analytic Hierarchy Process, Analytic Network Process, Multi-Criteria Decision Making, Pair-wise
Comparisons, Feedback, Fuzzy, Education.
Abstract: There exists wide range of software products to support decision making. Main disadvantage of those
software products is that they are commercial and relatively expensive and thus it prevents them to be used
by students or researchers. Also they are not suitable from pedagogical point of view. This paper introduces
two Microsoft Excel add-ins DAME and FVK that were developed for students to help them understand
basic principles of Multicriteria Decision Making. They don’t behave as a black box but display all results
of all intermediate calculations which are very important for educational purposes. The proposed software
packages are demonstrated on couple of illustrating examples of real life decision problems.
1 INTRODUCTION
Decision making in situations with multiple variants
is an important area of research in decision theory
and has been widely studied e.g. in (Fishburn, 1971),
(Gass, 2004), (Ramik, 2006), (Ramik, 2014), (Saaty,
1978), (Saaty, 1991), (Saaty, 2001). When teaching
decision making theory it is essential to support it
with appropriate computer program that
demonstrates its basic principles. There exists wide
range of computer programs that are able to help
decision makers to make good decisions, e.g. Expert
Choice (http://www.expertchoice.com), Decisions
Lens (http://www.decisionlens.com), Mind Decider
(http://www.minddecider.com), MakeItRational
(http://makeitrational.com) or Super Decisions
(http://www.superdecisions.com). Main
disadvantage of those programs is that they are
commercial and relatively quite expensive and thus
it prevents them to be used by students, researchers
or small companies. Also they are not suitable from
pedagogical point of view because they generally
displays just final results not the intermediate ones
which are essential to help students to understand
decision making theory.
Here we introduce two Microsoft Excel add-in
named DAME – Decision Analysis Module for
Excel and FVK which were mainly designed to
support the learning of the decision making theory.
Comparing to other software products for solving
multicriteria decision problems, DAME is free, able
to work with scenarios or multiple decision makers,
allows for easy manipulation with data and utilizes
capabilities of widespread spreadsheet Microsoft
Excel. Users can structure their decision models into
three levels – scenarios/users, criteria and variants.
Standard pair-wise comparisons are used for
evaluating both criteria and variants. For each pair-
wise comparison matrix there is calculated an
inconsistency index. There are provided three
different methods for the evaluation of the weights
of criteria, the variants as well as the scenarios/users
- Saaty's Method (Saaty, 1991), Geometric Mean
Method (Aguaron, 2003) and Fuller's Triangle
Method (Fishburn, 1971). Multiplicative and
additive syntheses are supported. FVK incorporates
possibility for expressing uncertainty by fuzzy
numbers and also takes into account
interdependences between criteria.
2 DAME
DAME works with all current versions of Microsoft
Excel from version 97. It consists of four individual
files:
DAME.xla – main module with user
510
Perzina R. and Ramik J..
Educational Microsoft Excel Add-ins - Solving Multicriteria Decision Making Problems.
DOI: 10.5220/0005494005100515
In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 510-515
ISBN: 978-989-758-107-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

interface, it is written in VBA (Visual Basic
for Applications),
DAME.dll – it contains special functions
used by the application, it is written in C#,
DAME.xll – it contains library for linking
C# modules with Excel called Excel-DNA
(http://exceldna.codeplex.com),
DAME.dna – configuration file.
All four files must be placed in the same folder
and macros must be permitted before running the
module (see Microsoft Excel documentation for
details). DAME itself can be executed by double
clicking on the file DAME.xla. After executing the
add-in there will appear a new menu item “DAME”
in the Add-ins ribbon (in older Excel versions the
menu item “DAME” will appear in the top level
menu). A new decision problem can be generated by
clicking on “New problem” item in the main DAME
menu, see figure 1.
Figure 1: New problem menu.
Then there will be shown a form with main problem
characteristics, see figure 2.
Figure 2: New problem characteristics.
In the top panel there are basic settings: number
of scenarios, criteria and variants. In case a user
doesn’t want to use scenarios or there is just a single
decision maker, the number of scenarios should be
set to one. In the second panel we can set how we
want to compare scenarios/users and criteria either
using pairwise comparison matrix or set weights
directly. Here we can also choose multiplicative or
additive synthesis model. In the last panel users can
chose how they want to evaluate variants according
to individual criteria. There are three options:
Pairwise – each pair of variants is compared
individually, Values max – indicates maximization
criterion where each variant is evaluated by single
value, e.g. price and Values min – indicates
minimization criterion where each variant is
evaluated by single value, e.g. costs. When user
confirms his options a new Excel sheet with forms is
created, where user can set names of all elements
and evaluate criteria and variants using pairwise
comparison matrices as shown on figure 3.
Figure 3: Pairwise comparison matrix.
In the pairwise comparison matrix users enter values
only in the upper triangle. The values in the lower
triangle are reciprocal and automatically calculated.
If criterion (variant) in the row is more important
than the criterion (variant) in the column user enters
values from 2 to 9 (the higher the value is the more
important is the criterion in the row). If criterion
(variant) in the row is less important than the
criterion (variant) in the column user enters values
from 1/2 to 1/9 (the less the value is the less
important is the criterion in the row). If criterion
(variant) in the row is equally important to the
criterion (variant) in the column user enters value 1
or leaves it empty. In the top right corner there is
calculated inconsistency index which should be less
than 0.1, if it is greater we should revise our
pairwise comparisons, so that they are more
consistent. In the very right column there are
calculated weights of individual criteria (variants)
based on the values in the pairwise comparison
matrix and selected evaluation method. The weights
w
k
based on geometric mean method are calculated
using the equation (1).
EducationalMicrosoftExcelAdd-ins-SolvingMulticriteriaDecisionMakingProblems
511

n
i
n
n
j
ij
n
n
j
kj
k
a
a
w
1
/1
1
/1
1
,
nk ,,2,1
(1)
where w
k
is weight of k-th criterion (variant), a
ij
are
values in the pairwise comparison matrix, and n is
number of criteria (variants).
The inconsistency index is calculated using the
formula (2).
ji
i
j
ij
w
w
a
nn
GCI
2
log
21
2
(2)
When we are entering values in individual pairwise
comparison matrices all weights are being instantly
recalculated, so we can see immediate impact of our
each individual entry. Matrix and graph with total
evaluation of variants is then shown at the bottom of
the sheet. The resulting vector of weights of the
variants
Z is given by the formula (3).
2132
WWZ
,
(3)
where
W
21
is the n1 matrix (weighing vector of the
criteria), i.e.
)(
)(
1
21
n
Cw
Cw
W
,
(4)
and
W
32
is the mn matrix:
),(),(
),(),(
1
111
32
mnm
n
VCwVCw
VCwVCw
W
,
(5)
where w(C
i
) is weight of the criterion C
i
, w(V
r
,C
i
) is
weight of variant V
r
subject to the criterion C
i
.
3 CASE STUDY – DAME
Here we demonstrate the proposed add-in DAME on
a decision making situation buying an “optimal”
refrigerator with 3 decision criteria and 3 variants.
The goal of this realistic decision situation is to find
the best variant from 3 pre-selected ones according
to 3 criteria: price (minimization criterion),
efficiency (pairwise) and design (pairwise). At this
stage we have just single decision maker, so the
parameter “Number of scenarios” is set to one.
Setting of parameters can be seen on the figure 4.
Figure 4: Case study – setting of parameters.
When we submit the form a new sheet is generated.
First we set names of criteria and variants, for
simplicity we use default names for variants (Var 1,
Var 2 and Var 3), see figure 5.
Figure 5: Case study – names of criteria and variants.
Next step is comparison of individual criteria using
pairwise comparison matrix with elements saying
how much more important is criterion in the row
than the criterion in the column, see figure 6.
Figure 6: Case study – criteria comparison.
We can see that inconsistency index is less than 0.1
therefore we can say that our pairwise comparisons
are consistent. In the very right column we can see
calculated weights of individual criteria.
Final step is evaluation of variants according to
individual criteria. Variants according the first
criterion (price) will be evaluated by actual price and
variants according the other two criteria (efficiency
and design) will be evaluated using pairwise
CSEDU2015-7thInternationalConferenceonComputerSupportedEducation
512

comparisons), see figure 7.
Figure 7: Case study – evaluation of variants.
As we can see both pairwise comparison matrices
are consistent, because their inconsistency indexes
are less than 0.1. In the top right matrix we can see
calculated weights of all variants (rows) according to
individual criteria (columns). At this stage synthesis
is calculated and we can see total evaluation of
variants in the last table on figure 8 and graphical
representation on figure 9. We can say that the best
variant is Var 3 with weight 0.40 followed by Var 1
with weight 0.34 and the last one is Var 2 with
weight 0.25.
Figure 8: Case study – total evaluation of variants.
Figure 9: Case study – total evaluation of variants - graph.
4 FVK
When applying Analytic Hierarchy Process (AHP)
in decision making one usually meets two
difficulties: when evaluating pair-wise comparisons
on the nine point scale we do not incorporate
uncertainty or when decision criteria are not
independent as they should be. In this paper these
difficulties are solved by a proposal of the new
method which incorporates uncertainty using pair-
wise comparisons by triangular fuzzy numbers, and
takes into account interdependences between
criteria.
The first difficulty is solved by fuzzy
evaluations: instead of saying e.g. “with respect to
criterion C element A is 2 times more preferable to
element B” we say “element A is possibly 2 times
more preferable to element B”, where “possibly 2” is
expressed by a triangular fuzzy number. In some real
decision situations, dependency of the decision
criteria occur quite frequently, e.g. the criterion price
is naturally influenced by the quality criterion. Here,
the dependency is modeled by a feedback matrix,
which expresses the grades of influence of the
individual criteria on the other criteria.
The interface between hierarchies, multiple
objectives and fuzzy sets have been investigated by
the author of AHP T.L. Saaty (Saaty, 1978). Later
on, (Laarhoven, 1983) extended AHP to fuzzy
pairwise comparisons. Saaty extended AHP to a
more general process with feedback called Analytic
Network Process (ANP) (Saaty, 1991), (Saaty,
2001). In this paper we extend the approaches from
(Buckley, 1985), (Chen, 1992), (Saaty, 2001) to the
case of feedbacks between the decision criteria as it
was specified in (Ramik, 2006) and (Perzina, 2008),
moreover we also supply an illustrating realistic
example to demonstrate the proposed method,
documented by the outputs from Microsoft Excel
add-in FVK that was developed for students to help
them understand and solve the proposed model.
FVK works with all current versions of
Microsoft Excel from version 97. It consists of two
individual files which must be place in the same
folder:
FVK.xla – main module with user
interface, it is written in VBA (Visual
Basic for Applications),
xlwVisio.xll – it contains special functions
used by the application which are linked
with Excel by module called XLW
(http://xlw.sourceforge.net).
FVK itself can be executed by double clicking
on the file FVK.xla. After executing the add-in there
will appear a new menu item “FVK” in the Add-ins
ribbon (in older Excel versions the menu item
“FVK” will appear in the top level menu). A new
decision problem can be generated by clicking on
“New problem” item in the main FVK menu. Then
there will be shown a form with main problem
characteristics, see figure 10.
EducationalMicrosoftExcelAdd-ins-SolvingMulticriteriaDecisionMakingProblems
513

Figure 10: New problem characteristics.
In the top part there are basic settings: Number of
criteria and variants. In the second part we can set
how we want to compare criteria either using
pairwise comparison matrix or set weights directly.
In the next part users can chose how they want to
evaluate variants according to individual criteria.
There are three options: Pairwise – each pair of
variants is compared individually, Values max –
indicates maximization criterion where each variant
is evaluated by single value, e.g. price and Values
min – indicates minimization criterion where each
variant is evaluated by single value, e.g. costs. In the
last part we can specify if we want to use
dependency among criteria. When user confirms his
options a new Excel sheet with forms is created,
where user can set all elements.
5 CASE STUDY – FVK
Here we analyze similar decision making situation
as we analyzed with DAME, but now using the
fuzzy ANP algorithm with a help of FVK
First we express the importance of the criteria
that is given by the pair-wise comparison matrix
C:
Figure 11: Pair-wise comparison matrix C.
Then we calculate the corresponding triangular
fuzzy weights, i.e. the relative fuzzy importance of
the individual criteria that are given in matrix
W
21
:
Figure 12: Matrix W
21
.
Next step is to make fuzzy evaluations of the
variants according to the individual criteria that are
given by the following 3 pair-wise comparison
matrices
A1, A2, A3:
Figure 13: Pair-wise comparison matrices A1, A2, A3.
The corresponding fuzzy matrix W
32
of fuzzy
weights is calculated as
Figure 14: Matrix W
32
.
In order to evaluate fuzzy feedback between the
criteria we apply again pair-wise comparison
method, then we obtain the following 3 pair-wise
comparison matrices
B1, B2, B3:
Figure 15: Matrices B1, B2, B3.
Then we obtain the fuzzy feedback matrix W
22
:
Figure 16: Fuzzy feedback matrix W
22
.
Finally we calculate the synthesis – the aggregated
triangular fuzzy values of the individual variants
Z.
The situation is graphically depicted in Figure 18.
Figure 17: Synthesis.
In the last step we rank the evaluations of the above
CSEDU2015-7thInternationalConferenceonComputerSupportedEducation
514
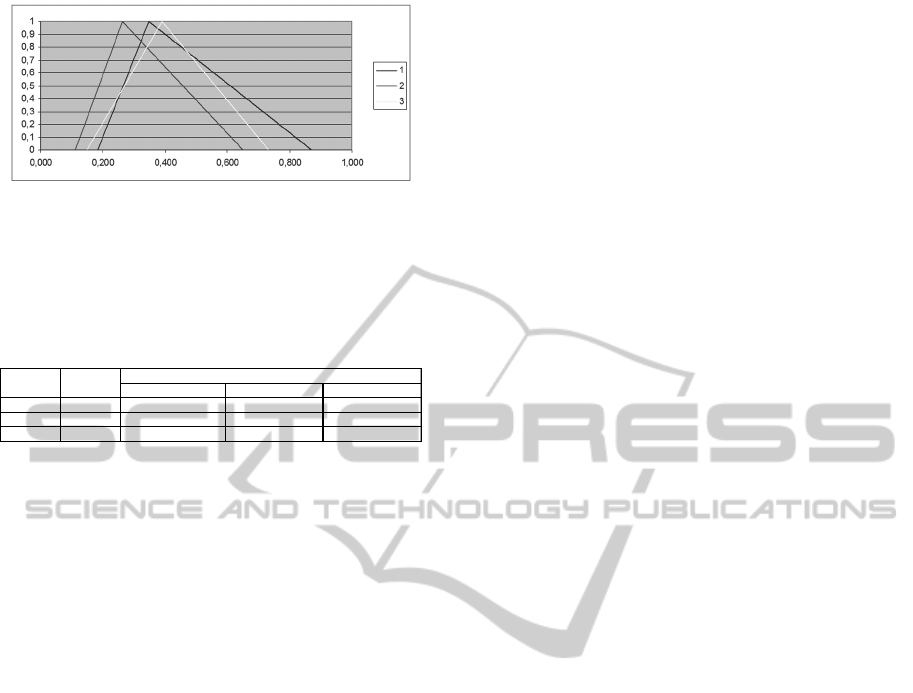
Figure 18: Total evaluation of fuzzy variants.
fuzzy variants resulting in the best decision. Here we
use ranking methods as described in section 4.3., i.e.
Center of gravity, L domination and R domination.
For the last two methods level α = 0.7 was used. The
results are in the following table.
Figure 19: Rank of variants.
6 CONCLUSIONS
In this paper we have proposed two Microsoft Excel
add-ins DAME and FVK which were developed for
students to help them understand and solve decision
making problems. Comparing to other decision
support programs they are free, able to work with
scenarios or multiple decision makers, allow for
dependency among criteria, can work with fuzzy
numbers, allows for easy manipulation with data and
utilizes capabilities of widespread spreadsheet
Microsoft Excel. On a realistic case study we have
demonstrated their functionality in individual steps.
These add-ins are regularly used by hundreds of
students in the course Decision Analysis for
Managers at the School of Business Administration
in Karvina, Silesian University in Opava. The
feedback from students is mostly positive and also
teachers of this subject observed increased students’
understanding of the decision support theory by
using these add-ins.
ACKNOWLEDGEMENTS
This research was supported by the grant project of
GACR No. 14-02424S.
REFERENCES
Aguaron, J., Moreno-Jimenez, J.M., 2003. The geometric
consistency index: Approximated thresholds.
European Journal of Operational Research 147, 137-
145.
Buckley, J.J., 1985. Fuzzy hierarchical analysis. Fuzzy
Sets and Systems 17, 1, p. 233-247.
Chen, S.J., Hwang, C.L. and Hwang, F.P., 1992. Fuzzy
multiple attribute decision making. Lecture Notes in
Economics and Math. Syst., Vol. 375, Springer-
Verlag, Berlin – Heidelberg.
Fishburn, P. C., 1971. A comparative analysis of group
decision methods, Behavioral Science (16), 538-544.
Gass, S.I., Rapcsák, T., 2004. Singular value
decomposition in AHP. European Journal of
Operational Research 154, 573–584.
Ramik, J., Perzina, R., 2006. Fuzzy ANP – a New Method
and Case Study. In: Proceedings of the 24th
International Conference Mathematical Methods in
Economics 2006, University of Western Bohemia.
Ramik, J., Perzina, R., 2008. Microsoft Excel Add-In for
Solving Multicriteria Decision Problems in Fuzzy
Environment. In: Proceedings of the 26th
International Conference Mathematical Methods in
Economics, Technical University of Liberec.
Ramik, J., Perzina, R., 2014. Solving Multicriteria
Decision Making Problems using Microsoft Excel. In:
Proceedings of the 32nd International Conference
Mathematical Methods in Economics, Palacky
University Olomouc.
Saaty, T.L., 1978. Exploring the interface between
hierarchies, multiple objectives and fuzzy sets. Fuzzy
Sets and Systems 1, 57-68.
Saaty, T.L., 1991. Multicriteria decision making - the
Analytical Hierarchy Process. Vol. I., RWS
Publications, Pittsburgh.
Saaty, T.L., 2001. Decision Making with Dependence and
Feedback – The Analytic Network Process. RWS
Publications, Pittsburgh.
Van Laarhoven, P.J.M. and Pedrycz, W., 1983. A fuzzy
extension of Saaty's priority theory. Fuzzy Sets and
Systems 11, 4, p. 229-241.
Center of gravity
L dominantion R dominantion
V
ar 1
0,466
121
V
ar 2 0,342 333
V
ar 3 0,424 212
Variant
Rank
xgi
EducationalMicrosoftExcelAdd-ins-SolvingMulticriteriaDecisionMakingProblems
515
