Setting Priorities

A Heuristic Approach for Cloud Data Center Selection

Ronny Hans, David Steffen, Ulrich Lampe, Bj

orn Richerzhagen and Ralf Steinmetz

Multimedia Communications Lab (KOM), TU Darmstadt, Rundeturmstr. 10, 64283 Darmstadt, Germany

Keywords:

Cloud Computing, Data Center, Quality of Service, Multimedia, Service, Heuristic.

Abstract:

A rising number of multimedia applications with Quality of Service requirements is delivered via cloud com-

puting platforms. To reduce latencies between data centers and customers, providers need to enhance and

utilize their cloud infrastructure by providing resources closer to the consumer. For planning such infras-

tructures and efﬁciently assigning existing resources, capable algorithms to solve the underlying optimization

problem are required. With our priority-based heuristic approach, we are able to reduce the computation time

by up to 99.99% compared to an exact approach, while retaining a favorable solution quality.

1 INTRODUCTION

Over the past years, cloud computing has developed

into a new paradigm for Information Technology (IT)

service delivery. It enables customers to use resources

according to their demand, independently of location

and time. The amount of services which are provided

via cloud data centers grows rapidly. While in 2012,

the ratio of overall Internet trafﬁc caused by commu-

nication with cloud data centers amounted to 46 %, it

has been predicted to reach a share of 69 % in 2017

(Cisco, 2013).

Beside the increasing quantity in demand, the

Quality of Service (QoS) requirements also grow.

Multimedia applications – such as Desktop as a Ser-

vice or cloud gaming – require low latencies, for ex-

ample. Such requirements pose new challenges re-

garding the service delivery for cloud infrastructure

providers. Even in industrial countries such as the

United States, with a well-developed cloud infrastruc-

ture, only a portion of users could be serviced with

sufﬁciently low latencies to enable services such as

cloud gaming (Choy et al., 2012).

Until a few years ago, cloud providers focused on

huge centralized data centers in only a few physical

locations. With the advent of QoS-aware multime-

dia services, data centers and compute resources that

are located closer to the user gain in importance. For

both, the appropriate planning of such extensive com-

pute infrastructures as well as the efﬁcient resource

allocation in existing infrastructures, appropriate al-

gorithms are required.

The remainder of this paper is structured as fol-

lows: In Section 2, we explain the speciﬁc problem.

In Section 3, we brieﬂy present our previously pub-

lished solution approaches including the mathemati-

cal model. In Section 4, we introduce our priority-

based heuristic approach, which is subsequently eval-

uated in Section 5. An overview of related work is

given in Section 6. Section 7 concludes the paper with

a brief summary and outlook on future work.

2 PROBLEM STATEMENT

In this work, we consider a cloud provider who aims

to provide the infrastructure for multimedia service

delivery. Therefore, a set of (potential or exist-

ing) data centers in different geographical locations

is assumed. Each data center may provide resource

units between a lower and a upper capacity bound.

The provider can choose between these data centers.

Thereby, for each data center certain ﬁxed costs, e. g.,

for construction or leasing, accrue. In addition, each

provisioned resource unit results in variable costs. For

the provided resource, the provider deﬁnes a set of rel-

evant QoS attributes and states a QoS guarantee with

respect to each user cluster and the deﬁned QoS at-

tribute.

The data centers should serve a set of geographi-

cally distributed user clusters. Thereby, a user cluster

represents a set of user with certain demand, which is

expressed in a standardized resource unit, i. e., num-

ber of servers. Regarding the delivered services, a

221

Hans R., Steffen D., Lampe U., Richerzhagen B. and Steinmetz R..

Setting Priorities - A Heuristic Approach for Cloud Data Center Selection.

DOI: 10.5220/0005494702210228

In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 221-228

ISBN: 978-989-758-104-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

user cluster has certain QoS requirements with respect

to each QoS attribute.

Under the assumption that prices are determined

by external market conditions, the problem of a

provider is the cost-minimal selection of appropriate

resources, as well as setting the respective resource

capacity. For the resource allocation to different user

clusters, the overall service demands of all user clus-

ters and the QoS requirements must be matched by

corresponding guarantees. In our former work, we re-

ferred to this problem as Cloud Data Center Selection

Problem (CDCSP) (Hans et al., 2013).

3 IP-/LP-BASED OPTIMIZATION

APPROACHES

In this section, we brieﬂy describe the mathematical

model for the CDCSP and previously published solu-

tion approaches.

3.1 Mathematical Model

The presented mathematical model is part of our for-

mer work (Hans et al., 2013). For the model several

formal notations are required. To begin with, we de-

ﬁne the basic entities:

• D = {1, 2,...,D

}: Set of (potential or existing)

data centers

• U = {1, 2, ...,U

}: Set of user clusters

• Q = {1, 2, ..., Q

}: Set of considered QoS at-

tributes

Based on these basic entities, the associated parame-

ters can be deﬁned as follows:

• S

: Service demand of user cluster u

• K

min

∈ R: Minimal capacity of data center d

• K

max

∈ R: Maximal capacity of data center d

• CF

∈ R: Fixed costs of selecting data center d

• CV

∈ R: Variable costs for per server unit in data

center d

• QG

d,u,q

∈ R: QoS guarantee of data center d w.r.t.

user cluster u for QoS attribute q

• QR

u,q

∈ R: QoS requirement of user cluster u

w.r.t. QoS attribute q

Finally, in order to model the CDCSP as optimization

problem, we use the following decision variables:

• x

: Selection of a data center d

• y

d,u

: Number of resource units provided by data

center d to user cluster u

Model 1: Cloud Data Center Selection Problem.

Min. C(x,y) =

∑

d∈D

×CF

∑

d∈D,u∈U

d,u

×CV

(1)

∑

d∈D

d,u

≥ S

∀u ∈ U (2)

∑

u∈U

d,u

≤ x

× K

max

∀d ∈ D (3)

∑

u∈U

d,u

≥ x

× K

min

∀d ∈ D (4)

d,u

≤ p

d,u

× K

max

∀d ∈ D, ∀u ∈ U (5)

d,u

(

1 if QG

d,u,q

≤ QR

u,q

∀q ∈ Q

0 else

(6)

∈ {0,1} ∀d ∈ D

d,u

∈ N ∀d ∈ D, ∀u ∈ U (7)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

∈ R,0 ≤ x

≤ 1 ∀d ∈ D

d,u

∈ R,y

d,u

≥ 0 ∀d ∈ D, ∀u ∈ U (8)

The described objective of the CDCSP constitutes a

linear, mixed-integer program, which is formalized in

Model 1. In the model, Eq. 1 deﬁnes the objective of

the problem. Thereby, the total cost C depends on the

decision variables x

and y

d,u

(Eq. 7) The binary vari-

ables x

indicate if data center d will be constructed

or leased. y

d,u

are integer variables that denote the

number of resource units a data center d provides to a

user cluster u. Eq. 2 represents the constraint that the

service demand of each user cluster needs to be satis-

ﬁed by the provided service units. Eqs. 3 and 4 assure

that the provided capacity of each data center lies be-

tween the given lower bound K

min

and the given upper

bound K

max

. Further, they functionally link the deci-

sion variables x and y. In Eq. 5 and Eq. 6 the variables

d,u

restrict the resource allocation between data cen-

ters and user clusters, depending on the fulﬁllment of

the QoS requirements. In Eq. 8 the binary and inte-

ger decision variables from Eq. 7 are substituted by

corresponding natural variables, which is required for

the LP-relaxed approach (cf. Section 3.2).

3.2 Solution Approaches

As stated earlier, the described model constitutes an

Integer Program (IP) and was published as Cloud

Data Center Selection Problem (Hans et al., 2013).

Such IPs can be solved using off-the-shelf algorithms,

such as branch-and-bound (Domschke and Drexl,

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

222

2004). This results in an exact (i. e., optimal) so-

lution. However, since branch-and-bound is based

on the principle of enumeration (Hillier and Lieber-

man, 2005), the computation time grows exponen-

tially with the number of decision variables in the

worst case. To overcome this drawback, we intro-

duced an initial heuristic approach based on the com-

mon concept of LP relaxation (Hans, 2013). Al-

though this approach signiﬁcantly reduces the com-

putation time, is still needs minutes for large problem

instances, which makes it inapplicable for on-demand

resource assignments.

4 PRIORITY-BASED HEURISTIC

APPROACH

The described CDCSP forms an extension of a ca-

pacitive facility location problem. Such problems can

be solved by using priority based approaches (An-

gelopoulos and Borodin, 2002). To efﬁciently ﬁnd

solutions for the CDCSP, we developed a priority-

based heuristic approach, where the user demand is

assigned to potential data centers in a stepwise man-

ner, following speciﬁc rules regarding user cluster

and data center selection. Since the approach cal-

culates an initial solution of the optimization prob-

lem, we named it Priority-based Start Heuristic, in

short CDCSP-PBSH. Our approach consists of sev-

eral phases, which are described in the subsequent

sections. Later on, we present a set of prioritization

and cost allocation rules in detail. Since we use a

generic approach, new rules can be easily added. Fi-

nally, we describe the conduction of concrete heuris-

tic approaches.

4.1 Generic Optimization Approach

Our approach is divided into ﬁve phases, as illustrated

in Figure 1. In the Selection Phase, the used data cen-

ters are determined. In the Allocation Phase, the ﬁ-

nal resource assignment is done. The purposes of the

other phases, namely the Initialization Phase, the Up-

date Phase, and the Finalization Phase, are primarily

the preparation of the required data structures and the

processing of interim as well as the ﬁnal results.

4.1.1 Initialization Phase

At the beginning of our procedure, a speciﬁc problem

instance of the CDCSP is analyzed and the required

data structure for the subsequent phases is created.

Algorithm 2 shows the corresponding pseudo code.

First of all, user clusters U are added to the list for

the residual user clusters U

res

. For each user clus-

ter appropriate data centers are determined, which are

able to provide QoS guarantees QG

d,u,q

according to

the QoS requirements QR

u,q

of the user cluster for all

QoS parameters q ∈ Q (cf. line 7 - 11). The result is

stored in a binary variable p

d,u

= {0,1} (cf. line 9),

which corresponds to the constraint in Eq. 6 in our

model. The permitted data centers for each user clus-

ter are stored in the list D

per

(cf. line 12). Further,

variables for the residual demand of the user clusters

res

and for the residual capacities of the data centers

res

are set (cf. line 3 and 16).

Algorithm 2: Initialization.

Start:

1: U

res

← U

2: for all u ∈ U do

3: S

res

← S

4: D

per

←

5: for all d ∈ D do

6: p

d,u

← true

7: for all q ∈ Q do

8: if QR

u,q

< QG

d,u,q

then

9: p

d,u

← false

10: end if

11: end for

12: if p

d,u

is true then D

per

← D

per

∪ {d} end if

13: end for

14: end for

15: for all d ∈ D do

16: K

res

← K

max

17: end for

4.1.2 Selection Phase

In this phase a ﬁrst feasible solution for the CDCSP is

determined in a stepwise manner. Algorithm 3 shows

the corresponding pseudo code. At the beginning of

each selection step, a user cluster u ∈ U

res

with a

residual service demand S

res

> 0 as well as a data cen-

ter d ∈ D

per

with a residual capacity K

res

> 0 are se-

lected (cf. line 3 and 4). The selection of a user cluster

depends on the priority rule (cf. Section 4.2), which

is set at the beginning of this phase. From the set of

possible data centers, the one with the lowest cost per

service unit – depending on the cost allocation rule

(cf. Section 4.3) – is selected (cf. Section 4.3). The

assignment of capacities y

d,u

depends on the resid-

ual demand of the selected user cluster S

res

and the

residual capacity K

res

of the selected data center (cf.

line 5).

Within this phase, a made assignment decision is

ﬁnal and will not be changed in later iterations. Ac-

cording to the assigned capacities, the residual de-

SettingPriorities-AHeuristicApproachforCloudDataCenterSelection

223

mand and the residual capacity are reduced (cf. line 6

and 7). All selected data centers are stored in the list

open

(cf. line 8). If the demand of a user cluster is

met or the capacity of a data center is exhausted, it

will not be taken into account in the subsequent itera-

tions (cf. line 9 and 12).

Algorithm 3: Determination of an Initial Solution.

Start: D

open

←

1: while |U

res

| > 0 do

2: if |D

per

| = 0 then exit without solution end if

3: u ← SelectUserCluster(U

res

)

4: d ← SelectDataCenter(D

per

)

5: y

d,u

← min(K

res

)

6: K

res

← K

res

− y

d,u

7: S

res

← S

res

− y

d,u

8: D

open

← D

open

∪ {d}

9: if S

res

= 0 then U

res

← U

res

\{u} end if

10: if K

res

= 0 then

11: for all u

∈ U

res

12: D

per

← D

per

\{d}

13: end for

14: end if

15: end while

4.1.3 Update Phase

In the previous phase, a set of data centers was opened

and stored in the list D

open

. This list serves as an im-

proved information base and is used instead of the ini-

tial list D, which included all possible data centers. In

the Update Phase, all assignments are reset and the

required data structure is recreated, whereby the pro-

cedure corresponds to the Initialization Phase.

4.1.4 Allocation Phase

The Allocation Phase is comparable to the the previ-

ously described Selection Phase. Again, the solution

is determined in a stepwise manner based on the prior-

itization and cost allocation rules. Since all data cen-

ters were determined in the Selection Phase, at least

the ﬁxed costs arise. Thus, the allocation of resources

can be improved by focusing on different goals, as

implemented by different priority and cost allocation

rules.

4.1.5 Finalization Phase

During the Selection Phase, the relevant data centers

were stored in the list D

open

. Based on its content, val-

ues need to be assigned to the decision variables x

Thereby, x

assumes the value one for all data cen-

ters in D

open

. The amount of assigned service units

is stored in y

d,u

. It assumes the value zero if no ser-

vice units were assigned between a data center and the

corresponding user clusters (cf. Algorithm 4).

Algorithm 4: Finalization of the Approach.

Start:

1: for all d ∈ D do

2: if d ∈ D

open

then

3: x

← 1

4: else

5: x

← 0

6: end if

7: for all u ∈ U do

8: if y

u,d

= null then y

u,d

← 0 end if

9: end for

10: end for

4.2 Priority Rules

A major challenge of priority based procedures is

the determination of the sequence in which the de-

manders are assigned to the supply locations (B

olte,

1994). Appropriate priority rules are required to sort

the demanders in a speciﬁc sequence. Beside the

demander, the selection of the supply locations can

also be supported by priority rules (Angelopoulos and

Borodin, 2002). For the CDCSP we focus on the fol-

lowing three quantity based prioritization rules which

sequences the used clusters w.r.t. the demand, the

available capacities, or both.

The Demand Priority Rule is used to order the

user clusters u ⊂ U

res

according to their residual ser-

vice demand S

res

> 0. The basic idea behind this rule

is to prefer user clusters with a higher service demand

to ensure a valid solution. Since the assignment takes

place in every single step of the procedure, the priori-

tization of the residual user clusters may change.

In contrast to the previous rule, the Capacity Pri-

ority Rule focuses on residual capacities K

res

of the

suitable data centers d ⊂ D

per

. Thereby, user clusters

with a lower total service supply are preferred.

Both rules have a low complexity and those may

be able to ﬁnd solutions with low computational ef-

fort. Nevertheless, they may lead to solutions with

a lower quality since they take only demand or sup-

ply into consideration. Thus, the third quantity based

prioritization rule, Buffer Priority Rule, combines

both preceding rules to overcome their disadvantages.

Thereby, a service buffer as the margin of residual

capacities and residual service demand of each user

cluster is calculated. User clusters with a lower ser-

vice buffer assume a higher priority.

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

224

Initialization

Phase

Selection

Phase

Choose Resources

Accounting

Solving Selection Problem Solving Allocation Problem

Initialization

Finalization

Initial Feasible

Solution of CDCSP

Specific CDCSP

Problem Instance

Allocation

Phase

Update

Phase

Finalization

Phase

Update

Choose Resources

Accounting

Figure 1: Phases of the Heuristic Approach.

4.3 Cost Allocation Rules

The selection of the data center is based on its costs,

which consist of variable and ﬁxed costs. Since the

total amount of delivered resources is unknown until

the end of the whole assignment procedure, the spread

of ﬁxed costs is a challenging task. The individual

costs of a service unit y

u,d

is given by the following

function.

C(u, d, base) = CV

+CF

∗ (1/base) (9)

Thereby, the spread of the ﬁxed cost depends on the

value of the artiﬁcial base parameter. With a larger

value of this parameter, the share of ﬁxed costs per

service unit decreases. Thus, the strategy for the de-

termination of the base parameter directly inﬂuences

the service assignment and is given by the cost alloca-

tion rules. In the subsequent section, we present two

main classes of cost allocation rules.

4.3.1 Static Cost Allocation Rules

Within these rules, the value of the base parameter is

determined once at the beginning of a heuristic ap-

proach and will not be changed any more. Within the

Max Capacity Cost Allocation Rule, the maximum ca-

pacity of a data center K

max

is considered. This rule

is based on the assumption that a data center is nearly

completely utilized. If this is not the case, the total

costs of a data center may be underestimated.

If a provider expects a utilization near the mini-

mum capacity of a data center K

min

, the Min Capacity

Cost Allocation Rule is more appropriate. Thereby,

the minimum capacity serves as the base parameter.

In case of a higher utilization, the costs per service

unit are overestimated.

To strike a balance, the Med Capacity Cost Allo-

cation Rule uses the medium value between the mini-

mum and the maximum capacity of a data center.

For a given set of already opened data centers, an-

other option is to neglect the ﬁxed costs completely.

This could be appropriate if the ﬁxed costs arise in

any case or if the number of provided service units is

very high. In this case, a sufﬁciently large value for

the base parameter is chosen. The corresponding rule

is named No Fixed Cost Allocation Rule.

4.3.2 Dynamic Cost Allocation Rules

In contrast to the static rules, the dynamic rules in-

clude the already existing assignments in the calcula-

tions. The value of the base parameter is calculated in

each iteration of our heuristic approach and considers

the current utilization of a data center.

The ﬁrst of our dynamic rules, Penalize First Cost

Allocation Rule, penalizes a user cluster which tends

to open a new data center d 6⊂ D

open

. In such a case,

the full ﬁxed costs are added to the cost function. If a

user cluster gets its services from an already opened

data center, only the variable costs are included into

the calculation. Thus, there is an incentive to use ex-

isting data centers, which is especially important dur-

ing the selection phase.

Another strategy is pursued by the Prefer Minimal

Utilization Cost Allocation Rule. This rule is based

on the assumption that the opened data centers need

to reach their minimum capacity constraint. Thus,

data centers with an utilization lower than the mini-

mum value get a higher priority. The cost function

of such data centers only includes the variable costs,

while cost function for data centers with an utiliza-

tion high than a minimum capacity includes addition-

ally the ﬁxed costs. Especially a scenario with a given

set of data centers, like the Allocation Phase, beneﬁts

from this rule.

The Current Utilization Cost Allocation Rule cal-

culates the ﬁxed costs based on the current utilization

of a data center. Thereby, the allocation of service

units between a data center and an user cluster re-

sults from the minimum of the residual demand and

the residual capacity. In contrast to the previous two

dynamic rules, the value of the ﬁxed costs which is

added to the cost function decreases with a higher uti-

lization.

SettingPriorities-AHeuristicApproachforCloudDataCenterSelection

225

Rules for

Selection Phase

Demand Priority Rule

Capacity Priority Rule

…

Buffer Priority Rule

Max Capacity Cost Allocation Rule

Min Capacity Cost Allocation Rule

Med Capacity Cost Allocation Rule

No Fixed Cost Allocation Rule

Penalize First Cost Allocation Rule

Current Utilization Cost Allocation Rule

…

Max Capacity Cost Allocation Rule

Min Capacity Cost Allocation Rule

Med Capacity Cost Allocation Rule

No Fixed Cost Allocation Rule

Penalize First Cost Allocation Rule

Current Utilization Cost Allocation Rule

…

Rules for

Allocation Phase

Specific Heuristic Procedute

Abstract Heuristic Procedure

Demand Priority Rule

Capacity Priority Rule

…

Buffer Priority Rule

Figure 2: Deduction of Speciﬁc Heuristic Approaches.

4.4 Deduction of Speciﬁc Heuristic

Approaches

In Section 4.1, we presented a heuristic approach as

an abstract solution approach for the CDCSP. For both

phases, the Selection Phase and the Allocation Phase,

we use priority rules for the user cluster selection

and cost allocation rules to choose the correspond-

ing data centers.For both phases, all described rules

are equally available. Nevertheless, some of them

are more suitable than others, e. g., the selection of

data centers with ignoring the ﬁxed costs very likely

leads to poor solutions. Figure 2 gives an overview of

the previously described rules and shows the deduc-

tion of a speciﬁc heuristic approach, i. e., the CDCSP-

PBSH[1], which is described in detail within the eval-

uation (cf. Section 5.2).

5 EVALUATION

5.1 Setup

In order to assess the capability of our heuristic ap-

proach, we prototypically implemented it in Java 8.

As the solver for the exact and the LP-relaxed ap-

proach, we used IBM ILOG CPLEX 12.5

, which

was accessed through the JavaILP middleware

Our evaluation focused on dependent variables,

computation time and solution quality, i. e., total

costs. As independent variables, we considered the

number of data centers and the number of user clus-

ters. These variables directly inﬂuence the number of

decision variables, and hence, the size of the solution

space.

http://www.ibm.com/software/integration/

optimization/cplex-optimizer/

http://javailp.sourceforge.net/

According to our former work (Hans et al., 2013),

the problem instance generation was based on the

2010 United States census

. Thereby we set the ser-

vice demands and different cost parameters according

the population of a randomly selected county and its

median income. We focused on latency as our sole

QoS parameter and set it corresponding to the require-

ments of multimedia services. For each test case, we

created 100 problem instances.

Based on the samples, we subsequently computed

the observed mean absolute computation times and

the macro-averaged ratio of total cost along with the

respective 95% conﬁdence intervals based on a t-

distribution (Kirk, 2007). The evaluation was con-

ducted on a workstation, equipped with a Intel Xeon

CPU E5-1620 v3 with 3.50 GHz and 16 GB of mem-

ory, operating under Microsoft Windows 7.

5.2 Results and Discussion

At the beginning we analyzed the performance and

the solution quality, i. e., the ratio cost. We used

the exact approach (CDCSP-EXA.KOM) and the LP-

relaxed approach (CDCSP-REL.KOM) of our for-

mer works and the proposed heuristic approaches

(CDCSP-PBSH.KOM) with all combinations of the

prioritization and cost allocation rules described in

this paper. Due to the large amount of evaluation re-

sults, we decided to present only two of them within

this paper. The ﬁrst approach was selected due to its

superior solution quality for a large set of test cases,

whereas the second was chosen due to its favorable

computation time.

• CDCSP-PBSH.KOM [1]: Selection: Buffer Prior-

ity Rule, Max Capacity Cost Allocation Rule; Al-

location: Buffer Priority Rule, Penalize First Cost

Allocation Rule

http://www.census.gov/geo/maps-data/data/

gazetteer.html

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

226

0.001

0.01

0.1

100

1000

10000

10 / 150 20 / 300 30 / 450 40 / 600

Mean Computation Time [s]

Test Case (|D| / |U|)

CDCSP-EXA.KOM

CDCSP-REL.KOM

CDCSP-PBSH.KOM [1]

CDCSP-PBSH.KOM [2]

Figure 3: Computation Time (Small Test Cases).

• CDCSP-PBSH.KOM [2]: Selection: Demand

Priority Rule, Max Capacity Cost Allocation

Rule; Allocation: Demand Priority Rule, Penalize

First Cost Allocation Rule

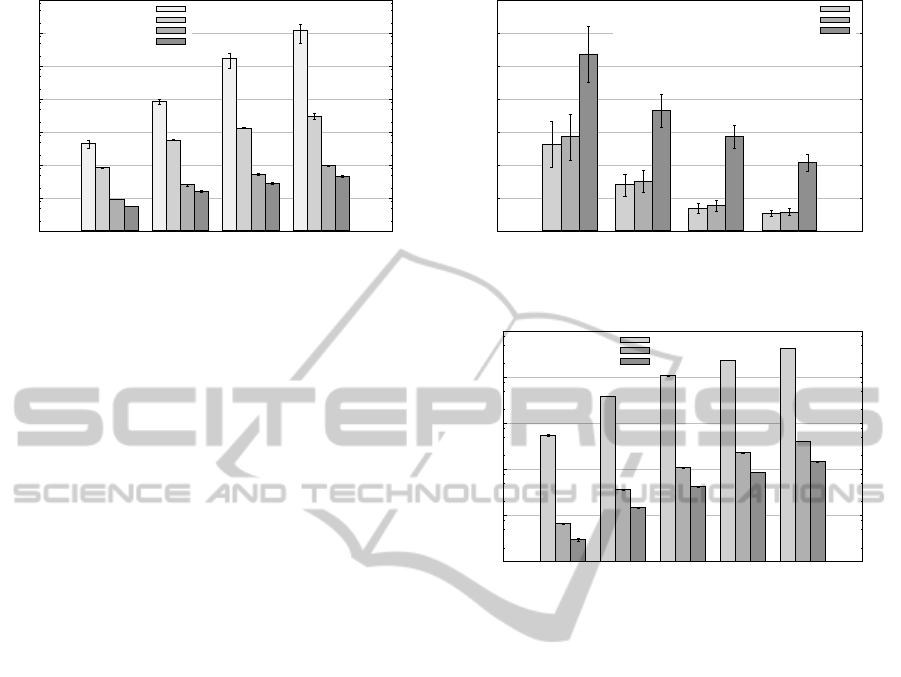
Figure 3 shows the computation time of the four ap-

proaches. The comparison between the exact and the

second heuristic approach (CDCSP-PBSH.KOM [2])

shows a statistical signiﬁcant improvement of 98.75%

for the ﬁrst test case (|D| = 10 / |U | = 150) and up

to 99.99% for the last test case (40 / 600). The so-

lution quality of the approaches is depicted in Fig-

ure 4. The chart shows the ratio of cost compared to

the exact approach. In the last test case (40 / 600),

the LP-relaxed approach causes 5.27% higher costs

compared to the exact approach and our ﬁrst heuristic

approach (CDCSP-PBMH.KOM [1]) causes 5.68%

higher costs. The fastest approach delivered the poor-

est solution quality with a cost increase of 20.68%.

In a second step, we used test cases with a larger

amount of potential data centers and user clusters to

evaluate the algorithms in large scale environments.

Due to the high computational effort, the exact ap-

proach is not feasible in such scenarios. Again, we

include the previously described heuristic approaches

in this setup.

Especially the results for the heuristic approach

CDCSP-PBSH.KOM [1] are very interesting. For the

chosen number of data centers and user clusters, we

are able to reduce the computation time by about 99%

compared to the LP-relaxed approach (cf. Figure 5),

while retaining the same solution quality, i. e., a cost

ratio of one.

Further, for the heuristic approach CDCSP-

PBSH.KOM [2], with a less complex prioritization

rule, we achieve an even better computation time.

However, the solution quality is signiﬁcantly worse

compared to the other approaches, with cost increases

ranging from 0.95% to 3.53%.

1.1

1.2

1.3

1.4

1.5

1.6

1.7

10 / 150 20 / 300 30 / 450 40 / 600

Ratio of Cost

Problem Size (|D| / |U|)

CDCSP-REL.KOM / CDCSP-EXA.KOM

CDCSP-PBSH.KOM [1] / CDCSP-EXA.KOM

CDCSP-PBSH.KOM [2] / CDCSP-EXA.KOM

Figure 4: Solution Quality (Small Test Cases).

0.01

0.1

100

1000

100 / 500 200 / 1000 300 / 1500 400 / 2000 500 / 2500

Mean Computation Time [s]

Test Case (|D| / |U|)

CDCSP-REL.KOM

CDCSP-PBSH.KOM [1]

CDCSP-PBSH.KOM [2]

Figure 5: Computation Time (Large Test Cases).

6 RELATED WORK

A lot of work focus on data center placement and re-

source allocation with different optimization goals,

such as the reduction of network latency or the re-

duction of total cost. Thereby different solution ap-

proaches like exact approaches or heuristic such as

Tabu Search so Simulated Annealing are used. In this

section, we present a set of selected papers, which are

most relevant regarding the work at hand.

(Chang et al., 2007) investigated in the consolida-

tion of the server infrastructure for the US army. The

authors formulated a optimization problem to mini-

mize the weighted distances between the data centers

and users. (Goiri et al., 2011) also analyze the place-

ment of data centers. Thereby, the objective is the

reduction of total costs under consideration of quality

requirements. The authors formulate an optimization

model and solved it with LP relaxation and a simu-

lated annealing heuristic. Both papers focus on data

center placement and do not provide algorithms for

run time resource allocation.

(Larumbe and Sans

o, 2012) formulated an op-

timization problem for cloud computing which in-

SettingPriorities-AHeuristicApproachforCloudDataCenterSelection

227

cludes: Location data centers, location of software

components, and routing. Therefore, the authors also

consider an exact optimization approach, which is pri-

mary appropriated for planing aspects. (Wang et al.,

2012) focus on mobile cloud gaming and propose an

approach for the minimization of the total costs of a

cloud provider taking the individual quality require-

ments of the users into account. The authors develop

a scheduling algorithm for assigning computation and

networking resources during run time. In contrast to

this work the authors do not formulate an optimiza-

tion problem.

(Choy et al., 2012) focuses in their work on the

availability on cloud gaming in the US. Therefore, the

authors analyze the cloud infrastructure provided by

Amazon and show that only 70 percent of the popula-

tion can use services. They propose the use of addi-

tional data centers or Edge Server to increase the cov-

erage. In contrast to our work, they does not propose

an optimization approach for the efﬁcient placement

of such data centers and servers.

In summary, to the best of our knowledge, our

work is the ﬁrst to include a detailed analysis of a

priority-based heuristic approach for cost-efﬁcient se-

lection of cloud data centers for QoS-aware services

provisioning. In this context, this paper provides a

generic heuristic approach, which allows substantial

reduction of computation time compared to previ-

ously presented approaches.

7 SUMMARY AND OUTLOOK

In this paper, we presented a heuristic approach to

a previously introduced optimization problem, the

Cloud Data Center Selection Problem. From this

generic approach, a variety of speciﬁc heuristic ap-

proaches can be deduced. Depending on the selected

prioritization and cost allocation rules, either very fast

heuristics approaches or heuristics with an outstand-

ing solution quality can be conﬁgured.

Based on the presented approach, we plan two ma-

jor enhancements in the future. First, we plan to de-

velop a best-of-breed approach, which combines the

beneﬁts of multiple heuristics. Second, we plan to de-

velop improvement procedures, such as tabu search or

simulated annealing, to further enhance the solution

quality of our approach.

ACKNOWLEDGEMENTS

This work has been sponsored in part by the German

Federal Ministry of Education and Research (BMBF)

under grant no. 01IS12054, by E-Finance Lab e.V.,

Frankfurt a.M., Germany (www.eﬁnancelab.de), and

by the German Research Foundation (DFG) in the

Collaborative Research Center (SFB) 1053 MAKI.

The authors are fully responsible for the content of

this paper.

REFERENCES

Angelopoulos, S. and Borodin, A. (2002). On the Power

of Priority Algorithms for Facility Location and Set

Cover. In Jansen, K., Leonardi, S., and Vazirani, V.,

editors, Approximation Algorithms for Combinatorial

Optimization. Springer.

olte, A. (1994). Modelle und Verfahren zur innerbe-

trieblichen Standortplanung. Physica. In German.

Chang, S.-J. F., Patel, S. H., and Withers, J. M. (2007). An

Optimization Model to Determine Data Center Loca-

tions for the Army Enterprise. In IEEE Military Com-

munications Conference.

Choy, S., Wong, B., Simon, G., and Rosenberg, C. (2012).

The Brewing Storm in Cloud Gaming: A Measure-

ment Study on Cloud to End-User Latency. In 11th

Annual Workshop on Network and Systems Support

for Games.

Cisco (2013). Cisco Global Cloud Index: Forecast and

Methodology, 2012-2017. Online Pubication.

Domschke, W. and Drexl, A. (2004). Einf

uhrung in Opera-

tions Research. Springer. In German.

Goiri,

I., Le, K., Guitart, J., Torres, J., and Bianchini, R.

(2011). Intelligent Placement of Datacenters for Inter-

net Services. In 31st Int’l Conf. on Distributed Com-

puting Systems.

Hans, R. (2013). Selecting Cloud Data Centers for QoS-

Aware Multimedia Applications. In Zimmermann,

W., editor, PhD Symposium at the 2nd European Conf.

on Service-Oriented and Cloud Computing.

Hans, R., Lampe, U., and Steinmetz, R. (2013). QoS-

Aware, Cost-Efﬁcient Selection of Cloud Data Cen-

ters. In 6th Int’l Conf. on Cloud Computing.

Hillier, F. and Lieberman, G. (2005). Introduction to Oper-

ations Research. McGraw-Hill, 8th edition.

Kirk, R. (2007). Statistics: An Introduction. Wadsworth

Publishing, 5th edition.

Larumbe, F. and Sans

o, B. (2012). Optimal Location

of Data Centers and Software Components in Cloud

Computing Network Design. In 12th IEEE/ACM Int’l

Symposium on Cluster, Cloud and Grid Computing.

Wang, S., Liu, Y., and Dey, S. (2012). Wireless Network

Aware Cloud Scheduler for Scalable Cloud Mobile

Gaming. In IEEE Int’l Conf. on Communications.

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

228