Stability and Sensitivity of Learning Analytics based Prediction

Models

Dirk T. Tempelaar

, Bart Rienties

and Bas Giesbers

Maastricht University, School of Business and Economics, PO Box 616, 6200 MD, Maastricht, The Netherlands

Open University U.K., Institute of Educational Technology, Walton Hal, Milton Keynes, MK7 6AA, U.K.

Rotterdam School of Management, PO Box 1738, 3000 DR, Rotterdam, The Netherlands

Keywords: Blended Learning, Dispositional Learning Analytics, e-tutorials, Formative Assessment, Learning

Dispositions.

Abstract: Learning analytics seek to enhance the learning processes through systematic measurements of learning

related data and to provide informative feedback to learners and educators. In this follow-up study of

previous research (Tempelaar, Rienties, and Giesbers, 2015), we focus on the issues of stability and

sensitivity of Learning Analytics (LA) based prediction models. Do predictions models stay intact, when the

instructional context is repeated in a new cohort of students, and do predictions models indeed change,

when relevant aspects of the instructional context are adapted? This empirical contribution provides an

application of Buckingham Shum and Deakin Crick’s theoretical framework of dispositional learning

analytics: an infrastructure that combines learning dispositions data with data extracted from computer-

assisted, formative assessments and LMSs. We compare two cohorts of a large introductory quantitative

methods module, with 1005 students in the ’13/’14 cohort, and 1006 students in the ’14/’15 cohort. Both

modules were based on principles of blended learning, combining face-to-face Problem-Based Learning

sessions with e-tutorials, and have similar instructional design, except for an intervention into the design of

quizzes administered in the module. Focusing on the predictive power, we provide evidence of both stability

and sensitivity of regression type prediction models.

1 INTRODUCTION

Learning analytics provide institutions with

opportunities to support student progression and to

enable personalised, rich learning (Bienkowski,

Feng, and Means, 2012; Oblinger, 2012; Siemens,

Dawson, and Lynch, 2013; Tobarra, Robles-Gómez,

Ros, Hernández, and Caminero, 2014). According to

Bienkowski et al. (2012, p. 5), “education is getting

very close to a time when personalisation will

become commonplace in learning”, although several

researchers (Greller and Drachsler, 2012; Stiles,

2012) indicate that most institutions may not be

ready to exploit the variety of available datasets for

learning and teaching. Many learning analytics

applications use data generated from learner

activities, such as the number of clicks (Siemens,

2013; Wolff, Zdrahal, Nikolov, and Pantucek, 2013),

learner participation in discussion forums (Agudo-

Peregrina, Iglesias-Pradas, Conde-González, and

Hernández-García, 2014; Macfadyen and Dawson,

2010), or (continuous) computer-assisted formative

assessments (Tempelaar, Heck, Cuypers, van der

Kooij, and van de Vrie, 2013; Tempelaar, Kuperus

et al., 2012; Wolff et al., 2013). User behaviour data

are frequently supplemented with background data

retrieved from learning management systems (LMS)

(Macfadyen and Dawson, 2010) and other student

admission systems, such as accounts of prior

education (Arbaugh, 2014; Richardson, 2012;

Tempelaar, Niculescu, Rienties, Giesbers, and

Gijselaers, 2012).

In Verbert, Manouselis, Drachsler, and Duval

(2012), six objectives are distinguished in using

learning analytics: predicting learner performance

and modelling learners, suggesting relevant learning

resources, increasing reflection and awareness,

enhancing social learning environments, detecting

undesirable learner behaviours, and detecting affects

of learners. Although the combination of self-report

learner data with learning data extracted from e-

tutorial systems (see below) allows us to contribute

156

Tempelaar D., Rienties B. and Giesbers B..

Stability and Sensitivity of Learning Analytics based Prediction Models.

DOI: 10.5220/0005497001560166

In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 156-166

ISBN: 978-989-758-107-6

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

to at least five of these objectives of applying

learning analytics, we will focus in this contribution

on the first objective: predictive modelling of

performance and learning behaviour (Baker, 2010;

Thakur, Olama, McNair, Sukumar, and Studham, S.,

2014). The ultimate goal of this predictive modelling

endeavour is to find out which components from a

rich set of data sources best serve the role of

generating timely, informative feedback and

signalling risk of underperformance. In designing

such prediction models, there is always a balance

between prediction accuracy at the one side, and the

generalizability of the prediction model at the other

side (Thakur et al., 2014). Models that are strongly

context specific will typically achieve high

prediction accuracy, but perform only within

contexts very similar to the one they are designed

for, and not outside such contexts. Relative

invariance of prediction models over several

modules making up an academic program is thus an

important aim in the design of prediction models. At

the same time, prediction models need to be

sufficiently context specific, for instance in order to

be able to analyse the effect of interventions into the

instructional system. In this study, we focus on both

of these issues within the empirical context of a

large module introductory quantitative methods. Our

study is a follow-up study of previous research,

Tempelaar, Rienties, and Giesbers (2014, 2015), in

which the role of formative assessment based LA is

analysed within one cohort of students. In the

current study, we extend our sample with a second

cohort, with the aim to investigate both the stability

of the prediction models over different cohorts, as

well as the sensitivity of those prediction models for

relevant changes in the instructional design.

2 APPLICATION CONTEXT

2.1 Dispositional Learning Analytics

Buckingham Shum and Deakin Crick (2012)

propose a dispositional learning analytics

infrastructure that combines learning activity

generated data with learning dispositions, values and

attitudes measured through self-report surveys,

which are fed back to students and teachers through

visual analytics. For example, longitudinal studies in

motivation research (Rienties, Tempelaar, Giesbers,

Segers, and Gijselaers, 2012; Järvelä, Hurme, and

Järvenoja, 2011) and students’ learning approaches

indicate strong variability in how students learn over

time in face-to-face settings (e.g., becoming more

focussed on deep learning rather than surface

learning), depending on the learning design, teacher

support, tasks, and learning dispositions of students.

Indeed, in a study amongst 730 students Tempelaar,

Niculescu, et al. (2012) found that positive learning

emotions contributed positively to becoming an

intensive online learner, while negative learning

emotions, like boredom, contributed negatively to

learning behaviour. Similarly, in an online

community of practice of 133 instructors supporting

EdD students, Nistor et al. (2014) found that self-

efficacy (and expertise) of instructors predicted

online contributions. And in a very recent overview

study into the role learner emotions in applications

of LA, Rienties and Alden Rivers (2014) distinguish

no less than hundred different facets of learner

emotions determining students’ learning behaviours.

However, studies combining LMS data with

intentionally collected data, such as self-report data

stemming from student responses to surveys, are the

exception rather than the rule in learning analytics

(Buckingham Shum and Ferguson, 2012; Greller and

Drachsler, 2012; Macfadyen and Dawson, 2010;

Tempelaar et al., 2013, 2015). In our empirical

contribution focusing on a large scale module in

introductory mathematics and statistics, we aim to

provide a practical application of such an

infrastructure based on combining longitudinal

learning and learner data. In collecting learner data,

we opted to use three validated self-report surveys

firmly rooted in current educational research,

including learning styles (Vermunt, 1996), learning

motivation and engagement (Martin, 2007), and

learning emotions (Pekrun, Goetz, Frenzel,

Barchfeld, and Perry, 2011). This operationalisation

of learning dispositions closely resembles the

specification of cognitive, metacognitive and

motivational learning factors relevant for the internal

loop of informative tutoring feedback (e.g., Narciss,

2008; Narciss and Huth, 2006). For learning data,

data sources are used from more common learning

analytics applications, and constitute both data

extracted from an institutional LMS (Macfadyen and

Dawson, 2010) and system track data extracted from

the e-tutorials used for practicing and formative

assessments (e.g., Tempelaar et al., 2014, 2015;

Wolff et al., 2013). The prime aim of the analysis is

predictive modelling (Baker, 2010) , with a focus on

the roles of (each of) 100+ predictor variables from

the several data sources can play in generating

timely, informative feedback for students, and

ultimately the stability and sensitivity of such

prediction models.

StabilityandSensitivityofLearningAnalyticsbasedPredictionModels

157

2.2 Case Study: Blended Learning of

Mathematics and Statistics using

e-tutorials and Formative

Assessment

Subjects in our study are freshmen students in

quantitative methods (mathematics and statistics) of

the business and economics school at Maastricht

University. This education is directed at a large and

diverse group of students, which benefits the

research design. Blackboard serves as a basic LMS

system to share module information to students.

Given the restricted functionality of this LMS in

terms of personalised, adaptive learning content with

rich varieties of feedback and support provision, two

external e-tutorials were utilised: MyStatLab (MSL)

and MyMathLab (MML). These e-tutorials are

generic LMSs for learning statistics and

mathematics developed by the publisher Pearson.

Please see Tempelaar et al. (2014, 2015), for a more

detailed description of these tools.

The MyLab functionality used in the module are

that of practicing (replacing traditional practicals),

formative assessment, and quizzing. Quizzing allows

students to achieve a bonus on the score of the final

written exam, determining the pass/fail decision for

the module. So although quizzing makes use of the

same materials as the self-steered formative

assessments, and the weight of quiz performance in

the pass/fail decision is limited, the quiz element

does entail some summative aspects beyond

important formative ones. And it has been in the

quizzing that we revised the instructional design of

the module. In the first cohort, quiz items were

randomly selected from the same pool of items

students could access in their formative assessments.

Thus by putting sufficient effort in self-assessment,

students could achieve knowledge about all item

types in the quiz (not with the exact items

themselves, since items are parametrized). To avoid

stimulating students to repeat formative assessments

over and over again only to learn all different item

types, we split all item pools into two non-

overlapping sub pools, one for self-assessments, the

other for quizzing. It is exactly this change,

prediction models might pick up from the LA

studies, if they appear to be sufficiently sensitive to

the instructional design.

3 RESEARCH METHODS

3.1 Research Questions

Combining empirical evidence on how students’

usage and behaviour in LMS influences academic

performance (e.g., Arbaugh, 2014; Macfadyen and

Dawson, 2010; Marks, Sibley, and Arbaugh, 2005;

Wolff et al., 2013), how the use of e-tutorials or

other formats of blended learning effects

performance (e.g., Lajoie and Azevedo, 2006), and

how feedback based on learning dispositions

stimulates learning (Buckingham Shum and Deakin

Crick, 2012), our study aims to discover the relative

contributions of LMSs, formative testing, e-tutorials,

and applying dispositional learning analytics to

student performance. The prime aim of the analysis

is predictive modelling (Baker, 2010; Wolff et al.,

2013), with a focus on the role each of these data

sources can play in generating timely, informative

feedback for students. In the investigation of

predictive modelling, we will focus on the stability

of prediction models, defined as the similarity of the

prediction models in the two subsequent cohorts,

and the sensitivity of the prediction models: will

they signal the revision in instructional design.

Q1 To what extent do distinct data sources, such

as (self-reported) learning dispositions of students,

LMSs and e-tutorial data (formative assessments)

predict academic performance over time?

Q2 To what extent are prediction models stable,

in the meaning that predictive modelling in both

cohorts results in invariant model structures with

similar weights of the prediction variables?

Q3 To what extent are prediction models

sensitive, in the meaning that predictive modelling

in both cohorts results in different models where the

instructional design of the module has been revised?

3.2 Methodology

3.2.1 Context of Study

The educational system in which students learn

mathematics and statistics is best described as a

‘blended’ or ‘hybrid’ system. The main component

is face-to-face: problem-based learning (PBL), in

small groups (14 students), coached by a content

expert tutor (Rienties, Tempelaar, Van den Bossche,

Gijselaers, and Segers, 2009; Schmidt, Van Der

Molen, Te Winkel, and Wijnen, 2009; Tempelaar,

Rienties, and Giesbers, 2009). Participation in these

tutorial groups is required, as for all courses based

on the Maastricht PBL system. Optional is the online

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

158

component of the blend: the use of the two e-

tutorials (Tempelaar et al., 2013). This optional

component fits the Maastricht educational model,

which is student-centred and places the

responsibility for making educational choices

primarily on the student (Schmidt et al., 2009;

Tempelaar et al., 2013). At the same time, due to

strong diversity in prior knowledge in mathematics

and statistics, not all students, in particular those at

the high end, will benefit equally from using these

environments. However, the use of e-tutorials and

achieving good scores in the practicing modes of the

MyLab environments is stimulated by making bonus

points available for good performance in the

quizzes.

The student-centred characteristic of the

instructional model requires, first and foremost,

adequate informative feedback to students so that

they are able to monitor their study progress and

their topic mastery in absolute and relative sense.

The provision of relevant feedback starts on the first

day of the course when students take two diagnostic

entry tests for mathematics and statistics (Tempelaar

et al., 2013). Feedback from these entry tests

provides a first signal of the importance for using the

MyLab platforms. Next, the MML and MSL-

environments take over the monitoring function: at

any time students can see their progress in preparing

the next quiz, get feedback on the performance in

completed quizzes, and on their performance in the

practice sessions. The same (individual and

aggregated) information is also available for the

tutors in the form of visual dashboards (Clow, 2013;

Verbert et al., 2012). Although the primary

responsibility for directing the learning process is

with the student, the tutor acts complementary to

that self-steering, especially in situations where the

tutor considers that a more intense use of e-tutorials

is desirable, given the position of the student

concerned. In this way, the application of learning

analytics shapes the instructional support.

3.2.2 Participants

From the two most recent cohorts of freshmen

(2013/2014 and 2014/2015) all students were

included who in some way participated in learning

activities (i.e., have been active in BlackBoard):

1005 and 1006 students respectively. A large

diversity in the student population is present: only

25% were educated in the Dutch high school system.

The largest group, 45% of the freshmen, were

educated according to the German Abitur system.

High school systems in Europe differ strongly, most

particularly in the teaching of mathematics and

statistics. Therefore, it is crucial that the first module

offered to these students is flexible and allows for

individual learning paths (Tempelaar, et al., 2009,

2013; Tempelaar, Kuperus, et al., 2012). In the

investigated course, students work an average 32.6

hours in MML and 20.7 hours in MSL, 30% to 40%

of the available time of 80 hours for learning in both

topics.

3.3 Instruments and Procedure

We will investigate the relationships between a

range of data sources, leading to in total 102

different variables. In the subsections that follow,

the several data sources are described that provide

the predictor variables for our predictive modelling.

3.3.1 Registration Systems Capturing

Demographic Data

In line with academic retention or academic

analytics literature (Marks et al., 2005; Richardson,

2012), several demographic factors are known to

influence performance. A main advantage of this

type of data is that institutions can relatively easily

extract this information from student admission, and

are therefore logical factors to include in learning

analytics models.

Demographic data were extracted from concern

systems: nationality, gender, age and prior

education. Since, by law, introductory modules like

ours need to be based on the coverage of Dutch high

school programs, we converted nationality data into

an indicator for having been educated in the Dutch

high school system. 24% of students are educated in

the Dutch higher education system, 76% of students

in international systems, mostly of continental

European countries. About 39% of students are

female, with 61% males. Age demonstrates very

little variation (nearly all students are below 20), and

no relationship with any performance, and is

excluded. The main demographic variable is the type

of mathematics track in high school: advanced,

preparing for sciences or technical studies in higher

education, or basic, and preparing for social sciences

(the third level, mathematics for arts and humanities,

does not provide access to our program). Exactly

two third of the students has a basic mathematics

level, one third has an advanced level. (See

Tempelaar, et al., 2009, 2013; Tempelaar, Kuperus,

et al., 2012 for detailed description.)

StabilityandSensitivityofLearningAnalyticsbasedPredictionModels

159

3.3.2 Diagnostic Entry Tests

At the very start of the course, so shaping part of

Week0 data, are entry tests for mathematics and

statistics all students were required to do. Both entry

tests are based on national projects directed at

signalling deficiencies in the area of mathematics

and statistics encountered in the transition from high

school to university (see Tempelaar, Niculescu, et

al., 2012 for an elaboration). Topics included in the

entry tests refer to foundational topics, often covered

in junior high school programs, such as basic

algebraic skills or statistical literacy.

3.3.3 Learning Dispositions Data

Learning dispositions of three different types were

included: learning styles, learning motivation and

engagement, and learning emotions. The first two

facets were measured at the start of the module, and

from the longitudinal perspective are assigned to

Week0 data. Learning style data are based on the

learning style model of Vermunt (1996). Vermunt’s

model distinguishes learning strategies (deep, step-

wise, and concrete ways of processing learning

topics), and regulation strategies (self, external, and

lack of regulation of learning). Recent Anglo-Saxon

literature on academic achievement and dropout

assigns an increasingly dominant role to the

theoretical model of Andrew Martin (2007): the

'Motivation and Engagement Wheel’. This model

includes both behaviours and thoughts, or

cognitions, that play a role in learning. Both are

subdivided into adaptive and mal-adaptive (or

obstructive) forms. Adaptive thoughts consist of

Self-belief, Value of school and Learning focus,

whereas adaptive behaviours consist of Planning,

Study management and Perseverance. Maladaptive

thoughts include Anxiety, Failure Avoidance, and

Uncertain Control, and lastly, maladaptive

behaviours include Self-Handicapping and

Disengagement. As a result, the four quadrants are:

adaptive behaviour and adaptive thoughts (the

‘boosters’), mal-adaptive behaviour (the ‘guzzlers’)

and obstructive thoughts (the ‘mufflers’).

The third component, learning emotions, is more

than a disposition: it is also an outcome of the

learning process. Therefore, the timing of the

measurement of learning emotions is Week4,

halfway into the module, so that students have

sufficient involvement and experience in the module

to form specific learning emotions, but still timely

enough to make it a potential source of feedback.

Learning emotions were measured through four

scales of the Achievement Emotions Questionnaire

(AEQ) developed by Pekrun et al. (2011):

Enjoyment, Anxiety, Boredom and Hopelessness.

All learning dispositions are administered through

self-report surveys scored on a 7-point Likert scale.

3.3.4 Learning Management System

User track data of LMS are often at the heart of

learning analytics applications. Also in our context

intensive use of our LMS, BlackBoard (BB), has

been made. In line with Agudo-Peregrina et al.

(2014), we captured tracking data from six learning

activities. First, the diagnostic entry tests were

administered in BB, and through the MyGrades

function, students could access feedback on their test

attempts. Second, surveys for learning dispositions

were administered in BB. Third, two lectures per

week were provided, overview lectures at the start of

the week, and recap lectures at the end of the week,

which were all videotaped and made available as

webcasts through BB. Fourth, several exercises for

doing applied statistical analyses, including a student

project, were distributed through BB, with a

requirement to upload solutions files again in BB.

Finally, communication from the module staff,

various course materials and a series of old exams

(to practice the final exam) were made available in

BB. For all individual BB items, Statistics Tracking

was set on to create use intensity data on BB

function and item level.

3.3.5 e-tutorials MyMathLab and

MyStatLab

Students worked in the MyMathLab and MyStatLab

e-tutorials for all seven weeks, practicing homework

exercises selected by the module coordinator. The

MyLab systems track two scores achieved in each

task, mastery score (MyLabMastery) and time on

task (MyLabHours). Those data were aggregated

over the on average 25 weekly tasks for

mathematics, and about 20 tasks for statistics, to

produce four predictors, two for each topic, for each

of the seven weeks. Less aggregated data sets have

been investigated, but due to high collinearity in data

of individual tasks, these produced less stable

prediction models.

The three (bonus) quizzes took place in the

weeks 3, 5 and 7. Quizzes were administrated in the

MyLab tools, and consisted of selections of practice

tasks from the two previous weeks. As indicated: the

single revision in the instructional design of the

course between the two class years is in the

inclusion of quiz items in the item pool availability

for self-assessment.

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

160

3.3.6 Academic Performance

Four measures of academic performance in the

Quantitative Methods module in both cohorts were

included for predictive modelling: score in both

topic components of the final, written exam, MExam

and SExam, and aggregated scores for the three

quizzes in both topics, MQuiz and SQuiz, where M

refers to the topic mathematics, and S refers to the

topic Statistics.

3.4 Data Analysis

Complete information was obtained for 874

respectively 879 students (87%) on the various

instruments. Prediction models applied in this study

are all of linear, regression type. More complex

models have been investigated, in particular

interaction models. However, none of these more

advanced model types passed the model selection

criterion that prediction models should be stable

over all seven weekly intervals. Collinearity existing

in track data in a similar way forced us to aggregate

that type of data into weekly units; models based on

less aggregated data such as individual task data

gave rise to collinearity issues.

4 RESULTS

The aim of this study being predictive modelling in a

rich data context, we will focus the reporting on the

coefficient of multiple correlation, R, of the several

prediction models. Although the ultimate aim of

prediction modelling is often the comparison of

explained variation, which is based on the square of

the multiple correlation, we opted for using R itself,

to allow for more detailed comparisons between

alternative models. Values for R are documented in

Table 1 for prediction models based on alternative

data sets, and for both cohorts. For data sets that are

longitudinal in nature and allow for incremental

weekly data sets, the growth in predictive power is

illustrated in time graphs for BB track data, MyLabs

track data and test performance data. To ease

comparison, all graphs share the same vertical scale.

4.1 Predictive Power per Topic

In the comparison of the several columns of

prediction accuracy in Table 1, one of the most

striking outcomes is that the predictive power for

mathematics uniformly dominates that for statistics,

in both cohorts, and for both performance measures

exam and quiz (with one single exception). The

difference is easy to explain: students enter

university with very different levels of prior

knowledge of and prior education in mathematics.

For that reason, demographics (containing the

dummy for high school math at advanced level) as

well as entry test contribute strongly in predictive

power. Statistics, not being part of the curriculum of

most European high school systems, does not profit

from the same type of predictors. This outcome

corroborates findings from previous research (Marks

et al., 2005; Richardson, 2012; Tempelaar et al.,

2013) that prior education seems to be a useful

factor to include in learning analytics modelling.

The single predictor performing equally well in both

topics represents learning dispositions: both learning

styles, and motivation and engagement variables, do

not differentiate between topics, signalling the

unique contribution that learning dispositions can

possess in LA based prediction models.

4.2 Predictive Power per Performance

Measure

In the comparison of predictive power of the two

performance measures, exam and quiz, of

corresponding topics and cohorts, we find less

articulated differences. Most predictor variables

predict exam performance with similar accuracy as

quiz performance. The clear exception to this

outcome relates the system tracking data collected

from the two MyLab systems: time in MML and

MSL, and mastery in MML and MSL. Given the

strong ties between the self-steered formative

assessment in the e-tutorials, and the quizzing

administered in the same e-tutorials, we find that

MyLab track data have much stronger predictive

power toward quiz performance, than toward exam

performance (the same is true for quiz performance

acting as predictor for later quizzes).

4.3 Predictive Power per Data Source

In a comparison of prediction accuracy of the

several data sources, the outcomes of this study are

fully in line with our findings in previous research

(Tempelaar et al., 2014, 2015). Most powerful

predictor is found in the cognitive data: scores on

entry tests, and scores in quizzes. From the moment

the first quiz data become available, other data

sources hardly contribute anymore in the prediction

of performance measures: see Figure 2. However:

the first quiz data are only available at the end of the

third week, about half way the module. More timely

StabilityandSensitivityofLearningAnalyticsbasedPredictionModels

161

data, already available from the start of the module

on, is found in the track data of the MyLab systems

(Figure 1, right panel). These data dominate the

predictive power of track data collected from the

LMS (Figure 1, left panel).

Table 1: Predictive power, as multiple correlation R, of various data sets and various timings, for four performance

measures, two cohorts.

Data source Timing

MExam

2013

SExam

2013

MQuiz

2013

SQuiz

2013

MExam

2014

SExam

2014

MQuiz

2014

SQuiz

2014

Demographics Week0 .43 .29 .39 .21 .24 .22 .27 .21

EntryTests Week0 .43 .30 .45 .24 .37 .28 .47 .29

Learning Styles Week0 .24 .22 .22 .23 .20 .23 .18 .25

Motivation & Engagement Week0 .30 .31 .33 .32 .19 .24 .23 .23

BlackBoard Week0 .12 .09 .16 .15 .19 .07 .16 .10

AllWeek0 Week0 .59 .46 .58 .43 .48 .43 .55 .43

BlackBoard Week1 .13 .13 .19 .16 .20 .08 .17 .11

MyLabs Week1 .37 .30 .48 .47 .34 .28 .44 .36

AllWeek1 Week1 .61 .50 .66 .57 .52 .49 .63 .53

BlackBoard Week2 .15 .14 .20 .17 .21 .10 .18 .11

MyLabs Week2 .39 .36 .50 .50 .36 .34 .45 .39

AllWeek2 Week2 .62 .52 .67 .64 .53 .52 .64 .58

BlackBoard Week3 .16 .14 .20 .17 .22 .11 .20 .11

MyLabs Week3 .47 .41 .61 .56 .41 .35 .47 .39

Quiz1 Week3 .67 .58 .86 .76 .60 .54 .81 .74

AllWeek3 Week3 .74 .66 .89 .81 .66 .64 .85 .79

Learning Emotions Week4 .48 .33 .49 .30 .32 .25 .38 .25

BlackBoard Week4 .16 .14 .22 .19 .24 .12 .21 .15

MyLabs Week4 .50 .45 .65 .60 .45 .40 .51 .40

AllWeek4 Week4 .79 .67 .90 .82 .76 .66 .86 .80

BlackBoard Week5 .17 .14 .22 .19 .24 .12 .21 .15

MyLabs Week5 .52 .50 .68 .66 .46 .44 .53 .46

Quiz2 Week5 .72 .61 .96 .93 .67 .64 .94 .93

AllWeek5 Week5 .77 .68 .97 .94 .72 .71 .95 .94

BlackBoard Week6 .17 .15 .22 .21 .25 .13 .22 .15

MyLabs Week6 .52 .51 .69 .66 .46 .45 .52 .46

AllWeek6 Week6 .78 .69 .97 .94 .73 .71 .96 .94

BlackBoard Week7 .18 .15 .22 .21 .26 .14 .23 .15

MyLabs Week7 .53 .51 .69 .67 .48 .46 .55 .47

Quiz3 Week7 .72 .61 1.00 1.00 .69 .66 1.00 1.00

AllWeek7 Week7 .78 .69 1.00 1.00 .75 .72 1.00 1.00

Note: MExam and SExam refer to exam scores in topics mathematics and statistics; MQuiz and SQuiz to the corresponding quiz score.

Figure 1: Predictive power of BB track data, and MML and MSL system data for six performance measures.

0,0

0,2

0,4

0,6

0,8

1,0

MExam2013

SExam2013

MQuiz2013

SQuiz2013

MExam2014

SExam2014

MQuiz2014

SQuiz2014

0,0

0,2

0,4

0,6

0,8

1,0

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

162

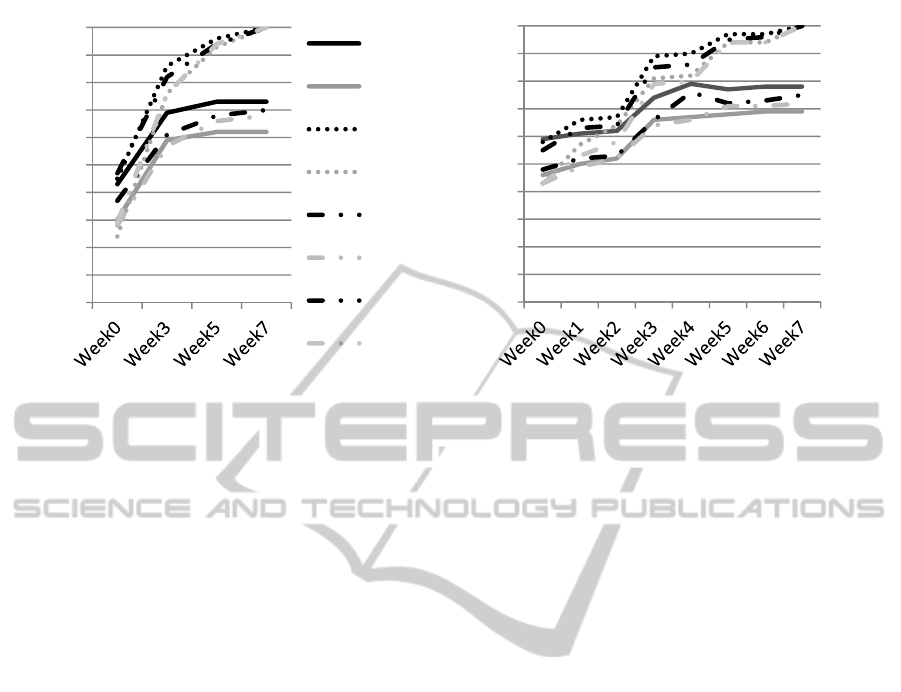
Figure 2: Predictive power of EntryTest and Quiz data, and all data combined for six performance measures.

4.4 Predictive Power per Cohort

Both Figures, as well Table 1, do also allow a

comparison of prediction accuracy between cohorts.

As to find an answer to the second and third research

question: stability and sensitivity of prediction

models. Stability follows from the strong similarities

between 2013 and 2014 outcomes. The pattern

reported in the previous section, with strongest

predictive power in the quiz data, followed by entry

test and e-tutorial track data, and least predictive

power in LMS track data, is equally visible for the

2013 cohort, as for the 2014 cohort. Beyond

predictive power itself, also the structure of the

regression models in the two cohorts (not reported

here) demonstrate strong correspondence. With one

exception: prediction accuracy of quizzes in the

2014 cohort, both for mathematics and statistics, is

at a much lower level than in the 2013 cohort. But it

was exactly this exception we expected on the basis

of the instructional redesign applied. Breaking the

strong link between items available for formative

assessment, and items used in quizzing, it was hoped

for to take out the strong stimulus to repeatedly

practice in the same item pool. Given that the lower

predictive power of quiz performance mainly comes

from the reduction in the contribution of the MyLab

track data, this is exactly what we aimed for in the

third research question: the prediction model is

sufficiently sensitive to signal the effects of the

instructional intervention, aiming to change students

learning behaviour.

5 DISCUSSION AND

CONCLUSION

In this empirical study into predictive modelling of

student performance, we investigated several

different data sources to explore the potential of

generating informative feedback for students and

teachers using learning analytics: data from

registration systems, entry test data, students’

learning dispositions, BlackBoard tracking data,

tracking data from two e-tutorial systems, and data

from systems for formative, computer assisted

assessments. In line with recommendations by

Agudo-Peregrina et al. (2014), we collected both

dynamic, longitudinal user data and semi-static data,

such as prior education. We corroborate our finding

in previous research (Tempelaar et al., 2015) that

the role of BlackBoard track data in predicting

student performance is dominated by the predictive

power of any of the other data components, implying

that in applications with such rich data available,

BlackBoard data have no added value in predicting

performance and signalling underperforming

students. This seems to confirm initial findings by

Macfadyen and Dawson (2010), who found that

simple clicking behaviour in a LMS is at best a poor

proxy for actual user-behaviour of students.

Data extracted from the testing mode of the

MyLab systems, the quiz data, dominate in a similar

respect all other data, including data generated by

the practicing mode of MyLabs, indicating the

predictive power of "true" assessment data (even if it

comes from assessments that are more of formative,

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

MExam2013

SExam2013

MQuiz2013

SQuiz2013

MExam2014

SExam2014

MQuiz2014

SQuiz2014

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

StabilityandSensitivityofLearningAnalyticsbasedPredictionModels

163

than summative type). However, assessment data is

typically delayed data (Boud and Falchikov, 2006;

Whitelock et al., 2014; Wolff et al., 2013), not

available before midterm, or as in our case, the third

week of the course. Up to the moment this richest

data component becomes available, entry test data

and the combination of mastery data and use

intensity data generated by the e-tutorial systems are

a second best alternative for true assessment data.

This links well with Wolff et al. (2013), who found

that performance on initial assessments during the

first parts of online modules were substantial

predictors for final exam performance.

A similar conclusion can be made with regards to

the learning disposition data: up to the moment that

assessment data become available, they serve a

unique role in predicting student performance and

signalling underperformance beyond system track

data of the e-tutorials. From the moment that

computer assisted, formative assessment data

become available, their predictive power is

dominated by that of performance in those formative

assessments. Dispositions data are not as easily

collected as system tracking data from LMSs or e-

tutorial systems (Buckingham Shum and Deakin

Crick, 2012). The answer to the question if the effort

to collect dispositional data is worthwhile (or not), is

therefore strongly dependent on when richer

(assessment) data becomes available, and the need

for timely signalling of underperformance. If timely

feedback is required, the combination of data

extracted from e-tutorials, both in practicing and test

modes, and learning disposition data suggests being

the best mix to serve learning analytics applications.

In contrast to Agudo-Peregrina et al. (2014), who

found no consistent patterns in two blended courses

using learning analytics, we did find that our mix of

various LMS data allowed us to accurately predict

academic performance, both from a static and

dynamic perspective. The inclusion of extensive

usage of computer-assisted tests might explain part

of this difference, as well as more fine-grained

learning disposition data allowed us to model the

learning patterns from the start of the module.

The inclusion of two different cohorts in this

study allows the investigation of two additional

crucial issues: that of stability and sensitivity of

prediction models. Evidence of both was found.

Both findings profit from the availability of a very

broad set of predictor variables, that proof to be

complementary in predicting performance. Being

complementary implies that the collinearity in the

set of predictors is limited. This limited collinearity

contributes to stability; within a set of predictors that

demonstrate stronger collinearity, prediction models

will tend to be more context dependent, less stable

over different contexts, such as cohorts. The broad

spectrum of predictor variables does also explain the

sensitivity of the prediction model to changes in the

instructional design. Without the inclusion of e-

tutorial track data, our LA based prediction model

would not have been able to signal the change in the

construction of quizzes. Thus, a broad set of

complementary predictor variables is crucial in the

successful application of LA.

To these stability and sensitivity aspects add

another one: that of feedback and intervention.

Feedback is informative if two conditions are

satisfied: it is predictive, and allows for intervention.

Feedback based on prior education may be strongly

predictive, but is certainly incapable of designing

interventions as to eliminate the foreseen cause of

underperformance (Boud and Falchikov, 2006;

Whitelock et al., 2014). Feedback related to learning

dispositions, such as signalling suboptimal learning

strategies, or inappropriate learning regulation, is

generally open to interventions to improve the

learning process (Lehmann et al., 2014; Pekrun et

al., 2011). Feedback related to suboptimal use of e-

tutorials shares that position: both predictive, and

open for intervention. The requirement of a broad

and complementary set of predictors thus needs a

completion: that of enabling intervention.

ACKNOWLEDGEMENTS

The project reported here has been supported and

co-financed by SURF-foundation as part of the

Learning Analytics Stimulus program.

REFERENCES

Agudo-Peregrina, Á. F., Iglesias-Pradas, S., Conde-

González, M. Á., and Hernández-García, Á. (2014).

Can we predict success from log data in VLEs?

Classification of interactions for learning analytics and

their relation with performance in VLE-supported F2F

and online learning. Computers in Human Behavior,

31, 542-550. doi: 10.1016/j.chb.2013.05.031.

Arbaugh, J. B. (2014). System, scholar, or students?

Which most influences online MBA course

effectiveness? Journal of Computer Assisted Learning.

doi: 10.1111/jcal.12048.

Baker, R. (2010). Data mining for education. International

encyclopedia of education, 7, 112-118.

Bienkowski, M., Feng, M., and Means, B. (2012).

Enhancing teaching and learning through educational

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

164

data mining and learning analytics: An issue brief. US

Department of Education, Office of Educational

Technology, 1-57.

Boud, D., and Falchikov, N. (2006). Aligning assessment

with longterm learning. Assessment & Evaluation in

Higher Education, 31(4), 399-413. doi:

10.1080/02602930600679050.

Buckingham Shum, S., and Deakin Crick, R. (2012).

Learning dispositions and transferable competencies:

pedagogy, modelling and learning analytics. Paper

presented at the 2nd International Conference on

Learning Analytics & Knowledge, Vancouver, British

Columbia.

Buckingham Shum, S., and Ferguson, R. (2012). Social

Learning Analytics. Journal of Educational

Technology & Society, 15(3). doi:

10.1145/2330601.2330616.

Clow, D. (2013). An overview of learning analytics.

Teaching in Higher Education, 18(6), 683-695. doi:

10.1080/13562517.2013.827653.

Greller, W., and Drachsler, H. (2012). Translating

Learning into Numbers: A Generic Framework for

Learning Analytics. Journal of Educational

Technology & Society, 15(3).

Hommes, J., Rienties, B., de Grave, W., Bos, G.,

Schuwirth, L., and Scherpbier, A. (2012). Visualising

the invisible: a network approach to reveal the

informal social side of student learning. Advances in

Health Sciences Education, 17(5), 743-757. doi:

10.1007/s10459-012-9349-0.

Järvelä, S., Hurme, T., and Järvenoja, H. (2011). Self-

regulation and motivation in computer-supported

collaborative learning environments. In S. Ludvigson,

A. Lund, I. Rasmussen and R. Säljö (Eds.), Learning

across sites: new tools, infrastructure and practices

(pp. 330-345). New York, NY: Routledge.

Lajoie, S. P., and Azevedo, R. (2006). Teaching and

learning in technology-rich environments. In P.

Alexander and P. Winne (Eds.), Handbook of

educational psychology (2 ed., pp. 803-821). Mahwah,

NJ: Erlbaum.

Lehmann, T., Hähnlein, I., and Ifenthaler, D. (2014).

Cognitive, metacognitive and motivational

perspectives on preflection in self-regulated online

learning. Computers in Human Behavior, 32, 313-323.

doi: 10.1016/j.chb.2013.07.051.

Macfadyen, L. P., and Dawson, S. (2010). Mining LMS

data to develop an “early warning system” for

educators: A proof of concept. Computers &

Education, 54(2), 588-599. doi:

10.1016/j.compedu.2009.09.008.

Marks, R. B., Sibley, S. D., and Arbaugh, J. B. (2005). A

Structural Equation Model of Predictors for Effective

Online Learning. Journal of Management Education,

29(4), 531-563. doi: 10.1177/1052562904271199.

Martin, A. J. (2007). Examining a multidimensional model

of student motivation and engagement using a

construct validation approach. British Journal of

Educational Psychology, 77(2), 413-440. doi:

10.1348/000709906X118036.

Narciss, S. (2008). Feedback strategies for interactive

learning tasks. In J. M. Spector, M. D. Merrill, J. J. G.

van Merrienboer and M. P. Driscoll (Eds.), Handbook

of Research on Educational Communications and

Technology (3 ed., pp. 125-144). Mahaw, NJ:

Lawrence Erlbaum Associates.

Narciss, S., and Huth, K. (2006). Fostering achievement

and motivation with bug-related tutoring feedback in a

computer-based training for written subtraction.

Learning and Instruction, 16(4), 310-322. doi:

10.1016/j.learninstruc.2006.07.003.

Nistor, N., Baltes, B., Dascălu, M., Mihăilă, D., Smeaton,

G., and Trăuşan-Matu, Ş. (2014). Participation in

virtual academic communities of practice under the

influence of technology acceptance and community

factors. A learning analytics application. Computers in

Human Behavior, 34, 339-344. doi:

10.1016/j.chb.2013.10.051.

Oblinger, D. G. (2012). Let's Talk... Analytics.

EDUCAUSE Review, 47(4), 10-13.

Pekrun, R., Goetz, T., Frenzel, A. C., Barchfeld, P., and

Perry, R. P. (2011). Measuring emotions in students’

learning and performance: The Achievement Emotions

Questionnaire (AEQ). Contemporary Educational

Psychology, 36(1), 36-48. doi:

10.1016/j.cedpsych.2010.10.002.

Richardson, J. T. E. (2012). The attainment of White and

ethnic minority students in distance education.

Assessment & Evaluation in Higher Education, 37(4),

393-408. doi: 10.1080/02602938.2010.534767.

Rienties, B., and Alden Rivers, B. (2014). Measuring and

Understanding Learner Emotions: Evidence and

Prospects. Learning Analytics Review 1, Learning

Analytics Community Exchange (LACE).

http://www.laceproject.eu/learning-analytics-

review/measuring-and-understanding-learner-

emotions/

Rienties, B., Cross, S., and Zdrahal, Z. (2015).

"Implementing a Learning Analytics Intervention and

Evaluation Framework: what works?" In B.

Motidyang and R. Butson (Eds.): Big data and

learning analytics in higher education. Springer,

Berlin.

Rienties, B., Tempelaar, D. T., Giesbers, B., Segers, M.,

and Gijselaers, W. H. (2012). A dynamic analysis of

social interaction in Computer Mediated

Communication; a preference for autonomous

learning. Interactive Learning Environments,

22(5),

631-648. doi: 10.1080/10494820.2012.707127.

Rienties, B., Tempelaar, D. T., Van den Bossche, P.,

Gijselaers, W. H., and Segers, M. (2009). The role of

academic motivation in Computer-Supported

Collaborative Learning. Computers in Human

Behavior, 25(6), 1195-1206. doi:

10.1016/j.chb.2009.05.012.

Schmidt, H. G., Van Der Molen, H. T., Te Winkel, W. W.

R., and Wijnen, W. H. F. W. (2009). Constructivist,

Problem-Based Learning does work: A meta-analysis

of curricular comparisons involving a single medical

StabilityandSensitivityofLearningAnalyticsbasedPredictionModels

165

school. Educational Psychologist, 44(4), 227-249. doi:

10.1080/00461520903213592.

Siemens, G. (2013). Learning Analytics: The Emergence

of a Discipline. American Behavioral Scientist, 57(10),

1380-1400. doi: 10.1177/0002764213498851.

Siemens, G., Dawson, S., and Lynch, G. (2013).

Improving the quality of productivity of the higher

education sector: Policy and strategy for systems-level

deployment of learning analytics: Solarresearch.

Stiles, R. J. (2012). Understanding and Managing the

Risks of Analytics in Higher Education: A Guide:

Educause.

Tempelaar, D. T., Heck, A., Cuypers, H., van der Kooij,

H., and van de Vrie, E. (2013). Formative Assessment

and Learning Analytics. In D. Suthers and K. Verbert

(Eds.), Proceedings of the 3rd International

Conference on Learning Analytics and Knowledge,

205-209. New York: ACM. doi:

10.1145/2460296.2460337.

Tempelaar, D. T., Kuperus, B., Cuypers, H., Van der

Kooij, H., Van de Vrie, E., and Heck, A. (2012). “The

Role of Digital, Formative Testing in e-Learning for

Mathematics: A Case Study in the Netherlands”. In:

“Mathematical e-learning” [online dossier].

Universities and Knowledge Society Journal (RUSC),

9(1). UoC.

Tempelaar, D. T., Niculescu, A., Rienties, B., Giesbers,

B., and Gijselaers, W. H. (2012). How achievement

emotions impact students' decisions for online

learning, and what precedes those emotions. Internet

and Higher Education, 15(3), 161–169. doi:

10.1016/j.iheduc.2011.10.003.

Tempelaar, D. T., Rienties, B., and Giesbers, B. (2009).

Who profits most from blended learning? Industry and

Higher Education, 23(4), 285-292.

Tempelaar, D. T., Rienties, B., and Giesbers, B. (2014).

Computer Assisted, Formative Assessment and

Dispositional Learning Analytics in Learning

Mathematics and Statistics. In M. Kalz and E. Ras

(Eds.), Computer Assisted Assessment. Research into

E-Assessment, pp. 67-78. Berlin, Springer:

Communications in Computer and Information

Science, Volume 439. doi: 10.1007/978-3-319-08657-

6_7.

Tempelaar, D. T., Rienties, B, and Giesbers, B. (2015). In

search for the most informative data for feedback

generation: Learning analytics in a data-rich context.

Computers in Human Behavior, 47, 157-167. doi:

10.1016/j.chb.2014.05.038.

Thakur, G., Olama, M. M., McNair, W., Sukumar, S. R.,

and Studham, S. (2014). Towards Adaptive

Educational Assessments: Predicting Student

Performance using Temporal Stability and Data

Analytics in Learning Management Systems. In:

Proceedings 20th ACM SIGKDD conference on

knowledge discovery and data mining: ACCESS, New

York city, NY.

Tobarra, L., Robles-Gómez, A., Ros, S., Hernández, R.,

and Caminero, A. C. (2014). Analyzing the students’

behavior and relevant topics in virtual learning

communities. Computers in Human Behavior, 31, 659-

669. doi: 10.1016/j.chb.2013.10.001.

Verbert, K., Manouselis, N., Drachsler, H., and Duval, E.

(2012). Dataset-Driven Research to Support Learning

and Knowledge Analytics. Journal of Educational

Technology & Society, 15(3), 133-148.

Vermunt, J. D. (1996). Metacognitive, cognitive and

affective aspects of learning styles and strategies: A

phenomenographic analysis. Higher Education, 31,

25–50. doi: 10.1007/BF00129106.

Whitelock, D., Richardson, J., Field, D., Van Labeke, N.,

and Pulman, S. (2014). Designing and Testing Visual

Representations of Draft Essays for Higher Education

Students. Paper presented at the LAK 2014,

Indianapolis.

Wolff, A., Zdrahal, Z., Nikolov, A., and Pantucek, M.

(2013). Improving retention: predicting at-risk

students by analysing clicking behaviour in a virtual

learning environment. In D. Suthers and K. Verbert

(Eds.), Proceedings of the 3rd International

Conference on Learning Analytics and Knowledge,

145-149. New York: ACM. doi:

10.1145/2460296.2460324.

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

166