Context-aware MapReduce for Geo-distributed Big Data

Marco Cavallo, Giuseppe Di Modica, Carmelo Polito and Orazio Tomarchio

Department of Electrical, Electronic and Computer Engineering, University of Catania, Catania, Italy

Keywords:

Big Data, MapReduce, Hierarchical Hadoop, Context Awareness, Partition Number.

Abstract:

MapReduce is an effective distributed programming model used in cloud computing for large-scale data anal-

ysis applications. Hadoop, the most known and used open-source implementation of the MapReduce model,

assumes that every node in a cluster has the same computing capacity and that data are local to tasks. How-

ever, in many real big data applications where data may be located in many datacenters distributed over the

planet these assumptions do not hold any longer, thus affecting Hadoop performance. This paper addresses

this point, by proposing a hierarchical MapReduce programming model where a toplevel scheduling system

is aware of the underlying computing contexts heterogeneity. The main idea of the approach is to improve

the job processing time by partitioning and redistributing the workload among geo-distributed workers: this is

done by adequately monitoring the bottom-level computing and networking context.

1 INTRODUCTION

In the last few years, the pervasivity and the

widespread diffusion of information technology ser-

vices such as social computing applications and smart

city services produced a signiﬁcant increase of the

amount of digital data, which in a single day may even

reach a few petabytes (Facebook, 2012).

The new term “Big Data” has been created to indi-

cate this phenomenon: it refers to collections of very

large datasets, that require unconventional tools (e.g

non-relational DBMS) to be managed and processed

within a reasonable time (Zikopoulos, P. and Eaton,

C., 2011). Big data analysis requires adequate in-

frastructure capable of processing so large amount of

data: parallel and distributed computing techniques

are commonly used to efﬁciently manipulate such

data. MapReduce is probably the most known parallel

programming paradigm that is nowadays used in the

context of Big Data (Dean and Ghemawat, 2004). It

is based on two functions, Map and Reduce: the ﬁrst

one generates data partitions based on a given user de-

ﬁned function, and the second one performs a sort of

summary operation on Map outputs. Apache Hadoop

is an open source implementation of the MapReduce

approach (The Apache Software Foundation, 2011);

in the last few years it has evolved by including many

features and reaching a high level of adoption both in

industry than in academic community. Hadoop has

been designed mainly to work on clusters of homoge-

neous computing nodes belonging to the same local

area network; data locality is one of the crucial factors

affecting its performance. However, in many recent

Big Data scenarios, it is not uncommon the need to

deal with data which are geographically distributed.

In fact, the design of geo-distributed cloud services

is a widespread trend in cloud computing, through

the distribution of large amounts of data among data

centers located in different geographical locations. In

these scenarios, the data required to perform a task

is often non-local, which, as mentioned before, may

severely affect the performance of Hadoop.

In this paper, we propose a novel job scheduling

strategy that is aware of data location. The proposed

approach takes into account the actual heterogeneity

of nodes, network links and of data distribution. Our

solution follows a hierarchical approach, where a top-

level entity will take care of serving a submitted job:

this job is split into a number of bottom-level, inde-

pendent MapReduce sub-jobs that are scheduled to

run on the sites where data reside. The remainder

of the paper is organized as follows. Section 2 pro-

vides some motivation for the work and also discusses

some related work. In Section 3 we introduce the sys-

tem design and provide the details of the proposed

strategy. Section 4 provides the details of the strategy

adopted to partition data and distribute the workload.

Finally, Section 5 concludes the work.

414

Cavallo M., Di Modica G., Polito C. and Tomarchio O..

Context-aware MapReduce for Geo-distributed Big Data.

DOI: 10.5220/0005497704140421

In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 414-421

ISBN: 978-989-758-104-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 BACKGROUND AND

RATIONALE

Well know implementations of MapReduce have been

conceived to work on a single or on a few clusters

of homogeneous computing nodes belonging to a lo-

cal area network. Hadoop (The Apache Software

Foundation, 2011), the most famous open source im-

plementation of the MapReduce paradigm, performs

very poorly if executed on data residing in geographi-

cally distributed datacenters which are interconnected

to each other by means of links showing heteroge-

neous capacity (Heintz et al., 2014).

The main problem is that Hadoop is unaware of

both nodes’ and links’ capacity, nor it is aware of the

type of application that is going to crunch the data.

This may yield a very bad performance in terms of job

execution time, especially in the case a huge amount

of data are distributed over many heterogeneous data-

centers that are interconnected to each other’s through

disomogeneous network links. In the literature two

main approaches are followed by researchers to ef-

ﬁciently process geo-distributed data: a) enhanced

versions of the plain Hadoop implementation which

account for the nodes and the network heterogeneity

(Geo-hadoop approach) ; b) hierarchical frameworks

which gather and merge results from many Hadoop

instances locally run on distributed clusters (Hierar-

chical approach).

Geo-hadoop approaches (Kim et al., 2011; Mat-

tess et al., 2013; Heintz et al., 2014; Zhang et al.,

2014) reconsider the phases of the job’s execution

ﬂow (Push, Map, Shufﬂe, Reduce) in a perspective

where data are distributed at a geographic scale, and

the available resources (compute nodes and network

bandwidth) are disomogeneous. In the aim of reduc-

ing the job’s average makespan

, phases and the rela-

tive timing must be adequately coordinated.

Hierarchical approaches (Luo et al., 2011; Jay-

alath et al., 2014; Yang et al., 2007) envision two (or

sometimes more) computing levels: a bottom level,

where several plain MapReduce computations occur

on local data only, and a top level, where a central en-

tity coordinates the gathering of local computations

and the packaging of the ﬁnal result. A clear advan-

tage of this approach is that there is no need to mod-

ify the Hadoop algorithm, as its original version can

be used to elaborate data on a local cluster. Still a

strategy needs to be conceived to establish how to re-

distribute data among the available clusters in order to

optimize the job’s overall makespan.

The execution time of a job. It is measured from the

time the job is submitted to the time results are gathered

The solution we propose belongs to the hierarchi-

cal category. We address the typical scenario of a

big company which has many branches distributed all

over the world producing huge amounts of business-

sensitive data that need to be globally processed on

demand. Examples of application domains that fall

in this scenario are electronic commerce, content de-

livery networks, social networks, cloud service provi-

sioning and many more. The Hadoop seems to offer

the computing model that best suits this situation, be-

cause of its capability of providing parallel computa-

tion on multiple pieces of data. Unfortunately, com-

pany sites may be disomogeneous in terms of com-

puting capabilities and the amount of stored raw data.

Also, the inter-site network links have very limited

and unbalanced bandwidth that is usually employed

to support many types of inter-site communication.

This makes the plain Hadoop unﬁt for the depicted

scenario.

We believe a hierarchical computing model may

help since it decouples the job/task scheduling from

the actual computation. The approach we propose in-

troduces a novel job scheduling algorithm which ac-

counts for the discussed disomogeneity to optimize

the job makespan. Basically, when a job is submitted,

a top-level entity (“Orchestrator” in the remainder of

the paper) will take care of serving the job. In par-

ticular, the job is split into a number of bottom-level,

independent MapReduce sub-jobs that are scheduled

to run on the sites where data reside. According to

the original data localization, the computing capac-

ity of involved sites and the available inter-site band-

width, the Orchestrator may decide to migrate data

(or pieces of them) from site to site before bottom-

level MapReduce jobs are eventually started. Finally,

the results of MapReduce sub-jobs are forwarded to

a top-level Reducer that will package and deliver the

ﬁnal result. Unlike previous works, our job schedul-

ing algorithm aims to exploit fresh information con-

tinuously sensed from the distributed computing con-

text (available site’s computing capacity and inter-site

bandwidth) to guess each job’s optimum execution

ﬂow.

3 DESIGN OVERVIEW

According to the MapReduce paradigm, a generic

computation is called job (Dean and Ghemawat,

2004). A generic job is submitted to a scheduling sys-

tem which is responsible for splitting the job in several

tasks and mapping tasks to a set of available machines

within a cluster. The performance of a job is measured

by its completion time (some refers to it with the term

Context-awareMapReduceforGeo-distributedBigData

415

Top-Level Job

Output Data

Result

Local Hadoop Job

Orchestrator

Top Level

Data Transfer

MasterGlobal Reducer

Execute Top-Level

MapTask

Reduce

Bottom Level

PushResult

TJEP

getTJEP

MoveData

Site1

Site3

Site2

Push Top-Level

Map Result

Site4

MapReduce

Figure 1: Overall architecture.

makespan), i.e., the time for a job to complete. That

time heavily depends on the job’s execution ﬂow de-

termined by the scheduling system and the computing

power of the cluster machines where the tasks are ac-

tually executed.

In a scenario where computing machines belong

to many geographically distributed clusters there is an

additional parameter that may affect the job perfor-

mance. Communication links among clusters (inter-

cluster links) are often disomogeneous and have a

much lower capacity than the communication links

among machines within a cluster (intra-cluster links).

Basically, if a scheduling system does not account for

the unbalanced capacity of both machines and com-

munication links, the overall job’s performance may

degrade dramatically.

The key point of our proposal for a hierarchical

MapReduce programming model is the need of a top-

level scheduling system which is aware of the un-

derlying computing context’s heterogeneity. We ar-

gue such awareness has to be created and augmented

by periodically “sensing” the bottom-level computing

context. Information retrieved from the computing

context is then used to drive the generation of the par-

ticular job’s execution ﬂow which maximizes the job

performance.

In Figure 1 the basic reference scenario addressed

by our proposal is depicted. Sites (datacenters) pop-

ulate the bottom level of the hierarchy. Each site

stores a certain amount of data and is capable of run-

ning plain Hadoop jobs. Upon receiving a job, a site

transparently performs the whole MapReduce process

chain on the local cluster(s) and returns the result of

the elaboration. All the system business logic de-

voted to the management of the geo-distributed paral-

lel computing resides in the top-level of the hierarchy.

Upon the submission of a Hadoop job, the business

logic schedules the set of sub-jobs to be disseminated

in the distributed context, gathers the sub-job results

and packages the overall computation result.

In particular, the system business logic is com-

posed of the following entities:

• Orchestrator. It is responsible for the generation

of a Top-level Job Execution Plan (TJEP). A TJEP

contains the following information:

– the Data Logistic Plan (DLP), which states how

data targeted by the job have to be re-organized

(i.e., shifted) among sites;

– the Sub-job Scheduling Plan (SSP), which de-

ﬁnes the set of Hadoop sub-jobs to be submitted

to the sites holding the data.

• Master. It is the entity to which Hadoop Jobs are

submitted. It calls on the Orchestrator for the gen-

eration of the TJEP, and is in charge of enforcing

the TJEP according to the information contained

in the DLP and the SSP.

• Global Reducer. It performs the top-level reduc-

tion of the results obtained from the execution of

Hadoop sub-jobs.

At design time two important assumptions were

made. First, at the moment only one Global Reducer

is responsible for collecting and reducing the data

elaborated by bottom-level sites. One may argue this

choice impacts on the overall performance, neverthe-

less it does not invalidate the approach. Anyway, this

assumption is going to be relaxed in future work. Sec-

ond, being this approach a pure hierarchical approach,

the top-level MapReduce job must be coded in such a

way that the applied operations are “associative”, i.e.,

may be performed recursively at each level of the hi-

erarchy and the execution order of the operations does

not affect the ﬁnal result (Jayalath et al., 2014).

In the scenario of Figure 1 four geo-distributed

sites are depicted that hold company’s business data

sets. The numbered arrows describe a typical execu-

tion ﬂow triggered by the submission of a top-level

job. This speciﬁc case envisioned a shift of data from

one site to another one, and the run of local MapRe-

duce sub-jobs on two sites. Here follows a step-by-

step description of the actions taken by the system to

serve the job:

1. A Job is submitted to the Master, along with the

indication of the data set targeted by the Job.

2. The Master forwards the Job request to the Or-

chestrator, to get the TJEP;

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

416

3. The Orchestrator elaborates and delivers a TJEP.

For the elaboration of the plan the Orchestrator

makes use of information like the distribution of

the data set among sites, the current computing

capabilities of sites, the topology of the network

and the current capacity of its links. A TJEP is

broken down in two section: 1) the DLP contain-

ing data-shift directives and 2) the SSP containing

data-elaboration directives;

4. The Master enforce the DLP. In particular, Site1

is ordered to shift data to Site4;

5. The actual data shift from Site1 to Site4 takes

place.

6. The Master enforces the SSP. In particular, top-

level Map tasks are triggered to run on Site2 and

Site4 respectively. We remind that a top-level Map

task corresponds to a Hadoop sub-job;

7. Site2 and Site4 executes local Hadoop jobs on

their respective data sets;

8. Results obtained from local execution are sent to

the Global Reducer;

9. The Global Reducer performs the reduction of

partial data;

10. Final result is pushed to the Master;

11. Final result is returned to the Job submitter.

One of the Orchestrator’s tasks is to monitor the

distributed context’s resources, i.e., the sites’ avail-

able computing capacity and the inter-site bandwidth

capacity. In Figure 2 the context monitoring infras-

tructure is depicted.

Top Level

Bottom Level

Site1

Site3

Site2

SDN-Enabled

Switch

Site4

Orchestrator

Nominal Capacity

Slot Capacity

Computing Availability Table

Slot Nom Avg ….

Site1

Site2

Site3

Site4

HeartBeat

Nominal

Free

Bandwidth Availability Table

Free Nom Avg ….

Link1

Link2

Link3

…

Figure 2: Context monitoring infrastructure.

As for the monitoring of the computing capac-

ity, each site periodically advertises its capacity to

the Orchestrator. Such capacity is expressed in ter-

aFlops, and represents the overall computing capac-

ity of the site for MapReduce purposes (overall nomi-

nal capacity). Further, we assume that sites enforce

a computing capacity’s allocation policy which re-

serves a given, ﬁxed amount of capacity to any sub-

mitted MapReduce job. Since the amount of com-

puting capacity potentially allocable to a single job

(slot capacity) may differ from site to site, sites are

also required to communicate that amount along with

the overall nominal capacity. By using this informa-

tion, the Orchestrator is able to build and maintain a

Computing Availability Table that keeps track of ev-

ery site’s instant and future capacity, average capac-

ity in time, and other useful historical statistics about

the computing capacity. The available inter-site link

capacity is instead “sensed” through a network in-

frastructure made of SDN-enabled (Open Networking

Foundation, 2012) switches. Switches are capable of

measuring the instant bandwidth occupied by incom-

ing and outgoing data ﬂows. The Orchestrator period-

ically enquires the switches to retrieve the bandwidth

occupation that is then fed to a Bandwidth Availabil-

ity Table, where statistics on the inter-site bandwidth

occupation are reported.

Information contained in these two tables are ex-

tremely useful to the Orchestrator when it comes to

elaborate an execution plan for a submitted job. The

awareness of the underlying distributed computing

context will guide the Orchestrator in deﬁning a path

which minimizes the overall job’s makespan. The

search for the path is committed to a scheduling sys-

tem that is embedded in the Orchestrator. In the fol-

lowing section, details on the strategy implemented

by the scheduling system are disclosed.

3.1 Job Scheduling System

Basically, the goal of the job scheduling system is to

generate a number of possible execution paths, and

to give each path a score. The path with the best

score will eventually be chosen as the execution path

to enforce. The calculation of the score for a given

path consists in the estimation of the path’s comple-

tion time; in the end, the path exhibiting the lowest

completion time (best score) will be selected.

If it may appear clear that the sites’ computing ca-

pacity and the inter-site bandwidth affect the overall

path’s completion time, some words have to be spent

on the impact that the type of MapReduce application

may have on that time. In (Heintz et al., 2014) authors

introduce the expansion/compression factor α, that

Context-awareMapReduceforGeo-distributedBigData

417

represents the ratio of the output size of the Map phase

to its input size. In our architecture focus is on the en-

tire MapReduce process (not just the Map phase) that

takes place in a site. Therefore we are interested in

proﬁling applications as a whole. We then introduce a

data Compression factor β

app

, which represents the

ratio of the output data size of an application to its

input data size:

app

Out putData

app

InputData

app

(1)

The β

app

parameter may be used to calculate the

amount of data that is produced by a MapReduce job

at a site, traverses the network and reaches the Global

Reducer. Based on that amount, the data transfer

phase may seriously impact on the overall top-level

job performance. The exact value for β

app

may not

be a priori known (MapReduce is not aware of the ap-

plication implementation). Section 3.2 will present an

approximate function that provides a good estimate.

We adopt a graph model to represent the job’s ex-

ecution path. Basically, a graph node may represent

either a data computing element (site) or a data trans-

port element (network link). Arcs between nodes are

used to represent the sequence of nodes in an exe-

cution path. A node is the place where a data ﬂow

arrives (input data) and another data ﬂow is gener-

ated (output data). A node representing a computing

element elaborates data, therefore it will produce an

output data ﬂow whose size is different than that of

input; a node representing a data transport element

just transports data, so input and output data coin-

cide. Nodes are assigned an attribute that describes

the Throughput, i.e., the rate at which node is capa-

ble of “processing” the input data. In the case of a

computing node the throughput represents the speed

at which the application’s input data are actually pro-

cessed, whereas in the case of a transport node the

throughput coincides with the link capacity. Actu-

ally, the throughput of a computing node is the rate

at which the node is capable of “processing” data

when running that speciﬁc application. This param-

eter is strictly application bound, as it depends on

how heavy is the type of computation requested by

the application. Like for the β

app

value, the exact

Throughput value is not a priori known; Section 3.2

discusses a sample based procedure employed to de-

rive the throughput of a computing node for a certain

application.

Nodes are also characterized by the β

node

at-

tribute, which in the case of a computing node is an

application-dependent parameter measuring the ratio

between input data and output data (β

app

), while in

the case of a transport node it will assume the ﬁxed

value 1 (in fact, a network link applies no data com-

pression).

Arcs between nodes are labeled with a number

representing the size of data leaving a node and reach-

ing the next one. The label value of the arc connecting

the j-th node with the (j+1)-th node is given by:

DataSize

j, j+1

= DataSize

j−1, j

× β

(2)

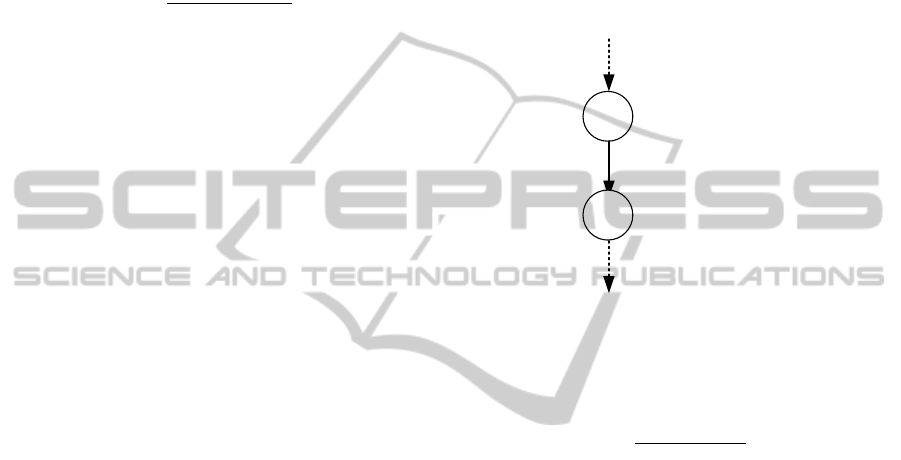
In Figure 3 an example of a branch made of two

nodes and a connecting arc is depicted:

DataSize

[ ]

Node

j, j+i

j+1

j-1, j

j+1, j+2

Throughput

j+1

[ ]

Figure 3: Nodes’ data structure.

Next, for the generic node j we deﬁne the execu-

tion time as:

DataSize

j−1, j

T hroughput

(3)

When a top-level job is submitted to the Master,

the scheduling system is requested to search for the

best execution path. The hard part of the scheduling

system’s work is the generation of all the potential

execution paths, each of which is going to be modeled

as a graph. The algorithm used to generate execution

paths is discussed in Section 4. We now put the focus

on how to calculate the execution time of a speciﬁc

execution path.

Figure 4 depicts a scenario of seven distributed

sites (S

through S

) and a geographic network which

interconnects the sites. One top-level job is requesting

to run a MapReduce application on the data sets (5 GB

sized each) located in the site S

and S

respectively.

Let us assume that one of the execution-paths gen-

erated by the scheduling system involves the move-

ment of data from S

site to S

, which will perform

the bottom-level MapReduce sub-job. Data placed

in site S

, instead, will be processed by the site it-

self; this case does not require any data transfer. The

Global reduce of the partial results produced by local

MapReduce sub-jobs will be executed in the node S1

(so partial results will have to move to that site before

the reducing occurs).

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

418

L63

Reduce

Execution Flow

5GB

β=0.8

L51

4GB

L31

4GB

5GB

4GB

5GB

β=0.8

Map

Execution Flow

Link

Global Reducer

Node

Input Data Node

Mapper Node

Switch/Router

Preview

https://drive.draw.io/#G0B_W8Th_ziojNTTl5RVY1anBSZWs

1 of 1 24/03/2015 9.16

Figure 4: Example of graph modeling an execution path.

In the right part of the picture the graph that mod-

els the execution-path for the just discussed conﬁgu-

ration is represented. Basically, a graph has as many

branches as the number of bottom-level MapReduce.

Branches are independent from each other’s and exe-

cute in parallel. Every branch starts at the node I (ini-

tial node) and ends at the Global reducer’s node. Next

to node I is the node where the data set interested by

the MapReduce computation initially resides. In the

example, the graph is composed of two branches. The

left branch models the elaboration of data initially re-

siding in the node S

, that are map-reduced by node

itself, and results are ﬁnally pushed to node S

(the

Global reducer) through link L

. Similarly, on the

right branch data residing in node S

are moved to

node S

through link L

, are map-reduced by node

and results are pushed to node S

through link L

We deﬁne the execution time of a branch to be the

sum of the execution times of the nodes belonging to

the branch; note that the Global reducer node’s execu-

tion time is left out of this sum. In particular, for the

left and the right branches of Figure 4 the execution

times will be respectively:

le f t

T hroughput

right

T hroughput

So in general, the execution time of a branch is

expressed as:

branch

N−1

∑

j=1

DataSize

j, j+1

T hroughput

j+1

(4)

being N the number of nodes in the branch.

Next we calculate the execution time for the

Global reducer node. The data pushed to that node

is the sum of the data coming from the two branches.

In the example, the execution time is given by:

4 + 4

T hroughput

So generalizing, the execution time of the Global

reducer is given by the summation of the sizes of the

data sets coming from all the branches over the node’s

estimated throughput. Let DataSize(K)

N−1,N

be the

data size of the k-th branch reaching the Global re-

ducer node. The execution time for the Global reducer

will be:

∑

K=1

DataSize(K)

N−1,N

T hroughput

(5)

being P the total number of branches in the graph.

Finally, the overall execution time estimated for the

speciﬁc execution path represented by the graph is

deﬁned as the sum of the Global reducer’s execution

time and the maximum among the branches’ execu-

tion times:

path

= max

1≤K≤P

(T (K)

branch

) + Throughput

(6)

In this formula we are assuming that the global

reduce phase will start as soon as the slowest (i.e.,

the one with the highest execution time) branch has

ﬁnished its execution.

Context-awareMapReduceforGeo-distributedBigData

419

The scheduling system can generate many job’s

execution paths. For each, the execution time is cal-

culated. In the end, the best to schedule will be, of

course, the one showing the lowest execution time.

3.2 Application Proﬁling

As mentioned earlier, both the computing node’s

Throughput, and the Compression factor β

app

are two

parameters strictly dependent on the type of applica-

tion requested by the top-level job. The estimate of

these parameters is determined by an application pro-

ﬁling procedure executed prior to the run of the job

on the requested data. The adopted approach, that re-

calls the one proposed in (Jayalath et al., 2014), is to

request sites that hold the data sets to run the job’s ap-

plication on a sample of data. The results will provide

an estimate of the parameters that will be used by the

scheduling system to calculate the best execution path

for the job.

The estimate is performed on a reference machine

having a computing power of 1 Gﬂops. Regarding the

Throughput, the objective is to evaluate the nominal

capability of a 1 Gﬂops machine to process the data

sample. So, the nominal Throughput is obtained by

dividing the sample data size by the data processing

time; the nominal β

app

, as well, is given by the ratio

between the output result size and the input sample

data size.

The nominal values obtained from the sites are

adequately averaged, and will constitute the ofﬁcial

estimate parameters for that speciﬁc application. In

particular, when it comes to calculate the Through-

put of a certain computing node of the graph (repre-

senting a site), that value is calculated by multiplying

the nominal Throughput times the number of Gﬂops

advertised by the node. This estimate makes the as-

sumption that the Throughput is a linear function of

the computing power.

4 EXECUTION PATHS

GENERATION

The scheduling system is in charge of generating a

number of potential execution paths for each top-level

job that is submitted. The variables that impact on

the generation of paths are the number of sites de-

voted to the running of MapReduce and the amount

of data each of those sites will be assigned. The num-

ber of potential paths may be very huge (and thus very

hard to compute in an acceptable time) if you consider

that data sets targeted by an application might be frag-

mented at any level of granularity, and each fragment

might potentially be moved to any of the available

sites for bottom-level computation.

We now formulate the problem of data fragmen-

tation and discuss the combinatorial approach we

adopted to generate the execution paths. Let us as-

sume that n, m and D be the number of nodes, the

number of mappers and the Application data size re-

spectively. In order to limit the number of potential

paths, the basic assumption we make is that all data

fragments must have the same size, and that the num-

ber of data fragments must be equal to the number of

sites available for computation (N

f rag

= n). The re-

sulting fragment size will then be:

Frag

size

(7)

A node may be assigned zero, one ore more frag-

ments to work on. Our algorithm will schedule

which nodes have to be appointed top-level mappers

and how many data fragments to assign each Map-

per. In order to generate all possible combinations

of mappers and the related assigned data fragments,

we leverage on the combinatorial and on the partition

number theory (Andrews, 1976).

By the notation P(n, m) we refer to the number

of partitions of the integer number n in the order m,

where m is the number of addends in which n is to be

partitioned. For instance, P(5, 2) is the number of par-

titions of the number 5 in 2 addends. It is easy to un-

derstand that P(5, 2) = 2 (being the two combinations

1+4 and 2 +3). If we had to partition the number 5 in

3 addends we would obtain P(5, 3) = 2 (combinations

1+2+2 and 1+3+1). We are going to use this tech-

nique to guess the number of possible ways the data

of an application may be partitioned into a bunch of

fragments. So, in the case that we have 5 data frag-

ments to distribute over 2 sites, two conﬁgurations are

possible: 1) 1 fragment on one site, 4 fragments on the

other one: 2) 2 fragments on one site, 3 on the other

one. Generalizing, the overall number of partitions of

a number n in all the orders m=1,2,..,n is:

P(n) =

∑

m=1

P(n, m) (8)

Of course, the fragment conﬁguration tell us just

the ways to “group” fragments for distribution, but the

distribution phase complicates the problem, as there

are many possible ways to distribute group of frag-

ments among sites. In the example concerning the

P(5, 2), 1 fragment may go to mapper1 (in site1) and

4 fragments may go to mapper2 (in site2), or vicev-

ersa. So for the distribution of fragments we have to

call on the partial permutation theory. The number of

possible ways of placing m mappers in n nodes is:

CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience

420

n,m

(n − m)!

(9)

In the end, the calculus of the number of all the

execution paths for a certain application has to con-

sider both the fragment distribution conﬁguration (eq.

8) and the partial permutation of mappers (eq. 9):

exepath

∑

m=1

P(n, m) ×

(n − m)!

(10)

For example, in the case of n=7 the number of gen-

erated paths will be around 18.000. For n=8 more

than 150.000 conﬁgurations were obtained. Treating

the problem of the generation of execution paths as an

integer partitioning problem allowed us to apply well

known algorithms working in constant amortized time

that guarantee acceptable time also on off-the-shelf

PCs (Zoghbi and Stojmenovic, 1994). For each con-

ﬁguration generated by the algorithm, a correspond-

ing graph is built. On each graph’s node, parame-

ters (computing capacity, link capacity, β) are then

assigned. Finally the graph’s execution time is com-

puted.

5 CONCLUSION

The increasing rate at which data grow have stimu-

lated through the years the search for new strategies

to overcome the limits showed by legacy tools that

have been used so far to analyze data. MapReduce,

and in particular its open implementation Hadoop, has

attracted the interest of both private and academic re-

search as the programming model that best ﬁt the need

for coping with big data. In this paper we address

the peculiar need to handle big data which by their

nature are distributed over many sites geographically

distant from each other. Plain Hadoop was proved to

be inefﬁcient in that context. We propose a strategy

which inspires to hierarchical approaches prior pre-

sented in other literature’s works. The strategy lever-

ages on the partition number and the combinatorial

theory to partition big data into fragments and efﬁ-

ciently distributes the workload among datacenters.

With respect to previous works, this exploits fresh

context information like the available computing and

the inter-site link capacity.

REFERENCES

Andrews, G. E. (1976). The Theory of Partitions, volume 2

of Encyclopedia of Mathematics and its Applications.

Dean, J. and Ghemawat, S. (2004). MapReduce: simpliﬁed

data processing on large clusters. In OSDI04: Pro-

ceeding of the 6th Conference on Symposium on op-

erating systems design and implementation. USENIX

Association.

Facebook (2012). Under the Hood: Scheduling

MapReduce jobs more efﬁciently with Corona.

https://www.facebook.com/notes/facebook-

engineering/under-the-hood-scheduling-mapreduce-

jobs-more-efﬁciently-with-corona.

Heintz, B., Chandra, A., Sitaraman, R., and Weissman, J.

(2014). End-to-end Optimization for Geo-Distributed

MapReduce. IEEE Transactions on Cloud Comput-

ing, PP(99):1–1.

Jayalath, C., Stephen, J., and Eugster, P. (2014). From

the Cloud to the Atmosphere: Running MapReduce

across Data Centers. IEEE Transactions on Comput-

ers, 63(1):74–87.

Kim, S., Won, J., Han, H., Eom, H., and Yeom, H. Y.

(2011). Improving Hadoop Performance in Intercloud

Environments. SIGMETRICS Perform. Eval. Rev.,

39(3):107–109.

Luo, Y., Guo, Z., Sun, Y., Plale, B., Qiu, J., and Li, W. W.

(2011). A Hierarchical Framework for Cross-domain

MapReduce Execution. In Proceedings of the Second

International Workshop on Emerging Computational

Methods for the Life Sciences, ECMLS ’11, pages 15–

22.

Mattess, M., Calheiros, R. N., and Buyya, R. (2013). Scal-

ing MapReduce Applications Across Hybrid Clouds

to Meet Soft Deadlines. In Proceedings of the 2013

IEEE 27th International Conference on Advanced In-

formation Networking and Applications, AINA ’13,

pages 629–636.

Open Networking Foundation (2012). Software-Deﬁned

Networking: The New Norm for Networks. White

paper, Open Networking Foundation.

The Apache Software Foundation (2011). The Apache

Hadoop project. http://hadoop.apache.org/.

Yang, H., Dasdan, A., Hsiao, R., and Parker, D. S. (2007).

Map-reduce-merge: Simpliﬁed relational data pro-

cessing on large clusters. In Proceedings of the 2007

ACM SIGMOD International Conference on Manage-

ment of Data, SIGMOD ’07, pages 1029–1040.

Zhang, Q., Liu, L., Lee, K., Zhou, Y., Singh, A.,

Mandagere, N., Gopisetty, S., and Alatorre, G. (2014).

Improving Hadoop Service Provisioning in a Geo-

graphically Distributed Cloud. In Cloud Computing

(CLOUD), 2014 IEEE 7th International Conference

on, pages 432–439.

Zikopoulos, P. and Eaton, C. (2011). Understanding Big

Data: Analytics for Enterprise Class Hadoop and

Streaming Data. McGraw Hill.

Zoghbi, A. and Stojmenovic, I. (1994). Fast algorithms for

generating integer partitions. International Journal of

Computer Mathematics, 80:319–332.

Context-awareMapReduceforGeo-distributedBigData

421