
Finding Maximal Quasi-cliques Containing a Target Vertex
in a Graph
Yuan Heng Chou
1
, En Tzu Wang
2
and Arbee L. P. Chen
3
1
Department of Computer Science, National Tsing Hua University, Hsinchu, Taiwan
2
Computational Intelligence Technology Center, Industrial Technology Research Institute, Hsinchu, Taiwan
3
Department of Computer Science, National Chengchi University, Taipei, Taiwan
Keywords: Dense Sub-graphs, Quasi-cliques, Maximal Quasi-cliques, Maximal Cliques.
Abstract: Many real-world phenomena such as social networks and biological networks can be modeled as graphs.
Discovering dense sub-graphs from these graphs may be able to find interesting facts about the phenomena.
Quasi-cliques are a type of dense graphs, which is close to the complete graphs. In this paper, we want to
find all maximal quasi-cliques containing a target vertex in the graph for some applications. A quasi-clique
is defined as a maximal quasi-clique if it is not contained by any other quasi-cliques. We propose an
algorithm to solve this problem and use several pruning techniques to improve the performance. Moreover,
we propose another algorithm to solve a special case of this problem, i.e. finding the maximal cliques. The
experiment results reveal that our method outperforms the previous work both in real and synthetic datasets
in most cases.
1 INTRODUCTION
Graphs have been used to model lots of real-world
applications for decades. For instance, biological
networks, social networks, and financial domains
can be modeled using graphs. In a graph, vertices
represent objects and edges represent the
relationships among objects. Finding dense sub-
graphs around certain important vertices is an
interesting problem in the graph research. In the web
network graph, (
Gibson, 2005) observe that a dense
sub-graph can correspond to spam link farms. In
social networks or blogospheres, the specific
vertices can be assigned as leaders or bloggers to
advertise new products or to lead fashions, as
observed by (
Agarwal, 2008) and (Goyal, 2008). In
the biology, (
Fratkin, 2006) and (Langston, 2005)
discover regulatory motifs in genomic DNA. (
Zou,
2007) find terrorist groups in a terrorist network by
matching a specified structure in the corresponding
graph.
Suppose that there is a terrorist network built by
an official security department. In the corresponding
graph, each vertex corresponds to a terrorist and
each edge denotes the partnership between two
individuals. Through a long time investigation,
polices aim at a terrorist as one of the suspects of a
terror attack. In order to identify the whole terrorist
group, dense sub-graphs containing the target vertex
corresponding to the suspect need to be found. We
measure whether a sub-graph is close enough by
checking whether it meets the definition of a quasi-
clique.
A graph is defined as a clique if an edge exists in
any pair of the vertices in the graph. Different types
of cliques, such as maximal cliques and maximum
cliques have been addressed. To model real
applications by graphs, incomplete situations need to
be considered. The concept of quasi-clique has
therefore been proposed. A quasi-clique represents
an almost clique as defined in (
Liu, 2008). A graph is
a quasi-clique if the degree of each vertex is larger
than or equal to ⌈γ × (N − 1)⌉, where γ is a parameter
between 0 and 1 and N is the number of vertices in
the graph. In this paper, we address a new problem
on finding maximal quasi-cliques from a graph,
which contain a specific target vertex. The maximal
quasi-clique in a graph is a quasi-clique not
contained by any other quasi-cliques.
Given a graph, the search space of finding quasi-
cliques from the graph is equivalent to the power set
of the number of vertices in it. In order to efficiently
find all maximal quasi-cliques of a target vertex, we
design several pruning strategies to reduce the
search space. In addition, we modify the Quick
5
Chou Y., Wang E. and Chen A..
Finding Maximal Quasi-cliques Containing a Target Vertex in a Graph.
DOI: 10.5220/0005498400050015
In Proceedings of 4th International Conference on Data Management Technologies and Applications (DATA-2015), pages 5-15
ISBN: 978-989-758-103-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

algorithm proposed in (Liu, 2008) for a comparison
with our proposed method, which is originally
designed for finding maximal quasi-cliques.
Moreover, we also propose an algorithm to
efficiently solve the special case on γ = 1. Two
synthetic datasets and one real dataset are used to
test the proposed methods, and the experiment
results demonstrate that our methods are better than
the modified Quick algorithm in most cases.
The remainder of this paper is organized as
follows. The related works are reviewed in Section
2. Then, the preliminaries are given in Section 3.
The modified Quick algorithm and our methods are
detailed in Section 4. Thereafter, the performance
evaluation on the proposed methods is presented in
Section 5. Finally, Section 6 concludes this work.
2 RELATED WORKS
The dense graph problems have been adopted on a
variety of applications, such as finding thematic
groups, organizing social events, and tag suggestion
(
Sozio, 2010), (Tsourakakis, 2013). A Clique, also
known as complete graph, is a typical dense graph,
in which vertices are all connected to each other.
The problem of finding a clique with a given size k
in a graph is NP-complete. In addition, to find all of
the maximal cliques is more difficult. (
Du, 2006)
have studied the techniques to enumerate all
maximal cliques in a complex network. For general
undirected graphs, Xiang et al. propose a color-
based technique to compute an upper bound of the
size of cliques in (
Xiang, 2013). If two vertices have
different colors, it means that no edge exists between
those two vertices. Since cliques are complete
graphs, the number of colors in the graph represents
the possible size of maximal clique able to be found.
A partitioning algorithm is designed in (
Xiang,
2013), which computes the maximum clique on
MapReduce using a branch and bound search. (
Zou,
2010) combine the maximal clique problem and the
top-k query. They assume that the graph data is
generally interfered in reality. This kind of graphs is
called uncertain graphs. In an uncertain graph,
vertices and edges have their own weights for
representing the probabilities of existence. When
they confirm that a sub-graph is a clique, its
corresponding score is calculated from the weights
of vertices and edges. Then, we can use the score to
prune some other vertices, which cannot form other
cliques with larger scores.
On the other hand, researchers consider quasi-
cliques, another type of dense graphs, which have
different definitions for different studies.
(
Tsourakakis, 2013) define the threshold for the
number of edges in a quasi-clique, and mention that
each vertex need connect to most other vertices in a
quasi-clique. (
Brunato, 2007) formulate two
parameters to define the quasi-clique. The first one
determines the number of neighbors of each vertex
in a quasi-clique, and the second one determines the
number of edges in the quasi-clique. (
Abello, 2002)
and (
Liu, 2008) have the similar definition for quasi-
cliques, which is based on the degree of each vertex
in the same sub-graph. (
Abello, 2002) propose an
algorithm for finding a single maximal quasi-clique.
(
Liu, 2008) propose the Quick algorithm for finding
maximal quasi-cliques in a graph. The basic idea of
this Quick algorithm is to use the depth-first order to
explore the search space. Then, they use several
pruning techniques to reduce the execution time. We
illustrate the detailed steps of the Quick algorithm in
Section 4 as a comparison of our method.
3 PRELIMINARIES
In this section, we describe the notations and terms
to be used in this paper, and formally define the
problem on finding maximal quasi-cliques for a
target vertex in a graph. Given a simple graph G =
(V, E), where V denotes a set of vertices and E
denotes a set of edges to represent objects and the
relationships among objects, respectively. That is, if
any two objects have a relationship, an edge between
the two corresponding vertices exists. An edge is
denoted using a form of (u, v) where u, v ∈ V. |V|
and |E| denote the number of vertices and the
number of edges in a graph, respectively. N
G
(v) = {u|
∀(u, v) ∈ E} denotes the neighbors of a vertex v in
G. |N
G
(v)| therefore denotes the degree of v in G.
dist
G
(u, v) denotes the distance between the vertex u
and the vertex v, which equals the minimum number
of edges to traverse from u to v in G. G' = (V', E') is
a sub-graph of G = (V, E) when V' ⊂ V, E' ⊂ E, and
for any u and v in V', if (u, v) ∈ E, then (u, v) ∈ E'.
In the following discussion, we also use a set of
vertices to represent the corresponding sub-graph.
Definition 1 (Quasi-Clique): Given a sub-graph G' =
(V', E') of G, where V' ⊂ V and E' ⊂ E, G' is defined
as a quasi-clique of v with respect to a parameter γ,
denoted QC(γ, v), where v ∈ V and 0 < γ ≤ 1, if G'
satisfies the following three conditions. 1) v ∈ V'. 2)
G' is connected, which means at least a path exists
between any two vertices in V'. 3) |N
G'
(v)| needs to
equal or exceed ⌈(|V'| − 1) × γ⌉, ∀v ∈ V', where ⌈(|V'|
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
6

−1) × γ⌉ is named the degree threshold and denoted
deg
γ
(V').
Example 1: As shown in Figure. 1, let the target
vertex be v
1
and γ be 0.5. G' = (V', E'), where V' =
{v
1
, v
2
, v
3
, v
5
} and E' = {(v
1
, v
2
), (v
1
, v
3
), (v
2
, v
3
), (v
2
,
v
5
), (v
3
, v
5
)} is a quasi-clique QC (0.5, v
1
), since G'
is connected, and for all vertices v ∈ V', |N
G'
(v)| ≥
deg
γ
(V') (= ⌈(4 − 1) × 0.5⌉ = 2).
Definition 2 (Maximal Quasi-Clique): Given a sub-
graph G' = (V', E') of G and G' is a quasi-clique of v
with respect to a parameter γ, where v ∈ V'; G' is
defined as a maximal quasi-clique of v with respect
to γ if G' is not a sub-graph of any other quasi-
cliques of v with respect to γ.
Example 2: As shown in Figure. 2, let γ be 0.6 and
the target vertex be v
2
, according to Definition 1, G'
= (V', E'), where V' = {v
1
, v
2
, v
3
, v
4
} and E' = {(v
1
,
v
2
), (v
1
, v
4
), (v
2
, v
3
), (v
2
, v
4
), (v
3
, v
4
)} is a quasi-clique
QC(0.6, v
2
). Since no other quasi-cliques QC(0.6, v
2
)
contain G', G' is a maximal quasi-clique of v
2
with
respect to 0.6.
Given a graph G = (V, E), a parameter γ ∈ (0, 1],
and a target vertex v ∈ V, the problem of finding
maximal quasi-cliques for v in G is to discover all
the sub-graphs G' where G' is a maximal quasi-
clique of v with respect to γ.
Figure 1: (Left) G' is a QC(0.5, v
1
).
Figure 2: (Right) G' is a QC(0.6, v
2
).
4 APPROACHES TO FINDING
MAXIMAL QUASI-CLIQUES
FOR A TARGET VERTEX
In this section, the solutions on finding maximal
quasi-cliques for a target vertex are detailed. In
Section 4.1, we discuss the Quick algorithm
proposed in (
Liu, 2008) and describe how to modify
it to solve our problem. This modification is used to
compare with our method in the experiments. Then,
we describe our solutions in Section 4.2.
4.1 The Quick Algorithm
Figure 3: The depth-first search tree of a group G.
Since any sub-graphs of G = (V, E) may have
chances of being quasi-cliques, the search space of
finding quasi-cliques is equivalent to the power set
of V. The Quick algorithm proposed by (
Liu, 2008)
uses depth-first search to find quasi-cliques. An
example of a depth-first search tree of a graph G
with four vertices {v
1
, v
2
, v
3
, v
4
} is shown in Figure.
3. Each node in the tree is associated with a sub-
graph which contains a set of vertices and the
corresponding edges in G. Moreover, the search
order follows the order of the vertex id, that is, the
sub-graphs with the smallest vertex id v
2
are
traversed after those with the smallest vertex id v
1
.
Notice that, if the smallest vertex ids of two sub-
graphs are the same such as {v
1
, v
2
} and {v
1
, v
3
}, we
compare the second smallest vertex id to decide the
search order and so on. As shown in Fig. 3, for each
internal node N in the tree, its children contain an
additional vertex and moreover, this additional
vertex must be with a larger vertex id than all of the
vertex ids of the vertices in N. For example, {v
1
, v
2
}
is one of the children of {v
1
}. The vertex used to
extend an internal node related to the sub-graph G' is
called a candidate vertex of G'. For instance, in
Figure. 3, let G' = (V', E') where V' = {v
2
, v
3
}, the
candidate vertex of G' is v
4
. The set of candidate
vertices of G' is denoted CV(G'), e.g., CV(G') = {v
3
,
v
4
} while V' = {v
1
, v
2
}. During traversing the whole
depth-first search tree, some lemmas used in the
Quick Algorithm to prune the candidate vertices are
discussed in the following.
Lemma 1: (
Liu, 2008) Given a sub-graph G' = (V', E')
of G, let ex_deg
min
(G') = min(|N
G
(v)|), ∀v ∈ V'. If G''
FindingMaximalQuasi-cliquesContainingaTargetVertexinaGraph
7

= (V'', E'') is a quasi-clique extended from G', then
|V''| ≤ ⌊ex_deg
min
(G')/γ⌋ + 1.
Figure 4: G' is a QC(0.5, v
1
).
ex_deg
min
(G') is the minimum degree of the
vertices in V', considering the edges in G. Since the
vertex degree in a quasi-click should be large
enough, i.e. at least ⌈(|V''| − 1) × γ⌉ for G'' to be a
quasi-clique, according to Lemma 1, the number of
vertices to be added to the sub-graph G' to form a
quasi-clique G'' is limited to be no larger than
⌊ex_deg
min
(G')/γ⌋ + 1 – |V'|, denoted U(G') (U for
upper bound). Once the number of vertices being
added to G' is larger than U(G'), the newly generated
sub-graph G'' cannot be a quasi-clique.
Example 3: As shown in Figure. 4, let γ be 0.5 and
the target vertex v
1
. The sub-graph G' = (V', E'),
where V' = {v
1
, v
2
, v
3
, v
5
, v
6
} and E' = {(v
1
, v
2
), (v
1
,
v
5
), (v
2
, v
3
), (v
2
, v
6
), (v
3
, v
5
), (v
3
, v
6
), (v
5
, v
6
)} is a
quasi-clique QC(0.5, v
1
). Also, ex_deg
min
(G') = 3,
and U(G') = ⌊3/0.5⌋+ 1 – 5 = 2.
Lemma 2: (Liu, 2008) Given a sub-graph G' = (V', E')
of G and G' is not a quasi-clique, let in_deg
min
(G') =
min(|N
G'
(v)|), ∀v ∈ V'. If G'' = (V'', E'') is a quasi-
clique extended from G', then |V''| ≥ |V'|+ n, where n
= the minimal value in {i | in_deg
min
(G') + i ≥ ⌈γ ×
(|V'| + i − 1)⌉}.
in_deg
min
(G') is the minimum degree of the
vertices in V', considering the edges in G'. If G' is
not a quasi-clique, |V''| should be large enough for
G'' to be a quasi-clique. According to Lemma 2, the
number of vertices to be added to the sub-graph G'
to form a quasi-clique G'' is limited to be no smaller
than the minimal value in {i | in_deg
min
(G') + i ≥ ⌈γ ×
(|V'| + i − 1)⌉}, denoted L(G') (L for lower bound).
Once the number of vertices being added to G' is
smaller than L(G'), the newly generated sub-graph
G'' cannot be a quasi-clique.
Example 4: As shown in Figure. 5, let γ be 0.6 and
the target vertex v
1
. The sub-graph G' = (V', E') is
not a quasi-clique QC(0.6, v
1
), where V' = {v
1
, v
2
, v
3
,
v
5
, v
6
} and E' = {(v
1
, v
2
), (v
1
, v
5
), (v
2
, v
3
), (v
3
, v
6
), (v
5
,
v
6
)}. Also, we have in_deg
min
(G') = 2, and L(G') = 1.
G' is extended to form G'' by adding v
10
as shown in
Figure. 6. Since G'' is a quasi-clique, |V''| ≥ |V'| +
L(G').
Figure 5: G' is not a QC(0.6, v
1
).
Figure 6: G'' is a QC(0.6, v
1
).
Definition 3 (critical vertices) (Liu, 2008)): Given a
sub-graph G' = (V', E') of G = (V, E), if there is a
vertex u ∈ V' such that |N
G'
(u)| < ⌈(|V'| − 1) × γ⌉, then
u is defined as a critical vertex of G'. The set of the
critical vertices of G' is denoted CritV(G').
Figure 7: G' is not a QC(0.6, v
1
).
Example 5: As shown in Figure. 7, let γ be 0.6 and
the target vertex v
1
. The sub-graph G' = (V', E'),
where V' = {v
1
, v
2
, v
3
, v
5
, v
6
} and E' = {(v
1
, v
2
), (v
1
,
v
5
), (v
2
, v
3
), (v
2
, v
6
), (v
3
, v
5
), (v
3
, v
6
), (v
5
, v
6
)} is not a
quasi-clique QC(0.6, v
1
). The vertex v
1
is a critical
vertex of G' since |N
G'
(v
1
)| = 2 < ⌈(5 − 1) × 0.6⌉ = 3.
Lemma 3: (
Liu, 2008) Given a sub-graph G'' = (V'',
E'') which is extended from G' = (V', E') where |V''|
> |V'| and G' has some critical vertices. If G'' is a
quasi-clique then at least ⌈(|V''| − 1) × γ⌉ - |N
G'
(u)| of
the neighbor vertices of u must be contained in V''-
V', ∀ u ∈ CritV(G').
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
8

Proof. Assume that a quasi-clique G'' = (V'', E'')
extended from G' = (V', E') and there is a critical
vertex u with N neightbor vertices in V''- V', where N
< ⌈(|V''| − 1) × γ⌉ - |N
G'
(u)|. Then, the degree of u in
G'', i.e., |N
G''
(u)|, is equal to N + |N
G'
(u)| < ⌈(|V''| − 1)
× γ⌉. By Condition 3 of quasi-cliques, if G'' is a
quasi-clique, |N
G''
(v)| ≥ ⌈(|V''
| − 1) × γ⌉, ∀ v ∈ V''. A
contradiction occurs. Accordingly, G'' is not a quasi-
clique.
The above three lemmas are used in (Liu, 2008)
to prune candidate vertices for each sub-graph
before they are extended. The detailed proofs are
described in (
Liu, 2008). We focus on the quasi-
cliques regarding a target vertex. The Quick
algorithm can be modified to solve our problem as
follows. The target vertex v is used as the root node
of the depth-first search tree in (
Liu, 2008). Then, we
renumber the other vertices in V – {v} and apply the
original Quick algorithm. This modified Quick
algorithm will be used to compare with our solutions
in the experiments.
4.2 The Target-extending Algorithm
Given a graph G = (V, E), a target vertex v ∈ V and a
parameter γ, any subsets of V – {v} and v may form
a quasi-clique of v with respect to γ if G is
connected. Therefore, the search space of finding
maximal quasi-cliques for a target vertex in G is the
power set of V.
Our baseline algorithm is described as follows.
We set the target vertex v as the root node to form a
sub-graph and select the neighbors of v to extend
this sub-graph. We use the neighbors of v to
generate combinations by the exhaustive method and
then extend the root node to form the new sub-
graphs using adding these combinations as shown in
Figure. 8. We detail the whole extending process as
follows, by which, maximal quasi-cliques for v can
be found if they exist. In the extending process, a
vertex being processed to extend a sub-graph G' to a
new sub-graph G'' is called the extending vertex of
G', and the set of the extending vertices denoted
EV(G'). For example, initially, the target vertex v is
the extending vertex. The neighbors (with vertex ids
larger than the extending vertices) of the extending
vertices of G' will be considered to extend the sub-
graph G', called the candidate vertices of G', and the
set of the candidate vertices of G' denoted CV(G').
For example, while v is the extending vertex, the set
of the candidate vertices is {v
2
, v
3
}. If G' adds some
candidate vertices to extend to G'' = (V'', E''), then
these candidate vertices of G' will become the
extending vertices of G'' for a further extension.
For example, in Figure 8, to extend the sub-graph
G' denoted {v, v
3
}, we have EV(G') = {v
3
} and
CV(G') = {v
4
}. Repeat this extending step until no
vertex can be added to form a new sub-graph, or all
vertices have been used.
Example 6: Given a sub-graph G' = (V', E') which
only contains the target vertex v. Assume that the
neighbors of v are {v
1
, v
2
, v
3
}, which form CV(G').
We generate the combinations of {v
1
}, {v
2
}, {v
3
},
{v
1
, v
2
}, {v
1
, v
3
}, {v
2
, v
3
}, {v
1
, v
2
, v
3
} from CV(G'),
and then add to G' to form the new sub-graphs.
To avoid enumerating the whole search tree of the
target vertex, in the following, we present some
pruning strategies. Lemmas 1-3 mentioned above are
also used in our solution. However, Lemma 1 needs
to be modified to match our baseline method, thus
generating the following Lemma 4.
Figure 8: A graph G and the corresponding search tree of
our baseline algorithm.
Lemma 4: Given a sub-graph G' = (V', E') of G, let
in_deg
min
(G') be min(|N
G'
(v)|), ∀v ∈ V' − EV(G'),
ex_deg
min
(G') be min(|N
G
(u)|), ∀u ∈ EV(G'), and
deg
min
(G') be min(in_deg
min
(G'), ex_deg
min
(G')). If
G'' = (V'', E'') is a quasi-clique extended from G',
|V''| ≤ ⌊deg
min
(G') / γ⌋ +1.
Proof. Assume that a quasi-clique G'' extended from
G' exists and |V''| > ⌊deg
min
(G') / γ⌋ +1. Then, there
must be a vertex u ∈ V', with the degree |N
G''
(u)| =
deg
min
(G'). We know that |N
G''
(u)| < ⌈(|V'| − 1) × γ⌉.
By Condition 3 of quasi-cliques, if G'' is a quasi-
clique, |N
G''
(u)| ≥ ⌈(|V'
| − 1) × γ⌉, ∀ v ∈ V'. A
contradiction occurs. Accordingly, G'' is not a quasi-
clique.
For each sub-graph G' = (V', E'), we can compute
U(G') and L(G') from Lemma 4 and Lemma 2,
respectively. These two boundaries U(G') and L(G')
can help to prune the combinations being extended
from a sub-graph G' if the number of vertices of the
combinations is larger than U(G') or less than L(G').
Suppose that a vertex u in V' is a critical vertex of
G'. If G' can be extended to form a quasi-clique G'' =
(V'', E''), at least one of the neighbors of u belongs to
{V''
−
V'}. In addition, if u is not the extending vertex
of G', G' cannot be extended to form a quasi-clique
FindingMaximalQuasi-cliquesContainingaTargetVertexinaGraph
9
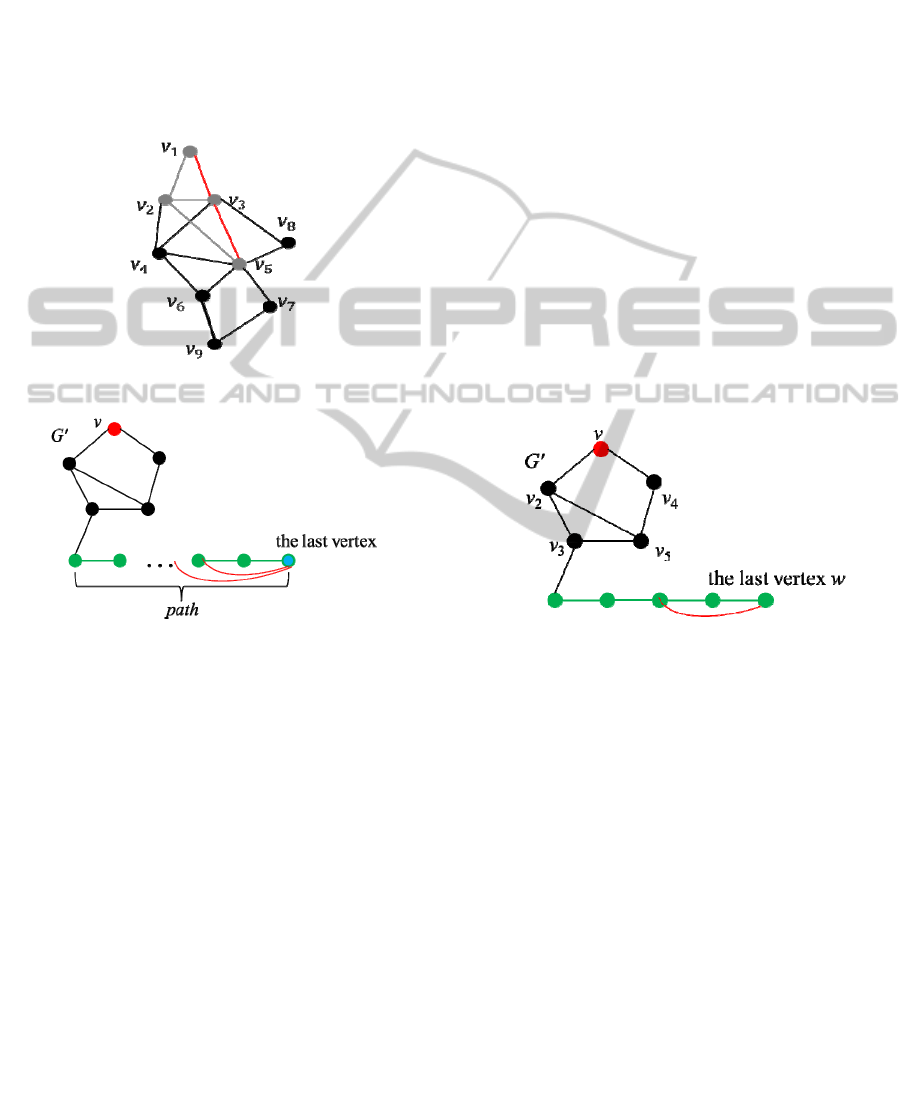
by Lemma 3. By applying Lemmas 2-4 to our
baseline algorithm, the number of sub-graphs can be
reduced and the depth of the search tree can be
limited.
Definition 4 (Hop
G'
(v)): Given a sub-graph G' = (V',
E') of G and let the target vertex be v, Hop
G'
(v)
denotes the maximum length of the shortest
distances between the target vertex v and all vertices
u ∈ V', i.e. max(dist
G'
(u, v)), ∀ u ∈ V', where
dist
G'
(u, v) is the shortest distance between u and v in
G'.
Figure 9: (Left) Hop
G'
(v
1
) is equal to 2 in a QC(0.6, v
1
) G'.
Figure 10: (Right) G'' is a QC(0.2, v).
Example 7: As shown in Figure. 9, let γ and the
target vertex be 0.6 and v
1
, respectively. The sub-
graph G' = (V', E'), where V' = {v
1
, v
2
, v
3
, v
5
} and E'
= {(v
1
, v
2
), (v
1
, v
3
), (v
2
, v
3
), (v
2
, v
5
), (v
3
, v
5
)} is a
quasi-clique QC(0.6, v
1
). Hop
G'
(v
1
) = 2 is the
maximum length of the shortest distances between
the target vertex v
1
and {v
2
, v
3
, v
5
} in G'.
Given a sub-graph G' = (V', E') of G and the
parameter γ, let the target vertex be v. There are
U(G') vertices able to be added to G' to form a
quasi-clique G'' = (V'', E''). We use Fdist(G') to
denote the maximum length of the shortest distances
between v and u, for all u ∈ V''.
Lemma 5: Given a sub-graph G' = (V', E') of G and
let the target vertex be v, if G'' = (V'', E'') is a quasi-
clique extended from G', dist
G
(v, u) is equal to or
less than Fdist(G'), for all u ∈ V''.
Proof. If we want to find the quasi-clique QC(γ, v)
extended from G', we can add at most U(G') vertices
into the sub-graph G' by Lemma 4. Consider the
connecting relation shown in Figure. 10. Given
U(G') vertices and U(G') − 1 edges, we use these
vertices and edges to form a simple path
as the path
shown in Figure. 10. Obviously, the distance of any
two vertices
in the path is maximized as the path
shown in Fig. 10 is the minimal requirement of a
connected graph. Since we need to satisfy the
requirement of deg
min
(G'), the last vertex in the path
needs to connect to the other vertices as the arc lines
in Figure. 10. We add an edge between G' and the
path to form G''.
Suppose that a vertex w exists to be added to
form a quasi-clique G'' and dist
G
(v, w) > Fdist(G').
The vertex w must connect to the last vertex to form
a longer path due to dist
G
(v, w) > Fdist(G').
Therefore, the number of vertices of G'' becomes |V'|
+ U(G') + 1. By Lemma 4, U(G') is the upper bound
which denotes the number of vertices can be added
to G' to form a quasi-clique. Therefore, G'' is not a
quasi-clique. A contradiction occurs. Accordingly, if
G'' = (V'', E'') is a quasi-clique extended from G',
dist
G
(v, u) is equal to or less than Fdist(G'), for all u
∈ V''.
Figure 11: G' is a QC(0.2, v).
From different situations of G', Fdist(G') has the
following three cases. (Case 1) If U(G') ≥ deg
min
(G'),
Fdist(G') = Hop
G'
(v) + U(G') − deg
min
(G') + 1. (Case
2) If U(G') < deg
min
(G') and U(G') + |EV(V')| ≥
deg
min
(G'), Fdist(G') = Hop
G'
(v) + 1. (Case 3) If
U(G') + |EV(V')| ≤ deg
min
(G'), the sub-graph G'
cannot be extended to form a quasi-clique and
Fdist(G') = -1.
Example 8 (Case 1): As shown in Figure. 11, let γ
and the target vertex be 0.2 and v, respectively. The
sub-graph G' = (V', E'), where V' = {v, v
2
, v
3
, v
4
, v
5
}
and E' = {(v, v
2
), (v, v
4
), (v
2
, v
3
), (v
2
, v
5
), (v
3
, v
5
), (v
4
,
v
5
)} is a quasi-clique QC(0.2, v). The extending
vertices of G' are v
3
and v
5
. By Lemma4, U(G') =
⌊deg
min
(G') / γ⌋ + 1 – |V'| = ⌊2 / 0.2⌋ + 1 – 5 = 6.
Since U(G') is larger than deg
min
(G'), there are
enough new vertices able to connect to the last
vertex w to let N
G''
(w) ≥ deg
min
(G'). Therefore,
Fdist(G') = dist
G
(v, w) = Hop
G'
(v) + U(G') −
deg
min
(G') + 1 = 7.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
10

Example 9 (Case 2): As shown in Figure. 12, let γ
and the target vertex be 0.4 and v, respectively. The
sub-graph G' = (V', E'), where V' = {v, v
2
, v
3
, v
4
, v
5
}
and E' = {(v, v
2
), (v, v
4
), (v
2
, v
3
), (v
2
, v
5
), (v
3
, v
5
), (v
4
,
v
5
)} is a quasi-clique QC(0.4, v). The extending
vertices of G' are v
3
and v
5
. |EV(V')| = 2. deg
min
(G') =
2 is bigger than U(G') = ⌊2 / 0.4⌋ +1 − 3 = 1 and less
than U(G') + |EV(V')| = 3. Since there are not enough
new vertices able to connect to the last vertex w, w
needs to connect to the extending vertices of G' to
let |N
G''
(w)| ≥ deg
min
(G'). Therefore, Fdist(G') =
Hop
G'
(v) + 1 = 2.
Figure 12: (Left) G' is a QC(0.4, v).
Figure 13: (Right) G' is a QC(0.4, v).
Figure 14: The search tree for {v, v2, v3, v4}.
Example 10 (Case 3): As shown in Figure. 13, let γ
and the target vertex be 0.4 and v, respectively. The
sub-graph G' = (V', E'), where V' = {v, v
2
, v
3
, v
4
, v
5
}
and E' = {(v, v
2
), (v, v
4
), (v, v
5
), (v
2
, v
3
), (v
2
, v
5
), (v
3
,
v
5
), (v
4
, v
5
)} is a quasi-clique QC(0.4, v). The
extending vertex of G' is v
3
and U(G') = ⌊2 / 0.4⌋ + 1
− 3 = 1. deg
min
(G') = 2 is equal to U(G') + |EV(V')|.
Since there are not enough neighbors of w in G', the
sub-graph G' cannot be extended to form a larger
quasi-clique. Therefore, we set Fdist(G') = -1.
Algorithm 1: The Target-Extending algorithm.
Input: A graph G = (V, E), a target vertex v
p
, and a
parameter γ.
Output: A result list RL, the set of maximal quasi-cliques
of v
p
with respect to γ in G.
1. Keep G into a two-dimensional array D[|V|][|V|].
D[i][j] = 1 means v
i
and v
j
are adjacent.
2. RL =
φ
and dist = 0
3. Put v
p
into the vertex set A
4. for j = 1 to |V| do
5. if D[p][j] = 1 then
6. Put v
j
into the set of candidate vertices CV(A).
7. Put v
p
into the set of extending vertices EV(A)
8. Recursive function RF(A, CV(A), EV(A), dist)
9. Compute the upper bound U(A) from Lemma 4
10. Compute the lower bound L(A) from Lemma 2
11. Select the critical vertices for A and put into
CritV(A) by Lemma 3
12. for each vertex v
u
in CritV(A) do
13. if v
u
∈ (A − EV(A))
14. Return
15. Compute Fdist(A) by Lemma 5.
16. if |A| = the maximal size A may have (from
Lemma 4) and dist > Fdist(A) then
17. return
18. else
19. Put CritV(A) into A
20. for i = L(A) to U(A) do
21. From EV(A) we choose i vertices to form a
combination and in this selection, at least one
vertex in CritV(A) should be contained. All
of these combinations generated are
individually merged with A and then put into
S.
22. for each vertex set U in S do
23. if U is a quasi-clique QC(γ, p) then
24. Add U to RL and update CV(U) and EV(U)
25. RF(U, CV(U), EV(U), dist + 1)
26. Return RL
Lemmas 2-5 can be used in our methods to
reduce the search space. The corresponding pruning
strategies are named Strategies 2-5. Since we only
focus on the maximal quasi-cliques, a sub-graph G'
= (V', E') need not be checked whether it is a QC(γ,
v) if we can find another quasi-clique G'' to contain
G' earlier. Therefore, we verify the sub-graphs with
the larger sizes and extend them in the search tree as
early as possible to find the large enough quasi-
clique quickly. This strategy is called Strategy 6 in
the following discussion. As shown in Figure. 14,
we first check whether the sub-graph corresponding
to N
4
is a quasi-clique, and then move to a larger
sub-graph corresponding to N
7
. If the sub-graph
corresponding to N
7
is a QC(γ, v), then the sub-
graphs contained in {v, v
2
, v
3
, v
4
} need not be
checked as they have no chances to be the maximal
quasi-cliques. By combining the baseline algorithm
with Strategies 2-6, the Target-Extending algorithm
is proposed. The pseudo code of this algorithm is
shown in Algorithm 1.
FindingMaximalQuasi-cliquesContainingaTargetVertexinaGraph
11

4.3 A Special Case
The quasi-clique G' is a complete graph when γ is
equal to 1. We only need to focus on the cliques
containing the target vertex in G. In fact, all vertices
in the cliques are the 1-hop neighbors of the target
vertex in G. We design another algorithm for the
special case on γ = 1, based on this concept.
4.3.1 The Target-clique Algorithm
Figure 15: The illustration of the Target-Clique Algorithm.
Given a graph G = (V, E) and a target vertex v ∈ V,
first, we put v into a vertex set A
1
and put the
neighbors of v in G to the candidate set CS(A
1
). Each
vertex in CS(A
1
) has a corresponding flag cv equal to
0 initially, which shows whether the vertex is
checked. The vertices in CS(A
1
) are sorted in a
descending order of their degree in G. Second, we
select a vertex u with cv equal to 0 from the first of
the sorted CS(A
1
), put it into a new vertex set A
2
, and
merge A
2
with A
1
. Then, we create a new candidate
set CS(A
2
) which collects vertices adjacent to u in
CS(A
1
). Those vertices are the common neighbors of
u and v in G. cv of u is set to 1 in CS(A
1
).
Algorithm 2: The Target-Clique algorithm.
Input: A graph G = (V, E), a target vertex v
p
Output: A result list RL, the set of maximal quasi-cliques
of v
p
with respect to γ in G.
1. Keep G into a two-dimensional array D[|V|][|V|].
D[i][j] = 1 means v
i
and v
j
are adjacent.
2. RL =
φ
3. Put v
p
into the vertex set A
1
4. for j = 1 to |V| do
5. if D[p][j] == 1 then
6. Put v
j
into CS(A
1
) and set v
j
.cv = 0
7. Recursive function RF(A
1
, CS(A
1
))
8. if |CS(A
1
)| ≤ 0 then
9. Put A
1
∪ CS(A
1
) into RL and return
10. else
11. Sort all vertices in CS(A
1
) into a decreasing
order of degree in G
12. for each vertex v
i
in CS(A
1
) do
13. if v
i
.cv = 0 then
14. Copy A
1
and v
i
into a new vertex set A
2
15. Set v
i
.cv = 1
16. for each vertex v
j
in CS(A
1
) do
17. if D[i][j] = 1 then
18. Add the vertex v
j
into CS(A
2
)
19. RF(A
2
, CS(A
2
))
20. return RL
We repeat the second step and create the new
vertex set A
i
until all the corresponding values
become 1 in CS(A
1
). A
i
merging with CS(A
i
) is a
clique that we want. We need not check whether the
obtained cliques are contained by some others
because this case will not be produced by our
method. The pseudo codes of the Target-Clique
algorithm are shown in Algorithm 2.
Example 11: As shown in Figure. 15, given a
graph G = (V, E), let the target vertex be v
1
, the table
shows the steps of the Target-Clique algorithm. We
add v
1
to A
1
and CS(A
1
) collects the neighbors of v
1
in G. Thereafter, CS(A
1
) is sorted according to the
degree to have the order list of <v
3
, v
6
, v
2
, v
5
>. We
select v
3
to join A
1
to form A
2
and CS(A
2
) collects the
common neighbors of v
1
and v
3
in G, that is <v
6
, v
2
>.
The vertex set A
2
is not an answer if CS(A
2
) contains
more than one vertex. Then, we select v
6
to join with
A
2
to form A
4
but CS(A
4
) is empty. The vertex set A
4
is a clique we demand because there are no common
neighbors of v
1
, v
3
and v
6
, and A
4
is not contained by
any other clique. Finally, we obtain three maximal
cliques {v
1
, v
5
}, {v
1
, v
3
, v
6
}, and {v
1
, v
3
, v
2
}, which
contain the target vertex v
1
in the graph G.
5 EXPERIMENTS
In this section, a series of experiments are performed
to evaluate our approach and the experiment results
are also presented and analyzed.
5.1 Experiment Setup
Table 1: The description of the experiment factors.
Factors Default Range Description
number of
vertices
5K 4K-8K
number of vertices in the
graph
average
degree
20 5-25
average degree of vertices
(the first dataset)
average
degree
300 100-500
average degree of vertices
(the second dataset)
Γ 0.5 0.1-0.9 parameter of quasi-cliques
Table 2: The description of the real data.
Vertices Edges Average degree Maximum degree
8,298 100,764 24 743
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
12

Since there are no approaches focusing on finding
maximal quasi-cliques from a graph, which contain
a specific target vertex, we compare the proposed
algorithms with the Quick algorithm. We use two
synthetic datasets for testing the proposed
algorithms. The first dataset is used to test the
methods for quasi-cliques and the second dataset is
used to test the Target-Clique algorithm. To generate
a synthetic graph G = (V, E), we first generate a
sufficient amount of vertices and randomly add
edges between any two vertices to make the sum of
edges equal to N × D
/ 2, were N is the number of
vertices and D is the average degree of vertices, both
of which are experiment factors. All of the
experiment factors are descripted in Table 1.
Moreover, we also use a real dataset named
Wikipedia vote network in the experiments, which is
related to a social network graph and obtained from
Stanford Large Network Dataset Collection
(https://snap.stanford.edu/data/). Its description is
shown in Table 2. All of the proposed algorithms are
implemented using C++ and performed on a PC with
the Intel i5-3210M 2.50GHz CPU, 8 GB of memory,
and under the windows7 64bits operating system. To
obtain a result point shown in the experiment, we
perform the process ten times to compute the
average value. For easily showing the experiment
results, we use a few symbols to indicate the
baseline algorithm and pruning lemmas. For
example, the baseline algorithm plus Strategy 2 and
Strategy 3 is denoted B+23.
5.2 Experiment Results
Figure 16: The running time on varying γ (the first
synthetic dataset).
The running time of the methods for quasi-cliques
on the synthetic dataset is shown in Figures. 16-19.
The running time on varying γ is shown in Figure.
16. As can be seen, our method is always better than
the modified Quick algorithm. The pruning strategy
from Lemma 5 works well when γ is small. Since the
large quasi-cliques may be found quickly, we can
ignore numerous small sub-graphs contained by the
large quasi-cliques. The larger γ is, the more the sub-
graphs need to be checked whether they are
contained by other quasi-cliques, reducing the
pruning capability of Lemma 5. Similarly, when
Strategy 6 is used, finding the large quasi-clique in
the very beginning can reduce the needing of
checking sub-graphs, making the running time to be
further reduced.
The running time on varying the average degree
of vertices is shown in Figure. 17. While the average
degree of vertices increases, the running time of our
method and that of the modified Quick algorithm
both exponentially grow. Under the condition of the
small average degree, our method is better than the
modified Quick algorithm. This is because the
modified Quick algorithm needs to consider the
combinations of the target vertex and the other
vertices in the first layer of the depth-first search
tree. However, we only consider the combinations of
the neighbors of the target vertex. Accordingly, we
generate fewer combinations. The running time on
varying the number of vertices is shown in Figure.
18. The number of vertices causes little impact to the
running time of our method, since more vertices
connecting to the target vertex need to be considered
with the growth of the total number of vertices.
The running time on the real data is shown in
Figure. 19. As can be seen, our method is still better
than the modified Quick algorithm. The pruning
strategy from Strategy 6 works well in this dataset.
In the experiments, we can see that B+23456
outperforms the modified Quick algorithm. In most
cases, the pruning capability of Strategy 6 is better
than that of Lemma 5.
Figure 17: The running time on varying average degree
(the first synthetic dataset).
Figure 18: The running time on varying number of
vertices (the first synthetic dataset).
FindingMaximalQuasi-cliquesContainingaTargetVertexinaGraph
13
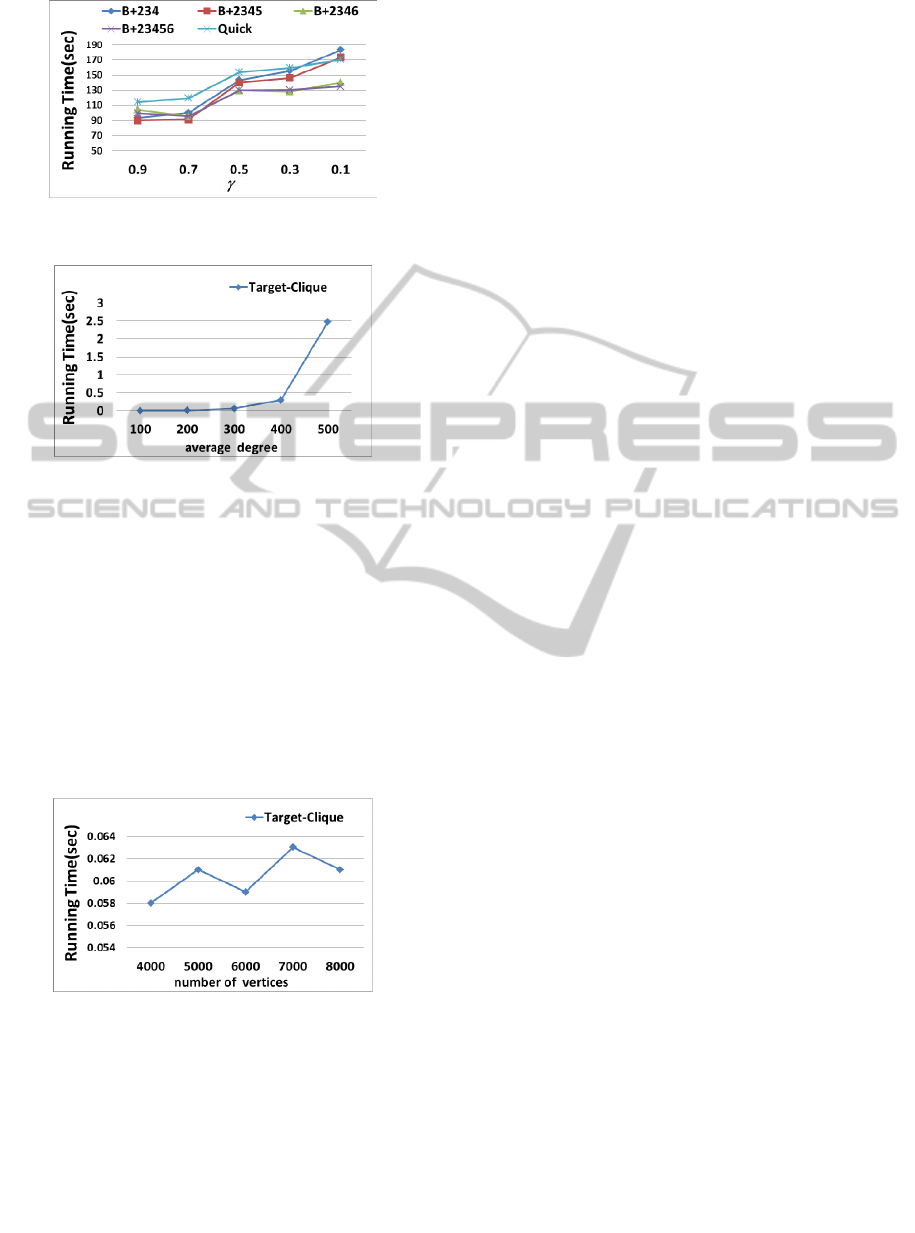
Figure 19: The running time of the real dataset.
Figure 20: The running time on varying γ (the second
synthetic dataset).
The running time of the Target-Clique algorithm
on the second synthetic dataset is shown in Figures.
20-21. The running time will exponentially grow
with the increase of the average degree. The number
of the possible vertex combinations will increase
with the increase of the vertices. However, the
number of vertices will not significantly affect the
running time of the Target-Clique algorithm. This is
because we only consider the neighbors of the target
vertex, which may or may not be affected by the
number of vertices.
Figure 21: The running time of varying number of vertices
(the second synthetic dataset).
6 CONCLUSIONS
In this paper, we solve the problem of finding
maximal quasi-cliques for a target vertex. Given a
graph G = (V, E), a parameter γ ∈ (0, 1] and a target
vertex v ∈ V, we find all of the maximal quasi-
cliques of v with respect to γ in G. We propose an
algorithm to solve this problem and use five pruning
techniques to improve the performance. These
techniques compute the maximum size and
minimum size of each sub-graph of G based on the
degrees of relevant vertices. The containment
relations between sub-graphs are also considered,
thus making most of the sub-graphs to be pruned
before quasi-clique checking. Moreover, we modify
the Quick algorithm (
Liu, 2008) to solve our problem
for a comparison with our method. The experiment
results, using a real and two synthetic datasets,
demonstrate that the pruning techniques are effective
and our algorithm outperforms the modified Quick
algorithm in most cases.
REFERENCES
Agarwal, N., Liu, H., Tang, L., Yu, P. S., 2008. Identifying
the Influential Bloggers in a Community. In
International Conference on Web Search and Data
Mining.
Abello, J., Resende, M. G. C., Sudarsky, S., 2002. Massive
quasi-clique detection. In 5th, Latin American
Symposium on Theoretical Informatics.
Brunato, M., Hoos, H. H., Battiti, R., 2007. On Effectively
Finding Maximal Quasi-Cliques in Graphs. Learning
and Intelligent Optimization. Springer-Verlag Berlin,
Heidelberg.
Du, N., Wu, B., Xu, L., Wang, B., Pei, X., 2006. A Parallel
Algorithm for Enumerating All Maximal Cliques in
Complex Network. In 6th, IEEE International
Conference on Data Mining Workshops.
Fratkin, E., Naughton, B. T., Brutlag, D. L., Batzoglou, S.,
2006. MotifCut: regulatory motifs finding with
maximum density sub-graphs. In ISMB (Supplement of
Bioinformatics).
Goyal, A., Bonchi, F., Lakshmanan, L. V. S., 2008.
Discovering Leaders from Community Actions. In
ACM 17th Conference on Information and Knowledge
Management.
Gibson, D., Kumar, R., Tomkins, A., 2005. Discovering
large dense subgraphs in massive graphs. In 31st,
International Conference on Very large data bases.
Langston, M. A., Lin, L., Peng, X., 2005. A combinatorial
approach to the analysis of differential gene
expression data: The use of graph algorithms for
disease prediction and screening. Methods of
Microarray Data Analysis, Springer, US, 4
th
edition.
Liu, G., Wong, L., 2008. Effective Pruning Techniques for
Mining Quasi-cliques. In European conference on
Machine Learning and Knowledge Discovery in
Databases.
Sozio, M., Gionis, A., 2010. The community-search
problem and how to plan a successful cocktail party. In
16th, ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
14

Tsourakakis, C. E., Bonchi, F., Gionis, A., Gullo, F., Tsiarli,
M. A., 2013. Denser than the Densest Subgraph:
Extracting Optimal Quasi-Cliques with Quality
Guarantees. In 19th, ACM SIGKDD international
conference on Knowledge discovery and data mining.
Xiang, J., Guo, C., Aboulnaga, A., 2013. Scalable
Maximum Clique Computation Using MapReduce. In
29th, IEEE International Conference on Data
Engineering.
Zou, L., Chen, L., Lu, Y., 2007. Top-K Subgraph Matching
Query in a Large Graph. In ACM first Ph.D. workshop
in CIKM.
Zou, Z., Li, J., Gao, H., Zhang, S., 2010. Finding Top-k
Maximal Cliques in an Uncertain Graph. In 26th,
IEEE International Conference on Data Engineering.
FindingMaximalQuasi-cliquesContainingaTargetVertexinaGraph
15
