The LARES Mission: An Opportunity to Teach General Relativity

Frame Dragging and Lense-Thirring Effect

A. Paolozzi

1,2

, C. Paris

2,1

, G. Sindoni

and A. Tartaglia

School of Aerospace Engineering and DIAEE, Sapienza University of Rome, Via Salaria 851, 00138 Rome, Italy

Centro Fermi, Via Panisperna 89, 00184 Rome, Italy

Applied Science and Technology Department, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Turin, Italy

Keywords:

LARES, General Relativity, Frame Dragging, Lense-Thirring Effect, SLR.

Abstract:

LARES is an Italian Space Agency mission devoted to test frame-dragging, a prediction of general relativity.

On February 2012 the satellite has been successfully put in orbit with the qualiﬁcation ﬂight of VEGA, the

new European Space Agency launcher. Basic concepts of general relativity are becoming more and more

familiar because of the part they play in science ﬁction movies. But frame-dragging (more formally known

as the Lense-Thirring effect), is so peculiar that it is a relatively unknown effect. The idea of this paper is to

start from the description of the experiment and then to push some parameters of the experiment to extreme

values in order to magnify the effects of relativity. This approach will provide not only the students and

general people but also professionals not strictly specialized in general relativity, with increased interest in

gravitational theories.

1 INTRODUCTION

Many concepts of special and general relativity,

though difﬁcult to understand in detail, are known to

be true even by non-specialists. Deﬂection of light

by a mass is an example. The phenomenon of grav-

itational waves is another. It is even possible, via

analogies, to explain that space and time are indeed

one single four-dimensional entity called spacetime.

More difﬁcult is the idea that time is not absolute but

ﬂows in different ways depending on the state of mo-

tion of the observer and on the strength of the grav-

itational ﬁeld. Time, being relative to the observer,

has been used in several science ﬁction movies so that

many people are aware of this effect even though it re-

mains an area for experts. Frame-dragging (Ciufolini,

2010) is another intriguing prediction of general rel-

ativity, but known only to specialists. The name

“frame-dragging” was given by Einstein in a private

communication with Ernst Mach (Einstein, 1913) be-

fore the general theory of relativity was published

(Einstein, 1915). But the ﬁrst mathematical deriva-

tion of this effect was performed few years later by

Josef Lense and Hans Thirring, two Austrian physi-

cists, that derived it in (Lense and Thirring, 1918).

Later a generalization was performed by Roy Kerr

that found an exact solution to the very complex non

linear equations of general relativity in the case of a

rotating mass (Kerr, 1963). However until few years

ago the smallness of this effect made its direct mea-

surement impossible. We need to come to the year

1997 to have the ﬁrst measurement with the LAGEOS

satellites (Ciufolini et al., 1997) that was later con-

ﬁrmed with an accuracy of about 10 % (Ciufolini and

Pavlis, 2004), and, using a different spacecraft (Grav-

ity Probe B), with an accuracy of 19 % (Everitt et al.,

2011). There are also other proposed experiments to

measure the frame-dragging such as GINGER (Bosi

et al., 2011)(DiVirgilio et al., 2014) planned in the

next few years. The LARES satellite, put in orbit with

the new VEGA launcher on the 13th February 2012

(Paolozzi and Ciufolini, 2013) (Paolozzi et al., 2015),

is expected to measure the Lense-Thirring effect with

an unprecedented accuracy of about 1 % (Ciufolini

et al., 2011)(Ciufolini et al., 2012a)(Ciufolini et al.,

2012b). While the equivalence principle, at the foun-

dation of general relativity, has a fundamental role

also in classical Galilei-Newton mechanics, gravita-

tional waves and frame-dragging have no counterparts

in classical theories. The use of science ﬁction and

relevant simulations could be seen as a way to involve

students and non specialists in science and technol-

ogy. In the following we will describe frame drag-

ging, recalling some basic principles of relativity, and

343

Paolozzi A., Paris C., Sindoni G. and Tartaglia A..

The LARES Mission: An Opportunity to Teach General Relativity - Frame Dragging and Lense-Thirring Effect.

DOI: 10.5220/0005498503430348

In Proceedings of the 7th International Conference on Computer Supported Education (CSEDU-2015), pages 343-348

ISBN: 978-989-758-108-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

the LARES experiment. Then we will push some pa-

rameters of the experiment to extreme values so as to

magnify the effects of relativity so well exploited in

science ﬁction.

2 FRAME-DRAGGING AND

LENSE-THIRRING EFFECT

We are so accustomed to very common physical phe-

nomena that we do not realize the deep concepts they

involve. The centrifugal force, or more generally any

inertial force, is a good example. Everyone has felt

those forces in a non-uniform motion. A car mov-

ing along a curve or accelerating induces an “appar-

ent force”: the inertial force or, in the ﬁrst case, more

speciﬁcally the centrifugal force. Those forces ex-

ist in the body ﬁxed reference frame, which is not

an inertial frame. But the next question is: what are

the inertial reference frames? According to the stan-

dard deﬁnition they correspond to observers not sub-

ject to any force. General relativity generalizes that

deﬁnition stating that all “freely falling” observers

are equivalent to inertial observers, but the free fall

depends on the mass-energy distribution in the uni-

verse. In fact masses distort spacetime, a fact mathe-

matically embodied in the elements of the metric ten-

sor, i.e. the mathematical tool expressing distances

and, more generally, the geometry of spacetime. The

warps in spacetime in turn determine the paths of

freely falling objects in the gravitational ﬁeld. These

paths are called geodesics in space-time. A person

(“an observer”) falling along a geodesic path is lo-

cally indistinguishable from a person in an inertial

reference frame. A massive body distorts spacetime,

furthermore, a rotating massive body will produce an

additional spacetime deformation. Since the Earth ro-

tates, it will produce such an additional spacetime dis-

tortion, though very weakly because it rotates very

slowly and is not very massive. In Newtonian me-

chanics a perfectly spherical and homogeneous body

will generate a gravitational ﬁeld in the same way as

if the entire mass was concentrated in the centre of

the sphere. The orbital plane of a satellite will re-

main ﬁxed, in the simpliﬁed hypothesis of absence of

non conservative forces, with respect to distant stars,

which in classical mechanics form an inertial refer-

ence frame. But if the body rotates, general relativity

predicts that also the orbital plane rotates very slowly.

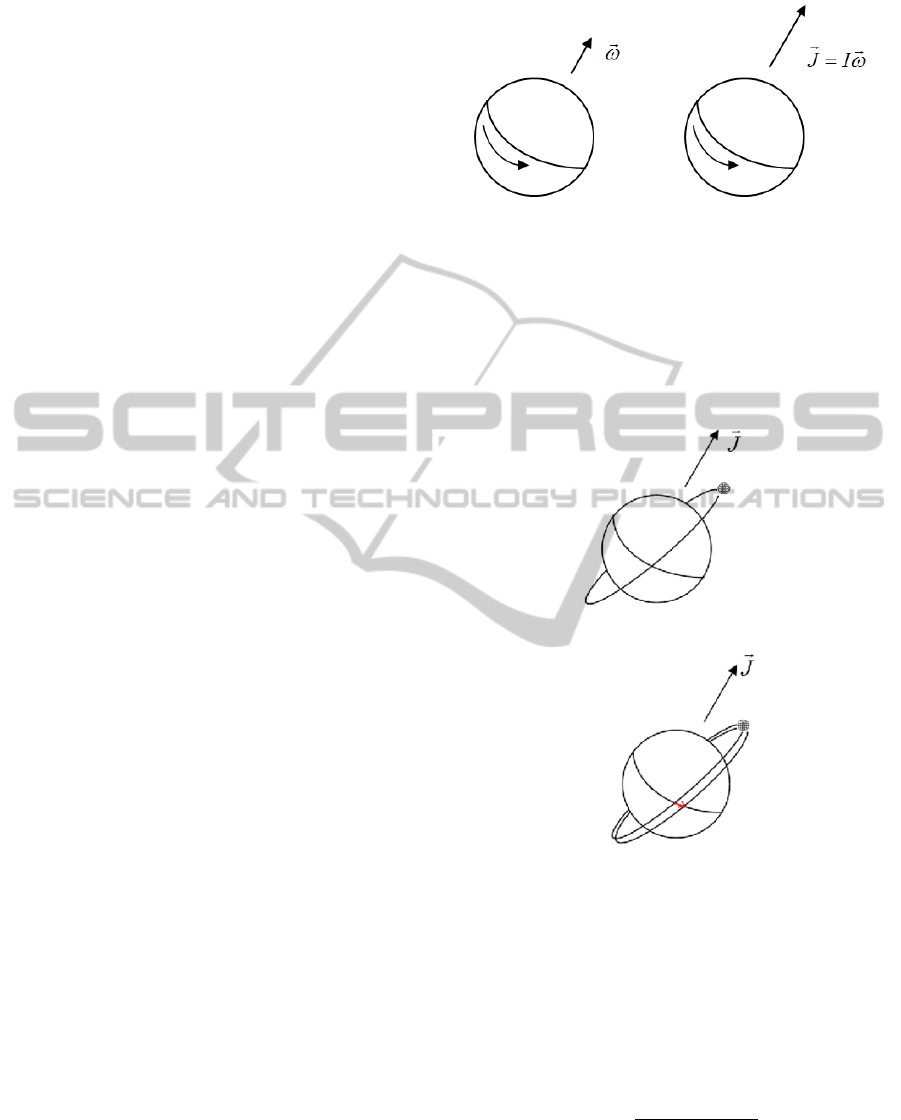
The classical angular momentum

−→

J of a body is a

vector deﬁned as I

−→

ω , where I represents the mass

property of the body (more rigorously called moment

of inertia) and

−→

ω the angular velocity vector which is

oriented as shown in Figure 1.

Figure 1: Representation of angular velocity (left) and of

angular momentum (right).

2.1 Lense-Thirring Effect

A graphical representation of what happens to the or-

bital plane of a satellite in classical and in general rel-

ativity theory is represented in Figure 2.

Figure 2: Orbital planes in a reference frame ﬁxed with re-

spect to distant stars. (Top) classical mechanics; (bottom)

general relativity. The red arrow shows the Lense-Thirring

nodal shift.

Mathematically, by representing the unit vector of

−→

J with

J, the angular velocity of the precession

−→

Ω

of the orbital plane of a satellite is (in the approxima-

tion of slow motion and weak ﬁeld) (Chandrasekhar,

1983):

−→

Ω

2GJ

(1 − e

)

3/2

J (1)

where

−→

Ω

is the Lense-Thirring precession of an

orbital plane, a and e the semimajor axis and the ec-

centricity of the orbit, c the speed of light and G the

gravitational constant.

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

344

2.2 Frame-dragging

More generally frame-dragging can be evaluated, for

a generic point of coordinates (a,θ), where θ is the co-

latitude. The longitude is not present because frame-

dragging is identical for points of any longitude.

The precession is given by (Tartaglia, 2000):

−→

Ω =

+ aA

+ R

sin

θ + aA

cos

θ(1 +

)

(2)

where

A =

(3)

J = Iω (4)

and

2GM

(5)

is the Schwarzschild radius and M the mass of the

central body. The Schwarzschild radius can be con-

sidered a radius inside which a mass is so concen-

trated that nothing can escape from it, not even light.

3 LARES SPACE EXPERIMENT

LARES is a passive satellite of the Italian Space

Agency (ASI) put in orbit on the 13 February 2012.

The position of the satellite is obtained by means of

about 50 laser stations belonging to the International

Laser Ranging Service (Pearlman et al., 2002). The

satellite was designed to minimize the effects of non

gravitational perturbations (Paolozzi et al., 2011) and

in particular thermal thrust (Ciufolini et al., 2014).

Alternative designs were studied earlier in (Ciufolini

et al., 2003) (Bosco et al., 2007). The main objec-

tive of the LARES mission is to measure the Lense-

Thirring effect, and to improve its previous measure-

ment (Ciufolini, 2010) (Ciufolini et al., 2012c) by one

order of magnitude (Ciufolini et al., 2010). The fea-

sibility of this goal has been demonstrated in (Ciu-

folini et al., 2013a) and by the recent data analysis

performed in (Ciufolini et al., 2012b) (Ciufolini et al.,

2013b).

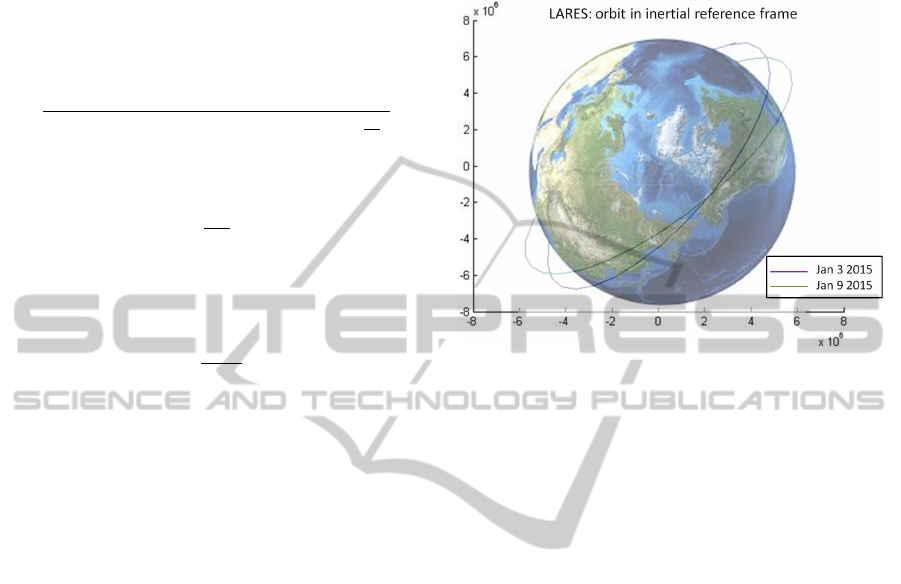
The fact that the Earth is neither spherical nor ho-

mogeneous causes the orbital plane to rotate as shown

in Figure 3 where the actual orbits of LARES, deter-

mined by laser ranging, are drawn. The experimental

value obtained for LARES orbit precession is of 1.706

degrees per day, as can be approximately veriﬁed in

Figure 3 using a protractor. An entire rotation of 360

degrees occurs in 211 days. The Lense-Thirring effect

is instead much smaller: only about 0.118/year. That

is, about 19 million times smaller than the classical

effect.

Figure 3: Real orbits of LARES six days apart one from

the other as seen from the north pole in an inertial reference

frame. Units in the axis are meters.

4 LIMIT CASES

In this section we will examine limit cases in which

the relativity effects are magniﬁed. We will suppose

ﬁrst the Earth rotating with a surface peripheral ve-

locity not far from the speed of light. We will then

consider LARES orbiting around a black hole with

the same “size” of the Earth. We shall discover that

LARES is too close to the event horizon of the black

hole and it would spiral down. However the orbit of

LARES will be considered stable also in this case.

4.1 Earth

Frame-dragging would be more pronounced if the

Earth angular momentum would increase. Consider-

ing the Earth undeformable and unbreakable, let us

imagine a limit case in which the Earth would rotate,

so that the surface almost reaches the speed of light.

In Figure 4 equations 1 and 2 are compared. In

particular the effect of the colatitude θ on frame drag-

ging is small even at the speed of light. Values of θ

are reported in the top left corner of the table.

So, without making signiﬁcant errors, we can, for

the sake of simplicity, assume θ = 90 degrees (i.e. a

point of the equator). In this case equation 2 yields

19.4 degrees/year. So summarizing we see that frame

dragging is very small around the Earth, no matter

how fast it rotates: for an Earth equator rotating at

TheLARESMission:AnOpportunitytoTeachGeneralRelativity-FrameDraggingandLense-ThirringEffect

345

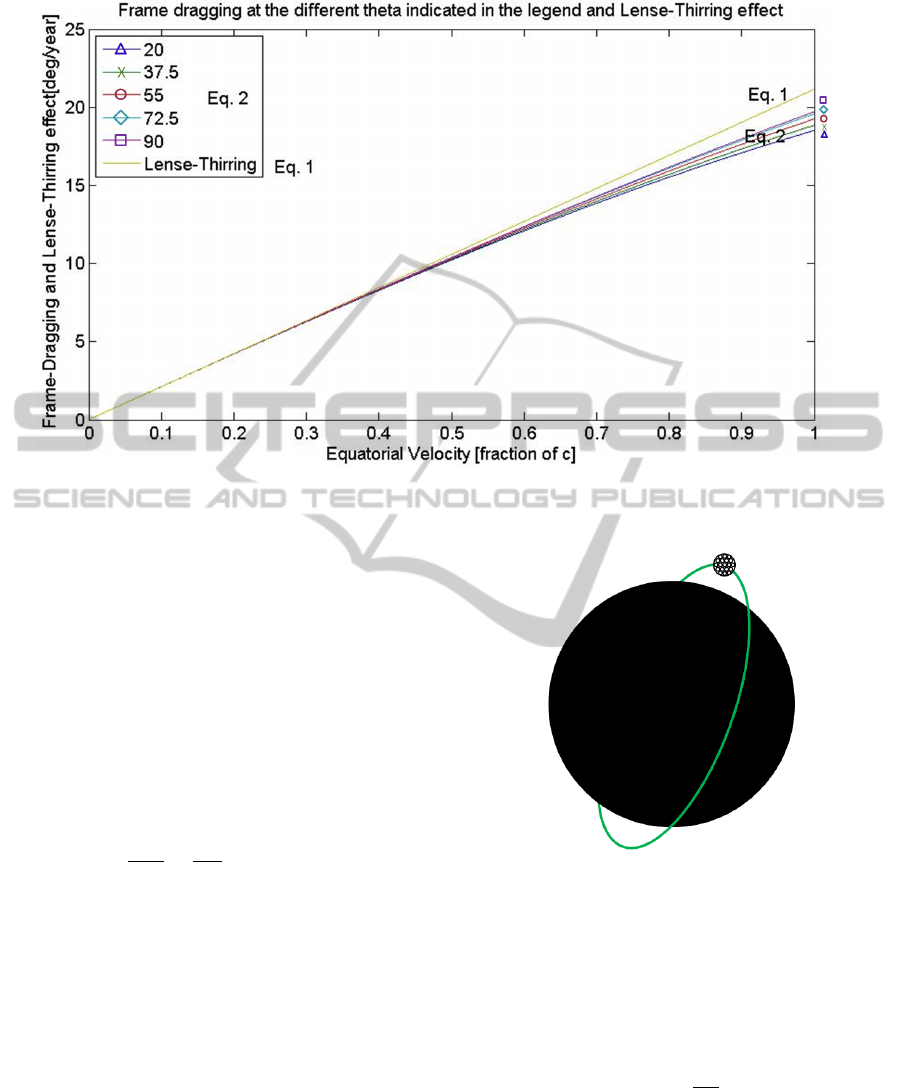
Figure 4: Frame-dragging for different values of θ and Lense-Thirring effect as a function of Earth peripheral speed (i.e. the

speed of points located in the Earth equator).

almost the speed of light, the effect on the LARES or-

bit would be only 19.4 degrees/year i.e., smaller than

the classical effect shown in Figure 3 due to the Earth

oblateness, which amounts to 623 degrees/year.

4.2 Rotating Black Hole

Suppose now to have a rotating black hole (techni-

cally it is called a Kerr black hole) whose inner event

horizon has the size of the Earth. This means that

the mass of the black hole, M

, would be (using the

Schwarzschild radius formula):

= 4.310

kg (6)

i.e. about 2160 solar masses. If the black hole

would not rotate, a small object (like LARES) could

not revolve in a stable orbit at the same distance at

which it rotates now. In fact the lowest possible cir-

cular orbit should have a radius of not less than 3 R

(i.e. a semimajor axis of about 20000 km), whereas

now LARES orbits at 7820 km from the center of the

Earth. In practice LARES would fall into the black

hole in a certain amount of time which is not the case

to calculate here. Just to pursue our example this as-

pect will be neglected and LARES will be considered

in a stable orbit around the black hole (Figure 5).

Let us ﬁrst recall that for a black hole it is not pos-

sible to separate the angular velocity from the moment

of inertia. In fact a black hole destroys all the infor-

mation falling inside it; all that can be “felt”, in the

Figure 5: A LARES satellite orbiting a black hole of the

“size” of the Earth.

surroundings outside the event horizon, is the mass,

the angular momentum and the charge. There is an

upper limit for the total angular momentum i.e. the

ratio A/R

can be at most 1/2, which means that the

highest possible angular momentum would be:

max

= G

(7)

The application of equation 2 in the case of the

black hole under concern with a value of J ranging

from zero to J

max

provides the curves reported in Fig-

ure 6 parameterized with the value of the colatitudes

θ listed in the box in the top left corner. The values

of frame-dragging in this example are extraordinarily

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

346

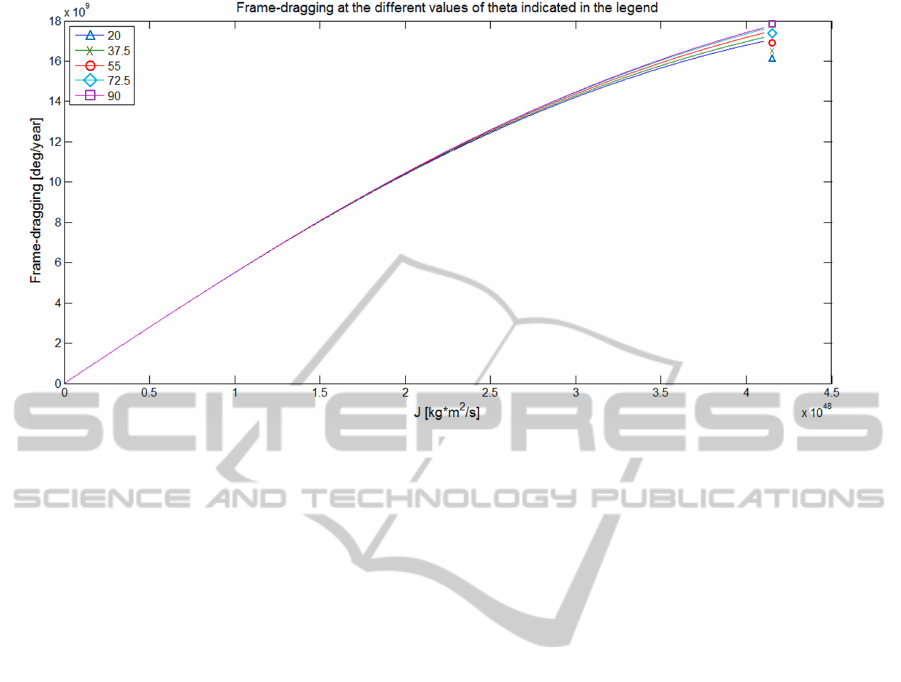
Figure 6: Frame-dragging for different values of θ (in the box on the upper left corner) as a function of the black hole angular

momentum.

high. At almost the maximum value of J, frame drag-

ging would be 16x10

deg/year i.e. the nodes of the

orbits would revolve at a rate of 1.4 rev/s.

5 CONCLUSIONS

The phenomenon of frame dragging has been de-

scribed using the LARES mission. The parameters of

the experiment have been pushed to unrealistic val-

ues, with the purpose of magnifying the effects of

relativity. An hypothetical LARES orbiting a rotat-

ing black hole, with event horizon of the same size as

the Earth has also been considered. The aim of the

study is mainly to attract the attention and interest of

non specialists to a tiny effect of general relativity, as

the frame dragging is. It is shown that the dragging

(or Lense-Thirring) effect becomes really important

only in the extreme case of a central rotating black

hole. Despite this fact the LARES mission will be

able to measure it around the Earth. The reader can

thus understand how delicate the experiment is and

what level of accuracy is needed to bring it to success.

ACKNOWLEDGEMENTS

The authors greatly acknowledge the Italian Space

Agency for supporting the LARES mission un-

der contracts I/043/08/0, I/043/08/1, I/034/12/0 and

I/034/12/1, and the International Laser Ranging Ser-

vice for tracking the satellite and providing the laser

ranging data.

REFERENCES

Bosco, A., Cantone, C., Dell’Agnello, S., delle Monache,

G., Franceschi, M., Garattini, M., and Napolitano, T.

(2007). Probing gravity in NEO with high-accuracy

laser-ranged test masses. International Journal of

Modern Physics D, 16:2271–2285.

Bosi, F., Cella, G., Virgilio, A. D., Ortolan, A., Porzio,

A., Solimeno, S., Cerdonio, M., Zendri, J., Allegrini,

M., Belﬁ, J., Beverini, N., Bouhadef, B., Carelli, G.,

Ferrante, I., Maccioni, E., Passaquieti, R., Stefani, F.,

Ruggiero, M. L., Tartaglia, A., Schreiber, K., Gebauer,

A., , and Wells, J.-P. R. (2011). Measuring gravito-

magnetic effects by multi ring-laser gyroscope. Phys-

ical Review D, 84:122002–1–23.

Chandrasekhar, S. (1983). The mathematical theory of

black holes. International Series of Monographs on

Physics. Oxford University Press.

Ciufolini, I. (2010). Frame-dragging, gravitomagnetism

and Lunar Laser Ranging. New Astronomy, 15:332–

337.

Ciufolini, I., Currie, D., and Paolozzi, A. (2003). The

LARES mission for testing the dynamics of general

relativity. In Proceedings of IEEE Aerospace Confer-

ence, volume 2, pages 693–703. IEEE.

Ciufolini, I., Lucchesi, D., Vespe, F., and Chieppa, F.

(1997). Measurement of gravitomagnetism. Euro-

physics Letters, 39:359.

Ciufolini, I., Monge, B. M., Paolozzi, A., Koenig, R., Sin-

doni, G., Michalak, G., and Pavlis, E. (2013a). Monte

Carlo simulations of the LARES space experiment to

TheLARESMission:AnOpportunitytoTeachGeneralRelativity-FrameDraggingandLense-ThirringEffect

347

test general relativity and fundamental physics. Clas-

sical and Quantum Gravity, 30.

Ciufolini, I., Paolozzi, A., Koenig, R., Pavlis, E., Ries, J.,

Matzner, R., Gurzadyan, V., Penrose, R., Sindoni, G.,

and Paris, C. (2013b). Fundamental physics and gen-

eral relativity with the LARES and LAGEOS satel-

lites. Nuclear Physics B - Proceedings Supplements,

243-244:180–193.

Ciufolini, I., Paolozzi, A., and Paris, C. (2012a). Overview

of the LARES mission: orbit, error analysis and tech-

nological aspects. Journal of Physics, Conference Se-

ries, 354:1–9.

Ciufolini, I., Paolozzi, A., Paris, C., and Sindoni, G. (2014).

The LARES satellite and its minimization of the ther-

mal forces. In Proceedings of IEEE International

Workshop on Metrology for Aerospace 2014. IEEE.

Ciufolini, I., Paolozzi, A., Pavlis, E., Ries, J., Koenig, R.,

Matzner, R., and Sindoni, G. (2010). The LARES

space experiment: LARES orbit, error analysis and

satellite structure. In General Relativity and John

Archibald Wheeler, pages 467–492. Springer Verlag.

Ciufolini, I., Paolozzi, A., Pavlis, E., Ries, J., Koenig, R.,

Matzner, R., Sindoni, G., and Neumayer, H. (2012b).

Testing general relativity and gravitational physics us-

ing the LARES satellite. European Physical Journal

Plus, 127(133).

Ciufolini, I. and Pavlis, E. (2004). A conﬁrmation of the

general relativistic prediction of the Lense-Thirring

effect. Nature, 431:958–960.

Ciufolini, I., Pavlis, E., Paolozzi, A., Koenig, R., Matzner,

R., Sindoni, G., and Neumayer, H. (2011). The Earth’s

frame dragging via laser ranged satellites: a response

to some considerations on the present-day results for

the detection of frame-dragging after the ﬁnal out-

come of GP-B by L. Iorio. European Physics Letters,

96:30002.

Ciufolini, I., Pavlis, E., Paolozzi, A., Ries, J., Koenig, R.,

Matzner, R., Sindoni, G., and Neumayer, H. (2012c).

Phenomenology of the Lense-Thirring effect in the

Solar System: measurement of frame-dragging with

laser ranged satellites. New Astronomy, 17:341–346.

DiVirgilio, A., Allegrini, M., Beghi, A., Belﬁ, J., Bev-

erini, N., Bosi, F., Bouhadef, B., Calamai, M., Carelli,

G., Cuccato, D., Maccioni, E., Ortolan, A., Passeg-

gio, G., Porzio, A., Ruggiero, M., Santagata, R., and

Tartaglia, A. (2014). A ring lasers array for fundamen-

tal physics. Comptes Rendus Physique, 15:866–874.

Einstein, A. (1913). Letter to Ernst Mach. Zurich, 25 June.

In C.W. Misner, K. T. and Wheeler, J., editors, Gravi-

tation, page 544. Freeman (1973).

Einstein, A. (1915). The ﬁeld equations of gravitation (orig-

inal title: Feldgleichungen der gravitation). Preussis-

che Akademie der Wissenschaften: Sitzungsberichte,

2:844–847.

Everitt, C., DeBra, D., Parkinson, B., Turneaure, J., Con-

klin, J., Heifetz, M., and et al. (2011). Gravity Probe

B: ﬁnal results of a space experiment to test general

relativity. Physical Review Letters, 106.

Kerr, R. (1963). Gravitational ﬁeld of a spinning mass as

an example of algebraically special metrics. Physical

Review Letters, 11:237–238.

Lense, J. and Thirring, H. (1918). Uber den einﬂuss-

der eigenrotation der zentralkorper auf die bewegung

der planeten und mondenach der Einsteinschen grav-

itationstheorie[on the inﬂuence of the proper rota-

tion of central bodies on the motions of planets and

moons according to Einstein’s theory of gravitation].

Physikalische Zeitschrift, 6:163.

Paolozzi, A. and Ciufolini, I. (2013). LARES successfully

launched in orbit: satellite and mission description.

Acta Astronautica, 91:313321.

Paolozzi, A., Ciufolini, I., Paris, C., and Sindoni, G.

(2015). LARES: a new satellite speciﬁcally designed

for testing general relativity. International Journal of

Aerospace Engineering, 2015:9.

Paolozzi, A., Ciufolini, I., and Vendittozzi, C. (2011). En-

gineering and scientiﬁc aspects of LARES satellite.

Acta Astronautica, 69:127–134.

Pearlman, M., Degnan, J., and Bosworth, J. (2002). The

international laser ranging service. Advances in Space

Research, 30:135–143.

Tartaglia, A. (2000). Detection of the gravitomagnetic clock

effect. Classical and Quantum Gravity, 17:783.

CSEDU2015-7thInternationalConferenceonComputerSupportedEducation

348