
Determining Top-K Candidates by Reverse Constrained Skyline
Queries
Ruei Sian Jheng
1
, En Tzu Wang
2
and Arbee L. P. Chen
3
1
Department of Computer Science, National Tsing-Hua University, Hsinchu, Taiwan
2
Computational Intelligence Technology Center, Industrial Technology Research Institute, Hsinchu, Taiwan
3
Department of Computer Science National Chengchi University, Taipei, Taiwan
Keywords: Top-K Queries, Range Queries, Skyline Queries, Reverse Skyline Queries, Quad-tree Index.
Abstract: Given a set of criteria, an object o is defined to dominate another object o' if o is no worse than o' in each
criterion and has better outcomes in at least a specific criterion. A skyline query returns each object that is
not dominated by any other objects. Consider a scenario as follows. Given three types of datasets, including
residents in a city, existing restaurants in the city, and candidate places for opening new restaurants in the
city, where each restaurant and candidate place has its respective rank on a set of criteria, e.g., convenience
of parking, we want to find the top-k candidate places that have the most potential customers. The potential
customers of a candidate place is defined as the number of residents whose distance to this candidate is no
larger than a given distance r and also regard this candidate as their skyline restaurants. In this paper, we
propose an efficient method based on the quad-tree index and use four pruning strategies to solve this
problem. A series of experiments are performed to compare the proposed method with a straightforward
method using the R-tree index. The experiment results demonstrate that the proposed method is very
efficient, and the pruning strategies very powerful.
1 INTRODUCTION
In the past decade, various spatial queries on spatial
databases have attracted much attention, such as the
k-nearest-neighbor (kNN) queries, the reverse k-
nearest-neighbor queries (RkNN), the range queries,
and the skyline queries. There are also many studies
focusing on the skyline computation since it plays an
important role in the applications of multi-criteria
decision making. Given a d-dimensional dataset, a
data point p is said to dominate another data point q
if it is better than or equal to q in all dimensions and
with at least one dimension better than that of q. A
data point is defined to be a skyline point if no data
points can dominate it. Many different approaches
have been proposed for efficient skyline
computation, such as BNL (Borzsonyi, 2001), D&C
(Borzsonyi, 2001), Bitmap (Tan, 2001), SFS
(Chomicki, 2003), LESS (Godfrey, 2005), BBS
(Papadias, 2005), SaLSA (Bartolini, 2006), ZSearch
(Lee, 2007), and OSP (Zhang, 2009).
Sharifzadeh and Shahabi (Sharifzadeh, 2006)
addresses the spatial skyline queries which consider
the Euclidean distances between a set of query
points and a set of data points. Deng et al. (Deng,
2007) addresses the multi-source skyline query and
proposes efficient algorithms on its query processing
in road networks. Chen and Lian (Chen, 2009) and
Fuhry et al. (Fuhry, 2009) propose the metric skyline
query, whose dynamic attributes are defined in the
metric space. Papadias et al. (Papadias, 2005) is the
first paper that mentions the dynamic skyline in
which the preference on an attribute is defined to be
better close to the requirement of the user. Dellis and
Seeger (Dellis, 2007) introduces the reverse skyline
query, which is a special skyline query and has the
similar concept to reverse k-nearest-neighbor queries.
Given a query point q, the reverse skyline query
returns the data points whose dynamic skyline
results contain q. For example, two features
including manufacture year and engine displacement
are considered while buying a second-hand car. The
operator of a second-hand car shop may want to
retrieve the number of customers who consider a
specific car as their dynamic skyline results for
deciding whether to import this car. We can make
more profitable decisions through the reverse
skyline query. On the other hand, the reverse k-
101
Jheng R., Wang E. and Chen A..
Determining Top-K Candidates by Reverse Constrained Skyline Queries.
DOI: 10.5220/0005498601010110
In Proceedings of 4th International Conference on Data Management Technologies and Applications (DATA-2015), pages 101-110
ISBN: 978-989-758-103-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

nearest-neighbor (RkNN) query (Kang, 2007), (Korn,
2000), (Lin, 2003), (Stanoi, 2000), (Stanoi, 2001),
(Tao, 2004), (Wu, 2008), (Yang, 2001) has also
received significant research attentions since it was
introduced in (Korn, 2000). An RkNN query
regarding a query point q finds all data points which
regard q as one of their corresponding k nearest
neighbors. Since q is close to such data points, q is
said to have high influence on these data points. The
RkNN answer set with respect to q is called the
influence set of q (Korn, 2000).
In some applications, skyline queries may be
issued with a range constraint. Consider a scenario
as follows. There are some office buildings and
restaurants located in a city. Each restaurant has its
own scores in different criteria such as service or
average price. A lot of workers from the office
buildings have to find a restaurant for lunch. They
may issue a range query with a distance r to indicate
that only the restaurants within this distance will be
considered. Moreover, they most likely will choose
the skyline restaurants within this distance to have
lunch. That is, a worker may issue a constrained
skyline query to find their target restaurants. For a
restaurant, we define its popularity by the number of
times it appears as an answer in the constrained
skyline queries issued from the workers. The
popularity of a restaurant can be computed by
reverse constrained skyline queries.
Now assume we want to open new restaurants in
the city at several candidate locations. We want to
determine top-k candidates based on their popularity
such that a good business can be expected. For
solving this novel top-k query, in this paper, we
propose a basic method and an advanced method.
Three pruning strategies are provided for reducing
the number of competitors while computing the
number of potential customers for each candidate.
Moreover, a pruning strategy focuses on reducing
the number of customers which cannot be the
potential customers of a target candidate. Rooted at
these four strategies, the advanced method
outperforms the basic method, substantially reducing
the computation time. The experiment results
demonstrate that the pruning strategies have a strong
pruning power.
The remainder of the paper is organized as
follows. The formal problem definition and a basic
solution to this problem are given in Section 2. An
advanced solution and its index structures are
described in Section 3. The performance evaluation
on the proposed algorithm is reported in Section 4.
Finally, Section 5 concludes this work.
2 PRELIMINARIES
In this section, we formally define the problem to be
solved and also propose a basic solution for it.
2.1 Problem Formulation
Referring to the scenario mentioned in Section 1, we
have two datasets including a set of office buildings
(customers) and a set of existing restaurants. In
addition, we have another dataset of candidates for
opening new restaurants. All of the datasets are on a
two dimensional space used to represent their
locations and moreover, the datasets of candidates
and the existing restaurants have the other n
attributes representing the features of the restaurants
such as service or average price.
Assume each customer finds a restaurant within
a distance r from his/her location. This search area
forms a circle with the center being the location of
the customer and a radius of r as shown in Figure 1,
where the triangle point represents the customer. If a
restaurant is located within this search area and is
the skyline point among all restaurants in this area
considering the other n attributes, this restaurant gets
one point from the corresponding customer. For
example, there are five restaurants located in the
search area as shown in Figure 1. The values of the
other 2 attributes of these restaurants representing
service ranking and food ranking are (6, 3), (5, 4),
(4, 5), (7, 5), and (6, 6), respectively. As a result, the
three restaurants with attributes (6, 3), (5, 4), and (4,
5) are skyline restaurants in this search area
(assuming smaller values of the attributes are better).
Each of them gets one point from the corresponding
customer.
Figure 1: An illustration of the search area of a customer.
The problem of determining the top-k candidates
by reverse constrained skyline queries is formally
defined as follows. There are three sets of data
points on a two dimensional space, representing
customers, competitors, and candidates. Moreover,
the competitors and candidates have the other n
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
102
attributes. Given the above three datasets and a
distance r, we return k data points which have the
highest scores from the set of candidates. The
scoring function is mentioned as above and in
addition, when we compute the score of a candidate,
we only consider the dominating relationship
between the candidate and competitors but not the
candidate and other candidates.
2.2 The Basic Solution
The basic approach to this novel top-k query is
based on the R-tree index (Guttman, 1984). We
assume that the R-tree indices of the set of customers
R and the set of competitors C are constructed in
advance. Each data point in the set of candidates is
kept in a sequence. We sequentially process each of
them to compute their corresponding scores and then
return the top-k results.
For a candidate, we trace the index of customers
to find the customers whose distance to the
candidate is less than r. On the other words, a range
query with a center equal to the location of the
candidate and a distance r is issued. The returned
customers are kept in another sequence. Then, for
each returned customer, another range query is
issued to find the competitors whose distance to the
customer is less than r. The index of competitors can
help to efficiently answer this query. After that, we
compare the candidate with the corresponding
competitors on the other n attributes to check
whether the candidate is a skyline point. If yes, it
gets one score from the corresponding customer.
Following the above steps, the score of each
candidate can be computed.
3 TOP-K QUERY PROCESSING
In this section, an advance approach to solving the
top-k query considering dominating relationship is
proposed. The index structure used in this approach
is discussed in Subsection 3.1 and then we detail this
approach in Subsection 3.2.
3.1 The Index Structures
The advance approach is based on two types of
index structures. One is built for customers, while
the other is built for competitors. Each of them is an
instance of quadtree. A quadtree index is a tree data
structure in which each internal node has four
children. Quadtree is often used to partition a two-
dimensional space by recursively subdividing it into
four quadrants (regions). Initially, we subdivide the
whole space into four regions with equal sizes. If a
new region still contains objects, it will be further
subdivided into four smaller regions as well. A
region will be recursively subdivided into smaller
regions until no objects contained in a region or the
amount of objects in a region is less than a suitable
number.
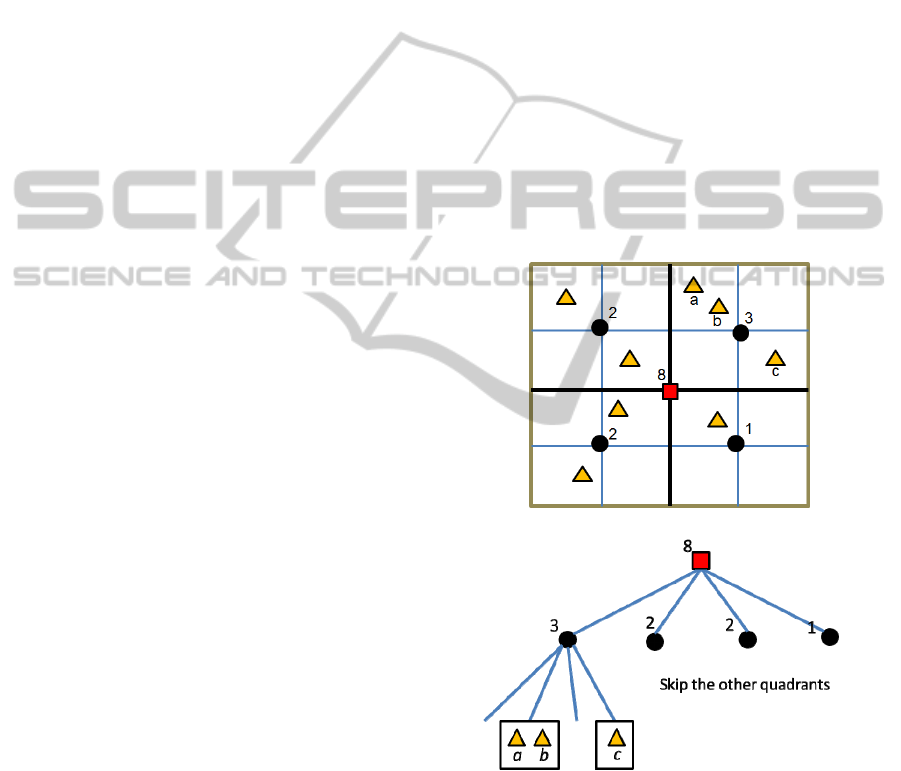
We use the quadtree structure to index customers,
called amount-quadtree. In each internal node, we
additionally record the amount of the customers in
its child nodes. An example is shown in Figs. 2(a)
and 2(b). The triangle points are regarded as
customers. As mentioned, while computing the
quadtree index, the whole space is recursively
subdivided into smaller regions. The circles are
viewed as the internal nodes of amount-quadtree and
moreover, the square point is the root node of
amount-quadtree. As shown in Fig. 2(b), for the root
node and each internal node, we record the amount
of the customers in it corresponding child node.
(a) An example of the index structure of customers.
(b) An illustration of amount-quadtree.
Figure 2: Examples of the index structure of customers
and amount-quadtree.
We also use the quadtree structure to index
competitors, called superiority-quadtree. Again,
initially, we subdivide the whole space into four
regions with equal sizes. If a new region still
contains objects, it will be further subdivided into
four smaller regions as well. In each internal node,
DeterminingTop-KCandidatesbyReverseConstrainedSkylineQueries
103
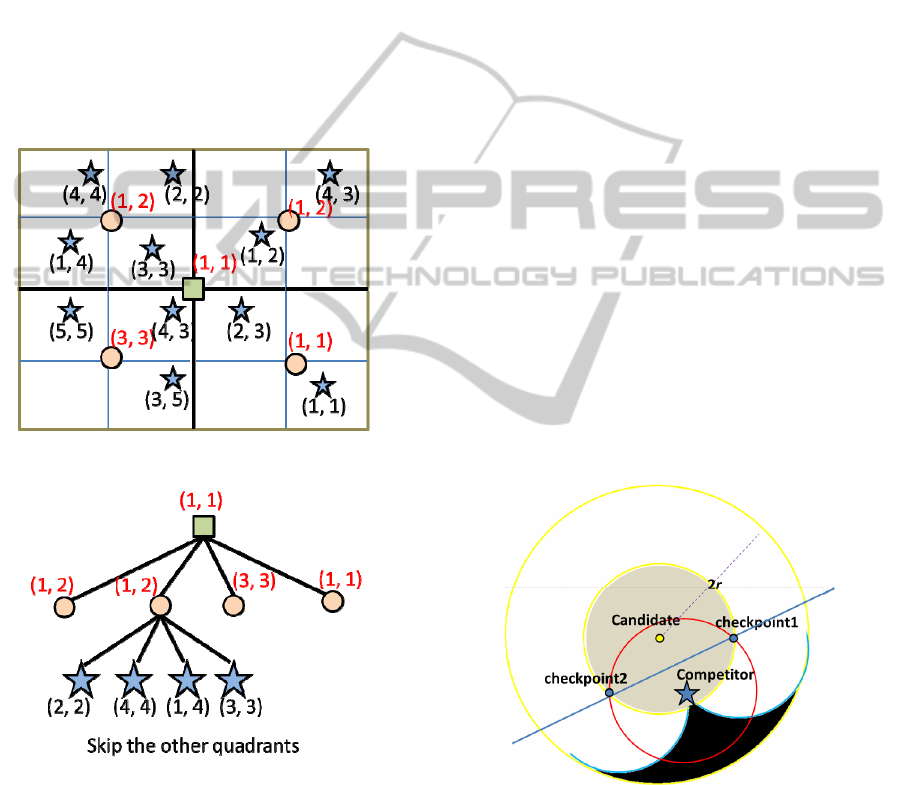
we additionally record the best value of each n
dimension with respect to its child nodes. An
example is shown in Figs. 3 and 4. The star points
are regarded as competitors. The circles are used to
represent the internal nodes of superiority-quadtree.
The square is the root of superiority-quadtree. As
shown in Fig. 4, we use the second quadrant to
explain the concept of superiority-quadtree. We find
the best values in x-dimension and y-dimension from
all of the child nodes of a corresponding internal
node. Suppose that we prefer the smaller value in
both x-dimension and y-dimension. The data point
(1, 4) is the competitor that has the best value in x-
dimension. The data point (2, 2)
is the competitor
that has the best value in y-dimension. Then, we
record (1, 2) in the corresponding internal node.
Figure 3: An example of the index structure of competitor.
Figure 4: An illustration of superiority-quadtree.
3.2 The Advanced Solution
In the following, we first introduce four strategies
used in our advanced algorithm for efficiency
enhancement, three of which are used to reduce the
amount of competitors and the other one is used to
reduce the amount of customers when computing the
score values for candidates. Then, we detail the
advanced algorithm.
Property 1. Given a candidate, if the distance
between the candidate and a specific competitor is
larger than 2r, this competitor cannot affect the score
of the given candidate.■
This property is quite straightforward. The
influence region of the competitor, i.e., the circle
with a center equal to the location of the competitor
and a radius of r cannot overlap the influence region
of the candidate since the distance between the
candidate and competitor is larger than 2r.
Accordingly, this competitor cannot affect the score
of the candidate.
Property 2. Given a candidate, the competitors
which cannot dominate the given candidate cannot
affect the score of the candidate.■
For a candidate, the competitors who cannot
dominate the candidate cannot decide whether the
candidate is a skyline result or not, no matter where
the locations of the competitors are. Since only the
skyline results can get the score from a customer,
these competitors cannot affect the score of the
candidate. On the other hand, if a candidate is
dominated by a specific competitor, we can ensure
that the candidate cannot get any score from the
customers located at the overlap of the two
corresponding influence regions. This is because due
to the competitor, the candidate cannot be the
skyline result with respect to the customers in the
overlap.
Figure 5: An example of Property 3.
Property 3. Given a competitor within a distance r
to a specific candidate, which dominates the specific
candidate, the competitor forms a do-not-care area
in which the other competitors need not be
considered while computing the score of the specific
candidate.■
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
104

We use an example shown in Fig. 5 to introduce
the do-not-care area with respect to a competitor and
detail the concept of Property 3. As mentioned in
Property 3, there are two intersection points
(denoted checkpoint1 and checkpoint2 in Fig.5)
generated by the influence region of the start-shape
competitor and that of the specific candidate. A line,
passing through checkpoint1 and checkpoint2,
partitions the circle with the center equal to the
location of the candidate and a radius of 2r into two
semicircles, one of which contains the candidate
while the other one contains the start-shape
competitor. The area formed by the semicircle
containing the start-shape competitor subtracting the
influence region of checkpoint1 and that of
checkpoint2 is the do-not-care area with respect to
the start-shape competitor. The dark black area
shown in Fig.5 is the do-not-care area with respect
to the start-shape competitor.
Any other competitors located at the do-not-care
area need not be considered to compare with the
specific candidate. This is because the overlap of the
influence region of the candidate and that of another
competitor located at the do-not-care area is always
fully contained in the overlap of the influence region
of the candidate and that of the start-shape
competitor. To the customers in the overlap of the
influence region of the candidate and that of another
competitor located at the do-not-care area, the
candidate need not be compared with the competitor
since the candidate is already dominated by the start-
shape candidate, not able to get scores from the
customers.
Figure 6: An example of Property 4.
Property 4. Given a competitor which dominates a
specific candidate, any customers located in the
overlap of the two corresponding influence regions
formed by the candidate and competitor cannot
contribute scores to the candidate.■
As shown in Fig. 6, suppose that we prefer small
values in both attributes, the candidate with (3, 5) is
dominated by the competitor with (2, 4). Any
customers located in the overlap of the two
corresponding influence regions formed by the
candidate and competitor will not contribute scores
to the candidate since to these customers, the
candidate always cannot be the skyline results due to
the competitor who dominates it.
Algorithm 1: (The ECE algorithm).
Input: amount-quadtree of customers R, superiority-
quadtree of competitor S, candidates, r, and k
Output: Top-k results from candidates
Main function ( ):
1 For each candidate c
2 Trace amount-quadtree to compute the number of
customers located within a distance r to c
3 Sort
the candidates into a decreasing order
according to the number of counted
customers.
4 Compute the scores for the first k candidates in
the sorted list. The smallest score is used to be
the threshold T and these k candidates are
regarded as potential results
7 For the unchecked candidate c in the sorted list
8 If the number of customers located within a
distance of r to c < T
9 Prune c
10 else
11 Compute the score of c
12 If the score of c is larger than T
13 T = the score of c
14 Replace the candidate with the smallest score
in the potential result by c
15 Return the top-k results
The advanced algorithm named ECE (Efficient
Candidate Elimination) detailed in the following is
based on the amount-quadtree index of customers
and the superiority-quadtree index of competitors.
We assume that the amount-quadtree index and the
superiority-quadtree index are constructed in
advance. The pseudo codes of the ECE method are
shown in Algorithm 1.
First, we sequentially process each candidate by
tracing amount-quadtree from the root to get the
number of customers located in the influence region
of a candidate. By using the amount-quadtree index
structure, we can efficiently get the number of
customers located in the influence region of a
corresponding candidate because in some cases, we
can obtain the number of customers from the records
of the internal nodes, without reaching for leaves.
After that, we sort the candidates into a decreasing
order according to the number of customers located
in their corresponding influence regions. For each
DeterminingTop-KCandidatesbyReverseConstrainedSkylineQueries
105

candidate in the sorted list, we calculate its exact
score. Once we get k exact scores, the smallest score
is used to be the lower bound. The candidates in the
sorted list with the number of customers located in
the corresponding influence regions can be pruned
as they have no chances of being the top-k results. In
the following, we focus on how to compute the exact
score of a candidate.
By Properties 1-3, we can prune most of the
competitors that need not be considered while
computing the exact score for a specific candidate.
For a specific candidate, we first prune the
competitors with a distance to it more than 2r by
Property 1. Then, by using the superiority-quadtree
index structure, we can efficiently get the
competitors that dominate the candidate because of
the record kept in the internal node. When traversing
superiority-quadtree, if the records kept in the
internal node are dominated by the target candidate,
we can prune the competitors in that branch by
Property 2 since the competitors who cannot
dominate the target candidate cannot affect the score
of the candidate. Then, by sequentially checking the
competitors that dominate the target and are with a
distance to the candidate smaller than r, we can
prune the competitors located in the corresponding
do-not-care area. After the above checking, the
remainder competitors are really taken into accounts
for computing the exact score of the target candidate.
At the very beginning, issuing a range query from
the target candidate, we find the customers that we
need to check. Before processing each
corresponding customer, we can reduce the number
of customers to be checked by Property 4. After all
of the above pruning check, we use the concept of
Basic to compute the exact score for the target
candidate.
4 EXPERIMENTS
In this section, a series of experiments are performed
to evaluate our approaches and the experiment
results are also presented and analyzed.
4.1 Experiment Setup
We use the data generator RandD to generate three
synthetic datasets with the independent, correlated,
and anti-correlated distributions as shown in Table
1. All objects in the datasets have coordinates within
the range of ([0, 2000], [0, 2000]). The competitors
and candidates have two attributes within a range of
([0, 2000], [0, 2000]). We also conduct the
experiments on a real dataset, obtained from the
website (http://www.census.gov/geo/www/tiger). Its
distribution is shown in Fig. 7. The real dataset
represents the resident locations in Los Angles. The
data size of this real dataset is approximate 360K.
We regard this data points as the customers. We also
generate 100K of the competitors and 1K of the
candidates with two attributes by the independent
generator [RandD]. The coordinates of each object
are within the range of ([0, 3100], [0, 1800]) and the
two attributes are within the range of ([0, 3100], [0,
3100]).
Four variables including r, number of customers,
number of competitors, and number of candidates
are used to be the factors in the experiments as
shown in Table 2. Moreover, k is set to 5 in the
experiments. All of the algorithms are implemented
in C++ and performed on a PC with the Intel Core
i5-2500 3.30GHz CPU, 8GB main memory, and
under the windows7 64bits operating system.
Table 1: The distributions of the test datasets.
Distribution Description
Independent
The attributes of each data point are
generated uniformly and randomly.
Correlated
If a data point has an attribute with low
value, the other attributes of this data
point may likely have low values as well.
Anti-
Correlated
If a data point has an attribute with a
low value, the other attributes of this
data point may likely have high values.
Table 2: Experimental factors.
Factors Default Range
# of customers 200K 150K - 300K
# of competitors 5K 3K - 6K
# of candidates 500 250 - 1000
R 200 160 - 240
Figure 7: The data distribution of the real dataset.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
106
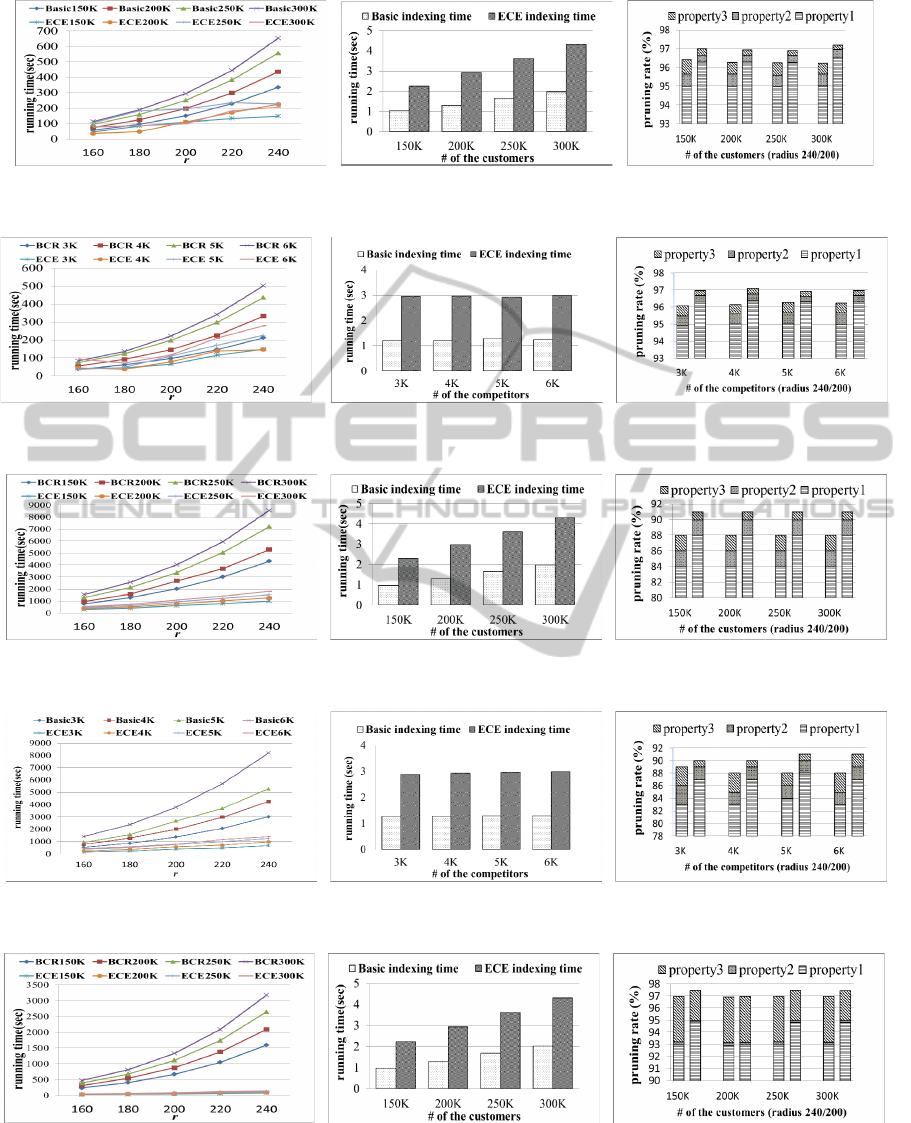
(a) Execution time. (b) Indexing time. (c) Pruning rate.
Figure 8: The varying number of customers on the independent dataset.
(a) Execution time. (b) Indexing time. (c) Pruning rate.
Figure 9: The varying number of competitors on the independent dataset.
(a) Execution time. (b) Indexing time. (c) Pruning rate.
Figure 10: The varying number of customers on the correlated dataset.
(a) Execution time. (b) Indexing time. (c) Pruning rate.
Figure 11: The varying number of competitors on the correlated dataset.
(a) Execution time. (b) Indexing time. (c) Pruning rate.
Figure 12: The varying number of customers on the anti-correlated dataset.
DeterminingTop-KCandidatesbyReverseConstrainedSkylineQueries
107

(a) Execution time. (b) Indexing time. (c) Pruning rate.
Figure 13: The varying number of competitors on the anti-correlated dataset.
4.2 Experiment Results
As mentioned, we use three synthetic datasets in the
experiments, including the independent dataset, the
correlated dataset, and the anti-correlated dataset.
The results on varying number of competitors and
the results on varying number of customers are
shown in Figs. 8-13. The running time of these two
methods is shown in the type (a) of Figs. 8-13.
(a) Execution time.
(b) Pruning rate.
Figure 14: The varying number of candidates on the
independent dataset.
When r becomes large, the curve of running time
becomes sharp. This is because a large distance r
may have more chances of making the number of
competitors and customers large. Obviously, in both
of the two methods, the more the r value is, the
longer the running time will be. Moreover, the more
the competitors and customers are, the longer the
running time will be. In each case, the running time
of ECE is much shorter than that of Basic, since
ECE computes the upper bound of the score for each
candidate and also uses four strategies to
substantially reduce the computation of calculating
the exact scores.
(a) Execution time.
(b) Pruning rate.
Figure 15: The varying number of candidates on the
correlated dataset.
The indexing time of the two methods is shown in
the type (b) of Figs. 8-13. The indexing time of ECE
is a bit longer than that of Basic, yet both of them
use just several seconds for dealing with customers
at the scale of approximate 200K even 300K. These
two methods both are practicable in the index
construction phase.
The pruning capabilities of the strategies on
reducing the number of competitors are shown in the
type (c) of Fig. 8-13. As can be seen, the pruning
capability of each strategy is different in each
synthetic dataset, yet overall, the pruning rate of
adopting these three properties is quite high in each
dataset, e.g., over 90%, and even achieving
approximate 97% in the independent dataset. The
pruning rate is defined as the radio of pruned data
points. We show the pruning rate with the executing
order of adopting Properties 1, 2, and 3.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
108

The results on varying number of candidates are
shown in Figs. 14-16. The running time and the
pruning rate are shown in the types (a) and (b) of
Figs. 14-16, respectively. The indexing time is fixed
due to the fixed number of customers and that of
competitors. Similarly, ECE outperforms Basic in
terms of running time. The pruning rates are also
quite high in this experiment. Moreover, the
experiment results on the real dataset are shown in
Fig. 17. From the experiment results shown above,
we conclude that under the environment of setting a
reasonable r and a reasonable k, even varying the
number of customers, competitors, or candidates,
ECE outperforms Basic.
(a) Execution time.
(b) Pruning rate.
Figure 16: The varying number of candidates on the anti-
correlated dataset.
Figure 17: Execution time on the real dataset.
5 CONCLUSION
In this paper, we make the first attempt to issue a
new top-k query which takes into account reverse
constrained skyline queries on spatial data. Given
three types of datasets, including customers,
candidates, and competitors, and a restricted
distance of r, the novel top-k query returns k
candidates with the most potential customers. We
propose a basic method denoted Basic, and an
advanced method named ECE to solve this problem.
The basic method uses the R-tree index while ECE is
rooted at the extended quad-tree index. Three
pruning strategies are provided for reducing the
number of competitors while a pruning strategy is
provided to focus on reducing the number of
customers unable to contribute the score for a target
candidate, when computing the score for each
candidate. Based on these four strategies, ECE
outperforms the basic method, substantially reducing
the computation time.
REFERENCES
Bartolini, I., Ciaccia, P., Patella, M.: SaLSa, 2006.
Computing the skyline without scanning the whole
sky. In: Proceedings of the ACM International
Conference on Information and Knowledge
Management. CIKM.
Borzsonyi, S., Kossmann, D., Stocker, K., 2001. The
skyline operator. In: Proceedings of the International
Conference on Data Engineering. ICDE.
Chomicki, J., Godfrey, P., Gryz, J., Liang, D., 2003.
Skyline with presorting. In: Proceedings of the
International Conference on Data Engineering. ICDE.
Chen, L., Lian, X., 2009. Efficient processing of metric
skyline queries. In: Proceedings of the IEEE Trans.
Knowl. Data Eng. TKDE.
Dellis, E. and Seeger, B., 2007. Efficient Computation of
Reverse Skyline Queries. In: Proceedings of the
International Conference on Very Large Data Bases.
VLDB.
Deng, K., Zhou, X., Shen, H.T., 2007. Multi-source
skyline query processing in road networks. In:
Proceedings of the International Conference on Data
Engineering. ICDE.
Fuhry, D., Jin, R., Zhang, D., 2009. Efficient skyline
computation in metric space. In: Proceedings of the
International Conference on Extending Database
Technology. EDBT.
Gargantini, I, 1982. An effective way to represent
quadtrees. In: Proceedings of the Communications of
the ACM. CACM.
Guttman, A., 1984. R-Trees: A Dynamic Index Structure
for Spatial Searching. In: Proceedings of the ACM’s
Special Interest Group on Management Of Data.
SIGMOD.
Godfrey, P., Shipley, R., Gryz, J., 2005. Maximal vector
computation in large data sets. In: Proceedings of the
International Conference on Very Large Data Bases.
VLDB.
DeterminingTop-KCandidatesbyReverseConstrainedSkylineQueries
109

Stanoi, I., Agrawal, D., Abbadi, A.E., 2000. Reverse
nearest neighbour queries for dynamic databases. In:
Proceedings of the ACM’s Special Interest Group on
Management of Data. SIGMOD.
Korn, F., Muthukrishnan, S., 2000. Influence sets based on
reverse nearest neighbor queries. In: Proceedings of
the ACM’s Special Interest Group on Management Of
Data. SIGMOD.
Lin, K.I., Nolen, M., Yang, C., 2003. Applying bulk
insertion techniques for dynamic reverse nearest
neighbor problems. In: Proceedings of IDEAS.
IDEAS.
Kang, J. M., Mokbel, M.F., Shekhar, S., Xia, T., Zhang,
D., 2007. Continuous evaluation of monochromatic
and bichromatic reverse nearest neighbors. In:
Proceedings of the International Conference on Data
Engineering. ICDE.
Lin, X., Yuan Y., Zhang, Q., Zhang, Y., 2007. Selecting
Stars: The k Most Representative Skyline Operator.
In: Proceedings of the International Conference on
Data Engineering. ICDE.
Lee, K. C. K., Zheng, B., Li, H., Lee, W.C., 2007.
Approaching the skyline in Z order. In: Proceedings of
the International Conference on Very Large Data
Bases. VLDB.
Papadias, D., Tao, Y., Fu, G., Seeger, B., 2005.
Progressive skyline computation in database systems.
In: Proceedings of the ACM Transactions on Database
Systems. TODS.
Papadias, D., Zhang, J., Mamoulis, N., Tao, Y., 2003.
Query Processing in Spatial Network Databases. In:
Proceedings of the International Conference on Very
Large Data Bases. VLDB.
Stanoi, I., Riedewald, M., Agrawal, D., Abbadi, A.E.,
2001. Discovery of influence sets in frequently
updated databases. In: Proceedings of the Interna-
tional Conference on Very Large Data Bases. VLDB.
Sharifzadeh, M., Shahabi, C., 2006. The Spatial Skyline
Queries. In: Proceedings of the International
Conference on Very Large Data Bases. VLDB.
Tan, K.L., Eng, P.K., Ooi, B.C., 2001. Efficient
progressive skyline computation. In: Proceedings of
the International Conference on Very Large Data
Bases. VLDB.
Tao, Y., Papadias, D., Lian, X., 2004. Reverse knn search
in arbitrary dimensionality. In: Proceedings of the
International Conference on Very Large Data Bases.
VLDB.
Wu,W.,Yang, F., Chan, C.Y., Tan,K.-L., 2008. Finch:
Evaluating reverse k-nearest-neighbor queries on
location data. In: Proceedings of the International
Conference on Very Large Data Bases. VLDB.
Yang, C., Lin, K.-I., 2001. An index structure for efficient
reverse nearest neighbor queries. In: Proceedings of
the International Conference on Data Engineering.
ICDE.
Zhang, S., Mamoulis, N., Cheung, D.W., 2009. Scalable
skyline computation using object-based space
partitioning. In: Proceedings of the ACM’s Special
Interest Group on Management Of Data. SIGMOD.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
110
