
Two-player Ad hoc Output-feedback Cumulant Game Control
Chukwuemeka Aduba
1
and Chang-Hee Won
2
1
Arris Group Inc., Horsham, PA 19044, U.S.A.
2
Department of Electrical and Computer Engineering, Temple University, Philadelphia, PA 19122, U.S.A.
Keywords:
Cost Cumulant Game Control, Nash Game, Neural Networks, Output-feedback, Statistical Control.
Abstract:
This paper studies a finite horizon output-feedback game control problem where two players seek to opti-
mize their system performance by shaping the distribution of their cost function through cost cumulants. We
consider a two-player second cumulant nonzero-sum Nash game for a partially-observed linear system with
quadratic cost function. We derive the near-optimal players strategy for the second cost cumulant function by
solving the Hamilton-Jacobi-Bellman (HJB) equation. The results of the proposed approach are demonstrated
by solving a numerical example.
1 INTRODUCTION
Game theory is the study of tactical interactions in-
volving conflicts and cooperations among multiple
decision makers called players with applications in
diverse disciplines such as management, communi-
cation networks, electric power systems and con-
trol (Zhu et al., 2012), (Charilas and Panagopoulos,
2010), (Cruz et al., 2002). Stochastic differential
game results from strategic interactions among play-
ers in a random dynamic system (Basar, 1999). In
stochastic optimal control, there is a player and cost
function to be optimized while in stochastic differ-
ential games, there are multiple players and separate
cost function to be optimized by each player.
In most practical control engineering applications,
not all the states are measurable. The system model
may consists of unknown disturbances usually ex-
pressed as process noise while the inaccuracies in
measurement are usually expressed as measurement
noise. An approach to account for the unmeasurable
states is to estimate those states using an estimator
before utilizing the states in a controller in a feedback
control system. This approach is part of a general-
ized method to analyzing linear stochastic systems by
applying the concept of certainty equivalence prin-
ciple (Van De Water and Willems, 1981) or related
separation principle (Wonham, 1968). Bensoussan et
al. (Bensoussan and Schuppen, 1985) investigated
the stochastic optimal control problem for partially-
observed system with exponential cost criterion and
proved that separation theorem does not hold for such
scenario. (Zheng, 1989) investigated both optimal
and suboptimal approach to output feedback control
for a linear system with quadratic cost function while
the solvability of the necessary and sufficient condi-
tions for the existence of a stabilizing output feed-
back solution for a continuous-time linear systems
was studied in (Geromel et al., 1998). Aberkane et
al. (Aberkane et al., 2008) investigated the output
feedback solution for generalized stochastic hybrid
linear systems and provided a dynamic system prac-
tical example. The infinite-horizon output feedback
Nash game for a stochastic weakly-coupled system
with state-dependent noise was studied in (Mukaidani
et al., 2010). In addition, the necessary conditions
for the existence of Nash equilibrium were given in
(Mukaidani et al., 2010). Klompstra (Klompstra,
2000), extended risk-sensitive control to discrete time
game theory and solved the Nash equilibrium for the
partially observed state of a 2-player game.
In this paper, we are motivated to extend the
above-referenced studies by considering higher-order
statistics of cost function. In particular, we consider
a second cumulant nonzero-sum Nash game for a
partially-observed system of two players on a fixed
time interval where the players shape the distribution
of their cost cumulantfunction to improvesystem per-
formance. This form of dynamic game finds applica-
tion in satellite and mobile robot systems. The second
cumulant of cost function is equivalent to the vari-
ance of the cost function. However, the optimization
of cost function distribution through cost cumulant
was initiated by Sain (Sain, 1966), (Sain and Liberty,
53
Aduba C. and Won C..
Two-player Ad hoc Output-feedback Cumulant Game Control.
DOI: 10.5220/0005503300530059
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 53-59
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

1971) while Won et al. (Won et al., 2010), extended
the theory of cost cumulant to second, third and fourth
cumulants for a nonlinear system with non-quadratic
cost and derived the corresponding HJB equations.
The reminder of this paper is organized as fol-
lows. In Section 2, we state the mathematical pre-
liminaries and formulate the second cumulant game
problem. Section 3 states the necessary condition for
the existence of Nash equilibrium solution while Sec-
tion 4 derives the players strategy based on solving
the coupled Hamilton-Jacobi-Bellman (HJB) equa-
tions which is the main result of this paper. Section 5
describes the numerical approximate method for solv-
ing the coupled HJB equations while a numerical ex-
ample is solved in Section 6. Finally, the conclusions
are given in Section 7.
2 PROBLEM FORMULATION
Consider a 2-player linear state dynamics and mea-
sured output described by the linear Itˆo-sense stochas-
tic differential equation.
dx(t) = A(t)x(t)dt +
2
∑
k=1
B
k
(t)u
k
(t)dt + G(t)dw
1
(t),
dy(t) = C(t)x(t)dt + D(t)dw
2
(t),
(1)
where t ∈ [t
0
,t
F
] = T, x(t) ∈ R
n
is the state, u
k
(t) ∈
U
k
⊂ R
m
is the k-th player strategy, k = 1, 2 and w
1
(t),
w
2
(t) are Gaussian random process defined on a prob-
ability space (Ω
0
, F,P) where Ω
0
is a nonempty set,
F is a σ-algebra of Ω
0
and P is a probability mea-
sure on (Ω
0
, F).x(t
0
) = x
0
is the initial state vec-
tor with covariance matrix P
0
. The Gaussian ran-
dom process w
1
(t) has zero mean and covariance of
E(dw
1
(t)dw
′
1
(t)) = W
1
(t)dt and similarly the Gaus-
sian random process w
2
(t) has zero mean and covari-
ance of E(dw
2
(t)dw
′
2
(t)) = W
2
(t)dt. The noise pro-
cesses w
1
(t) and w
2
(t) are assumed independent with
E(dw
1
(t)dw
′
2
(t)) = E(dw
2
(t)dw
′
1
(t)) = 0 assuming
dw
1
, dw
2
have same dimension. Let Q
0
= [t
0
,t
F
) ×
R
n
,
¯
Q
0
denote the closure of Q
0
, i.e
¯
Q
0
= T × R
n
.
Assume there exist constants c
1
, c
2
> 0 ∈ R such that
kA(t)k +
2
∑
k=1
kB
k
k ≤ c
1
, kG(t)k ≤ c
2
, (2)
where A(.), B
k
(.),C(.), D(.), G(.) are elements of
C
1
([t
0
,t
F
]) with appropriate dimensions. Let a feed-
back strategy law be defined as u
k
(t) = µ
k
(t, x(t)), t ∈
T. Then, (1) can be written as
dx(t) = f
µ
k
(x(t))dt + G(t)dw
1
(t), x(t
0
) = x
0
,
(3)
where f
µ
k
(x) denotes A(t)x(t) +
∑
2
k=1
B
k
(t)u
k
(t).
There exist a bounded, borel measurable feedback
strategy µ
k
(x) : R
m
→ U
k
such that µ
k
(x) satisfies a
global Lipschitz condition: i.e there exists a constant
c
1
such that
kµ
k
(x
1
) − µ
k
(x
2
)k ≤ c
1
kx
1
− x
2
k,
(4)
k.k is the Euclidean norm and x
1
, x
2
∈ R
n
. Also, µ
k
(x)
satisfies linear growth condition
kµ
k
(x)k ≤ c
2
(1+ kxk).
(5)
Then, if Ekx(t)k
2
is finite, there is a unique solu-
tion to (1) which is a Markov diffusion process on R
n
(Fleming and Rishel, 1975). In order to assess perfor-
mance of (1), consider the cost function (J
k
) for the
k-th player given as:
J
k
(t
0
, x(t
0
), µ
1
, µ
2
) = x
′
(t
F
)Q
f
x(t
F
)+
Z
t
F
t
0
h
x
′
(s)Q(s)x(s)+
2
∑
i=1
µ
′
i
(s)R
ki
(s)µ
i
(s)
i
ds,
(6)
where k = 1, 2, x(t
F
) = x
f
, Q(s), Q
f
are symmetric
positive semi-definite and R
ki
(.) is symmetric positive
definite, which can also be represented as
J
k
(t
0
, x(t
0
), µ
1
, µ
2
) =
Z
t
F
t
0
L
k
(s, x, µ
1
, µ
2
)ds+ ψ
k
(x(t
F
)),
(7)
where k = 1, 2, L
k
is the running cost, ψ
k
is the ter-
minal cost and L
k
, ψ
k
both satisfy polynomial growth
condition. Let the state estimate be ˆx(t) and the state
estimate error be ¯x(t) where x(t) is the state true value.
Then, the state estimation error ¯x(t), is given as
¯x(t) = x(t) − ˆx(t).
(8)
The filtered state estimate ˆx(t) is given as
d ˆx(t) =A(t) ˆx(t)dt +
2
∑
k=1
B
k
(t)u
k
(t)
dt
+ K(t)
dy(t) −C(t) ˆx(t)dt
.
(9)
where K(t) is the Kalman Filter gain (Davis, 1977).
Lemma 2.1. The expected value of the cost func-
tion (6) conditioned on the σ-algebra generated by the
measured output (1) can be rewritten as
E
n
J
k
(t
0
, ˆx(t
0
), µ
1
, µ
2
)
o
=
Z
t
F
t
0
h
E
ˆx
′
(s)Q(s)ˆx(s)
+ tr
Q(s)P(s)
i
ds+
Z
t
F
t
0
h
2
∑
i=1
µ
′
i
(s)R
ki
(s)µ
i
(s)
i
ds
+ E
ˆx
′
(t
F
)Q
f
ˆx(t
F
)
+ tr
Q
f
P
f
,
(10)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
54

where k = 1, 2, ˆx(t
F
) = ˆx
f
, Q(.), Q
f
, P(.), P
f
are pos-
itive semi-definite, R
ki
(s) is positive definite for k = i
and positive semi-definite for k 6= i, P(.), P
f
are the
state error estimate covariances.
Proof. See (Davis, 1977) for single player case, a
two-player case follows similar derivation.
Furthermore, we utilize the backward evolution
operator, O
k
(µ
1
, µ
2
), as defined in (Sain et al., 2000):
O
k
(µ
1
, µ
2
) = O
k
1
(µ
1
, µ
2
) + O
k
2
(µ
1
, µ
2
),
O
k
1
(µ
1
, µ
2
) =
∂
∂t
+ f
′
(t, x, µ
1
, µ
2
)
∂
∂x
,
O
k
2
(µ
1
, µ
2
) =
1
2
tr
G(t)W
1
(t)G(t)
′
∂
2
∂x
2
,
(11)
with tr = trace in (11). To study the cumulant game of
cost function, the m-th moments of cost functions M
k
m
of the k-th player is defined as:
M
k
m
(t, ˆx, µ
1
, µ
2
) = E
n
(J
k
)
m
(t, x, µ
1
, µ
2
)|x(t) = x
o
,
(12)
where m = 1, 2. The m-th cost cumulant function
V
k
m
(t, ˆx) of the k-th player is defined by (Smith, 1995),
V
k
m
(t, ˆx) = M
k
m
−
m−2
∑
i=0
(m− 1)!
i!(m− 1− i)!
M
k
m−1−i
V
k
i+1
,
(13)
where t ∈ T = [t
0
,t
F
], x(t
0
) = x
0
, ˆx(t) ∈ R
n
. Next, we
introduce some definitions.
Definition 2.1. A function M
k
1
:
¯
Q
0
→ R
+
is an ad-
missible first moment cost function if there exists a
strategy µ
k
such that
M
k
1
(t, ˆx) = M
k
1
(t, ˆx;µ
1
, µ
2
),
(14)
for t ∈ T, ˆx ∈ R
n
, M
k
1
∈ C
1,2
(
¯
Q
0
). Also, V
k
1
is the
admissible first cumulant cost function for the k-th
player related to the moment function through the
moment-cumulant relation (13). In addition, µ
k
∈
U
M
k
, V
k
1
(t, ˆx) = V
k
1
(t, ˆx;µ
1
, µ
2
).
Definition 2.2. A class of admissible strategy U
M
k
is
defined such that if µ
k
∈ U
M
k
⊂ R
m
then µ
k
satisfies
the equality of Definition 2.1 for M
k
0
, M
k
1
. It should be
noted that first moment M
k
1
is the same as first cumu-
lant V
k
1
, M
k
0
= 1 and V
k
0
= 0.
Definition 2.3. Let V
k
1
be the k-th player admissible
cumulant cost functions. The player strategy µ
∗
k
is the
k-th player equilibrium solution if it is such that
V
1∗
2
(t, ˆx) = V
1
2
(t, ˆx;µ
∗
1
, µ
∗
2
) ≤ V
1
2
(t, ˆx;µ
∗
1
, µ
2
),
V
2∗
2
(t, ˆx) = V
2
2
(t, ˆx;µ
∗
1
, µ
∗
2
) ≤ V
2
2
(t, ˆx;µ
1
, µ
∗
2
).
(15)
for all µ
k
∈ U
M
k
where the set {µ
∗
1
, µ
∗
2
} is a Nash equi-
librium solution and the set {V
1∗
2
,V
2∗
2
} is the Nash
equilibrium value set.
Problem Definition. Consider an open set Q ⊂
Q
0
and let the k-th player cost cumulant functions
V
k
1
(t, ˆx) ∈ C
1,2
p
(Q) ∩C(
¯
Q) be an admissible cumulant
function where the set C
1,2
p
(Q) ∩C(
¯
Q) means that the
function V
k
1
satisfy polynomial growth condition and
is continuous in the first and second derivatives of Q,
and continuous on the closure of Q. Assume the ex-
istence of a near-optimal strategy µ
∗
k
∈ U
M
k
and near-
optimal value function V
k∗
2
(t, ˆx) ∈ C
1,2
p
(Q) ∩C(
¯
Q) for
the k-th player. Thus, a 2-player second cumulant out-
put feedback game problem is to find the Nash strat-
egy µ
∗
k
(t, ˆx) for the partially-observed linear state sys-
tem with k = 1, 2 which results in the near-optimal2
nd
value function V
k∗
2
(t, ˆx) given as
V
1∗
2
(t, ˆx) = min
µ
1
∈U
M
1
n
V
1
2
(t, ˆx;µ
1
, µ
2
)
o
,
V
2∗
2
(t, ˆx) = min
µ
2
∈U
M
2
n
V
2
2
(t, ˆx;µ
1
, µ
2
)
o
.
(16)
Remarks. To find the Nash equilibrium strategies
µ
∗
1
(t, ˆx), µ
∗
2
(t, ˆx), we constrain the candidates of the
near-optimal players strategy to U
M
1
,U
M
2
, and the
near-optimal value functions V
1∗
2
(t, ˆx),V
2∗
2
(t, ˆx) are
found with the assumption that V
1
1
(t, ˆx),V
2
1
(t, ˆx), are
admissible.
3 AD HOC OUTPUT FEEDBACK
CUMULANT GAME
Theorem 3: From the full-state feedback statisti-
cal control in (Won et al., 2010), the minimal 2
nd
value function V
k∗
2
(t, x) for (1) with zero measure-
ment noise satisfies the following HJB equation for
the k-th player:
0 = min
µ
k
∈U
M
k
(
O
k
(µ
∗
1
, µ
∗
2
)
h
V
k∗
2
(t, x)
i
+
∂V
k
1
(t, x)
∂x
′
G(t)W
1
G(t)
′
∂V
k
1
(t, x)
∂x
)
,
(17)
with the terminal condition V
k
j
(t
F
, x
F
) = 0, k = 1, 2,
j = 1, 2. Assuming separation principle (Wonham,
1968), the minimal 2
nd
value function V
k∗
2
(t, ˆx) for
(9) satisfies the following HJB equation for the k-th
player:
Two-playerAdhocOutput-feedbackCumulantGameControl
55

0 = min
µ
k
∈U
M
k
(
O
k
(µ
∗
1
, µ
∗
2
)
h
V
k∗
2
(t, ˆx)
i
+
∂V
k
1
(t, ˆx)
∂ˆx
′
K(t)W
2
K(t)
′
∂V
k
1
(t, ˆx)
∂ˆx
)
,
(18)
with terminal condition V
k
j
(t
F
, ˆx
F
) = 0, k = 1, 2, j =
1, 2, K(t) is the Kalman filter gain associated with
(1) after transformation through innovative process
(Kailath, 1968), (Davis, 1977).
Remark. The HJB equation (17) provides a neces-
sary condition for the existence of equilibrium solu-
tion of a 2-player, 2
nd
cost cumulant game. A sim-
ilar condition with proof is given for statistical con-
trol in (Won et al., 2010). Our approach in (18) is
termed ad hoc, since we assume that separation prin-
ciple holds for the stochastic linear system with 2
nd
cumulant function V
k
2
(t, ˆx).
4 TWO-PLAYER CUMULANT
GAME NASH STRATEGY
Theorem 4. Let the solution to the k-th player second
cumulant output feedback game be given by
µ
∗
k
(t, ˆx) = −
1
2
R
−1
kk
B
′
k
∂V
k
1
(t, ˆx)
∂ˆx
+ γ
2k
∂V
k∗
2
(t, ˆx)
∂ˆx
,
(19)
where γ
2k
is the Lagrange multiplier and V
k
1
,V
k
2
are
the first, second cumulant cost functions and solutions
of the following coupled HJB equations:
0 =O
k
(µ
−k
, µ
k
)
h
V
k
1
(t, ˆx)
i
+ M
k
0
(t, ˆx)L
k
(t, ˆx, µ
−k
, µ
k
),
0 =O
k
(µ
−k
, µ
k
)
h
V
k
2
(t, ˆx)
i
+
∂V
k
1
(t, ˆx)
∂ˆx
′
K(t)W
2
K(t)
′
∂V
k
1
(t, ˆx)
∂ˆx
,
(20)
where M
k
0
= 1, O
k
(.) is the backward operator, −k
represents not k; if k is 1 then −k is 2 and vice-versa.
Proof. From the system equation (1), (18) and assum-
ing that separation principle holds, the minimal 2
nd
value function V
k∗
2
(t, ˆx) satisfies the following HJB
equation for the k-th player.
0 = min
µ
k
∈U
M
k
(
O
k
(µ
∗
1
, µ
∗
2
)
h
V
k∗
2
(t, ˆx)
i
+
∂V
k
1
(t, ˆx)
∂ˆx
′
K(t)W
2
K(t)
′
∂V
k
1
(t, ˆx)
∂ˆx
)
,
(21)
with terminal condition V
k
j
(t
F
, ˆx
F
) = 0, k = 1, 2, j =
1, 2, K(t) is the Kalman filter gain. Since the first
cost cumulant function V
k
1
is admissible (def. 2.1),
the following coupled equations are satisfied
0 =O
k
(µ
−k
, µ
k
)
h
V
k
1
(t, ˆx)
i
+ M
k
0
(t, ˆx)L
k
(t, ˆx, µ
−k
, µ
k
),
0 =O
k
(µ
−k
, µ
k
)
h
V
k
2
(t, ˆx)
i
+
∂V
k
1
(t, ˆx)
∂ˆx
′
K(t)W
2
K(t)
′
∂V
k
1
(t, ˆx)
∂ˆx
,
(22)
where M
k
0
= 1, O
k
(.) is the backward operator and
the first line of (22) follows from the classical HJB
equation while the second line relates the second cu-
mulant function with the first cumulant function in the
HJB equation. Thus, converting (22) to unconstrained
optimization problem gives
0 = min
µ
k
∈U
M
k
(
O
k
(µ
−k
, µ
k
)
h
V
k
1
(t, ˆx)
i
+ M
k
0
(t, ˆx)L
k
(t, ˆx, µ
−k
, µ
k
) + γ
2k
(t)O
k
(µ
−k
, µ
k
)
h
V
k∗
2
(t, ˆx)
i
+ γ
2k
(t)
∂V
k
1
(t, ˆx)
∂ˆx
′
K(t)W
2
K(t)
′
∂V
k
1
(t, ˆx)
∂ˆx
)
,
(23)
where γ
2k
is the Lagrange multiplier. From backward
operator (11) using (9), (10) and expanding (23) gives
min
µ
k
∈U
M
k
(
∂V
k
1
(t, ˆx)
∂t
+ ˆx
′
(t)Q(t) ˆx(t)
+ tr
Q(t)P(t)
+
2
∑
i=1
µ
i
(t)R
ki
(t)µ
′
i
(t)
+
∂V
k
1
(t, ˆx)
∂ˆx
ˆx(t)
′
A(t)
′
+
2
∑
i=1
µ
i
(t)
′
B
i
(t)
′
+
1
2
tr
K(t)W
2
K(t)
′
∂
2
V
k
1
(t, ˆx)
∂ˆx
2
+ γ
2k
∂V
k∗
2
(t, ˆx)
∂t
+ γ
2k
∂V
k∗
2
(t, ˆx)
∂ˆx
ˆx(t)
′
A(t)
′
+
2
∑
i=1
µ
i
(t)
′
B
i
(t)
′
+
γ
2k
2
tr
K(t)W
2
K(t)
′
∂
2
V
k∗
2
(t, ˆx)
∂ˆx
2
+ γ
2k
∂V
k
1
(t, ˆx)
∂ˆx
′
K(t)W
2
K(t)
′
∂V
k
1
(t, ˆx)
∂ˆx
)
= 0.
(24)
Minimizing (24) with respect to µ
k
(t, ˆx) gives
µ
∗
k
(t, ˆx) = −
1
2
R
−1
kk
B
′
k
∂V
k
1
(t, ˆx)
∂ˆx
+ γ
2k
∂V
k∗
2
(t, ˆx)
∂ˆx
.
(25)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
56

Remark. The strategy for the k-th player µ
∗
k
(t, ˆx) de-
rived from the coupled HJB equation (22) is subop-
timal. In (22), the certainty equivalent principle has
been extended to the second cumulant output feed-
back game where a Kalman filter is used for state es-
timation.
5 NUMERICAL
APPROXIMATION METHOD
The analytical solutions of HJB equation (18) is dif-
ficult to find except for simple linear systems. San-
berg (Sandberg, 1998) showed that neural networks
(NN) with time-varying weights can be utilized to ap-
proximate uniformly continuous time-varying func-
tions. We are motivated by the work in (Chen
et al., 2007), to extend NN approach to cost cumu-
lant game. In this approach, NN is utilized to ap-
proximate the value function based on method of
least squares on a pre-defined region. The value
functions V
k
i
can be approximated as V
k
i
(t, ˆx) =
w
′
L
(t)Λ
L
( ˆx) =
∑
L
i=1
w
i
(t)γ
i
( ˆx) on t on a compact
set Ω → R
n
. Thus, we approximate the players
value functions V
k
m
as V
k
mL
(t, ˆx) = w
′
mkL
(t)Λ
mkL
( ˆx) =
∑
L
i=1
w
mki
(t)γ
mki
( ˆx), where w
mkL
(t) and Λ
mkL
( ˆx) are
vectors, and w
mkL
(t) = {w
mk1
(t), . . . , w
mkL
(t)}
′
and
Λ
mkL
( ˆx) = {γ
mk1
( ˆx), . . . , γ
mkL
( ˆx)}
′
are the vector neu-
ral network weights and vector of activation functions
and L is the number of the hidden-layer neurons. Us-
ing the approximated value functions V
k
mL
(t, ˆx) in the
HJB equations result in residual error equations. We
apply weighted residual method (Finlayson, 1972) to
minimize the residual error equations and then numer-
ically solve for the least square NN weights (Chen
et al., 2007).
6 SIMULATION
Consider a linear deterministic dynamic system in
(Zheng, 1989), where we introduce gaussian noise as
process and measurement noise. The stochastic sys-
tem is represented as
dx(t) = Ax(t)dt + B
1
u
1
(t)dt + B
2
u
2
(t)dt + Gdw
1
(t),
dy(t) = Cx(t)dt + Ddw
2
(t),
(26)
A =
−2 0 3 2
4 −2 1 3
2 3 −3 4
0 0 0 −2
, B
1
=
1
0
1
0
,
B
2
=
0
1
0
1
,C =
1 0 0 0.1
0 1 0 0.1
0 0 1 1
,
and the state variable x(t) is defined as: x(t) = [x
1
(t)
x
2
(t) x
3
(t) x
4
(t)]
′
. We assume that G and D in
(26) are 4 × 1 and 3 × 1 constant vectors given as
G = [1 1 1 1]
′
, D = [1 1 1]
′
and dw
1
(t), dw
2
(t) in
(26) as a Gaussian process with mean E{dw
1
(t)} =
E{dw
2
(t)} = 0 and covariance E{dw
1
(t)dw
1
(t)
′
} =
0.1 and E{dw
2
(t)dw
2
(t)
′
} = 0.1. In this example, we
study a 2-player 2
nd
cumulant ad hoc output feedback
Nash game. Here, we compute the suboptimal solu-
tion for the player strategy through solving the output
feedback 2
nd
cumulant game problem constraint on
the 1
st
cumulant cost function.
The first player cost function J
1
is
J
1
(t
0
, x(t
0
), u
1
(t
0
), u
2
(t
0
)) =
Z
t
F
t
0
x
2
1
(t) + x
2
2
(t)
+ x
2
3
(t) + x
2
4
(t) + u
2
1
(t)
dt + ψ
1
(x(t
F
),t
F
),
(27)
where ψ
1
(x(t
F
),t
F
) = 0 is the terminal cost and the
second player cost function J
2
is
J
2
(t
0
, x(t
0
), u
1
(t
0
), u
2
(t
0
)) =
Z
t
F
t
0
x
2
1
(t) + x
2
2
(t)
+ x
2
3
(t) + x
2
4
(t) + u
2
2
(t)
dt + ψ
2
(x(t
F
),t
F
),
(28)
where ψ
2
(x(t
F
),t
F
) = 0 is the terminal cost. The ac-
tivation function Λ
L
(x) for the value functions of the
players are the same and based on (Chen and Jagan-
nathan, 2008) which are formulated as
Λ
L
(x) =
M
2
∑
i=1
n
∑
j=1
x
j
!
2i
,
(29)
where in (29), M is an even-order of the approxima-
tion, L is the number of hidden-layer neurons, n is the
system dimension.
The input function Λ
L
(x) (29) is
Λ
L
=
x
2
1
, x
2
2
, x
2
3
, x
2
4
, x
1
x
2
, x
1
x
3
, x
1
x
4
, x
2
x
3
, x
2
x
4
, x
3
x
4
′
.
(30)
We transform this problem as an innovative process
(Kailath, 1968) in terms of state estimate using (8),
(9), (10) and solve for the Kalman filter gain. For
the NN series approximation, we choose a polynomial
function (30) of up to second-order (M = 2) in state
variable (i.e x is 2
nd
order) with length L = 10. Higher
order polynomial did not provide significant improve-
ment in the approximation accuracy. In the simula-
tion, the asymptotic stability region for states was ar-
bitrarily chosen as −5 ≤ x
1
≤ 5,−5 ≤ x
2
≤ 5,−5 ≤
Two-playerAdhocOutput-feedbackCumulantGameControl
57
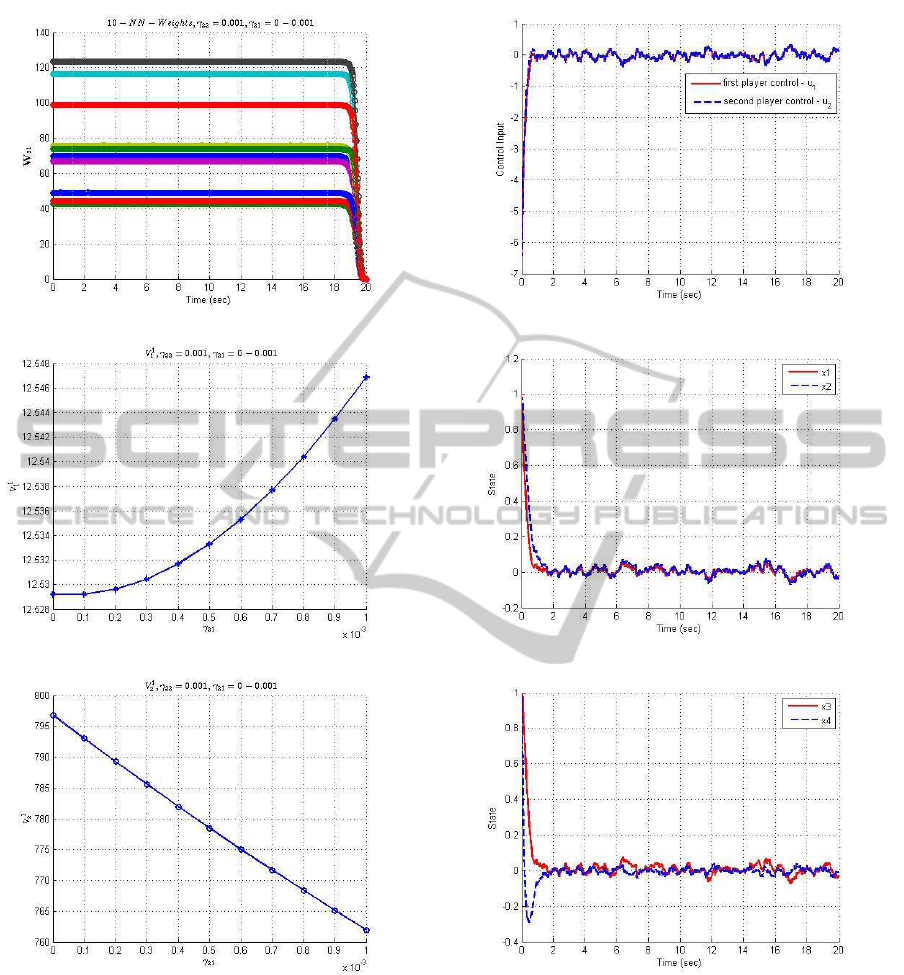
(a) NN Weights versus time
(b) V
1
1
versus γ
21
(c) V
1
2
versus γ
21
Figure 1: Neural Network Weights and Value Function.
x
3
≤ 5 and −5 ≤ x
4
≤ 5. The final time t
F
was 20 s and
w
′
11L
(t
F
)−w
′
21L
(t
F
) = {0} and w
′
12L
(t
F
)−w
′
22L
(t
F
) =
{0}. The initial condition was x(t
0
) = x
0
=[1 1 1 1]
′
.
Figs. 1(a) to 1(c) show the first player neural net-
work weights and value functions which are similar
to the second player, hence only the first player plots
are shown. Fig. 1(a), the neural network weights con-
verge to constants. Plots 1(b) to 1(c) show the first
and second value cumulant functions. From Fig. 1(b),
(a) Control trajectory
(b) State trajectory
(c) State trajectory
Figure 2: Control Strategy and State Trajectory.
it was observed that the value function V
1
1
increases
with increase in γ
21
while from Fig. 1(c), it was ob-
served that the value functions V
1
2
decreases as γ
21
increase. The Lagrange multipliers γ
2k
were selected
as constants. The Nash suboptimal controls, u
1
and
u
2
are shown in Fig. 2(a). It should be noted from
Fig. 2(a), that the Nash suboptimal controls for the
two players were solved for the 2
nd
cumulant game by
selecting γ
21
, γ
22
where the value functions are mini-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
58

mum which in our case were γ
21
= 0.001, γ
22
= 0.001.
In addition, we have the design freedom in γ
2k
val-
ues selection to enhance system performance. From
Figs. 2(b) to 2(c), the states converge to values close
to zero.
7 CONCLUSIONS
In this paper, we analyzed an output feedback cumu-
lant differential game control problem using cost cu-
mulant optimization approach. We investigated a lin-
ear stochastic system with two players and derived
a 2-player near-optimal strategies for the tractable
auxiliary problem. The efficiency of our proposed
method has been demonstrated using a numerical ex-
ample where a neural network series method was ap-
plied to solve the HJB equations.
REFERENCES
Aberkane, S., Ponsart, J. C., Rodrigues, M., and Sauter, D.
(2008). Output feedback control of a class of stochas-
tic hybrid systems. Automatica, 44:1325–1332.
Basar, T. (1999). Nash Equilibria of Risk-Sensitive Non-
linear Stochastic Differential Games. Journal of Opti-
mization Theory and Applications, 100(3):479–498.
Bensoussan, A. and Schuppen, J. H. V. (1985). Opti-
mal Control of Partially Observable Stochastic Sys-
tems with an Exponential-of-Integral Performance In-
dex. SIAM Journal of Control and Optimization,
23(4):599–613.
Charilas, D. E. and Panagopoulos, A. D. (2010). A sur-
vey on game theory applications in wireless networks.
Computer Networks, 54(18):3421–3430.
Chen, T., Lewis, F. L., and Abu-Khalaf, M. (2007). A
Neural Network Solution for Fixed-Final Time Op-
timal Control of Nonlinear Systems. Automatica,
43(3):482–490.
Chen, Z. and Jagannathan, S. (2008). Generalized
Hamilton-Jacobi-Bellman Formulation-Based Neural
Network Control of Affine Nonlinear Discrete-Time
Systems. IEEE Transactions on Neural Networks,
19(1):90–106.
Cruz, J. B., Simaan, M. A., Gacic, A., and Liu, Y. (2002).
Moving Horizon Nash Strategies for a Military Air
Operation. IEEE Transactions on Aerospace and
Electronic Systems, 38(3):989–999.
Davis, M. (1977). Linear Estimation and Stochastic Con-
trol. Chapman and Hall, London, UK.
Finlayson, B. A. (1972). The Method of Weighted Residu-
als and Variational Principles. Academic Press, New
York, NY.
Fleming, W. H. and Rishel, R. W. (1975). Determinis-
tic and Stochastic Optimal Control. Springer-Verlag,
New York, NY.
Geromel, J. C., de Souza, C. C., and Skelton, R. E. (1998).
Static Output Feedback Controllers: Stability and
Convexity. IEEE Transactions on Automatic Control,
43(1):120–125.
Kailath, T. (1968). An Innovations Approach to Least
Square Estimation Part I: Linear Filtering in Additive
White Noise. IEEE Transactions on Automatic Con-
trol, 13(6):646–655.
Klompstra, M. B. (2000). Nash equilibria in risk-sensitive
dynamic games. IEEE Transactions on Automatic
Control, 45(7):1397–1401.
Mukaidani, H., Xu, H., and Dragon, V. (2010). Static Out-
put Feedback Strategy of Stochastic Nash Games for
Weakly-Coupled Large-Scale Systems. In Proc. of the
American Control Conference, pages 361–366, Balti-
more, MD.
Sain, M. K. (1966). Control of Linear Systems According
to the Minimal Variance Criterion—A New Approach
to the Disturbance Problem. IEEE Transactions on
Automatic Control, AC-11(1):118–122.
Sain, M. K. and Liberty, S. R. (1971). Performance Measure
Densities for a Class of LQG Control Systems. IEEE
Transactions on Automatic Control, AC-16(5):431–
439.
Sain, M. K., Won, C.-H., Spencer, Jr., B. F., and Liberty,
S. R. (2000). Cumulants and risk-sensitive control:
A cost mean and variance theory with application to
seismic protection of structures. In Filar, J., Gaitsgory,
V., and Mizukami, K., editors, Advances in Dynamic
Games and Applications, volume 5 of Annals of the
International Society of Dynamic Games, pages 427–
459. Birkhuser Boston.
Sandberg, I. W. (1998). Notes on Uniform Approx-
imation of Time-Varying Systems on Finite Time
Intervals. IEEE Transactions on Circuit and
Systems-1:Fundamental Theory and Applications,
AC-45(8):863–865.
Smith, P. J. (1995). A Recursive Formulation of the Old
Problem of Obtaining Moments from Cumulants and
Vice Versa. The American Statistician, (49):217–219.
Van De Water, H. and Willems, J. C. (1981). The Cer-
tainty Equivalence Property in Stochastic Control
Theory. IEEE Transactions on Automatic Control,
AC-26(5):1080–1087.
Won, C.-H., Diersing, R. W., and Kang, B. (2010). Sta-
tistical Control of Control-Affine Nonlinear Systems
with Nonquadratic Cost Function: HJB and Verifica-
tion Theorems. Automatica, 46(10):1636–1645.
Wonham, W. M. (1968). On the Seperation Theorem
of Stochastic Control. SIAM Journal of Control,
6(2):312–326.
Zheng, D. (1989). Some New Results on Optimal and Sub-
optimal Regulators of the LQ Problem with Output
Feedback. IEEE Transactions on Automatic Control,
34(5):557–560.
Zhu, Q., Han, Z., and Basar, T. (2012). A differential
game approach to distributed demand side manage-
ment in smart grid. In IEEE International Conference
on Communications (ICC), pages 3345–3350.
Two-playerAdhocOutput-feedbackCumulantGameControl
59
