
Modeling and Simulation of Coalition Formation
V. Mashkov, J. Barilla, P. Simr and J. Bicanek
Department of Informatics, University J. E. Purkyne, Pasteurova 1, Usti nad Labem, Czech Republic
Keywords: Multi-agent Systems, Coalition Formation, Modeling, Simulation, Petri Nets.
Abstract: One of the challenges of agent technologies is to provide models of team or group activities in which agents
contact each other, negotiate and collaborate towards certain objectives. Such groups are related to multi-
agent systems. In context of multi-agent systems, separate agents can cooperate and join together in order to
execute the faced tasks in a more efficient way or in order to gain benefits. The paper deals with unselfish
agents which are concerned about the system’s global outcome, without regards for personal payoff. Coalition
formation is a very complex process which requires correct planning and preliminary modeling to be solved
effectively. In the paper, we considered the problem of modeling the coalition formation from unselfish
agents. There are several tools that allow providing and carrying out coalition formation modeling. In the
paper, we showed how the Petri Nets can be used for such modeling. For the purpose of simulation of coalition
formation the open access web application was developed.
1 INTRODUCTION
Rapid development of agent technologies has evoked
new research problems, among them the problem of
formation of the groups of agents. There are a number
of facets characterizing a group of agents, such as
duration of cooperation of agents in a group (long-
time or short-time); level of agents responsibility for
achieving the goal(s) of mission; extent to which the
agents are interested in their own benefits and in
successful achievement of the common group goal(s);
level of independence of agents to act; distribution of
roles among agents; interoperability and information
sharing among agents; etc. The variety of facets
predetermines the variety of possible groups of
agents. In this paper, we assume that at the beginning
the agents are forming the group called alliance.
Alliance is defined as a set of agents that agree to
share some of their private information and cooperate
eventually (Pechoucek, 2002). During alliance
formation, each agent receives public information
from the agents that have already agreed to participate
in the alliance. After performing analysis of this
information, some of the agents can take a decision
about preferences or even inability or refusals to
cooperate with particular agents, although giving
their agreement to participate in executing certain
tasks of the alliance. Thus, the alliance can be formed
with the account of the revealed refusals (Mashkov,
2004 and 2005).
As distinct from alliance, in coalition all of the
agents agree to cooperate with each other. We
consider coalition as a set of agents which agreed to
fulfill a single, well-specified goal. Coalition
members committed themselves to collaborate on the
within coalition shared goal. A coalition, unlike an
alliance, is usually regarded as a short-term
agreement among collaborative agents. Coalition is
formed from the agents of alliance every time when a
request is received from an in-need entity (client).
Depending on the tasks which should be executed to
satisfy the client, every agent of alliance makes its
own decision about the services and resources it can
deliver.
Several formal description techniques, methods
and tools are used when solving the task of alliance
and coalition formation. Here we list only some of
them, particularly: LOTOS (Koning, 1999); SDL
(Iglesias, 1998); language Z (d’Inverno, 1996); finite
state machines (Barbuceanu, 1995); agent UML
(Bauer, 2000); Petri Nets (Cost, 1999); Erlang/OTP
platform (Mashkov, 2010) etc.
In order to ensure the adequate modeling of
coalition formation and correct description of all the
elements of coalition formation process, we should
take into consideration such data as agents’
capabilities, their strategies, restrictions imposed on
329
Mashkov V., Barilla J., Simr P. and Bicanek J..
Modeling and Simulation of Coalition Formation.
DOI: 10.5220/0005504203290336
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 329-336
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

task execution and on the communications among the
agents, etc. This can be done by using Petri Nets.
Moreover, Petri Nets allow that the changes in the
above data can be readily accounted for in the
coalition formation modeling. It is also important that
several high-quality tools for working with Petri Nets
and for obtaining the characteristics of interest are
available nowadays. In view of this we performed
modeling of coalition formation with the help of Petri
Nets.
The rest of the paper is organized as follows.
Section 2 recapitulates the basics of Petri Nets and
gives a short overview of applications of Petri Nets in
different fields. Section 3 describes how Petri Nets
can be used for modeling of coalition formation.
Section 4 contains analysis of the results of the
performed modeling and the recommendations made
on their basis. Conclusions are finally made in
Section 5.
2 APPLICATION OF PETRI NETS
FOR SYSTEM MODELING
Petri Nets were designed by Carl Adam Petri in 1962
in his PhD Thesis ‘Kommunikation mit Automaten’
(Petri, 1966). The basic idea is to describe state
changes of system via transitions. The main elements
of Petri Net are places and transitions that may be
connected by directed arcs. Thus, the graphical
structure of a Petri Net is a bipartite directed graph.
Nodes of this graph are divided into two groups called
places and transitions. Arcs connect only nodes of
different groups. Transitions symbolize actions or
events, whereas places symbolize states or
conditions. When conditions are met, an action can be
performed (in terms of Petri Nets, transition “fires”).
Transition has a certain number of input and output
places representing the pre-conditions and post-
conditions of the event, respectively. Places can
contain a certain number (nonnegative integer) of
tokens. The presence of a token in a place is
interpreted as holding the truth of the condition
associated with the place. Tokens can be also
interpreted as available resources needed for carrying
out of an action. Since each place is marked with a
certain number of tokens, it is possible to write an m-
vector, where m is the total number of places. This m-
vector is called as marking and is denoted as M={m
1
,
m
2
,..,m
n
}, where m
i
, i=1..n, is the number of tokens in
place p
i
in marking M.
Petri nets can be defined mathematically as a
quadruple N = (P, T, Pre, Post), where:
P and T are finite, non empty, and disjoint sets;
P is the set of places (in the figures
represented by circles);
T is the set of transitions (in the figures
represented by rectangles);
Pre: P × T
N
0
is the pre-incidence function
that specifies the arcs from places to
transitions;
Post: T × P
N
0
is the post-incidence
function that specifies the arcs from transitions
to places;
Petri Nets are a powerful tool for modeling real
systems since they allow to take into consideration
such features of system activities as concurrency ( or
parallelism), synchronization, limited resources,
sequence, mutual exclusion (conflicts) etc.
Carl Adam Petri originally proposed Petri Nets
without any notion of time. However, for
performance evaluation and solving the scheduling
problems of dynamic systems, it is desirable and
useful to account time delays of the events associated
with transitions. Such Petri Nets are called as timed
Petri Nets if the delays are deterministically given or
as stochastic Petri Nets if the delays are
probabilistically specified. Application of timed Petri
Nets can be found in such areas as communication
protocols (Diaz, 1982), performance evaluation
(Masri, 2009), manufacturing (Toguyeni, 2006) etc.
In the stochastic Petri Nets, time was naturally
associated with activities that induce state changes.
Currently, Petri nets are broadly used as a tool for
designing, analyzing and modeling the parallel and
distributed systems. For example, Petri Nets can be
applied in such areas as telecommunications
(Billington, 1999) and transportation (List, 2004), for
description of automated industrial systems,
computer networks, wireless sensor networks,
system-on-chip, control applications, processor self-
testing (Mashkov, 2013) etc. Recently, Petri Nets
have also been applied in biology (Reddy, 1993), in
chemistry (Kuroda, 1994) and for modeling of
radiobiological mechanism (Barilla, 2014).
3 USING PETRI NETS FOR
MODELING OF COALITION
FORMATION
Coalition formation process depends considerably on
the strategies which agents of an alliance adhere to
and on the agents’ capabilities. In the paper, we
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
330
consider only the agents which are not self-interested,
i.e., they are more interested in achieving common
coalition goal rather than in gaining any benefits for
themselves. Thus, when an agent receives a request to
cooperate from another agent it will not refrain from
a reply, and it either accepts an offer or denies it.
We also assume that among the agents of alliance
there may be such agents that are not going to
cooperate with some agents of the same alliance.
Alliance in which at least one agent is not going to
cooperate with all other alliance agents is called as
restricted alliance (Mashkov, 2004).
The whole process of coalition formation can be
divided into small steps. At each step, the so-called
interim coalition which has not yet enough
capabilities to achieve the coalition goal is formed. At
every next step, interim coalition is extended by
adding a new agent of the alliance. This procedure
continues until coalition with enough capabilities is
formed. This last coalition got the name final
coalition. It is also assumed that during coalition
formation process an agent can be either in idle state
or in busy state. An agent can communicate with
other agents with the aim of interim coalition
formation only when he is in idle state.
Thus, Petri Net used for modeling coalition
formation should account such data as states of an
agent and durations of these states; the set of agents
with which agent is not going to cooperate; capability
of each agent; duration of each
communication/negotiation between any two agents.
In order to illustrate how Petri Nets can be used
for modeling of coalition formation, we consider
simple example when alliance consists of three agents
A
1
, A
2
and A
3
.
Agents adhere to their own preferences in
choosing the partner for negotiation. Agent’s
preferences are either derived from agent’s previous
experience or based on some chosen criteria. Thus,
agent’s preferences reflex the fact that the agent
differentiates between other agents according to his
willingness to negotiate with them.
In the example under consideration, the following
agents’ preferences are established:
A
1
: first tries to contact agent A
3
, then agent A
2
;
A
2
: first tries to contact agent A
3
, then agent A
1
;
A
3
: first tries to contact agent A
2
, then agent A
1
;
From these preferences it is easy to deduce the
negotiation when all three agents are idle. In our
example, this is negotiation between agents A
2
and
A
3
. It is also assumed that capabilities of agents A
2
and A
3
are enough to form the final coalition whereas
any interim coalition with agent A
1
will not have
enough capabilities. Petri Net for this particular case
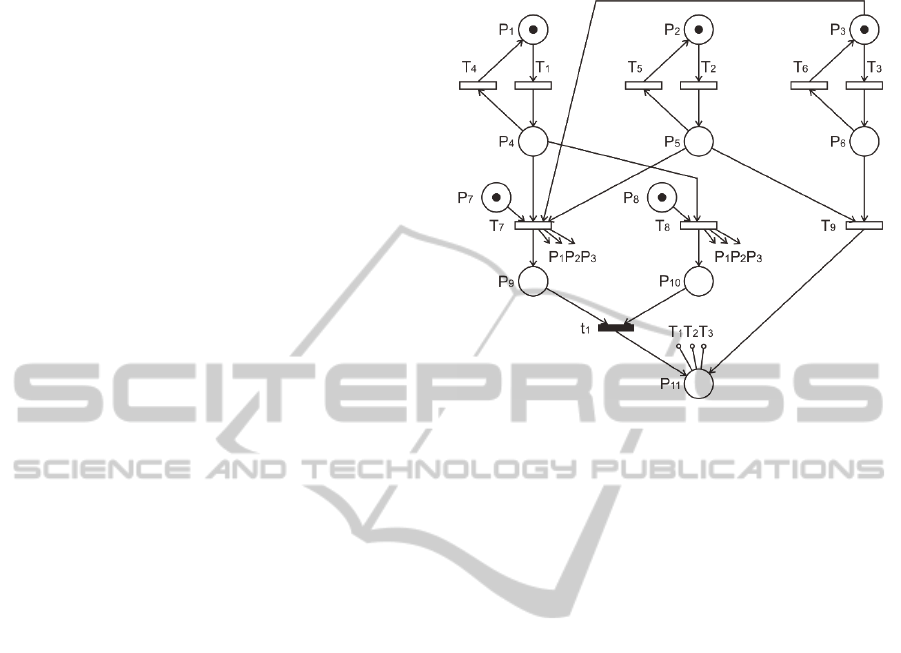
is depicted in Fig. 1.
Figure 1: Petri Net for coalition formation when alliance
consists of three agents.
In Fig. 1, places P
1
, P
2
and P
3
are associated with busy
states of the agents. Conversely, places P
4
, P
5
and P
6
are associated with the agents’ idle states in which
agents can negotiate to form coalitions. Places P
9
, P
10
and P
11
are associated with the events of interim and
final coalitions formation. For instance, if place P
9
contains a token, it means that interim coalition (A
1
,
A
2
) has been formed. Places P
7
and P
8
are used to
restrict the total number of negotiations between two
agents. The total number of negotiations is set as the
total number of tokens in the corresponding place. For
example, if place P
7
contains only one token, it means
that agents A
1
and A
2
will negotiate only once.
Timed transitions T
1
, T
2
and T
3
allow simulating
the amount of time when agents are busy, whereas
time transitions T
4
, T
5
and T
6
simulate the amount of
time when agents are idle and are ready to negotiate.
Timed transitions T
7
, T
8
and T
9
allow simulating the
amount of time allocated for negotiation between two
agents. Immediate transition t
1
simulates the logical
operation “AND”.
For more complex cases when the number of
agents is large, a special algorithm can be used to
determine the order of negotiations when all agents
are idle. The main idea behind the algorithm consists
in checking if the agent is intending (according to his
preference list) to contact the agent which already has
endeavored to contact him. The agents’ preferences
can be graphically depicted by using a sequence
diagram. For instance, for four agents the sequence
diagram is shown in Fig. 2.
ModelingandSimulationofCoalitionFormation
331

Figure 2: Sequence diagram of agents endeavors to
negotiate with.
In Fig. 2, agents’ preferences are shown as follows
A
1
: first A
3
then A
2
then A
4
or as (N-1)-tuple:
T
1
=(3,2,4)
A
2
: first A
1
then A
3
then A
4
or T
2
=(1,3,4)
A
3
: first A
2
then A
4
then A
1
or T
3
=(2,4,1)
A
4
: first A
3
then A
2
then A
1
or T
4
=(3,2,1)
The sequence diagram presented in Fig. 2 has
three main steps. At each step s, s=1,..N-1, the agents
try to get in touch with each other according to their
own preference list expressed by tuple T. For
example, at step 1 agent A
1
will contact agent A
3
,
while agent A
3
will contact agent A
2
. At step 2, agent
A
1
will try to contact agent A
2
. Since agent A
1
has
already received offer from agent A
2
at step 1, it
negotiates and forms the interim coalition with agent
A
2
. Proceeding from this consideration, we come to
the following negotiations order:
(A1, A2) and (A3, A4); then (A3, A2) and (A1, A4);
then (A1, A3) and (A2, A4).
For more complex cases when the number of
agents is large, negotiations order can be determined
according to the following algorithm.
Algorithm.
Input: Tuples T
i
, i=1,..,N; Sets R
i
S
, i=1,..,N, s=1,..,N-
1.
Output: Ordered List of negotiations L.
begin
For i:=1 to N do
begin
For s:=1 to N-1 do
begin
Choose s-th element of T
i
, i.e.,
e
s
Ti
If e
s
Ti
R
i
S
then include (i, e
s
Ti
)
in L at s-th step
end
end
return L
end
Where set R
i
S
contains numbers of agents which
have already contacted i-th agent by the s-th step.
This algorithm can be verified by using web
application available on
http://vtan.ujep.cz/pnsimulator-coalition.
It is worth noting that by using agent’s preferences
it is possible to model coalition formation when some
agents refuse to communicate and negotiate with each
other, i.e., deal with the agents of restricted alliance.
This is especially important when restricted alliance
includes large number of agents. In this case, Petri
Net modeling of coalition formation will allow to find
out the possible deadlocks and to estimate the
probabilities of their occurrences. A deadlock occurs
when current interim coalitions are unable to perform
coalition tasks and cannot be expanded due to refusals
of some agents to negotiate with each other.
In order to illustrate a possible deadlock which
leads to coalition formation failure, we consider a
slightly modified example with four agents (see Fig.
3).
Now, we assume that agents A
1
, A
2
, A
3
and A
4
have capabilities equaling to 2, 4, 6 and 7 respectively
and the required coalition capabilities R
C
are equal to
13. It is assumed that agent A
4
refuses to
communicate with agents A
1
and A
2.
This fact is
reflected in Fig. 3 as absence of transitions associated
with negotiations of agent A
4
with agents A
1
and A
2
.
As soon as agent A
3
forms an interim coalition either
with agent A
1
or with agent A
2
, coalition formation
process will fail, and the eventual situation will lead
to deadlock. Only coalition (A3, A4) can be
considered as final, and coalition formation process
can be considered as successful. In order to determine
the probability of formation of final coalition and
probability of coalition formation failure (i.e.,
deadlock), it is needed to provide solution of devised
Petri Net.
4 MODELING AND ITS RESULTS
Since Petri Net designed for modeling coalition
formation includes probabilistically defined timed
transitions, it relates to Stochastic Petri Nets. There
exist many modeling tools for solution of Stochastic
Petri Nets. For modeling coalitions with a small
number of agents, we chose Sharpe (Barilla, 2014) for
the following reasons:
- Sharpe provides graphical representation of
Petri Nets which is very illustrative;
- Sharpe has the tools for providing analysis of the
model;
- Sharpe has a friendly interface.
Step 1
Step 2
Step
3
A
1
A
2
A
3
A
4
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
332
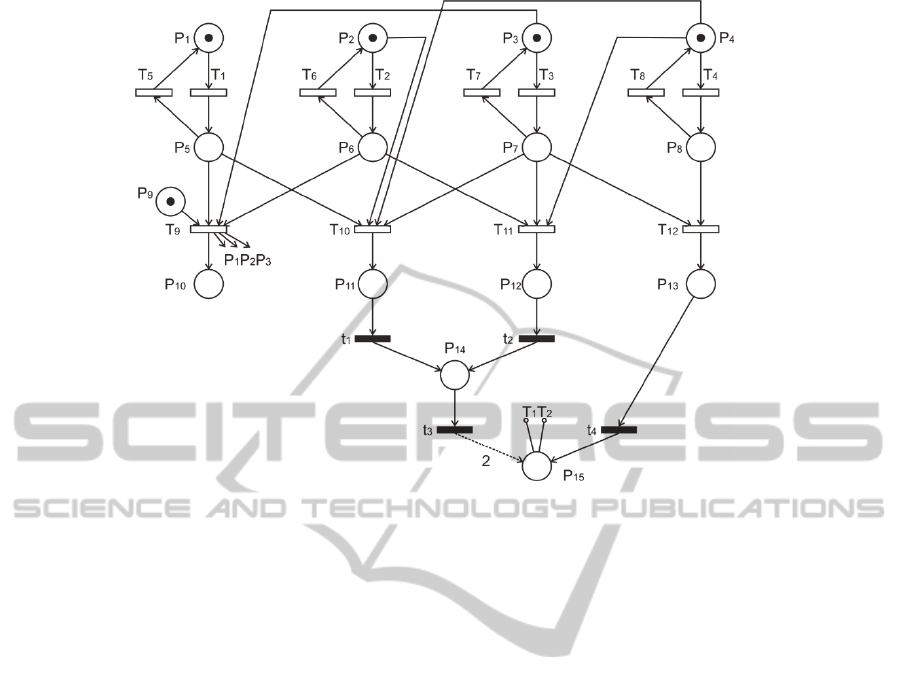
Figure 3: Petri Net for coalition formation when alliance consists of four agents.
Petri Nets simulating coalition formation when up to
four agents can be engaged in this process can be
plotted directly in the proper window of Sharpe.
Sharpe enables several outputs, such as:
- steady-state probability that the given place
is empty;
- probability that the given place is empty at
time t;
- expected number of tokens in the given
place at time t;
- throughput of the given transition at time t;
- utilization of given transition at time t; etc.
Given such options of Sharpe, it is possible to
determine several functional dependences for
coalition formation with three agents (see Fig. 1). For
instance, dependence of the time needed to form the
final coalition (i.e., coalition capable of performing
all coalition’s tasks) on the engaged periods of the
agents looks as presented in Fig. 4.
In Fig. 4, time needed to form the final coalition,
T
C
, and engaged period of agent, t
, are presented in
conditional units, which means that one can select
either milliseconds or seconds or hours or days, etc.,
depending on the problem to be solved. Given t
, the
probability of the event that final coalition will be
formed during time T
C
is equal to 0.95. From Fig. 4 it
is easy to conclude that functional dependence T
ft
is of polynomial growth.
Fig. 5 presents the probability of deadlock, P
d
,
determined by Sharpe when coalition is being formed
with four agents (see Fig. 3). Since agent A
4
refuses
to collaborate with agents A
1
and A
2
, each interim
coalition formed by any of these agents with agent A
3
will lead to deadlock. Thus, it is important for agent
A
4
to contact agent A
3
earlier than agents A
1
or A
2
have contacted it. Agent A
4
will be able to do this if
his engaged period t
is small. Fig. 5 provides
information about functional dependence P
ft
.
For the cases when total number of agents is large,
it is very difficult or even impossible to plot the
corresponding Petri Net into Sharpe. In the given
case, we suggest simulating the corresponding Petri
Net with the help of special web application available
on http://vtan.ujep.cz/pnsimulator-coalition.
Simulation of Petri Net is performed according to the
following algorithm.
Algorithm.
Step1. Draw lots for engaged and free periods of the
agents. In Petri Net, it results in putting a token into
the corresponding place.
Step 2. Determine the possible negotiations between
the agents according to their (agents’) states and
preferences.
Step 3. Form the interim coalitions.
Step 4. Expand the interim coalitions by way of their
joining if possible.
Step 5. Increment time by t
Step 6. Repeat Steps from 1 to 5 until final coalition
is formed.
ModelingandSimulationofCoalitionFormation
333
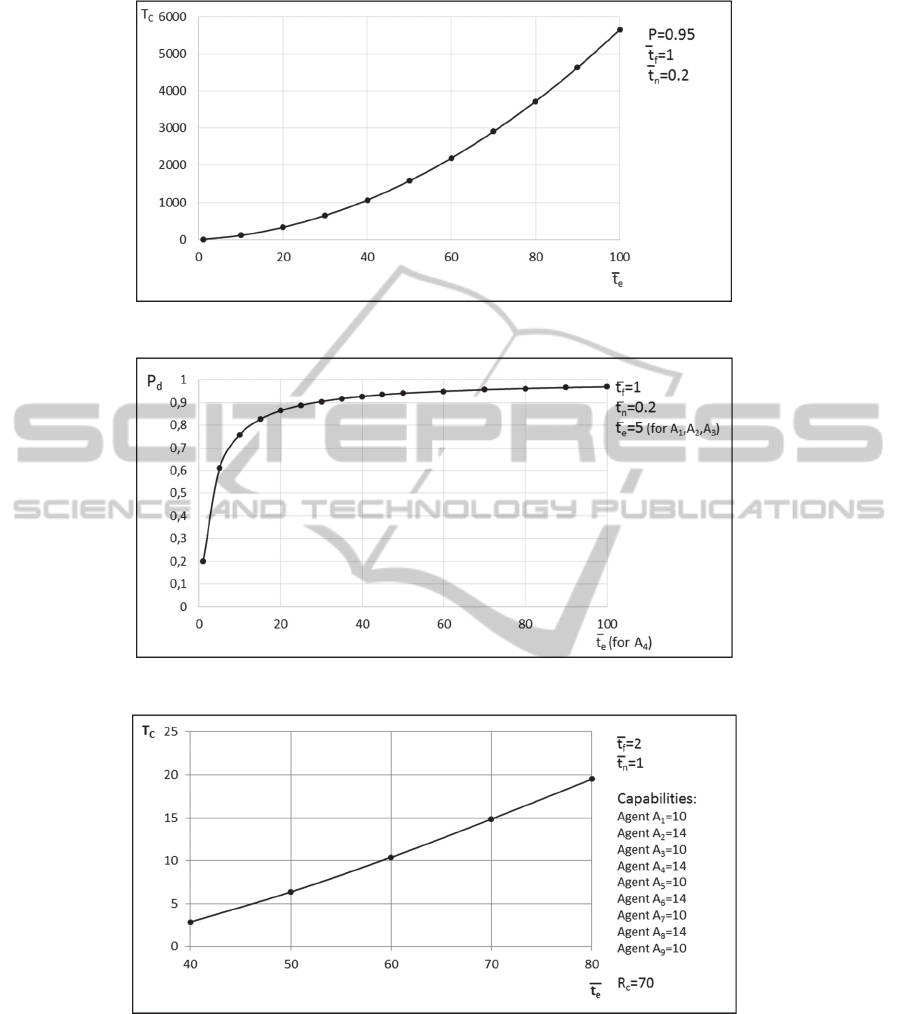
Figure 4: Time required to form the final coalition, T
C.
Figure 5: Probability of deadlock, P
d.
Figure 6: Functional dependence T
ft
for N=9.
The developed web application allows to set:
- total number of agents, N;
- capabilities required to perform all
coalition tasks R
C
(as positive integer);
- agent’s capabilities Cap(A
i
), i=1..N (as
positive integer for each agent separately);
- mean time of agent’s engaged period, t
;
- mean time of agent’s idle period, t
;
- mean time of negotiation between agents,
t
;
- agents’ preferences in the form of (N-1)-
tuple.
Unlike Sharpe, the developed web application
allows different probability density functions for
random variables t
e
, t
f
and t
n
, and thus, it gives a more
adequate model of real systems. The value of
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
334

increment t provides that the probability of agent’s
state change (from engaged to idle or vice versa) at
Step 1 of the algorithm is small. Approximately
dozens of repetitions of Step 1 are needed for agent’s
state change. Otherwise, the probability of omitting
the agent’s state change would be unacceptable.
The developed web application allows to set each
agent’s priorities in the order of negotiations, and, in
addition, it allows to model situations when some
agents will not communicate with each other.
This web application will enable to determine
some functional dependences which can be helpful
for its users. For example, functional dependence
T
ft
determined for the coalition formation
process with nine agents is shown in Fig. 6.
5 CONCLUSIONS
Our research deals with the issues of coalition
formation with unselfish agents of restricted alliance.
Agents of such alliance evaluate each other when
making decision about possible negotiations. We
consider that during the process of coalition
formation agents of the alliance can be either in a busy
or idle state. The amount of time when agent is in an
idle or busy state is random value. The time of each
negotiation between any two agents is also random
value. Thus, coalition formation process has many
parameters that are probabilistically defined. From
this it follows that it is very difficult to predict which
coalition capable of fulfilling coalition goal will be
formed and when. The situation when such coalition
will not be formed at all is also possible. The task of
estimating the probability of formation for all
possible coalitions and determining the mean time of
their formation can be solved by providing
appropriate modeling which will take into account
many characteristics of agents’ behavior and their
strategies. We preferred to use Petri Nets for such
modeling for the reasons mentioned above.
For providing analysis of the designed Petri Net
we propose to exploit the special tool called Sharpe
in case of small number of agents or use the
developed by us web application in case of large
number of agents. By using these facilities it is also
possible to find out deadlocks in coalition formation
process and determine the probabilities of their
occurrences when dealing with the agents of
restricted alliance. Agents of restricted alliance can be
informed about possible deadlocks before coalition
formation process begins and, thus, they will be
prepared and will know what to do to proceed with
formation of final coalition.
ACKNOWLEDGEMENTS
The authors would like to thank SHARPE developer
Prof. Kishor Trivedi for his kind help and
recommendations which facilitated preparing of this
paper.
REFERENCES
Barbuceanu, M., Fox, M. (1995) ‘COOL: A language for
describing coordination in multiagent system’, First
International Conference on Multi-agent Systems
(ICMAS-95), San Francisco, USA, pp.17-24.
Barilla, J., Lokajíček, M., Pisaková, H., Simr, P. (2014)
‘Simulation of the chemical stage in water radiolysis
with the help of Continuous Petri nets’, Radiation
Physics and Chemistry, (97), pp.262-269. DOI:
10.1016/j.radphyschem. 2013.12.019.
Bauer, B., Muller, J., Odell, J. (2000) ‘An extension of
UML by protocols for multi-agent interaction’,
International Conference on Multiagent Systems
(ICMAS’00), Boston, USA, pp.207-214.
Billington, J., Diaz, M., Rozenberg, C. (1999) ‘Application
of Petri nets to communication networks’, Advances in
Petri Nets, LNCS, (1), p.314.
Cost, R. et al. (1999) ‘Modeling agent conversation with
colored Petri nets’, J. Bradshaw, ed., Atonomous
Agents’99 Special Workshop on Conversation Policies.
Diaz, M. (1982) ‘Modeling and analysis of communication
and cooperation protocols using petri net based
models’, Computer Networks, 6(6), December 1982,
pp.419–441.
d’Inverno, M., Luck, M. (1996) ‘Formalising the contract
net as a goal-directed system’, W. de Velde and J.
Perram, ed., Agent Breaking Away, MAAMAW 96,
LNAI 1038, Springer-Verlag.
Iglesias, C., Garrijo, M., Gonzales, J., Velasco, J. (1998)
‘Design of multi-agent system using mas-
commonkads’, Proceedings of ATAL 98, Workshop on
Agent Theories, Architectures and Languages, LNAI
1555, Springer-Verlag, Paris, pp. 163-176.
Koning, J. (1999) ‘Algorithms for translating interaction
protocols into a formal description’, K. Ito, ed., IEEE
Interantional Conference on Systems (SMC-99), Tokio.
Kuroda, C., Ogawa, K. (1994) ‘Nonlinear-Waves in a
Shear-flow with a Diffusive Exothermic Reaction and
its Qualitative Reasoning’, Chemical Engineering
Science 49(16), pp. 2699-2708.
List, G. F., Cetin M. (2004) ‘Modeling traffic signal control
using Petri nets’, IEEE Trans. on Intelligent
Transportation Systems, (5), pp.177-187.
Mashkov, V., (2004) ‘Restricted alliance and coalition
formation’, Proc. of IEEE/WIC/ACM International
Conf. on Intelligent Agent Technology, Beijing, pp.329-
332.
Mashkov, V. (2005) ‘Tasks allocation among agents of
restricted alliance’, Proc. of 8th IASTED International
ModelingandSimulationofCoalitionFormation
335

Conf. on Intelligent systems and Control, ACTA Press,
Cambridge, MA, USA, pp.13-18.
Mashkov, V., Fiser, J. (2010) ‘Alliance and coalition
formation’, Int. Journal of Applied Computer Science,
18(1), Poland, pp.19-38.
Mashkov, V., Barilla, J., Simr, P. (2013) ‘Applying Petri
Nets to modeling of many-core processor self-testing
when tests are performed randomly’, Journal of
Electronic Testing (JETTA), 29(1), pp.25-34.
Masri, A., Bourdeaud’huy, T., Toguyeni, A. (2009) ‘A
component modular modeling approach based on
object oriented Petri nets for the performance analysis
of distributed discrete event systems’, 5th Int. Conf. on
Networking and Services ICNS, pp.222-227.
Pechoucek, M., Marik, V., Barta, J. (2002) ‘A knowledge-
based approach to coalition formation’, IEEE
Intelligent Systems, 7(3), pp.17-25.
Petri, C. A. Kommunikation mit Automaten. Bonn: Institut
fur Instrumentelle Mathematik, Schriften des IIM
(1966) Nr.3, 1962. Also, English translation
Communication with Automata, New York: Griffiss Air
Force Base, Tech., Rep., RADC-TR-65-377, 1(1).
Reddy, V. N., Mavrovouniotis, M. L. (1993) ‘Petri net
representation in metabolic pathways’, Proc. Int. Conf.
Intell. Syst. Mol. Biol. (1), pp.328-336.
Sahner, R. A., Trivedi, K. S. (1987) ‘Reliability modeling
using SHARPE’. IEEE Transactions on Reliability,
36(2), pp.186-193.
Toguyeni, A. (2006) ‘Design of modular and hierarchical
controllers for reconfigurable manufacturing systems’
IMACS Multiconference on Computational
Engineering in Systems Applications, (1), pp.1004-
1011.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
336
