
Synchronization of the Complex Dynamical Networks with a Gui Chaotic
Strange Attractor
Zhanji Gui
1
and Lan Kang
2
1
Department of Software Engineering, Hainan College of Software Technology, Qionghai, 571400, P.R. China
2
Department of Obstetric, Haikou Women and Children Hospital, Haikou, 570203, P.R. China
Keywords:
Gui Chaotic Strange Attractor, Neural Networks, Synchronization.
Abstract:
In this paper, impulsive neural networks with a Gui chaotic strange attractor is studied. By employing the
Lyapunov-like stability theory of impulsive functional differential equations, some criteria for synchronization
of impulsive neural networks are derived. An illustrative example is provided to show the effectiveness and
feasibility of the proposed method and results.
1 INTRODUCTION
In recent years, the additive neural networks have
been extensively studied, including both continuous
time and discrete-time settings, and applied to as-
sociative memory, model identification, optimization
problems, etc. Many essential features of these net-
works, such as qualitative properties of stability, os-
cillation, and convergence issues have been investi-
gated (Cao, 1999; Hopfield, 1982; Song and Zhang,
2008; Subashini and Sahoo, 2014; Wang and Huang,
2014).
However, as we well know, nonautonomous phe-
nomena often occur in many realistic systems. Partic-
ularly when we consider a long-term dynamical be-
haviors of a system, the parameters of the system usu-
ally will change with time. In addition, in many appli-
cations, the property of periodic oscillatory solutions
of cellular neural networks also is of great interest.
In fact, there has been considerable research on the
nonautonomous neural networks(Gopalsamy and He,
1994; Subashini and Sahoo, 2014) . The cellular neu-
ral networks with impulse effect are studied, where
the criteria on the existence, uniqueness and global
stability of periodic solution are obtained.Further, a
new chaos strange attractor was also found, known
as Gui chaos strange attractor(Zhang and Gui, 2009a;
Zhang and Gui, 2009b).
Another type of synchronization, impulsive syn-
chronization, has been developed(Amritkar and
Gupte, 1993; Anzo and Barajas-Ramłrez, 2014;
D¨orfler and Bullo, 2014; Wan and Cao, 2015; Xie
and Xu, 2014). It allows synchronization of chaotic
systems using only small impulses (Yang and Chua,
1999a) generated by samples of the state variables of
the driving system at discrete time instances. These
samples are called the synchronizing impulses and
they drive the response system discretely at these in-
stances. After a finite period of time, the two chaotic
systems behave in accordance with each other and
the synchronization of the two chaotic systems is
achieved. In other words, the asymptotic stability
property of the error dynamics between the driving
and response systems is reached. The impulsive syn-
chronization has been applied to a number of chaos-
based communication systems which exhibit good
performance for the synchronization purposes and for
security purposes (Yang and Chua, 1997; Yang and
Chua, 1999b) .
Motivated by the above discussions, the aim of
this paper is to study the synchronization of impul-
sive neural networks with a Gui chaotic strange attrac-
tor. By employing the Lyapunov-like stability theory
of impulsive functional differential equations, some
criteria for synchronization of impulsive neural net-
works are derived.
The remainder of the paper is organized as fol-
lows: Section 2 describes the issue of synchroniza-
tion of coupled impulsive systems with a Gui chaotic
strange attractor. In Section 3, some sufficient condi-
tions for the synchronization are derivedby construct-
ing suitable Lyapunov-like function. In Section 4, an
illustrative example is given to show the effectiveness
of the proposed method. Conclusions are given in
Section 5.
257
Gui Z. and Kang L..
Synchronization of the Complex Dynamical Networks with a Gui Chaotic Strange Attractor.
DOI: 10.5220/0005504902570262
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 257-262
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 PRELIMINARIES AND
PROBLEM FORMULATION
In this paper, we consider the following nonau-
tonomous cellular neural networks model with im-
pulses
dx
i
dt
= −a
i
x
i
(t) +
n
∑
j=1
b
ij
f
j
(x
j
(t)) + c
i
(t),
t > 0, t 6= t
k
,
∆x
i
(t
k
) = x
i
(t
+
k
) − x
i
(t
−
k
) = d
ik
x
i
(t
−
k
),
(1)
where i = 1, 2, . . . , n;k = 1, 2, . . . ;∆x
i
(t
k
) = x
i
(t
+
k
) −
x
i
(t
−
k
) are the impulses at moments t
k
and t
1
<
t
2
< . . .is a strictly increasing sequence such that
lim
k→∞
t
k
= +∞; x
i
(t) corresponds to the state of the
ith unit at time t, f
j
(x
j
(t)) denotes the output of the
jth unit at time t, b
ij
denotes the strength of the jth
unit on the ith unit at time t, c
i
(t) is the external bias
on the ith at time t, a
i
represents the rate with which
the ith unit will reset its potential to the resting state
when disconnected from the network and external in-
puts.
As usual in the theory of impulsive differential
equations, at the points of discontinuity t
k
of the solu-
tion t 7→ x
i
(t)we assume that x
i
(t
k
) ≡ x
i
(t
−
k
). It is clear
that, in general, the derivatives x
′
i
(t
k
) do not exist. On
the other hand, according to the first equality of (1)
there exist the limits x
′
i
(t
∓
k
). According to the above
convention, we assume x
′
i
(t
k
) ≡ x
′
i
(t
−
k
).
Throughout this paper, we assume that:
(H
1
) Functions f
j
(u) ( j = 1, 2, . . . , n) are Lipschitz
continuous and monotonically non-decreasing,
i.e., for all u
1
, u
2
∈ R = (−∞, ∞) there are con-
stants L
j
> 0 such that
0 6
f
j
(u
1
) − f
j
(u
2
)
u
1
− u
2
6 L
j
.
(H
2
) There exists a positive integer T , such that
t
k+T
= t
k
+ ω, d
i(k+T)
= d
ik
,
where k = 1, 2, . . . , i = 1, 2, . . . , n.
In (Gui and Ge, 2006) , the system (1) were found
to have a Gui chaotic strange attractor. Now we con-
sider the drive system in the form of the neural net-
works (1). For the purpose of synchronization, we
introduce the response system that is driven by (1) via
a set of signals
dy
i
dt
= −a
i
y
i
(t) +
n
∑
j=1
b
ij
f
j
(y
j
(t)) + c
i
(t),
t > 0, t 6= t
k
,
y
i
(t
+
k
) = 2d
ik
x
i
(t
−
k
) + (1− d
ik
)y
i
(t
−
k
),
(2)
where i = 1, 2, . . . , n, k = 1, 2, . . . . Letting e(t) = y
i
−
x
i
be synchronization error, where e(t) = (e
1
(t), e
2
(t),
. . . , e
n
(t))
T
, x
i
(t) and y
i
(t) are the state variables of
drive system (1) and response system (2). Thus,we
can derive the error dynamical system as follows:
(
˙e = − De(t) +WG(e(t)), t 6= t
k
,
e(t
+
k
) = (I − D
k
)e(t
−
k
), k = 1, 2, . . . ,
(3)
where
g
j
= f
j
(e
j
+ x
j
) − f
j
(x
j
),
G(e) = [g
1
, g
2
, . . . , g
n
]
T
.
I is identity matrix, and
D
k
=
d
1k
0 ·· · 0
0 d
2k
·· · 0
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ·· · d
nk
.
In fact, from the analysis above, we can see that (1)
and (2) are synchronized if and only if the equilib-
rium point of (3) is asymptotically stable for any ini-
tial condition.So the global impulsivesynchronization
problem can be solved if the controller gain matrices
d
ik
are suitably designed such that the zero solution of
(3) is globally asymptotically stable.
3 MAIN RESULTS
In this section, we will derive some sufficient condi-
tions for synchronization in the sense of the fact that
the error system (3)
Theorem 1. If there exist a positive constant ε >
0, α > 0, positive definite diagonal matrix P > 0, such
that
1. Linear matrix Inequality
−PD− D
T
P+ εL
2
M
λ
M
(W
T
W) − αP P
P −ε
< 0
(4)
where L
M
= max{L
j
}, λ
M
denote the largest eigen-
value of the matrix (∗).
2. τ < inf
k∈N
{t
k
− t
k−1
} < 1;
3. There exists a constant α such that
ln(ηβ
k
) + α(t
k
− t
k−1
) < 0, (5)
where β
k
= λ
2
M
(I − D
k
); then, the origin of system (3)
is globally asymptotically stable, which implies that
(1) and (2) are completely synchronized.
Proof. Construct a Lyapunov function in the form of
V(e(t)) = e
T
(t)Pe(t).
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
258

When t ∈ (t
k
− t
k−1
], the total derivative of V(e) with
respect to (3) is
˙
V(e) = ˙e
T
Pe+ e
T
P˙e,
=(−De+WG(e))
T
Pe
+ e
T
P(−De+WG(e))
= − e
T
(PD+ D
T
P)e
+ 2e
T
PWG(e).
Also, by the well-known inequality
2a
T
b 6 ε
−1
a
t
a+ εb
T
b,
for ∀ε > 0, we obtain
˙
V(e) 6 −e
T
(PD+ D
T
P)e+ ε
−1
e
T
PPe
+εL
2
M
λ
M
(W
T
W)G(e).
From the Assumption (H
1
), we can obtain
||G(e)||
2
6 L
2
M
||e||
2
This leads to
˙
V(e) 6 −e
T
(PD+ D
T
P)e+ ε
−1
e
T
PPe
+εL
2
M
λ
M
(W
T
W)e
T
e. (6)
From Linear matrix inequality (4) and (6), we have
˙
V(e) < αe
T
Pe = αV(e).
Let V(t) = V(e(t)), then
V(t) 6 V(t
+
k−1
)exp[α(t − t
k−1
)], (7)
where t ∈ (t
k−1
,t
k
], k ∈ N. From the second equation
in (3), we have
V(t
+
k
) = e
T
(t
+
k
)Pe(t
+
k
)
= [(I − D
k
)e(t
k
)]
T
P[(I − D
k
)e(t
k
)]
6 λ
2
M
(I − D
k
)V(t
k
)
= β
k
V(t
k
). (8)
For t ∈ (t
0
,t
1
], from (7) and (8), we have
V(t) 6 V(t
0
)exp[α(t − t
0
)], t ∈ (t
0
,t
1
],
which leads to
V(t
1
) 6 V(t
0
)exp[α(t
1
− t
0
)], t ∈ (t
0
,t
1
],
and
V(t
+
1
) 6 V(t
0
)β
1
exp[α(t
1
− t
0
)], t ∈ (t
0
,t
1
],
Similarly, for t ∈ (t
1
,t
2
],
V(t) 6 V(t
+
1
)exp[α(t − t
1
)],
6 V(t
0
)β
1
β
2
exp[α(t − t
0
)]
In general, for t ∈ (t
k−1
,t
k
],
V(t) 6 V(t
+
1
)exp[α(t − t
1
)],
6 V(t
0
)β
1
β
2
·· · β
k
exp[α(t − t
0
)] (9)
For t ∈ (t
k
,t
k+1
)], it follows from (5) and (9) that,
V(e(t)) 6 V(e(t
0
))β
1
β
2
·· · β
k
exp[α(t − t
0
)]
6 V(e(t
0
)){β
1
exp[ατ
1
]}{β
2
exp[ατ
2
]}
·· · {β
k
exp[ατ
k
]}exp[α(t − t
k
)]
6 V(e(t
0
))
exp[α(t − t
k
)]
η
k
(10)
From (10) , we can see that the trivial solution of sys-
tem (3) is globally asymptotically stable.This com-
pletes the proof.
4 AN ILLUSTRATIVE EXAMPLE
In order to demonstrate and verify the performance of
the proposed method, some numerical simulations are
presented in this section.
As is known to all that (1) can exhibit Gui chaotic
strange attractor (Zhang and Gui, 2009a; Zhang and
Gui, 2009b).In order to show it clearly, we give the
following example:
˙x
1
˙x
2
˙x
3
= −
x
1
x
2
x
3
+
1.2 −1.6 0
1.2 1.0 0.9
0 2.2 0.15
f
1
(x
1
)
f
2
(x
2
)
f
3
(x
3
)
+
c
1
(t)
c
2
(t)
c
3
(t)
x
i
(t
+
k
) = x
i
(t
k
) + d
ik
x
i
(t
k
), i = 1, 2, 3 k ∈ Z
+
,
(11)
where
d
1k
= 0.35, d
2k
= 0.4, d
3k
= 0.5,
f
j
(x
j
) = 0.5(|x
j
+ 1| − |x
j
− 1|), j = 1, 2.
Obviously, f
j
(x) satisfy (H
1
).
Now we investigate the influence of the period T
of impulsive effect on the system (11). Set
c
1
(t)
c
2
(t)
c
3
(t)
=
2− 2cost
2− 2sint
1+ cost
.
For T = 1, then (H
2
) isn’t satisfied. Periodic oscil-
lation of system (11) will be destroyed by impulses
effect. Numeric results show that system (11) still has
SynchronizationoftheComplexDynamicalNetworkswithaGuiChaoticStrangeAttractor
259

–1
0
1
2
3
4
x1
50 100 150 200
t
Figure 1: Time-series of the x
1
(t)of system (11).
0
2
4
6
8
10
x2
50 100 150 200
t
Figure 2: Time-series of the x
2
(t) of system (11).
2
4
6
8
10
x3
0 50 100 150 200
t
Figure 3: Time-series of the x
3
(t) of system (11).
a global attractor which can be a Gui chaotic strange
attractor(see Figs.1-4).
Every solutions of system (11) will finally tend to
the Gui chaotic strange attractor. As shown in Figs.
1-4, the system (11) possesses a Gui chaotic strange
attractor.
Now the response chaotic cellular neural network
1
2
3
4
x1
5
6
7
8
9
10
11
x2
6
8
10
x3
Figure 4: Phase portrait of Gui chaotic strange attractor of
system (11) with T = 1.
is designed as follows:
˙y
1
˙y
2
˙y
3
= −
y
1
y
2
y
3
+
1.2 −1.6 0
1.2 1.0 0.9
0 2.2 0.15
f
1
(y
1
)
f
2
(y
2
)
f
3
(y
3
)
+
c
1
(t)
c
2
(t)
c
3
(t)
y
i
(t
+
k
) = 2d
ik
x
i
(t
−
k
) + (1− d
ik
)y
i
(t
−
k
),
(12)
Remark 1. In (Zhang and Gui, 2009a; Zhang and
Gui, 2009b), the authors investigate the influence of
the period T of impulsive effect on the system (11).
If T =
2
5
π or T = 0.1π, then q = 5 or q = 20, respec-
tively, in (H
2
). According to Theorem 1 and Theo-
rem 2, the cellular neural networks model (11) has a
unique 2π-periodic solution which is globally asymp-
totically stable. For T =
2
5
π, γ
1
= 0.6, γ
2
= 0.85,
each positive solution tends to a unique positive 2π-
periodic solution with 5-impulses in a period. For
T = 0.1π, γ
1
= 0.4, γ
2
= 0.3, each positive solution
tends to a unique positive 2π-periodic solution with
20-impulses in a period.
Remark 2. If T = 1, then (H
2
) isn’t satisfied. Pe-
riodic oscillation of system (11) will be destroyed by
impulses effect. Numeric results show that system
(11) still has a Gui chaotic strange attractor(Zhang
and Gui, 2009a; Zhang and Gui, 2009b).
Let e(t) = y
i
− x
i
, then the error system (13) of
drive system (11) and respond system (12) is con-
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
260
structed as follow
˙e
1
(t)
˙e
2
(t)
˙e
3
(t)
= −
e
1
(t)
e
2
(t)
e
3
(t)
+
1.2 −1.6 0
1.2 1.0 0.9
0 2.2 0.15
·
f
1
(e
1
(t) + x
1
) − f
1
(x
1
)
f
2
(e
2
(t) + x
1
) − f
2
(x
2
)
f
3
(e
3
(t) + x
3
) − f
3
(x
3
)
e
1
(t
+
k
) = (1 − d
1k
)e
1
(t
−
k
),
e
2
(t
+
k
) = (1 − d
2k
)e
2
(t
−
k
),
e
3
(t
+
k
) = (1 − d
3k
)e
3
(t
−
k
).
(13)
e3
e2
e1
–1
–0.5
0
0.5
1
2 4 6 8
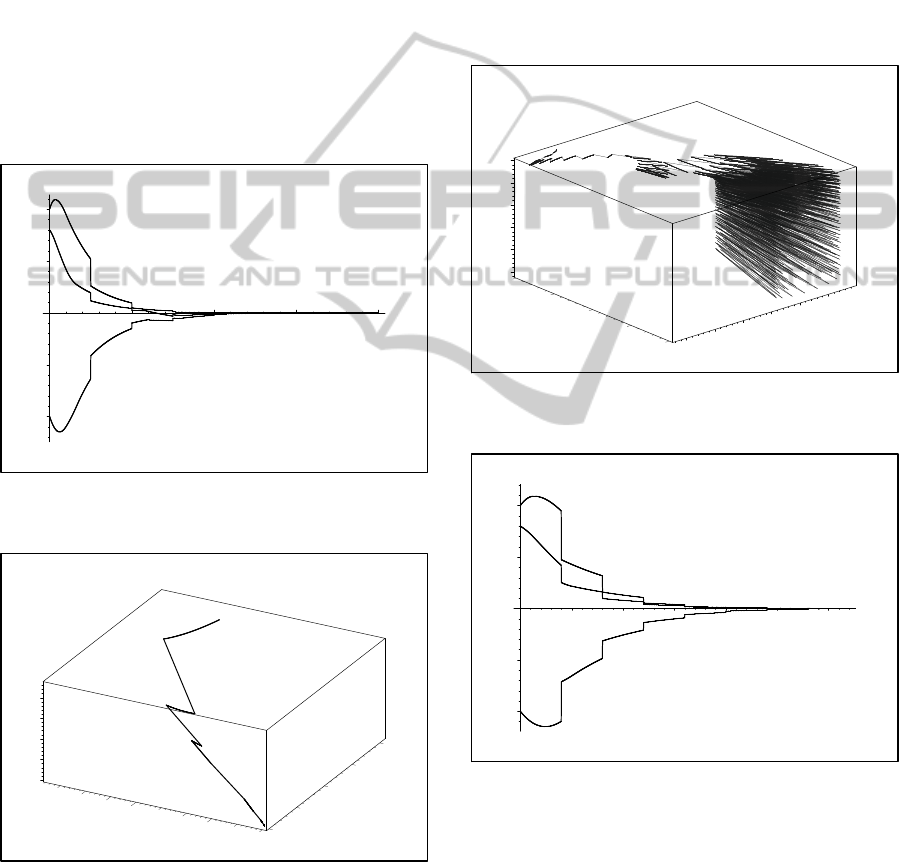
Figure 5: Synchronization errors between drive system (11)
and response system (12) with T = 1.
–0.0002
–0.00015
–0.0001
–5e–05
0
e1
–0.00016
–0.00014
–0.00012
–0.0001
–8e–05
–6e–05
–4e–05
–2e–05
0
e2
0
5e–07
1e–06
1.5e–06
2e–06
Figure 6: Phase portrait of Synchronization errors with T =
1.
If one choose L
1
= L
2
= L
3
= 1, η = 1.1, d
1k
=
0.35, d
2k
= 0.4, d
3k
= 0.5, It is easy to check the con-
ditions in Theorem 1 are satisfied. So, the system
(11) and (12) is synchronized. By Theorem 1, syn-
chronization can be obtained. The synchronization
performance is illustrated by Figs. 5,6. The numer-
ical simulations show that synchronization could be
quickly achieved.
Furthermore, if T = 0.4, set
c
1
(t)
c
2
(t)
c
3
(t)
=
2− 2sint
3− 3cost
1− 1sint
.
then, periodic oscillation of system (11) will be de-
stroyed by impulses effect. Numeric results show
that system (11) still has a Gui chaotic strange attrac-
tor(see Fig.7).
–2
0
2
4
6
8
x1
0
10
20
30
40
x2
0
500
1000
1500
2000
2500
x3
Figure 7: Phase portrait of Gui chaotic strange attractor of
system (11) with T = 0.4.
e3
e2
e1
–1
–0.5
0
0.5
1
0.5 1 1.5 2 2.5 3
Figure 8: Synchronization errors between drive system (11)
and response system (12) with T = 0.4.
It follows from Theorem 1 that systems (11) and
(12) are impulsively synchronized. Figs. 8 and 9 de-
pict the synchronizationerror of the state variables be-
tween the drive system and the response system.
SynchronizationoftheComplexDynamicalNetworkswithaGuiChaoticStrangeAttractor
261

–1.2e–12
0
e1
–8e–14
–6e–14
–4e–14
–2e–14
e2
–3e–16
–2e–16
–1e–16
0
1e–16
2e–16
3e–16
Figure 9: Phase portrait of Synchronization errors with T =
0.4.
5 CONCLUSIONS
In the paper,the synchronization of the impulses com-
plex dynamical network with a Gui chaotic strange at-
tractor and has been investigated based on the stabil-
ity analysis of impulsive functional differential equa-
tion. The criteria for the synchronization are derived.
An illustrative example is finally included to visual-
ize the effectiveness and feasibility of the developed
methods. Compared with the correspondingly previ-
ous works(Luo, 2008; Yang and Cao, 2007; Yang and
Cao, 2010; Zhang, 2009), our model of research is
new. As far as we know, There is no paper to deal
with such a problem.
ACKNOWLEDGEMENTS
This work was supported by the National Natural Sci-
ence Foundation of People’s Republic of China(Grant
no. 60963025), the Natural Science Foundation of
Hainan(Grant no.613166,112008).
REFERENCES
Amritkar, R. and Gupte, N. (1993). Synchronization of
chaotic orbits: the effect of a finite time steps. In Phys-
ical Review E. 47: 3889C3895.
Anzo, A. Barajas-Ramłrez J.G. (2014). Synchronization in
complex networks under structural evolution. In Jour-
nal of the Franklin Institute. 351: 358-372.
Cao, J. (1999). Global stability analysis in delayed cellular
neural networks. In Phys Rev E. 59: 5940-5944.
D¨orfler, F. and Bullo, F. (2014). Synchronization in com-
plex networks of phase oscillators: A survey. In Auto-
matica. 50: 1539-1564.
Gopalsamy, K. and He, H. (1994). Stability in asymmetric
hopfield nets with transmission delay. In Physics D.
76: 344C358.
Gui, Z. and Ge, W. (2006). Existence and uniqueness of
periodic solutions of nonautonomous cellular neural
networks with impulses. In Physics Letters A. 354:
84C94.
Hopfield, J. (1982). Neural networks and physical systems
with emergent collective computational abilities. In
Proc Nat Acad Sci USA. 79: 2554-2558.
Luo, R. (2008). Impulsive control and synchronization of
a new chaotic system. In Physics Letters A. 372:
648C653.
Subashini, M. M. and Sahoo, S. K. (2014). Pulse coupled
neural networks and its applications. In Expert Sys-
tems with Applications. 41: 3965-3974.
Song, Q. and Zhang, J. (2008). Global exponential stabil-
ity of impulsive cohencgrossberg neural network with
time-varying delays. In Nonlinear Anal Real World
Appl. 9:500C510.
Wan, D. and Huang, L. (2014). Periodicity and global expo-
nential stability of generalized CohenCGrossberg neu-
ral networks with discontinuous activations and mixed
delays. In Neural Networks. 51:80-95.
Wan, Y. and Cao, J. (2015). Periodicity and synchronization
of coupled memristive neural networks with supre-
mums. In Neurocomputing. 159:137-143.
Xie, C. and Xu, Y. (2014). ynchronization of time varying
delayed complex networks via impulsive control. In
Optik - International Journal for Light and Electron
Optics. 125:3781-3787.
Yang, T. and Chua, L. (1997). Impulsive stabilization for
control and synchronization of chaotic systems: the-
ory and application to secure communication. In IEEE
Transactions on Circuits and Systems-I. 44:976C988.
Yang, T. and Chua, L. (1999a). Generalized synchroniza-
tion of chaos via linear transformations. In Interna-
tional Journal of Bifurcation and Chaos. 9:215C219.
Yang, T. and Chua, L. (1999b). Impulsive control and syn-
chronization of non-linear dynamical systems and ap-
plication to secure communication. In International
Journal of Bifurcation and Chaos. 7:645C664.
Yang, Y. and Cao, J. (2007). Exponential lag synchroniza-
tion of a class of chaotic delayed neural networks with
impulsive effects. In Physica A. 386:492-502.
Yang, Y. and Cao, J. (2010). Exponential synchronization
of the complex dynamical networks with a coupling
delay and impulsive effects. In Nonlinear Analysis:
Real World Applications. 11: 1650-1659.
Zhang, C. (2009). Complete synchronization for impul-
sive cohencgrossberg neural networks with delay un-
der noise perturbation. In Chaos, Solitons and Frac-
tals. 42: 1664C1669.
Zhang, J. and Gui, Z. (2009a). Existence and stability of
periodic solutions of high-order hopfield neural net-
works with impulses and delays. In Journal of Com-
putational and Applied Mathematics. 224: 602-613.
Zhang, J. and Gui, Z. (2009b). Periodic solutions of nonau-
tonomous cellular neural networks with impulses and
delays. In Nonlinear Analysis: Real World Applica-
tions. 10: 1891-1903.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
262
