
A Fault Detection Scheme for Time-delay Systems using Minimum-order
Functional Observers
H. M. Tran and H. Trinh
School of Engineering, Faculty of Science, Engineering and Built Environment, Deakin University,
Geelong VIC 3217, Australia
Keywords:
Time-delay Systems, Fault Detection, Reduced-order Functional Observers, Residual Generators.
Abstract:
This paper presents a method for designing residual generators using minimum-order functional observers to
detect actuator and component faults in time-delay systems. Existence conditions of the residual generators
and functional observers are first derived, and then based on a parametric approach to the solution of a gener-
alized Sylvester matrix equation, we develop systematic procedures for designing minimum-order functional
observers to detect faults in the system. The advantages of having minimum-order observers are obvious from
the economical and practical points of view as cost saving and simplicity can be achieved, particularly when
dealing with high-order complex systems. Extensive numerical examples are given to illustrate the proposed
fault detection scheme. In all the numerical examples, we design minimum-order residual generators and
functional observers to detect faults in the system.
1 INTRODUCTION
Time-delay systems are commonly encountered in
various engineering complex systems. As cited in
(Duan and Patton, 2002; Fu et al., 2004; Wu and
Duan, 2007) time delays appear in practical processes
such as aviation industries, chemical processes, long
transmission lines and rolling mill systems. In fact,
when time delays appear in high complex systems,
they can cause the systems to be more vulnerable
to unexpected faults. Faults can enter the systems
via input or state delay. Normally, faults can cause
malfunctions of the system operations such as partly
break down or even whole system shutdown (Teh
and Trinh, 2013; Chen and Patton, 2012). Hence,
the problems of fault detection have been extensively
considered over the last several decades to improve
reliability and safety of system performance.
Accounting from the last several decades, there is
a wide range of approaches which are based on the
foundation of mathematics to build models in order to
detect system faults. One of the theories is applying
Kalman filter method to generate a residual based on
the difference between the ideal output and real out-
put of the system, this method can be seen in (Wang
et al., 2006; Zhong et al., 2003). Another trend in this
field is using geometric approach which can be seen
in (Meskin and Khorasani, 2009). Meanwhile, a very
common approach, which is used for fault detection,
is observer-based strategy. The basic idea behind the
observer-based approach is to estimate the state and
the output of the system from the measurements by
using some types of state observers, and then con-
struct a residual by a properly weighted output esti-
mation error. The residual is then examined for the
likelihood of faults (Duan and Patton, 1998; Duan and
Patton, 2001; Huong et al., 2014).
In this paper, the work on reduced-order func-
tional observers for dynamical systems (Darouach
et al., 1999; Darouach, 2001; Trinh and Ha, 2007;
Fernando et al., 2010; Trinh et al., 2004; Trinh and
Fernando, 2012; Fernando and Trinh, 2013) and (Fer-
nando and Trinh, 2014) are used to design a simple
and effective scheme to detect faults for time-delay
systems. We construct residual generators based on
the system outputs and minimum-order functional ob-
servers to trigger faults occurring in the systems. The
salient feature of our work is that the order of our de-
signed residual generators and observers is very low
and hence our fault detection scheme is very practical
and easy to implement. In the next section, we present
system description and problem statement. This is
then followed by preliminaries results and our pro-
posed fault detection scheme for time-delay systems.
Finally, three examples in Numerical Examples sec-
tion to illustrate the proposed theory can be seen.
64
Tran H. and Trinh H..
A Fault Detection Scheme for Time-delay Systems using Minimum-order Functional Observers.
DOI: 10.5220/0005506300640071
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 64-71
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 SYSTEM DESCRIPTION AND
PROBLEM STATEMENT
We consider the following time-delay system
˙x(t) = Ax(t) + A
d
x(t − τ) + Bu(t)
+E f(t), t ≥ 0,
y(t) = Cx(t),
x(t) = φ(t), t ∈ [−τ, 0),
(1)
where τ is a positive real number presenting the
known time delay in the state, x(t) ∈ R
n
, u(t) ∈ R
m
and y(t) ∈ R
p
are the state, input and output vector,
respectively. Unpredictable fault signals f(t) ∈ R
l
enter from the system input. A ∈ R
n×n
, A
d
∈ R
n×n
,
B ∈ R
n×m
, C ∈ R
p×n
and E ∈ R
n×l
are known con-
stant matrices. We assume that the pair (A,C) is ob-
servable, rank(C) = p, rank(E) = l. Furthermore, the
faults f(t) are assumed to be linear independent to
avoid vagueness situations which may appear when
some faults occur simultaneously. Hence, the resid-
ual generator may not detect faults because of zero
overall effects of faults.
Let us introduce a functional observer ω(t) of a
general q-order,1 ≤ q ≤ n. Here, ω(t) is an estimation
of a function Lx(t), L ∈ R
q×n
, where
˙
ω(t) = Nω(t) + Gy(t) + G
d
y(t − τ)
+Hu(t), t ≥ 0,
ω(t) = ϕ(t), t ∈ [−τ, 0),
(2)
ω(t) ∈ R
q
, N ∈ R
q×q
, G ∈ R
q×p
, G
d
∈ R
q×p
and
H ∈ R
q×m
are constant observer parameters which
will be determined such that ω(t) is an asymptotic es-
timation of the function Lx(t) when there is no fault
appearing in the system, i.e., f(t) = 0. Matrix L will
be determined for the purpose of fault detection.
Let us consider a residual generator r(t) which is
used to trigger faults in system (1) whenever the faults
appear, i.e., f(t) 6= 0,
r(t) = Tω(t) + Fy(t), (3)
where T ∈ R
1×q
and F ∈ R
1×p
are constant matrices
which will be detemined to satisfy the residual func-
tion such that
lim
t→∞
r(t) =
(
0 if f(t) = 0
c or undefined if f(t) 6= 0,
(4)
where c 6= 0, and f(t) = 0 implies a faultless condi-
tion, f (t) 6= 0 implies a faulty condition (Trinh et al.,
2013).
3 PRELIMINARIES RESULTS
Obviously, the reduced-order functional observers
and the residual generator can detect faults in systems
(1) if all the unknownparameters satisfy the following
conditions in Theorem 1.
Theorem 1. Under faultless conditions, ω(t) is an
asymptotic estimate of Lx(t) and residual genera-
tor r(t) function as (4) for any initial condition
φ(t), x(0), ω(0) and any u(t) if and only if
N is Hurwitz, (5)
NL+ GC− LA = 0, (6)
G
d
C− LA
d
= 0, (7)
H − LB = 0, (8)
TL+ FC = 0. (9)
Under fault conditions, residual r(t) satisfies (4)
if and only if all the parameters satisfy the conditions
(5)-(9) and
LE 6= 0. (10)
Proof. Let us define an error vector e(t) ∈ R
q
which
is the difference between the estimate ω(t) and the
function Lx(t) as follows
e(t) = ω(t) − Lx(t), t ≥ −τ. (11)
It follows from (1), (2) and (11), we obtain
˙e(t) = Ne(t) + (NL+ GC− LA)x(t)
+ (G
d
C− LA
d
)x(t − τ)
+ (H − LB)u(t) − LE f(t), t ≥ −τ.
(12)
Sufficiency: In the case of faultless conditions, i.e.,
f(t) = 0, if conditions (6)-(8) are satisfied then equa-
tion (12) is reduced to ˙e(t) = Ne(t). As a result, if
condition (5) is satisfied then the error e(t) asymptot-
ically tends to zero. Hence, the reduced-order func-
tional observer ω(t) is an estimation of the functional
Lx(t) as expected. Furthermore, by (1), (3) and (11),
residual r(t) can be expressed as follows
r(t) = Te(t) + (TL+ FC)x(t). (13)
It is clear that under no fault condition, the error
e(t) is expected to asymptotically tends to zero, thus
the residual is proposed to be zero and it happens if
condition (9) holds.
Necessity: Under no fault conditions, if condition
(5) is unsatisfied then even conditions(6)-(8) hold, the
error e(t) 6→ 0 with any initial condition of φ(t) and
x(0). Contrarily, if one of the conditions (6)-(8) is not
satisfied then even (5) holds, it is possible to find x(0)
to make e(t) 6→ 0.
AFaultDetectionSchemeforTime-delaySystemsusingMinimum-orderFunctionalObservers
65

Under fault conditions, if conditions (5)-(9) hold,
by (12) and (13), the residual is then governed by the
following equations
(
˙e(t) = Ne(t) − LE f(t),
r(t) = Te(t).
(14)
It follows from (14), r(t) can detect faults f(t) if
condition (10) is satisfied. This completes the proof
of Theorem 1.
The design of the functional observers and the
residual generator is now reduced to finding matrices
L, N, G, G
d
, H, T and F which satisfy Theorem 1.
4 FAULT DETECTION SCHEMES
This section is to determine the possible order of the
observer and the necessary parameters for designing
reduced-order functional observers and residual gen-
erator to detect faults in system (1). Note that, based
on the conditions in Theorem 1, whenever matrix L
is found, matrix H is determined from (8) and con-
dition (10) is checked. Moreover, other unknown pa-
rameters are solutions of equations (6), (7), (9) and
condition (5) holds. In order to simplify the three ma-
trix equations (6), (7) and (9), we employ the partition
method introduced in (Trinh and Fernando, 2012).
Let P ∈ R
n×n
be defined by
P =
C
+
C
⊥
, (15)
where C
+
∈ R
n×p
is the Moore-Penrose inverse of
matrix C, CC
+
= I
p
, and C
⊥
∈ R
n×n−p
is an orthog-
onal basis for the null space of matrix C, CC
⊥
= 0.
Then P is an invertible matrix (see, (Trinh and Fer-
nando, 2012)).
Now we define the following partitions
CP =
I
p
0
, (16)
LP =
L
1
L
2
, (17)
P
−1
AP =
A
11
A
12
A
21
A
22
, (18)
P
−1
A
d
P =
A
d11
A
d12
A
d21
A
d22
, (19)
where submatrices L
1
∈ R
q×p
, L
2
∈ R
q×(n−p)
, A
11
∈
R
p×p
, A
12
∈ R
p×(n−p)
, A
21
∈ R
(n−p)×p
, A
22
∈
R
(n−p)×(n−p)
, A
d11
∈ R
p×p
, A
d12
∈ R
p×(n−p)
, A
d21
∈
R
(n−p)×p
and A
d22
∈ R
(n−p)×(n−p)
.
Post-multiply both sides of equations (6), (7) and
(9) by matrix P, we have following equations
NLP+ GCP− LPP
−1
AP = 0, (20)
G
d
CP− LPP
−1
A
d
P = 0, (21)
TLP+ FCP = 0. (22)
Substitute equations (15)-(19) into (20)-(22), we
obtain
L
1
A
11
+ L
2
A
21
− NL
1
= G, (23)
L
1
A
d11
+ L
2
A
d21
= G
d
, (24)
F + TL
1
= 0, (25)
NL
2
− L
2
A
22
− L
1
A
12
= 0, (26)
L
1
A
d12
+ L
2
A
d22
= 0, (27)
TL
2
= 0. (28)
It is clear from equations (23), (24) and (25) that
matrices G, G
d
and F are computed when matrices
N, L
1
, L
2
and T are found. Consequently, the de-
sign of the observers and residual generator is now
reduced to determine matrices N, L
1
, L
2
and T such
that three conditions (26)-(28) are satisfied and con-
dition (5) holds.
4.0.1 Case 1: p >
2n
3
In this case, we consider the design of only first-order
functional observers and residual generators to detect
faults in the systems (1). We show that indeed it
is possible provided that the number of outputs
satisfying p >
2n
3
and that condition (10) is satisfied.
Theorem 2. If p >
2n
3
, first-order observers and
residual generators always exist to detect faults in the
system if the condition (10) is satisfied.
Proof. To design a first-order functional observer,
i.e., q = 1, N ∈ R
1×1
can be chosen to be any neg-
ative real number, i.e.,
N = s, s < 0. (29)
Note that s < 0 ensures the satisfaction of the con-
dition (5), i.e., N is Hurwitz. By letting L
2
= 0, equa-
tion (26) and (27) are reduced to
L
1
A
12
= 0, (30)
L
1
A
d12
= 0. (31)
We can express (30) and (31) as
L
1
A
12
A
d12
= 0. (32)
Since p >
2n
3
,
A
12
A
d12
∈ R
p×2(n−p)
is a col-
umn matrix, i.e., p > 2(n− p), thus a solution to (32)
where L
1
6= 0 always exists. Let N (X) be a matrix
of row basis vectors for the row-nullspace of X, i.e.,
N (X)X = 0. The solution to L
1
6= 0 according to (32)
exists when N (X) 6= 0. Therefore, solutions for L
1
can be computed by first finding
ˆ
L
1
according to
ˆ
L
1
= N
A
12
A
d12
, (33)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
66

and then choosing any row of
ˆ
L
1
as L
1
.
In (28) and since L
2
= 0, T 6= 0 can be arbitrarily
chosen to be any scalar, say, α where α 6= 0. Finally,
if the condition (10), LE 6= 0, is satisfied, where L =
L
1
0
P
−1
is obtained according to (17), matrices
H, G, G
d
and F can then be obtained from (8), (23),
(24) and (25), respectively. This completes the proof
of Theorem 2.
The effectiveness and the simplicity of this
scheme can be seen in Example 1 of the Numeri-
cal Examples section, in which a system with n = 4,
p = 3, m = 1 and l = 1 is taken under considera-
tion. For this system, according to Theorem 2, we
only need to design first-order observer and residual
generator to detect faults in the system.
4.0.2 Case 2: 1 ≤ p ≤
2n
3
In this case, first-order functional observers do not ex-
ist and we have to consider observers of higher or-
der. We present a solution to the three matrix equa-
tions (26)-(28) with the requirement that N has pre-
scribed distinct eigenvalues. For completeness, let us
first present a parametric solution (Duan, 1993) to the
generalized Sylvester matrix equation (26).
Let N ∈ R
q×q
with q distinct eigenvalues be de-
fined as follows
N = Q
−1
ΛQ, (34)
where Q ∈ R
q×q
is any freely chosen invertible ma-
trix, Λ = diag(s
1
, s
2
, ..., s
q
), s
i
6= s
j
for i 6= j and
Re(s
i
) < 0 for all i = 1, 2, ..., q.
With N as defined in (34), L
1
and L
2
satisfy-
ing (26) are given in the following parametric forms
(Duan, 1993)
L
1
= Q
U(s
1
)b
1
U(s
2
)b
2
... U(s
q
)b
q
⊤
,(35)
L
2
= Q
Z(s
1
)b
1
Z(s
2
)b
2
... Z(s
q
)b
q
⊤
,(36)
where b
i
∈ C
p
(i= 1, 2, ..., q) are free parameters satis-
fying b
i
=
¯
b
j
if s
i
= ¯s
j
, ¯s
j
denotes the complex conju-
gate of s
i
. Matrices U(s) ∈ R
p×p
and Z(s) ∈ R
(n−p)×p
are coprime polynomial matrices satisfying the fol-
lowing coprime factorization
(sI
n−p
− A
⊤
22
)
−1
A
⊤
12
= Z(s)U
−1
(s). (37)
The reader can refer to (Duan, 1993) for a numer-
ically reliable algorithm to compute Z(s) and U(s).
Also, as suggested in (Trinh and Fernando, 2012),
U(s) and Z(s) can be conveniently computed accord-
ing to the following equations
U(s) = det(sI
n−p
− A
22
)I
p
, (38)
Z(s) = adj(sI
n−p
− A
⊤
22
)A
⊤
12
, (39)
where det(.) and adj(.) denote the determinant and
the adjugate matrix of matrix (.), respectively. For
any given A
22
, the characteristic polynomial can be
obtained as follows
a(s) , det(sI
n−p
− A
22
)
= s
n−p
+ a
1
s
n−p−1
+ a
2
s
n−p−2
+ ... + a
n−p
, (40)
where the coefficients a
i
, i = 1, 2, ..., (n − p), are real
constants.
The adjugate matrix adj(.) is then obtained as fol-
lows
adj(sI
n−p
− A
⊤
22
) = ϒ
1
s
n−p−1
+ ϒ
2
s
n−p−2
+ ϒ
3
s
n−p−3
+ ... + ϒ
n−p
, (41)
where ϒ
i
, i = 1, 2, ..., n− p, are computed by using the
coefficients of a(s) and matrix A
22
as given below
ϒ
1
= I
n−p
,
ϒ
2
= ϒ
1
A
⊤
22
+ a
1
I
n−p
,
ϒ
3
= ϒ
2
A
⊤
22
+ a
2
I
n−p
,
.
.
.
ϒ
n−p
= ϒ
n−p−1
A
⊤
22
+ a
n−p−1
I
n−p
.
(42)
Theorem 3. A functional observer always exists with
q-order where q is the lowest order that matrix M (M
is defined in equation (45)) has row basis vectors for
the row-nullspace of M, N (M) 6= 0. Furthermore, the
proposed residual generator (3) can detect the faults
in systems if condition (10) holds.
Proof. Now, by substitute L
1
and L
2
from (35) and
(36) into the transpose of (27) and (28), we obtain
A
d12
A
d22
⊤
U(s
1
)b
1
U(s
2
)b
2
... U(s
q
)b
q
Z(s
1
)b
1
Z(s
2
)b
2
... Z(s
q
)b
q
Q
⊤
= 0, (43)
Z(s
1
)b
1
Z(s
2
)b
2
... Z(s
q
)b
q
(QT)
⊤
= 0. (44)
Since Q is an invertible matrix, let (QT)
⊤
=
t
1
t
2
. . . t
q
, t
i
6= 0, i = 1, 2, ..., q, are arbitrarily
chosen real numbers. It follows (43) and (44), we ob-
tain
Mβ = 0, (45)
where M ∈ R
(q+1)(n−p)×pq
, β ∈ R
pq×1
and
M =
¯
A
1
0 . . . 0
0
¯
A
2
. . . 0
.
.
.
0 0 . . .
¯
A
q
Z(s
1
)t
1
Z(s
2
)t
2
. . . Z(s
q
)t
q
,
¯
A
i
= A
⊤
d12
U(s
i
) + A
⊤
d22
Z(s
i
), i = 1, 2, . . . , q,
β =
b
⊤
1
b
⊤
2
. . . b
⊤
q
⊤
.
AFaultDetectionSchemeforTime-delaySystemsusingMinimum-orderFunctionalObservers
67

Let N (M) be a matrix of row basis vectors for the
row-nullspace of M, i.e., MN (M) = 0. Therefore, the
solutions for β 6= 0 in (45) exists iff N (M) 6= 0, and β
can be selected as any column of
ˆ
β, where
ˆ
β = N (M). (46)
This completes the proof of Theorem 3.
Remark 1: For the case
n
2
< p ≤
2n
3
, if M is a row
matrix, N (M) 6= 0 always exists, thus implies
q >
h
n−p
2p−n
i
. (47)
This leads to a method for searching for the or-
der q, we only need to search for the lowest q, which
satisfies Theorem 3, in the range of
2 ≤ q ≤
h
n−p
2p−n
+ 1
i
. (48)
Remark 2: For the case 1 ≤ p ≤
n
2
, M in (45) is
always a column matrix, thus its row basis vectors for
the row-nullspace, N (M) 6= 0, exists if M is not a full
rank matrix, that implies
rank(M) < qp. (49)
Based on Remark 2, q-order can be selected as the
smallest order that M satisfies condition (49).
It is concluded that since matrices T is arbitrarily
chosen, matrices L
1
, L
2
and N are determined through
this section, the parameters H, G, G
d
and F are calcu-
lated based on equations (8), (23), (24) and (25), re-
spectively. Matrix L is then achieved from the equa-
tion (17), we can check if condition (10) holds, i.e.,
LE 6= 0. Thus, all the conditions in the Theorem 1
are satisfied and the design of the reduced-order func-
tional observers and the first-order residual generator
to detect the faults in system (1) is completed. Ex-
amples 2 and 3 in the Numerical Examples section
illustrate the theory of this section.
5 NUMERICAL EXAMPLES
Example 1: In this example, we take consideration
of timely fault detection in a time-delay system with
n = 4, p = 3, m = 1, and l = 1. Since we have the case
where p >
2n
3
, and as discussed in Case 1 of Section 4,
we only need to design a residual generator based on
first-order observer to detect the faults in the system.
For this example, C =
I
3
0
, A, A
d
, B and E are
as given below
A =
−5 0 1 2
1 −1 0 −2
0 0 −3 −1
−2 2 0 −2
, B =
1
−2
4
−1
,
A
d
=
0 −1 0 0
0 0 0 −1
0 1 0 −2
1 0 0 −1
, E =
1
−1
2
−3
.
Now, the design of a first-order functional ob-
server and residual generator can be readily carried
out.
Since C is already in the desired form, i.e., C =
I
3
0
, so P is an identity matrix, i.e., P = I
4
. Ac-
cording to the partitions (18) and (19), submatrices
A
11
, A
12
, A
21
, A
22
, A
d11
, A
d12
, A
d21
and A
d22
are ob-
tained, where
A
11
A
12
A
21
A
22
=
−5 0 1
2
1 −1 0 −2
0 0 −3
−1
−2 2 0 −2
,
A
d11
A
d12
A
d21
A
d22
=
0 −1 0
0
0 0 0
−1
0 1 0 −2
1 0 0 −1
.
It is clear that
A
12
A
d12
is a column matrix
and thus its matrix of row basis vectors for the row-
nullspace exists, i.e., N
A
12
A
d12
6= 0. As a result,
a first-order functional observer exists.
For the design of first-order observer and first-
order residual generator, let us assign N = −3 and L
1
is computed according to (33), we obtain
L
1
=
−0.5571 −0.7428 0.3714
.
Since L
2
= 0 and according to (17), matrix L is
obtained as
L =
−0.5571 −0.7428 0.3714 0
.
With L as obtained above, condition (10) is found
to be satisfied since
LE = 0.9285 6= 0.
Hence, a first-order residual generator exists and
can be constructed to detect faults in the system. By
choosing T = −5, matrices H, G, G
d
and F are ob-
tained according to equations (8), (23), (24) and (25),
respectively, where
H = 2.4140,
G =
0.3714 −1.4856 −0.5571
,
G
d
=
0 0.9285 0
,
F =
−2.7854 −3.7139 1.8570
.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
68

Figure 1 shows that the residual generator can ef-
fectively detect the faults f(t) in the system. Fault
f(t) appears at time t = 20s and clears from t =
30s. During the time the fault happens, the resid-
ual generator triggers the fault, when there are no
faults, the residual generator converges to zero as ex-
pected. Note also that the residual is insensitive to
the input u(t) as expected. It is clear in this exam-
ple that, a significantly lower order (only first-order)
residual generator is designed using a first-order func-
tional observer. In contrast, existing fault detection
schemes using full-order or reduced-order state ob-
servers would give higher order schemes.
Example 2: This example is given to demonstrate
Case 2 (Section 4), where
n
2
< p ≤
2n
3
. Let us con-
sider a system which hasC =
I
3
0
and matrices A,
A
d
, B and E given as
A =
−1 0 0 1 −2
0 −5 3 4 0
1 1 −8 3 0
−4 0 2 −6 0
0 0 0 1 −1
, B =
1 0
0 1
1 −1
0 0
0 1
,
A
d
=
0 0 2 −1 0
0 −1 0 1 0
0 0 −1 3 0
−1 0 1 −2 0
0 1 0 0 −3
, E =
1 3
−1 1
2 −2
−3 2
2 −3
.
Thus, for this example, we have n = 5, p = 3, m =
2 and l = 2. Since
n
2
< p ≤
2n
3
, this falls into the Case
2 (Section 4) and thereforewe can carry out the design
of a reduced-order observer and a residual generator
to detect faults in the system.
Since C =
I
3
0
, thus P = I
5
and according
to (18) and (19), sub-matrices A
11
, A
12
, A
21
, A
22
,
A
d11
, A
d12
, A
d21
and A
d22
are obtained, where
A
11
A
12
A
21
A
22
=
−1 0 0
1 −2
0 −5 3 4 0
1 1 −8
3 0
−4 0 2 −6 0
0 0 0 1 −1
,
A
d11
A
d12
A
d21
A
d22
=
0 0 2
−1 0
0 −1 0 1 0
0 0 −1
3 0
−1 0 1 −2 0
0 1 0
0 −3
.
According to (40)-(42), we obtain the characteris-
tic polynomial and adjugate matrix as
a(s) = s
2
+ 7s+ 6,
adj(sI
n−p
− A
⊤
22
) = ϒ
1
s+ ϒ
2
,
where
ϒ
1
= I
2
, ϒ
2
=
1 1
0 6
.
Time(sec)
0 5 10 15 20 25 30 35 40 45 50
-15
-10
-5
0
5
10
15
20
25
30
Fault f(t)
Residual r(t)
Input u(t)
Figure 1: Residual generator using first-order observer ef-
fectively triggers fault in the system.
The pair of coprime polynomial matricesU(s) and
Z(s) are then calculated based on (38) and (39)
U(s) = (s
2
+ 7s+ 6)I
3
,
Z(s) = (ϒ
1
s+ ϒ
2
)A
⊤
12
.
As in Theorem 3 and Remark 1, now we search
for the lowest possible order q of the observers ω(t).
It follows equation (48) we have
2 ≤ q ≤ 3.
For the case that q = 2, let us assign the poles of N
to be at s
1
= −3, s
2
= −5 and choose Q to be Q = I
2
and TQ =
1 1
.
From (45), matrix M and the matrix of row basis
vectors for the row-nullspace of M are obtained
M =
14 10 −6 0 0 0
18 0 0 0 0 0
0 0 0 16 28 12
0 0 0 6 0 0
−4 −8 −6 −6 −16 −12
−6 0 0 −2 0 0
,
N (M) =
0 0.2339 0.3898 0 0.3509 −0.8187
⊤
.
Since N (M) 6= 0, the second-order observers ex-
ist for the system. Accordingly, β 6= 0 exists and is
obtained by taking any column of N (M ). Matrices
b
1
and b
2
are then obtained based on (45), where
b
1
=
0 0.2339 0.3898
⊤
,
b
2
=
0 0.3509 −0.8187
⊤
.
From (35) and (36), L
1
and L
2
are obtained
L
1
=
0 −1.4034 −2.3390
0 −1.4034 3.2747
,
L
2
=
−4.2103 0
4.2103 0
.
AFaultDetectionSchemeforTime-delaySystemsusingMinimum-orderFunctionalObservers
69

It follows (17) and P = I
5
, L =
L
1
L
2
and it is
easy to verify condition (10) that
LE =
9.3562 −5.1459
−4.6781 0.4678
6= 0.
Thus, all the conditions for Theorem 3 are satis-
fied and hence a second-order observer and first-order
residual generator exist and can be constructed to de-
tect faults in the system by determining all other un-
known parameters, where
N =
−3 0
0 −5
, T =
1 1
,
G =
14.5021 0.4678 −0.9356
−13.5665 3.2747 −5.6137
,
G
d
=
4.2103 1.4034 −1.8712
−4.2103 1.4034 0.9356
,
H =
−2.3390 0.9356
3.2747 −4.6781
,
F =
0 2.8069 −0.9356
.
Figure 2 indicates that the residual generator can
detect the faults f
1
(t) and f
2
(t) in the system. It is
clear in this example that the design of residual gen-
erator is very easy and systematic. Furthermore, the
order of the functional observer is very low compar-
ing to conventional FD schemes using full-order or
reduced-order state observers. This example thus fur-
ther highlights the attractiveness of the FD scheme
proposed.
Time(sec)
0 5 10 15 20 25 30 35 40 45 50
-30
-20
-10
0
10
20
Fault f
1
(t)
Fault f
2
(t)
Input u(t)
Residual r(t)
Figure 2: Residual generator based on second-order fuc-
tional observers detects faults in the system.
Example 3: This example is given to demonstrate
Case 2 (Section 4), where 1 ≤ p ≤
2n
2
. Let us con-
sider a system which has matrices A, B, and E as same
as in Example 2, however, matrices A
d
and C given as
A
d
=
−1 0 0 0 0
2 −1 0 0 0
1 −1 0 0 0
−1 0 0 0 0
0 1 0 0 0
, C =
1 0
0 1
0 0
0 0
0 0
⊤
.
Thus, for this example, we have n = 5, p = 2, m =
2 and l = 2. Since C =
I
2
0
, implies P = I
5
and
according to (18) and (19), sub-matrices A
11
, A
12
, A
21
,
A
22
, A
d11
, A
d12
, A
d21
and A
d22
are obtained, where
A
11
A
12
A
21
A
22
=
−1 0
0 1 −2
0 −5
3 4 0
1 1 −8 3 0
−4 0
2 −6 0
0 0 0 1 −1
,
A
d11
A
d12
A
d21
A
d22
=
−1 0
0 0 0
2 −1 0 0 0
1 −1 0 0 0
−1 0
0 0 0
0 1 0 0 0
.
Let us assign q = 2, the poles of N to be at s
1
=
−7, s
2
= −9, Q = I
2
and TQ =
1 1
. It follows
the same line as in the calculations of Example 2, the
matrix M in (45) is obtained as
M =
0 0 0 0 0 0 −16 −8 14
0 0 0 0 0 0 −30 −78 0
0 0 0 0 0 0 −20 10 6
0 0 0 0 0 0 8 −40 0
⊤
.
Since rank(M) = 3 < qp = 4, the condition (49)
holds and N (M) 6= 0 exists, where
N (M) =
0.3152 0.1686 −0.7354 −0.5757
⊤
.
Accordingly, b
1
and b
2
are obtained, where
b
1
= [
0.3152 0.1686
]
⊤
, b
2
= [
−0.7354 −0.5757
]
⊤
.
From (35) and (36), L
1
and L
2
are obtained
L
1
=
13.2368 7.0828
−17.6490 −13.8173
,
L
2
=
−10.1017 −15.6751 4.4123
10.1017 15.6751 −4.4123
.
It follows (17) and P = I
5
, L =
L
1
L
2
and it is
easy to verify that
LE =
41.8003 22.4096
−39.4781 −42.3809
6= 0.
Thus, all the conditions for Theorem 3 are satis-
fied and hence a second-order observer and a residual
generator exist and can be constructed to detect faults
in the system by determining all other unknown pa-
rameters, where
N =
−7 0
0 −9
, T =
1 1
,
G =
132.019 4.064
−193.791 −45.168
,
G
d
=
6.502 7.431
−15.559 −0.697
,
H =
3.135 21.597
−7.547 −28.331
, F =
4.412
6.734
⊤
.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
70
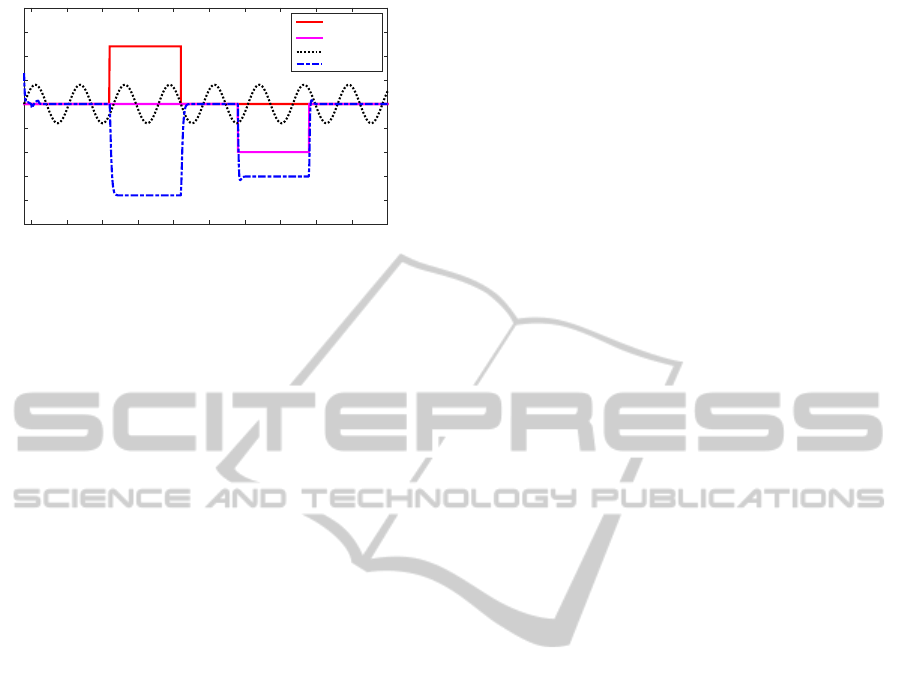
Time(sec)
0 5 10 15 20 25 30 35 40 45 50
-25
-20
-15
-10
-5
0
5
10
15
20
Fault f
1
(t)
Fault f
2
(t)
Input u(t)
Residual r(t)
Figure 3: Residual generator based on second-order func-
tional observers detects faults in the system.
Figure 3 indicates that a residual generator based
on a second-order observer can effectively detects the
faults f
1
(t) and f
2
(t) in the system. It clearly illus-
trates the Remark 2.
6 CONCLUSION
This paper has proposed a new fault detection scheme
using minimum-order functional observers to con-
struct residual generators to timely trigger actuator
faults in time-delay systems. The proposed approach
is based on solving a generalized Sylvester matrix
equation via a parametric approach. Existence con-
ditions and systematic procedures for designing the
proposed fault detection scheme have been presented.
The lowest possible order and the simplicity of the
approach are the hallmark of the proposed novel fault
detection scheme. Three examples have been con-
structed to prove the theory of the scheme.
REFERENCES
Chen, J. and Patton, R. J. (2012). Robust Model-Based Fault
Diagnosis for Dynamic Systems. Springer Publishing
Company, Incorporated.
Darouach, M. (2001). Linear functional observers for sys-
tems with delays in state variables. IEEE Transactions
on Automatic Control, 46(3):491–496.
Darouach, M., Pierrot, P., and Richard, E. (1999). De-
sign of reduced-order observers without internal de-
lays. IEEE Transactions on Automatic Control,
44(9):1711–1713.
Duan, G. and Patton, R. J. (2001). Robust fault detec-
tion using luenberger-type unknown input observers
- a parametric approach. International Journal of Sys-
tems Science, 32(4):533–540.
Duan, G.-R. (1993). Solutions of the equation av + bw =
vf and their application to eigenstructure assignment
in linear systems. IEEE Transactions on Automatic
Control, 38(2):276–280.
Duan, G. R. and Patton, R. J. (1998). Robust fault detection
in linear systems using luenberger observers. In IEE
Conference Publication, pages 1468–1473.
Duan, G. R., H. D. and Patton, R. J. (2002). Robust fault
detection in descriptor linear systems via generalized
unknown input observers. International Journal of
Systems Science, 33(5):369–377.
Fernando, T. and Trinh, H. (2013). A procedure for design-
ing linear functional observers. Applied Mathematics
Letters, 26(2):240–243.
Fernando, T. and Trinh, H. (2014). A system decomposition
approach to the design of functional observers. Inter-
national Journal of Control, 87(9):1846–1860.
Fernando, T. L., Trinh, H. M., and Jennings, L. (2010).
Functional observability and the design of minimum
order linear functional observers. IEEE Transactions
on Automatic Control, 55(5):1268–1273.
Fu, Y. ., Duan, G. ., and Song, S. . (2004). Design of un-
known input observer for linear time-delay systems.
International Journal of Control, Automation and Sys-
tems, 2(4):530–535.
Huong, D. C., Trinh, H., Tran, H. M., and Fernando, T.
(2014). Approach to fault detection of time-delay sys-
tems using functional observers. Electronics Letters,
50(16):1132–1134.
Meskin, N. and Khorasani, K. (2009). Robust fault detec-
tion and isolation of time-delay systems using a geo-
metric approach. Automatica, 45(6):1567–1573.
Teh, P. S. and Trinh, H. (2013). Design of unknown input
functional observers for nonlinear systems with appli-
cation to fault diagnosis. Journal of Process Control,
23(8):1169–1184.
Trinh, H. and Fernando, T. (2012). Functional observers
for dynamical systems, volume 420 of Lecture Notes
in Control and Information Sciences.
Trinh, H., Fernando, T., Emami, K., and Huong, D. C.
(2013). Fault detection of dynamical systems using
first-order functional observers. In 2013 IEEE 8th In-
ternational Conference on Industrial and Information
Systems, ICIIS 2013 - Conference Proceedings, pages
197–200.
Trinh, H., Fernando, T., and Nahavandi, S. (2004). Design
of reduced-order functional observers for linear sys-
tems with unknown inputs. Asian Journal of Control,
6(4):514–520.
Trinh, H. and Ha, Q. P. (2007). State and input simultane-
ous estimation for a class of time-delay systems with
uncertainties. IEEE Transactions on Circuits and Sys-
tems II: Express Briefs, 54(6):527–531.
Wang, H., Wang, C., Gao, H., and Wu, L. (2006). An lmi
approach to fault detection and isolation filter design
for markovian jump system with mode-dependent
time-delays. In Proceedings of the American Control
Conference, volume 2006, pages 5686–5691.
Wu, A. and Duan, G. (2007). On delay-independent stabil-
ity criteria for linear time-delay systems. International
Journal of Automation and Computing, 4(1):95–100.
Zhong, M., Ding, S. X., Lam, J., and Zhang, C. (2003).
Fault detection filter design for lti system with time
delays. In Proceedings of the IEEE Conference on
Decision and Control, volume 2, pages 1467–1472.
AFaultDetectionSchemeforTime-delaySystemsusingMinimum-orderFunctionalObservers
71
