Design of State Observers for Interconnected Time-delay Systems via a
Coordinate Transformation Approach
Wei Yin Leong and Hieu Trinh
School of Engineering, Deakin University,Waurn Ponds, VIC 3216, Australia
Keywords:
Reduced-order State Observers, Interconnected Systems, Time-delay Systems, Observability, Coordinate
Transformation.
Abstract:
This paper considers the design of state observers for interconnected time-delay systems using a coordinate
transformation method. Through such a transformation, the system that has interconnection and state delays is
metamorphosed into a new system that injects time-delay information into its input and output terms, before
reintroducing them back into the latter system, effectively coupling the delay terms into the IO injection
terms and eliminating the delay values from the state variables. Next, full-order and reduced-order observers
are designed based on the transformed system. Finally, the observed states of the transformed system that
correspond to the original system is used to deduce the estimates of the original system. A numerical example
is provided of an interconnected time-delay system.
1 INTRODUCTION
High volume information exchange of modern inter-
connected systems are driving the need for seamless
communication capabilities, while at the same time
pushing for an optimum usage of already saturated
communication channels. In a world where the ideal
case of instantaneous interactions between subsys-
tems is limited by the communication capabilities, the
occurrence of time delays is therefore inevitable. In
the context of state estimation for these subsystems,
the notion of time delays inflicted on the state vari-
ables of these subsystems, put constraints on the em-
ployment of prominent observer structures and its ex-
istence conditions.
Understanding the main constraints that come
from the observability properties is an important state
estimation issue to be addressed. For time-delay
free systems that are observable, the design of ob-
servers is straightforward as many existing observer
design techniques can be applied (Luenberger, 1971;
Darouach et al., 1994; Darouach, 2000; Hou and
Müller, 1992, 1994; Trinh, 1999; Trinh and Fernando,
2012) and others. However, the opposite is true
for time-delay systems (Bhat and Koivo, 1976; Fair-
man and Kumar, 1986; Pearson and Fiagbedzi, 1989;
Darouach et al., 1999; Trinh, 1999; Darouach, 2001;
Germani et al., 2002; Hou et al., 2002; Subbarao and
Muralidhar, 2008; Nam et al., 2014; Leong et al.,
2015) that put forward challenges and complications
into devising effective observer structures. In this pa-
per, it will be shown that the design of asymptotic
observers for time-delay systems can be approached
in such a way that a coordinate transformation (Hou
et al., 2002) is performed to convert the system to
another domain or coordinate that guarantees the ob-
servability of its new system matrices. Subsequently,
an observer can be designed to estimate the state vec-
tor of the transformed system that is algebraically
linked to the state vector of the original system. For
example, for z(t) = Mx(t), M is the transformation
matrix that formularizes the transitional relationship
between the state vector z(t) and x(t) of the trans-
formed and original system, respectively. In short, the
state variables of the original system is related to that
of the transformed system through a coordinate trans-
formation relationship (Hou et al., 2002). Eventually,
the prediction of the states of the former system ˆx(t)
can be deduced from the estimates of the latter system
ˆz(t) on the basis of the same coordinate transforma-
tion relationship.
The implementation of such a concept requires
the establishment of a coordinate transformation (Hou
et al., 2002) that governs the relationship between the
original system and the transformed system in such
a way that the transformation is bi-directional - the
transformed system can be reversed-transformed to its
original system. In other words, the state vector of an
86
Leong W. and Trinh H..
Design of State Observers for Interconnected Time-delay Systems via a Coordinate Transformation Approach.
DOI: 10.5220/0005508500860093
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 86-93
ISBN: 978-989-758-122-9
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

x-domain system can be conveniently convertible to
that of the state vector of a z-domain system and vice-
versa.
To the best of our knowledge, application of co-
ordinate transformation in enabling the design of ob-
servers for interconnected time-delay systems has not
been well considered. In view of the potential that
such a transformation would act as a stepping stone
towards the construction of observers for such a class
of systems, it is the aim of this paper to tap into the
incentive such a coordinate transformation approach
has to offer.
The rest of the paper is organized as follows:
Session 2 provides the structure of a general time-
delay system represented in the delay operator form.
It further explores the underlying motivation and pos-
sibility of a coordinate transformation inspired by the
work of Hou et al. (2002), upon the satisfaction of
the given Theorem 1. Next, a typical two-area in-
terconnected time-delay system is given and an ex-
planation provided on how best to take advantage
of the benefits inherent in the transformed system to
overcome the distinct limitations of an interconnected
time-delay system in terms of state observation. In
section 4, the construction of a coordinate transforma-
tion based on the idea of Hou et al. (2002) is carried
out. Subsequently, full-order and reduced-order ob-
servers are designed for the transformed system using
well-known and straightforward techniques. Finally,
conclusion is given in section 5.
2 SYSTEM DESCRIPTION
To begin, assume that a time-delay system can be
represented in two different coordinate systems, x-
coordinate and z-coordinate. In a conventional x-
coordinate system, the state vector is known as x(t)
and as z(t) in the new z domain.
If we define τ as a time-delay operator, a time-
delay system can be represented as the following gen-
eral form such that
˙x(t) = A(τ)x(t) +B(τ)u(t), (1)
x(t) =

φ
1
(t)
φ
2
(t)

, ∀t ∈ [−τ
max
, 0], (2)
y(t) = C(τ)x(t), (3)
where τ = {τ
i
} for systems with multiple time-delay
constants for i = 1, 2, ..., K and τ
max
= max
{
τ
i
}
. Vec-
tors x(t) ∈ R
n
, u(t) ∈ R
m
and y(t) ∈ R
p
are the state,
control input and output measurement, respectively.
Matrices A(τ) ∈ R
n×n
, B(τ) ∈ R
n×m
and C(τ) ∈ R
p×n
are known system polynomial matrices as a function
of τ operator.
The purpose of the embedment of time-delay op-
erator into the system matrices is twofold. The first
reason is to simplify the representation of the struc-
ture of time-delay systems to accommodate for po-
tentially a larger class of interconnected systems with
time-delay appearing in diverse forms and values; and
secondly, to standardize the time-delay system to the
notational form that is conducive for the subsequent
coordinate transformation to take place. To demon-
strate the usage of delay operator in a particular poly-
nomial matrix, the multiplication of the time-delay
operator of an element of a polynomial matrix with
a state variable, for instance
A(τ)x(t) =

3 + 2τ
1
− τ
2
2
τ
3
. . . . . .

x
1
(t)
x
2
(t)

produces

3x
1
(t)+ 2x
1
(t − τ
1
) − x
1
(t − 2τ
2
) + x
2
(t − τ
3
)
. . .

.
According to Hou et al. (2002), a coordinate trans-
formation can be performed to transform the system
into an equivalent z-coordinate system which offers
distinct advantages. With the computation of a poly-
nomial matrix T (τ) having a coordinate transforma-
tion relationship as
z(t) = T (τ)x(t), (4)
the system described in (1)-(3) can be transformed
into the following
˙z(t) =
¯
Az(t)+
¯
E(τ)y(t) +
¯
B(τ)u(t), (5)
y(t) =
¯
Cz(t), (6)
where
¯
E(τ)y(t) and
¯
B(τ)u(t) are the output and input
injection terms respectively.
¯
A and
¯
C are constant ma-
trices of appropriate dimensions that carry the forms
of
¯
A =






0 I
p
.
.
.
.
.
.
.
.
.
I
p
0






, (7)
¯
C =

I
p
0 · ·· 0

, (8)
in which p is the dimension of the system output with
reference to (3).
Apparently, one would now realize the distin-
guishable benefit that the coordinate-transformed sys-
tem (5)-(6) is unquestionably observable. Such a
characteristic is pivotal because the conformity to the
DesignofStateObserversforInterconnectedTime-delaySystemsviaaCoordinateTransformationApproach
87

observability criteria signifies the affirmation of the
existence of an observer for such a system. Addition-
ally, one would notice that the delay values associated
with the state vector x(t) brought about by the system
polynomial matrix A(τ) in (1) is no longer existent in
the new system of (5)-(6) as the value of
¯
A follows
(7). This is an indication that a shift of time-delay as-
sociation has happened, that the time-delay constants
are now tied to the output and input injection terms,
through
¯
E(τ) and
¯
B(τ) polynomial matrices, rather
than having a direct association with the state vec-
tor. In principal, the use of coordinate transformation
has redefined the time-delay problem in the state vec-
tor into a whole new problem of having time-delay
terms in the input and output which is much easier
to be dealt with. In comparison, the same time-delay
system in the pre-transformed form of (1)-(3) suffers
from a limited viability of observer construction.
In order to obtain a transformed system that pos-
sesses system matrices that are observable, one has
to construct a transform or coordinate change matrix
which in this case denoted as T(τ). Now, an impor-
tant question arises as to under what situation the co-
ordinate transformation is available? The possibility
of constructing such a matrix depends largely on a set
of conditions. The existence condition of the trans-
formation matrix is given in Hou et al. (2002) and for
convenience, it will be quoted as follows.
Theorem 1. (Hou et al., 2002) There exists a coordi-
nate transformation that transforms an original sys-
tem of (1)-(3) into an observable form of (5)-(6) if the
observability matrix Q
k
(τ) defined in the following is
column unimodular.
The observability matrix for (1)-(3) is given by
Q
k
(τ) =





C(τ)
C(τ)A(τ)
.
.
.
C(τ)A
k−1
(τ)





, (9)
where k ≤ n is the smallest integer such that
rank(Q
k
(τ)) = p for all τ.
Proof. The reader may refer to the proof detailed in
Hou et al. (2002).
In the sequel, the succeeding section explores the
construction of observers for an interconnected time-
delay system via coordinate transformation by capi-
talizing on the benefits of inherent observability in the
matrix pair

¯
C,
¯
A

.
3 COORDINATE
TRANSFORMATION OF AN
INTERCONNECTED
TIME-DELAY SYSTEM
Similar to that of (1)-(3) that is represented in τ time-
delay operator form, a class of interconnected time-
delay system having the form of
˙x
i
(t) = A
ii
x
i
(t)+
N
∑
j=1, j6=i
A
i j
x
j
(t − τ
ji
)
+ A
d
ii
x
i
(t − τ
ii
) + B
i
u
i
(t) (10)
y
i
(t) = C
i
x
i
(t); i = 1, 2, ..., N, (11)
can be conveniently expressed in the similar fash-
ion. It is important to note that the common nota-
tion would be slightly different when the system is
expressed in the general time-delay operator form. In
order to illustrate the process of coordinate transfor-
mation in terms of the mapping of notations, an exam-
ple of the following two-area interconnected system
will be utilized.
˙x
1
(t) = A
11
x
1
(t)+ A
12
x
2
(t − τ
21
) + A
d
11
x
1
(t − τ
11
)
+ B
1
u
1
(t), (12)
y
1
(t) = C
1
x
1
(t), (13)
˙x
2
(t) = A
22
x
2
(t)+ A
21
x
1
(t − τ
12
) + A
d
22
x
2
(t − τ
22
)
+ B
2
u
2
(t), (14)
y
2
(t) = C
2
x
2
(t), (15)
where i = 1, 2, x
i
(t) ∈ R
n
i
, u
i
(t) ∈ R
m
i
and y
i
(t) ∈ R
p
i
are the state, input and the measured output for the
i −th subsystem, respectively. Matrices A
ii
∈ R
n
i
×n
i
,
A
d
ii
∈ R
n
i
×n
i
, A
i j
∈ R
n
i
×n
j
, B
i
∈ R
n
i
×m
i
and C
i
∈
R
p
i
×n
i
are real known system matrices.
The system matrices for the system described in
(12)-(15) are chosen as
A
11
=

−0.2 −0.2
0 −0.1

, A
12
=

−0.6 0
−0.1 0.3

,
A
21
=

0 0
0 −0.1

, A
22
=

−0.6 −0.3
0.4 −0.2

,
A
d11
=

−0.6 0
0 −0.1

, A
d22
=

−0.6 0
0.3 −0.3

,
C
1
=

1 0

, C
2
=

1 0

.
For the convenience of representation, the delay
constants in the system equations are mapped to τ
i
notation as follows:
τ
1
= τ
11
, τ
2
= τ
21
, τ
3
= τ
22
and τ
4
= τ
12
.
Obviously, the system is entangled with four dif-
ferent delay terms in its state variables. For this rea-
son, the application of standard design techiques that
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
88

Original x-
Coordinate
System,
ẋ(t)
Transformed
z-Coordinate
System,
ż(t)
y(t)
Coordinate
Transformation
u(t)
y(t)
y(t-τ
K
)
τ
1,
τ
2,
...τ
K
Γ
1
, Γ
2,
...Γ
K
y(t-τ
2
)
y(t-τ
1
)
Γ
y(t)
...
B
2
, B
3,
...B
K
¯¯ ¯
u(t-τ
K
)
u(t-τ
2
)
u(t-τ
1
)
...
B
1
¯
τ
1,
τ
2,
...τ
K
Figure 1: Coordinate transformation of the system.
requires that the observability criteria to be true be-
comes out of the question when it comes to the de-
sign of observer for such a system. Traditionally, this
results in a state observation problem that requires a
complicated solution or observer structure to account
for the time-delay terms implicit in the system state
variables.
It is therefore of crucial importance to have a
means to overcome this observability problem and
limitation of the time-delay terms in the state vari-
ables by working on a less restrictive alternative sys-
tem that is backward convertible to the original sys-
tem. Before a coordinate transformation is taking
place, it is convenient to represent the system in the
time-delay operator form as previously shown. In this
case, the system polynomial matrices in the form of
(1)-(3) would be easily computed as
A(τ) =



−0.6τ
1
− 0.2 −0.2
0 −0.1τ
1
− 0.1
0 0
0 −0.1τ
4
−0.6τ
2
0
−0.1τ
2
0.3τ
2
−0.6τ
3
− 0.6 −0.3
0.3τ
3
+ 0.4 −0.3τ
3
− 0.2



(16)
B(τ) =



−0.1 0
0.1 0
0 0.4
0 0.1



, (17)
C(τ) =

1 0 0 0
0 0 1 0

. (18)
Now, a coordinate transformation relationship
T (τ) can be obtained and is given as
T (τ) =

C(τ)
C(τ)A(τ) −
¯
E
1
(τ)C(τ)

, (19)
such that
z(t) = T (τ)x(t), (20)
where

¯
E
2
(τ)
¯
E
1
(τ)

=C(τ)A(τ)
2
Q
+
k
(τ), and that
Q
+
k
(τ) is the pseudoinverse of Q
k
(τ) obtained in (9).
The system can now be transformed into
˙z(t) =
¯
Az(t)+
¯
E(τ)y(t) +
¯
B(τ)u(t), (21)
y(t) =
¯
Cz(t), (22)
where
¯
E(τ) =

¯
E
1
(τ)
¯
E
2
(τ)

∈ R
n
z
×p
,
¯
B(τ) = T (τ)B(τ).
Or equivalently, when (16)-(18) are used, the spe-
cific transformed system obviously becomes that of
˙z(t) =
¯
Az(t)+ Γy(t) + Γ
1
y(t − τ
1
) + Γ
2
y(t − τ
2
)
+ Γ
3
y(t − τ
3
) + Γ
4
y(t − τ
4
) + Γ
5
y(t − 2τ
1
)
+ Γ
6
y(t − 2τ
3
) + Γ
7
y(t − τ
1
− τ
2
)
+ Γ
8
y(t − τ
1
− τ
4
) + Γ
9
y(t − τ
2
− τ
3
)
+ Γ
10
y(t − τ
2
− τ
4
) +
¯
B
1
u(t)+
¯
B
2
u(t − τ
1
)
+
¯
B
3
u(t − τ
2
) +
¯
B
4
u(t − τ
3
)
+
¯
B
5
u(t − τ
4
), t ≥ 0, (23)
y(t) =
¯
Cz(t), (24)
where pair

¯
C,
¯
A

is observable,
10
∑
i=1
Γ
i
and
5
∑
j=2
¯
B
j
are
the delayed output and input injection terms to be
DesignofStateObserversforInterconnectedTime-delaySystemsviaaCoordinateTransformationApproach
89

computed during the coordinate transformation pro-
cess and will be covered in the next section. z(t) ∈
R
n
z
, u(t) ∈ R
m
and y(t) ∈ R
p
are respectively the
state, input and the measured output of the trans-
formed system. Matrices
¯
A ∈ R
n
z
×n
z
,
¯
C ∈ R
p×n
z
,
Γ
i
∈ R
n
z
×p
, 1 ≤ i ≤ 10 and
¯
B
j
∈ R
n
z
×m
, 2 ≤ j ≤ 5,
are known constant matrices.
Note that the state vector z(t) has no association
of delay terms in comparison to the original system.
The coordinate transformation is illustrated in Figure
1 in which the transformed system in z-coordinate,
receives the same control input information u(t) as
the original x-coordinate system, and eventually pro-
duces the same output measurements y(t) as the orig-
inal system. In other words, the functionality of the
transformed and original system is virtually the same.
3.1 Design of a Full-order Observer
The structure of a typical Luenberger observer for
the transformed system is shown below. It is worth-
noting that part of this observer structure follows the
standard Luenberger structure except for the addi-
tional delayed input and output injection terms. The
use of these injection terms renders the relaxation of
the observer existence condition which in this case the
observability criteria.
˙
ˆz(t) = (
¯
A − L
¯
C)ˆz(t) + {L + Γ}y(t) + Γ
1
y(t − τ
1
)
+ Γ
2
y(t − τ
2
) + Γ
3
y(t − τ
3
) + Γ
4
y(t − τ
4
)
+ Γ
5
y(t − 2τ
1
) + Γ
6
y(t − 2τ
3
)
+ Γ
7
y(t − τ
1
− τ
2
) + Γ
8
y(t − τ
1
− τ
4
)
+ Γ
9
y(t − τ
2
− τ
3
) + Γ
10
y(t − τ
2
− τ
4
)
+
¯
B
1
u(t)+
¯
B
2
u(t − τ
1
) +
¯
B
3
u(t − τ
2
)
+
¯
B
4
u(t − τ
3
) +
¯
B
5
u(t − τ
4
), t ≥ 0, (25)
where L is a matrix of appropriate dimension.
3.2 Design of a Reduced-order
Observer
The objective of a reduced order observer is to esti-
mate a function f (t) ∈ R
(n
z
−p)
defined as:
f (t) = Lz(t), (26)
where L =

0
(n
z
−p)×p
I
n
z
−p

∈ R
(n
z
−p)×n
z
is a
full-row rank matrix such that

¯
C
L

is non-singular.
The reduced-order observer structure that we pro-
pose for the transformed z-domain system is
ˆ
f (t) = w(t) + Ey(t), (27)
˙w(t) = Nw(t) +Jy(t) + M
1
y(t − τ
1
) + M
2
y(t − τ
2
)
+ M
3
y(t − τ
3
) + M
4
y(t − τ
4
) + M
5
y(t − 2τ
1
)
+ M
6
y(t − 2τ
3
) + M
7
y(t − τ
1
− τ
2
)
+ M
8
y(t − τ
1
− τ
4
) + M
9
y(t − τ
2
− τ
3
)
+ M
10
y(t − τ
2
− τ
4
) + Hu(t) + K
1
u(t − τ
1
)
+ K
2
u(t − τ
2
) + K
3
u(t − τ
3
)
+ K
4
u(t − τ
4
), t ≥ 0, (28)
where
ˆ
f (t) ∈ R
n
z
, u(t) ∈ R
m
and y(t) ∈ R
p
are the
reduced-order state estimates, input and output re-
spectively. Matrices E, N, J, M
i
, 1 ≤ i ≤ 10, H, K
j
,
1 ≤ j ≤ 4 are matrices of appropriate dimensions. The
construction of a reduce-order observer requires that
these unknown matrices to be obtained.
As soon as the state estimates of the z-coordinate
system are obtained, the state of the x-coordinate sys-
tem can be approximated by recovering them from the
z-coordinate state estimates, for instance, ˆx(t) and ˆz(t)
are related through the linear function of
ˆx(t) = T
+
(τ)ˆz(t), (29)
where T
+
(τ) of appropriate dimension is the pseu-
doinverse of T (τ) obtained from equation (19).
4 NUMERICAL EXAMPLE
Consider the previous example of an interconnected
time-delay system where the system polynomial ma-
trices have been worked out to be (16)-(18). The time-
delay values are chosen to be τ
1
= 5, τ
2
= 5, τ
3
= 5
and τ
4
= 5 for simulation purposes.
According to Theorem 1, an observability matrix
Q
k
(τ) has to be computed, and provided that it is
column unimodular, the system can be transformed
into an observable form of (5)-(6). It is found that
rank(Q
2
(τ)) = p, which signifies that the following
Q
2
(τ) is column unimodular.
Q
2
(τ) =



1 0 0 0
0 0 1 0
−0.6τ
1
− 0.2 −0.2 −0.6τ
2
0
0 0 −0.6τ
3
− 0.6 −0.3



,
(30)
It then follows that a left-inverse Q
+
2
(τ) exists to
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
90

be
Q
+
2
(τ) =




1 0 0 0
−3τ
1
− 1 −3τ
2
−5 0
0 1 0 0
0 −2τ
3
− 2 0 −
10
3




.
By definition of (19), the coordinate transforma-
tion T (τ) is derived as
T (τ) =



1 0 0 0
0 0 1 0
0.1τ
1
+ 0.1 −0.2 −0.2τ
2
0
0.15τ
4
0 0.3τ
3
+ 0.2 −0.3



,
(31)
which eventually produces
¯
E(τ) =



−0.7τ
1
− 0.3
−0.15τ
4
−0.08τ
1
− 0.06τ
1
2
− 0.02
−0.03τ
4
− 0.09τ
1
τ
4
−0.4τ
2
−0.9τ
3
− 0.8
0.08τ
2
− 0.06τ
1
τ
2
+ 0.12τ
2
τ
3
−0.09τ
2
τ
4
− 0.39τ
3
− 0.18τ
3
2
− 0.24



(32)
and
¯
B(τ) =



−0.1 0
0 0.4
−0.03 − 0.01τ
1
−0.08τ
2
−0.015τ
4
0.12τ
3
+ 0.05



. (33)
This z-coordinate system can be easily converted
into the form of (23)-(24) and therefore the detailed
conversion process will be omitted here.
4.1 Full-order Observer
A full-order observer is designed for such a sys-
tem utilizing the structure given in (25). Selecting
the poles to be

−3; −4; −5; −6;

, the ob-
server gain matrix L can be obtained through the well-
known pole-assignment technique and the calculated
observer parameters are given as follows.
L =



11 0
0 7
30 0
0 12



, Γ =



−0.3 0
0 −0.8
−0.02 0
0 −0.24



,
Γ
1
=



−0.7 0
0 0
−0.08 0
0 0



, Γ
2
=



0 −0.4
0 0
0 0.08
0 0



,
Γ
3
=



0 0
0 −0.9
0 0
0 0.39



, Γ
4
=



0 0
−0.15 0
0 0
−0.03 0



,
Γ
5
=



0 0
0 0
−0.06 0
0 0



, Γ
6
=



0 0
0 0
0 0
0 −0.18



,
Γ
7
=



0 0
0 0
0 −0.06
0 0



, Γ
8
=



0 0
0 0
0 0
−0.09 0



,
Γ
9
=



0 0
0 0
0 0.12
0 0



, Γ
10
=



0 0
0 0
0 0
0 −0.09



,
¯
B
1
=



−0.1 0
0 0.4
−0.03 0
0 0.05



,
¯
B
2
=



0 0
0 0
−0.01 0
0 0



,
¯
B
3
=



0 0
0 0
0 −0.08
0 0



,
¯
B
4
=



0 0
0 0
0 0
0 0.12



, and
¯
B
5
=



0 0
0 0
0 0
−0.015 0



.
Subsequently, with the attainment of ˆz(t) from the
observer, state estimates of x-coordinate system ˆx(t)
can be deduced directly from the state estimates of z-
coordinate system ˆz(t) through equation (29) where
T
+
(τ) is computed as:
T
+
(τ) =




1 0 0 0
1
2
τ
1
+
1
2
−τ
2
−5 0
0 1 0 0
1
2
τ
4
τ
3
+
2
3
0 −
10
3




.
−5 0 5 10 15 20 25 30 35
−6
−4
−2
0
2
4
6
8
10
t − τ
X−state vs. Observed X−state
x1−hat(t) vs. x1(t)
ˆx
1
(t) z-system
x
1
(t) x-system
0 5 10 15 20 25 30 35 40
t
Figure 2: State vector, x
1
(t) from the original system vs.
ˆx
1
(t) derived from the observer of the transformed system.
DesignofStateObserversforInterconnectedTime-delaySystemsviaaCoordinateTransformationApproach
91

Simulation of the z-domain full-order observer
was carried out and comparisons between the x state
variables and its estimates are plotted as below.
−5 0 5 10 15 20 25 30 35
−5
−4
−3
−2
−1
0
1
2
3
t − τ
X−state vs. Observed X−state
x2−hat(t) vs. x2(t)
ˆx
2
(t) z-system
x
2
(t) x-system
0 5 10 15 20 25 30 35 40
t
Figure 3: State vector, x
2
(t) from the original system vs.
ˆx
2
(t) derived from the observer of the transformed system.
−5 0 5 10 15 20 25 30 35
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
2.5
t − τ
X−state vs. Observed X−state
x3−hat(t) vs. x3(t)
ˆx
3
(t) z-system
x
3
(t) x-system
0 5 10 15 20 25 30 35 40
t
Figure 4: State vector, x
3
(t) from original system vs. ˆx
3
(t)
derived from the observer of the transformed system.
−5 0 5 10 15 20 25 30 35
−3
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
t − τ
X−state vs. Observed X−state
x4−hat(t) vs. x4(t)
ˆx
4
(t) z-system
x
4
(t) x-system
0 5 10 15 20 25 30 35 40
t
Figure 5: x
4
(t) from original system vs.
b
x
4
(t) derived from
the observer of the transformed system (x
4
(t) 6= z
4
(t))
4.2 Reduced-order Observer
A reduced-order observer of the structure mentioned
in (27)-(28) is constructed. The computed parameters
are as follows.
E =

3 0
0 4

, N =

−3 0
0 −4

,
J =

−8.12 0
0 −13.04

, M
1
=

2.02 0
0 0

,
M
2
=

0 1.28
0 0

, M
3
=

0 0
0 3.21

,
M
4
=

0 0
0.57 0

, M
5
=

−0.06 0
0 0

,
M
6
=

0 0
0 −0.18

, M
7
=

0 −0.06
0 0

,
M
8
=

0 0
−0.09 0

, M
9
=

0 0.12
0 0

,
M
10
=

0 0
0 −0.09

, H =

0.27 0
0 −1.55

,
K
1
=

−0.01 0
0 0

, K
2
=

0 −0.08
0 0

,
K
3
=

0 0
0 0.12

, and K
4
=

0 0
−0.015 0

.
From (26), since essentially, f (t) =

z
3
(t)
z
4
(t)

,
therefore,
ˆ
f (t) =

ˆz
3
(t)
ˆz
4
(t)

. Again, ˆx
2
and ˆx
4
can be
deduced according to equation (29) as soon as
ˆ
f (t)
and the measurable output y(t) are available.
Simulation of the z-domain reduced-order ob-
server was carried out and the comparison between
the x state vector and its deduced estimates are shown
below.
−5 0 5 10 15 20 25 30 35
−5
−4
−3
−2
−1
0
1
2
3
t − τ
X−state vs. Observed X−state
x2−hat(t) vs. x2(t)
ˆx
2
(t) z-system
x
2
(t) x-system
0 5 10 15 20 25 30 35 40
t
Figure 6: x
2
(t) from the original system vs. ˆx
2
(t) derived
from the observer of the transformed system.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
92

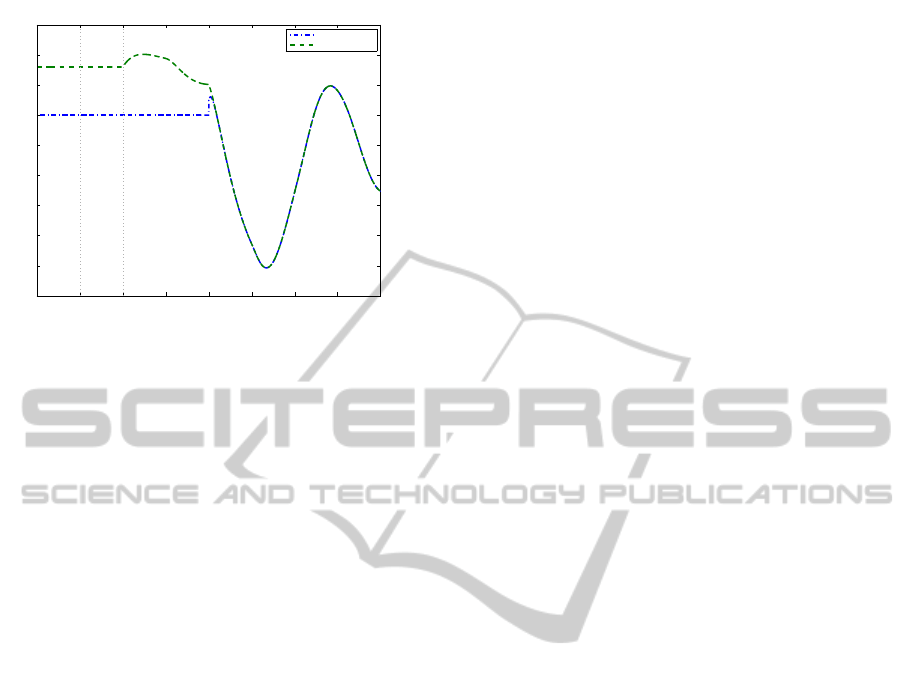
−5 0 5 10 15 20 25 30 35
−3
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
t − τ
X−state vs. Observed X−state
x4−hat(t) vs. x4(t)
ˆx
4
(t) z-system
x
4
(t) x-system
0 5 10 15 20 25 30 35 40
t
Figure 7: x
4
(t) from the original system vs. ˆx
4
(t) derived
from the observer of the transformed system.
5 CONCLUSIONS
This paper has applied a state transformation method
of Hou et al. (2002) into the design of state observers
for interconnected time-delay systems. Through the
use of a coordinate transformation, an equivalent sys-
tem of different coordinates has been established, ef-
fectively redefining the restrictive time-delay problem
in the state vector into a less complex problem of hav-
ing time-delay terms in the input and output. This
in turn opens up the opportunity of accommodating
well-established standard observer design techniques
for delay-free linear systems which have otherwise
lacked viability in the original interconnected time-
delay system. Numerical results show that, for the
coordinate-transformed time-delay system, observers
of desirable asymptotic convergence properties may
be designed using estimation theory available for
delay-free systems. Further work is needed in order
to meet constraints imposed on the flow of informa-
tion in an interconnected system. Hence some forms
of distributed or decentralized observer schemes will
be a possible topic for future research.
REFERENCES
Bhat, K. and Koivo, H. (1976). An observer theory for time
delay systems. Automatic Control, IEEE Transactions
on, 21(2):266–269.
Darouach, M. (2000). Existence and design of functional
observers for linear systems. IEEE Transactions on
Automatic Control, 45(5):940–943.
Darouach, M. (2001). Linear functional observers for sys-
tems with delays in state variables. IEEE Transactions
on Automatic Control, 46(3):491–496.
Darouach, M., Pierrot, P., and Richard, E. (1999). De-
sign of reduced-order observers without internal de-
lays. IEEE Transactions on Automatic Control,
44(9):1711–1713.
Darouach, M., Zasadzinski, M., and Xu, S. J. (1994).
Full-order observers for linear systems with unknown
inputs. IEEE Transactions on Automatic Control,
39(3):606–609.
Fairman, F. and Kumar, A. (1986). Delayless observers for
systems with delay. IEEE Transactions on Automatic
Control, 31(3):258–259.
Germani, A., Manes, C., and Pepe, P. (2002). A new
approach to state observation of nonlinear systems
with delayed output. IEEE Transactions on Automatic
Control, 47(1):96–101.
Hou, M. and Müller, P. (1992). Design of observers for lin-
ear systems with unknown inputs. IEEE Transactions
on Automatic Control, 37(6):871–875.
Hou, M. and Müller, P. (1994). Design of decentral-
ized linear state function observers. Automatica,
30(11):1801–1805.
Hou, M., Zítek, P., and Patton, R. J. (2002). An observer de-
sign for linear time-delay systems. IEEE Transactions
on Automatic Control, 47(1):121–125.
Leong, W. Y., Trinh, H., and Fernando, T. (2015). A prac-
tical functional observer scheme for interconnected
time-delay systems. International Journal of Control,
(in press, DOI: 10.1080/00207179.2015.1025429).
Luenberger, D. (1971). An introduction to observers. IEEE
Transactions on Automatic Control, 16(6):596–602.
Nam, P., Pathirana, P., and Trinh, H. (2014). ε-bounded
state estimation for time-delay systems with bounded
disturbances. International Journal of Control,
87(9):1747–1756.
Pearson, A. and Fiagbedzi, Y. (1989). An observer for time
lag systems. IEEE transactions on Automatic Control,
34(7):775–777.
Subbarao, K. and Muralidhar, P. C. (2008). A state observer
for LTI systems with delayed outputs: Time-varying
delay. In American Control Conference, 2008, pages
3029–3033. IEEE.
Trinh, H. (1999). Linear functional state observer for
time-delay systems. International Journal of Control,
72(18):1642–1658.
Trinh, H. and Fernando, T. (2012). Functional Observers
for Dynamical Systems. Lecture Notes in Control and
Information Sciences. Springer, Berlin, Heidelberg.
DesignofStateObserversforInterconnectedTime-delaySystemsviaaCoordinateTransformationApproach
93