
Gaussian Mixture Measurements for Very Long Range Tracking
Qian Zhang, Taek Lyul Song
Department of Electronic Systems Engineering, Hanyang University, Hanyang, Republic of Korea
K
eywords:
Nonlinear Estimation, Very Long Range Tracking, Gaussian Mixtures, GMM-ITS.
Abstract:
Target tracking with very long range is studied in this paper. Such tracking problem has severe measurement
nonlinearity that will cause consistency problems and large tracking errors. Gaussian mixture measurements
are obtained by dividing the measurement likelihood into several Gaussian components. The Gaussian Mixture
Measurement-Integrated Track Splitting (GMM-ITS) is applied to very long range tracking scenarios. The
simulation results show that the GMM-ITS can produce consistency in the filtering results crucial to the filter
performance. Furthermore, it is also able to estimate the target state accurately with small tracking errors.
1 INTRODUCTION
Phased array radar can produce measurements which
are very accurate in the range direction and very in-
accurate in the cross range direction. Very long range
tracking with phased array radar is an interesting but
challenging problem. Due to the thin, curved, con-
tact lens-like shape of the measurement uncertainty
region in the Cartesian coordinates, this problem is
also known as the contact lens problem (Tian and Bar-
Shalom, 2009). The contact lens problem results in
severe measurement nonlinearity that leads to corre-
sponding consistency problems for traditional nonlin-
ear filtering techniques such as the extended Kalman
filter (EKF) (Bar-Shalom et al., 2001), the unscented
Kalman filter (UKF) (Julier and Uhlmann, 2004) and
the particle filter (PF) (Ristic et al., 2004). When esti-
mating the state of a dynamic system, a state estimator
is called consistent if the estimation errors based on
a finite number of samples (measurements) are con-
sistent with their theoretical statistical properties: (a)
have mean zero; (b) have covariance matrix as calcu-
lated by the filter (Bar-Shalom et al., 2001).
The converted measurement Kalman filter
(CMKF) (Bar-Shalom et al., 2001) transforms the
polar measurement to Cartesian coordinates and
implements the Kalman filter purely in the Cartesian
coordinates. As the converted measurements always
use a decreased accuracy in the range direction,
the CMKF can produce consistent filtering results.
However, measurement transformation will result in
the CMKF with significant loss in range accuracy. To
reduce the corresponding loss in range accuracy, the
measurement covariance adaptive extended Kalman
filter (MCAEKF) employing the measurement co-
variance adaptive (MCA) rule was proposed in (Tian
and Bar-Shalom, 2009) to address the contact lens
problem. The MCA rule guarantees the consistency
of the linearized EKF by artificially increasing the
measurement uncertainty region. If the MCA rule
is not satisfied, the standard deviation of the range
measurement is increased in the MCAEKF. By
modifying the covariance matrix of the measure-
ments, the MCAEKF can yield consistent filtering
results and avoid overall loss in range accuracy. The
MCAEKF also has advantages in tracking accuracy.
Unfortunately, it causes significant loss in accuracy
at the early stage of filtering due to the artificially
enlarged range measurement covariance. In order
to prevent this loss, consistency-based Gaussian
mixture filtering (CbGMF) (Tian and Bar-Shalom,
2014) approximates the inaccurate track using a set
of sub-tracks so that the MCA rule is satisfied at the
sub-track level. In the CbGMF, if there is at least one
sub-track that covers the true target state, the consis-
tency of the whole set of sub-tracks is guaranteed. To
control complexity, the CbGMF removes sub-tracks
that are far away from the true target state and sets
an upper limit for the total number of sub-tracks.
Simulation results of (Tian and Bar-Shalom, 2014)
indicate that CbGMF overcomes the loss in accuracy,
but still results in a small degradation in consistency.
The original and partial version of the Gaus-
sian Mixture Measurement-Integrated Track Split-
ting (GMM-ITS) is proposed in (Muˇsicki and Evans,
2006). In this paper, we solve the contact lens prob-
457
Zhang Q. and Song T..
Gaussian Mixture Measurements for Very Long Range Tracking.
DOI: 10.5220/0005509404570464
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 457-464
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

lem using the GMM-ITS. The key idea of the GMM-
ITS is that both the non-linear (non-Gaussian) target
measurement likelihood and the target state proba-
bility density function (pdf) are approximated by a
Gaussian mixture of components (Muˇsicki, 2009).
For very long range target tracking, the GMM-ITS
should divide a curved (contact lens-shaped) uncer-
tainty measurement region (non-Gaussian) into sev-
eral components. Then, each predicted track com-
ponent uses each measurement component to obtain
a new track component. Finally, the track compo-
nent pruning and merging are performed to control
the complexity of the algorithm.
The remainder of the paper is structured as fol-
lows. The details about the contact lens problem are
presented in Section 2. Section 3 describes the GMM-
ITS solution. A simulation study in Section 4 shows
the effectiveness of this solution , followed by the
conclusions.
2 PROBLEM STATEMENT
In this paper, we consider a two-dimensional mea-
surement situation with range and azimuth. The tar-
get follows the continuous white noise acceleration
(CWNA) motion model (Bar-Shalom et al., 2001) and
the state vector components are ordered as
x = [x, y, ˙x, ˙y]
′
(1)
The dynamic model is given by
x
k
= Fx
k−1
+ ν
k−1
(2)
where the state propagation matrix
F =
1 T
0 1
⊗ I
2
(3)
does not change with time, ν
k−1
is a sequence of zero
mean, white Gaussian noise with covariance
Q
k−1
=
T
3
/3 T
2
/2
T
2
/2 T
⊗ diag(q
x
,q
y
) (4)
T is the sampling time, I
2
is 2 × 2 identity matrix, q
x
and q
y
are power spectral densities.
The measurements are taken in polar coordinates
and given by
b
k
= h(x
k
) + ω
k
(5)
where
h(x
k
) =
r
k
θ
k
=
q
x
2
k
+ y
2
k
tan
−1
y
k
x
k
(6)
ω
k
=
ω
r
k
ω
θ
k
(7)
R
T
V
r
R
T
V
V
r
V
The origin
The measurement
uncertainty region
Figure 1: An example of the curved measurement uncer-
tainty region
The measurement noise ω
r
k
and ω
θ
k
are assumed to
be mutually independent white Gaussian with zero
means and standard deviations σ
r
and σ
θ
, respec-
tively. We also use B
k
to denote the set of all mea-
surements up to time k
B
k
=
n
b
k
,B
k−1
o
= {b
k
,b
k−1
,..., b
1
}. (8)
In this paper, the raw measurements (range and an-
gle) in the polar coordinates are converted to pseudo
measurements in the Cartesian coordinates. The con-
verted measurements can be expressed as
z
k
= Hx
k
+ ϖ
k
(9)
where the converted measurement noise ϖ
k
=
ω
x
k
,ω
y
k
′
is non-Gaussianstate-dependent and ω
x
k
and
ω
y
k
are correlated. The measurement matrix H is
H = [ I
2
0
2
] (10)
where 0
2
is 2× 2 zeros matrix. In the same way, Z
k
denotes the set of all measurements up to time k
Z
k
=
n
z
k
,Z
k−1
o
= {z
k
,z
k−1
,...,z
1
}. (11)
For very long range tracking scenarios, the con-
tact lens problem appears when the target states in
the Cartesian coordinates are updated with nonlin-
ear measurements from a different coordinate system
(e.g., the polar coordinates). As the range measure-
ment is very accurate compared to the angle measure-
ment for very long range target tracking, the mea-
surement uncertainty has a very thin, curved, contact
lens-like shape in the Cartesian coordinates. An ex-
ample of the uncertainty region of such a measure-
ment is presented in Figure 1. We can determine from
the basic geometry that the cross-range uncertainty
increases while the range becomes larger. Since the
accuracy in range does not change, the measurement
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
458

uncertainty region takes on an increasingly curved
shape as the range increases. If the measurement non-
linearity becomes too severe, the conventional filters
(e.g., the EKF, the UKF and the PF) develop a sig-
nificant consistency problem. In order to prevent this
problem, the CMKF always reduces the accuracy in
range and the MCAEKF artificially modifies the mea-
surement covariance at the early stages of the filter-
ing. Besides, the CbGMF approximates an inaccurate
track by a set of sub-tracks.
3 THE GMM-ITS SOLUTION
In the GMM-ITS, the a posteriori target state esti-
mate pdf is updated by the Bayes formula, given by
p(x
k
|Z
k
) =
p(z
k
|x
k
)p(x
k
|Z
k−1
)
p(z
k
|Z
k−1
)
(12)
where p(z
k
|x
k
) is the likelihood of the measurement
z
k
, p(x
k
|Z
k−1
) denotes the propagated state pdf from
time k − 1 to k and the prior likelihood of measure-
ment is
p(z
k
|Z
k−1
) =
Z
x
k
p(z
k
|x
k
)p(x
k
|Z
k−1
)dx
k
. (13)
Then, the equation (12) can be expressed as
p(x
k
|Z
k
) =
p(z
k
|x
k
)p(x
k
|Z
k−1
)
R
x
k
p(z
k
|x
k
)p(x
k
|Z
k−1
)dx
k
. (14)
As the likelihood function of the converted measure-
ment p(z
k
|x
k
) is not Gaussian, the GMM-ITS seeks to
approximate both p(z
k
|x
k
) and p(x
k
|Z
k−1
) by Gaus-
sian mixtures.
3.1 GMM Likelihood Approximation
In order to approximate p(z
k
|x
k
) using a Gaussian
mixture, we first divide the measurement uncertainty
into several segments.
Suppose at time k, the measurements are r
k
and
θ
k
with standard deviations σ
r
and σ
θ
, respectively.
If we divide the measurement uncertainty into N seg-
ment, the angle of each segment is
θ
k,i
= θ
k
− ασ
θ
+
i−
1
2
·
2× ασ
θ
N
,i = 1,. ..,N
(15)
with standard deviations
σ
θ,i
=
1
2
·
2× ασ
θ
N
(16)
where α is the constant number selected to provide
sufficient coverage.
T
D
V
r
D
V
u
Figure 2: An example of Gaussian mixture measurement
The range of each segment is the same, given by
r
k,i
= r
k
,i = 1,.. ., N (17)
with standard deviations
σ
r,i
= ασ
r
(18)
Each segment i is approximated by a Gaussian whose
mean value and covariance are z
k,i
and R
k,i
respec-
tively:
z
k,i
= r
k,i
cos(θ
k,i
)
sin(θ
k,i
)
(19)
R
k,i
= T
k,i
σ
2
r,i
0
0 (r
k,i
σ
θ,i
)
2
T
T
k,i
(20)
with the rotation matrix T
k,i
defined by
T
k,i
=
cos(θ
k,i
) −sin(θ
k,i
)
sin(θ
k,i
) cos(θ
k,i
)
(21)
To reflect the probability mass of the segment, a
weight is associated with each segment, which sat-
isfies
λ
k,i
∝ exp{−
(θ
k,i
− θ
k
)
2
2σ
2
θ
} (22)
N
∑
i=1
λ
k,i
= 1 (23)
Then, the function p(z
k
|x
k
) is approximated by
p(z
k
|x
k
) =
N
∑
i=1
λ
k,i
N (z
k,i
;Hx
k
,R
k,i
) (24)
where N denotes the number of measurement com-
ponents and N (x;m, P) is the Gaussian pdf of vari-
able x with mean m and covariance P. In equation
(24), each element of the Gaussian mixture is termed
a “measurement component”. Figure 2 shows an ex-
ample of the Gaussian mixture measurement model,
which contains seven components. For the contact
lens problem, each measurement component is pre-
sented by an α-sigma ellipse and the area of each el-
lipse is the same . Besides, the target is displayed by
the cross.
GaussianMixtureMeasurementsforVeryLongRangeTracking
459

3.2 GMM-ITS Target Tracking
In this subsection, we consider one update cycle start-
ing with the a posteriori state estimate at time k − 1,
and ending with a posteriori state estimate at time k.
At time k− 1, the target state pdf is approximated by
a Gaussian mixture
p(x
k−1
|Z
k−1
) =
C
k−1
∑
c=1
ξ
k−1,c
p(x
k−1
|c,Z
k−1
) (25)
where each element is termed a “track component”
with indexc and the total numberof track components
is C
k−1
. In equation (25), ξ
k−1,c
denotes the relative
probability that the track component c is true based
on the measurement set Z
k−1
,
ξ
k−1,c
∆
= p
c|Z
k−1
(26)
and
C
k−1
∑
c=1
ξ
k−1,c
= 1. (27)
The probability density function p(x
k−1
|c,Z
k−1
) is
the target state pdf assuming that track component c
is true and follows a Gaussian distribution:
p(x
k−1
|c,Z
k−1
) = N
x
k−1
; ˆx
k−1|k−1
(c),P
k−1|k−1
(c)
(28)
where ˆx
k−1|k−1
(c) and P
k−1|k−1
(c) denotes the up-
dated state estimate and error covariance of the track
component c at time k − 1 respectively.
3.2.1 Track Prediction
In equation (12), the predicted target trajectory state
pdf p(x
k
|Z
k−1
) is calculated by
p(x
k
|Z
k−1
) =
Z
x
k−1
p(x
k
|x
k−1
) p(x
k−1
|Z
k−1
)dx
k−1
(29)
From the dynamic model of the target, we can observe
that
p(x
k
|x
k−1
) = N (x
k
;Fx
k−1
,Q
k−1
) (30)
Then, substituting (25) and (30) into (29)
p(x
k
|Z
k−1
) =
Z
x
k−1
p(x
k
|x
k−1
)
×
C
k−1
∑
c=1
ξ
k−1,c
p(x
k−1
|c,Z
k−1
)dx
k−1
(31)
Interchanging the integral and summation yield
p(x
k
|Z
k−1
) =
C
k−1
∑
c=1
ξ
k−1,c
p(x
k
|c,Z
k−1
) (32)
where
p(x
k
|c,Z
k−1
) = N
x
k
; ˆx
k|k−1
(c),P
k|k−1
(c)
(33)
and each predicted track component comes from the
standard Kalman filter prediction formulae
ˆx
k|k−1
(c) = F ˆx
k−1|k−1
(c) (34)
P
k|k−1
(c) = FP
k−1|k−1
(c)F
T
+ Q
k−1
(35)
3.2.2 Track Update
Thus, both the measurement likelihood p(z
k
|x
k
) and
target prediction p(x
k
|Z
k−1
) are approximated by
Gaussian mixtures, given by (24) and (32) respec-
tively. Then, each measurement component updates
each predicted track component, generating a new up-
dated track component at time k.
The prior likelihood of measurement is given by
p(z
k
|Z
k−1
) =
Z
x
k
p(z
k
|x
k
)p(x
k
|Z
k−1
)dx
k
(36)
Applying (24) and (32), and interchanging the inte-
gral and summation, we can obtain
p(z
k
|Z
k−1
) =
N
∑
i=1
λ
k,i
p(z
k,i
|Z
k−1
) (37)
where
p(z
k,i
|Z
k−1
) =
C
k−1
∑
c=1
ξ
k−1,c
p(z
k,i
|c,Z
k−1
)
=
C
k−1
∑
c=1
ξ
k−1,c
N (z
k,i
; ˆz
k
(c),S
k,i
(c))
(38)
and
ˆz
k
(c) = H ˆx
k|k−1
(c); (39)
S
k,i
(c) = HP
k|k−1
(c)H
T
+ R
k.i
. (40)
ˆz
k
(c) and S
k,i
(c) are produced by the standard Kalman
filter using the measurement components and pre-
dicted track components.
Substituting (24), (32) and (37) into (14), the
a posteriori target state estimate pdf at time k can be
calculated as
p(x
k
|Z
k
) =
N
∑
i=1
λ
k,i
p(z
k,i
|x
k
)
C
k−1
∑
c=1
ξ
k−1,c
p(x
k
|c,Z
k−1
)
p(z
k
|Z
k−1
)
=
C
k−1
∑
c=1
N
∑
i=1
ξ
k−1,c
λ
k,i
p(z
k,i
|x
k
)p(x
k
|c,Z
k−1
)
p(z
k
|Z
k−1
)
×
p(z
k,i
|c,Z
k−1
)
p(z
k,i
|c,Z
k−1
)
=
C
k−1
∑
c=1
N
∑
i=1
ξ
k−1,c
λ
k,i
p(z
k,i
|c,Z
k−1
)
p(z
k
|Z
k−1
)
× p(x
k
|c,z
k,i
,Z
k−1
)
(41)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
460

which is reshaped into
p(x
k
|Z
k
) =
C
k
∑
c
+
=1
ξ
k,c
+
p(x
k
|c
+
,z
k
,Z
k−1
) (42)
where c
+
= {i, c} denotes the new track component
created by applying measurement component i to pre-
dicted track component c. Furthermore, the number
of new track components at scan k increases to
C
k
= C
k−1
· N. (43)
The probability of the new track component is deter-
mined by the Bayes formula
ξ
k,c
+
∆
= p(c,i|Z
k
)
=
p(z
k
|c,i,Z
k−1
)p(i|c,Z
k−1
)p(c|Z
k−1
)
p(z
k
|Z
k−1
)
(44)
Since the probability of the measurement component
i does not depend on the previous measurements or
the target state,
p(i|c,Z
k−1
) = λ
k,i
(45)
Thus,
ξ
k,c
+ =
λ
k,i
ξ
k−1,c
p(z
k
|c,i,Z
k−1
)
p(z
k
|Z
k−1
)
(46)
where
p(z
k
|c,i,Z
k−1
) = N (z
k,i
; ˆz
k
(c),S
k,i
(c)) (47)
and the prior measurement likelihood p(z
k
|Z
k−1
) can
be calculated from (37). The relative probabilities
ξ
k,c
+ satisfy
C
k
∑
c
+
=1
ξ
k,c
+ = 1 (48)
The state estimate of the new track component is
given by
p(x
k
|c
+
,z
k
,Z
k−1
) = N (x
k
; ˆx
k|k
(c
+
),P
k|k
(c
+
)) (49)
where ˆx
k|k
(c
+
) and P
k|k
(c
+
) are the mean value and
the covariance matrix respectively, calculated by the
standard Kalman filter update
ˆx
k|k
(c
+
) = ˆx
k|k−1
(c) + K
k
(c
+
)(z
k,i
− H ˆx
k|k−1
(c))
(50)
P
k|k
(c
+
) = (I− K
k
(c
+
)H)P
k|k−1
(c) (51)
with the Kalman gain
K
k
(c
+
) = P
k|k−1
(c)H
T
S
−1
k,i
(c) (52)
and S
k,i
(c) is given by (40).
3.2.3 Track Component Management
As described above, each measurement component is
used to update each predicted track component and a
new track component is generated. Obviously, the to-
tal number of track components grows exponentially
over time. Thus, a practical implementation should be
applied to control their number.
Existing available methods include track compo-
nent pruning and component subtree removal (remov-
ing track components with low probability) (Black-
man and Popoli, 1999), as well as track component
merging. Track component merging merges track
components that have similar states into one track
component.
In this paper, the GMM-ITS implements the prun-
ing and merging method proposed in (Singer et al.,
1974), which proposes merging of all track compo-
nents with the common measurement sequence.
3.2.4 Track Outputs
The track outputs usually consist of the mean and er-
ror covariance of the target estimate pdf, given by
ˆx
k|k
=
C
k
∑
c
+
=1
ξ
k,c
+ ˆx
k|k
(c
+
) (53)
P
k|k
=
C
k
∑
c
+
=1
ξ
k,c
+ (P
k|k
(c
+
) + ˆx
k|k
(c
+
) ˆx
T
k|k
(c
+
))
− ˆx
k|k
ˆx
T
k|k
(54)
4 SIMULATION EXPERIMENTS
In this section, we evaluate the performance of the
GMM-ITS in four scenarios where the target starts at
different range from the sensor. We also compare it to
the MCAEKF and the CbGMF.
In the simulation, the standard deviations of the
measurements in range and azimuth are σ
r
= 0.2 m
and σ
θ
= 10
−3
rad, respectively. The sampling inter-
val is T = 1 s, and the simulated time interval is 70
s. We choose the power spectral densities, q
x
= q
y
=
10
−3
m
2
/s
3
. The target has the same initial velocity
of [200, 300] m/s in different scenarios and the sensor
always locates the origin.
A two-point differencing method (Bar-Shalom
et al., 2001) employing the unbiased measurement
conversion (Longbin et al., 1998) from polar to Carte-
sian coordinates is used in the initialization of all fil-
ters. The results are obtained from 100 Monte Carlo
runs.
GaussianMixtureMeasurementsforVeryLongRangeTracking
461

0 10 20 30 40 50 60 70
50
100
150
200
250
300
time (s)
RMSE in Position (m)
MCAEKF
CbGMF
GMM−ITS
(a) RMSE in position
0 10 20 30 40 50 60 70
0
0.2
0.4
0.6
0.8
1
1.2
1.4
time (s)
RMSE in Range (m)
MCAEKF
CbGMF
GMM−ITS
(b) RMSE in range
0 10 20 30 40 50 60 70
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
time (s)
NEES
MCAEKF
CbGMF
GMM−ITS
NEES−1
NEES−2
(c) NEES and 99% probability regions
Figure 3: Results from the medium range scenario.
We compare the accuracy of the filters using root
mean square error (RMSE) (Bar-Shalom et al., 2001)
in position and range. The normalized (state) estima-
0 10 20 30 40 50 60 70
0
500
1000
1500
2000
2500
3000
time (s)
RMSE in Position (m)
MCAEKF
CbGMF
GMM−ITS
(a) RMSE in position
0 10 20 30 40 50 60 70
0
1
2
3
4
5
6
7
8
9
10
time (s)
RMSE in Range (m)
MCAEKF
CbGMF
GMM−ITS
(b) RMSE in range
0 10 20 30 40 50 60 70
2
3
4
5
6
7
8
9
time (s)
NEES
MCAEKF
CbGMF
GMM−ITS
NEES−1
NEES−2
(c) NEES and 99% probability regions
Figure 4: Results from the long range scenario.
tion error squared (NEES) (Bar-Shalom et al., 2001)
can be used to determine whether a filter is consistent.
The results are presented in Figures 3-6.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
462
0 10 20 30 40 50 60 70
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
time (s)
RMSE in Position (m)
MCAEKF
CbGMF
GMM−ITS
(a) RMSE in position
0 10 20 30 40 50 60 70
0
2
4
6
8
10
12
14
16
18
time (s)
RMSE in Range (m)
MCAEKF
CbGMF
GMM−ITS
(b) RMSE in range
0 10 20 30 40 50 60 70
2
3
4
5
6
7
8
9
10
11
12
time (s)
NEES
MCAEKF
CbGMF
GMM−ITS
NEES−1
NEES−2
(c) NEES and 99% probability regions
Figure 5: Results from the very long range scenario
In scenario 1, the target is initially located at
[105, 250] km (the medium range). The GMM-ITS
divides the measurement into N = 6 components and
0 10 20 30 40 50 60 70
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
time (s)
RMSE in Position (m)
MCAEKF
CbGMF
GMM−ITS
(a) RMSE in position
0 10 20 30 40 50 60 70
0
5
10
15
20
25
30
time (s)
RMSE in Range (m)
MCAEKF
CbGMF
GMM−ITS
(b) RMSE in range
0 10 20 30 40 50 60 70
2
3
4
5
6
7
8
9
10
11
12
time (s)
NEES
MCAEKF
CbGMF
GMM−ITS
NEES−1
NEES−2
(c) NEES and 99% probability regions
Figure 6: Results from the extremely long range scenario.
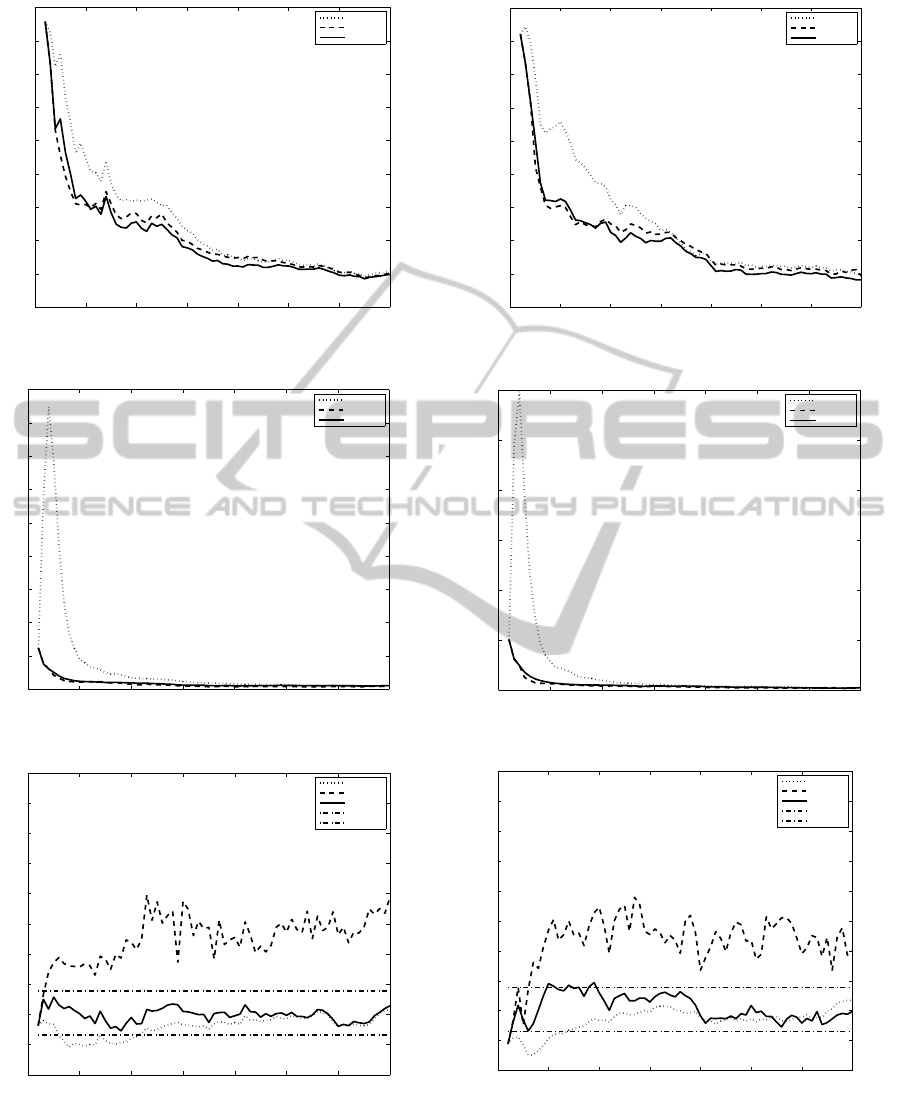
chooses α = 3 at each time k. Figures 3a, 3b and 3c
shows the performance of the MCAEKF, the CbGMF
and the GMM-ITS. These three filters have nearly the
GaussianMixtureMeasurementsforVeryLongRangeTracking
463

same position accuracy (see Figure 3a) and good con-
sistency (see Figure 3c). From Figure 3b, we can see
that both the GMM-ITS and the CbGMF have signifi-
cantly smaller range errors in the early states than the
MCAEKF.
The target starts from [1050,2500] km (the long
range) in scenario 2. In the GMM-ITS, the measure-
ment likelihood is approximated by N = 12 compo-
nents with α = 3. In this scenario, as shownin Figures
4a, 4b and 4c, the GMM-ITS and the CbGMF have
obviously improved accuracy in position and range
over the MCAEKF and do not exhibit loss in range
accuracy in the early stage of filtering. We can clearly
see that the GMM-ITS and the MCAEKF are consis-
tent in Figure 4c; however, in this case, the CbGMF
has a small degradation in consistency (the NEES is
around 5 instead of 4) (Tian and Bar-Shalom, 2014).
In scenario 3 and 4, the target starts much further
away from [4500,2200] km (the very long range) and
[8500,5500] km (the extremely long range), respec-
tively. Obviously, the contact lens issue is much more
of a problem than in scenario 1 and 2. In scenario
3, the parameters of the GMM-ITS are N = 24 and
α = 3.5. In order to guarantee the consistency of the
GMM-ITS, N = 48 and α = 4 are chosen in scenario
4. Figures 5a and 6a show that the GMM-ITS per-
forms better than the CbGMF and the MCAEKF in
the position RMSE. Furthermore, as shown in Figure
5c and Figure 6c, the GMM-ITS and the MCAEKF
are consistent, but the CbGMF is not.
5 CONCLUSIONS
For very long range target tracking, traditional filters
such as the EKF and the UKF are ill-equipped to solve
the contact lens problem. However, the MCAEKF
maintains consistency by using a bigger standard de-
viation of the range measurement. As a result, the
MCAEKF exhibits significant loss in range accuracy
in the early stage of filtering. The CbGMF represents
the distribution of the target state by a dynamic set
of Gaussian mixtures and can avoid the problem the
MCAEKF suffers. However, the CbGMF is consis-
tent only in the small range scenario. In the GMM-
ITS, both the measurement likelihood and the target
state pdf are approximated by a set of Gaussian mix-
tures. As shown in the simulation experiments, the
GMM-ITS is always consistent in different range sce-
narios and has small errors in positon and range. To
best of our knowledge, no other Gaussian mixture ap-
proach thus far guarantees sufficient consistency and
tracking accuracy, which are crucial to filter perfor-
mance.
ACKNOWLEDGEMENTS
This work was supported by Defense Acquisition Pro-
gram Administration and Agency for Defense Devel-
opment, Korea under the contract UD140081CD.
REFERENCES
Bar-Shalom, Y., Li, X.-R., and Kirubarajan, T. (2001). Esti-
mation with Application to Tracking and Navigation.
John Wiley and Sons.
Blackman, S. and Popoli, R. (1999). Design and Analysis
of Modern Tracking Systems. Artech House.
Julier, S. J. and Uhlmann, J. K. (2004). Unscented filtering
and nonlinear estimation. Proceedings of the IEEE,
92(3):401–422.
Longbin, M., Ziaoquan, S., Yiyu, Z., and Bar-Shalom, Y.
(1998). Unbiased converted measurements for track-
ing. IEEE Transactions on Aerospace and Electronic
Systems, 34(3):1023–1027.
Muˇsicki, D. (2009). Bearings only single-sensor tar-
get tracking using gaussian mixtures. Automatica,
45(9):2088–2092.
Muˇsicki, D. and Evans, R. (2006). Measurement gaussian
sum mixture target tracking. In 9th International Con-
ference on Information Fusion, Florence, Italy.
Ristic, B., Arulampalam, S., and Gordon, N. (2004). Be-
yond the Kalman Filter. Artech House.
Singer, R. A., Sea, R., and Housewright, K. B. (1974).
Derivation and evaluation of improved tracking fil-
ters for use in dense multi-target environments. IEEE
Transactions on Information Theory, 20(4):423–432.
Tian, X. and Bar-Shalom, Y. (2009). Coordinate conver-
sion and tracking for very long range radars. IEEE
Transactions on Aerospace and Electronic Systems,
45(3):1073–1088.
Tian, X. and Bar-Shalom, Y. (2014). A consistency-based
gaussian mixture filtering approach for the contact
lens problem. IEEE Transactions on Aerospace and
Electronic Systems, 50(3):1636–1646.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
464
