
A Domain Specific Platform for Engineering Well Founded Measurement
Applications
Florent Bourgeois
1,2
, Philippe Studer
1
, Bernard Thirion
1
and Jean-Marc Perronne
1
1
Universit
´
e de Haute Alsace, MIPS EA 2332, 12 rue des Fr
`
eres Lumi
`
ere, F-68093 Mulhouse, France
2
Actimage GmbH, Hafenstraße 3, 77694 Kehl, Germany
Keywords:
Metrology, Measuring Process, Mobile Measurement Applications, Development Platform.
Abstract:
Mobile platforms, such as smartphones, are now embedding more processing and communication capabilities
than ever. They offer generally a set of standard built-in sensors to measure their surroundings and potentially
increase their knowledge about the environment. Moreover their communication capabilities allow easy access
to external devices and remotely accessible sensing nodes or more general services. Nevertheless, despite their
obvious ability to provide rich data visualization, only a few applications propose using mobile platforms as
a flexible and user-friendly measuring process assistant. This paper proposes the description of a system able
to model and design mobile and well-founded domain specific measuring processes, supporting physical as
well as non-physical quantities. The soundness of the application and its conformance to metrology rules is
ensured through the use of quantities semantic, dimensional analysis and adherence to the representational
theory of measurement. The conformance verification gives to non-metrology specialists the ability to design
and configure rigorous mobile applications dedicated to assist an end-user in its usual and specific measuring
needs and habits, while limiting erroneous results due to manipulation errors.
1 INTRODUCTION
In recent years, we have seen the global widespread
use of powerful sensors embedded into smartphones
(Daponte et al., 2013). Sensors increase our capabil-
ity to measure things, which is an unbelievable oppor-
tunity for craftsmen who need to know their work sur-
roundings. Moreover, sensors are useful tools in ev-
eryday activities such as cooking, health care, sport or
interior design. This leads to the recurring use of mea-
suring operations and vocabulary. They are so useful
and widespread in popular culture that anyone is able
to define a way to measure a table length, the weight
of a person or the temperature of a room. Further-
more, people naturally use units in order to commu-
nicate obtained values.
Nevertheless, accidents such as the loss of the
Mars Climate Orbiter (Stephenson et al., 1999) re-
minds us that errors in measurements can lead to
disastrous situations and are quite difficult to detect.
Even though this example is critical, it shows that
even experts are subject to make mistakes, which
means that non-specialists are, a fortiori, likely to ob-
tain wrong results. Such wrong results can waste time
and affect production for craftsmen which may have
important economic repercussions.
The newly built-in mobile sensors, such as ac-
celerometers, gyroscope, barometer, compass, GPS,
etc. are not always straightly compatible with users’
needs. Indeed, they present values that were not ac-
cessible to users a few years ago. For example, if a
user wants to know about the tilt of a surface, he might
try to use his mobile gyroscope. But this requires pre-
cise knowledge of what the sensor returned values are
and how to evaluate a tilt indication from these values.
This kind of problem can be alleviated by using a do-
mains specific measuring assistant. As an illustration,
a typical application is described.
The application proposes to the user to estimate
the production of a solar panels installation using lo-
calization data to define the positions of the panels.
The measuring process requests the user to place the
mobile device on the roof. Using the embedded sen-
sors, the application gathers data on the geolocation,
the orientation and the inclination of the device. With
such data the application knows the solar panels the-
oretical position. Then the application is able to esti-
mate quantities such as the weather condition of the
location and mean daylight time. If the user then in-
puts the surface and the kind of solar panels, it is pos-
309
Bourgeois F., Studer P., Thirion B. and Perronne J..
A Domain Specific Platform for Engineering Well Founded Measurement Applications.
DOI: 10.5220/0005512103090318
In Proceedings of the 10th International Conference on Software Engineering and Applications (ICSOFT-EA-2015), pages 309-318
ISBN: 978-989-758-114-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

sible estimate their production of electricity.
It might also be interesting to extend this scenario
by adding the ability to consider the roof nature, the
weight of the solar panels, the kind of roof covering
products. Such data might be interesting to estimate if
the roof can bear the installation. Also, most of solar
panels owners are looking for electricity cost savings.
It is then possible to estimate the money saved thanks
to the installation. Furthermore since the installation
comes with a price, it would be possible to estimate
the time required to cover the installation price with
savings.
This application makes use of physical and non
physical quantities altogether in order to produce its
result. These quantities belong to different measure-
ment scales (c.f. Section 2). The complexity of the
calculation is not unbearable, but it is subject to mis-
takes and wrong calculations when using such differ-
ent quantity kinds.
Metrology, the science of measurement, defines
rules to follow during measuring. Thanks to these
rules it is possible to avoid erroneous results due to
manipulation errors. Basics of this science are known
by everyone but advanced rules are only accessible
to specialists. Such a situation is not satisfactory con-
sidering the growing number of measuring tools users
can access and the risk of increased measurement er-
rors. The mentioned errors encompass the absence
of references leading to conversions errors, the lack
of knowledge in the sensors characteristics, process
steps omission, mishandled operations on quantities
and false decisions based on poor quality results.
Based on an interdisciplinary approach combining
quantities semantic, dimensional analysis and repre-
sentative theory of measurement, as well as software
modeling, software engineering and software archi-
tectures, this paper proposes a model-driven approach
for building well-founded mobile measurement ap-
plications. First an architect has to model a domain
specific measuring process. The obtained models are
then validated for coherence with real world accord-
ing to the process inputs semantic specified by the em-
ployed sensor models. Following the use of model-
driven principles and tools allows for creating an ap-
plication that conforms to the validated models. The
resulting application supports the end-user when he
tries to apply the measuring process while ensuring
more confidence in the produced results.
This paper presents related works by presenting
the metrology rules deduced from the literature and
the various development existing in the domain. Af-
terward, it shows the requirement analysis which lead
then to our design and prototype. Last, the paper con-
cludes by presenting future developments.
2 RELATED WORK
2.1 Metrology: Foundations, Standards
Metrology is an active research domain covering all
of the sciences. Several foundational frameworks ex-
ist to model the domain. Some based on mathemat-
ics such as (Khan and Finkelstein, 2013), others on
algebra like (Domotor and Batitsky, 2010) or some
on the Representational Theory of Measurement in-
cluding (Mari, 2013). Within this section we present
the standard of metrology used to represent observa-
tions. Then we point out that quantities are not only
numbers and present the importance of constraints on
their manipulations. And last we explain the terms of
measuring process and uncertainty.
2.1.1 Measurement Standards
Metrology is the science used to communicate about
the surrounding world in terms of measurable objects
properties. Being multidisciplinary, it is used in any
physical science (i.e. mechanics, physics) but also in
psychological sciences (i.e. IQ, pain). International
standards have been created lately to ease this pro-
cess. The Joint Committee for Guides in Metrology
(JCGM) published a unified vocabulary in (OIML
et al., 2012), the International Vocabulary of Metrol-
ogy (VIM), which defines itself as a common ref-
erence to anyone looking to perform measurements.
The VIM defines a quantity as the property of a phe-
nomenon, body, or substance, where the property has
a magnitude and a reference. The most usual kind of
reference is a measurement unit. Quantities are clas-
sified by quantity kinds.
Physical properties, represented by quantity kinds
(e.g. length, time, speed), are associated one to
another with physical laws. Hence the quantity kinds
are organized using systems of quantities based on a
set of base quantities and derived quantities, which
result from algebraically combining quantities. The
most recognized system is the International System
of Quantities (ISQ) described by (ISO, 2009). This
system presents the advantage that any quantity kind
can be represented using a combination of seven base
quantities through multiplication and division oper-
ations. The SI has been created upon this standard.
(BIPM, 2006) describes the International System of
units (SI) which presents one specific unit for each
quantity kind. Other quantities are represented as a
combination of these base units. Also some of the
derived units are called by a special name, whose pur-
pose is to ease the notation of complex derived units.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
310

The reader is referred to the NIST diagrams
1
for an overview of the ISQ and SI. Ultimately only
SI units should be used to communicate but non-SI
units are still used widely. Therefore, even though it
is possible to convert from one unit to another, this
can lead to misunderstanding when quantities are
communicated. (Astarita, 1997) shows that using a
system of quantities allows us to use dimensional
analysis. This method is able to check quantity
equation homogeneity, to find equation simplification
and also to determine the appropriate scaling of a
quantity.
2.1.2 Representational Theory of Measurement
Nowadays it is natural to use quantity values associ-
ated with SI units to describe objects. This quanti-
tative representation is so widespread that the non-
expert tends to think that he simply is manipulat-
ing numbers. However, on a more foundational per-
spective, the representational theory of measurement
(RTM), initiated by Stevens (Stevens, 1946), explains
the relations between the empirical observation of
events and their formal representation and manipu-
lation as quantities. (Krantz et al., 1971) explains
how to extract from the different empirical relations
on object properties a system of operations that can
be safely applied on the formal representation and are
still relevant in the real world.
Since several quantity kinds have the same mathe-
matical structure, the notion of scales is introduced. A
scale represents a given set of permissible operations
for a quantity as illustrated in table 1. (Hand, 1996)
denotes that the scale attributed to a given observa-
tion result depends on the knowledge of the property
analyzed and the value assignment method. Such a
knowledge enables us to detect when common opera-
tions cannot be applied (e.g. mean of values).
It is important to note that RTM is not only re-
served for the measurement of physical quantities,
but also for more subjective measurements of quan-
tities, such as those performed in psychosocial sci-
ences. This implies quantities that are not only repre-
sented by numbers but also by symbols because of the
possibility to use nominal scales in order to categorize
various properties (i.e. color, gender).
2.1.3 Measuring Process and Uncertainty
Although several processes can define a given object
property, some are more convenient than others and
can have an impact on uncertainties.
1
http://physics.nist.gov/cuu/Units/SIdiagram2.html
The definition of a domain specific measuring pro-
cess is a difficult task. Indeed, the process has to de-
fine any interacting parts to obtain the result. (Ellison
et al., 2000) explains that it is possible to ease this task
using a cause and effect diagram with input branches
for the method, the operator, the instruments, the en-
vironment and the subject under consideration.
Defining the right measuring process also implies
an uncertainty estimation process. This uncertainty
results from instruments precision limitations and the
combination of the different errors induced by the
measurement process (Farrance and Frenkel, 2012).
The Uncertainty of Measurement Guide (OIML et al.,
2008), or GUM, is the international reference con-
cerning uncertainty estimation. It presents the vocab-
ulary and the methods for handling uncertainty.
2.2 Metrology in Computer Science
In this section we present an overview of the develop-
ments that integrate metrology and computer science.
2.2.1 Representing Observations
The encoding of metrological concepts in software
occurs at different conceptual levels : ontological,
modeling, units or dimensions encoding, etc. (Foster,
2013) discusses the lack of a standard formalization
of the concepts, which brought an environment with
no cohesion, every system using measurements being
based on its own implementation or encoding.
(Fowler, 1997) specifies a model for observation
and measurement. This model proposes considering
categories which are defined as a range of values for
a given quantity. An observation holds a protocol
to perform the measurement. Hence with the cate-
gories and the protocol it is possible to model any
measurement of physical and non physical quantities.
Derived from this model, the Open Geospatial Con-
sortium proposed (ISO, 2011), which describes Ob-
servations and Measurements (O&M). This is a stan-
dard for modeling quantities in geographic informa-
tion systems. It is able to represent measurements of
any domain as long as the process description is pro-
vided. Physical quantities are represented by a num-
ber and a unit of measurement encoded as identifiers
recognized by the system. An XML schema of O&M
is provided by the Open Geospatial Consortium.
On a more ontological level, quantities represent
knowledge about a physical object. This is made
through the use of a standardized vocabulary, which
ontologies are used for. So it is natural to find on-
tologies that represent quantities and units. (Hodgson
et al., 2013) presents QUDT ontologies which rep-
resent any system of quantities associated with its di-
ADomainSpecificPlatformforEngineeringWellFoundedMeasurementApplications
311

Table 1: Representation of the four basic measurement scales (inspired from (Stevens, 1946)).
Scale Elements relation Acceptable Operations Example
Nominal Categorized = (is a) Gender, Colors
Ordinal Ordered =, < IQ, school grades
Interval Equidistant magnitude =, <, + Temperatures (
◦
F,
◦
C)
Ratio Equidistant magnitude and Absolute zero =, <, +, ∗ Weight, Length
mensions and system of units. While QUDT proposes
a base reusable in any software to handle units and
quantities, it does not resolve issues such as the units
presenting the same dimension. Such issues appear
typically with mechanical torque and energy having
the same dimension but different units and also with
dimensionless units as angles and counts.
(Rijgersberg et al., 2011) and (Rijgersberg, 2013)
present OM, which is “an Ontology of units of Mea-
sure and related concepts”. They also compare OM to
related existing ontologies. It appears that OM tends
to propose more capabilities than other ontologies
thanks to its ability to operate dimensional analysis.
Indeed, to propose a dimensional analysis that is more
accurate and avoids conflicts, OM proposes defining
applications domains for quantities and units. Know-
ing the domain of an end-user, it is possible to reduce
unit conflicts. However and according to (Rijgers-
berg, 2013) their interpretation of the term scale is
different from that of RTM. Thus it would not be pos-
sible to represent non physical measurements. OM
proposes web services whose purposes are to share
measurements data in the semantic web.
The Unified Code For Units of Measure (UCUM),
presented by (Schadow and McDonald, 2009), is a
coding system intended to include all units of mea-
sures being contemporarily used. The document
presents a language capable of expressing any unit.
Prefixed units can be created using units and prefixes.
Also, UCUM has been able to define a language with
no conflict as long as the non-SI units do not use SI
prefixes. Consequently it is a simple and efficient way
to represent quantities as a structure composed of a
number and a UCUM coded unit.
(Cmelik and Gehani, 1988) describe a way to use
preprocessing in order to write source code embeding
quantities and units. The direct usage of such entities
in the source code makes comprehension easier when
modeling physical properties and recall that the data
manipulated are more than simple numbers. One unit
is defined as the base unit for each quantity. In order
to accept different units, it is possible to define a new
one by selecting the unit it is based on and a conver-
sion factor to this unit. Thanks to this operation the
user can code by using the usual units and the pre-
processor will do the conversion. Libraries based on
this idea such as (Schnabel and Watanebe, 2013) are
still used. While useful, such method has no impact
beyond the code level.
2.2.2 Quantities Processing
Most implementations essentially propose encoding
the observations. We now focus on systems able to
manipulate the quantities.
(Rijgersberg, 2013) shows that OM is able to han-
dle dimensional analysis. When an equation based on
quantities is proposed, a web service is able to de-
termine if the equation is dimensionally correct and
if the units used are coherent. Their framework pro-
poses an abstraction of mathematical operations and a
workflow that has to be processed to achieve the cal-
culation. Indeed, in calculations performed by mathe-
matical tools such as MATLAB, the semantic data has
to be removed and treated separately from the numer-
ical data in order to generate separate numerical and
semantic results that are then combined. The units of
the results are assigned using dimensional analysis.
(Botts and Robin, 2007), who use O&M as a basis
to express quantities, is a framework dedicated to the
representation of processes implying the transforma-
tion of input stimuli to output measurement quanti-
ties. Initially aimed at processing sensors data, O&M
is also able to represent operations on quantities. In-
deed it is possible to consider such operations as pro-
cesses which stimuli and output are quantities. Yet,
the framework is not able to deduce the resulting
quantity kind from the input quantities or to determine
whether an operation is possible. Indeed the O&M
framework does not provide implementation for the
different features of interest or for the units. So its ca-
pabilities of mathematical operations are bound to the
user knowledge and the implementations used.
The same limitations are found in most of the
tools. Indeed, since the frameworks to represent ob-
servations are limited to physical quantities most of
the time, they rarely consider the Representational
Theory of Measurement. Consequently the opera-
tions they accept to perform are limited to additions
of quantities of the same quantity kind, or multiplica-
tion and division of quantities, such as (Schnabel and
Watanebe, 2013) proposes.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
312

2.2.3 Uncertainty Calculation
Uncertainty calculation is of particular importance for
measurement. Some frameworks propose implemen-
tations of such calculations.
(Hall, 2006) proposes computing the measuring
process output values and uncertainties from the dif-
ferent inputs. The measuring process is built as a
set of interconnected components which represent the
different operations performed. The components im-
plement the uncertainty propagation law and recur-
sively request the uncertainty value of their inputs
from the previous components.
The OpenTURNS framework (EDF et al., 2013)
implements an uncertainty propagation methodology.
It requires a description of the measuring process as
an equation. Knowing this equation, and the values of
the inputs, OpenTURNS is able to compute the out-
puts uncertainty values of any measuring process.
2.2.4 Workflow
Being both the source of errors and the list of activi-
ties, leading to the measurement result, the measuring
process is of first interest. Frameworks able to model
a measuring process are presented here.
Simple activities such as using sensors and mathe-
matical operations on quantities are described as pro-
cesses by (Botts and Robin, 2007). Moreover, their
model proposes process chains which are composite
processes able to sequence several simples processes,
leading to complete measuring processes.
Measuring processes, being simply the applica-
tion of observations and calculations activities con-
strained by a specific order, present the same charac-
teristics as any kind of workflow. The essential dif-
ference is the format of the inputs and outputs which
represent quantities. (WFMC, 1999) describes work-
flows as the automation of a business process pre-
senting several activities, processing any kind of data
and connected through transitions. Such a standard
description may be used to model a measuring pro-
cess, considering that an activity is the production of a
quantity through the use of a sensor or a mathematical
operation. A workflow transition condition might be
enabled by the presence of a quantity resulting from
an upstream activity. But it might also be enabled by
a user action, such as turning on a sensor.
3 REQUIREMENTS ANALYSIS
The previous section presented several frameworks
that aim to implement metrology concepts and rules.
Although a lot of works exist, we did not find any
solution able to model and design a mobile applica-
tion which assists an end-user during his own mea-
suring process and asserts that the application model
is coherent with the rules of metrology. This section
adopts a stakeholders point of view to present the re-
quirements analysis for a development platform that
a software architect can use in order to create such a
domain specific measurement application.
3.1 Developing Organisation
As a developing organisation, the industrial partner of
this project aims to propose a family of applications
dedicated to assist craftsmen during their daily work.
The application described in the introduction is one
of them, other examples are applications dedicated to
the estimation of room’s covering costs and assistance
of interior design. The production of such a family
of applications sharing similar properties will be sup-
ported by a model-driven development approach. In
this approach, a platform architect has to engineer do-
main specific measurement platforms and measure-
ment processes based on the description of end-user
domains.
3.2 End-users
End-users think with their specific business domain
vocabulary in mind while the architect configuring an
application manipulates platform descriptions as well
as metrology concepts. A main requirement is to pro-
pose tools to reduce this semantic gap.
A specific measuring process model must be built
according to the description of a process an end-user
can formulate. This description yields knowledge
about the specific hardware and the measuring and
visualization instruments the end-user intends to use.
In addition to the prescription of quantities and units
for the process inputs and outputs, the end-user might
define uncertainties with maximum ranges. Thus, the
platform has to be able to compute the uncertainties
implied by the measuring process and propose to de-
fine the inputs estimated worst cases uncertainties de-
rived from the end-user instruments and outputs un-
certainties.
To resume, in order to be valid the application
must :
• Produce the quantities the end-user requires.
• Be based on methods and specific instruments
handled by the end-user.
• Produce a result with an uncertainty range con-
form to the end-users requirements.
ADomainSpecificPlatformforEngineeringWellFoundedMeasurementApplications
313

Such a measuring process assistant becomes re-
ally pertinent when it is supported by the computing
capabilities of mobile devices which would be able to
accompany the end-user during his daily work. It is a
further requirement to be able to generate applications
targeting specific mobile devices.
3.3 Metrology Specialist
The different required metrology concepts are : repre-
sentations of observable attributes of objects, dimen-
sional analysis, uncertainty evaluation and measure-
ment scales brought by the Representational Theory
of Measurement. Indeed, the ability to handle non-
physical quantities is needed by the typical intended
end-user domains (e.g. type of roof tile). Since nei-
ther the end-users nor the architect are metrology spe-
cialists the purpose is to propose a platform which
can be used by these non specialists. So, the plat-
form must be able to deduce from a formal repre-
sentation of quantities the performable operations and
their impact in order to propose to the end-users a
verified result. Moreover, the model has to embed
enough knowledge about the empirical relations be-
tween properties manifested in the real world and
quantity semantics in order to deduce the correctness
of the operations performed on the values resulting
from the measurements. The term quantity semantics
encompasses any metadata (i.e. numbers, symbols,
scales, etc.) which allows to represent an information
based on the concepts and rules of metrology.
Thanks to the quantity semantics, a model check-
ing tool dedicated to metrology will be able to pro-
cess the whole model and assert its coherence. To
achieve this assertion, the model checker must be able
to interpret the quantities manipulation functions and
proceed dimensional analysis as well as restrictions
based on the measurement scales. To enhance usabil-
ity by non-specialists, each quantity has to be asso-
ciated to a default measurement scale. Indeed, the
different quantities brought in the process are consid-
ered captured by a real or virtual sensor able to di-
rectly measure the quantity. This naturally associate
a measured quantity to a given scale. Moreover, each
specific sensor description may contain an associated
measurement scale.
Finally, any observable property might ultimately
become a quantity. It is therefore necessary for the
platform to be open and give the possibility to a spe-
cialist to define new importable quantities.
3.4 Architect
The role of the architect is to design a domain spe-
cific measurement platform (c.f. figure 1). This role
implies two complementary activities. First, during a
platform engineering activity he configures the plat-
form, based on an end-user domain description. Sen-
sor specific models and formal representations are
used to reduce the gap between end-user and architect
language levels. Then, using a configured platform,
the architect realizes a process engineering activity.
During this activity he models and verifies the domain
specific measuring processes based on an end-user de-
scription. The description provided by the end-user
contains knowledge about the end-user usual measur-
ing activities and their sequencing. From this descrip-
tion the architect builds a workflow model of the mea-
suring process. To this end, the platform has to pro-
vide tools to compose workflows. This encompasses
activities requiring the user participation to measure a
quantity, activities applying automatic measurement
operations and sequencing of activities.
Process
engineering
<Activity>
<Role>
Domain Specific
Measurement
Platform
Designer
<Product>
Measuring
process model
realize
in charge of
out
in
Architect
played by
in
Platform
engineering
<Activity>
<Product>
Domain Specific
system configuration
realize
in charge of
out
<Product>
Process
description
<Product>
Sensors
models
<Product>
Target model
inin
in
<Product>
Domain model
in
Figure 1: Architect Activities.
The measuring process model can contain any
kind of function the end-user might need. These func-
tions are classified as :
• Measuring, this implies the use of measuring in-
struments to generate quantity values. These
functions imply the association of quantity se-
mantics to the values.
• Processing, this implies the use of mathematical
operations on the quantity values. These functions
imply the manipulation of the quantities seman-
tics according to the process performed.
• Presenting, this implies the use of specific inter-
faces to display the quantity values. These func-
tions suppress the quantities semantics and con-
vert the results to adequate formats.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
314
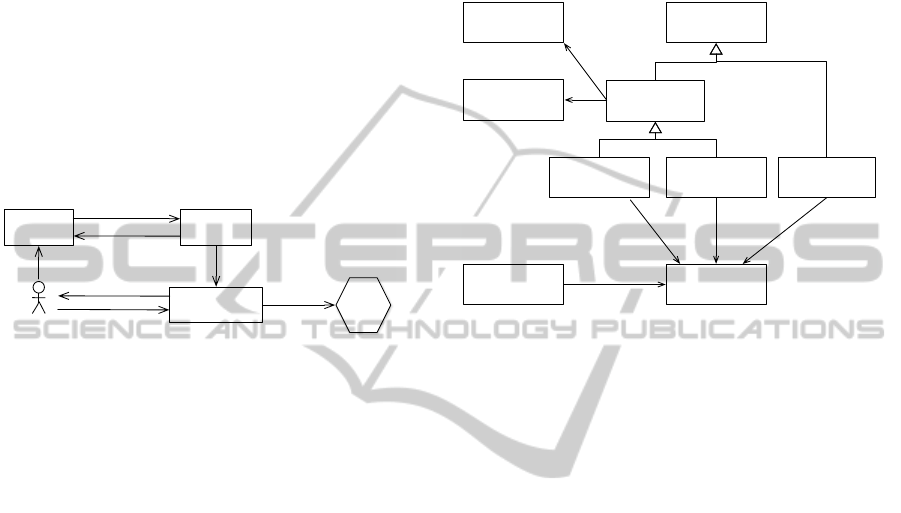
4 DESIGN AND PROTOTYPE
The generation of a mobile application relies on a
suite of interpreted tools following a model driven ap-
proach (c.f. figure 2). Each tool produces a model
which is consumed by the next tool. The three main
tools are a Process Modeler to compose a measuring
process model, sequence activities, edit the associated
displays and define the targeted devices, a Metrol-
ogy Core which verifies the conformance of the pro-
cess model to the metrology rules and a Model Trans-
former which transforms the process model into an
application model that governs the behavior of the
Mobile Embedded Application. The Model Trans-
former also transforms the process model into a for-
mat used to estimate uncertainties.
Error in model
Architect
Model
Transformer
Metrology
Core
Process model
Process
Modeler
Use
Verified model
Uncertainty
Valid model
MEA
Executable
model
Figure 2: Domain Specific Measurement Platform.
4.1 The Process Modeler
The Process Modeler is the tool the architect uses to
generate a process model (called MEASURE model).
This model is the result of the transposition of the
end-user measuring practices in the software domain,
taking into account the measuring devices he owns
and handles. The MEASURE model is composed of
a workflow layer and a measure layer.
The workflow layer, models the sequencing of the
measuring activities. The activities model measur-
ing operations and transitions model quantities eval-
uations. The Process Modeler allows the architect to
produce the workflow by sequencing activities imply-
ing either automatic (i.e. combination of quantities)
or user involved (i.e. use of a sensor to grab a quan-
tity value) metrological operations. To assist the user,
any user involved activity proposes an associated user
interface. Depending on the activity, this interface
presents guidelines, interactions to input values, or
displays of captured data needing a confirmation.
The measure layer models the real operationaliza-
tion of the process activities as found in the presented
application. To easily create new measuring mod-
els or reconfigure existing ones, this layer leverages
on a connectable component model paradigm. Such
paradigm offers combinatory capacities allowing the
architect to re-use models or part of them in order to
propose new behaviors. Figure 3 presents the compo-
nent model. Three main component classes describe
the system functions presented in section 3 and guide
the modeling activity. Indeed, the architect builds
the MEASURE model according to the user descrip-
tion. This description is based on sensors, quantities
manipulations and presentations which are modeled
by classes inheriting respectively from the Measurer,
Processor and Presenter components.
Component
Measurer Presenter Processor
Connector
out in ins
ExternalInterface
Unit
Link
source
sink
outs
Communication
Interface
Figure 3: Components model.
The ExternalInterface components represent in-
puts or outputs. They associate a communication in-
terface with the element meant to capture the mea-
sured value and a unit which specifies the associated
semantic. The Processor components represent alge-
braic manipulation of the quantities.
Sensors and presenters are highly dependent on
the application domain. Indeed, a domain specific
application description may include specialized sen-
sors and presenters. Therefore, the Process Modeler
proposes to extend a basic configuration of the plat-
form with specific sensors and presenters libraries ac-
cording to the needs. Such extensions usually impact
the platform’s three tools. It is likely that the archi-
tect would not be able to perform these extensions.
Then, a metrology specialist might be required to han-
dle their implementation. These extension activities
may typically occur during the early stage of the plat-
form usage. When several developments have been
performed using the platform, the different domain
specific extensions architect might need will likely be
available as imports.
This capacity to extend the platform according to
the specific application domain reduces the semantic
gap between the architect and an end-user. Indeed,
these extensions give to the architect the ability to
build a MEASURE model using the elements and vo-
cabulary of the description furnished by the end-user.
ADomainSpecificPlatformforEngineeringWellFoundedMeasurementApplications
315

4.2 The Metrology Core
Section 2 highlighted that quantities and units add
knowledge to refer the measured values to the ob-
served world. Also, dimensions and scales are con-
cepts able to define if an operation on quantities leads
to a meaningfull result. The Metrology Core is a
model checking tool whose purposes is to use such
concepts to verify the MEASURE model in order to
assert that the quantities generated through the mea-
suring process can be used in order to draw valid con-
clusions on the real world. The Metrology Core en-
codes knowledge in first-order predicate logic based
and uses the Prolog language to reason about that
knowledge.
Metrology concepts are modeled with a set of
clauses and predicates that can be considered as being
at a meta level. These clauses and predicates are then
instantiated to represent and verify a specific MEA-
SURE model. A fundamental principle of the metrol-
ogy core is to convert each quantity kind into a canon-
ical representation. Hence a set of rules has been de-
signed that associate one concept to another :
• a base quantity kind to a base unit ; for example :
aliasedU(mile,length).
• a base quantity kind to a canonical representation
that also allows the treatment of derived units : ?-
simplifyURep(length,Res). unifies with :
Res = [power(length,1)].
• a unit to a measurement scale:
defaultScale(celsius,interval).
The representation of units is a prolog implementation
of (Rijgersberg et al., 2011) class diagram of unit of
measure. The scale of a derived quantity is deduced
from the set of operations leading to it. The measure-
ment scale resulting from a combination of quantities
is the most restrictive scale of the participating quan-
tities scales or the scale implied by the operation it-
self. A MEASURE model is then straightforwardly
transformed into a Prolog model. In fact, each MEA-
SURE model component has a predicate counterpart.
For example, the Measurer and Presenter components
become input and output predicates.
The role of an input predicate is to extract a canon-
ical representation and a measurement scale from the
unit of a Measurer component.
Similarly, the role of an output predicate is to ex-
tract a canonical representation from the unit of a Pre-
senter component. This canonical representation is
then compared by unification with the canonical rep-
resentation of the variable resulting from the predicate
representing the component it is connected to.
The Processor components are associated to alge-
braic operation clauses. These clauses apply dimen-
sional analysis and scale coherence analysis, through
unification, according to the algebraic operation the
components model. If the analysis present no issues,
the result is a variable holding the canonical repre-
sentation and the scale resulting from the operation
application.
Listing 1 shows an excerpt of prolog generated
by the Metrology core on a simple solar panel price
calculation process illustrated by figure 4. The uni-
fication returns true meaning that the process model
does not present any issue considering the dimen-
sional analysis and the measuring scales coherence.
This example uses on purpose different units such as
mile, meter, are, euro, dollar to show that the unifica-
tion is done as long as the units are convertibles from
one to another.
Area
product
textIn (mile)
I_L1
textIn (metre)
I_L2
textDisp
(squareMetre)
Out_Area
Price
product
textIn
(euro/are)
I_PP
textDisp
(dollar)
Out_Price
Figure 4: Solar panel price MEASURE model.
Listing 1: Solar panel price process verification.
?- input(mile,I_L1),
input(metre,I_L2),
input(unitQuotient(euro,are),I_PP),
operation(multiplication,I_L1,I_L2,Area),
output(Area, squareMetre),
operation(multiplication,Area,I_PP,Price),
output(Price,dollar).
Our Metrology Core is not limited to physical
quantities, as listing 1 suggests it by using money
quantities. As long as a base quantity is associated to
the units and a scale is associated to the base quantity,
it is possible to use all types of quantities.
As mentioned in the Process Modeler description,
it is possible to import domain specific extensions to
the platform. Such extensions are handled through the
prolog consult mechanism.
4.3 The Model Transformer
To propose a process uncertainties estimation during
the process validation phase, the Model Transformer
translates the measuring process to the OpenTURNS
framework (EDF et al., 2013) and let this framework
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
316

evaluate the uncertainties. This solution requires con-
sidering the on-line adaptation of the measuring pro-
cess. Indeed, applications are able to consider their
surrounding using sensor values, it is then possible to
generate a process which considers the surrounding
state such as the luminosity, the temperature or the
end-user experience with the application to adapt the
activities sequencing. Such on-line adaptation implies
that the uncertainty estimation process has to consider
all the possible measuring sequences, but highly im-
proves the resulting quality due to flexibility and con-
text aware usage. The Model Transformer deduces
from the MEASURE model the possible activities se-
quencing and submits them to the uncertainty estima-
tion.
The Model Transformer also generates the Mo-
bile Embedded Application’s executable components
configuration model (c.f. Section 4.4) if the model’s
uncertainty estimation matches the user needs. Also,
any model created by an architect can be reused in
an other application as is. Indeed, the communica-
tion between the different components being seman-
tically checked quantities, it is possible to exchange
any component by a compliant one. This feature im-
plies modeling modularity and reusability. The con-
struction of applications is then facilitated by pre-
senting complex structures as simple components im-
ported from previous constructions. All the complex-
ity of building the application is hidden in the Model
Transformer.
4.4 The Mobile Embedded Application
After building and verification of MEASURE mod-
els, the next step concerns the generation of specific
mobile embedded applications.
A Mobile Embedded Application instantiates and
executes a MEASURE model. Since the MEASURE
model is built on a component model, the application
runtime is also built on the same paradigm. Such
choice presents two advantages. First keeping the
same paradigm will ease the transformation between
the MEASURE model and the application descrip-
tion. Second, in later evolutions of the application
it might be possible to embed the Process Modeler in
the final application, enabling an experimented user
to modify the process it is performing considering not
forecasted situations. The modifications on the model
could then be added dynamically to an application.
In order to propose such capabilities, we defined
the MEASURE model executable counterparts as
connectable components activated by a synchronous
model of computation. The application proposes
three main elements. A process builder which con-
nects and configures the components handling the
measuring process the user will follow. A process
executer which is able to sequence the components
of the process enabling the user to perform its mea-
suring process. A components library which con-
tains the MEASURE model executable counterparts
defined for the specific mobile platform the applica-
tion is installed on.
Internally all operations rely on a canonical repre-
sentation of units. Hence conversions only happens at
the inputs and outputs. Each Measurer or Presenter
component is associated to a specific component han-
dling the interaction with sensor or display and with a
component handling the conversions between the re-
ceived or wanted quantity unit
We made a prototype implementation using Ob-
jective C to target iOS devices. Currently it is possible
to generate the component configuration from a de-
scription based on the application network model and
to execute this network. We implemented the iPhone
5 embedded gyroscope, a bluetooth communicating
laser rangefinder and textual input as sensors, simple
math operations as processes and text presenter.
In this section we highlighted that designing a Do-
main Specific Measurement Platform able to generate
an application to assist an end-user during its mea-
surement activities based on a verified measuring pro-
cess requires combining several technologies. A way
to tackle the induced complexity is to rely on a model
driven approach.
5 CONCLUSION, FUTURE WORK
This paper introduced that non-metrology specialists
may have access to more and more embedded sen-
sors and measuring tools. This can lead to erroneous
deductions in a measurement scenario. These errors
encompass conversions errors, communication issues,
sensors misuse, process steps omission, mishandled
operations on quantities and false decisions based on
poor quality results.
The importance of metrology concepts in measur-
ing activities is highlighted and a general framework
to reduce the mentioned errors occurrences is de-
duced from the literature. It appears that even though
metrology is an active domain of research, metrol-
ogy sensitive software frameworks do not cover all
the concepts mentioned in the design of well founded
measuring assistant applications.
An analysis, using a stakeholders point of view,
showed the requirements such a system has to ful-
fill. To try to integrate the various implied aspects,
a model driven approach was used.
ADomainSpecificPlatformforEngineeringWellFoundedMeasurementApplications
317

Following requirements analysis, a software ar-
chitecture based on three distinct tools and a plat-
form embedded application was presented. Each tool
is a response to the presented requirements. A Pro-
cess Modeler enables an architect to model an end-
user process. Proposing importable sensors and do-
main specific vocabulary, it indexes the communica-
tion and sensors issues. A Metrology Core, based
on dimensional analysis and measurement scales ver-
ification asserts that the measuring process presents
no mishandled operations on quantities. A Model
Transformer translates the process model to the Open-
TURNS framework to estimate results uncertainties.
This tool also transforms the process model into an
executable model consumed by a Mobile Embedded
Application.
Based on this architectures and a model-driven ap-
proach the paper also presented a functional proto-
type using executable connectable components and a
Metrology Core implemented in Prolog.
Further work consist in strengthening the meta-
models of the process model and the model consumed
by the embedded application to further automatize the
transformations. Open issues include the analysis of
the impact and the implementation of the workflow
layers in each of the tools presented, process exten-
sions using more elaborated operations (e.g. statis-
tics) and implication of targeted mobile platforms in
the process modeling.
REFERENCES
Astarita, G. (1997). Dimensional analysis, scaling, and or-
ders of magnitude. Chemical Engineering Science,
52(24):4681 – 4698.
BIPM (2006). SI brochure, 8th edition - the international
system of units (SI).
Botts, M. and Robin, A. (2007). OpenGIS sensor model
language (SensorML) implementation specification.
OpenGIS Implementation Specification OGC 07–000.
Cmelik, R. F. and Gehani, N. H. (1988). Dimensional anal-
ysis with c++. Software, IEEE, 5(3):21–27.
Daponte, P., Vito, L. D., Picariello, F., and Riccio, M.
(2013). State of the art and future developments of
measurement applications on smartphones. Measure-
ment, 46(9):3291 – 3307.
Domotor, Z. and Batitsky, V. (2010). An algebraic–analytic
framework for measurement theory. Measurement,
43(9):1142 – 1164.
EDF, EADS, and PhiMeca (2013). Reference guide Open-
TURNS version 1.1.
Ellison, S. L. R., Rosslein, M., Williams, A., et al. (2000).
Quantifying uncertainty in analytical measurement. In
Eurachem/CITAC Guide. Eurachem.
Farrance, I. and Frenkel, R. (2012). Uncertainty of mea-
surement: A review of the rules for calculating uncer-
tainty components through functional relationships.
The Clinical Biochemist Reviews, 33(2):49–75.
Foster, M. P. (2013). Quantities, units and computing. Com-
puter Standards & Interfaces, 35(5):529 – 535.
Fowler, M. (1997). Analysis patterns: reusable object mod-
els. Addison Wesley Professional.
Hall, B. D. (2006). Component interfaces that support mea-
surement uncertainty. Computer Standards & Inter-
faces, 28(3):306 – 310.
Hand, D. J. (1996). Statistics and the theory of measure-
ment. Journal of the Royal Statistical Society. Series
A (Statistics in Society), 159(3):pp. 445–492.
Hodgson, R., Keller, P. J., Hodges, J., and Spivak, J. (2013).
QUDT - quantities, units, dimensions and types.
ISO (2009). Iso 80000-1:2009 quantities and units – part 1:
General. International Standards Organization.
ISO (2011). ISO 19156:2011 geographic information –
observations and measurements. International Stan-
dards Organization.
Khan, S. and Finkelstein, L. (2013). Mathematical mod-
elling in the analysis and design of hard and soft mea-
surement systems. Measurement, 46(8):2936 – 2941.
Krantz, D., Luce, D., Suppes, P., and Tversky, A. (1971).
Foundations of Measurement, Vol. I: Additive and
Polynomial Representations. NY Academic Press.
Mari, L. (2013). A quest for the definition of measurement.
Measurement, 46(8):2889 – 2895.
OIML, BIPM, CEI, IFCC, ILAC, ISO, UICPA, and UIPPA
(2008). Evaluation of measurement data - guide to
the expression of uncertainty in measurement - JCGM
100:2008 (GUM) - NF ENV 13005:2009.
OIML, BIPM, CEI, IFCC, ILAC, ISO, UICPA, and UIPPA
(2012). International vocabulary of metrology – ba-
sic and general concepts and associated terms (VIM).
JCGM 200:2012 [ISO/IEC guide 99].
Rijgersberg, H. (2013). Semantic support for quantitative
research. PhD thesis, s.n.], S.l.
Rijgersberg, H., Wigham, M., and Top, J. L. (2011). How
semantics can improve engineering processes: A case
of units of measure and quantities. Advanced Engi-
neering Informatics, 25(2):276 – 287.
Schadow, G. and McDonald, C. J. (2009). The unified code
for units of measure. Regenstrief Institute and UCUM
Organization: Indianapolis, IN, USA.
Schnabel, M. C. and Watanebe, S. (2013). Boost c++ li-
braries boost.units 1.1.0.
Stephenson, A. G., LaPiana, L. S., Mulville, D. R., Rut-
ledge, P. J., Bauer, F. H., Folta, D., Dukeman, G. A.,
Sackheim, R., and Norvig, P. (1999). Mars climate or-
biter mishap investigation board phase I report novem-
ber 10, 1999.
Stevens, S. S. (1946). On the theory of scales of measure-
ment. Science, 103(2684):677–680.
WFMC (1999). Terminology and glossary. Technical Re-
port WFMC-TC-1011, Issue 3.0, Workflow Manage-
ment Coalition.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
318
