Relative Height Estimation using Omnidirectional Images

and a Global Appearance Approach

Yerai Berenguer, Luis Pay

a, Adri

an Peidr

o and Oscar Reinoso

Departamento de Ingenier

ıa de Sistemas y Autom

atica, Universidad Miguel Hern

andez de Elche,

Avda. de la Universidad s/n. 03202, Elche (Alicante), Spain

Keywords:

Height Estimation, Omnidirectional Images, Radon Transform, Computer Vision.

Abstract:

This work presents a height estimation method that uses visual information. This method is based on the

global appearance of the scenes. Every omnidirectional scene is described with a global appearance descriptor

without any other transformation. This approach is tested with our own image database. This database is

generated synthetically based on two different virtual rooms. One of the advantages of generating the images

synthetically is that noise or occlusions can be added to test the robustness of the algorithms. This database

is formed by a set of omnidirectional images captured from different points of these rooms and at different

heights. With these scenes we build the descriptor of each image and we use our method to estimate the

relative height of the robot. The experimental results show the effectiveness and the robustness of the method.

1 INTRODUCTION

When a mobile robot has to do a task in an unknown

environment, it must carry out two fundamental steps.

On one hand, it must create an internal representation

of the unknown environment (map) and on the other

hand it must be able to estimate its position within

the map. The robot uses the information extracted

from the environment by the different sensors that it is

equipped with. This information is compared with the

data stored in the map to estimate the position of the

robot. There are many kinds of sensors that provide

useful information to the robot, such as touch sensors,

encoders, laser or vision sensors.

Vision sensors have properties that make them

very useful in mobile robotics. These sensors provide

a very rich information from the environment and they

have multiple possible conﬁgurations. In this work

we use the omnidirectional conﬁguration. We can ﬁnd

many previous works that use omnidirectional images

in navigation tasks, such as (Winters et al., 2000).

The classic developments in mobile robotics us-

ing visual sensors, are based on the extraction and de-

scription of some landmarks from the scenes. These

landmarks can be either natural or artiﬁcial, such

as SIFT (Scale-Invariant Feature Transform) (Lowe,

1999) and SURF (Speeded-Up Robust Features) (Bay

et al., 2006) descriptors.

More recently some works propose using the

global information of the images to create the de-

scriptors. These techniques have demonstrated to be

a good option to solve the localization and navigation

problems in 2D. (Chang et al., 2010) and (Pay

a et al.,

2010) are two examples of this.

Nowadays, the UAVs (Unmanned Aerial Vehi-

cles) are very popular and versatile platforms that can

do several tasks in the ﬁeld of mobile robotics. Some

researchers have faced previously the problem of lo-

calization with this platform, such as (Mondragon

et al., 2010).

Comparing to previous works, the contribution

of this paper is to extend the use of global descrip-

tors based on omnidirectional images to estimate the

height of the robot. Furthermore we use the omnidi-

rectional images as the vision sensor provides them,

without additional transformations (i.e. we do not

convert them to panoramic images because it would

suppose an additional computational cost, as shown

in (Amor

os et al., 2014)). We only build a global-

appearance descriptor for each omnidirectional im-

age based on the Radon transform. The procedure to

obtain this descriptor is summarized in the following

section.

In this research the UAV does not change its in-

clination with respect to the z axis. It will be able

to estimate the relative height between two different

positions along this axis. The Figure 6 shows the sys-

tem scheme that we use in this work, in this scheme

202

Berenguer Y., Payá L., Peidro A. and Reinoso O..

Relative Height Estimation using Omnidirectional Images and a Global Appearance Approach.

DOI: 10.5220/0005512302020209

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 202-209

ISBN: 978-989-758-123-6

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

we can observe the axes directions, the focus of the

camera (F) and the focus of the mirror (F

The experiments with our method have been car-

ried out with our own synthetic image database. This

database has been created with two synthetic environ-

ments of two different rooms.

The remainder of this paper is structured as fol-

lows. Section 2 introduces the method we use to de-

scribe global appearance, the Radon transform. Sec-

tion 3 presents the algorithm we have designed for

height estimation. Section 4 describes the image

database used in this research. Section 5 presents the

experiments and results. At last section 6 outlines the

conclusions.

2 GLOBAL-APPEARANCE

DESCRIPTORS:

RADON TRANSFORM

Methods based on the global appearance of the scenes

constitute a robust alternative compared with meth-

ods based on landmark extraction. This is because

global appearance descriptors represent the environ-

ment through high level features that can be inter-

preted and handled easily.

This section presents the image descriptor we have

used to describe the scenes. It is based on global ap-

pearance without any segmentation or local landmark

extraction.

When designing a new description method, we

should take into account several features. This de-

scriptor should have a compression effect in the im-

age information. These should be a correspondence

between the distance of two descriptors and the dis-

tance of the two positions where the images were cap-

tured. The computational cost to calculate and com-

pare them should be low, so that this descriptor can be

used in real time. It should provide robustness against

noise, illumination changes, occlusions and position

changes of the objects in the environment. Further-

more it should have information of the orientation the

robot had when it captured the image. In Section 5 we

will check if these features are met.

We make use of the Radon transform which is de-

scribed in (Radon, 1917). Previous research demon-

strate the efﬁcacy of this descriptor in shape descrip-

tion and segmentation such as (Hoang and Tabbone,

2010) and (Hasegawa and Tabbone, 2011).

The Radon transform in 2D consists of the inte-

gral of a 2D function over straight lines (line-integral

projections).

This transform is invertible. The inverse Radon

transform reconstructs an image from its line-integral

projections.

The Radon transform can be deﬁned as:

R { f (x, y)} = λ

(p,φ) =

+∞

−∞

f (x, y)δ(p −

−→

p )dxdy (1)

Where f (x,y) is the function to transform. δ is the

Dirac delta function (δ(x) = 1 when x = 0, and δ(x) =

0 elsewhere). The integration line is speciﬁed by the

radial vector

−→

p that is deﬁned by

−→

p =

−→

p · p where

−→

is a unitary vector in the direction of

−→

p . p is the

−→

module deﬁned by:

p = |

−→

p | (2)

p ≡ αcos φ + βsinφ (3)

The line-integral projections evaluated for each az-

imuth angle, φ, produce a 2D polar function, λ

, that

depends on the radial distance p and the azimuth an-

gle φ.

−→

r is a cluster of points which are perpendicular

−→

p .

The Radon transform calculation of an image

im(x,y) along the line c

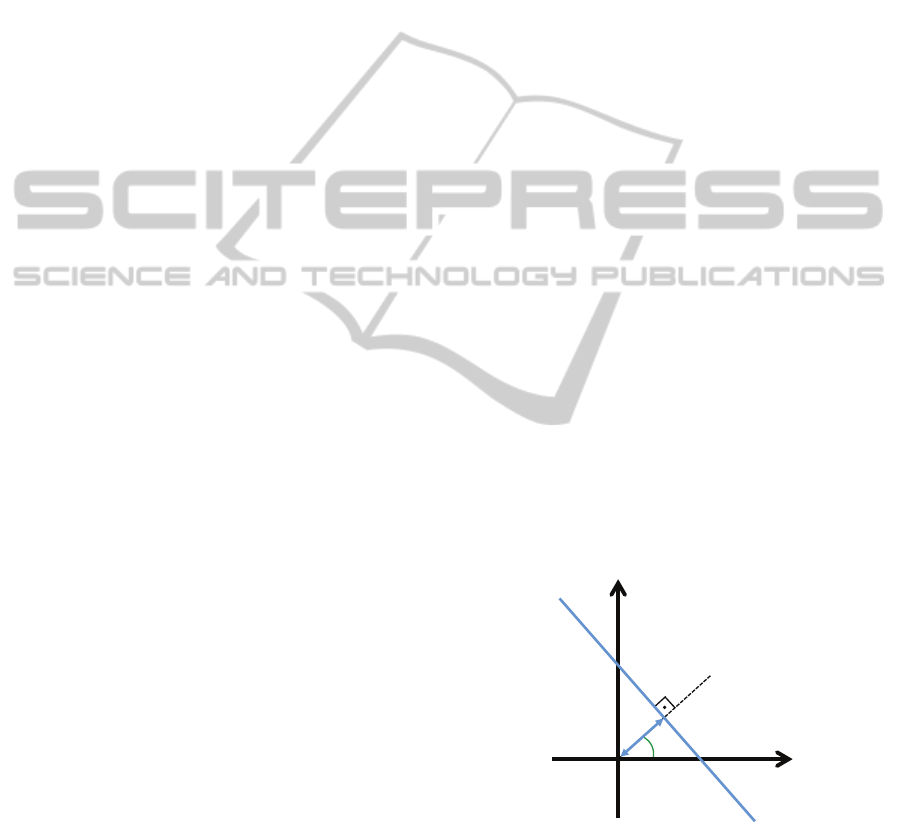
(d, φ) (Figure 1) is given by

the following equivalent expression:

R {im(x,y)} =

im(x

cosφ−y

sinφ+y

cosφ)ds

(4)

where







cosφ sinφ

−sinφ cosφ







(5)

Figure 1: Line parametrization through the origin distance

d and the angle between the normal line and the x axis, φ.

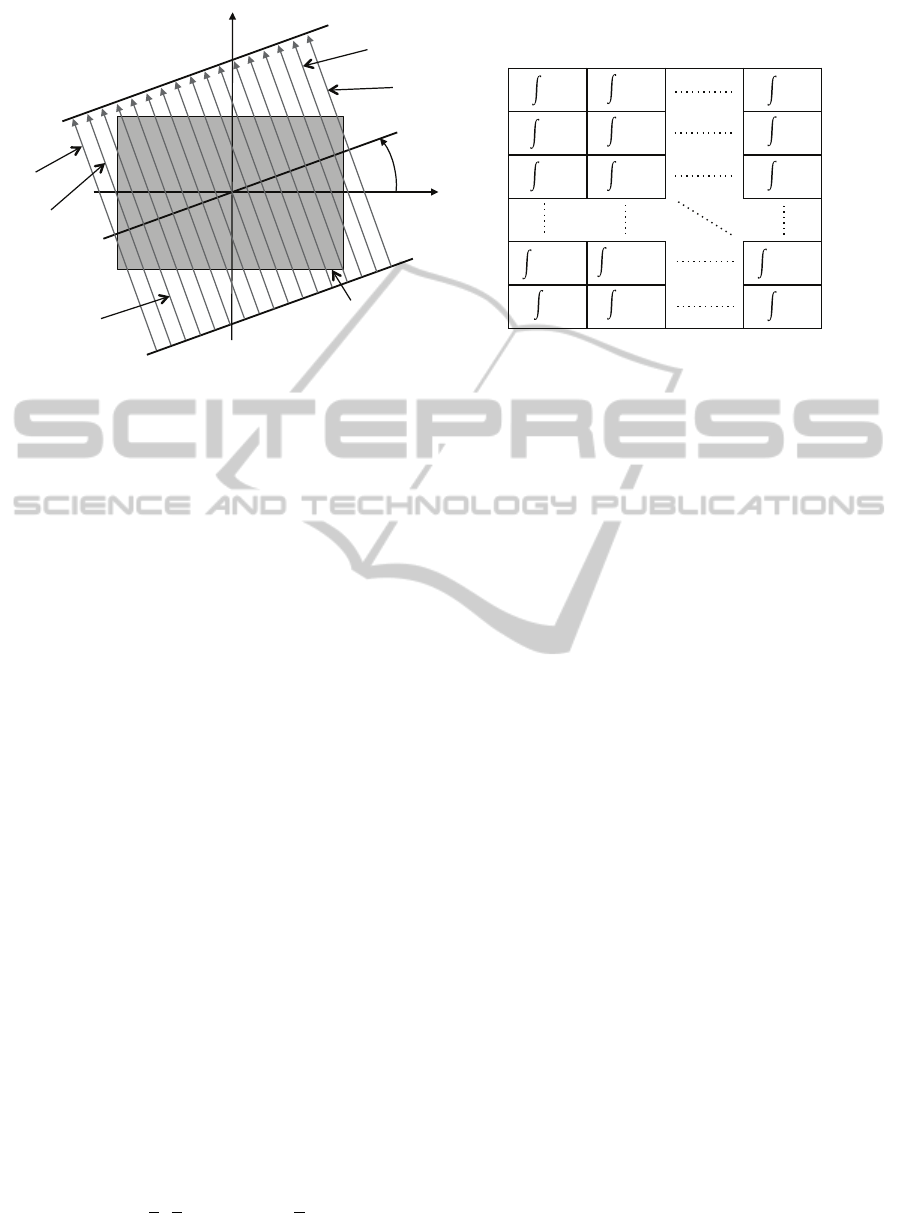
When the Radon transform is applied to images,

it calculates the image projections along the speciﬁed

directions through a cluster of line integrals along par-

allel lines in this direction. The distance between the

parallel lines is usually one pixel. The Figure 2(a)

shows the integration paths to calculate the Radon

RelativeHeightEstimationusingOmnidirectionalImagesandaGlobalAppearanceApproach

203

im(x,y)

()%

(

(a)

φ=1º

φ=359º

φ=0º

!!!

Radon Transform Matrix

(b)

Figure 2: (a) Integration paths to calculate the Radon transform of the image im(x, y) in the φ direction. (b) Radon transform

matrix of the image im(x,y).

transform of an image in the φ direction, and the Fig-

ure 2(b) shows the construction process of the Radon

transform.

The Figure 3 a sample black and white image, on

the left, and its Radon transform, on the right. Fur-

thermore it shows graphically the process to calculate

the Radon transform.

2.1 Radon Transform Properties

The Radon transform has several properties that make

it useful in localization tasks using images. These

properties are the following:

• Linearity: The Radon transform has the linear-

ity property as the integration operation is a linear

function of the integrand:

R {α f + βg} = αR { f } + βR {g} (6)

• Shift: The Radon transform is a variant operation

to translation. Translation of the two-dimensional

function, by a vector

−→

= (x

), has the trans-

lation effect on each projection, this translation is

given by a distance

−→

r · (cos φ,sin φ).

• Rotation: If the image is rotated an angle φ

implies a shift φ

of the Radon transform along

the variable φ. (columns shift).

• Scaling: A scaling of f by a factor b implies a

scaling of the d coordinate and amplitude by a fac-

tor b, and implies a scaling of the Radon transform

by a factor 1/b.



o

= |b|λ



,φ



(7)

3 HEIGHT ESTIMATION

The Radon transform has been used extensively in

medical imaging applications and in shape descrip-

tion in scenes. However we have not found any pre-

vious application to robot localization and height es-

timation. In this section, we present a method based

on the Radon transform to obtain a topological height

estimator. The method provides information of the

direction and the magnitude of the vertical displace-

ment of the robot using only omnidirectional images

captured by a camera mounted on the robot.

The method compares an image captured at a de-

terminate height with another image captured at an-

other height. As a result, the relative height between

both images must be estimated.

3.1 Compression-expansion of the

Radon Transform

The key of the method resides in the differences be-

tween the Radon transform of two scenes captured al

different heights. If the vertical displacement is up-

wards, then the objects in the omnidirectional scene

tend to move towards the center of the image. This

produces that the information in the columns of the

Radon transform move towards the center row. And

vice-versa, if the displacement is downwards, the in-

formation in the columns moves outwards the center

row. This effect is related to scaling property of the

Radon transform, Equation (7).

This feature produces a characteristic change in

the Radon Transform. When the robot moves up-

wards, the information in the columns of the Radon

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

204

100

150

200

0.2

0.4

0.6

0.8

φ=0º

φ=45º

,-&

(a)

!"#$%&'("%)*$(+&

,-&

φ(degrees)

=0º

"" $""

!%%

!""

φ=0º

φ=45º

(b)

Figure 3: (a) Example image. (b) Radon transform of the example image.

transform tends to move towards the central row

(compression effect), and when the robot moves

downwards, the information in the columns tends to

move outwards the central row (expansion effect).

The method we use to estimate the height of the robot,

is based on these effects.

The Figure 4 shows an example of this fea-

ture, two omnidirectional images captured at differ-

ent heights (1m and 1.5m) and their corresponding

Radon transforms. In this ﬁgure it is possible to ob-

serve that in the second image the objects have moved

towards the center of the omnidirectional image and

the Radon transform presents a ”compression” effect

with respect the central row.

00 300

100

150

200

250

00 300

100

150

200

250

!"#$%&'("%)*$(+& !"#$%&'("%)*$(+&

,-./0'&1&2+&

,-./0'&1&234+&

5$+6(-)).$%&78-9'&

Figure 4: Example of the Radon transform compression.

3.2 POC (Phase Only Correlation)

In this subsection we present the method we use to

compare two Radon transforms.

In general, a function in the frequency domain

is deﬁned by its magnitude and its phase. Some-

times, only the magnitude is taken into account and

the phase information is usually discarded. However,

when the magnitude and the phase features are exam-

ined in the Fourier domain, it follows that the phase

features contain also important information because

they reﬂect the characteristics of patterns in the im-

ages.

Oppenheim and Lim have demonstrated this by re-

constructing images using the full information from

the phase with unit magnitude. This shows that the

images resemble the originals, in contrast to recon-

structing images using the full information from the

magnitude with uniform phase(Oppenheim and Lim,

1981).

POC, proposed in (Kuglin and Hines, 1975), is

an operation made in the frequency domain that pro-

vides a correlation coefﬁcient between two images

(Kobayashi et al., 2004). In our case we compare

two Radon transforms but this does not affect the POC

performance because the Radon transform can be in-

terpreted as an image.

The correspondence between two images im

(x,y)

and im

(x,y) calculated by POC is given by the fol-

lowing equation:

C(x, y) = F

−1



(u,v)·IM

∗

(u,v)

(u,v)·IM

∗

(u,v)



(8)

Where IM

is the Fourier transform of the image

1 and IM

∗

is the conjugate of the Fourier transform

RelativeHeightEstimationusingOmnidirectionalImagesandaGlobalAppearanceApproach

205

#!!!"

$!!!"

%!!!"

&%!!!"

&$!!!"

&#!!!"

%!!!" '!!!"$!!!"#!!!"!"&#!!!"&$!!!"&%!!!"&'!!!"

()*+,-""

./01,"

2345)6"#"

2345)6"$"

2,3-5"708,9+"$"

2,3-5"708,9+"#"

:1)*,+"#"

:1)*,+"$"

:/-;,+"

<))-"

=1)6,-;)+"

!"#$%&"'(")*+*

(a)

!"&A!!"&#!!!"&#A!!"

#A!!"

#!!!"

A!!"

#A!!"

$!!!"

#!!!"

A!!"

&A!!"

&#!!!"

&#A!!"

&$!!!"

()*+,-""

./01,"

2345)6"#"

2345)6"$"

;1)*,+"#"

;1)*,+"$"

;/-<,+"

=))-"

>1)6,-<)+"

!"#$%&"'(")*,*

(b)

Figure 5: (a) Plane of the environment 1. (b) Plane of the environment 2. (Dimensions in millimeters).

F’

! ! !

! !

! !!!

Origin

max

Image plane

Mirror equation:

Figure 6: Scheme of the hyperbolic mirror used to capture

the synthetic omnidirectional images were built.

os the image 2. F

−1

is the inverse Fourier transform

operator.

max{C(x,y)} is a coefﬁcient that takes values in

the interval [0,1] and it measures the similitude be-

tween the two images. This measure is invariant un-

der translations in the original image. To estimate the

similitude between two images we have used the fol-

lowing expression:

dist(im

,im

) = 1 − max{(C(x,y)} (9)

Furthermore, it is possible to estimate the rela-

tive displacements between the two images ∆

and ∆

along both axes by:

(∆

,∆

) = argmax

(x,y)

{C(x,y)} (10)

!"#$%&"'(")*+* !"#$%&"'(")*,*

Figure 7: Example of an omnidirectional image of each En-

vironment.

If we use Radon transforms instead of images, the

value ∆

is equal to the relative orientation of the robot

when capturing the two images.

This way, POC is able to compare two images in-

dependently on the orientation and it is also able to

estimate this change in orientation.

3.3 Height Estimation Method

The height estimation method is based on the con-

cepts described in the previous two subsections. It is

invariant to rotation with respect to the z axis thanks

to the use of POC to compare the Radon transforms.

The method works as follows.

The robot takes an omnidirectional image from its

ﬁrst position and saves its Radon transform. Then the

robot moves upwards or downwards, captures a new

omnidirectional image and saves its Radon transform.

The next step consists in detecting the height dif-

ference between the images. Since it produces a com-

pression effect in the Radon transform with respect to

the central row, our procedure consists in applying a

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

206

! "!!! #!!!

!$%

!$&

!$'

()*+,-.//0

! "!!! #!!!

!$%

!$&

!$'

()*+,-.//0

! "!!! #!!!

!$#

()*+,-.//0

!"#$%&%'('#)*#+

#)*#./01#h.%213# 4"#$%&%'('#)*#+

#)*#./01#h.%213#

!#6#4#

!"#$ !%#$

!&#$

0 500

000

500

000

downwards

upwards

!"#$%&"'(&)%*++,%

-.+/0"11'.2%3#4).0%4#$45$#)"6%

!"#$

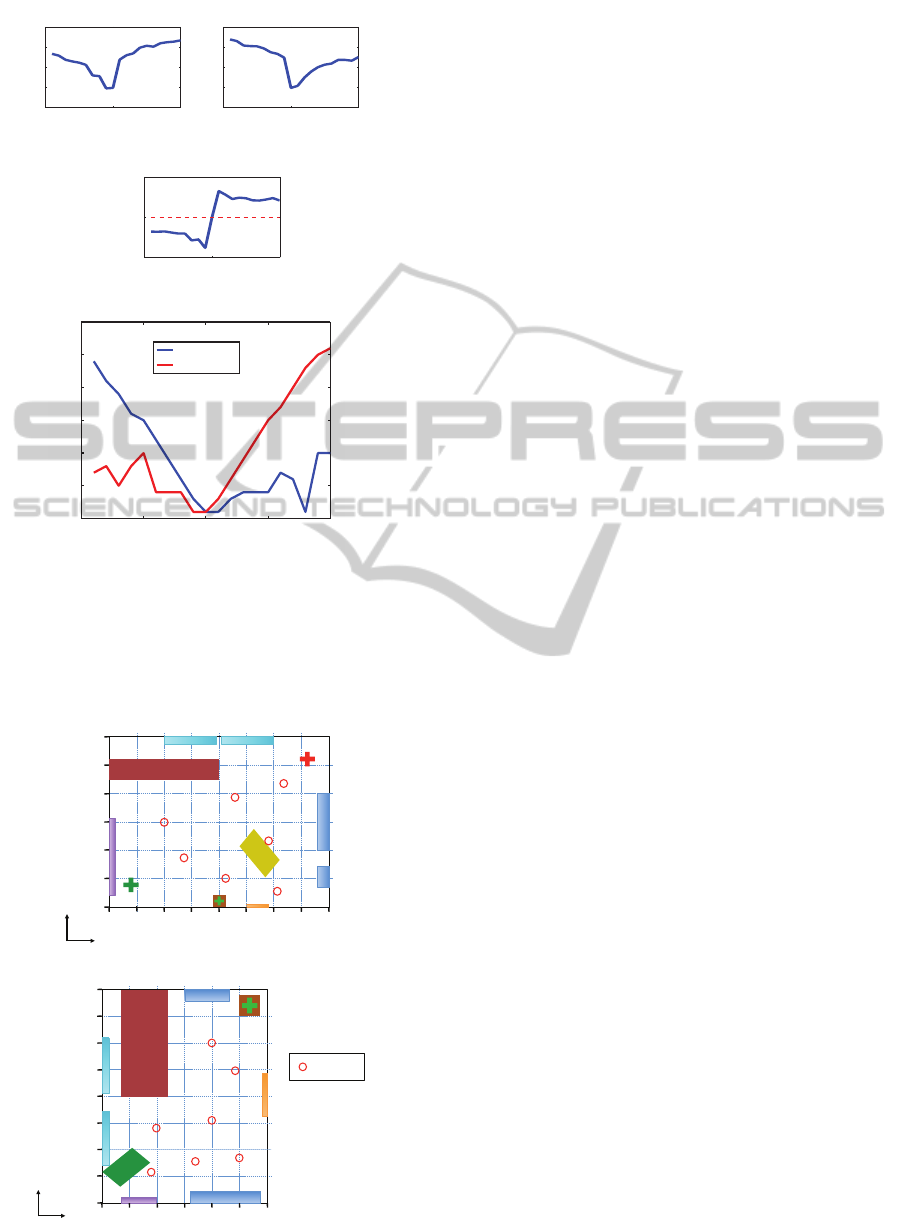
Figure 8: Minimum of the vectors (a) V

(case 1) and (b)

(case 2). (c) Difference between (a) and (b). (d) a

fac-

tor which is proportional to the real relative height between

each image and the test image. This example is in the envi-

ronment 1 with the following position: x = 0 mm and y = 0

mm.

#!!!"

$!!!"

%!!!"

&%!!!"

&$!!!"

&#!!!"

%!!!" '!!!"$!!!"#!!!"!"&#!!!"&$!!!"&%!!!"&'!!!"

!"#$%&"'(")*+*

!"#$!!"#%!!!"#%$!!"

%$!!"

%!!!"

$!!"

%$!!"

&!!!"

%!!!"

$!!"

#$!!"

#%!!!"

#%$!!"

#&!!!"

!"#$%&"'(")*+*

,&-$.&"-*

Figure 9: Positions of the test images in each Environment.

scale factor a to each column of the ﬁrst Radon trans-

form and comparing the result with the second Radon

transform using POC. Then, the distance is obtained

using Equation (9). This step is repeated increasing

the compression factor a in each step, until the com-

pression does not make sense, because the transform

has no relevant information. In this moment the robot

has a vector of distance values V

calculated with

POC, each element of the vector corresponds to one

value of the compression factor a. The a factor, that

has produced the minimum of the vector of distances

, is a magnitude proportional to the relative height,

The problem in this point is that the robot does

not know the translation direction (upwards or down-

wards). If the translation is upwards the second

Radon transform suffers a compression but if the

translation is downwards then the ﬁrst Radon trans-

form is the one that suffers a compression.

To take this problem into account:

Firstly, the robot compresses gradually the ﬁrst

Radon transform and carries out the method described

in the foregoing paragraph, to obtain the a

factor, but

in this case the robot also has to save the minimum

magnitude d

min

in the vector of distances V

. This

case would be the correct one if the robot was moved

upwards

Secondly, the robot repeats the process compress-

ing the second image. This case would be the correct

case if the robot was moved downwards.

Finally, the robot has two factors: a

from the ﬁrst

case and a

from the second case, and it has two d

min

distances: d

min1

and d

min2

. The minimum between

min1

and d

min2

determines which is the correct case.

At the end of the process the robot has a magni-

tude a

proportional to the vertical displacement and,

depending or the correct case, the displacement has

been upwards (case 1) or downwards (case 2).

4 IMAGE DATABASE

In order to check the performance of the proposed

technique, we have created two virtual environments

which represent two different rooms. In these envi-

ronments it is possible to create an omnidirectional

image from any position. The Figure 5 shows a

scheme of both environments.

The omnidirectional images have 250x250 pixels

and they have been created using the hyperbolic mir-

ror which is described in Figure 6. The parameters

used in the mirror equation are a = 40 and b = 160.

Several images have been captured in both envi-

ronments. In each environment several positions have

RelativeHeightEstimationusingOmnidirectionalImagesandaGlobalAppearanceApproach

207

0 500

000

500

000

!"#$%&"'(")*+*

,&'-%(..$&"*/01)&%*02*

31)405*6($76)*8''9*

(a)

0 500

000

500

000

!"#$%&"'(")*+*

,&'-%(..$&"*/01)&%*02*

31)405*6($76)*8''9*

(b)

0 500

000

500

000

!"#$%&"'(")*+*

,&'-%(..$&"*/01)&%*02*

31)405*6($76)*8''9*

(c)

0 500

000

500

000

!"#$%&"'(")*+*

,&'-%(..$&"*/01)&%*02*

31)405*6($76)*8''9*

(d)

Figure 10: (a) Experiments in the environment 1 with the reference image at height=100 mm. (b) Experiments in the environ-

ment 1 with the reference image at 1000 mm. (c) Experiments in the environment 2 with the reference image at 100 mm. (d)

Experiments in the environment 2 with the reference image at 1000 mm.

been chosen on the ﬂoor and a set of images above

these positions were captured to carry out the experi-

ments. The minimum height is 100 mm, and the max-

imum 2000 mm, with a step of 100 mm. In the Fig-

ure 4 there is an example of two different images at

different heights. And the Figure 7 shows one omni-

directional image of each environment.

5 EXPERIMENTS AND RESULTS

In this section the results of the experiments with

our height estimation method are shown. As ex-

posed in section 3, one of the necessary steps is

to differentiate the direction of the translation (up-

wards or downwards). To distinguish this, it is nec-

essary to calculate the difference between both val-

ues: min(V

)−min(V

). This difference determines

which minimum is the lowest and it determines which

is the correct direction (upwards or downwards). The

Figure 8 shows an example of this. In this ﬁgure we

take the image captured at 1000 mm as reference. The

Figure 8(a) and the Figure 8(b) show the minimum of

the vectors V

(case 1) and V

(case 2). The Figure

8(c) shows the difference between both vectors. If

the difference is negative, the correct case is the case

1 and if the difference is positive, the correct case is

the case 2. In Figure 8(d) the a

factor is represented

for each height in both cases (case 1: downwards and

case 2: upwards). This factor is proportional to the

real relative height between each image and the ref-

erence image. As we can observe in Figure 8(c), the

correct case for heights lower than 1000 mm is the

case 1 (downwards) and for heights higher than 1000

mm is the case 2 (upwards). This determines that in

Figure 8(d) the blue line to the left of 1000 mm indi-

cates the translation magnitude downwards the refer-

ence image and the red line to the right of 1000 mm

indicates the translation magnitude upwards the ref-

erence image. We can observe that the functions are

quite linear.

The Figure 8 is a speciﬁc example to show the

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

208

method steps. To demonstrate the correct perfor-

mance of our method we have done a whole set of

experiments in both virtual environments at different

positions. The Figure 9 shows the positions where the

images were captured in each environment to carry

out the experiments. We use a total of 14 positions

with 20 images in each position.

In the Figure 10, the results of these experiments

can be observed. The red line shows the magnitude of

translation upwards and the blue line shows the mag-

nitude of translation downwards. We can observe that

these experiments demonstrate that the method is very

linear for values of relative height around 1 meter.

6 CONCLUSIONS

In this work a method to estimate the height of the

robot has been presented. This method uses omnidi-

rectional images and transforms them with the Radon

transform to make the descriptors of each image. Fur-

thermore it compares the descriptors and ﬁnally es-

timates the relative height of the robot. Taking into

account the changes that Radon transforms of scenes

suffer when the robot changes its height.

The experiments included in this paper use our

own image database created synthetically from two

different environments. The results demonstrate that

the method is able to estimate the relative height be-

tween two images with robustness and linearity.

The method is invariant to rotation with respect to

the ﬂoor plane because the POC comparison is invari-

ant to shifts of the Radon transform.

The results of this work encourage us to continue

this research line. It will be interesting to do the

experiments with real images and also with images

which have noise, occlusions or changes in lighting

conditions. Furthermore we think that the study of

movements in 6 degrees of freedom will be interest-

ing to investigate.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish govern-

ment through the project DPI2013-41557-P.

REFERENCES

Amor

os, F., Pay

a, L., Reinoso, O., and Valiente, D. (2014).

Towards relative altitude estimation in topological

navigation tasks using the global appearance of visual

information. VISAPP 2014, International Conference

on Computer Vision Theory and Applications, 1:194–

201.

Bay, H., Tuytelaars, T., and Gool, L. (2006). Surf: Speeded

up robust features. Computer Vision at ECCV 2006,

3951:404–417.

Chang, C., Siagian, C., and Itti, L. (2010). Mobile

robot vision navigation and localization using gist and

saliency. IROS 2010, Int. Con on Intelligent Robots

and Systems, pages 4147–4154.

Hasegawa, M. and Tabbone, S. (2011). A shape descrip-

tor combining logarithmic-scale histogram of radon

transform and phase-only correlation function. In

Document Analysis and Recognition (ICDAR), 2011

International Conference on, pages 182–186.

Hoang, T. and Tabbone, S. (2010). A geometric invari-

ant shape descriptor based on the radon, fourier, and

mellin transforms. In Pattern Recognition (ICPR),

2010 20th International Conference on, pages 2085–

2088.

Kobayashi, K., Aoki, T., Ito, K., Nakajima, H., and Higuchi,

T. (2004). A ﬁngerprint matching algorithm us-

ing phase-only correlation. IEICE Transactions on

Funda- mentals of Electronics, Communications and

Computer Sciences, pages 682–691.

Kuglin, C. and Hines, D. (1975). The phase correlation

image alignment method. In Proceedings of the IEEE,

International Conference on Cybernetics and Society,

pages 163–165.

Lowe, D. (1999). Object recognition from local scale-

invariant features. ICCV 1999, Int. Con. on Computer

Vision, 2:1150–1157.

Mondragon, I., Olivares-M

ended, M., Campoy, P.,

Mart

ınez, C., and Mejias, L. (2010). Unmanned aerial

vehicles uavs attitude, height, motion estimation and

control using visual systems. Autonomous Robots,

29:17–34.

Oppenheim, A. and Lim, J. (1981). The importance of

phase in signals. Proceedings of the IEEE, 69(5):529–

541.

Pay

a, L., Fern

andez, L., Gil, L., and Reinoso, O. (2010).

Map building and monte carlo localization using

global appearance of omnidirectional images. Sen-

sors, 10(12):11468–11497.

Radon, J. (1917). Uber die bestimmung von funktio-

nen durch ihre integralwerte langs gewisser mannig-

faltigkeiten. Berichte Sachsische Akademie der Wis-

senschaften, 69(1):262–277.

Winters, N., Gaspar, J., Lacey, G., and Santos-Victor, J.

(2000). Omni-directional vision for robot navigation.

IEEE Workshop on Omnidirectional Vision, pages 21–

28.

RelativeHeightEstimationusingOmnidirectionalImagesandaGlobalAppearanceApproach

209