
Fault Detection by Backwards Analysis in Coloured Workflow Nets
Vasilii Ganishev
1
, Olga Fengler
2
and Wolfgang Fengler
2
1
Department of Applied Mathematics, National Research University ”Moscow Power Engineering Institute”,
Moscow, Russia
2
Faculty of Computer Science and Automation, Computer Architecture Group, TU Ilmenau, Ilmenau, Germany
Keywords:
Workflow Nets, Fault Detection, Backwards Analysis, Coloured Petri Nets.
Abstract:
The increasing complexity of the business processes requires automated methods for trouble-shooting and
debugging of the process model in operation. This paper proposes mechanism of fault detection based on the
concept of backwards reachability for the coloured workflow nets. The formal verification methods defined
for coloured Petri nets such as state space method or place invariants declaration suffer from fast-growing
computational complexity. The article offers the set of firing rules for backwards token-play on coloured
workflow net. This method helps to detect resource-related failures of the two most common types: ”the
missing arc” fault (the resource was not initialized) and ”wrong expression fault” (there is no proper resource).
1 INTRODUCTION
Rapid growth of business process integration and
complexity causes the need for detailed modeling not
only of the structure but also the behavior during ex-
ecution. The workflow networks provide better func-
tionality for modeling the execution of the process.
But the interaction of the resource is not included in
the classical concept. Looking at the behavior from
the viewpoint of resources allows a more detailed de-
scription of the business process.
Creating a mechanism for error detection is a pri-
ority issue. If the model is too complicated, it is dif-
ficult to create error-free net. There are formal veri-
fication methods such as state space method (draw-
ing the reachability graph) or place invariants (in-
troduction of the special logical expressions for net
marking). But they either suffer from rapid growth
of computational complexity (state explosion in state
space method) or are too complex to automate and
need manual preparation (place invariants) (Jensen
and Kristensen, 2009). The backwards analysis based
on the theory of duality in Place/Transition nets (Laut-
enbach, 2003) proved to be a very powerful tool
for fault detection and reachability analysis in Petri
nets. The interpretations of this method have been al-
ready proposed for predicate/transition nets (Muller
and Schnieder, 2007), probability propagation nets
(Lautenbach and Susewind, 2012) and also BPMN di-
alect used in YAWL (Scharfe, 2013).
However, there are some papers proposing some
variations of the backwards analysis for coloured
Petri nets, for example (Bouali et al., 2009). Unfor-
tunetely some faults cannot be detected by this ap-
proach, such as the ”missing arc” fault (resource was
not initialized) as it is shown in the work (Ganishev,
2013).
This paper provides a set of firing rules that adapts
backwards reachability analysis to the concept of
coloured Petri nets as well as coloured workflow nets.
The detection of two types of the resource-related
faults (”missing arc fault” and ”wrong expression
fault”) will be shown in the example net. These faults
are resource-related in the concept of coloured work-
flow nets, because the control flow itself has to sat-
isfy the requirement of soundness. It makes the oc-
currence of such faults impossible there.
2 COLOURED WORKFLOW
NETS
The classic concept of workflow nets does not sup-
port the distinction of the resources that are neces-
sary in carrying out the process. For a detailed view
of the processes and the modeling of the competition
between resources the concept of coloured workflow
nets has been proposed (van der Aalst et al., 2011).
In this paper we use the definition of coloured
Petri net, which differs from classic one given in
(Jensen, 1991), (Kristensen et al., 1998). Two types
88
Ganishev V., Fengler O. and Fengler W..
Fault Detection by Backwards Analysis in Coloured Workflow Nets.
DOI: 10.5220/0005513000880094
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 88-94
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

of capacity are introduced and the guard function is
excluded from consideration.
A coloured Petri net (CPN) formally is a tuple
CPN = (P, T, F, C, K, M, m0) satisfying the require-
ments below:
• P is a finite set of places:
P 6= ; (1)
• T is a finite set of transitions:
T 6= , (2)
P ∩ T = ; (3)
• F is an arc expression function. F models the re-
lationship between states and transitions:
F ⊆ T × P ∪ P × T, (4)
F 6= ; (5)
Elements: (p,t) is a precondition and (t,p) is a
postcondition;
• C is a set of (logical) colours (types):
C
N
0
⊆ N
0
×C, (6)
C
∞
N
0
⊆ (N
0
+ ∞) ×C; (7)
• K is a capacity, the maximal possible number of
tokens with one colour in place:
P → C
∞
; (8)
K
s
is a total capacity:
P → N
∞
; (9)
• M is a multiplicity of arc:
F → N; (10)
• m0 is an initial marking:
P → C
∞
0
; (11)
0 ≤ m0 ≤ k(p); (12)
The definitions of enabled transitions, reachability
and fire rules used in this paper are the same as the
classic ones (Jensen, 1991).
By introducing this definition of CPN to the clas-
sic concept of workflow nets come out the coloured
workflow nets (CWN) similar to the concept proposed
(van der Aalst et al., 2005). A CWF notation covers
the control-flow perspective, the resource perspective
and the data/case perspective. ”A token in a place of
type Case refers to a case and some or all of its at-
tributes. Tokens in a place of type Resource represent
resources. Places of type CxR hold tokens that refer
to both a case and a resource” (van der Aalst et al.,
2005). However we will treat CxR places as Case
places in this paper, because they show the same be-
havior during the execution of the process. These nets
satisfy the following constraints (van der Aalst et al.,
2005):
1. A CWN where all places of type Resource are re-
moved should correspond to a Sound Workflow
Net (sound WF-net).
2. The expression of each arc contains only one ap-
pearance of each element of set C per conjunction
for resource place. That means that only one to-
ken of each colour can be taken from the place or
come to it.
3. The capacity of each resource place is one. That
means that only one token of each colour allowed
to remain in the place at the moment.
This extension does not break limitations of the
classic concept (there should be no increase in the
number of tokens) (van der Aalst et al., 2011), be-
cause at any time classic constraints could be reached
by unfolding.
A coloured workflow net should also satisfy fol-
lowing limitations of classical concept (van der Aalst
and van Hee, 2002):
1. Every transition is on the way to end place.
2. There has to be no dead transitions, that can’t be
enabled by execution.
Fig. 1 shows an example of a coloured workflow
net. It models the actions of a worker, who needs
a resource for his work. The resource should be re-
leased at the end of the work. Place ”Start” is an ini-
tial place. The transition ”Init” initializes the business
process. Place ”Ready” models the worker’s readi-
ness to start the work. The place ”Res” models the
resource place. The transition ”Use” shows the cap-
ture of the resource by the worker. The place ”Work”
models the process of working. The transition ”Free”
models the termination of the work and the release
of the resource. The place ”Done” is the termination
(end) place of the single instance of the business pro-
cess. The transition ”Finish” prepares the net for the
next run. The place ”End” shows the termination of
the whole run of the business process. The transition
”t*” provides liveness of the net.
FaultDetectionbyBackwardsAnalysisinColouredWorkflowNets
89

Figure 1: The example of the coloured workflow net.
3 FAULT DETECTION BY
BACKWARDS ANALYSIS
The automatic detection of resource-related faults can
help to manage resources in complex business mod-
els. Especially it may be very helpful in combina-
tion with auto-generated CWN or CPN from existing
logs provided by business model, so called Play-In
(van der Aalst, 2011). The methods for the back-
wards analysis in classic Petri nets concept or con-
cepts of other High Level Petri nets cannot be used
for the coloured Petri nets or workflow nets:
• in classic dual nets the transformation of the to-
kens when firing is not taken in account;
• in various types of higher Petri nets the transfor-
mation is modeled with the help of the activation
vector (or activation function), but the concept of
coloured Petri nets does not use activation vectors.
3.1 Double-marked Coloured Workflow
Net
The concept of the double-marked Petri nets was
first introduced by Kurt Lautenbach (?) based on
the theory of the dual spaces in order to do diag-
noses in Petri nets. First approaches were proposed
for place/transition nets (Lautenbach, 2003) and then
applies to some other classes of High Level Petri
nets (Muller and Schnieder, 2007), (Lautenbach and
Susewind, 2012).
The algorithm behind this approach can be de-
scribed as follows:
• In forward firing (normal case) the net works as
classic coloured net.
• If the net is dead, but the terminal state is
not yet reached, the end place (or places) will
be marked with so called initial T-marking
(transition-marking). Now places fire rather than
transitions, and the net works backwards.
One element of the CPN, the set of colours cannot
be simply dualized as in other classes of High Level
Petri nets (Muller and Schnieder, 2007). This leads
to the inability to use the theory of the dual spaces
directly.
The main point of this paper is the introduction of
the neutral element, that helps to avoid this limitation
of CPN, and special firing rules to deal with it.
Formally a double-marked coloured Petri net is a
tuple DMCPN = (P, T, C
∗
, K, M, m
0
), where all ele-
ments except C
∗
and m
0
are defined as in the original
concept of coloured Petri nets. C
∗
and m
0
are defined
as follows:
• C
∗
is a set of (logical) colours (types) plus neutral
element ’*’
• m
0
is a tuple of the initial marking. m
0
= { m
P
0
,
m
T
0
}, where m
P
0
is the initial place-marking and
m
T
0
is the initial transition-marking. At the begin-
ning of the backwards analysis the transitions to
the end places are marked with neutral element.
By dividing a set of places into two subsets (Case
places and Resource places) and introducing transi-
tion t
∗
we come to informal definition of double-
marked coloured workflow net (DMCWN).
3.2 Firing Rules
Following firing rules are required for DMCWN op-
eration. They represent the adaptation of the set of
rules in (Scharfe, 2013) for the concept of CWN and
they consider the neutral element.
There are two types of firing rules with neutral
element: α-firing rules (all firing places are not
marked) and β-firing rules (some firing places are
marked).
Simple α-firing Rule
Let the transition t be marked with a neutral element.
The place which has only one pre-transition is en-
abled for α-firing rule if there is a neutral token in the
pre-transition and there is no P-token in this place. By
firing the post-transition of te marked place receives a
neutral token and pre-transition loses its marking.
This rule can be illustrated as follows (Fig. 2, Fig.
3).
Special α-firing Rules
Special α-firing rules are the adaptation of Special
α-firing rules in classic Petri nets for coloured nets.
Special α-firing Rule 1
Let the transition t be marked with a neutral element.
If there are two or more places that are enabled with
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
90
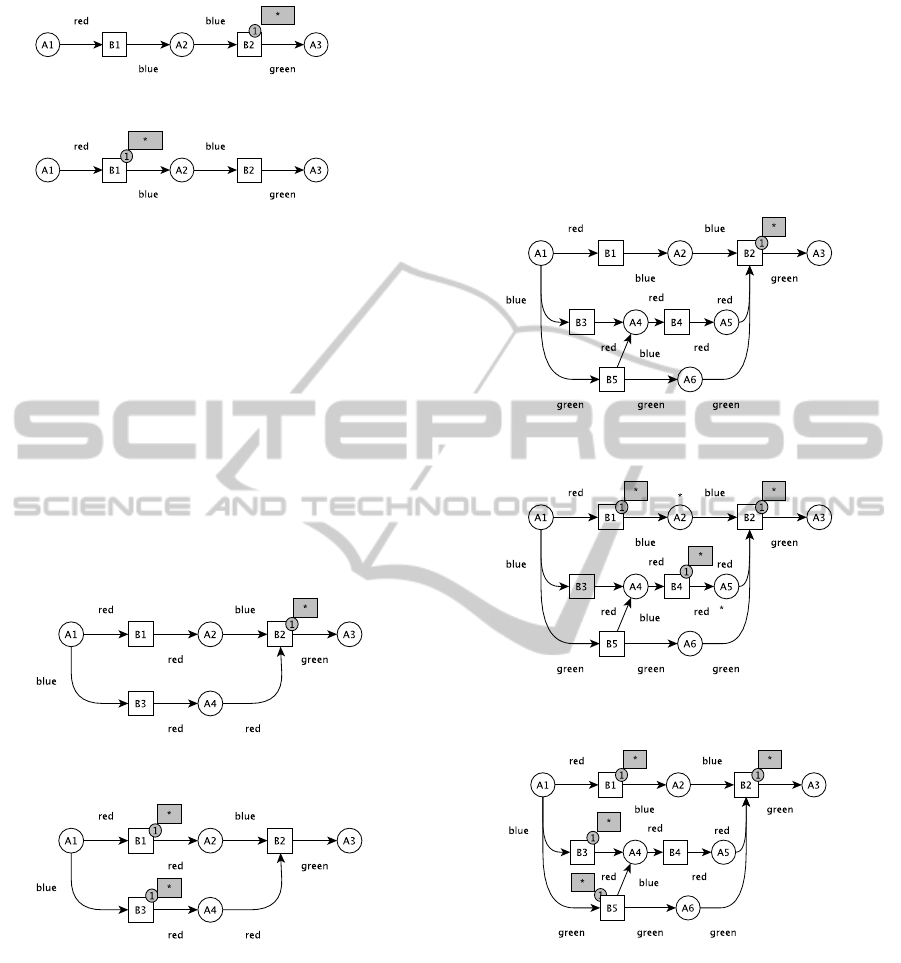
Figure 2: Simple α-firing rule.
Figure 3: Simple α-firing rule after firing.
actual T-marking and all these places have identical or
different post-transitions, then all places fire simulta-
neously. By firing every post-transition gets a neutral
token and the pre-transition loses its marking. It could
be shown with the following formula.
enabled:
∃t : m
T
(t) =
0
∗
0
; ∃p
j
, j ∈ (0, n),n ≥ 2,
(t, p
j
) ∈ F ∧ (p
j
,t
i
) ∈ F,i ≥ 1
(13)
firing:
m
T
(t) =
00
∧ ∀im
T
(t
i
) =
0
∗
0
. (14)
This rule can be illustrated as follows (Fig. 4, Fig.
5)
Figure 4: Special α-firing rule 1 before firing.
Figure 5: Special α-firing rule 1 after firing.
Special α-firing Rule 2
Let the transition t be marked with a neutral element.
If there are two or more places, which have t as the
pre-transition, and all these places have identical or
different post-transitions, a total firing is not possi-
ble. Then the enabled places fire and are marked with
symbol ’*’. They should not fire again. By firing the
post-transition gets a neutral token. When all places
have fired, then t loses its marking and each symbol
’*’ from places should be removed. It could be shown
with the following formula:
enabled:
∃t : m
T
(t) =
0
∗
0
; ∃p
j
, j ∈ (0, n),n ≥ 2,
(t, p
j
) ∈ F ∧ (p
j
,t
i
) ∈ F,i ≥ 1;
∃k : k > 0 (t, p
k
) ∈ F ∧ (p
k
,t
k
) ∈ F;
(15)
firing:
m
T
(t) =
00
; ∧ ∀k m
T
(t
k
) =
0
∗
0
∧ m
P
(p
k
) =
0
∗
0
; (16)
Figure 6: Special α-firing rule 2 before firing.
Figure 7: Special α-firing rule 2 after partial firing.
Figure 8: Special α-firing rule 2 after total firing.
If all have fired:
∀ jm
P
(p
j
) =
0
∗
0
⇒ m
P
(p
j
) =
00
. (17)
This rule can be illustrated as follows (Fig. 6, Fig.
7, Fig. 8)
β-firing Rule
This rule applies, if the application of α-firing rules is
not possible.
Let the transition t be marked with a neutral ele-
ment. If there is a place p, which has t as the pre-
transition, but it contains P-token, then the transition
FaultDetectionbyBackwardsAnalysisinColouredWorkflowNets
91

t changes its marking on the expression of the arc that
goes from p to t. Now the transition t can not change
its marking.
enabled:
∃ t : m
T
(t) =
0
∗
0
; ∃p(t, p) ∈ F ∧
(p,t
∗
) ∈ F, m
P
(p) 6=
00
;
(18)
firing:
m
T
(t) = (t, p). (19)
This rule can be illustrated as follows (Fig. 9, Fig.
10)
Figure 9: Special β-firing rule before firing.
Figure 10: Special β-firing rule after firing.
β-firing Rule (case of multiple places)
Let the transition t be marked with a neutral element.
If there are places p
1
,.. ., p
n
, which have t as the
pre-transition, but k places contain P-tokens, then the
transition t changes its marking on the expressions of
the arcs that go from p
k
to t. Each expression is sepa-
rated from others with the symbol ’/’. The places that
contain no P-tokens fire with α-firing rules. Now the
transition t may not change its marking.
enabled:
∃t : m
T
(t) =
0
∗
0
; ∃p
j
, j ∈ (0, n),n ≥ 2,
(t, p
j
) ∈ F ∧ (p
j
,t
i
) ∈ F,i ≥ 1;
∃k : k > 0 m
P
(p
k
) 6=
00
;
(20)
firing:
m
T
(t) = (t, p
m1
)/.../(t, p
mk
),
m
1
... m
k
∈ m ⊆ n ∧ m
T
(t
d
) =
0
∗
0
,
d ∈ n ∧ d /∈ m.
(21)
This rule can be illustrated as follows (Fig. 11,
Fig. 12)
4 EXAMPLES OF FAULT
DETECTION
”Missing arc” Fault. Let us illustrate the function-
ality of backwards analysis in coloured workflow nets
in following example (Fig. 13). It is the net from pre-
vious chapter (p. 2), but with following differences:
Figure 11: Special β-firing rule (case of multiple places)
before firing.
Figure 12: Special β-firing rule (case of multiple places)
after firing.
Figure 13: Example net for ”Missing arc” fault. The dead
net.
there is no arc from the transition ”Init” to the place
”Res” (the resource cannot be initialized).
When the place ”Ready” is marked, then the tran-
sition ”Use” cannot fire because the resource is re-
quired (Fig. 14). Then the transition ”Finish” will be
marked with the neutral element.
The place ”Done” is enabled for special α-firing
rule 2 (”Res” cannot fire, because it also needs to-
ken from ”Use”). After that the place ”Work” is en-
abled for simple α-firing rule 1. When the transition
”Use” is marked, there is no place that is enabled for
α-firing rules. But we can use β-firing rule for the
place ”Ready”. It changes the marking in ”Use” to
Worker. After that the net should be analyzed (Fig.
14).
For the analysis of the fault the incidence matrix,
the P- and T-reachability graphs are required. The in-
cidence matrix looks as follows:
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
92

Figure 14: Example net for ”Missing arc” fault. After back-
ward analysis.
-Worker 0 0 0 Worker
Worker -Worker 0 0 0
0 -Resource Resource 0 0
0 Worker -Worker 0 0
0 0 Worker -Worker 0
0 0 0 Worker -Worker
The columns illustrate the transitions in order of
firing. And the rows illustrate the places in order that
they get marking.
The P- and T-reachability graphs look as follows
(the order is the same as in the incidence matrix):
0 Worker 0 0 0 0
0 Worker 0 0 0
As we can see, the P-marking of the place
”Ready” and T-marking of the transition ”Use” are
the same. But according to incidence matrix for firing
this transition needs the token ”Resource” from the
place ”Res” as well. To solve this problem the place
”Res” should be initialized with this token.
”Wrong expression” Fault. The second example
also repeats the example from previous chapter (p. 2),
but now the expression of the arc from the transition
”Use” to the place ”Work” will be ”Bummer”.
When the places ”Work” is marked, then the tran-
sition ”Free” cannot fire because it needs a token
”Worker” from ”Work” (Fig. 15). Then the transition
”Finish” will be marked with the neutral element.
The place ”Done” is enabled for special α-firing
rule 2 (”Res” cannot now fire, because it also needs
Figure 15: Example net for ”Wrong expression” fault. Dead
net.
Figure 16: Example net for ”Wrong expression” fault. After
backward analysis.
token from ”Use”). We can use β-firing rule for the
place ”Work”. It changes the marking in ”Free” to
Worker. After that the net should be analyzed (Fig.
16).
The incidence matrix looks as follows (the differ-
ence with the previous example that it has initializa-
tion of ”Res”):
-Worker 0 0 0 Worker
Worker -Worker 0 0 0
Resource -Resource Resource 0 0
0 Worker -Worker 0 0
0 0 Worker -Worker 0
0 0 0 Worker -Worker
The P- and T-reachability graphs look as follows:
0 0 0 Bummer 0 0
0 0 Worker 0 0
As we can see, the P-marking of the place ”Work”
and T-marking of the transition ”Free” are different.
The incidence matrix shows that they are connected.
To solve this problem one can either change the ex-
pression of the arc from ”Work” to ”Free” to ”Bum-
mer” or change the marking of the place ”Work” to
”Worker” (by changing the expression of arc from
pre-transition).
5 CONCLUSIONS
The coloured workflow nets provide very powerful
functionality for modeling and describing the behav-
ior of business processes and resource management,
but the debugging and resource-related fault detection
in many cases has to be performed manually.
In this work the mechanism of the backwards
analyses for automated troubleshooting and fault de-
tection in coloured workflow net is proposed. The two
sets of firing rules for the double-marked coloured
workflow net were formulated and described. This
method allows finding resource-related faults in the
FaultDetectionbyBackwardsAnalysisinColouredWorkflowNets
93

business process with minimal amount of resources
and time.
However the question about the efficiency and the
computational complexity of the proposed concept re-
mains open. Also a comparative study with existing
approaches (Rabbi et al., 2010a), (Rabbi et al., 2010b)
has to be done.
REFERENCES
Bouali, M., Barder, P., and Schon, W. (2009). Backward
reachability analysis of colored petri nets. In The Eu-
ropean Safety and Reliability Conference (ESREL09),
Prague, Czech Republic. Taylor and Francis Group.
Ganishev, V. (2013). Use of high level petri nets for mod-
eling of adaptive workflow systems, in german: An-
wendung von hoeheren erweiterten petri netzen fuer
die modellierung von adaptiven workflow-systemen.
Master’s thesis, TU Ilmenau, Ilmenau, Germany.
Jensen, K. (1991). Coloured petri nets: A high level lan-
guage for system design and analysis. In Rozenberg,
G., editor, Advances in Petri Nets 1990, volume 483 of
Lecture Notes in Computer Science, pages 342–416.
Springer Berlin Heidelberg.
Jensen, K. and Kristensen, L. M. (2009). Coloured Petri
Nets. Springer-Verlag Berlin Heidelberg, Cambridge,
MA, USA.
Kristensen, L. M., Christensen, S., and Jensen, K. (1998).
The practitioners guide to coloured petri nets. In-
ternational Journal on Software Tools for Technology
Transfer, 2(2):98–132.
Lautenbach, K. (2003). Duality of Marked Place/Transition
Nets. University Koblenz-Landau, Koblenz, Germany.
Lautenbach, K. and Susewind, K. (2012). Probability
Propagation Nets and Duality, volume 11 of Ar-
beitsberichte des Fachbereichs Informatik. University
Koblenz-Landau, Koblenz, Germany.
Muller, J. and Schnieder, E. (2007). Duality in high level
petri-nets - a basis to do diagnoses. In Simulation Con-
ference, 2007 Winter, pages 629–636.
Rabbi, F., Wang, H., and MacCaull, W. (2010a). Compens-
able workflow nets. In Dong, J. and Zhu, H., editors,
Formal Methods and Software Engineering, volume
6447 of Lecture Notes in Computer Science, pages
122–137. Springer Berlin Heidelberg.
Rabbi, F., Wang, H., and MacCaull, W. (2010b). Yawl2dve:
An automated translator for workflow verification. In
Secure Software Integration and Reliability Improve-
ment (SSIRI), 2010 Fourth International Conference
on, pages 53–59.
Scharfe, C. (2013). Modeling of Adaptive Business
Processes, in german: Modellierung von adaptiven
Geschaeftsprozessen, Thesis. PhD thesis, TU Ilme-
nau, Ilmenau, Germany.
van der Aalst, W. (2011). Process Mining. Discovery, Con-
formance and Enhancement of Business Processes.
Springer-Verlag.
van der Aalst, W., Jrgensen, J., and Lassen, K. (2005). Lets
go all the way: From requirements via colored work-
flow nets to a bpel implementation of a new bank sys-
tem. In Meersman, R. and Tari, Z., editors, On the
Move to Meaningful Internet Systems 2005: CoopIS,
DOA, and ODBASE, volume 3760 of Lecture Notes in
Computer Science, pages 22–39. Springer Berlin Hei-
delberg.
van der Aalst, W. and van Hee, K. (2002). Workflow Man-
agement: Models, Methods, and Systems. MIT Press,
Cambridge, MA, USA.
van der Aalst, W., van Hee, K., ter Hofstede, A., Sidorova,
N., Verbeek, H., Voorhoeve, M., and Wynn, M.
(2011). Soundness of workflow nets: classification,
decidability, and analysis. Formal Aspects of Comput-
ing, 23(3):333–363.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
94
