
New Schedulability Analysis for Real-Time Systems based on MDE
and Petri Nets Model at Early Design Stages
Mohamed Naija
1
, Samir Ben Ahmed
1
and Jean-Michel Bruel²
1
Laboratory of Computer for Industrial Systems, INSAT, Tunis, Tunisia
²Institute of Computer Science Research, IRIT, Toulouse, France
Keywords: Real-Time Embedded Systems, Concurrency Model, MARTE, Schedulability Analysis, Petri Nets, Design.
Abstract: Transforming a software functional model that describes the underlying application to a concurrency model
is considered as a critical issue in the model-based approaches for Real-Time Embedded Systems (RTES)
development process. The formal methods have proven to be useful for making the development process
reliable at a high abstraction level. Based on this approach, this current research proposes a generic
approach to task construction that allows early detection of unfeasible design. Having a component-oriented
specification as entry, the first stage of the methodology consists in the workload model specification. The
workload model represents the system end-to-end computations triggered by an external stimulus and
subject to hard real-time constraints. This model is then mapped into a Petri Nets formalism to perform P-
invariant method and generate all transactions in an optimized way. The refinement of the transaction set in
a Schedulability Analysis Model defining an optimized threading strategy model. The latter presents the set
of units of execution taken into account by the scheduler of the system and their scheduling parameters. We
illustrate the advantages and effectiveness of the proposed method by constructing a concurrency model for
a combined Cruise Control System and Anti-lock Braking System.
1 INTRODUCTION
In the development of Real-Time Embedded
Systems (RTES), component-oriented high-level
specifications are used to manage complexity. Each
software component encapsulates the
implementation of a specific functionality which is
accessible only through the input and output access
points. In that context, the software application is
described in a component-based model (called also
functional model) still being independent of any
specific platforms. Hence, this functional model
(Mraidha et al, 2011) constitutes a first step in the
definition of a structure able to fulfil requirements
for the system.
After building a logical component model, it is
necessary to synthesize a mapping of functional
blocks on threads in order to support the verification
of non-functional requirements (NFP) at early
design stages. The choice of the threading strategy
defines how the system reacts due to an external
event or a timer. Finding the adequate number of
threads and the good grouping of functions to
threads relies mainly on the designer experience
towards the definition of a concurrency model of the
system.
Thus, the real-time application is described in a
concurrency model that runs on a given target
hardware platform and satisfies timing constraints.
To this end an abstracted run-time model of the
platform has to be assumed.
In fact, the scheduling analysis phase makes it
possible to predict and validate the concurrency
model before the design stage. An analysis carried
out earlier makes it possible to guide the designer in
the construction of a valid design model with respect
to the threading strategy.
In this paper, we incorporate mapping functional
blocks on threads problem in the design
optimization. Since threading strategy is NP-hard
problem, it is recommended to apply formal
techniques intended to reduce the problem impact.
This allows the construction and the validation of
the concurrency model that is reliable at early design
stage. The proposed approach adopts the model-
driven engineering. Indeed, the system behavior that
is in response to external stimuli and platform
resources are annotated with MARTE (OMG, 2008)
330
Naija M., Ben Ahmed S. and Bruel J..
New Schedulability Analysis for Real-Time Systems based on MDE and Petri Nets Model at Early Design Stages.
DOI: 10.5220/0005514003300338
In Proceedings of the 10th International Conference on Software Engineering and Applications (ICSOFT-EA-2015), pages 330-338
ISBN: 978-989-758-114-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

profile stereotypes. This input model, also called
Workload model, is at the same level of abstraction
of the functional model. After that, the mapping
from UML into Petri Nets is performed in order to
generate a concurrency model. Finally, the obtained
concurrency model is automatically validated by
using traditional schedulability tests.
The present paper is organized as follows.
Section 2, provides an overview of the main
concepts of Petri Nets. In section 3 related work is
discussed. In section 4 a description of the proposed
methodology is given. Section 5 gives experimental
evaluation results. Finally, section 6 concludes the
paper and sketches some future work.
2 OVERVIEW OF PETRI NETS
In this section we provide enough information about
Petri Nets to understand how and why we use them
in our approach.
2.1 Formal Definition
Petri Nets (Murata, 1989) can be defined as 4-tuplet:
PN = (P, T, IN, OUT) (1)
where:
• P = {p
1
, p
2
, . . . , p
n
} is a finite set of places n > 0;
• T = {t
1
, t
2
, . . . , t
m
} is a finite set of transitions m
> 0;
• IN: (P × T)↦ℕ is the backward incidence
function;
• OUT: (P × T)↦ℕ is the forward incidence
function.
Each system state is represented by a marking M of
the net. The notation M(p) denotes the number of
tokens in place p in marking M. M
0
is the initial
marking of the net. A transition t is said to be
enabled if and only if each place p
i
in the common
pre-set of t has a token.
2.2 Structural Analysis of Petri Nets
Structural analysis makes it possible to prove some
properties regardless of the evolution of the marking
(without constructing the reachability graph). This
analysis can be applied through the method of place
invariant, which requires calculating the matrix of
incidence presented by definition 1.
Definition 1
The incidence matrix C of a PN = (P, T, IN, OUT) is
an (n × m) integer matrix whose rows correspond to
places and whose columns correspond to transitions.
The column t ϵ T denotes how the firing of t affects
the marking of the net (Narahari and Viswanadham,
1985):
C (t, p) = OUT (p
i
, t
j
) – IN (p
i
, t
j
) (2)
The solutions of the equation C
X = 0 are called
place invariants (P-invariants). A proper P-invariant
is a solution of C
X = 0 if X ≠ 0.
A P-invariant indicates that the number of tokens
remains unchanged in all reachable markings. In P-
invariant, tokens cannot evolve or disappear. They
can “move” from one place in a system net to
another and “change” their marking, i.e., inner state
(Frumin and Lamazova, 2014). So P-invariant
proves the conservative property of the net, i.e.,
places that can be fired with the same token (Murata,
1989). This analysis method can be used to prove
concurrency (places fired with the same token) and
mutual exclusion (same place fired with different
tokens) properties.
3 RELATED WORK
There have been a number of approaches proposed
for real-time applications enabling early analysis of
non-functional requirements. We will discuss in the
following the methodologies that focuses in
concurrency mapping from different structural
models.
COMET (Gomaa, 2000), proposes a
methodology for designing real-time and distributed
applications which integrates concurrency concepts
and uses the UML notation. It is here proposed to
support generation of concurrency models after the
definition of functional blocks of the system and
their connections. The concurrent real-time model
of the system is then designed in terms of active and
passive objects without supporting schedulability
validation.
In (Saksena and Karvelas, 2000) a method for
mapping the execution of active object methods
(actions) into threads is proposed. However, the
authors discuss two threading strategies: (i) a single
thread solution: where all actions are implemented
by a single thread and events are queued by priority,
and (ii) multi-threading solution: where threads
change their priority based on messages they handle.
Unfortunately, while the single threaded
implementation is analyzable and practically
applicable the multi-threading solution is difficult to
analyze or inapplicable (Bartolini et al., 2005).
NewSchedulabilityAnalysisforReal-TimeSystemsbasedonMDEandPetriNetsModelatEarlyDesignStages
331
In (Bartolini et al., 2005) the authors propose a
mapping process considering EDF schedulability
tests. In particular, the author defines two algorithms
to generate the task real-time scheduling parameters.
Nevertheless, there is not automated support for the
test which is an ad-hoc test (Mraidha et al., 2011).
In the same vein, (Kodase et al., 2003) have
introduced a mapping process of a structural model
to task model but only for a single-processor system.
In (Mraidha et al, 2011) OPTIMUM
methodology is provided for MARTE models
considering schedulability analysis at early stages.
Optimum is able to generate a concurrency model
from activity diagram. Although this work supports
MARTE notation, some elements of activity
diagrams will not be processed, this leads to the
impossibility of transforming complicated activity
diagram into set of task.
Other efforts have been specifically tailored to
automotive architectures. In (Wozniak et al., 2014)
(Mehiaoui et al., 2013) the partitioning of the set of
functions and signals in tasks and messages has been
treated in the design optimization. They assume that
each function is assigned to exactly one task unlike
these approaches, our approach proposes
methodological rules to build concurrency model
when actions are involved in multiple transactions.
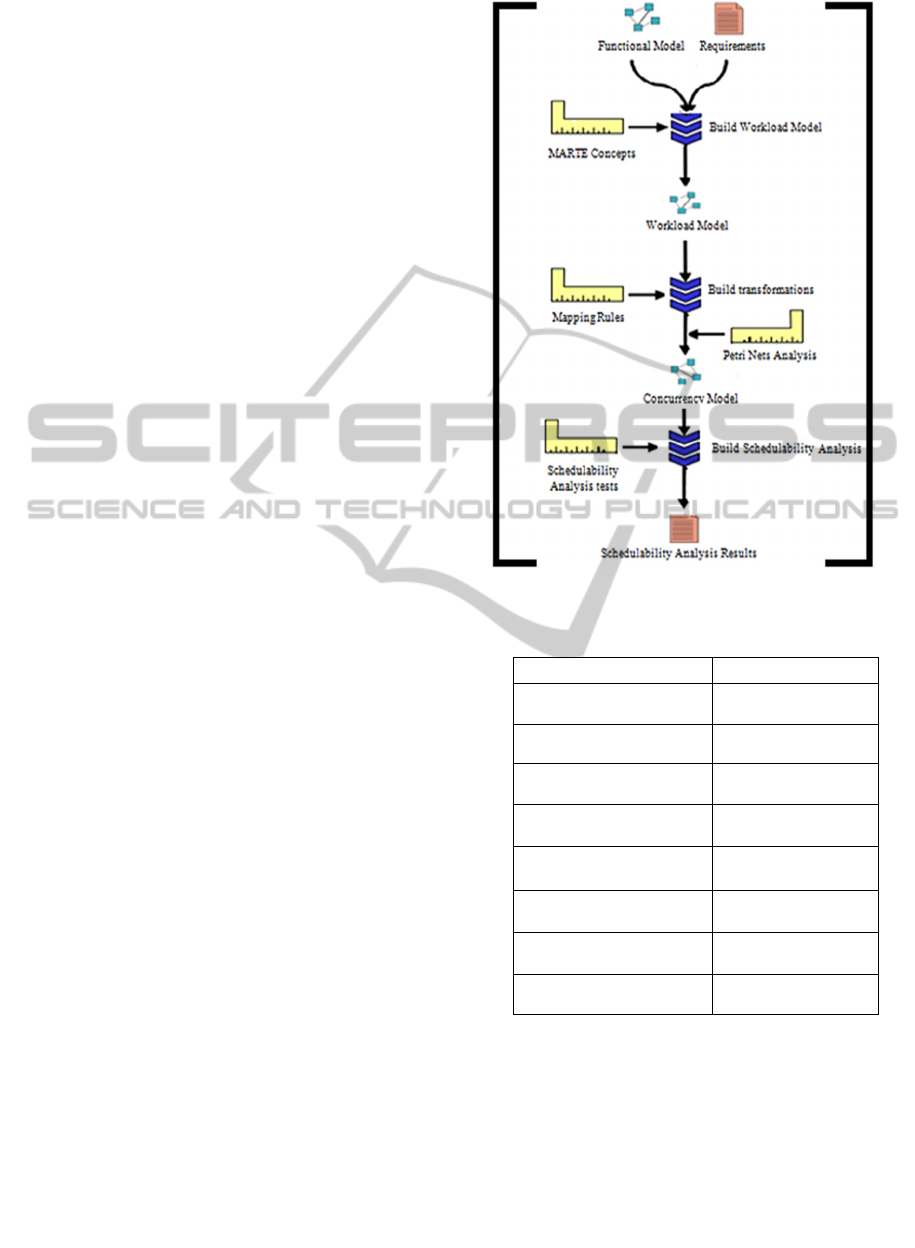
4 METHODOLOGY
The proposed methodology intended the
construction and the validation of the concurrency
model at early design stage. The methodology
defines a process depicted on Figure 1: (i) the first
step consists in workload model that describe system
end-to-end scenarios and timing requirements
annotated with MARTE profile, (ii) this model is
mapped into Petri Nets formalism in order to
generate concurrency model and (iii) finally,
schedulability Analysis Results that describes the
evaluated concurrency model is provided.
The idea of performing scheduling analysis
based on MARTE models assumes that all the
information that is needed for the analysis is already
part of the MARTE model. Therefore, concurrency
model contains all necessary information for an
analysis (tasks, shared resources, platform,
scheduling algorithms, execution times, etc.). In
Table 1 all used stereotypes offered by UML
MARTE profile are presented.
The following subsections give details of the
intermediate models produced by our methodology.
Figure 1: Methodology Process.
Table 1: MARTE Elements of our methodology.
MARTE Stereotype UML Extensions
«gaPlatformResources» Classifier
«saExecHost» Classes, Objects
«saCommHost» Classes, Objects
«schedulableResource» Classes, Objects
«saSharedResources» Classes, Objects
«saEndtoEndFlow» Activities
«gaWorkloadEvent» Initial-Node
«saStep» Methods
4.1 Workload Model
The definition of a well-formed analyzable model in
case of component-oriented specifications has two
steps. The first consists of gathering the components
structure and defining the workload behavior of the
system, the second representing platform resources.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
332

4.1.1 Workload Behavior
The workload behavior is built from the functional
model that is specifying the flow of the executed
actions during a certain system mode. Therefore,
workload situations are defined by activity diagram
stereotyped with MARTE «gaWorkloadBehavior»
stereotype. The latter (HadjKacem et al., 2012) is
able to expose the dynamics of a system and depict a
great degree of resemblance to the Petri Nets.
At this level, we focus on the MARTE
annotations applied to the activity diagram. Indeed,
end-to-end real-time constraints (deadline
properties) are specified on transactions, that is,
chains of operation activations enabled by external
stimuli. Each transaction is stereotyped
«saEndtoEndFlow». However, an event (e.g., timers,
internal event and external occurrences) that triggers
the behavior of a system and precedes all the action
is annotated with MARTE «gaWorkloadEvent»
stereotype. Each event is annotated with the property
«arrivalPattern» in order to fix its period. In
addition, any activity/action which represents the
execution of an operation is extended with the
«saStep» stereotype and has an execution time
(execTime property) specified for a given execution
host (host property).
4.1.2 Platform Resources
To this end an abstracted view of the execution
platform resources is assumed to have execution
time estimation for steps. Thus, the processor
resources are represented as components with the
«saExecHost» stereotype, bus resources are with the
«saCommHost» stereotype and platform resources
are stereotyped by «gaPlatformResources». To be
executed, a software resource must obviously be
mapped on processors or busses. Involved shared
resources should also be described.
4.2 Generation of Concurrency Model
In order to generate a concurrency model from a
workload behavior this stage consists of three steps:
(1) Mapping Workload Behavior diagram to Petri
Nets, (2) identify transactions in Petri Nets model
and (3) allocate actions in transactions to threads.
4.2.1 Mapping Workload Behavior Diagram
to Petri Nets
The first step consists in mapping the workload
behavior to Petri Nets formalism. Petri Nets
(Murata, 1989) are formal models based on strict
mathematical theories. They are powerful and
appropriate for modeling and analyzing systems
with parallelization, synchronization and confliction.
The mapping process consists of the deriving
activity diagram elements (nodes, transitions,
signals, actions, and synchronisation bar) and
MARTE annotations into Petri Nets elements. In
that context, several methods (Yang et al., 2010)
(HadjKacem et al., 2012) proposed mapping rules to
enhance formal analysis. In this paper, the rules for
transforming activity diagram elements into Petri
Nets are similar to those proposed in previous
literatures.
4.2.2 Transaction Identification
Once the mapping process is realized, the second
stage consists of determining all transactions in the
nets running in concurrency. A transaction is defined
as a sequence of actions performed in the end-to-end
processing in response to an external event. The
general problem is quite difficult because there are a
high number of transactions that derive all possible
system modes. Thus, to identify all transactions of
an optimized way we propose using the method of
invariants based on Petri Nets formalism.
Place invariant indicates a set of places in which
the number of tokens remains unchanged in all
reachable markings. As a consequence, it
corresponds to a constraint on the states and system
activities that will always be verified, regardless of
its evolutions.
As already mentioned, the solutions of the
equation C
X = 0 are called place invariants (P-
invariants). The solution is called proper if X≠ 0. In
this work we are interested only in proper place
invariants describing all the operations that will be
performed by the same token in only one
transaction. Thus, the set of places p
i
with X
i
> 0,
called the support of the P-invariant, is considered as
only transaction. The execution order of the
operation sequence in a specific transaction is given
by the crossing transitions order.
4.2.3 Generation of the Task Set
After identifying the transactions, it is necessary to
specify the so-called schedulable Resources. These
are units of execution taken into account by the
scheduler of the system, called tasks in scheduling
literature (Radermacher et al., 2010). The task set is
constructed by mapping all actions of the same
transaction to one task i.e. the execution operations
belonging to the place invariants must be assigned to
threads of execution. In fact, we apply a transaction-
NewSchedulabilityAnalysisforReal-TimeSystemsbasedonMDEandPetriNetsModelatEarlyDesignStages
333

based task model generation (to get one single
thread of execution for each transaction). Note that,
a software resource can be mapped into more than
one thread. However, she is denoted as a critical
sections needed to manage multi-threading whose
code must be protected.
Among these assumptions, the synchronization
protocol, used to protect the access to the shared
resource, must be considered in the concurrency
model. In this paper, we use a classical solution
(Mraidha et al., 2011) (Mzid et al., 2014) that
considers the Priority Ceiling protocol (Goodenough
and Sha, 1988) as a synchronization protocol in
order to avoid deadlocks at the implementation
level.
4.3 Schedulability Analysis
To this end, at this level, execution actions, shared
resources and synchronization protocol are
specified. This concurrency model is independent
from any particular Real-Time Operating System
(RTOS) in order to fulfill the MDA principals.
To be analyzable, we assume that the
schedulability analysis model must specify: (1)
threads, here called schedulable resources, along
with their scheduling parameters, (2) the allocation
of threads to hardware resources (e.g. processors)
and (3) the scheduler algorithm used by the
processing resources stereotyped <<SaExecHost>>
defined in the Workload model.
Note how the specification of scheduling
algorithm must be coherent with scheduling
parameters for tasks. A task is characterized by its
priority P
i
, its execution time C
i
, its activation period
T
i
, its blocking time B
i
and its deadline D
i
that
represents end-to-end limit in which a task must
complete its execution. The information on
deadlines was already provided in the Workload
Behavior. Let us remark that (Bartolini et al., 2005)
a task activated by an event is considered to be
periodic or aperiodic. In the case of a task that is
activated by another task cannot be assigned a
period. Anyway, dependencies between tasks allow
setting some priority orders i.e., t
j
may not be
executed before t
i
when t
j
depends on the output of
t
i
. Then, we assume that succeeding tasks have
higher priority than preceding ones. Tasks
dependencies are derived from the dependencies of
the functions mapped into them. Since a task is
strictly sequential, the worst case execution time
(WCET), denoted as C
i
, is given by the sum of
computational cost of the all actions contained in the
task. Note that if a task have more than one
execution path, the maximum execution time is
considered. Due to the presence of shared resources,
a task is also characterized by a blocking time B
i
.
The blocking time accounts for the time a higher-
priority task has to wait, before acquiring the lock,
since a lower-priority task owns this lock. The
computation of this term depends on the worst case
execution time C
i
of the task that owns the access to
the shared resource.
The Schedulability Analysis Model, as defined,
contains all the needed information to perform the
schedulability tests.
5 AUTOMOTIVE CASE STUDY
In this section we illustrate the application of our
methodology to an automotive case study
constructed by merging two subsystems consisting
of a CCS (Cruise Control System) (Anssi et al.,
2011) and ABS (Anti-lock Braking System)
(Mraidha et al., 2011).
The cruise control system maintains the vehicle
speed according to driver inputs. This subsystem
holds the correct distance from the vehicle in front to
prevent collisions through Diagnosis function (to
detect errors or inconsistencies in acquired data) and
Limphome function (decides which action to take in
case of detected error). Note that this Diagnosis
function is connected also to the ABS subsystem in
order to disable the anti-locking function in case a
fault is detected.
The ABS subsystem is composed of three
elementary functions: Dataprocessing (acquiring
data coming from the sensor), Diagnosis (to detect
errors or inconsistencies in acquired data) and
AntiLockControl (calculating the command to send
to the actuator).
5.1 Workload Model
5.1.1 Workload Behavior
The end-to-end computation represents the
processing load of the system. It represents the
different steps (functions) executed in the system
and triggered by one or more external stimuli. Each
step can be linked to a successor step with a control
flow. In our methodology, the application workload,
called Workload Behavior, is represented with a
UML activity diagram annotated with MARTE
profile in order to specify timing information. The
timing information contains both timing description
(computational budget, activation event, etc.) and
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
334

timing constraints (operation deadlines). Figure 2
shows the description of the workload behavior
scenario.
Figure 2: System-level end-to-end scenario.
The end-to-end computations, stereotyped
«saEndtoEndFlow», are activated by the both
external events acquisitionforABS and
acquisitionforDiagnosis with periods T
1
= 60 ms and
T
2
= 100 ms, respectively. The AntiLockControl step
is a successor step for both Dataprocessing and
Diagnosis steps. This precedence relation is modeled
with a merge node in activity diagram which
represents here the ‘or’ operator. In fact, the Limp
home step is a successor step of Diagnosis. This is
modeled with a decision node in the activity
diagram. From this, when it occurs, Diagnosis step
has two successor steps. The timing information of
each step is specified through exec- Time property.
5.1.2 Platform Resources
As explained previously, at this stage of the
methodology, a very abstract view of the system
hardware resources is needed to have an estimation
of execution time for steps. This estimation is used
to perform feasibility tests with respect to expressed
end-to-end deadlines and external events activation
rates. Execution nodes and communication resources
are specified with MARTE «saExecHost» and
«saCommHost» stereotype.
At this level, scheduling algorithm and operating
system resource concept must be specified in order
to perform feasibility tests and coordinate the
concurrent access of tasks to shared resources if
exist. This platform model is modeled in the
schedulability analysis stage (see Figure 4).
5.2 Generation of Concurrency Model
5.2.1 Mapping Workload Behavior Diagram
to Petri Nets
In order to generate concurrency model from the
workload model, a preliminary transformation of the
end-to-end scenario in Petri Nets is required. This
transformation is applied in graphical and formal
forms. Figure 3 depicts the mapping of the
Workload model of combined CCS and ABS sub-
systems to Petri Nets.
Figure 3: Petri Nets Model.
The initial node corresponding to the launching of
the scenario of the system (e.g, acquisitionABS and
acquisitionDiagnosis) is transformed into a place
marked with an initial token. Tokens are used to
simulate the dynamic behavior of systems. Activity
node is transformed into a place without any token at
the beginning connected to a transition by means of
an output arc. Thus, actions such as DataProcessing,
Diagnosis, AntiLock and LimpHome are transformed
to places without any token at the beginning.
A transition represents cause/effect places
relations and is enabled if its each input place that
contains tokens. The Diagnosis step can cross one
among all outgoing flows according to related guard
conditions. The crossing of the transition t
2
ensures
fusion of several incoming places (DataProcessing
and Diagnosis) to a single outgoing place
(AntiLock).
NewSchedulabilityAnalysisforReal-TimeSystemsbasedonMDEandPetriNetsModelatEarlyDesignStages
335

5.2.2 Transaction Identification
This stage of the methodology consists of
determining all transactions in Petri Net model
running in concurrency using the place-invariants
method. We use this analysis method to prove
concurrency (places fired with the same token) and
mutual exclusion (same place fired with different
tokens) properties. Corresponding to the Petri Nets
model (Figure 3), the input matrix IN, the output
matrix OUT and the incidence matrix C are
presented in the following:
t1 t2 t3 t4
1 0 0 0 p1
0 1 0 0 p2
IN = 0 0 0 0 p3
0 0 1 0 p4
0 1 0 1 p5
0 0 0 0 p6
t1 t2 t3 t4
0 0 0 0 p1
1 0 0 0 p2
OUT = 0 1 0 0 p3
0 0 0 0 p4
0 0 1 0 p5
0 0 0 1 p6
t1 t2 t3 t4
-1 0 0 0 p1
1 -1 0 0 p2
C = 0
1 0 0 p3
0 0 -1 0 p4
0 -1 1 -1 p5
0 0 0 1 p6
The initial marking M
0
of the net, representing
the initial distribution of tokens in places, is an
integer vector given by:
M
0
= (1 0 0 1 0 0) (3)
So, M
0
indicates that only p
1
and p
4
are marked with
only one token.
The solution based on matrix multiplication of
C X = 0 are called place invariants. For instance, the
vector X
1
= (1 1 1 0 0 0) and X
2
= (0 0 1 1 1 1) are P-
invariants, their multiplication by the incidence
matrix satisfies the property C X
1
=0 and C X
2
=0.
Note that each value in X
1
and X
2
vectors
corresponds to conservative places that can be fired
with the same token in all marking of the net.
A P-invariant indicates that the number of tokens
in all reachable markings satisfies some linear
invariant. For example, the invariant X
1
mean that all
reachable markings M of places p
1
, p
2
and p
3
denoted as M(acquisitionABS), M(DataProcessing)
and M (AntiLock) satisfy the initial marking
(in M
0
the sum of the tokens in p
1
, p
2
and p
3
is equal
to 1). The invariant X
2
mean that all reachable
markings M of places p
3
, p
4
, p
5
and p
6
satisfy the
initial marking (is equal to1):
M (acquisitionABS) + M (DataProcessing)
+ M (AntiLock) = 1
(4)
M (acquisitionDiagnosis) + M (Diagnosis)
+ M (LimpHome) + M (AntiLock) =1
(5)
From these results, we identified two transactions:
T
1
(acquisitionABS, DataProcessing and AntiLock)
with sequential order of execution and T
2
(acquisitionDiagnosis, Diagnosis, LimpHome
andAntiLock) with sequential order of execution
between both acquisitionDiagnosis and Diagnosis
steps and decision execution between both
Diagnosis and LimpHome steps.
5.2.3 Generation of the Task Set
After identifying the transactions, it is necessary to
specify the so-called schedulable Resources. In this
case study we have specified two transactions T
1
and
T
2
running all function of the system. Schedulable
Resources are identified from transactions, we apply
a transaction-based task model generation (to get
one single thread of execution for each transaction).
In our combined CCS and ABS sub-systems, we
obtain two different threads namely task1
(acquisitionforABS, DataProcessing and
AntiLockControl) and task2
(acquisitionforDiagnosis, Diagnosis, LimpHome and
AntiLockControl).
The action AntiLockControl is shared among the
two threads. This critical section is added in resource
platform and extended with the property of actions
SharedResources which actually represents a mutual
exclusion.
5.3 Schedulability Analysis
Eventually, software resource must to be obviously
allocated to processors for schedulability analysis. In
Figure 4 the two threads task1 and task2 with
priorities are included in the platform resources
SaResources to perform schedulability analysis.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
336

Figure 4: Platform Resource Model.
Thus, in this case study the scheduling algorithm
(FixedPriority) has been chosen for the execution
host hecu stereotyped as «saExecHost» and the
synchronization protocol (Priority Ceiling) has been
specified to avoid deadlocks.
The Schedulability Analysis Model, as defined
in the previous subsection, contains all the needed
information to perform the schedulability analysis
tests. Table 2 gives a tabular description of the
concurrency model showing the different parameters
required to perform schedulability analysis.
Table 2: Schedulability analysis model.
Task T
i
C
i
B
i
P
i
D
i
task1
60 25 15 20 60
task 2
100 25 0 10 100
Consequently, a schedulability analysis test can be
carried out on this model (table 2). Such test
calculates the worst case response times for each
schedulable Resource. Note that the worst-case
response time includes the blocking time B
i
. Table 3
summarizes the results of the schedulability analysis
obtained. The property isSched of the
«saEndtoEndFlow» stereotype indicates the
schedulability of each task. The response times of
the two tasks are lower than their deadlines. Thus,
this concurrency model satisfies the timing
constraints of the system.
Table 3: Schedulability analysis results.
Task Response Time isSched
task1 40 True
task 2 25 True
The evaluation of the concurrency model is
produced as an artifact of our methodology in the
form of a Schedulability Analysis Results provided
to the designer. This evaluation can guide the
designer for the refinement toward a design and an
implementation model of the system.
6 CONCLUSIONS
In this paper, we propose a methodology of
transforming workload models to concurrency
models for schedulability with hard real-time
constraints expressed at specification phase. Our
method is integrated in the software life-cycle since
the very beginning that automates the transition from
functional model to design model. The proposed
approach is based on identifying transactions
through a formal method, which can compute the
optimal solution. After identifying transactions, the
so-called schedulable Resource is specified to
perform schedulability analysis. Such approach
provides a guideline for the designer to find an
implementable concurrency model describing a real-
time application of an optimized way. The feasibility
of our approach has been successfully assessed
through an automotive case study. The future tasks
we have assigned to ourselves is to define empirical
and comparative studies to provide quality indicators
and to measure the benefits of our proposal.
REFERENCES
Anssi,S., Tucci-Piergiovanni, S., Kuntz,S., Gerard,S. and
Terrier, F., 2011. Enabling scheduling analysis for
AUTOSAR systems. In ISORC ’11, 14
th
IEEE
International Symposium on Object-Oriented Real-
Time Distributed Computing.IEEE Computer Society.
Bartolini, C., Lipari, G. and Natale, M. D.,2005. From
Functional Blocks to the Synthesis of the Architectural
Model in Embedded Real-time Applications. In RTAS’
05, Proceedings of the 11th IEEE Real-Time and
Embedded Technology and Applications Symposium
,San Francisco, CA, USA. IEEE Computer Society.
Frumin, D. and Lamazova, I., 2014. Branching Process of
Conservative Nested Petri Nets. In VPT’14, second
international workshop on Verification and Program
Transformation. EPiC Series, vol.25,pp 19-35.
Gomaa, H., 2000. Designing Concurrent, Distributed and
Real-Time Applications with UML. Addison-Wesley.
Goodenough, J. B. and Sha, L., 1988. The priority ceiling
protocol: A method for minimizing the blocking of
high priority Ada tasks, volume 8. ACM.
HadjKacem, Y., Mahfoudhi,A., Magdich, A., Karamti, W.
and Abid, M., 2012. Using MDE and Priority Time
NewSchedulabilityAnalysisforReal-TimeSystemsbasedonMDEandPetriNetsModelatEarlyDesignStages
337

Petri Nets for the schedulability analysis of embedded
systems modeled by UML activity diagrams. In
ECBS‘12, 19
th
Annual IEEE International Conference
and Workshops on the Engineering of Computer
Based Systems. IEEE Computer Society.
Kodase, S., Wang, S. and Shin, K.G.,2003. protocol: A
Transforming Structural Model to Runtime Model of
Embedded Software with Real-time Constraints. In
DATECE’03, Design, Automation and Test in Europe
Conference and Exhibition. IEEE Computer Society.
Mehiaoui,A.,Wozniak, E., Natale, M.D., Zeng, H.,
Mraidha, C., Tucci-Piergiovanni, S. and Gerard, S.,
2013. A Two-step Optimization Technique for
Functions Placement, Partitioning, and Priority
Assignment in Distributed Systems. In LCTES’13,
14thconference on Languages, Compilers and Tools
for Embedded Systems. ACM.
Mraidha, C., Tucci-Piergiovanni, S. and Gerard,S.,2011.
Optimum: a marte-based methodology for
schedulability analysis at early design stages. In ACM
SIGSOFT Software Engineering Notes, 36(1):1–8.
Murata,T., 1989. Petri nets: Properties, analysis and
applications. In Proceedings of the IEEE, vol. 77, no.
4, pp. 541-580.
Mzid, R., Mraidha, C., Babau, J.P. and Abid, M., 2014.
SRMP: A Software Pattern for Deadlocks Prevention
in Real-Time Concurrency Models. In QoSA’14, 10th
International Conference on Quality of Software
Architectures, France. ACM SIGSOFT.
Narahari, Y. and Viswanadham, N., 1985. On the
invariants of coloured Petri Nets. In Proceedings of 6
th
European Workshop on Petri Net Theory and
Applications, pp. 330-345.
OMG Object Management Group., 2008. A UML Profile
for MARTE: Modeling and Analysis of Real-Time
Embedded systems, Beta 2, Object Management
Group.
Radermacher, A., Mraidha, C., Tucci-Piergiovanni, S. and
Gérard,S.,2010. Generation of schedulable real-time
component implementations. In ETFA’10, 15
th
IEEE
International Conference on Emerging Technologies
and Factory Automation. IEEE Computer Society.
Saksena, M. and Karvelas, P., 2000. Designing for
Schedulability Integrating Schedulability Analysis
with Object-Oriented Design. In ECRTS’00, 12th Euro
micro Conference on Real-time Systems,
Stockholm,Sweden. IEEE Computer Society.
Wozniak, E., Natale, M.D., Zeng, H., Mraidha, C., Tucci-
Piergiovanni, S. and Gerard, S., 2014. Assigning Time
Budgets to Component Functions in the Design of
Time-Critical Automotive Systems. In ASE’14, 29 th
International Conference on Automated Software
Engineering. ACM.
Yang, N., Yu, H., Sun,H. and Qian,Z., 2010. Mapping
UML activity diagrams to Analyzable Petri Net
Models. In QSIC ’10, 10th International Conference
on Quality Software, pages 369–372, Washington,DC,
USA. IEEE Computer Society.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
338
