
Norm Selection for Evaluation Criterion for Placement Planning of
Active Damping Devices in Structure
Kou Miyamoto
1
, Jinhua She
2,3
, Hiroshi Hashimoto
4
and Min Wu
3
1
Interdisciplinary Graduate School of Science and Engineering, Tokyo Institute of Technology,
4259 Nagatsuta-cho, Midori-ku, Yokohama, Kanagawa 226-8503, Japan
2
School of Engineering, Tokyo University of Technology, 1404-1 Katakura, Hachioji, Tokyo 192-0982, Japan
3
School of Automation, China University of Geosciences, Wuhan 430074, China
4
Master Program of Innovation for Design and Engineering, Advanced Institute of Industrial Technology
1-10-40 Higashiooi, Shinagawa-ku, Tokyo 140-0011, Japan
Keywords:
Active Damping Device (ADD), Active Vibration Control, Combinatorial Optimization, Norm, Placement
Planning.
Abstract:
Active vibration control has been widely investigated in civil engineering. This study considers the problem
of selecting a norm for an evaluation criterion for the planning of the placement of active damping devices
(ADDs) in a structure in active vibration control. Using a 4-degree-of-freedom system as an example, we
compare the commonly used 2-norm and ∞-norm, and show that the 2-norm is a suitable choice for the
performance index of the placement planning of ADDs.
1 INTRODUCTION
Since active structural control exhibits good control
performance, it has been attracting great attention. An
active structural control system has been designed us-
ing many control methods, for example, classical con-
trol (Gucu, 2006), modern control (She et al., 2010),
advanced control (Zhang et al., 2014), and predictive
control (Tsuji et al., 2012).
Due to the constraints on the cost and structure,
active damping devices (ADDs) have usually been
placed only on the top floor or at the base of the
structure. However, the situation has been changed in
the last decade. Along with the progress of the tech-
nologies in mechatronics in recent years, both of the
cost and the size of ADDs have been reduced greatly.
This provides flexibility in the selection and place-
ment of an active structural control system (For ex-
ample, (Tokkyokiki Corporation, 2015)).
Take a four-story building as an example. An
ADD was placed on the first floor in (Yoshida et al.,
1995), on the second floor in (Gucu, 2006), and on
all floors in (She et al., 2010). However, no explana-
tions for the placement were given. And it is ques-
tionable why they placed the ADDs in those way and
whether or not it is really necessary to place ADDs on
all floors. To solve these problems, we introduced the
2-norm of a control system to evaluate the control per-
formance (Miyamoto and She, 2015). In this study,
we extend the result in (Miyamoto and She, 2015) and
explore the commonly used norms for the purpose of
evaluating the placement planning of ADDs.
2 STRUCTURAL MODEL OF
4-STORY AND CONTROL
SYSTEM
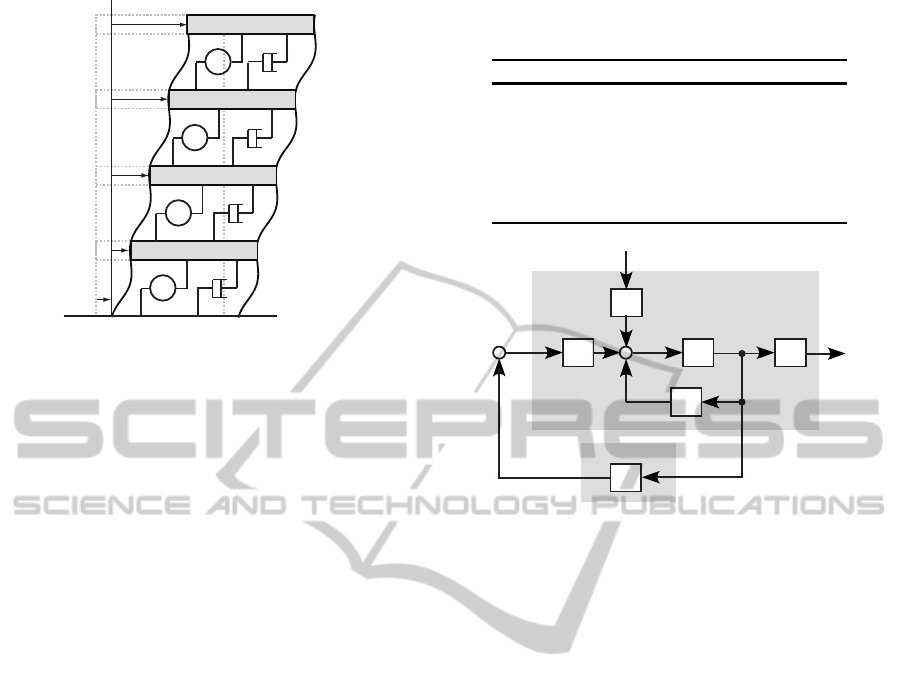
To make the discussion simple, we use a four-story
structure (Figure 1) in this paper. The achievedresults
can easily be extended to an n-story structure. The
motion of the system is described by
M
s
¨x(t) +C
s
˙x(t) + K
s
x(t) = E
u
u(t) + E
g
¨x
g
(t), (1)
where
x(t) = [x
1
(t), x
2
(t), x
3
(t), x
4
(t)]
T
,
u(t) = [ f
u1
(t), f
u2
(t), f
u3
(t), f
u4
(t)]
T
,
M
s
= diag{m
1
, m
2
, m
3
, m
4
},
C
s
=
c
1
+ c
2
−c
2
0 0
−c
2
c
2
+ c
3
−c
3
0
0 −c
2
c
3
+ c
4
−c
4
0 0 −c
4
c
4
,
117
Miyamoto K., She J., Hashimoto H. and Wu M..
Norm Selection for Evaluation Criterion for Placement Planning of Active Damping Devices in Structure.
DOI: 10.5220/0005520201170122
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 117-122
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
m
1
m
2
m
3
m
4
x
g
x
1
x
2
x
3
x
4
c
1
c
2
c
3
c
4
k
1
k
2
k
3
k
4
u1
f
u2
f
u3
f
u4
f
Figure 1: Dynamic model of four-story structure.
K
s
=
k
1
+ k
2
−k
2
0 0
−k
2
k
2
+ k
3
−k
3
0
0 −k
3
k
3
+ k
4
−k
4
0 0 −k
4
k
4
,
E
u
=
b
1
− b
2
0 0
0 b
2
− b
3
0
0 0 b
3
− b
4
0 0 0 b
4
,
E
g
= [m
1
, m
2
, m
3
, m
4
]
T
,
where the meanings of the parameters and variables
are given in Table 1. And E
u
indicates the placement
of ADDs, and b
i
(i = 1,2,3,4) in E
u
is given by
b
i
=
0, the ith floor does not have an ADD,
1, the ith floor has an ADD.
(2)
The state-space equation is
˙
ξ(t) = Aξ(t) + Bu(t) + B
d
¨x
g
(t),
y(t) = Cξ(t),
(3)
where the state vector is ξ(t) =
x
T
(t), ˙x
T
(t)
T
, the
output is y(t) = x(t), and
A =
0 I
4
−M
−1
s
K
s
−M
−1
s
C
s
, B =
0
−M
−1
s
E
u
,
B
d
=
0
−E
, C =
I
4
0
, E = [1, 1, 1, 1]
T
.
In order to verify the relationship between the
placement of ADDs and control effect, it is necessary
to construct a control system. In this study, we con-
struct a simple optimal control system by minimizing
the following performance index
J =
Z
∞
0
ξ
T
(t)Qξ(t) + u
T
(t)Ru(t)
dt, (4)
where Q (≥ 0) and R (> 0) are weighting matrices
such that (Q
1/2
,A) is observable. A feedback control
Table 1: Meanings of parameters and variables (i =
1,2,3, 4).
Symbol Meaning
m
i
[kg] Mass of the ith story
c
i
[Ns/m] Damping of the ith story
k
i
[N/m] Stiffness of the ith story
x
i
Displacement of the ith story
f
ui
Output of the ith ADD
x
g
Displacement of the ground
B
A
B
d
d(t)
x(t)x(t)
.
Controller
s I
−1
K
Plant
u(t)
C
y(t)
Figure 2: Configuration of optimal active-structural-control
system.
law is given by
u(t) = Kξ(t), (5)
K = −R
−1
B
T
P, (6)
A
T
P+ PA+ Q− PBR
−1
B
T
P = 0. (7)
As a result, the transfer function of the system from
the input to the output is
G(s) = C[sI − (A + BK)]
−1
B, (8)
where s is the operator of the Laplace transform. An
optimal state-feedback active-structural-control sys-
tem is shown in Figure 2.
3 SELECTION OF NORM FOR
PLANNING INDEX
First, we consider the norms for a signal. A norm of a
signal u(t) = [u
1
(t), u
2
(t), ·· · , u
n
(t)]
T
, kuk, has the
following properties:
1. kuk ≥ 0;
2. kuk = 0 ⇔ u(t) = 0, ∀t;
3. kauk = |a|kuk, ∀a ∈ R; and
4. ku + vk ≤ kuk + kvk .
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
118

Table 2: Relationships of the norms between input, output,
and system.
kuk
2
kuk
∞
pow(u)
kyk
2
kGk
∞
∞ ∞
kyk
∞
kGk
2
kGk
1
∞
pow(y) 0 ≤ kGk
∞
kGk
∞
1-norm, 2-norm, and ∞-norm of the signal are defined
as follows.
kuk
1
=
n
∑
i=1
Z
∞
−∞
|u
i
(t)|dt, (9)
kuk
2
=
Z
∞
−∞
u
T
(t)u(t)dt
1/2
, (10)
kuk
∞
= sup
t
|u
i
(t)|. (11)
On the other hand, if
pow(u) =
lim
T→∞
1
2T
Z
T
−T
u
T
(t)u(t)dt
1/2
(12)
exist, we call the signal a power signal. Note that
a nonzero signal can have zero average power. So,
Property 2 does not hold for (12) and pow(·) is not a
norm.
For a stable system, G(s), its H
2
norm is
kGk
2
=
1
2π
Z
∞
−∞
Trace
n
G
T
(− jω)G( jω)
o
dω
1/2
=
1
2πj
I
Trace{G
T
( ¯s)G(s)}ds
1/2
,
(13)
and its H
∞
norm is
kGk
∞
= sup
0≤ω≤∞
σ
max
{G( jω)} . (14)
Note that, for a square matrix Φ = [φ
ij
] ∈ C
n×n
,
Trace in (13) is Trace{Φ} =
∑
n
i=1
φ
ii
, and σ
max
(Φ) in
(14) is the maximum singular value of Φ.
The definitions of induced norms givethe relation-
ships of the norms between the input, u(t), the out-
put, y(t), and the system G(s) (Table 2) (Doyle et al.,
2009):
kGk
1
= sup
kuk
∞
6=0
kyk
∞
kuk
∞
, (15)
kGk
2
= sup
kuk
2
6=0
kyk
∞
kuk
2
, (16)
kGk
∞
= sup
kuk
2
6=0
kyk
2
kuk
2
= sup
pow(u)6=0
pow(y)
pow(u)
. (17)
It is clear from the above relationships that, to sup-
press the vibration caused by an earthquake and/or a
typhoon, it is suitable to use the 1-normor the ∞-norm
of the system from the disturbance to the output to
evaluate the effect caused by a disturbance, because
the worst output caused by the disturbances can be
evaluate by the 1- or ∞-norms of the system.
However, those norms may not be suitable for the
evaluation of the placement of active damping de-
vices. The reason is as follows. To suppress vibra-
tion quickly and efficiently, for a given control input
with limited power, the bigger the output produced by
the control input is, the more desirable the system is.
From this viewpoint, the use of the 2-norm of the sys-
tem from the control input to the output is suitable for
the planning of the placement of ADDs. We use a nu-
merical example to examine and this and compare the
use of norms in the next section.
Let k be the number of ADDs. The placement
problem is divided into two cases:
(1) k is not fixed: The optimal problem is
max
b
1
,b
2
,b
3
,b
4
∈{0,1}
kGk
2
. (18)
(2) k is fixed: The optimal problem is
max
b
1
,b
2
,b
3
,b
4
∈{0,1},
∑
4
i=1
b
i
=k
kGk
2
. (19)
Note that these combinatorial optimization problems
are an integer programming problem, and can easily
be solved using well-known solvers.
4 NUMERICAL EXAMPLE
For simplicity, we only verify and compare the 2-
norm and ∞-norm of the system in this section.
The parameters of a four-story structure are
(Yoshida et al., 1995)
m
1
= 0.828, m
2
= m
3
= 0.842, m
4
= 0.640,
k
1
= 400, k
2
= 1600, k
3
= 1302, k
4
= 160,
c
1
= 7.5, c
2
= c
3
= c
4
= 0.02.
(20)
For the design of a control system, the weighting ma-
trices in (4) were chosen to be
Q = 300× diag{100, 100, 100, 100, 1, 1, 1, 1}, R = I
k
,
(21)
where k is the number of ADDs.
This study used the ground acceleration data of
Noto Peninsula earthquake [Figure 3 (a) and (b)],
which has a low frequency, and Kobe earthquake
[Figure 3 (c) and (d)], which features randomness,
as disturbances in simulations (Japan Meteorological
Agency, 2015).
The peak-to-peak values (PPVs) of the maximum
displacements for Noto Peninsula earthquake for dif-
ferent placement plans of ADDs are shown in Table
NormSelectionforEvaluationCriterionforPlacementPlanningofActiveDampingDevicesinStructure
119

(a)
(c)
-400
-200
0
200
400
50
403020100
t [s]
x
g
[cm/s ] (Noto)
2
..
x
g
[cm/s ] (Kobe)
2
..
Spectrum (x 10
-3
)
400
300
200
100
0
Spectrum (x 10
-9
)
1086420
Frequency [Hz]
(b)
(d)
20
15
10
5
0
10
86420
Frequency [Hz]
-800
-400
0
400
50403020100
t
[s]
Figure 3: Input earthquake waves: (a) Noto Peninsula earthquake, (b) Power spectrum of Noto Peninsula earthquake; (c)
Kobe earthquake; and (d) Power spectrum of Kobe earthquake.
Table 3: Relationship between the placement of ADDs (up-
per row) and the PPV of the maximum displacement for
Noto Peninsula earthquake [cm] (lower row).
Sys1234 Sys123 Sys124 Sys12
7.27 (4F) 7.39 (4F) 7.66 (4F) 7.85 (4F)
Sys134 Sys13 Sys14 Sys1
7.98 (4F) 8.15 (4F) 8.50 (4F) 8.84 (4F)
Sys234 Sys23 Sys24 Sys2
11.36 (4F) 11.54 (4F) 11.95 (4F) 12.18 (4F)
Sys34 Sys3 Sys4
13.33 (4F) 13.65 (4F) 15.68 (4F)
3. In the table, the word in the parentheses in the
right column shows the place where the maximum
displacement occurred; and SysXYZ indicates that
the control system has ADDs at the X-th, Y-th, and
Z-th floors, for example, Sys1234 means that it has
ADDs at the first to the fourth floors.
Tables 3 and 4 show that the ascending order of the
maximum PPV for the placement of ADDs is almost
the same for those two quite different earthquakes.
And Sys1 has the minimum PPV for the use of one
ADD, Sys12 is for two and Sys123 is for three ADDs.
Let PPV
(max)
SysN
be the maximum PPV of SysN. The
relative difference of the PPV for the placement of
ADDs is defined to be
δ
SysN
=
PPV
(max)
SysN
− PPV
(max)
Sys1234
PPV
(max)
Sys1234
× 100%. (22)
Table 4: Relationship between the placement of ADDs (up-
per row) and the PPV of the maximum displacement for
Kobe Peninsula earthquake [cm] (lower row).
Sys1234 Sys123 Sys124 Sys12
10.83 (4F) 11.02 (4F) 11.45 (4F) 11.81 (4F)
Sys134 Sys13 Sys234 Sys14
11.98 (4F) 12.25 (4F) 12.63 (4F) 12.86 (4F)
Sys1 Sys23 Sys24 Sys2
13.41 (4F) 20.34 (4F) 21.41 (4F) 21.90 (4F)
Sys34 Sys3 Sys4
23.79 (4F) 24.27 (4F) 29.17 (4F)
It is in the range of 2-56% for Noto earthquake and
2-17% for Kobe earthquake for three ADDs; in the
range of 8-83% for Noto earthquake and 9-120% for
Kobe earthquake for two ADDs; and in the range of
22-116% for Noto earthquake and 23-169% for Kobe
earthquake for one ADD. This clearly shows that,
while the increase of the ADDs improves the control
performance, suitable placement of ADDs also dra-
matically changes the control performance. Observ-
ing the above results yields the follows. First, since
the smallest difference of δ
SysN
between the use of
one and four ADDs for a suitable placement is about
22%, that between two and four is about 8%, and that
between three and four is about 2%; there is no need
to place ADDs at all floors. Second, the largest differ-
ence of δ
SysN
is as large as 146% for different place-
ment of the same number of ADDs. So, if we choose
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
120

Table 5: Norms of active structural control system for (21).
Placement H
2
H
∞
Sys1234 0.01161 0.004301
Sys123 0.01118 0.004300
Sys134 0.01111 0.004282
Sys124 0.01109 0.004294
Sys13 0.01064 0.004281
Sys12 0.01054 0.004293
Sys14 0.01048 0.004275
Sys1 0.009854 0.004274
Sys234 0.008719 0.003894
Sys23 0.008106 0.003886
Sys24 0.007717 0.003819
Sys34 0.007048 0.003454
Sys2 0.006763 0.003805
Sys3 0.006102 0.003388
Sys4 0.004640 0.001951
(a)
(b)
16
14
12
10
8
6
Max. PPV dis. (Noto) [cm]
12
10864
||
G||
2
(x 1000)
R
2
= 0.9769
30
25
20
15
10
Max. PPV dis. (Kobe) [cm]
12
10864
||
G||
2
(x 1000)
R
2
= 0.9334
Figure 4: Relationship between the maximum PPV of the
output and the H
2
norm of the system for (a) Noto Peninsula
earthquake and (b) Kobe earthquake.
suitable floors to place devices, we can use a small
number of ADDs to achieve satisfactory aseismic ef-
fect.
Table 5 shows the calculated results of the H
2
and
H
∞
norms of G(s) for different placement of ADDs.
The relationships between the maximum PPV of the
output and the H
2
norm is shown in Figure 4, and
that between the maximum PPV and the H
∞
norm is
shown in Figure 5.
(a)
(b)
17
16
15
14
13
Max. PPV dis. (Noto) [cm]
4.5
4.03.53.02.52.01.5
||
G||
∞
(x 1000)
34
32
30
28
26
24
Max. PPV dis. (Kobe) [cm]
4.5
4.03.53.02.52.01.5
||
G||
∞
(x 1000)
Figure 5: Relationship between the maximum PPVs of the
outputs and the H
∞
norm of the system for (a) Noto Penin-
sula earthquake and (b) Kobe earthquake.
It is clear from Figures 4 and 5 that the maximum
PPV of the output is basically in inverse proportion to
the H
2
or H
∞
norms of the system. And all of the co-
efficients of determination, R
2
, are larger than 0.9 in
Figure 4. However, the H
∞
norms of the system with
good control performance all almost have the same
value, 0.043, as shown in Table 5. Recall that the H
∞
norm of an SISO system is the peak gain value of its
Bode plot. It is easy to understand that the values be-
come almost identical when a vibration mode is sup-
pressed. As a result, if we use the H
∞
norm of the
system as a performance index to evaluate the place-
ment of ADDs, it may just show good control perfor-
mance for those disturbances with the frequency cor-
responding to the peak gain value of the Bode plot,
and does not guarantee the aseismic effect for distur-
bances with other frequencies. From this viewpoint,
we can say that it is not suitable to use the H
∞
norm of
a control system to evaluate the placement planning.
On the other hand, as shown in (13), the H
2
norm
of a control system is the square root of the area of its
frequency-response gain. It is basically different for
different placement of ADDs. So, it is suitable to use
the H
2
norm of the transfer function from the control
input to the output to evaluate the placement planning.
Another question is if the reduction of the number
of ADDs results in the increase of the power of the
control input of each ADD. To answer this question,
we plot the relationship between the maximum PPVs
NormSelectionforEvaluationCriterionforPlacementPlanningofActiveDampingDevicesinStructure
121
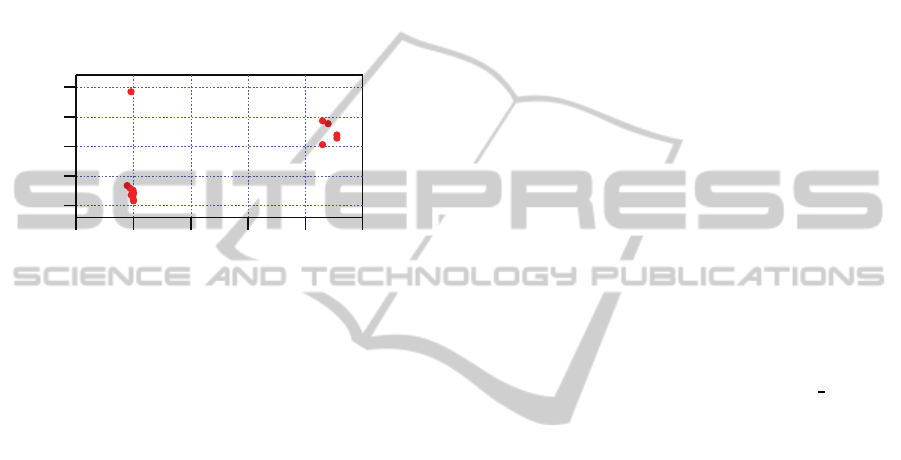
of the outputs and the 2-norms of the control inputs
for Kobe earthquake in Figure 6. The figure shows
that the power of the control input has no significant
correlation. For example, Sys1 uses less input power
than Sys23 does, but it yields much better control per-
formance. So, good control performance produced by
the control system with a small number of devices,
which are given by the optimal placement (18), does
not mean the increase of control-input power. This
also shows the importance of the optimal placement
of ADDs.
Sys1
Sys14
Sys234
Sys13
Sys134
Sys12
Sys124
Sys123
Sys1234
Sys4
30
25
20
15
10
Max. PPV dis. (Kobe) [cm]
1.81.61.41.21.00.8
||
u
i
||
2
/ ||u
1234
||
2
}
Sys3
Sys34
Sys2
Sys24
Sys23
{
Figure 6: Relationship between the maximum PPVs of the
outputs and the 2-norms of the control inputs for Kobe
earthquake.
5 CONCLUSION
In this study, we considered the problem of the place-
ment of ADDs to perform active structural control.
To suitably evaluate the placement planning, we ex-
amined the 1-, 2-, and ∞-norms of a control system
from the control input to the output; and employed
the H
2
norm for the evaluation. We used a four-story
structure as an example to demonstrate the validity of
the selection. The following points were clarified.
1. Increasing the number of ADDs does not neces-
sarily lead to the improvement of control perfor-
mance. Placing a small number of ADDs at suit-
able floors achieves satisfactory control result.
2. The H
2
norm of the transfer function from the
control input to the output is suitable for a per-
formance index to find out an optimal placement
of ADDs.
ACKNOWLEDGEMENTS
This study was supported in part by the National
Natural Science Foundation of China under Grants
61473313 and 61210011; and by the Grant-in-Aid for
Scientific Research (C), Japan Society for the Promo-
tion of Science (JSPS) under Grant 26350673.
REFERENCES
Doyle, J., Francis, B., and Tannenbaum, A. (2009). Feed-
back Control Theory. Dover Publications, New York.
Gucu, R. (2006). Sliding mode and PID control of structural
system against earthquake. Mathematical and com-
puter modeling, 44:314-328.
Japan Meteorological Agency (2015) Mea-
sured data of severe earthquakes for
main earthquakes. [Online available]
http://www.data.jma.go.jp/svd/eqev/data/kyoshin/
jishin/index.html (accessed on 26 September, 2014)
Miyamoto, K. and She, J. (2015). Optimal Planning of Ac-
tuators in Structure Using H
2
Norm as Planning Index.
Transactions of the Japan Society of Mechanical En-
gineers Series C, (under review).
She, J., Sekiya, K., Wu, M., and Lei, Q. (2010). Ac-
tive Structural Control with Input Dead Zone Based
on Equivalent-Input-Disturbance Approach. In Proc.
of the 36th Annual conference of the IEEE Indus-
trial Electronics Society (IECON 2010), pages 47-52,
IEEE.
Tokkyokiki Corporation (2015). Vibration con-
trol Technology ω series. [Online available]
http://www.tokkyokiki.co.jp/product/product
o.html
(accessed on 26 September, 2014)
Tsuji, T., Nakamura, H., and Kagimura, S. (2012). Stud-
ies on an active preview control of structures and
applicability of predicted earthquake motions. Jour-
nal of Japan Society of Civil Engineers, Ser. A1
(Structural Engineering & Earthquake Engineering),
68:110-123.
Yoshida, K., Kang, S., and Kim, T. (1995). LQG Con-
trol and H
∞
Control of Vibration Isolation for Multi-
Degrees-of-Freedom Systems. Transactions of the
Japan Society of Mechanical Engineers Series C,
61:975-980.
Zhang, H., Wang, R., Wang, J., and Shi, Y. (2014). Ro-
bust finite frequency H
∞
static-output-feedback con-
trol with application to vibration active control of
structural systems. Mechatronics, 24:354-366.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
122
