
Challenges when Creating Variable-structure Models
Alexandra Mehlhase, Daniel Gomez Esperon and Thomas Karbe
Software Engineering, Technische Universit
¨
at Berlin, Ernst-Reuter-Platz 7, 10587, Berlin, Germany
Keywords:
Variable-structure models, Mathematical models, Differential equations, Modeling guidelines.
Abstract:
Variable-structure models can switch their system of equations during a simulation, allowing for a change
of level of detail or behavior. The need for this kind of models has been well-established, and there are
simulation environments that can handle them. While most research papers on this topic focus on language
and tool issues regarding variable-structure models, in this paper, we will shed some light on the pragmatics
of actually creating such a model in a reusable way. During the construction of a variable-structure model, the
modeler will face several challenges, such as the initialization of new modes during mode switches. We will
collect and discuss the most important challenges and, if possible, provide rules of thumb on how to handle
these challenges appropriately.
1 INTRODUCTION
According to Mahr, modeling means always to create
a model of something for some purpose (Mahr, 2008).
Thus, on the one hand, a model is always an abstract
representation of some other entity. Only some of its
properties are taken over to the model, while others
are left out on purpose. On the other hand, the se-
lection of those properties is guided by the purpose
of the model. In (Top, 1993) the author gives a more
specific explanation:
The modeling problem is to construct the most
simple artifact that allows an adequate answer
to a given query.
Therefore, the quality of a model could be judged by
the simplicity of the model, as long as it fulfills its
purpose.
This means that the main challenge in modeling is
to find the right level of abstraction to answer a given
query. It should not include any information that is
not necessary for the answer, but all information that
is needed.
In the field of mathematical models with
differential-algebraic equations (DAEs), there are two
major factors that add complexity to the modeling
problem. First, models tend to become quite large and
are therefore split into submodels, which are models
on their own for some part of the problem domain
which can be reused. Second, during the course of a
simulation sometimes different aspects of the problem
are of interest or needed in a different level of detail.
An example of this is the model of an airplane
taking off on a runway, then increasing height, and
finally arriving at traveling height. Since in this ex-
ample three different stages of a flight are simulated,
there should be three specific models, one for each
stage. Then, the flight simulation should switch be-
tween the different models when appropriate.
Models with different states between which they
can switch during simulation depending on the cur-
rent situation are called variable-structure models.
Each state in such a model is called a mode, and the
model can switch between modes through transitions.
While simulating such a model one mode is always
active and represents a state of the modeled system.
When a transition is activated through a guard, a new
mode becomes active. The new mode then needs to
be initialized and the simulation continues in the new
mode.
It is well-established that there is a need for
variable-structure models and that they can gener-
ally be handled in a simulation environment (Heinzl
et al., 2012), (Elmqvist et al., 1993). However, these
environments are mostly prototypes or experimental
frameworks for now. In these specialized frameworks
the models need to be reimplemented in the language
specific to the framework. Common simulation envi-
ronments like Dymola (Dassault Systems, 2015) and
Simulink (The MathWorks Inc., 2013a) provide only
limited support of variable-structure models.
Therefore, there is not much experience with mod-
eling large models or how to adapt models, which al-
101
Mehlhase A., Gomez Esperon D. and Karbe T..
Challenges when Creating Variable-structure Models.
DOI: 10.5220/0005521601010110
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 101-110
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

ready exist, in simulation environments like Dymola
or Simulink. Using modes and transitions between
modes gives modelers a much wider tool set, but it
also introduces new challenges that have to be con-
sidered. In non-variable-structure models, the mod-
eler just had to find appropriate start values for the
one model. Now, he also has to decide when and
how often a mode switch should take place, and for
each mode switch, how to initialize the newly acti-
vated mode.
In this paper, we regard modeling of variable-
structure models, since it is already shown in differ-
ent papers that variable-structure models can be sim-
ulated. We present a collection of challenges that
often occur when creating variable-structure models,
and give rules of thumb (RoT) to handle them. These
challenges and ruled of thumb are regarded indepen-
dent of the domain and hold true for models which are
described with differential-algebraic equations.
Chapter 2 gives a basic overview of the state of
the art in variable-structure modeling and simulation.
Chapter 3 covers the architecture of variable-structure
models regarding their equations, variables and inter-
faces. In Chapter 4 the initialization routines are dis-
cussed in detail while Chapter 5 focuses on guards of
transitions. Chapter 6 summarizes the evaluation of
the proposed rules of thumb. Chapter 7 concludes
the paper and presents future works.
2 STATE OF THE ART
General purpose modeling languages like Modelica
(by the Modelica Association (The Modelica Asso-
ciation, 2012)) and Matlab Simulink are well estab-
lished but their support for variable-structure models
is very limited. This special form of modeling has
been investigated for more than twenty years (Heinzl
et al., 2012). Many different experimental languages
and simulation environments have been developed to
model and simulate changes in model structure.
One of these tools is MOSILAB (Nytsch-Geusen
et al., 2005), (GENSIM Project, 2007), which uses
a Modelica-like language to describe the models.
The modes and transitions are described through a
Statecharts-like (Harel, 1987) view. The simulation
is realized through an integrated simulation engine.
In MOSILAB only Index-0 models can be simulated
since no index-reduction is integrated yet.
Another approach is the experimental language
SOL which provides a language and a simulator (Zim-
mer, 2010). The variable-structure simulation frame-
work of SOL can handle higher-index models.
Another tool often used is Ptolemy (Ptolemaeus,
2014) which also enables the modeler to use different
modes.
Other approaches to describe variable-structure
models in specific languages are the theorem prover
for hybrid systems called KeYmaera (Platzer and
Quesel, 2008), the functional language Hydra (Nils-
son et al., 2003), the event based approach of DEVS
(Pawletta et al., 2002), the Matlab/Simulink libraries
SimEvents (Clune et al., 2006), and Stateflow (The
MathWorks Inc., 2013b).
A framework to model and simulate variable-
structure models without having to implement the
modes in a new language is introduced in (Mehlhase,
2013). Here, common simulation environments are
used to simulate each mode whilst the mode changes
are handled by the framework.
The current state of the art is that variable-
structure models can be modeled and simulated.
There are algorithms, tools and frameworks to sim-
ulate and test such models. A formalization ap-
proach to tackle challenges of hybrid systems, to
which variable-structure models belong, is described
in (Mosterman and Biswas, 1997).
Yet, it is not well-established what has to be con-
sidered and what challenges occur compared to clas-
sical modeling.
3 BASIC ARCHITECTURE OF
VARIABLE-STRUCTURE
MODELS
It is important to understand the principles and goals
in classical modeling before discussing the challenges
of variable-structure modeling in detail.
A real system usually consists of many related
components. Each of these components is also a sys-
tem and can consist of components itself. It is there-
fore built hierarchically. This approach is necessary
to be able to build systems out of components and ex-
change components if necessary.
While modeling such a system it is helpful to use
the same approach and create a model that has com-
ponents which can again consist of components. A
model that describes a part of a whole will be called
component. Components on one hierarchy level can
be connected through the variables in their interfaces.
An interface is a collection of variables and compo-
nents can have an arbitrary number of interfaces. Fig-
ure 1 shows three components (A, B, C) connected
through their interfaces (circles appended to the com-
ponents). These interfaces are connected through
equations (rectangles on connecting line) which de-
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
102
scribe the relation between these interfaces. We will
call these equations relation-equations to not confuse
them with Modelica connect-equations since they do
not have the same semantics. The relation-equations
can be any kind of equation to specify the connec-
tion of interfaces. Therefore, the relation-equations
are a more general description and abstract the Mod-
elica connect-equations as well as Simulink connec-
tions between interfaces.
A
B C
{a
1
}
a
1
= f (b
1
)
{b
1
}
{a
2
}
a
2
= c
2
{c
2
}
{b
2
, b
3
}
b
2
= 2 ∗c
1
b
3
= c
1
{c
1
}
Figure 1: Model with three components.
Each component encapsulates behavior and
should be usable in different contexts. A created com-
ponent can therefore be used many times as long as
the interfaces of the component can be connected.
When looking at variable-structure models, the
exchange of components itself needs to be mod-
eled. Therefore, it is sensible to encapsulate such ex-
changes in components to enable reusability.
3.1 Modes and Transitions
A variable-structure model generally consists of an ar-
bitrary number of modes. A mode is a component
which can be exchanged during simulation through
another component.
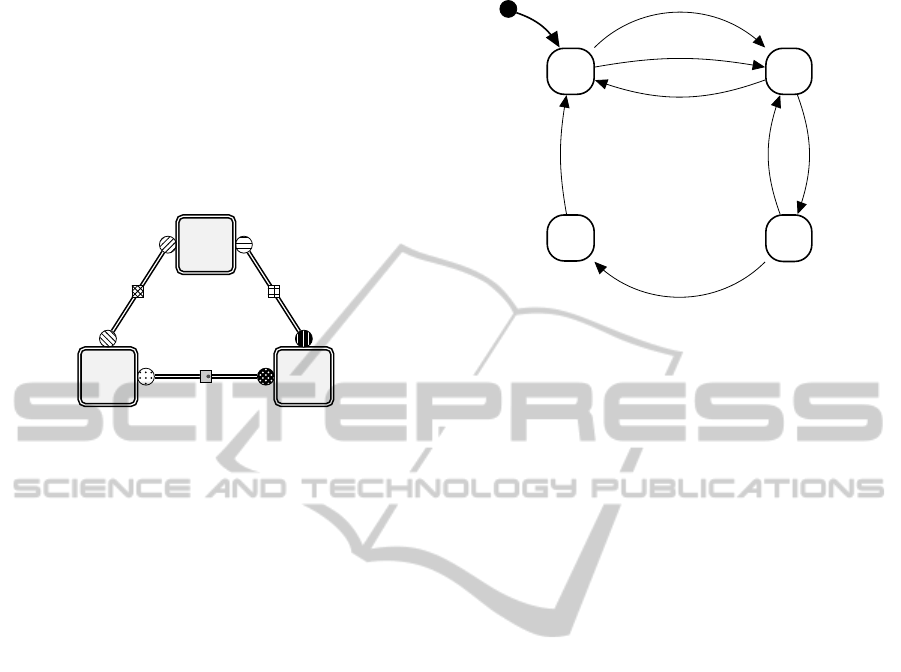
Figure 2 shows a simple variable-structure model
in a Statecharts-like syntax. The model consists of
four modes (A, B, C and D) and is always represented
by one of them.
Like in Statecharts an initial mode has to be de-
fined. Furthermore, the first mode might need to be
initialized with user-defined values. This initializa-
tion process is equivalent in classical modeling. In
this example mode A is the initial mode and is initial-
ized through init.
Each transition leads from one mode to another.
A transition is activated when a guard (e.g. a1
g
, b1
g
)
becomes true. When a transition is activated, the sim-
ulation of a mode stops and the new mode needs to
be identified. This new mode needs to be initialized
through a routine defined in the transition. During the
mode switch the simulation time does not continue.
A B
C
D
a1
g
⇒ B1
i
a2
g
⇒ B2
i
c1
g
⇒ D
i
d
g
⇒ A2
i
b1
g
⇒ A1
i
b1
g
⇒ C
i
b2
g
⇒ B3
i
init
Figure 2: Variable-structure model with four modes.
Simulation time only moves on during the simulation
of a mode.
A transition therefore consists of the following in-
formation:
• Pre mode
• Post mode
• Guard
• Initialization routine.
3.2 Modes in Components
So far we have looked at components and their rela-
tion and modes in general. Now we take a look at
modes inside a component. Models usually consist of
components which can often be used in other mod-
els. Many modeling tools/languages (e.g. Modelica)
have libraries with components. These can be used to
create a specific model. The same should be possible
with components containing modes. To accomplish
this the modes and components have to fulfill certain
criteria.
3.2.1 Interfaces
Figure 3 shows a model with two components.
Component A has two modes, therefore it is repre-
sented by either the component A1 or A2 at a specific
simulation time. If the interfaces of A1 and A2 are
identical, the relation-equations to the component B
do not have to change during a mode switch.
Only the intern variables and equations of A
change.
RoT-1 uniform interface I: For reusable compo-
nents all modes in the component should have the
same interfaces.
ChallengeswhenCreatingVariable-structureModels
103
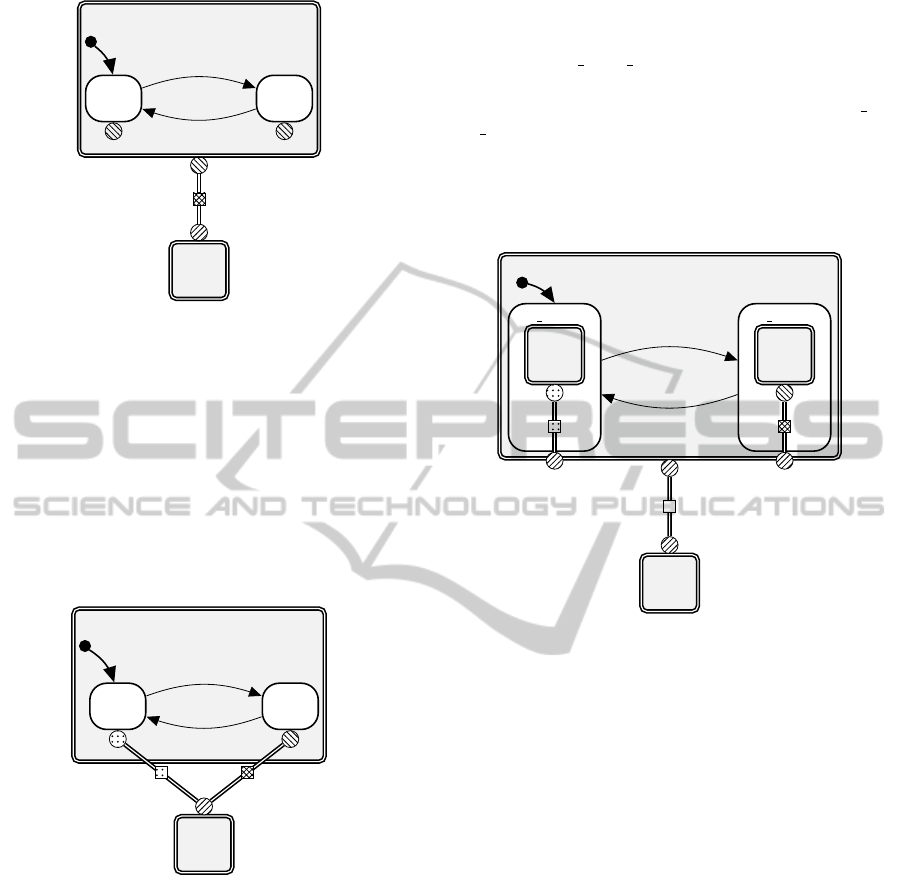
A
A1 A2
a1
g
⇒ A2
i
a2
g
⇒ A1
i
init
B
Figure 3: Component A consists of two modes with identi-
cal interfaces.
When this model is simulated, it starts with the
compositions of A1 and B since A1 is the initial mode
of A. When the transition is activated, the component
A2 is initialized and the simulation of the composition
of A and B is resumed.
If the interfaces of the modes are not identical, the
mode switch is not as simple. The mode switch can-
not be defined locally since the relation-equations to
the other components also need to change.
A
B
A1 A2
a1
g
⇒ A2
i
a2
g
⇒ A1
i
init
Figure 4: Model with two components. Component A has
two modes with different interfaces.
Figure 4 shows such an example. Such a model
can be created but the advantage of reusability is lost
since component A with its modes cannot be used in
other models without adapting the context the com-
ponent is used in. In Figure 4 the relation-equations
are different for the two modes, represented through
the two separate connecting lines. The goal is to cre-
ate components with modes which can be used in
different models the same way a component without
modes can be used.
The interfaces of the modes should be adapted
to be the same in all modes. Adapting the inter-
faces is straight forward since the individual relation-
equations of the modes can be used to define the new
interface which then matches the needed one. Fig-
ure 5 shows this approach graphically. New modes
are created (A1 a, A2 a) that wrap the old modes (A1,
A2) to adapt the interfaces. The old modes (A1, A2)
are then only components and the new modes (A1 a,
A2 a) consist of the old mode and the old relation-
equation with the new interface.
The mode switch is again local inside a compo-
nent and Component B needs no information about
the mode switch.
A1 a A2 a
A
B
A1 A2
a1
g
⇒ A2
i
a2
g
⇒ A1
i
init
Figure 5: Model with adapted interfaces.
RoT-2 uniform interface II: If modes in compo-
nents do not have the same interface, the modes
should be encapsulated by an adapter mode.
3.2.2 Variables and Equations Inside Modes
The different combinations of active modes with other
components must lead to a solvable system of equa-
tions. In Figure 4, this means the composition of A1
and B as well as A2 and B must be a solvable system
of equations.
RoT-3 solvable combinations I: All reachable mode
combinations must lead to a solvable system of
equations.
For the simulation in current environments it is a
necessary requirement that the number of equations
and number of unknown variables in a model are
equal. As presented in (Broman, 2010) one can depict
a Constrained Delta C
∆
for each component. This C
∆
represents the delta of equations to unknown variables
for each component. A model can only be simulated
if the C
∆
is zero. Otherwise the system of equations
is not solvable. In a component consisting of com-
ponents the relation-equations as well as the variables
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
104

and equation of each component are taken into ac-
count.
To define encapsulated components with modes
the C
∆
has to be the same in all modes. Otherwise the
modes are not locally exchangeable since the overall
C
∆
would differ from zero if the context of the com-
ponent does not change during a local mode switch.
RoT-4 solvable combinations II: All modes in a
component must have the same C
∆
for locally de-
finable mode switches.
4 INITIALIZATION
To understand the importance of a correct initializa-
tion it is necessary to look at the basics first. The ini-
tialization of a set of differential-algebraic equations
influences the results and sometimes even the stability
of the simulation’s results significantly.
A steady-state is often sought after for the initial-
ization to minimize the possibility of wrong results
(Casella et al., 2011).
When regarding variable-structure models it is not
only necessary to find a consistent set of values for the
start of the simulation. Instead, for each mode switch
a separate initialization needs to take place. This ini-
tialization mostly depends on the state the model was
in when the transition was activated and it is not suf-
ficient to use static values. The initialization routine
is part of the transition since only the transition has
information about the previous and the next mode.
RoT-5 initialization: Each transition must define
an initialization routine.
4.1 Using the Last State of the Old
Mode
The easiest way to initialize a mode is by starting
the simulation where the old mode left off. An ex-
ample of this is a pendulum (mode 1) becoming a
falling mass (mode 2) when the centrifugal force is
smaller than zero. In this case the simulation of the
falling mass should start at the exact position and ve-
locity where the pendulum simulation left off. As-
suming both modes have the necessary variables x,
y, vx and vy representing the position and velocity, a
simple one-to-one-mapping is possible that maps the
old state to the new state.
If the modes of a transition do not have the same
variables, such a one-to-one-mapping of values is not
possible. For the above example the pendulum mode
might only have the variables for the angle ϕ and the
angular velocity der ϕ. The falling mass on the other
hand needs the Cartesian coordinates. In this scenario
a calculation needs to take place to transform the old
state to the new state (mapping).
RoT-6 initialization Function: The initialization
can use the previously simulated data of the old
mode to initialize the next mode through a map-
ping.
4.2 Using Past Data
In variable-structure models it is not only possible to
exchange components but also to delete or generate
new components. In case an added component has
not previously been in the model it might not be suffi-
cient to use only the previously calculated simulation
results. An example of such a model is a pipe net-
work where some of the pipes where cut off through
valves at the beginning of the simulation. When a
valve opens, further pipes need to be simulated. The
modeler has to give information about the state the
new pipe or pipes should be in after a transition.
RoT-7 component Generation: The initialization
can use external data.
Another scenario might be that a pipe gets cut off,
which enforces a mode switch and later on the pipe is
added again. In such a case it can be sensible to use
the old state of the pipe for its initialization. Meaning
that not only the past data of the previous mode is
necessary in the initialization routine but also the past
data of this mode’s own previous state.
RoT-8 state Storage: The initialization has access
to previous states of the new mode.
4.3 Time Consuming Transitions
Transitions also require modeling since they describe
the whole switching process from one mode to an-
other. This model did for now not need any simu-
lation time and was not simulated by a solver. The
simulation of the previous mode stopped and so did
the simulation time until the next mode’s simulation
was started.
Sometimes such an abrupt change is not feasible
and leads to discontinuities in the simulation’s results,
which should usually be avoided. Therefore, transi-
tions can be modeled with their own mode. Mean-
ing that for a desired switch from A to B there ex-
ists a third mode AB which models the transition. Of
course, then there need to be transitions from A − AB
and AB − B but since the mode AB is created merely
ChallengeswhenCreatingVariable-structureModels
105
for the transition from A to B the two transitions can
usually be kept quite simple.
Two different kinds of in-between modes are pos-
sible:
1. Deriving the in-between Mode from the modes
A and B: An in-between mode can be derived
by simulating both modes simultaneously. Dur-
ing the simulation of the in-between mode results
of the two modes are weighted. The simulation
is started with the old mode weighted with 100%
and the new mode with 0% and altered until the
old mode has a weight of 0% and the new one of
100%. The mode switch should then not have any
discontinuities in the important variable’s values.
This approach is possible when the level of detail
is changed. If the behavior changes, it is usually
not the case that during a switching period both
modes are valid. A drawback of this method is
that during the mode switch two systems of equa-
tions are used, which makes the simulated system
of equations quite large.
2. Creating a new in-between Mode: A new mode
can be defined that models the mode switch with
equations exclusively for this mode switch. This
is for instance useful for clutches. In one mode
the clutch is disengaged in the other one engaged.
The transition is neither possible to model with
the one or the other mode since the clutch is some-
where in between.
This approach is possible when there is a switch
in behavior. Usually this means that more modes
need to be regarded than were obvious.
RoT-9 Time Consuming Transitions: For complex
transitions an in-between mode should be intro-
duced.
4.4 Jump Into the Past
The above initializations assumed that the simula-
tion of the next mode starts where the old simula-
tion stopped. Sometimes, it is necessary that the new
mode’s simulation does not start exactly where the old
simulation left off. If the current mode is less detailed,
the deviation that causes the transition event might be
detected too late. In such a case it is useful to go back
in time during a mode switch to let the new mode’s
simulation start off at a time step when the result was
more accurate. Then, a critical point can be calculated
anew to make certain that the values are correct. Fur-
thermore, it allows to calculate the new start values in
a region when the old mode is still in a state where it
was valid, e.g. steady-state.
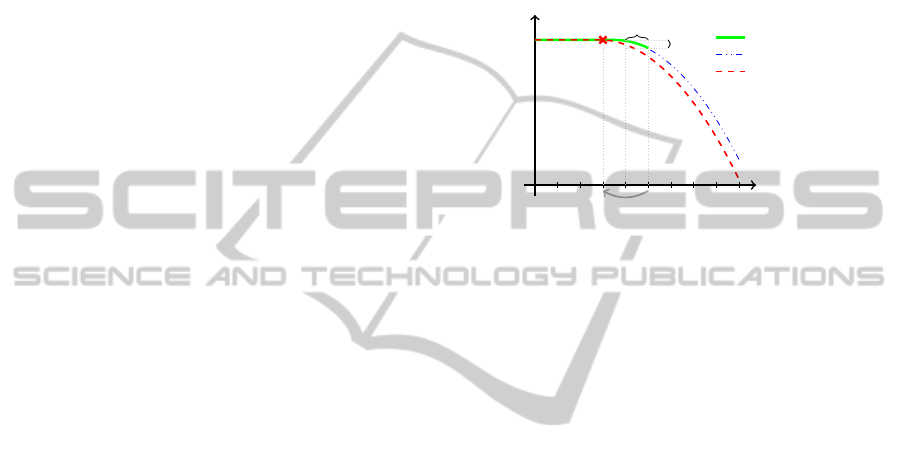
Figure 6 shows how the results of such a simula-
tion might look like. It is assumed that a less detailed
mode is used with a variable x. The delta between
the values of x from two time steps is used to acti-
vate a transition. Since the mode is assumed to be
less detailed, the variable might not change as fast as
it would in a more detailed mode. When the transition
is activated there is a time jump into the past and the
more detailed mode is initialized with past data.
Time
x
t
x
Jump
less detailed
detailed
detailed
h
∆x
Figure 6: Mode switch with a jump into the past
Here the modeler has to decide how far the sim-
ulation time should be reset. For the specified time,
initialization values need to be available.
RoT-10 past states: The initialization has access to
past states to allow for steps back in time.
4.5 Initialization for Modes in
Components
The approaches above regarded the initialization in
general and they are valid for transitions on the high-
est hierarchy level and on the component level.
When looking at the component level, the scope of
the components has to be considered. Since the idea
of a component is to encapsulate behavior, a compo-
nent can only use data available in this component.
This applies to modes in a component as well as to
the transitions between these modes.
Consider Figure 7 which presents a model with
two components. One component represents a pipe
which is split into 100 elements to calculate the mass
(m), pressure (p) and temperature (T) accurately. The
other mode only has 10 elements and is less detailed.
This gives us the means to calculate the values of the
above variables more or less accurately during the
simulation. The pipe is connected on one side to a
throttle which calculates a mass flow out of the pipe
depending on the temperature and pressure from the
pipe’s end and a parameter P. The pressure and tem-
perature are assumed to be inputs for the throttle while
the mass flow is the output.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
106

Pipe
Pipe detailed
elements = 100
Pipe simple
elements = 10
extend transition(t id): init new
t id: guard ⇒ init
init
Throttle
m f low = f (p, T, P)
p, T , m f low
p, T , m f low
p, T , m f low p, T , m f low
Figure 7: Pipe model with components Pipe and Throttle.
The initial state of the model is the pipe with 100
elements connected with the throttle. When a mode
switch occurs, for instance because the temperatures
in the elements do not differ much anymore, the new
mode with only 10 elements needs to be initialized.
In this case it is sensible to combine 10 elements into
one new element, e.g. t1
new
= mean(t1
old
, . . .t10
old
),
m
new
= sum(m1
old
, . . . , m10
old
).
During a mode switch as described above the val-
ues of T and p change during the initialization rou-
tine. When the pressure and temperature change, the
mass flow through the throttle also has to change since
it depends on T and p. The local mode switch in the
pipe implicitly changes a value of the throttle. This
also means that the switch is not local. As soon as
output variables (p, T ) change their values and influ-
ence connected components, the initialization is not
restricted to the component the mode switch is in.
To make sure that this does not occur one should
abstain from changing output values during a local
mode switch. This might of course be difficult to en-
sure in acausal modeling since during the modeling of
the components the outputs are not defined and are de-
pendent on the context. In a modeling language with
causal behavior this is easier to realize since the in-
put/output relation is hard coded.
RoT-11 change of outputs: The initialization in a
component should not change output values.
Since the above rule cannot be ensured all the
time, there need to be possibilities and rules to han-
dle initialization routines implicitly to change values
from other components. There are different possibili-
ties which can be assumed during such mode switches
in components:
1. Everything not specified should stay the same.
This means that only the values of the variables
in the switching component are influenced. All
other components without a mode switch try to
keep their values. This usually means that the pa-
rameters and state variables will keep their values
whereas other variables might change their values,
e.g. mass f low changes while P keeps its value
even though this leads to a discontinuity in the
mass flow.
2. Everything not specified must stay the same:
This means that all variables and parameters from
components without a mode switch must keep
their values. Therefore, it would not be allowed
to change the values of output variables during an
initialization routine. If all outputs keep their val-
ues, values of other components do not have to
change.
3. Local transitions know the global context: This
means that transitions have access to the con-
text they are in and can therefore initialize other
components. This is often an approach in state
machines and their parallel components (Harel,
1987). In the context of modeling this does not
seem feasible since the context of a component
should be exchangeable and a component should
have a local scope. Otherwise it would not be pos-
sible to use a component with modes in different
contexts.
4. Extension of local transitions: This means that
the user can extend or redefine local transitions in
one of the higher hierarchy levels if necessary. In
most cases it should suffice to use the local transi-
tions but sometimes it is not possible to initialize
the new mode and its context correctly through
the local initialization routine. If this is the case,
it should be possible to overwrite the local transi-
tion on a higher hierarchy level and redefine the
initialization routine. To accomplish this a tran-
sition should have an ID. This ID can be used to
identify the transition to be overwritten. Since this
new routine is on a higher hierarchy level, it can
use data from its current hierarchy level and is not
limited to the local scope of the old transition.
In the example above such an extended transition
is used to overwrite the initialization routine of
the local mode with init new. In this routine one
might define that the value P should change rather
than the value of m f low to avoid discontinuities.
We suggest a mix of the first and fourth approach.
When nothing else is specified the values of parame-
ters and state variables should keep their values. But
to make the initialization more flexible the modeler
should have the means to overwrite or extend a transi-
tion to specify a global initialization which takes the
variables of other components into account.
RoT-12 change of Outputs: The initialization can
be extended on a higher level.
ChallengeswhenCreatingVariable-structureModels
107

5 GUARDS
A transition is activated when its guard becomes true.
During its activation the transition leads to a mode
switch which uses the initialization routines already
discussed. As a result of the modularization and the
local scope of components the guards of transitions
inside of components can only depend on the local
data of that component’s currently simulated mode.
Otherwise the components would again not be ex-
changeable since it would be context dependent.
5.1 Basics
The most basic decision regarding transitions is when
a mode switch should occur. In some cases this is sim-
ple as with the already discussed pendulum example.
When the centrifugal force (F
centri
) is below zero the
mass of the pendulum will not continue on its circular
path. The mass will begin to fall which leads to dif-
ferent equations to describe the behavior. The guard
would therefore be F
centri
< 0.
When looking at changes in the behavior it is often
possible to look at the real system and fragment the
behavior in different phases depending on the mathe-
matical description which is necessary for the differ-
ent phases. If two phases of a real system do not need
different sets of equations to describe their behavior,
there do not need to be two modes in a mathematical
model. If the phases are obvious, it is often possible
to find obvious guards when to switch. It is important
though that the guards are chosen in a manner that
avoids many switches back and forth between two
modes in a short time (also called chattering). This
can be avoided by using hysteresis in the guards or by
demanding that a mode is active for a minimum time.
RoT-13 avoid chattering: Chattering between two
modes should be avoided.
Regarding variable-structure models which switch
their level of detail, the guard is usually not clear since
both modes describe basically the same system only
with a different granularity. The modeler has to de-
cide when the switch of detail needs to take place.
The modeler already decided about the granularity of
the modes when he created them and probably has a
basic idea why and when this switch should occur. As
was shown and discussed in Figure 6 the choice of the
guard can influence the simulation significantly.
When in doubt the modeler should use the more
detailed mode for longer periods than necessary in-
stead of switching too early. If the results are ac-
curate enough, one can change the guard to use the
more detailed mode for a shorter time to enhance per-
formance. It should always be the goal though not to
reduce the accuracy.
RoT-14 preserve accuracy: For variability in detail
start with a simulation using the detailed mode for
a longer time and then reduce this period.
In classical modeling it is common practice to
try to initialize a model in a steady-state. This usu-
ally leads to an easier and stable initialization of the
model. This should also be the goal for variable-
structure models. Therefore the guards should be cho-
sen in a steady-state to make the initialization easier
and safer.
RoT-15 steady-state initialization: A mode switch
should occur when the previous mode is in a
steady-state.
5.2 Guards for Modes in Components
The rules above also apply for the guards of tran-
sitions between modes in components. But if there
are many components each having modes and there-
fore transitions between these modes, also other chal-
lenges have to be regarded.
We present challenges by examples of two mode
switches but it can be generalized to more switches.
5.2.1 Two Simultaneous Mode Switches
It might be necessary that two components switch
their modes at the same time. This is for instance sen-
sible if both components change their level of detail
and a mix between a detailed and a less detailed com-
ponent is not feasible. The problem is that the mode
switches are in components with each having a local
scope. This means that the transitions do not have
knowledge about the mode switches in other compo-
nents. Similar to extending a transition’s initialization
to a higher level, a guard can be described on a top
level to synchronize transitions.
RoT-16 synchronized guards: Describe the guard
on a top level to synchronize simultaneous mode
switches.
During modeling it might happen that two transi-
tions in two components have the same guard depend-
ing on variables with the same values over time (pos-
sible through the interfaces). In this case, the simula-
tion environment might be able to detect both guard
activations. Both local transitions can then take place
simultaneously.
As already discussed local transitions can implic-
itly influence values from other components which
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
108

can lead to problems when two transitions are acti-
vated at the same time. A question is in which order
the transition’s initialization routines are evaluated.
This order might influence the behavior of the whole
model since values from the first initialization might
be overwritten by the second. If this problem occurs,
the modeler should overwrite the local transitions by
a transition on a higher hierarchy level again.
When conditions are not completely equal since
they were locally defined but the user would like to
have them switch in the same instant, a new transition
should also be defined which can activate local tran-
sitions or overwrite them to specify the wanted mode
switches in the components.
RoT-17 synchronized initializations: Describe the
initialization on a top level to avoid conflicts during
simultaneous mode switches.
5.2.2 Two Consecutive Mode Switches
A mode switch in one component might influence the
initial values of another component if values of out-
puts were changed. This can lead to a problem if a
value is changed which is used as a guard in a tran-
sition. If this value changes in a way that the guard
is skipped, a necessary mode switch would not occur
and might render the whole simulation’s results unus-
able.
This should be avoided either by checking that no
other guards are passed during the initialization or by
overwriting a transition on a higher hierarchy level.
RoT-18 skipped guards: Consider skipped guards
during the initialization routine of other transi-
tions.
6 EVALUATION
The proposed rules of thumb are based on real world
examples, which where modeled and simulated in the
DySMo framework. A short description of three of
these models is given in the following.
Air-condition Model (Mehlhase et al., 2012):
This is an example of a variable-detail model where
components can be removed. To remove components
it was necessary to adapt the interfaces of the com-
ponents remaining in the model. For the initializa-
tion routines initialization functions and past data was
needed. In this example about 60% of simulation time
was saved through the variable-structure approach.
Rocket Model (Mehlhase et al., 2014): This
model describes a rocket flight with three stages.
The component representing the propulsion had three
modes: Starting the propulsion calculated with its
chemical reactions, constant propulsion, no propul-
sion. The model had six modes in all and through the
variable-structure approach and the RoT presented in
this paper we where able to reduce the simulation time
from 50 seconds to about 4 seconds (with all switches
included) without loss of accuracy.
Automatic gear Box Model (Ehrich, 2012): This
model consists of many components with different
modes, which leads to many possible combinations of
components. Furthermore, in between modes where
defined for this model. It was essential to heed the
rules of thumbs for hierarchical models to create a
consistent model (e.g. RoT-9,11,15).
Other examples where also implemented but not
published yet.
Another major evaluation was done through a
formalization describing hierarchical, compositional
variable-structure models and how to simulate them.
This formalization is based on Object-Z and was used
as basis for the implementation of the DySMo frame-
work. We plan to publish the formalization in a
follow-up paper. The presented rules of thumb also
provide information on what a simulation environ-
ment should support.
We therefore think that the rules of thumb pre-
sented here give valuable hints on how to handle
variable-structure models.
7 CONCLUSION AND FUTURE
WORK
In this paper, we gave a basic overview on challenges
a modeler has to face when creating variable-structure
models and libraries of components with modes. It
is supposed to serve as a basic guideline for model-
ers that helps them to understand and differentiate the
different challenges they are facing, and to find rules
of thumb for each of them.
As foundation for our analysis we first introduced
the two aspects of variable-structure models, which
together cause these challenges: the mechanism to
switch between different modes during simulation,
and the division of models into different components.
The presented challenges can be categorized into
three different categories: structural challenges, re-
garding the interfaces of modes and components
(section 3), challenges regarding the initialization of
new modes (section 4), and challenges regarding the
guards and the timing of mode switches (section 5).
Altogether, we discussed several challenges and
gave 18 rules of thumb to help modelers solve them.
ChallengeswhenCreatingVariable-structureModels
109

This set of challenges discussed in this paper is not
supposed to be complete in any sense, but instead
aims at covering the most important issues.
A formalization that helped us to make sure that
the assumptions and ideas presented here are valid
will be presented separately in a future publication.
A very interesting next step to support the ac-
tual modeling activity is the augmentation of mod-
els, components, and modes with specific informa-
tion. Such information could include assumptions un-
der which a component should behave as desired, and
information on the expected outcome and level of de-
tail for a component. To express such information in
an easy and efficient way, a domain-specific language
is required.
Furthermore, a tool environment is needed, which
supports the modeling of structure changes in com-
ponents and their simulation. Such a tool should be
able to detect modeling problems and propose fixes
for such problems in order to support the modeler
whenever needed. This paper is a step towards the
requirements and possible analysis for such a tool.
REFERENCES
Broman, D. (2010). Meta-Languages and Semantics for
Equation-Based Modeling and Simulation. PhD the-
sis, Link
¨
oping University.
Casella, F., Sielemann, M., and Savoldelli, L. (2011).
Steady-state initialization of object-oriented thermo-
fluid models for homotopy methods. In Proceedings
of the 8th International Modelica Conference, pages
86–96.
Clune, M., Mosterman, P., and Cassandras, C. (2006).
Discrete event and hybrid system simulation with
simevents. In Proceedings of the 8th International
Workshop on Discrete Event Systems, pages 386–387.
Dassault Systems (2015). Dassault systems.
www.dynasim.se. Accessed: January 2015.
Ehrich, A. (2012). Modellierung und Simulation eines Au-
tomatikgetriebes mit Strukturdynamik. Master’s the-
sis, Technische Universit
¨
at Berlin.
Elmqvist, H., Cellier, F. E., and Otter, M. (1993). Object-
oriented modeling of hybrid systems. In Proceedings
of the European Simulation Symposium (ESS’93), So-
ciety of Computer Simulation, pages 31–41.
GENSIM Project (2007). MOSILAB. http://mosim.swt.tu-
berlin.de/wiki/doku.php?id=projects:mosilab:home.
Accessed: February 2015.
Harel, D. (1987). Statecharts: A visual formalism for com-
plex systems. Science of Computer Programming,
8(3):231–274.
Heinzl, B. et al. (2012). Bcp - a benchmark for teaching
structural dynamical systems. In Mathematical Mod-
elling 7(1), pages 896–901.
Mahr, B. (2008). Ein Modell des Modellseins - Ein Beitrag
zur Aufkl
¨
arung des Modellbegriffs. In Modelle. Ul-
rich Dirks, Eberhard Knobloch.
Mehlhase, A. (2013). A Python framework to create and
simulate models with variable structure in common
simulation environments. Mathematical and Com-
puter Modelling of Dynamical Systems, 20(6):566–
583.
Mehlhase, A. et al. (2014). An example of beneficial
use of variable-structure modeling to enhance an ex-
isting rocket model. In Proceedings of the 10th
International Modelica Conference, pages 707–713.
Link
¨
oping University Press.
Mehlhase, A., Kr
¨
uger, I., and Schmitz, G. (2012). Variable
structure modeling for vehicle refrigeration applica-
tions. In Proceedings of the 9th International Model-
ica Conference, pages 927–934. Link
¨
oping University
Electronic Press.
Mosterman, P. J. and Biswas, G. (1997). Formal specifica-
tions for hybrid dynamical systems. In Proceedings of
the 15th International Joint Conference Artificial In-
telligence IJCAI-97, pages 568–573.
Nilsson, H., Peterson, J., and Hudak, P. (2003). Functional
hybrid modeling. In Proceedings of 5th Int. Work-
shop on Practical Aspects of Declarative Languages,
volume 2562 of Lecture Notes in Computer Science,
pages 376–390.
Nytsch-Geusen, C. et al. (2005). Mosilab: Development of
a modelica based generic simulation tool supporting
model structural dynamics. In Proceedings of the 4th
International Modelica Conference, pages 527–535.
Pawletta, T., Lampe, B., Pawletta, S., and Drewelow, W.
(2002). A devs-based approach for modeling and sim-
ulation of hybrid variable structure systems. In Mod-
elling, Analysis, and Design of Hybrid Systems, Lec-
ture Notes in Control and Information Sciences, vol-
ume 279, pages 107–129. Springer Berlin Heidelberg.
Platzer, A. and Quesel, J. D. (2008). Keymaera: A hybrid
theorem prover for hybrid systems (system descrip-
tion). In Proceedings of the 4th international joint
conference on Automated Reasoning (IJCAR ’08),
pages 171–178.
Ptolemaeus, C., editor (2014). System Design, Modeling,
and Simulation using Ptolemy II. Ptolemy.org.
The MathWorks Inc. (2013a). MATLAB, Simulink 2013b.
Natick, Massachusetts, United States.
The MathWorks Inc. (2013b). MATLAB, Stateflow 2013b.
Natick, Massachusetts, United States.
The Modelica Association (2012). Modelica - a uni-
fied object-oriented language for physical systems
modeling - language specification version 3.3.
www.modelica.org/documents/ModelicaSpec33.pdf.
Accessed: February 2015.
Top, J. (1993). Conceptual Modelling of Physical Systems.
PhD thesis, University of Twente.
Zimmer, D. (2010). Equation-based modeling of variable-
structure systems. PhD thesis, Eidgen
¨
ossische Tech-
nische Hochschule ETH Z
¨
urich.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
110
