GR-TNCES: New Extensions of R-TNCES for Modelling and

Verification of Flexible Systems under Energy and Memory

Constraints

Oussama Khlifi

1,2

, Olfa Mosbahi

, Mohamed Khalgui

and Georg Frey

LISI Laboratory, INSAT, University of Carthage, Tunis, Tunisia

Polytechnic School of Tunisia, University of Carthage, Tunis, Tunisia

Chair of Automation, Saarland University, Saarbrücken, Germany

Keywords: Distributed Discrete Event Control System, Adaptive System, Reconfiguration, Modeling, Formal

Verification, Model Checking, Energy Control, Memory Control.

Abstract: This study deals with the formal modeling and verification of Adaptive Probabilistic Discrete Event Control

Systems (APDECS). A new formalism called Generalized Reconfigurable Timed Net Condition Event

Systems (GR-TNCES) is proposed for the optimal functional and temporal specification of APDECS. It is

composed of behavior and control modules. This formalism is used for the modeling and control of

unpredictable as well as predictable reconfiguration processes under memory and energy constraints. A

formal case study is proposed to illustrate the necessity of this formalism and a formal verification based on

the probabilistic model checker Prism.

1 INTRODUCTION

Adaptive Probabilistic Discrete Event Control

Systems (APDECS) such as chirurgical robots are

able to change their behaviors with an unpredictable

way during run-time processes. Reconﬁguration is

the qualitative change in the structure, functionality,

and algorithms of the control systems (Radu et al.,

2011). This is due to qualitative changes of goals of

control, the controlled system or of the environment

the system behaves within. Partial failures,

breakdowns, or even human intervention may cause

such changes (Yang et al., 2013). Thus, the

development of Probabilistic Reconfigurable

Discrete Event Control Systems (PRDECS) is not an

easy activity to perform since they should be

adapted to their environment under functional,

memory, energy and real-time constraints. Many

systems and protocols run under devices with

limited memory and energy resources, so the system

could violate them during an adaptation process. For

this reason, we should have real-time reconﬁgurable

supervised control architecture in order to evaluate

and improve its performance. In this work, we focus

on the optimal modeling and verification of

PRDECS running under memory and energy

constraints.

In general, all requirements for DECS can be

reduced to two general properties: value correctness

and temporal correctness (Kopetz, 2003). These can

be further split up into two corresponding questions:

Will the system respond to an input change with the

correct output change (value correctness)? and Will

it do so within the correct time bounds (temporal

correctness)?

Many researchers have tried to deal with the

formal modeling of control systems with potential

reconﬁgurations. Wu and Zhou (2011) presented

intelligent token Petri nets. In their model, tokens

represent job instances to carry real-time knowledge

about system states and changes. It is like smart

cards in practice such that the dynamical changes of

a system can be easily modeled. Dumitrache et al.,

(2000) developed a real-time reconﬁgurable

supervised control architecture for large-scale

manufacturing systems in order to evaluate

performance of the control architecture. Ohashi and

Shin (2011) established a model based control

design for reconfigurable manufacturing systems

(RMS) using state transition diagrams and a general

graph representation. Kalita and Khargonekar (2002)

deﬁned a hierarchical structure. It allows reusability

and rapid reconfigurability of the controller while

the machining system is reconﬁgured.

373

Khliﬁ O., Mosbahi O., Khalgui M. and Frey G..

GR-TNCES: New Extensions of R-TNCES for Modelling and Veriﬁcation of Flexible Systems under Energy and Memory Constraints.

DOI: 10.5220/0005523503730380

In Proceedings of the 10th International Conference on Software Engineering and Applications (ICSOFT-EA-2015), pages 373-380

ISBN: 978-989-758-114-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

All the aforementioned studies have tried to

describe the reconfigurability and reﬂect the

characteristics of APDECS. Nevertheless, some of

them do not consider the temporal constraints. Most

of them do not treat unpredictable, probabilistic and

infinite characteristics of APDECS. Since these

formalisms are not able to cope with these systems,

this study tries to model APDECS using a direct

method by deﬁning a new formalism that is an

extension of R-TNCES. We assign new controllers

for the memory and energy resources at run-time

process to cover the problem of resources violation.

We should not have a deadlock problems caused by

lack of resources at reconfiguration process. We

suppose that each firing transition consumes one

token from the energy and memory reserves. A new

formalism called Generalized Reconﬁgurable Timed

Net Condition/Event Systems (GR-TNCES) is

proposed for the optimal functional and temporal

speciﬁcation of systems. It is deﬁned by a behavior

module and a control module. This formalism is

used to model and verify a formal case study to

show its suitability.

The paper is organized as follows: the next

section describes the preliminaries on top of which

our new formalism is built. Section 3 introduces our

new formalism and its formalization. A case study is

provided in section 4. Finally, section 5 concludes

the paper.

2 BACKGROUND

In this section, we present reconfigurable

probabilistic discrete event systems and their formal

verification. We thereafter expose the formalisms

TNCES (Hanisch et al., 1997) and R-TNCES

(Zhang et al., 2013), which extend Petri nets for the

modeling of adaptive control systems, and the

related existing tools.

2.1 Verification of Reconfigurable

Probabilistic Systems

Adaptive probabilistic systems are modular,

extensible and reconfigurable (Sharifloo and

Spoletini, 2013). These systems have an

unpredictable behavior that could change during a

run-time process (Forejt et al., 2012). Hence, we

need an expressive formalism for their optimal

modeling and verification. CTL is used to specify

functional properties of a reconfigurable system

(Zhang et al., 2013). It offers facilities for the

specification of properties to be checked. The

process of checking whether a temporal formula

holds for a system is called model checking (Martin

and

Christian, 2009). Probabilistic model checking is

an automated method to verify quantitative

properties based on Probabilistic Computation Tree

Logic (PCTL) (Forejt et al., 2012). Due to

qualitative changes of goals of system control or of

the environment the system behaves within, we are

focusing on a new method for the optimal modeling

of probabilistic reconfigurable systems under

memory and energy constraints.

2.2 Modeling Formalisms and Tools

In this section, we introduce two formalisms

extending Petri nets which are useful to model

distributed reconfigurable control systems.

2.2.1 Timed Net Condition/Event System

A Timed Net Condition/Event Systems (TNCES)

have modular structures which can be basic or

composite (Salem et al., 2014). It allows the

representation of hierarchical models and provides a

way to express exchange of event and the state of

information. It is a suitable formalism for systematic

structured modeling of automated objects, machines

and processes (Hanisch et al., 1997). A TNCES, as

shown in Figure 1 is formalized as a tuple as

follows:

NCES = (P, T, F, W, CN, EN, C

, C

out

,V,m0)

Where:

• P (respectively, T) is a non-empty ﬁnite set

of places (respectively, transitions),

• F is a set of ﬂow arcs F ⊆ (P × T) ∪ (T ×

P),

• W :(P × T) ∪ (T × P) →{0, 1} maps a

weight to a ﬂow arc, W(x, y) > 0 if (x, y) ∈

F, and W(x, y)=0 otherwise, where x, y ∈ P

∪ T,

• CN (respectively, EN) is a set of condition

(respectively, event) signals with CN ⊆ (P

× T) (respectively, EN ⊆ (T × T)),

• C

(respectively, E

) is a set of condition

(respectively, event) inputs,

• C

out

(respectively, E

out

) is a set of condition

(respectively, event) outputs

• V : T →{∨, ∧} maps an event-processing

mode (

AND or OR) to each transition,

• m0: P →{0, 1} is the initial marking.

ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications

374

Figure 1: Example of a TNCES.

2.2.2 Reconfigurable Timed Net

Condition/Event Systems

An R-TNCES, as defined in (Zhang et al., 2013) is

an extension of the formalism TNCES with a

specific function of self-reconﬁguration. It is a

structure RTN = (B, R), where R is the control

module consisting of a set of reconfiguration

functions R = {r

1,...,rm}. The reconfiguration

function is a structure r= (Cond, S, X). Cond→ (true,

false) is the precondition of r. S is the structure

modification instruction. X is the state processing

function that links the states before and after the

reconfiguration process. B is the behavior module

which is a union of multi TNCES, represented as

follows:

B =(P, T, F, W, CN, EN, DC, V, Z0) (3)

where: (i) P (respectively, T) is a superset of places

(respectively, transitions), (ii) F ⊆ (P × T) ∪ (T × P)

is a superset of flow arcs, (iii) W: (P × T) ∪ (T ×P)

→{0, 1} maps a weight to a flow arc, W(x, y) > 0 if

(x, y) ∈ F, and W(x, y)=0 otherwise, where x, y ∈ P

∪ T, (iv) CN ⊆ (P × T) (respectively, EN ⊆ (T × T))

is a superset of condition signals (respectively, event

signals), (v) DC: F ∩ (P × T) → {[l1,h1],...,[

l|F n (P ×

T)|, h|F n (P × T)|]} is a superset of time constraints on

output arcs, where ∀ i ∈ [1, |F ∩ (P × T)|], l

i, hi ∈

N, and l

i, < hi, (vi) V : T →{∨ , ∧ } maps an event-

processing mode (AND or OR) for every transition,

(vii) Z

0= (M0, D0), where M0 : P → {0, 1}is the

initial marking and D

0: P →{0} is the initial clock

position. R-TNCES is a novel formalism for

adaptive systems. But this formalism cannot deal

with probabilistic running under memory and energy

constraints.

3 CONTRIBUTION: GR-TNCES

System modeling and control is not a trivial activity

because a failure can be critical for the safety of

human beings, e.g., air and railway traffic control

(Suender et al., 2011). This process consumes an

amount of memory and energy resources that is

estimated depending on the chosen scenario. To

cover these goals, a new formalism, called (GR-

TNCES), which is an extension of Petri Nets, is

proposed. It is deﬁned by behavior and control

modules. It is necessary to guarantee the state

feasibility before and after probabilistic

reconﬁgurations under memory and energy

constraints. We aim to guarantee the optimal

functional and to be sure that never we will face a

scenario in which the system has to establish a

reconfiguration process with insufficient memory or

energy resources.

3.1 Motivation

Reconfiguration can be unpredictable, i.e., we do not

have any idea about the behavior of the system in

the future (Carlo, 2011). Memory and Energy

resources are mandatory to run all processes. So,

before running the system and applying a

reconfiguration, we have to check that there are

enough memory and energy resources. We propose a

real-time probabilistic reconﬁgurable supervised

control architecture. We add a new parameter on the

arcs of the model to design the probability of this

TNCES branch. We design also controllers for the

supervision of the memory and energy resources

during running processes.

3.2 Formalization

We present in this section the formalism (GR-

TNCES) for the optimal modeling of unpredictable

systems under memory and energy constraints.

3.2.1 Generalized R-TNCES

We define the formalism GR-TNCES that is a

network of R-TNCES. It is a structure G = {∑ R-

TNCES}. R-TNCES = (B, R), where R is the control

module consisting of a set of reconﬁguration

functions {r1, r2, r3, r4,.}. B is the behavior module

that is a union of multi TNCES, represented as

follows:

B = (P, T, F, W, CN, EN, DC, V, Z

)

Where:

• P (respectively, T) is a non-empty ﬁnite set of

places (respectively, transitions),

• F is a set of ﬂow arcs F ⊆ (P × T) ∪ (T × P),

• W :(P × T) ∪ (T × P) →{0, 1} maps a weight

to a ﬂow arc, W(x, y) > 0 if (x, y) ∈ F, and

W(x, y)=0 otherwise, where x, y ∈ P ∪ T,

GR-TNCES:NewExtensionsofR-TNCESforModellingandVerificationofFlexibleSystemsunderEnergyandMemory

Constraints

375

• CN (respectively, EN) is a set of condition

(respectively, event) signals with CN ⊆ (P × T)

(respectively, EN ⊆(T × T)),

• DC: F (P ×T) → {[l, h ]} is a superset of time

constraints on output arcs,

• V: T →{∨, ∧} maps an event-processing mode

(AND or OR) to each transition,

• Z

= (T0, D

) where T

: P →{0, 1} is the initial

marking and D0 : P →{0} is the initial clock

position.

Let TN = P ×T ×F ×W × CN × EN × DC × V

be the set of all feasible net structures that can be

performed by a system. Given a TNCES:

β=(P’,T’,F’,W’,CN’,V’, DC’

,Z’0), TN(β) = (P’, T’,

F’ , W’, CN’, EN’, DC’, V’) denotes its net

structure, where TN(β) ∈ ∑ TN. We have P’ ⊆ P, T’

⊆ T, F’ ⊆ F, W’⊆ W, CN’ ⊆ CN, EN’⊆ EN, DC’ ⊆

DC, and ∀t ∈ T, V’ (t) =V (t). Each reconfiguration

is controlled by the controller. It is a structure:

R = {Condition Cond, Probability P

’, Energy E’,

Memory M’, Structure S, State X}

Let

•r (respectively, r•) denotes the original

(respectively, target) TNCES before (respectively,

after) the reconﬁguration function r is applied, where

TN(

•r), TN(r•) ∈ ∑ TN. A reconﬁguration function r

is a structure r = (Cond, P

, E, M, S, X). A

reconfiguration r is enabled at a state if the following

conditions are fulfilled.

Cond → {true, false}: the precondition of r,

’: P

: F→ [0..1] TNCES probability which

could be a functional (internal to the TNCES) or a

reconfiguration probability,

’: P→ [0..max] : controls the energy

requirements by the TNCES to token number of

energy in the controller, else the second

reconfiguration probability is chosen,

’ : P → [0..max]: controls the memory

requirements by the TNCES to token number of

memory, else the second adaptation probability is

chosen,

S : TN(•r) → TN(r•) : is the structure

modiﬁcation instruction for reconfiguration scenario,

X : last state (•r) → initial state (r•) : is the state

processing function, where last state (•r)

(respectively, initial state (r•)) denotes the last

(respectively, initial) state of •r (respectively, r•)

before (respectively, after) the application of r.

A state machine speciﬁed by an TNCES, which

is called Structure_changer, is deﬁned to describe

the control module. In this state machine, each place

corresponds to a speciﬁc TNCES of the GR-TNCES

model. Thus, each transition corresponds to a

reconﬁguration function. The fact that a place sp

gets a token implies that the TNCES, to which sp

corresponds, is selected. If a transition st (∀st ∈ sp

• )

ﬁres, then it removes the token away from sp and

brings it into a place sp’

with sp’ ∈ st•. Firing st

implies that a reconﬁguration function is applied.

The Structure_changer is formalized as follows:

Structure_changer = (P, T, F, V, M

, P

)

Where ∀t ∈ T, |•t| = |t•| =1, ∑M

(P)=1, which means

state and only one TNCES is performed at any time.

The controller manages the GR-TNCES model using

the Structure_changer model. Each place of this

structure contains the whole information about the

corresponding TNCES e.g. its energy and memory

requirements (number of states in this TNCES).

Each state consumes one token from the energy and

memory reserve. So before enabling the

reconfiguration, tokens are removed from the

reserve. Only memory tokens are added to the

model’s memory at the end of the adaptation

process. Energy reserve will be removed from the

battery. Then, the battery will be charged

periodically.

3.2.2 Dynamics of GR-TNCES

The dynamic describes the behavior of this control

operation. Before moving the token from one place

to the next state, The structure modiﬁcation

instruction S guides the GR-TNCES from TN(•r) to

TN(r•), including the condition/event signals among

them. The state processing function X maps the last

state of •r before the application of r to a feasible

initial state of r•, from which the reconﬁgured

system goes on running. The dynamics of an GR-

TNCES is represented in this section by referring to

self-modiﬁcation nets and net rewriting systems. The

states of an GR-TNCES are deﬁned as follows.

A state of G is a pair (TN(β), State(β)), where

TN(β) denotes the net structure of G and State(β)

denotes a state of G. The evolution of an GR-

TNCES depends on what events, energy and

memory constraints (reconﬁguration functions or

transitions) take place. Using this GR-TNCES, a

reconﬁguration function r = (Cond, P’, E’, M, S, X)

is enabled at state (TN(β), State(β)) if the new

original following conditions are met.

1) TN(β) = TN(•r), i.e., TN(β) is equal to the net

structure of •r and if the firing time

constraints are fulfilled,

2) Cond = true: its precondition is fulﬁlled,

3) E

> Cost TNCES (E

’): E

’ (token number)

is removed from the energy reserve,

4) M

> Cost TNCES (M

’), M

’ (token cost) is

removed from the memory controller. When

the reconfiguration is over, these memory

ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications

376

tokens are added to the memory initial

reserve.

After ﬁring a reconﬁguration function r at the

state (TN(β), State(β)), the system evolves into a

new state (TN(β’), State(β’)), M

’ : the memory

reserve is returned to the memory controller but the

consumed energy E

’ is removed from the reserve

. This reserve will be charged after a time period.

For a transition t in an GR-TNCES, the ﬁrst

condition of its ﬁring is that it must be in the current

active TNCES. It should be enabled. On this basis,

the ﬁring rule of a transition in an GR-TNCES is the

same as that in a TNCES. Note that, in an GR-

TNCES, a reconﬁguration function always has a

higher priority than a transition.

4 CASE STUDY

In this paper, the authors aim just to expose this new

formalism using a simple case study. Let’s assume a

formal reconfigurable probabilistic system to be

composed of two Modules: Module1 labeled as

GRTN1 and Module2 named as GRTN2

communicating by an event signal ev0. P1 is the

initial state. The first module contains Three TNCES

with different probabilities. The first TNCES TN1 is

labeled with the probability 0.3. It is composed of 4

states (p2, p3, p4, p5) and 4 transitions (t2, t3, t4,

t5). The second TNCES TN2 has 0.1 as a reachable

probability, contains 3 states (p6, p7, p8). The last

one is composed of (p10, p11, p12, p13).

The second module GRTN2 is activated once the

third TNCES TN3 is selected by module1. It sends

an event ev

0 for the activation of module2. We

suppose that during this reconfiguration process at

the transition t1, our system has to run 5 successive

cycles of the chosen TNCES. Initially, this controller

contains 12 tokens in its energy reserve and 10

tokens in its memory reserve as shown in Figure 2.

Before applying the reconfiguration scenario, the

controller uses the Struture_changer for the

selection of the adaptation process. Figure 3 shows

the Structure_changer of the use case model. It

contains two state machines that correspond to these

two modules GRTN1 and GRTN2.

Rec1, Rec2 and Rec3 are the different

reconfiguration processes and TN1, TN2 and TN3

are respectively the 3 TNCES of the probabilistic

model. For the second module GRTN2, we have 2

places N1 and N3 to represent the TNCES. Using

this Structure_changer the memory and energy

controllers could easily supervise the general model.

This control is done through the estimation of the

amount of resources located in the places of this

TNCES. During the reconfiguration process, the

system removes the tokens of the chosen TNCES

from the system reserve (energy and memory). After

this reconfiguration the memory tokens are added to

the system’s memory once it is free and not used by

the system.

Figure 2: Use Case Controller Model.

Figure 3: Running Example Model.

GR-TNCES:NewExtensionsofR-TNCESforModellingandVerificationofFlexibleSystemsunderEnergyandMemory

Constraints

377

This case study is a useful example to present the

necessity of this new formalism for modeling finite,

probabilistic and reconfigurable systems. We start

by the deactivation of the memory and energy

controllers to test its results on the system behavior.

Then, we activate the control process. Therefore, we

explain and discuss its role and how it affects the

system’s model. A based verification model

checking technique using Prism is applied to

validate this new modeling formalism.

4.1 Verification of GR-TNCES

We use Prism as a model checker to check the safety

of each reconfiguration scenario that can be applied

to the system. The Computation Tree Logic (CTL)

(Zhang et al., 2013) and the probabilistic

computation tree logic (PCTL) (Forejt et al., 2012)

are used to specify the deadlock and the probability

of properties which will be verified on the system.

Typical properties which can be verified are

boundedness of places, liveness of transitions, and

reachability of states (Dubinin et al., 2006). We

could detect if there is a deadlock and be sure that

the model meets user requirements. To evaluate the

interest of the controllers, we should disable it to

check its effects on the system. The following CTL

formula is applied for the deadlock detection:

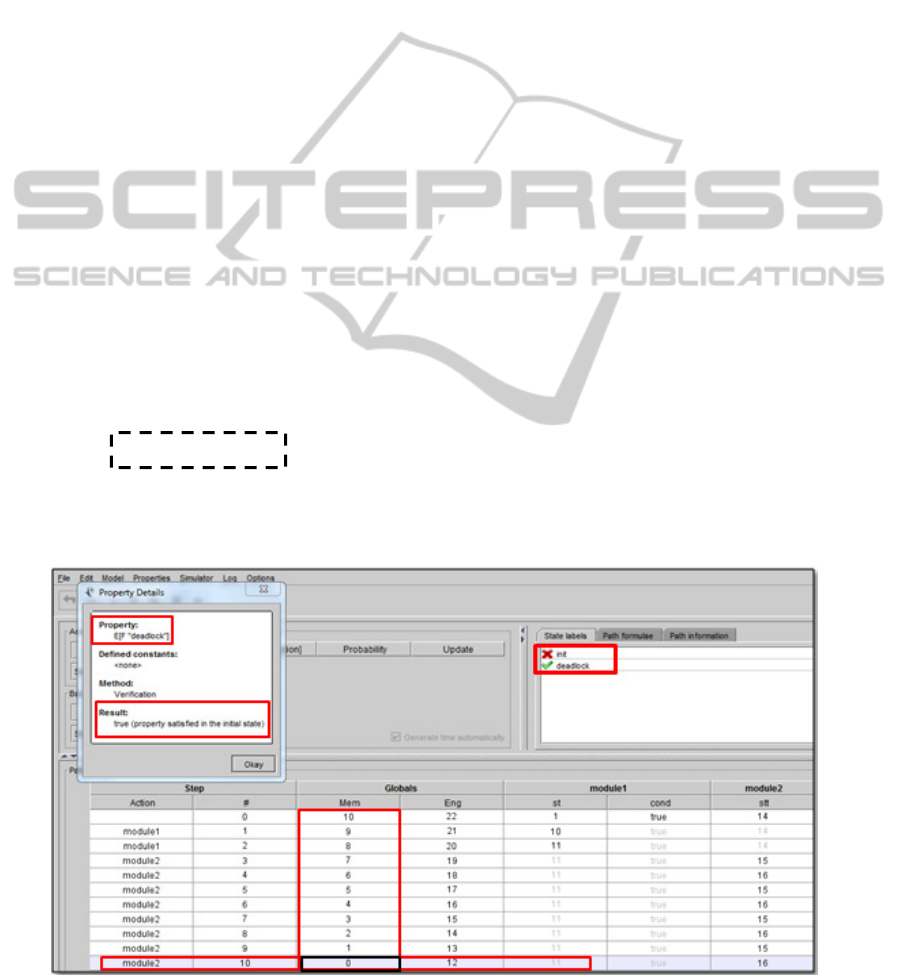
E[F " deadlock "]

This formula is proven to be true by Prism as

shown in the screenshot in Figure 4. So, there is a

deadlock (ticked with the green color) at the state

p16. It is because the controller was inactive. It is

due to the violation of memory resources at run-time

process as shown at step 10. There are no memory

resources. The system does not manage its resources

in the optimal way. We notice that there is no

addition of the memory tokens to the memory

resources at the end of each TNCES cycle. So it is

quickly exhausted by a false using way.

When the simulation progresses to establish the

adaptation process that is composed of 5 successive

cycles, we have a blocking situation caused by the

lack of these resources. At the fifth cycle, at state

p16 the system becomes in deadlock and cannot

progress during this critical reconfiguration scenario.

This is our dangerous problem, we consider it as a

critical situation at run-time adaptation process e.g.,

the system has to fulfill a list of tasks, but it could

not establish the whole operation due to the violation

of its memory, or energy resources.

The former case shows that the system is blocked

when we disable the energy and memory controllers.

Now, we reactivate these controllers. Using this new

configuration, we try to check the system at a new

unpredictable adaptation scenario using Prism model

checker. By the activation of the control, we hope to

run all the reconfiguration processes.

We aim that the system finishes this adaptation

situation successfully without any blocking

situations. After a successful simulation, we reach

the end of the adaptation scenario. We verify that the

model meets users’ requirements. So any adaptation

process does not lead to a deadlock state as proven

by the Red Cross.

Figure 4: Prism Deadlock State Detection.

ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications

378

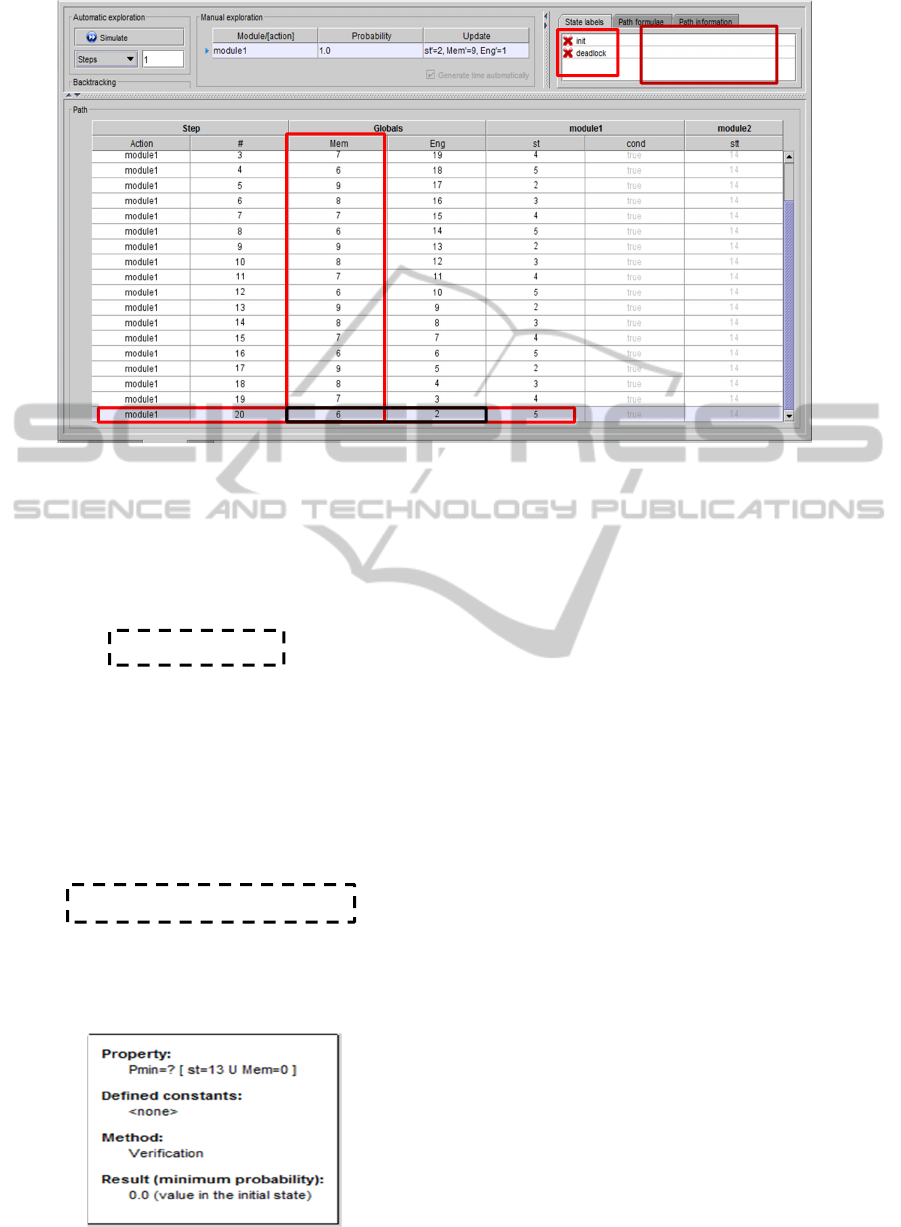
Figure 5: Simulation with Control.

We see also that the reconfiguration process is

finished and the amount of memory resources

increases at the end of each TNCES as mentioned in

the logic of this controller. The following CTL

formula is checked and proven to be false.

E[F " deadlock "]

We use now the probabilistic logic PCTL for

probabilistic quantification of described properties

(Forejt et al., 2012). We have proven that there is no

chance for the system to reach the end of the

TNCES without memory or energy resources. Prism

certifies that the probability to reach this state is

zero. The following PCTL formula is an example of

the checked properties:

Pmin=? [ st=13 U Mem=0 ]

This formula is evaluated and proven by Prism

with zero probability that the system reaches state

13which is the last state of the reconfiguration

process with no resources in reserves.

Figure 6: Prism Screenshot for Memory Verification.

4.2 Discussion: Comparison to Other

Works

As shown in this Figure 5 and Figure 6, all user

requirements are satisfied: we have done all the

reconfiguration processes without any deadlock (the

five successive cycles). The controllers run well,

they manage the memory and energy resources as

predicted before. Thanks to this new formalism GR-

TNCES, we could model and control all

unpredictable reconfigurable systems running under

memory and energy constraints. R-TNCES or its

previous extension could not deal with this kind of

systems. R-TNCES just deals with finite

reconfigurable systems; it could not model

probabilistic systems under resource constraints. It

cannot control system’s resources during a running

process or an adaptation scenario. High level Petri

Nets could also not deal with this kind of systems.

They could not express the probabilistic aspects and

the unpredictable behaviors during the running

processes.

5 CONCLUSIONS

This paper has proposed GR-TNCES, a new

formalism for modeling and veriﬁcation of adaptive

probabilistic discrete event control systems running

under memory, energy and real-time constraints.

Compared to the previous studies on formal

methods, the functional and temporal speciﬁcations

Deadlock

GR-TNCES:NewExtensionsofR-TNCESforModellingandVerificationofFlexibleSystemsunderEnergyandMemory

Constraints

379

are optimized; new modeling formalism to cover this

systems with resources control is developed.

Therefore an GR-TNCES is a new extension of the

formalism R-TNCES. It focuses on probabilistic,

adaptive, distributed event control systems running

under some constraints. Formalization and the

dynamics of GR-TNCES are proposed. A formal

case study is taken as a whole running example.

Prism as a probabilistic model checker was used to

show that GR-TNCES is a convenient formalism for

modeling and analyzing APDECS thanks to the

formal case study. A visual environment named

ZiZo is now under building to concretize these

contributions for the modeling and control of infinite

adaptive probabilistic systems running under various

constraints. In our future works, we will apply this

formalism to model the protocol IPV4 Zeroconf that

is an adaptive probabilistic system.

REFERENCES

Zhang, J., Khalgui, M., Li, Z., Mosbahi, O., and Al-

Ahmari, A.M. (2013). “R-TNCES: A Novel

Formalism for Reconfigurable Discrete Event Control

Systems.” Systems, Man, and Cybernetics: Systems,

IEEE Transactions on 43.4 (2013): 757-772.

Radu, C., Senior, IEEE, M., Lars, G., Marta, K., Raffaela,

M., “Dynamic QoS Management and Optimization in

Service-Based Systems”, In Software Engineering,

IEEE Transactions, May. 2011.

Salem, M. O. B., Mosbahi, O., and Khalgui, M.,”Pcp-

based solution for resource sharing in reconfigurable

timed net condition/event systems”. ADECS 2014,

Hanisch, H.-M., Thieme, J., Luder, A., and Wienhold, O.

(1997). “Modeling of plc behavior by means of timed

net condition/event systems”, In Emerging

Technologies and Factory Automation Proceedings,

1997. ETFA ’97., 1997 6th International Conference.

Wu. N. Q. and Zhou, M. C. “Intelligent token Petri nets

for modelling and control of reconﬁgurable automated

manufacturing systems with dynamical changes,”

Trans. Inst. Meas. Control, vol. 33, no. 1, pp. 9–29,

Feb. 2011.

Dumitrache, I., Caramihai, S. I. and Stanescu, A. M.

“Intelligent agent based control systems in

manufacturing,” in Proc. IEEE Int. Symp. Intell.

Control, 2000, vol. 1, pp. 369–374.

Ohashi, K. and Shin, K. G “Model-based control for

reconﬁgurable manufacturing systems,” in Proc. IEEE

Int. Conf. Robot. Autom., 2011, pp. 553–558.

Kalita, D. and Khargonekar, P. P. “Formal veriﬁcation for

analysis and design of logic controllers for

reconﬁgurable machining systems,” IEEE Trans.

Robot. Autom., vol. 18, no. 4, pp. 463–474, Aug.

2002.

H. Kopetz, “Time-triggered real-time computing”. Annual

Reviews in Control 27 (2003) 3–13, 2003.

Forejt, V., Kwiatkowska, M., Parker, D. Qu, H., and

Ujma. M., “Incremental Runtime Verification of

Probabilistic Systems”, Proc. 3rd International

Conference on Runtime Verification (RV'12), 2012.

Yang, L., Huai-Kou, M., Senior, M., Yan, M., Pan, L.,

“Nondeterministic Probabilistic Petri Net — A New

Method to Study Qualitative and Quantitative

Behaviors of System “,Journal of Computer Science

and Technology , Jan. 2013.

Suender, C., Vyatkin, V., and Zoitl, “A. Formal validation

of downtime less system evolution in embedded

automation controllers”. ACM Transactions on

Embedded Control Systems, 2011.

Dubinin, V., Hanisch, H., and Karras, S. “Building of

reachability graph extractions using a graph rewriting

system”. In proceedings of the 7th International

Conference of Science and Technology, NITis 2006.

Sharifloo, A.M, and Spoletini, P, “LOVER: Light-weight

fOrmal Verification of adaptivE systems at Run time”

Formal Aspects of Component Software, pp 170-177,

2013.

Carlo Ghezzi. “Engineering evolving and self-adaptive

systems: An overview”. In Software and Systems

Safety - Specification and Verification, pages 88{102.

2011.

Martin L. and Christian S., “A brief account of runtime

verification”. Journal of Logic and Algebraic

Programming, 78(5):293 {303, 2009}.

ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications

380