
Transformation from R-UML to R-TNCES: New Formal Solution for
Verification of Flexible Control Systems
Mohamed Oussama Ben Salem
1,2
, Olfa Mosbahi
2
, Mohamed Khalgui
2
and Georg Frey
3
1
Tunisia Polytechnic School, University of Carthage, Tunis, Tunisia
2
LISI Laboratory, INSAT, University of Carthage, Tunis, Tunisia
3
Chair of Automation and Energy Systems, Saarland University, Saarbr
¨
ucken, Germany
Keywords:
UML, R-TNCES, Model Transformation, Modeling, Model-based Verification, PCP, Shared Resource.
Abstract:
Unified Modeling Language (UML) is currently accepted as the standard for modeling software and control
systems since it allows to concentrate on different aspects of the system under design. However, UML lacks
formal semantics and, hence, it is not possible to apply, directly, mathematical techniques on UML models
to verify them. UML does not feature explicit semantics to model flexible control systems sharing adaptive
shared resources either. Thus, this paper proposes a new UML profile, baptized R-UML (Reconfigurable
UML), to model such reconfigurable systems. The profile is enriched with a PCP-based solution for the
management of resource sharing. The paper also presents an automatic translation of R-UML into R-TNCES,
a Petri Net-based formalism, to support model checking.
1 INTRODUCTION
The Unified Modeling Language (UML) is a semi for-
mal language developed by the Object Management
Group to specify, visualize and document models of
both software and non-software systems. Driven by
software engineering industries, it became well devel-
oped and supported with dozens of tools (Bahill and
Daniels, 2003). UML provides two types of diagrams
to create a specific profile for a given system: struc-
tural and behavioral. The first is designed to visual-
ize and document the static aspects of systems, while
the second aims at visualizing the dynamic aspects
(Warmer and Kleppe, 1998). UML has unquestion-
able advantages as a technique for visual modeling,
nevertheless, it does not guarantee that the generated
models are correct. Actually, no step of system devel-
opment, including the modeling one, is spared from
human errors. Consequently, the cost to detect and
remove such defects considerably increases through
the system development (Fenton and Neil, 1999).
The idea of being able to, more or less au-
tomatically and systematically, verify and validate
UML-based models has been around for a while,
so there is a rather large body of literature on the
topic. For example, the authors in (Lilius and Pal-
tor, 1999) use statecharts and sequence diagrams in
a combined manner to check temporal logic formu-
las over a statechart-based description of the system,
and the model checker produces, then, counterexam-
ples through sequence diagrams. Another approach
is described in (Cardoso and Sibertin-Blanc, 2001)
where sequence diagrams are formally translated into
Petri nets, based on the UML collaborations pack-
age metamodel. The authors check the correctness
of the sequence diagrams through the resulting Petri
nets. A work described in (Cortellessa and Mirandola,
2000) uses the sequence diagram in conjunction with
use cases and deployment diagrams to obtain queu-
ing network models for performance evaluation. An
execution graph from the sequence diagram is later
obtained thanks to a given algorithm. Another work
reported in (Mikk et al., 1998) translated Statecharts
into PROMELA, the input language of SPIN verifica-
tion system, whereas (Lam, 2007) formally analyzed
activity diagrams using NuSMV model checker to de-
termine the correctness of activity diagrams. The au-
thors in (King and Pooley, 1999) produce Petri net
models starting from UML diagrams, however, they
only describe the methodology at an intuitive level,
through an example and no translation procedure is
described. The work described in (Bondavalli et al.,
1999) proposed new UML stereotypes to enrich UML
diagrams with dependability aspects. The purpose
is to exploit the latter to build generally distributed
stochastic Petri net models. The authors didn’t focus
64
Ben Salem M., Mosbahi O., Khalgui M. and Frey G..
Transformation from R-UML to R-TNCES: New Formal Solution for Verification of Flexible Control Systems.
DOI: 10.5220/0005523700640075
In Proceedings of the 10th International Conference on Software Paradigm Trends (ICSOFT-PT-2015), pages 64-75
ISBN: 978-989-758-115-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

on an automatic translation, but rather on detecting
the dependability aspects from the UML diagrams.
We see in the previous related works that no one
of our community was interested in modeling the re-
configuration aspect which is featured by many con-
trol systems and their shared resources. Neverthe-
less, reconfiguration has become, nowadays, a cru-
cial feature to consider when designing new embed-
ded systems. It is actually the ability to dynamically
improve the latter’s performance and quality of ser-
vice at run-time, according to well defined conditions
(Salem et al., 2015b). Increasing safety constraints
and growing expected flexibility pushed developers
to focus on designing systems that are able to fit
their environment and shifting user requirements un-
der functional and temporal constraints (Salem et al.,
2015a). In this work, a reconfiguration scenario is
assumed to be any run-time automatic operation that
modifies the system’s structure by adding or remov-
ing tasks or resources according to user requirements
in order to adapt the whole architecture to its envi-
ronment (Salem et al., 2014). Whence, we propose,
in this work, a new UML profile, baptized R-UML
(Reconfigurable UML), endowed with a formal se-
mantics enabling UML to model flexible control sys-
tems sharing adaptive shared resources. R-UML re-
lies on UML’s extensibility mechanisms to enhance
class and statechars diagrams, respectively called R-
CD and R-StD henceforth. The latter are extended
to support Priority Ceiling Protocol (PCP), a well-
known synchronization protocol for shared resources.
It was proved in (Salem et al., 2014) the relevance of
this protocol to solve the issue of concurrent access
to adaptive shared resources in reconfigurable control
systems. We propose then a new solution to trans-
late R-UML into Reconfigurable Timed Net Condi-
tion/Event Systems (R-TNCES) (Zhang et al., 2013),
a Petri net-based formalism to model flexible con-
trol systems. An application of formal verification is,
then, performed and aims to (dis)prove certain prop-
erties of the system using a formal model. This contri-
bution is original since R-TNCES is a new and origi-
nal formalism for reconfigurable systems, and no one
in our community worked on the translation of UML
into R-TNCES to combine their respective assets, i.e.
the easiness and relevance of UML for visual model-
ing and the formal semantics of R-TNCES to verify
and validate models.
This paper is organized as follows: the next sec-
tion describes useful preliminaries for the reader. Sec-
tion 3 introduces a running example which will be
used throughout the paper to prove the relevance of
our contribution. We expose, in Section 4, the new
profile R-UML and a solution to translate the latter
into R-TNCES. We finish the paper in Section 5 by a
conclusion and an exposition of our future works.
2 BACKGROUND
We start, in this section, by presenting the formalisms
TNCES (Hanisch et al., 1997) and R-TNCES (Zhang
et al., 2013) which extend Petri nets for the model-
ing of adaptive control systems. We provide, then, an
overview of the well-known PCP.
2.1 Timed Net Condition/Event System
The formalism was introduced by (Hanisch et al.,
1997). A TNCES is a tuple:
T NCES = {P,T, F, m
0
,Ψ,CN,EN,DC} (1)
where (i) P = {p
1
, p
2
,..., p
n
} is a finite set of
places; (ii) T = {t
1
,t
2
,...,t
m
} is a finite set of transi-
tions; (iii) F ⊆ (P ×T ) ∪ (T ×P) is a finite set of flow
arcs between places and transitions; (iv) m
0
is initial
marking; (v) CN ⊆ (P × T ) is a finite set of condition
arcs; (vi) EN ⊆ (T × T ) is a finite set of event arcs.
Ψ is input/output structure of TNCES module
which is represented by the following tuple:
Ψ = {C
in
,E
in
,C
out
,E
out
,Bc,Be,Cs, Dt} (2)
where (i) C
in
defines a finite set of TNCES mod-
ule condition input signals; (ii) E
in
defines a finite
set of TCNES module event input signals; (iii) C
out
defines a finite set of TNCES module condition out-
put signals; (iv) E
out
defines a finite set of TCNES
module event output signals; (v) Bc ⊆ C
in
× T is
a set of TNCES module input condition arcs; (vi)
Be ⊆ En × T is a set of TNCES module input event
arcs; (vii) Cs ⊆ P × C
out
is TNCES module output
condition arcs; (viii) Dt ⊆ T × E
out
is a set of TNCES
module output event arcs.
Time intervals are assigned to the pre-transition
flow arcs F ⊆ P × T , which impose time constrains to
the firing of the transition:
DC = {DR,DL,D
0
} (3)
where (i) DR represents the set of minimum times
that the token should spend at particular place before
the transition can fire; (ii) DL is the final set of limi-
tation time that defines maximum time that the place
may hold a token (if all the other conditions for tran-
sition firing are met); (iii) D
0
is the initial set of the
clocks associated with the places.
TransformationfromR-UMLtoR-TNCES:NewFormalSolutionforVerificationofFlexibleControlSystems
65
2.2 Reconfigurable Timed Net
Condition/Event System
An R-TNCES, as defined in (Zhang et al., 2013), is a
structure RTN=(B, R), where R is the control module
consisting of a set of reconfiguration functions R =
r
1
,...,r
n
and B is the behavior module that is a union
of multi TNCESs, represented as
B = (P,T,F,W,CN, EN,DC,V,Z) (4)
where: (i) P (respectively, T) is a superset of
places (respectively, transitions), (ii) F ⊆ (P × T ) ∪
(T × P) is a superset of flow arcs, (iii) W: (P ×
T ) ∪ (T × P) → {0,1} maps a weight to a flow
arc, W (x,y) < 0 if (x,y) ∈ F, and W(x, y)=0 oth-
erwise, where x,y ∈ P ∪ T , (iv) CN ⊆ (P × T ) (re-
spectively, EN ⊆ (T × T )) is a superset of condi-
tion signals (respectively, event signals), (v) DC :
F ∩ (P × T ) → {[l
1
,h
1
],...,[l
|F∩(P×T)|
,h
|F∩(P×T)|
} is
a superset of time constraints on output arcs, where
i ∈ [1,|F ∩ (P × T )|], l
i
,h
i
∈ N, and l
i
< h
i
, (vi) V :
T → {∨,∧} maps an event-processing mode (AND
or OR) for every transition, (vii) Z = (M
0
, D
0
), where
M
0
: P → {0,1} is the initial marking and D
0
: P →
{0} is the initial clock position.
2.3 Priority Ceiling Protocol
The Priority Ceiling Protocol (PCP) (Goodenough
and Sha, 1988) in real-time computing is a synchro-
nization protocol for shared resources to avoid un-
bounded priority inversion and mutual deadlock due
to wrong nesting of critical sections. In this protocol,
each resource R is assigned a priority ceiling Cl(R),
which is equal to the highest priority of the tasks that
may lock it. A task can acquire a resource only if
the resource is free and has a higher priority than the
priority ceiling of the rest resources in lock by other
tasks.
Let us assume a system to be composed of the
tasks T
1
, T
2
, T
3
and T
4
(having respectively the in-
creasing priorities 1, 2, 3 and 4) and two resources R
and Q: R can be used by T
1
and T
2
and Q by T
1
and
T
4
. Then, Cl(R)=2 and Cl(Q)=4. Thus, T
2
is blocked
if it tries to block R which is free when Q is locked.
3 RUNNING EXAMPLE
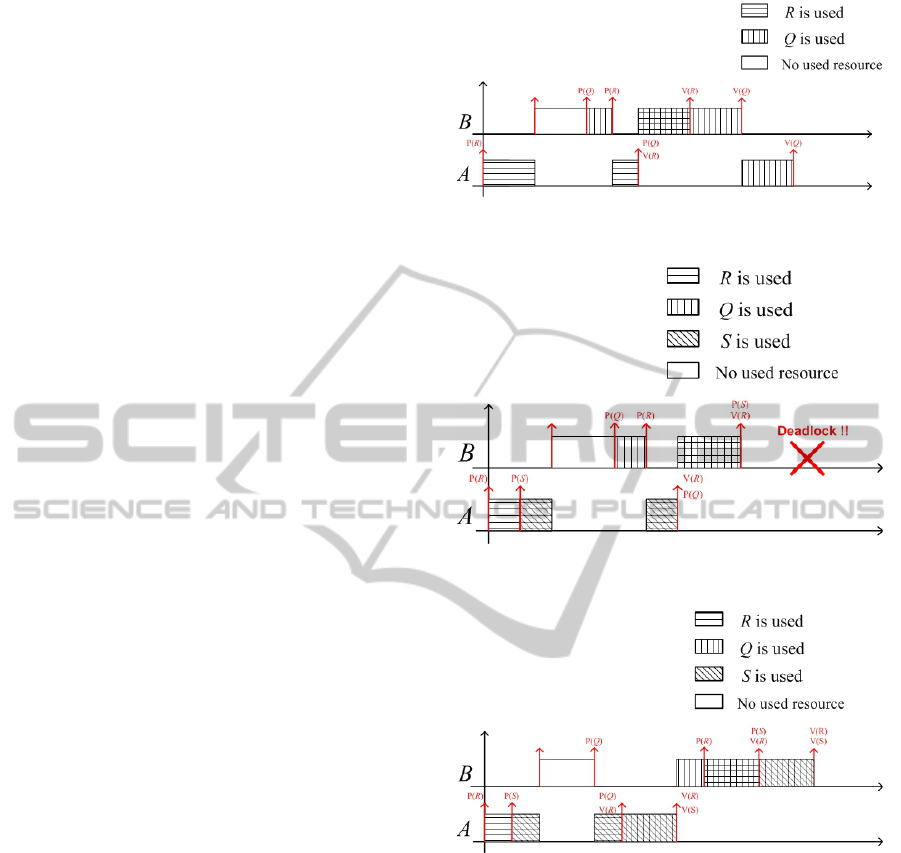
Let us assume a reconfigurable discrete event system
to be composed of two tasks A and B. We suppose that
these two tasks share initially the resources Q and R
(as shown in Figure 1) before applying a reconfigu-
ration scenario which will add a new resource S (to
Figure 1: Behavior of A and B before a reconfiguration sce-
nario.
Figure 2: Behavior of A and B after a reconfiguration sce-
nario.
Figure 3: A and B behaviors after using PCP.
be used by both A and B). This case was not treated
in any related work and forms a new problem dealing
with reconfigurable resources. We suppose that B has
the highest priority (B > A ). We suppose that the sys-
tem is safe before the reconfiguration scenarios. But,
once the reconfiguration is applied, a deadlock cer-
tainly occurs according to Figure 2. In fact, A starts
by using R and then S before being interrupted by B
due to the latter’s higher priority. B is then blocked
because it tries to lock R (P(R)) which is dill hold by
A. A continues progressing until it frees R (V(R)) and
B interrupts it. When B asks for S (P(S)), it is inter-
rupted because S is hold by A. A is in its turn blocked
because it is asking for Q which is hold by B. A dead-
lock occurs thus, because A is waiting for Q while B
for S. Regarding to this situation, we apply the PCP
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
66

on this running example which solves the deadlock
issue as illustrated in Figure 3.
This running example features two tasks sharing
three adaptive resources like in (Salem et al., 2014),
however, the tasks’ behavior and the reconfiguration
scenario are different. Besides, in (Salem et al.,
2014), a deadlock occurs because A is waiting for S
while B for Q, whereas, in this work, it occurs be-
cause A is waiting for Q while B for S.
4 CONCEPTION AND
VALIDATION OF FLEXIBLE
CONTROL SYSTEMS
We expose, in this section, the new profile R-UML
to model and validate flexible control systems sharing
adaptive resources. A new solution is proposed, then,
to transform an R-UML into an R-TNCES.
4.1 R-UML
In this section, we define how to model the structure
and the behavior of a flexible control system using
R-UML. The contribution is applied on the running
example of Section 3.
4.1.1 Structure Modeling
UML provides the class diagram to show the logical
structure of a system. This diagram highlights con-
ceptual connections showing the relations between
the system’s modules or components, each of which
having its distinctive properties defined by a class. It
is possible to extend the core semantics of UML and
express new properties by using stereotypes. The lat-
ter is a mechanism to categorize an element. Thus,
we extend the contribution proposed in (Lobov et al.,
2005) and define the following eight stereotypes of
the class’s attribute:
• << input >>: the given attribute is a system in-
put;
• << out put >>: the given attribute is a system
output;
• << in >>: the given attribute is a system module
input;
• << out >>: the given attribute is a system mod-
ule output;
• << eventInput >>: the given attribute is a sys-
tem module event input;
• << eventOut put >>: the given attribute is a sys-
tem module event output;
• << integer >>: the given attribute is an integer;
• << boolean >>: the given attribute is a boolean
attributed which can be evaluated to TRUE or
FALSE.
The description above distinguishes between sys-
tem and module. System denotes the whole system
under control, whereas module a part of the system.
A system may actually have internal connections be-
tween the modules specified by means of the stereo-
types << in >> and << out >>, and a module may
provide to the controller the connections that are spec-
ified by means of the stereotypes << input >> and
<< out put >>. Two system modules may also be
interconnected by an event which is an action which
occurrence may be detected by another module in the
system. An event is different from an input/output,
since the first is just a signal informing that a cer-
tain action took place. The << eventInput >> and
<< eventOut put >> stereotypes respectively repre-
sent the event inputs and outputs that a module may
have.
The information provided by a class diagram can
be formally written as a tuple:
ClD = {C,A,M, S,α, β} (5)
where (i) C = {cl
1
,c1
2
,...,cl
n
} is a fi-
nite set of classes in class diagram ClD;
(ii) A = {attr
1
,attr
2
,...,attr
n
} is a final set
of attributes that belong to the classes; (iii)
M = {setlnput,resetInput,setOut put,resetOut put,
setCeiling} is a set of methods of the classes;
(iv) S is a set of stereotypes / S = {<< in >>
,<< out >>,<< input >>, << out put >>
,<< eventInput >>, << eventOut put >>, <<
integer >>,<< boolean >>}; (v) α : st
i
→ attr
j
is
a function that maps the stereotype st
i
from S to the
attr
j
from A; (vi) β : attr
i
→ cl
j
is a function that
maps attribute to the class.
According to the previous class diagram defini-
tion, we create two classes to model the running ex-
ample of Section 3: a class named Task to model, as
its name suggests, the different tasks of the system,
and a second one, named Resource, to model the dif-
ferent reconfigurable shared resources. We instantiate
for each task or resource an object from the corre-
sponding class.
The class Task, as showed in Figure 4, has an
integer-stereotyped attribute, named priority, trans-
lating the task’s priority. It also has a boolean-
stereotyped one, added, indicating whether the task
in added to the system (added=TRUE) or not
(added=FALSE), depending on the applied reconfig-
uration scenario. The Figure 5 shows that the class
TransformationfromR-UMLtoR-TNCES:NewFormalSolutionforVerificationofFlexibleControlSystems
67

Resource features an integer-stereotyped attribute,
named ceiling, translating the ceiling that each re-
source has according to PCP definition in Section 2.3.
The class also features a method named setCeiling
that recompute a resource’s ceiling after applying a
reconfiguration scenario. This method’s code will be
detailed later. Just as tasks, resources have a boolean-
stereotyped attribute, added, because a reconfigura-
tion scenario may add or remove a task or a resource
(Salem et al., 2014).
Figure 4: The Task class.
Figure 5: The Resource class.
Running Example 1
The static description of a system is often made
through the class diagram. This simplifies the
modeling by synthesizing the common charac-
teristics and covering a large number of objects.
However, it is sometimes useful or even neces-
sary to add an object diagram. The latter al-
lows, depending on the situation, to illustrate the
class diagram (showing an example that explains
the model), clarify certain aspects of the sys-
tem (by highlighting imperceptible details in the
class diagram), express an exception (by mod-
eling specific cases of non-generalizable knowl-
edge) or take an image (snapshot) of a system
at a given time. The class diagram models the
rules, whereas the object diagram models facts.
Often the class diagram is a model to instanti-
ate the binders in order to obtain the object dia-
gram (Rumbaugh et al., 1991). Thus, we propose
here to realize the object diagram of the running
example described in Section 3. The said dia-
gram illustrated in Figure 6 features two objects
of the Task class (modeling the tasks A and B)
and three of the Resource class (modeling the re-
sources R, Q and S) while highlighting the links
between them.
4.1.2 Behavior Modeling
UML features the State diagram as powerful tool to
represent the behavior of an object which is the im-
plementation of a particular class. We define for the
system or its components a set of states which they
may take. Each state is distinguished by its name.
The change of the states is represented via transitions.
The latter specify the laws that cause the change of
the state and the consequences of the change. The
rules which fire transitions may be expressed by event
and guard which is a boolean expression that has to be
evaluated to TRUE to fire the transition. A given tran-
sition may be fired through three manners: an event (if
a certain action took place somewhere in the system),
a guard (if the certain properties are assigned with the
particular values) or combination of both. The differ-
ent states are interconnected by transitions which de-
termine the rules that cause transition to fire and the
consequences of a transition’s firing. Events, guards
and the combination of both specify these rules. A
time event, after (n) where n is a positive integer, is
also used to specify that n time units should elapse be-
fore the transition may fire. Events may also be spec-
ified by << eventInput >> or << eventOut put >>
stereotyped attributes. A transition firing may be ac-
companied by the activation of an action which can
modify some properties of the system. This activa-
tion may call attribute-modifying methods defined in
the classes, such as setlnput, resetInput, setOutput, re-
setOutput and setCeiling.
We extend the contribution proposed in (Lobov
et al., 2005) and formally represent a state diagram
by the tuple:
StD = {St,Tr, Ev,G,Ac, γ,δ, ε,ζ} (6)
where (i) St = {st
1
,st
2
,...,st
n
} is a finite set
of states in a state diagram StD; (ii) Tr =
{tr
1
,tr
2
,...,tr
m
} is a finite state of transitions in a state
diagram StD; (iii) Ev is a finite set of events in transi-
tions of StD; (iv) G is a finite set of the guards in StD;
(v) Ac is a final set of actions; (vi) γ : ev
i
→ tr
j
is a
function that maps the event ev
i
of Ev to the transition
tr
j
of Tr; (vii) δ : gr
k
→ tr
j
is a function that maps
the guard gr
k
of Gr to the transition tr
j
of Tr; (viii)
ε : act
l
→ tr
j
is a function that maps the action act
l
of
Ac to the transition tr
j
of Tr; (ix) ζ : tr j → {st
b
,ste} is
a function that maps transition tr
j
of Tr to the pair of
states st
b
and st
e
, where st
b
is the state from which the
transition is taken and st
e
is the next state if tr
j
fires.
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
68

Figure 6: The running example’s object diagram.
According to the reconfiguration feature expected
from the system, we define a reconfigurable state dia-
gram as a structure:
R − StD = (B,R) (7)
where (i) B is the behavior module that is a union
of multi StD; (ii) R is the control module consisting
of a set of reconfiguration functions R={r
1
,...,r
n
}.
A reconfiguration function r
i
makes the necessary
changes to the system after a reconfiguration scenario
in accordance with the definition given in Section 1.
Hence, we define r as the structure:
r = (η, θ,ι) (8)
where (i) η : t
i
→ {0, 1} is a function controlling
tasks, η(t
i
) = 1 if the task t
i
is added to the system,
η(t
i
) = 0 otherwise; (ii) θ : res
j
→ {0,1} is a function
controlling resources, θ(res
j
) = 1 if the resource res
i
is added to the system and θ(res
j
) = 0 otherwise; (iii)
ι : (res
j
,t
i
) → {0,1}, ι(res
j
,t
i
) = 1 if res
j
is used by t
i
in this triggered reconfiguration scenario, ι(res
j
,t
i
) =
0 otherwise.
According to the previous definitions, we define in
this section the Resource class’s method, setCeiling,
as follows:
if θ(res) == 1
for i:=1 to |Tasks|
if η(t
i
) == 1 AND ι(res,t
i
) == 1
AND t
i
.priority > res.ceiling
res.ceiling := t
i
.priority
We propose, then, R-StD diagrams to model a task
and a resource on the basis of PCP definition and
the reconfiguration feature expected from the system.
Thus, we propose the R-StD illustrated in Figure 7 to
model a reconfigurable shared resource:
Figure 7: The shared resource’s R-StD.
A resource may actually be free or hold by a task
T
i
. Thus, we propose the states ”Free”, ”Hold by T
i
”
and ”Hold by T
n
” where R may be exclusively hold by
a task from a set of n different tasks (n is an integer
∈ (1, +∞)). The guards associated to the transitions
leaving the state Free guarantee the respect of PCP
rules before locking a resource, i.e. a task T may hold
a given resource if, first, the latter is free and, sec-
ondly, the resources hold by other tasks have a ceiling
lower than T’s dynamic priority, a condition verified
by the guard named X. E3.i is an event coming from
T
i
and asking to unlock R.
We propose, then, a second R-StD, illustrated in
Figure 8 to model a reconfigurable task:
The task’s R-StD is composed of the following
states: (i) Idle: as its names suggests, the task is idle,
(ii) Execute: the task is running, (iii) Wait: the task
was interrupted by another one, so it is waiting, (iv)
P(R): the task T is asking to lock a resource R, (v)
Q(R): the task T is unlocking the resource R. The R-
TransformationfromR-UMLtoR-TNCES:NewFormalSolutionforVerificationofFlexibleControlSystems
69

Figure 8: The task’s R-StD.
StD of a task T should include as many P(R) and Q(R)
as the resources it may lock, but, in this running ex-
ample, we decide that T will use just one resource
(R).The different events indicated on the figure above
stand for:(i) E2: an event confirming the lock of Rby
T, (ii) E8.1 and E8.2: when T switches from Idle to
Execute, the event E8.1 forces the running tasks with
lower priorities to switch from Execute to Wait. T’s
E8.1 is actually the E8.2 of tasks with lower priorities.
Whence, the E8.2 on Figure 8 is an event announcing
that a task with a higher priority than T’s switched
from Idle to Execute, (iii) E9.1: when T switches from
Execute to Idle, the event E9.1 will force the waiting
tasks with lower priorities to switch from Wait to Exe-
cute. T’s E9.1 is actually the E9.2 of tasks with lower
priorities. Whence, the E9.2 is translating that a task
with a higher priority that T’s has switched from Ex-
ecute to Idle.
Running Example 2
Now that we formalized R-StD and proposed
patterns to model control tasks and shared re-
sources, we can model our running example. We
propose, as examples and respectively in Figure
9 and Figure 10, the modeling of the control task
A, which uses the resources Q, R and S, and the
resource R which is shared by the tasks A and B.
In our case study, the different resources have
the same modeling since they have the same ceil-
ing and are used by the same tasks. We choose to
model the resource R as shown in Figure 10. The
guards named X are used to guarantee that, when
a task T tries to lock the resource, all the other
resources, whose ceilings are not lower than the
task’s priority, are free or hold by T. Thus, we
avoid any eventual deadlock and see the rele-
vance of the PCP.
Figure 9: The task A’s R-StD.
Figure 10: The resource R’s R-StD.
4.2 Transformation
We present, in this section, R-TNCES-based models
using PCP to solve the issue of concurrent access to
adaptive shared resources. We propose, then, a new
solution to translate R-StD models into the said R-
TNCES-based ones. A formal verification is, then,
performed to prove the relevance of our contribution.
4.2.1 PCP-based Solution for Resource Sharing
in R-TNCES
We aim in this section to check the safety of each
reconfiguration scenario by enriching the Recon-
figurable Timed Net Condition/Event System (R-
TNCES) with the PCP protocol. We propose, then, to
use new patterns introduced in (Salem et al., 2014) to
model reconfigurable discrete event systems accord-
ing to R-TNCES by using PCP. This contribution is
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
70

original since R-TNCES is an original formalism for
reconfigurable systems, but lacks of useful mecha-
nisms to manage reconfigurable shared resources.
Formalization
We present in this section the formalization of
Distributed Reconfigurable Control Systems (DRCS)
sharing resources.
DRCS
The authors in (Salem et al., 2014) assume a
DRCS D to be composed of n
1
networked reconfig-
urable sub-systems sharing n
2
resources. They extend
the formalization of DRCS in (Zhang et al., 2013) by
adding the new set of resources as follows:
D = (
∑
R − T NCES,ϖ,
∑
M,
∑
R) (9)
where: (i)
∑
R − T NCES is a set of n
1
R-TNCES,
(ii) ϖ a virtual coordinator handling
∑
M, a set of
Judgment Matrices, (iii)
∑
R, a set of n
2
shared
resources.
Shared Resources
On the basis of PCP’s definition and the flexibility
expected from the DRCS, a resource R is defined as
follows :
R = (Rec,S,Cl) (10)
where: (i) Rec (Reconfiguration) indi-
cates whether R is added to the system /
Rec ∈ {added,!added}, (ii) S indicates the state of R
/S ∈ { f ree,hold by a task i}, (iii) Cl is used for the
ceiling of R.
Tasks
Based on the expected reconfiguration of the sys-
tem, the authors in (Salem et al., 2014) defines a task
T by:
T = (Rec, S) (11)
where: (i) Rec (Reconfiguration) indi-
cates whether T is added to the system /
R ∈ {added,!added}, (ii) S indicates the state
of T /S ∈ {idle,execute,wait, P(R
i
),V (R
i
)} and
P(R
i
) means locking R and V (R
i
) unlocking it.
Modeling
The authors in (Salem et al., 2014) proposes new
solutions to introduce PCP in R-TNCES to avoid any
blocking problem after reconfiguration scenarios. An
R-TNCES model is proposed for each resource of
∑
R and task of
∑
R − T NCES.
Shared Resources
Each shared resource is modeled by an R-TNCES
as shown in Figure 11. The latter is composed of
three TNCES modeling the resource’s reconfiguration
(Rec), state (S) and ceiling (Cl). Here is the modeling
of a resource R:
Figure 11: A shared resource’s modeling.
Control Tasks
The authors in (Salem et al., 2014) model each
task T by an R-TNCES to be composed of two
TNCESs as shown in Figure 12: the first one is illus-
trating its reconfiguration (Rec), the second its state
(S).
Figure 12: A task’s modeling.
4.2.2 R-Std Translation into R-TNCES
The paper proposes Table 1 which is given above
to show the correspondence between R-StD and R-
TNCES. The numbers given in parentheses show the
reference to the formulas that give details on the syn-
tax used in the table.
The seven translation rules are explained here-
after:
TransformationfromR-UMLtoR-TNCES:NewFormalSolutionforVerificationofFlexibleControlSystems
71

Table 1: Correspondence table for R-StD translation into R-TNCES.
Rules R-StD R-TNCES
Rule 1 St (6) P (4)
Rule 2 Tr (6) T (4)
Rule 3 {st
b
,st
e
} := ζ(tr) (6) {p
out
, p
to
} ⊆ P ; { f a
1
, f a
2
} ⊆ F (4)
Rule 4 gr := δ
−1
(tr) (6) ci ∈ C
in
(2) ; co ∈ C
out
(2) ; ca ∈ CN (1)
Rule 5 ac := ε
−1
(tr) (6) ei ∈ E
in
(2) ; eo ∈ E
out
(2) ; ea ∈ EN (1)
Rule 6 ev := ζ
−1
(tr) (6) AND << eventInput >>:= α
−1
(ev) (5) ei ∈ E
in
(2) ; eo ∈ E
out
(2) ; ea ∈ EN (1)
Rule 7 ev := ζ
−1
(tr) (6) AND ev is an after(n) event n ∈ DR ; ∞ ∈ DL (1) (2) (3)
Figure 13: The illustrative example’s R-TNCES.
• Rule 1: A state St in an R-StD corresponds to a
place P in an R-TNCES;
• Rule 2: A transition Tr in an R-StD corresponds
to a transition too (T) in an R-TNCES;
• Rule 3: Each transition tr in an R-StD is mapped
to a pair of states, st
b
and st
e
, where the first is the
state from which tr is taken and the second is the
next state if tr fires. The corresponding transition
(t) and two places (p
out
and p
to
) will be created
using, respectively, Rule 2 and Rule 1. Rule 3
creates actually in the R-TNCES a flow arc, f a
1
,
linking p
out
to t, and another one, f a
2
, linking t to
p
to
;
• Rule 4: In an R-StD, some guards can be mapped
to some transitions. A guard gr corresponds to
a condition arc, ca, in an R-TNCES. A condition
output signal, co, is added to the place from which
ca is leaving and a condition input signal, ci, to the
place which is pointed by ca;
• Rule 5: In an R-StD, some actions can be mapped
to some transitions. An action ac corresponds to
an event arc, ea, in an R-TNCES. An event output
signal, eo, is added to the place from which ea is
leaving and an event input signal, ei, to the place
which is pointed by ea;
• Rule 6: In an R-StD, each <<eventInput>>-
stereotyped event, ev, is translated into an event
arc, ea, in the corresponding R-TNCES. An event
output signal, eo, is added to the place from which
ea is leaving and an event input signal, ei, to the
place which is pointed by ea;
• Rule 7: An R-StD may feature after(n)-typed
events, where n ∈ N
N
N
∗
. If so, n is added to DR,
the set of minimum times that the token should
spend at particular place before the transition can
fire, and ∞ to DL, the set of limitation time that de-
fines maximum time that the place may hold a to-
ken, since the place from which the after(n)-typed
event is leaving may indefinitely hold the token.
4.2.3 Verification
We propose in this section to check the relevance of
the our solution and the contribution of PCP in solv-
ing several issues threatening a DRCS’s safety and
deadlock-freedom. Thus, we start by modeling the
running example of Section 3 in UML and then trans-
forming the latter in R-TNCES according to (Zhang
et al., 2013).
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
72

Figure 15: The taks A and B’s modeling using PCP.
Figure 14: Screenshot from SESA.
Thus, we don’t call out the PCP. We obtain the
model illustrated in Figure 13. To verify it, we use
model-checking which is a technique for automat-
ically verifying the correctness properties of finite-
state systems. Model checking for R-TNCES is based
on its reachability graphs. ZiZo (Salem et al., 2015b)
is a new and effective software environment for the
analysis of R-TNCES, which computes the set of
reachable states exactly. It exports, then, files ex-
ploitable by the model-checker SESA (Starke and
Roch, 2002). Typical properties which can be ver-
ified are boundedness of places, liveness of transi-
tions, and reachability of states. In addition, tempo-
ral/functional properties based on Computation Tree
Logic (CTL) specified by users can be checked man-
ually. We apply, then, the CTL formula AG EX TRUE
which checks the deadlock-freedom of the system.
The said formula turned out to be false as shown in
Figure 14, meaning that the system features a dead-
lock issue.
Whence, we call out the solution we proposed in
the previous sections. We start by modeling the two
tasks and the three resources in R-StD and transform,
then, the models to R-TNCES based on the transfor-
mation rules specified in Section 4.2.2. We obtain,
thus, the R-TNCES model of the tasks A and B illus-
trated in Figure 15.
Once the R-TNCES model of the DRCS is en-
riched with PCP, the next step is to verify whether
the models meet users requirements. So, any recon-
figuration scenario dealing with adding/removal of re-
sources does not lead to a blocking situation. The fol-
lowing e-CTL formula is applied:
AG EX true (12)
This formula is proven to be true by SESA as
shown in the screenshot in Figure 16, so there is no
deadlock in our R-TNCES.
Figure 16: Screenshot from SESA.
We also check the safety property by checking if
a given resource may be simultaneously locked by
two different tasks. The following CTL formula is
checked:
EF p22 AND p23 (13)
where p22 is the place translating that the resource
R is locked by the task A; p22 means that B locks R.
This formula is proven to be false as illustrated in Fig-
ure 17.
Figure 17: Screenshot from SESA.
The formula 13 is applied six times of the R-
TNCES modeling, changing at each time p22 and p23
by the places which correspond to the ones translating
that the resource R (and then Q and S) is locked by the
task A (and then B). We check thus whether a given
resource can be locked by the two tasks at the same
time. The six formulas turned out to be false. We
TransformationfromR-UMLtoR-TNCES:NewFormalSolutionforVerificationofFlexibleControlSystems
73

are sure, then, that our system doesn’t feature a dead-
lock issue caused by a concurrent access to shared re-
sources after a reconfiguration scenario.
5 CONCLUSIONS
Our work consisted, through this paper, in propos-
ing a new UML profile, the R-UML, to model and
verify flexible control systems sharing adaptive re-
sources. Whence, we chose to enhance class and
statecharts diagrams to support PCP. We proposed,
then, a new and original solution to translate the gen-
erated R-UML models into R-TNCES-based patterns
which were proposed in (Salem et al., 2014). This
aims at proving the correctness of the R-UML mod-
els by performing model-checking on the generated
R-TNCES models. The relevance of our contribution
was proved thanks to model-checking using ZiZo, a
new R-TNCES editor, simulator and model-checker
(Salem et al., 2015b). This approach is original since
R-TNCES is a new formalism dedicated to flexible
control systems modeling and ZiZo is a new tool sup-
porting the said formalism.
The next step is to apply this contribution on
BROS, a new surgical robotic platform (Salem et al.,
2015a). BROS is a flexible system since it can run
under different operating modes: it is reconfigurable.
The concurrent access to adaptive shared resources is
present in the said system, which can be rather haz-
ardous in such medical systems. Whence, applying
our contribution on BROS can be very relevant to cer-
tify that the robotic platform is safe and does not run
any risk after any reconfiguration scenario.
ACKNOWLEDGEMENTS
This research work is carried out within a MOBIDOC
PhD thesis of the PASRI program, EU-funded and ad-
ministered by ANPR (Tunisia). The BROS national
project is a collaboration between ARDIA, the Ortho-
pedic Institute of Mohamed Kassab, eHTC and IN-
SAT (LISI Laboratory) in Tunisia and Saarland Uni-
versity in Germany.
REFERENCES
Bahill, T. and Daniels, J. (2003). Using objected-oriented
and uml tools for hardware design: A case study. Sys-
tems Engineering, 6(1):28–48.
Bondavalli, A., Majzik, I., and Mura, I. (1999). Auto-
mated dependability analysis of UML designs. In
Object-Oriented Real-Time Distributed Computing,
1999.(ISORC’99) Proceedings. 2nd IEEE Interna-
tional Symposium on, pages 139–144. IEEE.
Cardoso, J. and Sibertin-Blanc, C. (2001). Ordering actions
in sequence diagrams of UML. In Information Tech-
nology Interfaces, 2001. ITI 2001. Proceedings of the
23rd International Conference on, pages 3–14. IEEE.
Cortellessa, V. and Mirandola, R. (2000). Deriving a queue-
ing network based performance model from UML
diagrams. In Proceedings of the 2nd international
workshop on Software and performance, pages 58–70.
ACM.
Fenton, N. E. and Neil, M. (1999). A critique of soft-
ware defect prediction models. Software Engineering,
IEEE Transactions on, 25(5):675–689.
Goodenough, J. B. and Sha, L. (1988). The priority ceil-
ing protocol: A method for minimizing the blocking of
high priority Ada tasks, volume 8. ACM.
Hanisch, H.-M., Thieme, J., Luder, A., and Wienhold,
O. (1997). Modeling of PLC behavior by means
of timed net condition/event systems. In Emerging
Technologies and Factory Automation Proceedings,
1997. ETFA’97., 1997 6th International Conference
on, pages 391–396. IEEE.
King, P. and Pooley, R. (1999). Using UML to derive
stochastic petri net models. In Proceedings of the 15th
UK Performance Engineering Workshop, pages 45–
56.
Lam, V. S. (2007). A formalism for reasoning about UML
activity diagrams. Nordic Journal of Computing,
14(1):43–64.
Lilius, J. and Paltor, I. P. (1999). The production cell: An
exercise in the formal verification of a UML model.
Lobov, A., Lastra, J. M., and Tuokko, R. (2005). Applica-
tion of UML in plant modeling for model-based ver-
ification: UML translation to TNCES. In Industrial
Informatics, 2005. INDIN’05. 2005 3rd IEEE Inter-
national Conference on, pages 495–501. IEEE.
Mikk, E., Lakhnech, Y., Siegel, M., and Holzmann,
G. J. (1998). Implementing statecharts in PROME-
LA/SPIN. In Industrial Strength Formal Specification
Techniques, 1998. Proceedings. 2nd IEEE Workshop
on, pages 90–101. IEEE.
Rumbaugh, J., Blaha, M., Premerlani, W., Eddy, F.,
Lorensen, W. E., et al. (1991). Object-oriented model-
ing and design, volume 199. Prentice-hall Englewood
Cliffs.
Salem, M. O. B., Mosbahi, O., and Khalgui, M. (2014).
PCP-based solution for resource sharing in reconfig-
urable timed net condition/event systems. In ADECS
2014, Proceedings of the 1st International Workshop
on Petri Nets for Adaptive Discrete-Event Control Sys-
tems, co-located with 35th International Conference
on Application and Theory of Petri Nets and Con-
currency (Petri Nets 2014), Tunis, Tunisia, June 24,
2014., pages 52–67.
Salem, M. O. B., Mosbahi, O., Khalgui, M., and Frey, G.
(2015a). BROS - a new robotic platform for the treat-
ment of supracondylar humerus fracture. In HEALTH-
INF 2015 - Proceedings of the International Confer-
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
74

ence on Health Informatics, Lisbon, Portugal, 12-15
February, 2015, pages 151–163.
Salem, M. O. B., Mosbahi, O., Khalgui, M., and Frey, G.
(2015b). ZiZo: Modeling, simulation and verifica-
tion of reconfigurable real-time control tasks sharing
adaptive resources. application to the medical project
BROS. In HEALTHINF 2015 - Proceedings of the
International Conference on Health Informatics, Lis-
bon, Portugal, 12-15 February, 2015, pages 20–31.
Starke, P. H. and Roch, S. (2002). Analysing signal-net sys-
tems. Professoren des Inst. f
¨
ur Informatik.
Warmer, J. B. and Kleppe, A. G. (1998). The object con-
straint language: Precise modeling with uml (addison-
wesley object technology series).
Zhang, J., Khalgui, M., Li, Z., Mosbahi, O., and Al-Ahmari,
A. M. (2013). R-TNCES: A novel formalism for re-
configurable discrete event control systems. Systems,
Man, and Cybernetics: Systems, IEEE Transactions
on, 43(4):757–772.
TransformationfromR-UMLtoR-TNCES:NewFormalSolutionforVerificationofFlexibleControlSystems
75
