Pulley-type Ring Resonator and Optimization

Dong-Po Cai

, Chii-Chang Chen

and Chien-Chieh Lee

Department of Optics and Photonics, National Central University, 32001 Jhongli, Taiwan

Optical Sciences Center, National Central University, 32001 Jhongli, Taiwan

Keywords: Ring Resonators, Nano-optics.

Abstract: In this work, we propose a guideline to design the high Q-factor ring resonators. To keep the optical energy

in the ring, the radiation loss of the ring should be reduced. The difference of the propagation constant

between the bus waveguide and the ring should be enlarged to prevent from the light in ring to be coupled

back to the bus waveguide. The phase difference of the light between the bus waveguide and ring should be

adjusted to obtain the destructive interference at the output port (critical coupling). From these points

mentioned above, we compare the 6 types of ring resonators. We conclude that the high Q-factor pulley-

type ring resonator can be more easily designed. The experimental Q-factor of the pulley-type ring

resonators with ring radius of only 4.43µm can be obtained up to 1.73×10

1 INTRODUCTION

The microring resonator is an important and

versatile integrated optics component. For example,

several devices such as filter (Little et al., 1997),

gyroscope (Matsko et al., 2004) and optical switch

(Almeida and Lipson, 2005) can be constructed by

the microring resonator. In the past decade, several

types of microring resonator are developed such as

the single microring with single bus waveguide

(Terrel et al., 2009) or double bus waveguides

(Nawrocka et al., 2006), the racetrack type (Menon

et al., 2004) and the multiple microrings type (Poon

et al., 2004). However, to decrease the device

dimension, the reduction of the ring size is required.

The disadvantage of above microring structures is

the huge bending or radiation loss from the

microring resulting in the lower Q-factor. In order to

obtain the high Q-factor, the size of the above

microring structures must be increased to reduce the

bending loss or radiation loss. The microdisk and

microring with the pulley-type coupling

configuration, pulley coupler, have been reported for

the applications of integrated optical isolators and

sensor devices in Ref. (Hu et al., 2008) and

(Hosseini et al., 2010) respectively. The Q-factor of

the ring resonators with pulley-coupler has been

reported to be 10,000 to 210,000, respectively.

However, the performance of the pulley-type ring

resonators has not been compared to that of the other

types of ring resonators.

In this work, we propose a guideline to design

the high Q-factor ring resonators. We compare the 6

types of ring resonators. We conclude that the high

Q-factor pulley-type ring resonator can be more

easily designed.

2 SIMULATION

To design the high Q-factor ring resonators, the

optical energy should be kept in the ring. First, the

radiation loss of the ring should be reduced.

Secondly, the difference of the propagation constant

between the bus waveguide and the ring should be

enlarged to prevent from the light in ring to be

coupled back to the bus waveguide.

Thirdly, the phase difference of the light between

the bus waveguide and ring should be adjusted to

obtain the destructive interference at the output port

(critical coupling). Fine tune of the dimensions of

the ring should be performed.

Table 1 shows the dimension parameters that can

be varied for finely tuning the ring resonators to

obtain the high Q-factor. We can observe that only

the bus waveguide width change one property of the

ring resonators, . Therefore, in this work we finely

tune the performance of the ring resonators by

changing the bus waveguide width.

Cai D., Chen C. and Lee C..

Pulley-type Ring Resonator and Optimization.

DOI: 10.5220/0005523800250028

In Proceedings of the 6th International Conference on Optical Communication Systems (OPTICS-2015), pages 25-28

ISBN: 978-989-758-116-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Dimension parameter of ring resonators and the

influences on the properties of ring resonators.

Dimension Parameters Influences

Ring radius

L, , λ

Gap

, κ, λ

Ring waveguide width

L, , λ

Bus waveguide width



Refractive index

λ, 

L: the length of cavity, β: the propagation constant

: the resonant wavelength, : the coupling coefficient.

In this study, we adopt the 2-D finite-difference

time- domain method (2-D FDTD) to investigate the

energy decay in the ring resonators. The microring

resonator of the 6 types to be studied are

schematically shown in Fig. 1(a)-(e).

The refractive index of bus waveguides and the

ring is 3.48. The background refractive index is

unity. The inner radius, R0, and the outer radius, R1,

of the ring are 4.33m and 4.53m, respectively.

The inner radius, R2, and outer radius, R3, of the

curved bus waveguide is 4.68m and 4.88m. The

ring waveguide width, d1, and the bus waveguide

width, d3, are both 0.2m. The gap, d2, between the

ring and the bus waveguide is 0.15m. The light at

the wavelength of 1550nm in the TM polarization is

launched into the waveguide.

Figure 1: (a) Schematic drawing of the pulley-type

microring resonator. (b)-(e) Schematic drawing of the

various ring resonators.

Fig. 2(a) shows the bending loss per propagation

distance of the single ring waveguide and the two

concentric ring waveguides. The single ring

waveguide with the central radius, Rc, defined as

(R0+R1)/2 is schematically shown in Fig. 2(b). Fig.

2(c) illustrates the two concentric ring waveguides.

The gap between two waveguides is 0.15 m. The

inner and outer waveguide widths are 0.2m and

0.23 m, respectively. We launch an impulsed light

in the ring and to obtain the bending loss per

propagation distance of ring waveguide.

We can observe that the bending loss of the two

concentric ring waveguides is lower than that of the

single ring waveguide. This is due to the fact that the

outer waveguide of the concentric ring waveguides

can collect the light of the radiation loss of the inner

waveguide. Since the light in the outer waveguide

can be coupled back to the inner waveguide, the

bending loss of the ring can be reduced.

Figure 2: (a) Bending loss per propagation distance of

single ring waveguide and two concentric ring waveguides

for different Rc. (b) and (c) Schematic drawing of single

ring waveguide and two concentric ring waveguides,

respectively.

Table 2: Q-factors and Db for the 6 ring resonator

structures illustrated in Figure 1.

Structure Q-factor



Fig. 1(a)

7×10

3.4372

1.4×10

1.2103

Fig. 1(b)

1.24×10

10.2

1.98×10

5.367

Fig. 1(c)

7.16×10

10.2

9.06×10

5.367

Fig. 1(d)

3.6×10

4.465

5.8×10

1.355

0.2418

Fig. 1(e)

2.83×10

9.6078

5.86×10

Fig. 1(f)

1.79×10

9.7684

3.6×10

OPTICS2015-InternationalConferenceonOpticalCommunicationSystems

3 FABRICATION AND

CHARACTERISATION

We fabricate the pulley-type microring resonators by

using the e-beam lithography. The SOI with the top

silicon layer of 250 nm thick and the buried oxide

layer of 3m thick is used. The sample is prebaked

on the hotplate with 90

C during 1 minute. The E-

beam writer, RAITH150-TWO, with the

acceleration voltage 20 kV and the aperture size of

30m is employed to define the pattern of the

pulley-type ring resonators. The ring waveguide

width, the gap width, the bus waveguide width and

the radius of ring are chosen to be 0.2, 0.15, 0.23

and 4.43m, respectively. The grating coupler is

employed to couple the light into and out of the ring

resonators with the optical fibers. The period of

grating is 620 nm. The duty cycle of grating

couplers is gradually varied from 13 % to 50 % with

the step of 1.6 %. The taper segments with the

length of 150m are used to connect the bus

waveguide and the grating coupler. The developer

(MF-319: TMAH=99%: 1%) is used to remove the

unexposed photoresist during 20 seconds. After

developing, the sample is rinsed by deionized water

(DI water) during 20 seconds to remove the residual

developer. Finally, the sample is dried by the N2 gas.

Before etching, the sample is hard baked on the

hotplate with 100

C during 10 minutes to firm the

photoresist. The pattern of the pulley-type ring

resonators and the grating couplers are transferred to

the SOI wafer by the reactive-ion etching (RIE) with

the power of 160 W, the working pressure of 80

mTorr, CF

(48 SCCM) (SCCM stands for cubic

centimeter per minute at standard conditions for

temperature and pressure) and CHF

(12 SCCM).

The etching depth of device is around 150 nm. After

the dry etching, the acetone (ACE) is used to remove

the residual photoresist. The scanning electron

micrograph (SEM) image of the pulley-type ring

resonator, the grating coupler and the schematic

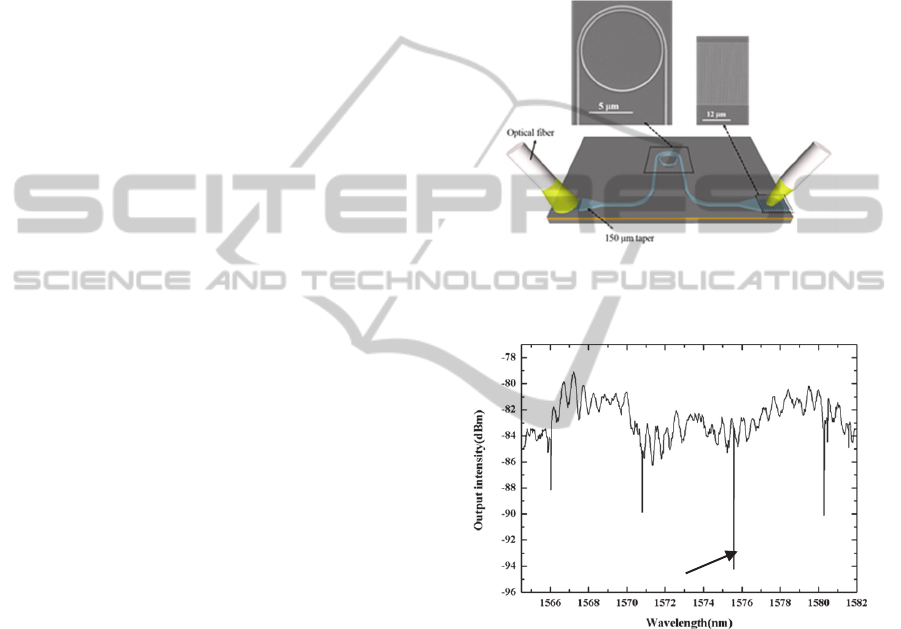
structure of device are shown in Fig. 3.

To characterize the pulley-type ring resonator,

the broadand amplified spontaneous emission (ASE)

light source and the optical spectrum analyzer are

employed.

The output power spectrum of the pulley-type

microring resonator is shown in Fig. 4. The vertical

axis is presented in dBm scale. The deepest notch is

located at 1575.65 nm as the bus waveguide width is

0.23m. The Q-factor of 1.73×10

is obtained by

employing the Lorentz curve fitting. The shift of the

resonance wavelength between the design and the

experimental result is around 9.69 nm due to the

fabrication error. This work shows that by changing

the bus waveguide width to achieve the critical

coupling, the maximal energy of the traveling light

at the resonance wavelength of 1575.65 nm stored in

the ring resonator can be optimized. The measured

Q-factor of 1.73×10

is lower than the theoretical Q-

factor of 7× 10

. This is due to the fact that the

roughness of the waveguide surface can scatter the

traveling light out of the pulley-type ring resonator.

Figure 3: Schematic drawing of the characterisation setup

including the SEM micrograph of the pulley-type ring

resonator and the grating couplers.

Figure 4: Measured spectrum of the pulley-type ring

resonator.

4 DISCUSSION AND

CONCLUSION

In Ref. (Hu et al., 2008); (Hosseini et al., 2010), the

microdisk with the radius of 20m is fabricated on

the As

platform. The Q-factors are 2.1×10

and

1.5×10

for the TM and TE modes, respectively. (Hu

et al., 2008) The Si

microdisk with the radius of

20m is fabricated on the SiO

platform. The Q-

factor characterized by the launched source in the

TE mode is 6×10

.(Hosseini et al., 2010) In our

work, the radius is only 4.43m. However, we can

Q=1.73x10

Pulley-typeRingResonatorandOptimization

obtain the Q-factor with the same order of

magnitude. Our result shows that the pulley-type

ring resonator can be ameliorated by enlarging 

and shows the possibility to obtain the ring

resonators with higher Q factor if the ring radius is

enlarged or the sidewall roughness of the

waveguides is improved.

In our previous work, we propose a fast method

to calculate the coupling length of the concentrically

curved waveguides using the conformal mapping.

(Cai et al., 2012) Fig. 5 shows the schematic

refractive index profile of the concentrically curved

waveguides before and after conformal mapping.

We can observe that the effective index of the outer

waveguide is higher that of the inner waveguide.

This implies that the propagation constant of the two

curved waveguides is not inherently identical. In the

case of the directional couplers with straight

waveguides, the 100% energy coupling is not

possible. However, in the case of the ring resonators,

the critical coupling can be achieved due to the fact

that the circumference of the ring the integer

multiple of the resonant wavelength, even if the

propagation constant of the concentrically curved

waveguides is not identical. Therefore, the fine

tuning of the outer concentrically curved waveguide

width can achieve the critical coupling. Since the

effective refractive index of the outer curved

waveguide is higher than that of the inner waveguide,

the radiation loss of the ring can be reduced due to

the good optical confinement of the higher refractive

index profile of the outer curved waveguide.

(a)

(b)

Figure 5: (a) Refractive index profile of two concentrically

curved waveguides (b) Refractive index profile after

conformal mapping.

In summary, the rigorous FDTD method has

been employed to analyse the 6 types of ring

resonators. Since the bending loss per propagation

distance of the two concentrically curved

waveguides is lower than that of the single curved

waveguide, the pulley-type ring resonator can

provide lower optical loss.

In this work, we fabricate the pulley-type ring

resonator based on the SOI platform. The Q-factor

of the pulley-type ring resonator is measured to be

1.73×10

as the bus waveguide width of 0.23m

and the ring radius of 4.43m. The Q-factor might

be ameliorated by smoothing the sidewall of

waveguide. The high Q-factor of the pulley-type

ring resonator with tiny radius is helpful for the

miniaturization of the integrated optical devices.

REFERENCE

B. E. Little, S. T. Chu, H. A. Haus, J. Foresi, and J.-P.

Laine, J. Lightwave Technol. 15, 998 (1997).

A. B. Matsko, A. A. Savchenkov, V. S. Ilchenko, and L.

Maleki, Opt. Comm. 233, 107 (2004).

V. R. Almeida and M. Lipson, Opt. Lett. 30, 2733 (2005).

M. Terrel, Michel J. F. Digonnet, and S. Fan,

“Performance comparison of slow-light coupled-

resonator optical gyroscopes,” Laser & Photon. Rev.

3,452 (2009).

M. S. Nawrocka, T. Liu, X. Wang, and R. R. Panepucci,

“Tunable silicon microring resonator with wide free

spectral rang,” Appl. Phys. Lett. 89, 071110 (2006).

V. M. Menon, W. Tong, and S. R. Forrest, “Control of

Quality Factor and Critical Coupling in Microring

Resonators Through Integration of a Semiconductor

Optical Amplifier,” IEEE Photon. Technol. Lett. 16,

1343 (2004).

Joyce K. S. Poon, J. Scheuer, Y. Xu, and A. Yariv,

“Designing coupled-resonator optical waveguide delay

lines,” J. Opt. Soc. Am. B 21, 1665 (2004).

J. Hu, N. Carlie, N. Feng, L. Petit, A. Agarwal, K.

Richardson and L. Kimerling, “Planar waveguide-

coupled, high-index-contrast, high-Q resonator in

chalcogenide glass for sensing,” Opt. Lett., 33, 2500

(2008)

E. S. Hosseini, S. Yegnanarayanan, A. H. Atabaki, M.

Soltani and A. Adibi, “Systematic design and

fabrication of high-Q single-mode pulley-coupled

planar silicon nitride microdisk resonators at visible

wavelength,” Opt. Express, 18, 2127 (2010).

D. P. Cai, C. C. Chen, C. C. Lee, and T. D. Wang, “Study

of Coupling Length of Concentrically Curved

Waveguides,” IEEE Photon. J. 4, 80 (2012).

OPTICS2015-InternationalConferenceonOpticalCommunicationSystems