
Secure Physical Access Control with Strong Cryptographic Protection
Jan Hajny, Petr Dzurenda and Lukas Malina
Department of Telecommunications, Brno University of Technology, Technicka 12, Brno, Czech Republic
Keywords:
Authentication, Identification, Security, Proofs Of Knowledge, Physical Access Control, Cryptography.
Abstract:
This paper is focused on the area of physical access control systems (PACs), particularly on the systems for
building access control. We show how the application of modern cryptographic protocols, namely the cryp-
tographic proofs of knowledge, can improve the security and privacy protection in practical access control
systems. We propose a novel scheme SPAC (Secure Physical Access Control) based on modern cryptographic
primitives. By employing the proofs of knowledge, the authentication process gets more secure and privacy
friendly in comparison to existing schemes without negative influence on the implementation complexity or
system performance. In this paper, we describe the weaknesses of existing schemes, show the full crypto-
graphic specification of the novel SPAC scheme including its security proofs and provide benchmarks on
off-the-shelf devices used in real commercial systems. Furthermore we show, that the transition from an old
insecure system to strong authentication can be easy and cost-effective.
1 INTRODUCTION
We use physical access control systems (PACs) many
times a day. We open parking lot gates, office com-
plex doors or operate elevators by attaching our chip-
cards or RFID (Radio Frequency Identification) tags
to electronic readers. Using PACs, the identification
and authentication process is easy and fast. The chip-
card just transmits the identifier stored in its memory
to the reader. In more advanced systems, a crypto-
graphic authentication protocol is additionally imple-
mented to avoid the eavesdropping of identifiers by
attackers.
Although the PAC systems are often used in very
security-sensitive areas, such as power plants, large
industrial sites, banks or critical communication in-
frastructures, their security is often very low. There
are many known attacks exploiting improper crypto-
graphic protocol design or wrong implementation of
PAC systems.
In this paper, we describe the general PAC archi-
tecture (Section 2), show the weaknesses of popu-
lar existing systems (Section 3), identify the features
necessary for next-generation PACs (Section 3.1) and
propose a novel cryptographic scheme based on mod-
ern cryptographic primitives that remove most of the
weaknesses and provides additional features for pri-
vacy protection (Section 4). To prove the practical
readiness for implementation, we show the perfor-
mance benchmarks of primitives used in our scheme
on devices used in real, commercial PAC systems
(Section 6). Finally, we show that the new scheme
based on strong cryptography is easily implementable
into existing applications (Section 6.1).
2 GENERAL ARCHITECTURE
OF PHYSICAL ACCESS
CONTROL SYSTEMS
The general architecture of physical access control
systems is described in this section. Regardless the
manufacturer, the existing commercial systems usu-
ally respect the architecture shown in Fig. 1.
Although some modifications might occur in con-
crete implementations, we will assume this architec-
ture because it sufficiently reflects the most of existing
systems and perfectly reflects the implementation we
are aiming at with our scheme. We provide the list of
key PAC devices and describe their roles in the system
here.
• User Device: a smartcard or a smartphone used
by a user for authentication. The User Device
transmits the identifier or executes the authenti-
cation protocol with a reader via RFID interface.
220
Hajny J., Dzurenda P. and Malina L..
Secure Physical Access Control with Strong Cryptographic Protection.
DOI: 10.5220/0005524202200227
In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 220-227
ISBN: 978-989-758-117-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: General architecture of physical access control
systems.
The expected range is upto 5 centimeters.
• Reader: a simple device receiving the identi-
fier or authentication data. In trivial implementa-
tions, the reader just re-sends data received from
RFID interface to Access Terminal via a one-
way Wiegand three-wire interface. In more com-
plex implementations, the Reader is able to ver-
ify the cryptographic data received and re-send
user’s identifier only in case he provided correct
proofs. In this case, the Reader is often equipped
by SAM (Secure Access Module). Using SAM,
the verification of cryptographic data might be
faster and more secure due to the use of special
cryptographic co-processors. The SAM might be
realized by a programmable smartcard such as
JavaCard (Oracle, 2015) or MultOS card (Mul-
tOS, 2015).
• Access Terminal: a device connected to Read-
ers by one-way Wiegand interface and to Cen-
tral Servers by two-way interface (possibly LAN).
The Access Terminal maintains a list of identi-
fiers of authorized users. This list gets updated
from Central Servers. After receiving an identi-
fier from the Reader, the Terminal checks its list
and decides about the authorization.
• Central Server: the Central Server is the central
point of administration. Using Central Server, it
is possible to add, remove, block and manage all
users. The information necessary for authentica-
tion (user identifiers, their keys) are distributed to
other devices from here.
• User Database: all user information is stored in a
central database directly connected to the Central
Server.
The weakest point of the above described architec-
ture from the security perspective is the communica-
tion between the User Device and the Reader. That is
given by its wireless nature and the fact that it is not
protected physically (like the other interfaces might
be, for example by running wires inside walls or pri-
vate areas of the building). Therefore, most crypto-
graphic protocols are aiming on securing the commu-
nication between users’ smartcards and SAMs inside
Readers. We provide a short overview of existing so-
lutions in the next section.
3 STATE OF THE ART IN PACS
We analyze the existing solutions used for physical
access control in this section. We’ve chosen the most
spread technologies. Although precise data regarding
the market shares are not available, the technologies
and manufacturers included represent the majority of
all systems deployed. We included NXP’s Mifare and
DESfire; HID’s Prox and iClass; and Legic Prime
and Advant.
Mifare Classic
NXP’s Mifare Classic introduced in 1994 is the
most popular technology used in physical access
control systems. Although very old and insecure, the
technology is still used in many applications, even
those security sensitive. The authentication protocol
is based on a unique 4B card identifier UID. In some
implementations, the card just reveals UID to the
Reader without any authentication protocol. In that
case, UID can be easily eavesdropped and used by an
attacker for impersonation. In other implementations,
an authentication protocol depicted in Fig. 2 is
used. The protocol is considered insecure due to
many existing practical attacks (Courtois et al., 2008;
Courtois, 2009; Garcia et al., 2009) on the encryption
algorithm CRYPTO1.
Mifare DESfire
The insufficient security of the CRYPTO1 algorithm
used in the Mifare Classic made NXP improve the
cryptographic protection and release Mifare DESFire.
The old encryption algorithm was replaced by 3DES
algorithm. The authentication protocol is depicted
SecurePhysicalAccessControlwithStrongCryptographicProtection
221

Figure 2: Mifare authentication protocol.
Figure 3: DESfire authentication protocol.
in Fig. 3. The authentication protocol was further
improved in Mifare DESFire EV1 which supports
the AES encryption algorithm (NIST, 2001). The
protocol itself remained without major changes.
However, even Mifare DESFire was successfully
attacked, although the attacks (Oswald and Paar,
2011; Markantonakis, 2012) were aimed on imple-
mentation, not cryptographic weaknesses.
HID Prox and HID iClass
The HID Prox technology contains no cryptographic
protection. HID iClass employs an authentication
protocol based on the 3DES algorithm. The proto-
col is depicted in Fig. 4. There are attacks on this
protocol available (Meriac, 2010).
Figure 4: HID iClass authentication protocol.
Legic Prime and Legic Advant
Legic Prime has weak proprietary cryptographic pro-
tection (SRLabs, 2015). Legic Advant is protected
by symmetric block algorithms (DES (NIST, 1999),
3DES, AES).
Based on the analysis of existing technologies above,
we conclude that the majority of existing physical
access control systems used in practice is based ei-
ther on missing/insufficient cryptographic protection
(Mifare Classic, HID Prox, Legic Prime) or obso-
lete algorithms (DES, 3DES). The rest of analyzed
systems is based on AES, originally a block cipher
designed for data encryption. None of the analyzed
solutions is using modern authentication protocols
based on the provable security concept allowing for-
mal proofs, such as zero-knowledge protocols, Σ-
protocols (Cramer, 1997) or proofs of knowledge.
Privacy-enhancing features, such as the unlinkabil-
ity of verification sessions, are not considered. All
schemes implemented are symmetric, thus employing
shared keys. That makes non-repudiation difficult in
the systems. Furthermore, the symmetric keys must
be present at both User Devices and Readers. That
makes the risk of their extraction higher since Read-
ers can be captured and analyzed by attackers.
3.1 Our Contribution
We specify a novel cryptographic scheme addressing
the above identified weaknesses in the next sections.
In particular, the SPAC scheme is designed to provide
the following features.
• Provable Security: our SPAC scheme is based
on cryptographic primitives with provable se-
curity, particularly on the interactive Schnorr-
based proof of knowledge of discrete logarithm
(Schnorr, 1991) in the RSA group (Rivest et al.,
1978). We provide the full security analysis in
Section 5.
SECRYPT2015-InternationalConferenceonSecurityandCryptography
222
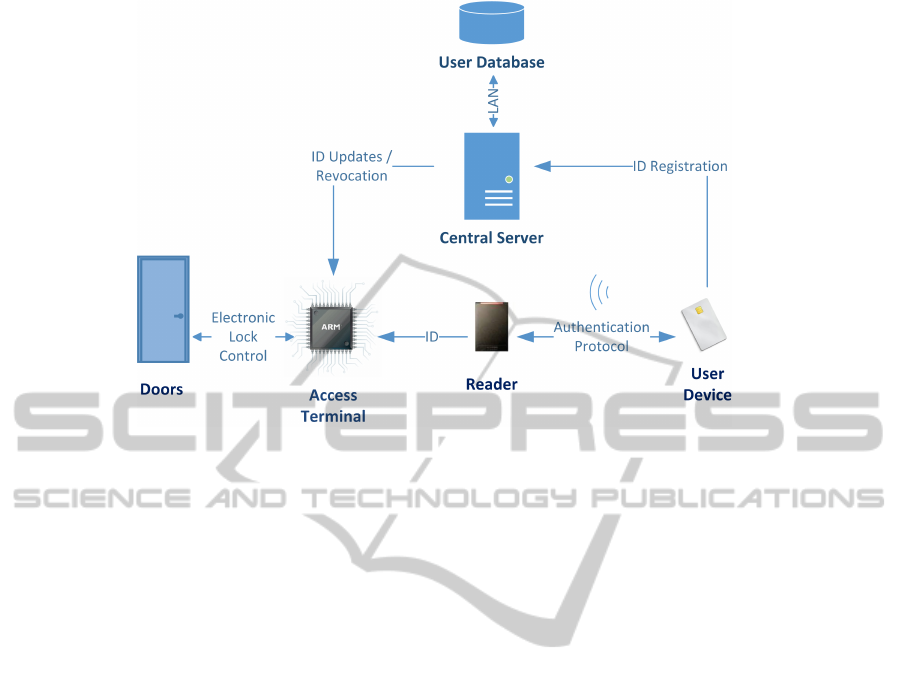
Figure 5: SPAC architecture.
• Privacy Protection Features: the SPAC scheme
provides features for the protection of users’ pri-
vacy and digital identity, namely user ID hiding
and authentication sessions unlinkability.
• Non-repudiation: the SPAC scheme is based on
asymmetric cryptography. The user is proving his
identity using a private cryptographic key known
only by him, not by anyone else. Therefore, users
cannot repudiate their past transactions like in
symmetric schemes.
• Local Key Storage: unlike existing schemes, the
user authentication key is stored in user’s device
only, not in the verifier’s device. That makes the
key protection much easier.
• Computational and Communication Effi-
ciency: the SPAC scheme is computationally
efficient enough to run on low-resource devices
as smartcards and SAMs. The communication is
realized by a simple 3-way protocol. We prove
the computational and communication efficiency
by describing the implementation results in
section 6.
4 SPAC CRYPTOGRAPHIC
SPECIFICATION
4.1 Notation
For various proofs of knowledge or representation,
we use the efficient CS notation introduced by Ca-
menisch and Stadler (Camenisch and Stadler, 1997).
The protocol for proving the knowledge of discrete
logarithm of c with respect to g is denoted as PK{α :
c = g
α
}. The symbol “:” means “such that”, “|”
means “divides”, “|x|” is the bitlength of x and “x ∈
R
{0,1}
l
” is a randomly chosen bitstring of maximum
length l. G is a set of the respective group generators.
All operations are in Z
∗
n
, where n = rs and r,s are ran-
dom large safe primes over 512 bits long. H denotes
a hash function.
4.2 Scheme Overview
The SPAC scheme complies with the general concept
of PAC systems described in section 2. The SPAC
scheme is depicted in Fig. 5. The scheme is com-
posed of following protocols.
1. Setup: all cryptographic parameters are gener-
ated and distributed to participating devices here.
2. Registration: User Device generates its private
key, computes his public identifier and registers
this identifier at the Central Server here.
3. Authentication: User Device proves the own-
ership of his private key corresponding to a regis-
tered identifier to the Reader, Reader forwards the
identifier to the Terminal that decides about grant-
ing/rejecting the access.
4. Revocation: in case some user needs to be
revoked, the whitelist of valid identifiers is
updated at Terminals by the Central Server.
SecurePhysicalAccessControlwithStrongCryptographicProtection
223

User Device Reader’s SAM
Preshared parameters: g,n
Private: w, ID = g
w
mod n
Private: φ(n) = (r −1)(s − 1)
PK{w : ID = g
w
mod n}
−−−−−−−−−−−−−−−−−−−−−−−−−−−−→
ID
−−−−−−−−−−−−→
(to Terminal)
Figure 6: Authentication protocol in CS notation.
Setup Protocol
The public parameters of Z
∗
n
group (modulus n,
generator g) and general parameters (k - user key
size, l - challenge size, m - protocol error rate) are
generated and distributed by the Central Server to
all participating devices. Private parameters (the
factorization of n) are distributed to SAM modules
of Readers. This phase can be realized by existing
means of cryptography or by simply pre-sharing all
values in software, thus we don’t cover it in more
details.
Registration Protocol
User Device generates a random private key
w ∈
R
{0,1}
k
and computes the identifier
ID = g
w
mod n. By means of traditional cryp-
tography or personal interaction, the ID is registered
at Central Server and distributed to Terminals.
Authentication Protocol
The authentication protocol is the key part of the
scheme. It runs between the User Device and the
SAM module of the Reader. The Reader sends user’s
ID to the Terminal after the protocol is successfully
finished. If the ID is valid (present on Terminal’s
whitelist), the access is granted by, e.g., unlocking an
electronic door lock.
The authentication protocol is realized by a stan-
dard interactive proof of knowledge of discrete loga-
rithm protocol (Camenisch and Stadler, 1997) based
on Schnorr protocol (Schnorr, 1991). The authenti-
cation protocol is depicted in CS notation in Fig. 6.
Using this protocol, the User Device provides a cryp-
tographic proof that he knows a private key w to its
unique identifier ID. If the proof is constructed cor-
rectly, the Reader’s SAM learns ID and is convinced
that the User Device knows corresponding w. How-
ever, w is never disclosed.
The proof of knowledge can be practically imple-
mented as a Σ-protocol (Cramer, 1997) depicted in
full notation in Fig. 7. An interactive version us-
ing a random challenge e generated by the Reader,
instead of a non-interactive version based on Fiat-
User Device Reader’s SAM
Preshared parameters: g,n
Private: w, ID = g
w
mod n
Private: φ(n) = (r −1)(s − 1)
r
1
∈
R
{0,1}
k+l+m
¯
ID = g
r
1
mod n
¯
ID
−−−−−−−−−→
e
0
∈
R
{0,1}
l
←−−−−−−−−−−
e = H (g,n,
¯
ID,e
0
)
z = r
1
− ew
z
−−−−−−−−−−−→
ID = (
¯
IDg
−z
)
e
−1
mod φ(n)
mod n
ID
−−−−−−−−−−−−→
(to Terminal)
Figure 7: Authentication protocol in full notation.
Shamir heuristic (Fiat and Shamir, 1987), is cho-
sen due to Reader’s hardware limitations (no clocks,
limited memory). First, the User Device chooses a
randomization value r
1
and computes corresponding
commitment
¯
ID.
¯
ID is sent to the SAM. The SAM
module responds with a randomly generated chal-
lenge e
0
. The User Device closes communication by
sending the response z = r
1
−ew. In the response, the
private key is perfectly hidden by r
1
and e. From the
knowledge of φ(n) and the answer z, the SAM mod-
ule is able to compute ID and send it to the terminal
that decides about its validity.
5 SPAC SECURITY ANALYSIS
The authentication protocol used in our scheme is
based on standard cryptographic constructions, there-
fore the security proof follows the standard approach
for proofs of knowledge systems (Rosen, 2006).
We prove completeness, soundness and semi-honest
verifier zero-knowledge of the protocol.
Completeness
Completeness property proves that honest, valid users
who know private key w are almost
1
always accepted
by the protocol. We prove the completeness from the
authentication verification equation:
1
Except low probability given by the protocol error rate
P
Err
= 2
−m
SECRYPT2015-InternationalConferenceonSecurityandCryptography
224

ID ≡ (
¯
IDg
−z
)
e
−1
mod φ(n)
≡ (g
r
g
−(r−ew)
)
e
−1
mod φ(n)
≡
≡ (g
r+ew−r
)
e
−1
mod φ(n)
≡ g
ewe
−1
mod φ(n)
≡ ID (mod n)
(1)
Soundness
Soundness property proves that dishonest, invalid
user who does not know the private key w, is accepted
by the protocol with negligible probability. We prove
soundness by proving that a user who does not know
w is able to correctly answer at most 1 challenge e.
We prove soundness by following the proof de-
scribed in (Camenisch and Shoup, 2003).
Theorem 1. Under the assumptions that factoring of
n is hard and log
g
ID is unknown, given a modulus
n, along with elements g,ID, it is hard to compute
integers a,b such that
1 ≡ g
a
ID
b
mod n and (a 6= 0 or b 6= 0). (2)
Proof. Suppose there is an algorithm A that inputs
n,g,ID and outputs a,b valid in (2). Then we can
use A to either factor n or compute log
g
ID, both
violating assumptions. The output (a, b) satis-
fies 1 ≡ g
a
ID
b
≡ g
a
g
αb
≡ g
a+αb
mod n, therefore
a + αb ≡ 0 mod ord(g). We have two cases:
Case 1. Let us consider a + αb = 0. Then discrete
logarithm log
g
ID can be efficiently computed as
log
g
ID = α = −
a
b
. Case 1 violates the discrete
logarithm assumption.
Case 2. Let us consider a + αb 6= 0. A can be used to
factor n by choosing α in random, inputting (n,g,g
α
)
and getting the output (a,b). Using (a +αb), which is
a non-zero multiple of φ(n), the adversary can factor
n. To efficiently compute a proper factor of n, the ad-
versary can use the technique originally developed for
RSA (Boneh, 1999). Case 2 violates the factorization
assumption.
Using the Theorem 1, we can prove soundness like in
(Camenisch and Shoup, 2003), thus by constructing
the knowledge extractor and assuming that the factor-
ization of n is hard. The extractor uses the standard
rewinding technique, thus inputs two different valid
answers z,z
0
on two different challenges e,e
0
with the
fixed first step
¯
ID. The verification equation must
hold for both answers:
ID ≡ (
¯
IDg
−z
)
e
−1
mod φ(n)
ID ≡ (
¯
IDg
−z
0
)
e
0−1
mod φ(n)
therefore
ID
e
≡ (
¯
IDg
−z
)
ID
e
0
≡ (
¯
IDg
−z
0
)
Now we divide the equations and get:
ID
e−e
0
≡ g
−z+z
0
That equation can be transformed into:
ID ≡ g
(−z+z
0
)/(e−e
0
)
From the Theorem 1, the User must have used
log
g
ID, since the factorization of n is unknown.
Based on the Case 1 of Theorem 1, (e − e
0
) di-
vides (−z + z
0
), therefore the extractor can extract
w =
−z+z
0
e−e
0
. We reached the contradiction to the
original assumption.
Honest Verifier Zero-Knowledge
Zero-knowledge property guarantees that no informa-
tion about private w leaks from the protocol. That
is proven by the existence of a simulator M that is
able to simulate all the protocol values indistinguish-
ably from real protocol values without the knowledge
of w. Therefore, if all protocol values can be simu-
lated without the knowledge of w, they do not release
any information about w. The protocol simulator is
constructed in the standard way (Damg
˚
ard, 2000) and
works in following steps:
1. M randomly generates an answer z
0
from the in-
terval < 2
klm
− 2
kl
,2
klm
>,
2. M randomly generates a challenge e
00
∈
R
{0,1}
l
,
3. M computes the first message of the protocol
¯
ID
0
= ID
e
00
g
z
0
mod n.
The simulated values
¯
ID
0
, e
00
, z
0
are then computation-
ally indistinguishable from the real run of the proto-
col.
6 IMPLEMENTATION
Many existing cryptographic schemes remain only
theoretical because their computational complexity is
too high for practical implementations on restricted
devices like smart cards and card readers equipped
by only very limited hardware. Therefore, we pro-
vide detailed analysis and benchmarks of the primi-
tives used in our scheme on real, off-the-shelf hard-
ware commonly used in PAC systems. We focus on
operations inside Reader’s SAM module because that
is the weakest point of the systems. Other devices
are more computationally powerful (Central Server -
standard server, Terminal - ARM-based system, User
Device - NFC-enabled smartphone or smartcard with
cryptographic co-processor).
SecurePhysicalAccessControlwithStrongCryptographicProtection
225

Figure 8: Benchmarks of SAM modules.
From the cryptographic specification of the au-
thentication protocol in Section 4, the primitive op-
erations are easily identifiable. For the authentication
protocol implementation, the SAM module must be
able to efficiently compute:
• 1 random number generation (RNG),
• 1 modular inversion (Minv),
• 2 modular exponentiation (Mpow),
• 1 modular multiplication (Mmul).
We measured the time necessary for the compu-
tation of the above specified operations in a modular
group with 1024 b modulus and parameters k = 160,
l = 160, m = 80. The smartcards Oberthur Id-one
v7.0-a (JavaCard), ML3-36K-R1 (MultOS) and ML2-
80K-65 (MultOS) were used. These cards are com-
monly used as SAM modules. The results of indi-
vidual operations and the total verification time are
shown in Fig. 8. We present the arithmetic mean of
25 measurements.
The total time needed for the user verification
varies according to the module used from 300 to 800
ms. The best choice for our protocol is the Mul-
tOS ML2 card (marked green in the graph). Fur-
ther speed-up is possible by using pre-computation
techniques and better implementation of some opera-
tions (e.g., the modular inverse operation is currently
implemented naively using modular exponentiation).
However, we consider even the times measured fast
enough for practical implementations.
The implementation on the User Device is easier.
If smartphones are used, no resource restrictions ap-
ply due to enormous computational power of modern
devices. In case smartcards are required, the MultOS
ML2-80K-65 is again the best choice for implementa-
tion. All operations of the cryptographic proof require
167 ms on this device.
Figure 9: Compatibility of SPAC with existing PAC sys-
tems.
Based on the times measured, it is possible to
compute the total time of the protocol, including com-
putations on the user’s smartcard and the SAM mod-
ule. The total time excluding communication is 484
ms without optimization. This value proves the prac-
tical implementability of the scheme since the indus-
try limit is considered 0.5 s for physical access control
protocols.
6.1 Compatibility with Existing
Applications
Novel systems are sometimes difficult to practically
implement into existing systems. Usually, it is diffi-
cult to completely replace all devices in existing sys-
tems. The SPAC scheme proposed in this paper was
created in cooperation with an industrial PAC system
manufacturer who required backward compatibility.
Therefore, we designed the SPAC scheme in a way
that allows re-using of some existing components,
namely the Central Server, User Database and the Ter-
minals. Only the Reader and the User Device must be
re-designed because a new authentication protocol is
used. The components and protocols that need new
implementation are marked red in Fig. 9.
7 CONCLUSIONS
The paper contains cryptographic specification of a
SECRYPT2015-InternationalConferenceonSecurityandCryptography
226

novel physical access control scheme called SPAC. In
comparison to existing schemes, SPAC is based on
modern asymmetric primitives, that provide features
currently unavailable in existing systems, such as
provable security, local key storage, non-repudiation
and authentication session randomization. Although
the scheme is based on asymmetric cryptography,
it is very fast even when implemented on resource-
limited devices. In the section focused on implemen-
tation, we show, that the verification part realized on a
smartcard SAM module takes around 300 ms and the
proving part implemented on user’s smartcard takes
around 170 ms. Moreover, we expect a significant
speed-up in the optimized version of our implementa-
tion, which is our next step.
ACKNOWLEDGEMENTS
Research described in this paper was financed by the
National Sustainability Program under grant LO1401,
Technology Agency of the Czech Republic project
TA04010476 ”Secure Systems for Electronic Ser-
vices User Verification” and by the Czech Science
Foundation under grant no. 14-25298P. For the re-
search, infrastructure of the SIX Center was used.
REFERENCES
Boneh, D. (1999). Twenty years of attacks on the rsa cryp-
tosystem. NOTICES OF THE AMS, 46:203–213.
Camenisch, J. and Shoup, V. (2003). Practical verifiable
encryption and decryption of discrete logarithms. In
Advances in Cryptology - CRYPTO 2003, pages 126–
144. Springer-Verlag.
Camenisch, J. and Stadler, M. (1997). Proof systems for
general statements about discrete logarithms.
Courtois, N., Nohl, K., and O’Neil, S. (2008). Algebraic
attacks on the crypto-1 stream cipher in mifare classic
and oyster cards. IACR Cryptology ePrint Archive.
Courtois, N. T. (2009). The dark side of security by ob-
scurity and cloning mifare classic rail and building
passes, anywhere, anytime.
Cramer, R. (1997). Modular Design of Secure Yet Practical
Cryptographic Protocols.
Damg
˚
ard, I. (2000). Efficient concurrent zero-knowledge in
the auxiliary string model. In Preneel, B., editor, Ad-
vances in Cryptology — EUROCRYPT 2000, volume
1807 of Lecture Notes in Computer Science, pages
418–430. Springer Berlin Heidelberg.
Fiat, A. and Shamir, A. (1987). How to prove your-
self: Practical solutions to identification and signature
problems. In Advances in Cryptology - CRYPTO 86,
volume 263 of Lecture Notes in Computer Science,
pages 186–194. Springer Berlin / Heidelberg.
Garcia, F. D., van Rossum, P., Verdult, R., and Schreur,
R. W. (2009). Wirelessly pickpocketing a mifare clas-
sic card. In Security and Privacy, 2009 30th IEEE
Symposium on, pages 3–15. IEEE.
Markantonakis, K. (2012). Practical relay attack on contact-
less transactions by using nfc mobile phones. Radio
Frequency Identification System Security: RFIDsec.
Meriac, M. (2010). Heart of darkness-exploring the un-
charted backwaters of hid iclasstm security. Heart.
MultOS (2015). Multos webpage. ”http://
www.multos.com”.
NIST (1999). Federal information processing standards
publication (FIPS 46-3). Data Encryption Standard
(DES). -.
NIST (2001). Federal information processing standards
publication (FIPS 197). Advanced Encryption Stan-
dard (AES). -.
Oracle (2015). Java card webpage. ”http://
www.oracle.com/technetwork/java/embedded/javacard/
overview/index.html”.
Oswald, D. and Paar, C. (2011). Breaking mifare desfire
mf3icd40: Power analysis and templates in the real
world. In Cryptographic Hardware and Embedded
Systems–CHES 2011, pages 207–222. Springer.
Rivest, R., Rivest, R., Shamir, A., and Adleman, L. (1978).
A method for obtaining digital signatures and public-
key cryptosystems. COMMUNICATIONS OF THE
ACM, 21:120–126.
Rosen, A. (2006). Concurrent Zero-Knowledge With Addi-
tional Background by Oded Goldreich. Springer.
Schnorr, C. P. (1991). Efficient signature generation by
smart cards. Journal of Cryptology, 4:161–174.
SRLabs (2015). ”https://srlabs.de/analyzing-legic-prime-
rfids/”.
SecurePhysicalAccessControlwithStrongCryptographicProtection
227
