Comparison of Two Radar-based Scanning-techniques for the Use in

Robotic Mapping

Paul Fritsche and Bernardo Wagner

Institute for Real Time Systems, Leibniz University Hanover, Applestr. 9A, Hanover, Germany

Keywords:

Radar, Trilateration, Mono-static Radar Network, Amplitude Sensing Ratio, 2D-Scanner, Robotic Mapping,

Occupancy Grid Mapping, Sensor-fusion.

Abstract:

This paper will introduce two radar-based scanning-methods and evaluate their application in robotic mapping.

Both approaches base upon a rotary joint, but with a fundamentally different angle estimation method to

estimate object locations inside the scanning area. The ﬁrst part of this paper describes the relevant theory

behind both techniques and presents our considerations on erroneous inﬂuences. The focus of the second

part of this paper is laying on experiments. We discuss the results of our experiments and take a look on the

usability of both methods for occupancy grid mapping.

1 INTRODUCTION

The following article introduces two scanning meth-

ods, for mapping purposes in mobile robotics. Our

ﬁrst method is based on a rotating mono-static radar

network, which determines the positions of objects

inside the scanning area via a continuously running

lateration algorithm. Our second method is based on

rotating radar sensors with an angle offset and a deter-

mination of the positions of objects through the Am-

plitude Sensing Ratio (ASR) technique.

A precise model of the environment is essential

in many areas of mobile robotics and builds the fun-

dament for localization and navigation. Commonly,

popular sensors like laser-scanners, sonar-sensors and

stereo-cameras have established themselves as state

of the art for most tasks in mobile robotics. Neverthe-

less, radar sensors frequently appear in ﬁeld and res-

cue robotics (Adams et al., 2012) (Tadokoro, 2009),

but are seldom used to perform tasks like mapping

and localization. Radar can penetrate certain materi-

als, basically non-conductors, which provides advan-

tages in dusty, foggy, rainy or other harsh environ-

ments. But, limited resolution, noisy data, inﬂuence

of optical effects like refraction, reﬂection and ab-

sorption make the application in mobile robotics chal-

lenging.

The use of radar sensors in mobile robotics is

challenging but not impossible. The ﬁrst appearance

of radar sensors in the robotic community is tracing

back to the Australian Centre for Field Robotics in the

early nineties, where fundamental work on probabilis-

tic SLAM algorithms in combination with radar was

developed (Clark and Whyte, 1998). Because of their

limited resolution and other aforementioned draw-

backs, radar sensors are not very suitable to use in

indoor environments. Nevertheless, (Detlefsen et al.,

1993) were investigating the use of radar sensors in

an industrial environment and (Marck et al., 2013) in

an ofﬁce. As far as we can see, most radar sensor

principles in mobile robotics are based on mechan-

ical beam-forming. Usually, the radar beam is fo-

cussed via a parabolic antenna and panned mechan-

ically over the environment. Electrical beam-forming

through phased array antennas is not seen very often

in mobile robotics rather in automotive systems of the

car industry.

Besides beam-forming techniques, position esti-

mation can be achieved through lateration, which is

a common technique in radar networks for aircraft

surveillance. Lateration is a measurement method,

where the position of a point target is calculated of

distance information from n Sensors with known lo-

cations. The term trilateration refers to the measure-

ment of three distances to deﬁne the position of an ob-

ject (in contrast to triangulation, where three angles

are used to calculate an object’s position). The esti-

mation of surfaces with ultra-wide band (UWB) radar

networks has been studied experimentally in lab envi-

ronments, especially with lateration by (Mirbach and

Menzel, 2011) , envelopes of spheres by (Kidera et al.,

2008) and inverse boundary scattering algorithms by

365

Fritsche P. and Wagner B..

Comparison of Two Radar-based Scanning-techniques for the Use in Robotic Mapping.

DOI: 10.5220/0005524303650372

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 365-372

ISBN: 978-989-758-122-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

(Sakamoto, 2007). But, we can not see a link to the

ﬁeld of robotic mapping with mobile robots, where

laser scanners are dominating. ASR techniques on a

rotary joint are common techniques in ground-based

radar systems for air-trafﬁc control (Agilent, 2014).

For our experiments, we use frequency modulated

continuous wave (FMCW) radar sensors, which pro-

vide distance but no angle information of objects in-

side the observation area. The sensors work in 24

GHz ISM band and accordingly are limited in Ger-

many to a bandwidth B of 250 MHz, which corre-

sponds to a theoretical distance resolution ∆d of 0.6

m in dependency of the speed of light c

(See Equa-

tion 1).

∆d =

(1)

The resolution ∆d of a radar sensor is equal to its

minimum detection range. The availability of sensors

with a high resolution depends on national and inter-

national bandwidth regulations. An UWB channel be-

tween 22 GHz to 26,65 GHz has been closed in 2013,

but is moved to 79 GHz for automotive purposes re-

cently (Schmid and Neubauer, 2007, p. 20).

A radar’s resolution is its capability to distinguish

objects. If the difference between the radial distances

of two or more objects to the sensor is less than its

resolution, then the sensor merges the two or more

distance information to one. Additionally, the detec-

tion of objects depends on their radar cross section

(RCS) and the background noise of the environment.

This article is organized as follows. In Section 2,

we present a short overview, how position estimation

via lateration and ASR techniques are solved. Besides

the theory and introduction to common terms, we ex-

plain the ghost target and non-point target problems

in radar networks which are based on lateration. Ad-

ditionally, we describe inﬂuences of errors related to

the power and range measurement accuracy of radar

sensors. The reader who is familiar to these topics

might go directly to Section 3, where the sensor prin-

ciples are described in the beginning. Further in this

section, we will describe our experiments, which re-

sults are discussed in Section 4. A brief summation of

the obtained knowledge is given in Section 5.

2 MATERIALS AND METHODS

Estimating the position of an object with a radar net-

work can be solved by standard lateration methods or

ASR techniques. In order to deﬁne an object’s posi-

tion in two-dimensional space, at least two sensors are

necessary. In case of lateration, two radii from two

range measurements at different positions can break

down the object’s position to two possible locations.

Usually, only one location is plausible due to the an-

tenna’s direction. In case of the ASR technique, the

position of an object can be estimated through the dif-

ference in the receiver power at two antennas which

are located at the same position but pointing into dif-

ferent directions. In this paper, we investigate the us-

ability of both methods in combination of a rotating

scanning unit to generate occupancy grid maps.

2.1 Principle of the Lateration

Technique

Lateration is a measurement principle to estimate the

positions of points with distance informations to a

known locations. If the distance to an unknown point

is given, then this point must be laying on a radius

(two-dimensional case) around our location. If two

locations are known, then two radii result in an inter-

section, which is the position of the point. Figure 1

demonstrates the basic of operation of the lateration

principle.

Ghost targets

Ant

✲

✻

Figure 1: The position of objects O can be estimated via the

distances d, which are measurend from different sensors.

Ghost targets represent a geometrical ambiguity.

For a two-dimensional space, n objects O

(i=1..n)

and m sensors S

(j=1..m) result in m · n equations

of circle. The euclidean distances between the sen-

sor positions S

S j

) and the object positions

) are given by the following equations:

− x

)

+ (y

− y

)

= d

S j

− x

)

+ (y

S j

− y

)

= d

i j

− x

)

+ (y

− y

)

= d

(2)

The distance between an Object O

and an Sensor

is deﬁned as d

i j

. The general description of the lin-

ear system of equations can be achieved through sub-

tracting the last equation (j=m) of Equations 2 from

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

366

all other equations ( j = 1...m − 1) (Schneider, 2013,

p. 8).







2 · (x

− x

) 2 · (y

− y

)

2 · (x

− x

) 2 · (y

− y

)

2 · (x

Sm−1

− x

) 2 · (y

Sm−1

− y

)

















− x

+ y

− y

− d

− x

+ y

− y

− d

Sm−1

− x

+ y

Sm−1

− y

− d

im−1

− d







A ·~o

(3)

In reality, every sensor outputs measurement val-

ues with errors. The difference from the true value

occur due to limited accuracy and resolution. Hence,

the system of equations does not result in one sin-

gle solution if it is overdetermined. The system of

equation gets overdetermined if the radar network has

more sensors than the dimension of its measurement

space. Commonly, overdetermined systems of equa-

tion with no single solution get resolved through re-

gression. The most popular solution is the least mean

square method (Schneider, 2013, p. 8) (F

olster, 2006,

p. 39).

Like it can be seen in Figure 1, ghost targets can

appear in radar networks. Ghost targets represent a

wrong data association, because like it is shown in

Equation 2, four objects can be theoretically calcu-

lated if two objects are placed in front of two sen-

sors. Ghost target appear if the sensor’s resolution is

smaller than the half antenna distance (d

Ant

). A de-

tailed derivation of the ghost target cases can be seen

in (Rabe et al., 2009).

In order to resolve the ghost target problem,

olster and Rohling, 2005) present the button-up

data association method. In two-dimensional space,

at least three radar sensors are required. In order to

distinguish ghost objects from real objects, the ob-

servation area in front of the sensor network is dis-

cretized into a ﬁnite set of possible object positions.

Then, a simple minimum distance calculation is done.

For each point, an error value E(x, y) can be calcu-

lated from the square of the minimum distance of the

point to the sensor S

minus the distance d

i j

between

object O

and sensor S

, summarized over all n sen-

sors (See Equation 4).

E(x, y) =

∑

i=1



min

i j

∈OL

i j

− d(x, y))



(4)

This calculation results in the lowest error values

at points that are closest to the real objects. After-

wards, a threshold distinguishes likely ghost target

from real objects.

2.2 Principle of the ASR Technique

Every location in front of an antenna, is connected to

a different antenna gain factor. For example, if we

walked on a radius around a loudspeaker with closed

eyes, we would have a feeling when we would be

walking directly in front of it, because then the sound

appears to be louder. A similar effect is used for the

ASR technique. If we point two radar antennas in

slightly different directions, then the power at the re-

ceiver antennas would not be equal, due to different

antenna gains.

Angle α

Power at receiver antenna P

Angle α

ASR

Figure 2: The position of an object O inside the observation

area can be estimated via the difference of power of into

different direction facing receiver antennas.

The measured power at the receiver antenna P

an object depends on the angle α between antenna and

object. Two sensors, which are facing into different

directions, but placed at the same location, measure

the same distance but different power P

. If a function

for the power in dependency of the angle position of

the object is given, then the object’s position can be

estimated via the ASR function (See Figure 2).

ComparisonofTwoRadar-basedScanning-techniquesfortheUseinRoboticMapping

367

The angle of an object inside the observation area

can be estimated through the Amplitude Sensing Ra-

tio (ASR). In a two-dimensional case, the ASR for

the azimuth is deﬁned by a delta signal (∆) and a sum

signal (

∑

), which are derived from the powers at the

receiver antennas (B

uhren, 2008, p. 34-35).

ASR =

∆

− P

+ P

(5)

In order to obtain information in three-

dimensional space, the elevation needs to be

estimated through an additional sensor beam.

2.3 Consideration on Erroneous

Inﬂuences

Estimating the position of objects with lateration and

ASR requires sensors with very high range or power

accuracy. Nevertheless, every sensor has a measure-

ment error. In case of lateration, the maximum po-

sition measurement error σ

can be approximated

by the maximal range measurement error σ

max

of all

sensors and the angle α (See Equation 6). The range

measurement accuracy is deﬁned by the root-mean-

square (rms) measurement error σ

(Curry, 2005, p.

167). Figure 3 clariﬁes the relation between the range

measurement error σ

, the angle α and the position

measurement error σ

graphically.

2·σ

sinα

2·σ

sinα

Figure 3: Area of ambuguity, which is caused by the two

rms-errors σ

and σ

If the ratio between distance of the object and the

antenna distance gets higher, then the rhomb-shaped

area of ambiguity gets wider. In Figure 5, it can be

seen that the area of ambiguity of a point target ap-

pears almost to be a line. From Equation 6, it can

be seen that the accuracy of a lateration based radar

network is getting very bad at the sides of the sensor

network, where α is approaching zero.

≈

max

sinα

(6)

The rms error σ

depends basically on the signal-

to-noise ratio of the received signal. The signal-to-

noise ratio is higher and results accordingly in a bet-

ter accuracy, if the RCS of an object is higher. Conse-

quently, our radar principle results in better position

estimations for objects with high RCS. But, objects

with a high RCS are entering the observation area of

a rotating scan earlier from the sides then objects with

a lower RCS, hence an object with high RCS suffers

more from the position estimation error σ

Besides the range measurement accuracy, the res-

olution of a radar sensor has important impact on the

reliability of the scan results. A radar sensor will not

distinguish two point targets, if they are inside a so

called resolution cell. For example, a radar with a

resolution of 1 m, can not differ between two or more

objects which are inside a band, with the wide of 1

m, around the sensor and would output the detection

of only one range value somewhere between those

two objects. The lateration technique results only in

correct position estimation if all sensors of the radar

network are measuring the same distance to the same

point. But, single point targets are very rare in stan-

dard environments. Usually, every sensor of a radar

network measures the distance to a different point tar-

get, which results in wrong position estimations.

The precondition for the ASR technique is the

placement of sensors at the same location. The closer

the antennas are placed to each others, the more ex-

actly is the result and the same centres of reﬂection

of a target can be assumed in a ASR radar network.

Unfortunately, the accuracy and resolution of the re-

ceiver power P

can not be deﬁned, because it is de-

pending on the RCS of the object as well (See radar

equation). There is a ﬂuctuation of the RCS, which

can be explained by the Swerling Models. A. Ludloff

explains in (Ludloff, 1998, p. 3-14) how the ﬂuctua-

tion can be modelled. The model is based on the idea

that one radar target exists of multiple reﬂector ele-

ments, which are distributed over the volume of the

target. The model assumes the reﬂector elements to

be isotropic and with the same RCS and neglects the

effects of reﬂection or shadows among themselves.

Through overlapping of reﬂected radar waves on this

multiple isotropic reﬂector elements, phase differ-

ences result in complex interferences. This model ex-

plains the appearance of high ﬂuctuation of the RCS

(and accordingly the receiver power), even if the as-

pect angle is changed only slightly. To sum it up, an

exact estimation of the RCS, even of standard geome-

tries, is not possible in the real world and ﬂuctuation

effects disturb the reliability of the position estimation

results via ASR techniques.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

368

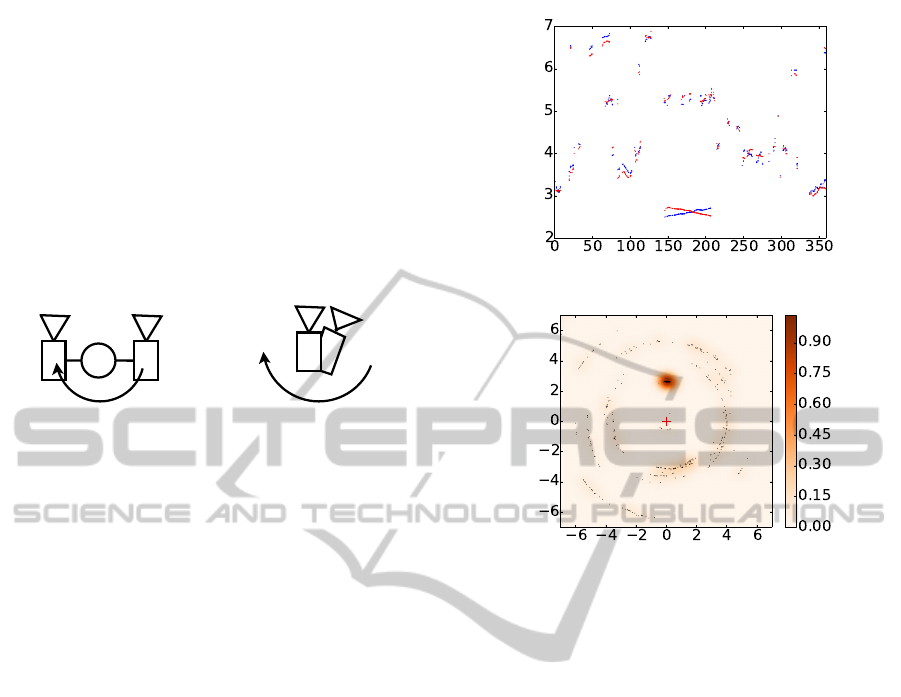
3 EXPERIMENTS

The following section describes ﬁrst experiments with

both sensor principles. Therefore, two scans at the

same location but with different sensor principle have

been performed. Both sensor principles, the lateration

technique and the ASR technique, have been set up

on a rotating platform. Our radar sensors work with a

center frequency of 24 GHz with a bandwidth of 250

MHz, which is the reason for the low resolution. Fur-

thermore, our radar beam is not very focussed. The

setup of both experiments can be seen in Figure 4.

β β

Figure 4: The left drawing shows the scanner with the lat-

eration setup. The right drawing presents the ASR setup.

Both setups are based on a rotating joint and its angle posi-

tion β.

Our ﬁrst scans have been performed in an indoor

environment. We neglect that we perform a 2D scan

inside a 3D environment. In order to have a landmark,

we were placing a point target (an aluminium corner

reﬂector), at the same hight like our sensor unit, inside

our scan area. A serial of scans of a hallway with both

principles has been performed for further evaluation.

3.1 Single Scan with the Lateration

Technique

In order to evaluate the sensor principle, we were per-

forming ﬁrst scans of standard objects in an indoor

environment. The goal of the ﬁrst experiment is to

ﬁnd out about error inﬂuences in our sensor princi-

ple. As mentioned before, a limited resolution can be

problematic in an indoor environment, like our ofﬁce.

There might be metallic radiators, steal-beams behind

the walls, computer towers and many other objects

that can have a RCS huge enough of being detected by

our radar sensor. Our ﬁrst scan results are presented

in Figure 5.

The measurement contains the accumulation of

ﬁve 360

◦

degree scans with a step size of 0.7

◦

de-

grees. Not every measurement cycle leads to a suc-

cessful position estimation. A successful position es-

timation can be processed if both sensors detect an

object.

The probability of occurrence of two objects, with

a smaller difference of their radial distances to the

sensor than the radar’s resolution, is high, hence we

p(0)

and d

in m

y in m

x in m









Figure 5: Above: This diagram presents the distance infor-

mations of the two sensors during a 360

◦

scan of the ro-

tating platform. It can be seen that the corner reﬂector is

the only trustful point target in our ofﬁce environment (See

red circle). The characteristics of the distances of the two

sensors d

and d

is caused by the rotation of the platform,

where one sensor is approaching and the other sensor gets

more far away during a rotation. The distances of non point

target do not have a symetric characteristic. Below: This

diagram depicts a top view on our scanning area. The red

cross represents the location of the sensor unit. The point

target results in an accumulation of distance values. The

remaining spread is only cause by the sensor measurement

error σ

. Accordingly, the point target has the highest prob-

ability p(0) for its correct position estimation.

can rarely trust our scan results, if performed in an

indoor environment. For fundamental research, our

radar sensors with an resolution of approximately 0.6

m are sufﬁcient.

3.2 Single Scan with the ASR Technique

For our investigation on the ASR technique, we were

using exactly the same scene and same sensors. In-

stead of placing the sensor at two different positions,

the ASR technique works the best if both sensors are

placed close as possible, but with a small shift regard-

ing the antenna direction. Our scan results are pre-

sented in Figure 6.

The measurement contains the accumulation of

ComparisonofTwoRadar-basedScanning-techniquesfortheUseinRoboticMapping

369

p(0)

and P

in dBy in m

x in m

Figure 6: Above: This diagram depicts the power at the

receiver antennas P

and P

during a 360

◦

scan. The non-

point target effect does not effect the results. The main er-

ror inﬂuence is caused by the low resolution and the wide

beam size of the radar sensor. An angle estimation of ob-

jects through the ASR in an traditional way is impossible,

because of the non-uniform distribution of the power val-

ues. Below: This diagram presents a 2D scan of our ofﬁce

environment via the ASR technique. The red cross shows

the location of the sensor unit.

ﬁve 360

◦

degree scans with a step size of 0.7

◦

degrees

as well. The distribution of the powers at the receiver

antennas is not suitable for a traditional ASR based

position estimation, because the high amount of ob-

jects does not allow to develop regression functions

for the ASR of our experiment. Nevertheless, we can

assume to have an object perpendicular in front of the

sensor unit if the ASR is close to zero. The ASR

method requires, besides calibration of the range mea-

surement of the sensors an calibration of the antenna

directions.

3.3 Scan of Hallway

In order to compare the suitability for robotic map-

ping of both sensor principles, a serial of scans has

been recorded of a hallway. To avoid inﬂuences of

control and odometry errors of our robots, all scans

have been performed at known poses (See Figure 7).

The locations of the sensor unit have been cho-

*****************

Figure 7: Ground truth of the ofﬁce environment with scan

positions of the sensor unit.

sen under the consideration of the minimal detectable

distance of the radar sensors, which is equal to their

resolution. The minimal detectable distance is a rea-

son, why radar sensors with low resolution are only

suitable for outdoor environments with larger scale.

Like mentioned before, a 2D experiment in per-

formed in a 3D environment, hence metallic objects

with rectangular shape elements, like ofﬁce lamps, get

layered into the map as well. Occupancy grid maps,

which are obtained via classical inverse sensor model

(Elfes, 1989), are presented in Figure 8.

Figure 8: Above: This occupancy grid map is built from

raw data of the lateration technique. The wide spread of the

sensor data is caused by non point target situations. Below:

This map is obtained from of the ASR technique.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

370

4 RESULTS AND DISCUSSION

This section will give an interpretation of the obtained

results of the experiments, which have been described

in Section 3.

Figure 5 presents the results of one single scan in-

side an ofﬁce environment, where a point target has

been placed. The position of the point target gets es-

timated very well and the remaining spread of the es-

timated points is caused by the range measurement

error σ

of the sensors. Tests with different distances

between corner reﬂector and sensor unit have proven,

that a rhomb-shaped area of ambiguity is achieved.

This has been explained for a static case on Figure 3.

The position of non point targets gets not estimated

very well. The sensors measure distances to different

points. This results in a non symmetric characteristics

of the distance values d

and d

. Consequently the lat-

eration algorithm calculates the wrong positions.

Figure 2 presents the result of a single scan with

the ASR technique. The corner reﬂector gets the high-

est accumulation of detected object locations, like in

case of the lateration technique. Theoretically, the

characteristics of the receiver powers P

and P

sup-

posed to have a phase difference equal to the angle

shift of the antenna directions. But, the fact that we

can not place both sensors in exactly the same point

leads to the fact that again we can not measure exactly

the same point target. Furthermore, we can not guar-

antee both antenna diagrams to be exactly the same

due to fabrication tolerances. Nevertheless, we can

assume a position of an object, if the ASR is close to

zero.

In order to evaluate if the lateration and ASR tech-

nique are suitable for robotic mapping, we built two

occupancy grid maps with an inverse sensor model

(Thrun et al., 2005, p. 279-300) which we applied on

the raw data that has been recorded during a scan of

a hallway (See Figure 7). The wide of the hallway is

approximately 2m and it has a curve at 20m. Figure 8

displays both results. The ASR technique results in a

quite good map. Consequently, we see possibilities to

map even indoor environments with radar sensors of

low resolution. The minimum detection range, which

is equal to the resolution of the sensor, should be con-

sidered (See Equation 1). To enhance the result of the

lateration technique, more sensors should be used. In

general, both principles suffer from bad resolution of

the radar sensors. Optical effects like double reﬂec-

tions inside a narrow hallway have a negative effect

on the methods as well.

5 CONCLUSION

Robust localization and navigation in hazardous and

tough environments are still a difﬁcult issue in ﬁeld

robotics research. Dust, rain, fog or inadequate illu-

mination are conditions, which make popular sensors,

such as laser scanners or cameras, not suitable. Radar

overcomes the aforementioned difﬁculties.

In this article, we were investigating two new

scanning methods for mobile robotics and took a

closer look on failure inﬂuences. We were focusing

on three inﬂuences. First, the range measurement er-

ror of the sensor itself. Second, the inﬂuence of wrong

position estimation due to non point targets regarding

the lateration technique. Third, we investigated if the

received power of the receiver antenna is reliable for

position estimation, in an environment with multiple

targets. We discovered that the inﬂuence of non point

targets has a huge inﬂuence, especially in a setup with

only two sensors. This effect can be scaled down by

increasing the number of sensors.

There exists several mapping algorithms. An

overview is given by Thrun in (Thrun, 2002, p.7).

Thrun introduces algorithms, which are suitable for

mapping with unknown robot poses, which is named

simultaneous localization and mapping (SLAM). In

this article, we focus on mapping with known poses,

which is simpler. But, mapping with known poses is

leading to more promising results, because odometry

and control errors do not inﬂuence the map. Occu-

pancy grid mapping with Bayes ﬁlter is the most pop-

ular probabilistic representation of a map. Our pro-

posed scanning methods are suitable for occupancy

grid mapping with a classical inverse sensor model.

As far as we can see, the ASR technique results in

better maps.

The proposed radar-based scanning methods are

an alternative to mechanical and electrical beam-

forming methods. Mechanical beam-forming tech-

niques require an antenna and electrical beam-

forming techniques need phase array radars, which

are commonly more expansive. Although no antenna

construction is required, our methods needs more than

one sensor.

From one single 360

◦

-scan of a radar-scanner,

which pivots mechanically a focused beam over a sur-

rounding, a more continues distribution of the mea-

surement can be expected. Our proposed methods

base on antennas with a very large beam width and

objects with a high RCS occlude a larger scene conse-

quently. However, the lateration technique is record-

ing more than one measurement of an object dur-

ing one scan rotation, which raises the possibility

of a correct detection of an object. An advantage

ComparisonofTwoRadar-basedScanning-techniquesfortheUseinRoboticMapping

371

over techniques with focused beams is the possibil-

ity to perform 3D scans as well, which would be me-

chanically complicated in case of mechanical beam-

forming techniques and is only known in combination

with electrical beam-forming radars. Unfortunately,

the lateration technique suffers more from bad accu-

racy and resolution, wrong calibration or asynchro-

nism of measurements than traditional techniques.

The detection of different centres of reﬂection is the

main problem of the lateration technique. The ASR

technique results in pretty well raw data, although a

traditional ASR curve approximation is not possible

in an environment with multiple objects. In this arti-

cle we propose the simple solution of ﬁltering all data,

with a threshold close to a ASR of zero. This results

in less wrong position estimations than the lateration

technique.

REFERENCES

Adams, M., Mullane, J., and Jose, E. (2012). Robotic Nav-

igation and Mapping with Radar. ARTECH HOUSE.

Agilent (2014). Techniques for Precision Validation of

Radar System Performance in the Field. Agilent Tech-

nologies.

uhren, M. (2008). Simulation und Verarbeitung von

Radarziellisten im Automobil. PhD thesis, Universit

Stuttgart.

Clark, S. and Whyte, H. D. (1998). The design of a high

performance mmw radar system for autonomous land

vehicle navigation. In Field and Service Robotics.

Curry, G. R. (2005). Radar System Performance Modeling.

Artech House.

Detlefsen, J., Rozmann, M., and Lange, M. (1993). 94 hgz

3-d imaging radar sensor for industrial environments.

EARSeL Advance in Remote Sensing.

Elfes, A. (1989). Using occupancy grid mapping for mobile

robot perception and navigation. IEEE Computer.

olster, F. (2006). Erfassung ausgedehnter Objekte durch

ein Automobil-Radar. PhD thesis, Technische Univer-

sit

at Hamburg-Harburg.

olster, F. and Rohling, H. (2005). Data association and

tracking for automotive radar networks. IEEE Trans-

actions in Intelligent Transportations Systems.

Kidera, S., Sakamoto, T., and Toru, S. (2008). High-

resolution and real-time three-dimensional imaging

algorithm with envelopes of spheres for uwb radars.

IEEE Transactions on Geoscience and Remote Sens-

ing.

Ludloff, A. (1998). Praxiswissen Radar und Radarsig-

nalverarbeitung. vieweg.

Marck, J. W., Mohamoud, A., and Houwen, Eric vd

qnd Hejster, R. v. (2013). Indoor radar slam . a radar

application for vision and gps denied environments. In

10th European Radar Conference.

Mirbach, M. and Menzel, W. (2011). A simple surface es-

timation algorithm for uwb pulse radas based on tri-

lateration. IEEE International Conference on Ultra-

Wideband.

Rabe, H., Denicke, E., Armbrecht, G., Musch, T., and

Rolfes, I. (2009). Considerations on radar localiza-

tion in multi-target environments. Advances in Radio

Science.

Sakamoto, T. (2007). A fast algorithm for 3-dimensional

imaging with uwb pulse radar systems. IEICE Trans-

action on Communication, pages 636–644.

Schmid, G. and Neubauer, G. (2007). Bestimmung der ex-

position durch ultra-wideband technologien. Techni-

cal report, Bundesamt f

ur Strahlenschutz.

Schneider, M. (2013). LSB-Methode Bestimmung von Dis-

tanzunterschieden mittels parametrierter Schwebun-

gen. PhD thesis, Universit

at Rostock.

Tadokoro, S. (2009). Rescue Robotics - DDT Project on

Robots and Systems for Uraban Search and Rescue.

Springer.

Thrun, S. (2002). Robotic Mapping: A Survey. School of

Comuputer Science.

Thrun, S., Burgard, W., and Fox, D. (2005). Probalistic

Robotics. The MIT Press.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

372