Implementation of Evolving Fuzzy Models of a Nonlinear Process

Radu-Emil Precup

, Emil-Ioan Voisan

, Emil M. Petriu

Mircea-Bogdan Radac

and Lucian-Ovidiu Fedorovici

Department of Automation and Applied Informatics, Politehnica University of Timisoara,

Bd. V. Parvan 2, 300223, Timisoara, Romania

School of Electrical Engineering and Computer Science, University of Ottawa, 800 King Edward, K1N 6N5,

Ottawa, ON, Canada

Keywords: Evolving Takagi-Sugeno-Kang Fuzzy Models, Experimental Results, Input Selection Algorithm, Pendulum

Dynamics.

Abstract: This paper presents details on the implementation of evolving Takagi-Sugeno-Kang (TSK) fuzzy models of

a nonlinear process represented by the pendulum dynamics in the framework of the representative

pendulum-crane systems. The pendulum angle is the output variable of the TSK fuzzy models that are

obtained by online identification. The rule bases and the parameters of the TSK fuzzy models are

continuously evolved by an online identification algorithm (OIA) that adds new rules with more

summarization power and modifies the existing rules and parameters. The OIA is associated with an input

selection algorithm that guides the modelling in terms of ranking the inputs according to their importance

factors. Three TSK fuzzy models evolved by the OIA are exemplified. The performance of the new

evolving TSK fuzzy models is illustrated by experimental results conducted on pendulum-crane laboratory

equipment.

1 INTRODUCTION

As shown in (Angelov, 2002; Sayed Mouchaweh et

al., 2002; Lughofer, 2011, 2013; Precup et al.,

2015), the evolving Takagi-Sugeno-Kang (TSK)

fuzzy models are characterized by the continuous

online learning for rule base learning. In this regard,

an online identification algorithm (OIA) generally

continuously evolves the rule bases and the

parameters of the TSK fuzzy models, and the models

are built online by adding new or removing old local

models (i.e., the adding mechanism). A useful

classification of OIAs dedicated to evolving TSK

fuzzy models is given in (Dovžan et al., 2014),

where the OIAs are organized in three categories.

First, the adaptive algorithms must start with the

initial structure of the TSK fuzzy model (given by

other algorithms or by the experience of the

specialist), the number of space partitions/clusters

does not change over time, and only the parameters

of the membership functions (m.f.s) and the local

models are adapted. Second, the incremental

algorithms, represented by RAN (Platt, 1991),

SONFIN (Juang and Lin, 1998), SCFNN (Lin et al.,

2001), NeuroFAST (Tzafestas and Zikidis, 2001),

DENFIS (Kasabov and Song, 2002), eTS (Angelov

and Filev, 2004), FLEXFIS (Lughofer and Klement,

2005) or PANFIS (Pratama et al., 2014), implement

only adding mechanisms. Third, the evolving

algorithms, besides the adding mechanism,

implement removing and some of them also merging

and splitting mechanisms.

Building upon the recent results on evolving

TSK fuzzy models given in (Precup et al., 2012c,

2014), this paper gives details on the implementation

of evolving TSK fuzzy models of a representative

nonlinear process represented by the pendulum

dynamics in the framework of pendulum-crane

systems. As shown in (Precup et al., 2014), the

pendulum-crane systems are important as

translational electromechanical systems. The crane

control systems can carry out either the cart position

control or the position control of the cart and the

downward or upward angle control of the pendulum

as well. The process models for crane systems can

give the cart position (Precup et al., 2014) or the

pendulum angle (Precup et al., 2012c).

Some recent examples of TSK fuzzy models for

the pendulum dynamics, i.e., the pendulum angle is

the output variable, are presented in the literature

Precup R., Voisan E., Petriu E., Radac M. and Fedorovici L..

Implementation of Evolving Fuzzy Models of a Nonlinear Process.

DOI: 10.5220/0005524700050014

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 5-14

ISBN: 978-989-758-122-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

with focus on fuzzy control. The parameters of TSK

fuzzy models are tuned in (Al-Hadithi et al., 2012)

by the parameters’ weighting method that exhibits

low computational effort. Fuzzy state observers are

combined with TSK fuzzy models in

(Kolemishevska-Gugulovska et al., 2012). Type-2

TSK fuzzy models that alleviate the noise of training

data and that account for mismatched m.f.s are

proposed in (Li and Sun, 2012; Li et al., 2014). TSK

fuzzy models with perturbations and state

multiplicative noises are suggested in (Chang and

Huang, 2014). The quasi-Linear Parameter Variation

formulation of TSK models is discussed in

(Allouche et al., 2014). The dynamic decoupling

concept is introduced in (Chiu, 2014) by the virtual

input dynamics, which decouples the system

uncertainty and the control signal in each rule. The

modelling errors between nonlinear dynamic

systems and TSK fuzzy models are analyzed in (Tsai

and Chen, 2014). The so-called universal TSK fuzzy

models for discrete-time non-affine nonlinear

systems are proposed in (Gao et al., 2015).

Three evolving TSK fuzzy models are proposed

in this paper, namely models with one, two and three

inputs. These models are derived by an OIA that

belongs to the incremental algorithms according to

the classification given in (Dovžan et al., 2014). The

OIA adds new rules with more summarization power

and modifies the existing rules and parameters, and

it is associated with an input selection algorithm that

guides the modelling in terms of ranking the inputs

according to their importance factors.

This paper offers twofold new contributions with

respect to the previously discussed state-of-the-art,

expressed as the functionalities of the OIA. First, the

OIA is inspired from (Angelov and Filev, 2004), and

it offers rule bases and parameters that continuously

evolve by adding new rules with more

summarization power, the existing rules and

parameters are modified in terms of using the

potentials of new data points. Second, an input

selection algorithm is inserted in the OIA.

These contributions are advantageous compared

to the state-of-the-art because, as shown in (Precup

et al., 2014) but for crane control systems, the OIA

ensures a relatively simple and transparent

implementation. In addition, the OIA derives TSK

fuzzy models with improved performance proved for

a complex nonlinear process represented by the

pendulum dynamics. This paper applies and adapts

the results obtained in (Precup et al., 2014) for the

cart position models to the pendulum angle models.

The new functionalities of the OIA and the TSK

fuzzy models proposed in this paper are compared

with the TSK fuzzy models obtained by three OIAs:

the adaptive algorithm ANFIS (Jang, 1993) and the

incremental algorithms DENFIS and FLEXFIS. The

comparison shows that the proposed evolving TSK

fuzzy models ensure the performance enhancement

on the validation data.

This paper is structured as follows: an overview

on the OIA is presented in the next section. The case

study concerning the derivation and validation of the

new TSK fuzzy models for the pendulum dynamics

in the framework of pendulum-crane systems are

treated in Section 3. The comparison of model

performance is included. The conclusions are

highlighted in Section 4.

2 ONLINE IDENTIFICATION

ALGORITHM

The steps of the OIA are obtained by the relatively

simple reformulation of the results given in

(Angelov and Filev, 2004; Precup et al., 2014)

focusing on the cost-effective implementation of the

recursive procedure. The OIA consists of the

following steps that can be organized in terms of the

flowchart, omitted here for the sake of simplicity:

Step 1. The rule base structure is initialized, i.e.,

the parameters in the rule antecedents are initialized.

This is carried out such that to have a single rule,



, where

is the number of rules. The

subtractive clustering (Takagi and Sugeno, 1985) is

applied to compute the parameters of the TSK fuzzy

models using the first data point

, where the

expression of the data point p at the discrete time

step k is

,]...[

121 Tn

kkkk

ppp



p

(1)

T indicates the matrix transposition, the data point in

the input-output data space

1n

,]...[

]...[][

1121







nTnn

pppp

yzzzy

(2)

the rule base of the affine-type TSK fuzzy models is

,...1 ,... THEN

IS AND ... AND IS IF: Rule

110

Rnniiii

nini

nizazaay

LTzLTzi



(3)

where

,...1 , njz



are the input variables, n is the

number of input variables,

,...1 ,...1 ,

njniLT

Rji



are the input linguistic terms,

is the output of the

local model in the rule consequent of rule

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

,...1 ,

nii 

and

,...0 ,...1 ,

nlnia

Rli



are the

parameters in the rule consequents.

Using the algebraic product t-norm to model the

AND operator and the weighted average

defuzzification method in the TSK fuzzy model

structure, the output y of the TSK fuzzy model is

,]1[

111







































yyy

πz

(4)

where the firing degree of the rule i is

,...1 ),(...)()(

))(),...,(),((AND)(

2211

Rninii

niniii

nizzz

zzz





 z

(5)

the normalized firing degree of the rule i is

,...1 ,/

iii





















(6)

and the vector

,...1 ,

ni π

in (4) is the parameter

vector of the rule i (Precup et al., 2014)

,...1 ,]...[

210 R

iniiii

niaaaa π

(7)

The parameters are initialized in terms of (Angelov

and Filev, 2004)

,1)( , ,1 ,1

,4.0 , ,]0...00[

])(...)()([

112111







pzz

πππθ

Pnk

(8)

where

)1()1( 



nnnn

is the covariance matrix, I

is the

)1( nn

order identity matrix,

,0 ,const 

is a large number,

is an

estimation of the parameter vector in the rule

consequents at the discrete time step k, and

,0 , 

is the spread of all Gaussian input m.f.s

,...1 ,...1 ,

njni

Rji



of the fuzzy sets of the input

linguistic terms

,...1 ,...1

],))(/4(exp[)(

njni

zzrz

jijsjji





(9)

and

,...1 ,...1 ,

njniz

Rji



are the centres of these

m.f.s.

in (8) is the first cluster centre,

is the

centre of the rule 1 and also a projection of

the axis z defined in (2), and

)(

in (8) is the

potential of

The input selection algorithm suggested in

(Precup et al., 2014) is next applied in order to select

the important input variables from all possible input

variables. This algorithm consists of the following

steps that are organized as sub-steps of this step 1 of

the OIA:

Sub-step 1.1. The algorithm is initialized by

setting the values of the

10 , 



, that represents

the importance threshold, and

10 , 

, that

stands for the significance threshold.

Sub-step 1.2. The input variable

njz

...1 , 

, is

applied to the initial TSK fuzzy model, the outputs

of the initial TSK fuzzy model at the discrete

time moment k,

Dk ...1



, are read, where D is the

number of input-output data points. The change

range

for the input variable

njz

...1 , 

, is

calculated

min

max

,, kjkjz







(10)

and the importance factor

of the input variable

njz

...1 ,



, is calculated as well

max















jjj

zzz

(11)

The most important input variable is characterized



. As shown in (Precup et al., 2014), large

values of

and

indicate a big influence of the

input variable

njz

...1 ,



, and small values of

and

indicate a relatively unimportant input

variable

njz

...1 ,



Sub-step 1.3. The importance of all input

variables is ranked according to the values of the

importance factors

njI

...1 ,



Sub-step 1.4. All input variables that fulfil the

condition





(12)

are removed. The condition (12) points out that the

input variable

njz

...1 ,



, is unimportant, so it is

justified to remove it. This sub-step gives the set of

remaining

input variables, which are selected out

of the initial n input variables,



Sub-step 1.5. The closely related input variables

are recognized to carry out the independent input

variable testing by the calculation of the correlation

functions

),(

zzCorr

1),(0 



zzCorr

, between

the selected input variables

and

nji ...1, 

ImplementationofEvolvingFuzzyModelsofaNonlinearProcess



)])([(),(

jkjikiji

zzzzzzCorr





















(13)

where

and

are the means of vectors

and

nji ...1, 

, respectively, and



and



are the

variances of

and

nji ...1, 

, respectively.

respectively. If the following condition is fulfilled:

,),( 

zzCorr

(14)

then the input variable

is closely related with the

input variable

. The condition (14) is used in

keeping the independent input variables among the

selected input variables. The condition (14) also

helps in removing one of the two input variables

. Therefore, this sub-step leads to the set of

remaining

independent input variables out of the

selected input variables,

nn 

Step 2. At the next time step, k is set to





and the next data sample

is read.

Step 3. The potential of each new data sample is

computed in terms of (Precup et al., 2014)

,).( ,)(

,)( ],2

)1)(1/[()1()(































kkk

kkkk

ppp

kkP p

(15)

Step 4. The potentials of the centres of existing

rules (clusters) are recursively updated by (Angelov

and Filev, 2005)

,)()()(2/

)()1()(

)1(



























kklklk

lklk

dPPk

PkP

(16)

where

)(

P p

is the potential at the discrete time

step

k of the cluster centre, which is a prototype of

the rule l.

Step 5. The possible modification or upgrade of

the rule base structure is carried out using, as

described in (Angelov and Filev, 2004; Precup et al.,

2014), the potential of the new data compared to the

potential of existing rules’ centres. The rule base

structure is modified if certain conditions are

fulfilled.

Step 6. The parameters in the rule consequents

are updated using the Recursive Least Squares

(RLS) algorithm (Takagi and Sugeno, 1985; Chiu,

1994)

,...2 ,

(

ˆˆ

111

1111

kkk

kkkkkk

















ψCψ

CψψC

θψψCθθ

(17)

where the initial conditions are given in (4), and the

output of the TSK fuzzy model in (4) is expressed in

terms of the vector form

].] 1[...] 1[] 1[[

,]...[ ,

TTT

zzzψ

πππθθψ





(18)

Step 7. The output of the evolving TSK fuzzy model

at the next discrete time step

1k

is predicted using

the particular form of (18)

1 k

y θψ



(19)

The algorithm continues with the step 2 until all data

points from the set of input-output data

}...1|{ Dk



(20)

are read. The step 1 is conducted offline, and the

steps 2 to 7 are conducted online.

3 FUZZY MODELS AND

EXPERIMENTAL VALIDATION

A laboratory setup that contains a pendulum-cart

system described in (Turnau et al., 2008) has been

used in the development and validation of the

evolving TSK fuzzy models. The state equations of

the process in the pendulum-cart system are

presented in (21).

The variables in (21) are:

– the cart position

(the distance between the cart and the centre of the

rail),

– the angle between the upward vertical and

the ray pointing at the centre of mass cart,

– the

cart velocity,

– the pendulum angular velocity, u

– the control signal represented by a constrained

PWM voltage signal,

0||

max

 uu

– the

equivalent mass of the cart,

– the mass of the

pole and load, and

– the distance from the axis of

rotation to the centre of mass. The parameters in

(21) are:

– the moment of inertia of the

pendulum-cart system with respect to the axis of

rotation,

– the ratio between the control force and

the control signal,

– the ratio between the control

force and

– the dynamic cart coefficient, and

– the rotational friction coefficient. The

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

34222

4422

()

[ sin ] [sin ]cos

()() () ()

/[ cos ],

()

[ sin ]cos[sin

() ()

p p

cp cp cp cp

dd d d

cp cp

Jfx

fpx

xx gx x

mml mml mml mml

mml

fpx

xxxxg

mml mml l

 

 

 

 

 

















  







 





]

()

/[ cos ],

()

mml



















(21)

parameter values used in the experimental setup are

(Turnau et al., 2008; Precup et al., 2014)

s/rad. m N 1065.6 /m, N 5.0

s/m, N 548.0 N, 4.9

,mkg 00292.0 m, 0110

kg, 052.0 kg, 76.0 ,5.0

max











fsf

J.l

mmu

(22)

The OIA presented in the previous sections has been

applied in order to obtain the evolving TSK fuzzy

models of the pendulum dynamics, i.e.

xy 

. This

section gives a part of the results. The OIA has been

coded as an extension of the implementation in

terms of eFS Lab (Ramos and Dourado, 2004; Aires

et al., 2009) of the OIAs given in (Angelov and

Filev, 2004; Precup et al., 2014).

Setting the sampling period to 0.01 s, the control

signal

u has been generated as two weighted sums of

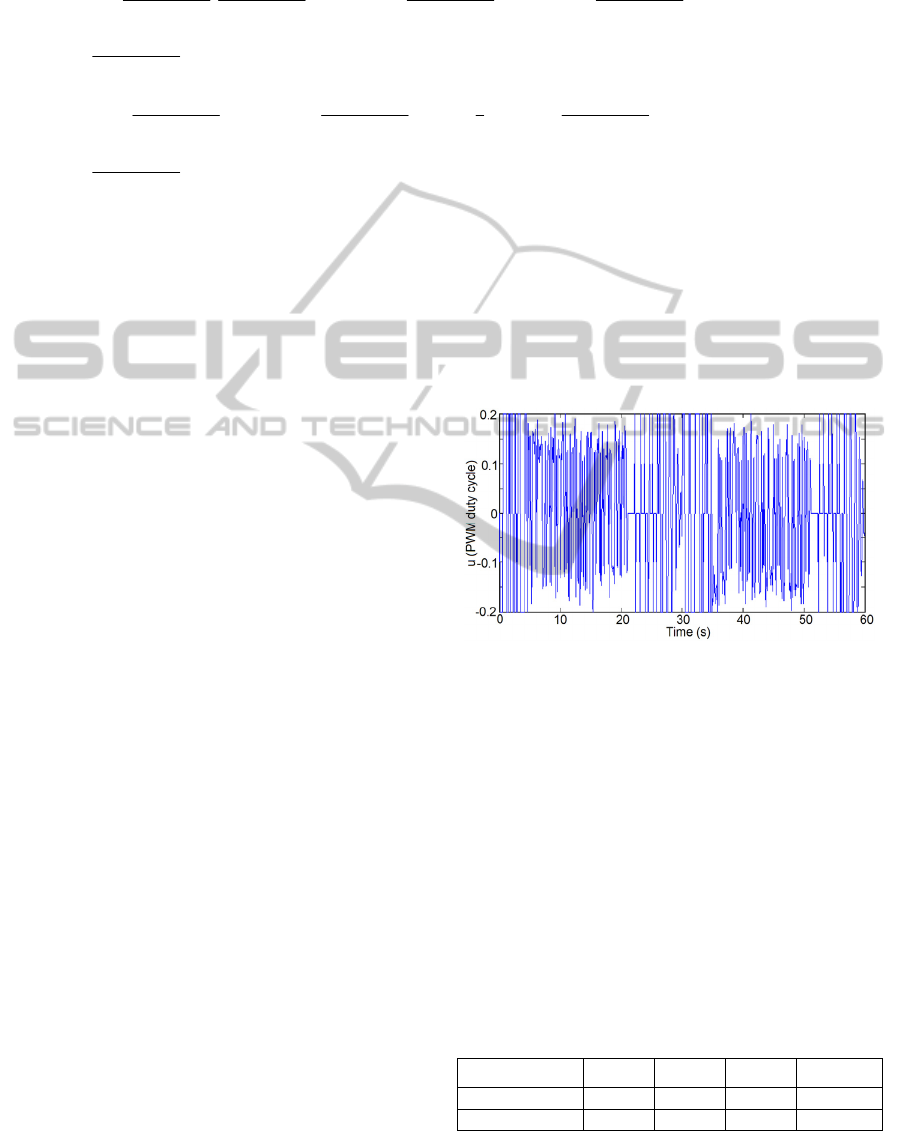
pseudo-random binary signals according to Figure 1

that covers different ranges of magnitudes. As

shown in (Precup et al., 2012c, 2014), this process

input has been applied to the laboratory setup to

generate the input-output data points

....1 ),,( Dky

z

Figure 1 leads to a total number

of 6000 data points separated in training data and

validation data. The first

2500D

data points (the

time frame from 0 s to 25 s) in Figure 1 belong to

the validation data, the rest of

3500D

data points

(the time frame from 25 s to 60 s) in Figure 1 belong

to the testing (validation) data, and the process

output

y will be illustrated as follows.

The input selection algorithm included in the

step 1 of the OIA has been applied for three values

of the importance threshold, namely

4.0





3.0

and

2.0

, and one value of the

significance threshold,

5.0





. This leads to three

TSK fuzzy models with the following inputs: the

TSK fuzzy model 1, with the input

1k

, the TSK

fuzzy model 2 with the inputs

1k

and

1k

, and the

TSK fuzzy model 3 with the inputs

1k

and

2k

. The output of these three TSK fuzzy models is

. The inputs of the fuzzy models have been

obtained from delayed system inputs and/or outputs

extracted from the training and validation data sets.

The value of the parameter



in the step 1 of the

OIA has been set to

10000





Figure 1: Control signal versus time: training data and

testing data.

The TSK fuzzy model 1 has evolved to

2

rules.

The parameter values of the TSK fuzzy model 1,

computed by the OIA for

1n

, are presented in

Table 1.

The evolutions of the system output (i.e., the

pendulum angle)

y versus time of the TSK fuzzy

model 1 and of the real-world process (the

laboratory setup) are presented in Figure 2. Figure 2

gives the responses of the TSK fuzzy model 1 and of

the process for the validation data and shows the

poor behaviour of this model. The system output for

the validation data is not illustrated as follows.

Table 1: Parameter values of TSK fuzzy model 1.

Rule number i

1 0 0.0424 5.3009 –1.6296

2 0.1156 0.0424 5.3689 0.3121

ImplementationofEvolvingFuzzyModelsofaNonlinearProcess

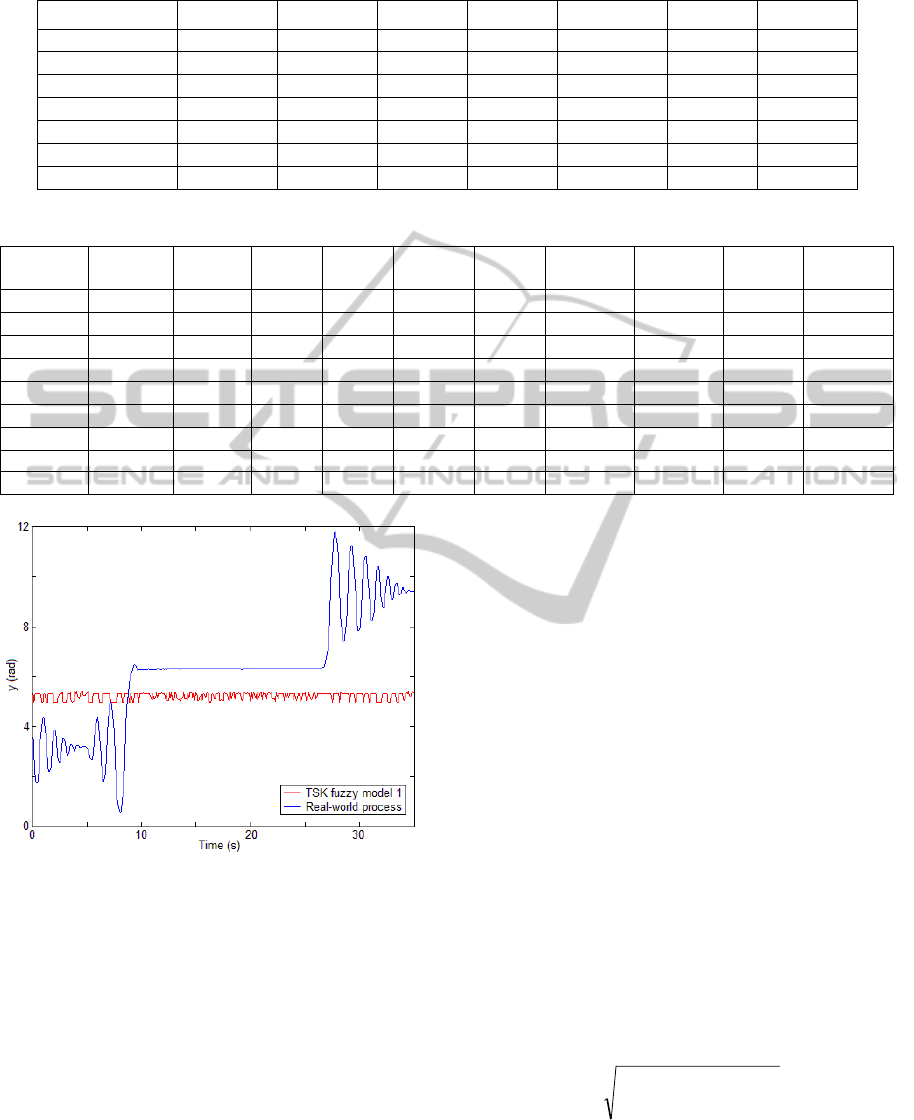
Table 2: Parameter values of TSK fuzzy model 2.

Rule number i

1 0 0 0.0424 1.2502 0.6903 1.0025 0.4226

–0.1167

3.1861 0.0424 1.2502 0.0639

–0.5125

0.9956

–0.1167

2.3332 0.0424 1.2502 0.6877

–1.1108

0.6857

4 0 6.2186 0.0424 1.2502

–0.4733

0.0435 1.0744

–0.1167

6.2186 0.0424 1.2502

–0.6956 –0.0229

1.1099

6 0 6.1161 0.0424 1.2502

–0.4597 –0.1376

1.0472

7 0 5.9841 0.0424 1.2502

–0.5298

0.7453 1.0385

Table 3: Parameter values of TSK fuzzy model 3.

Rule

number i

1 0 0 0 0.0424 1.2502 1.2502 0.1161 0.2383 2.1021

–0.9404

–0.1175

3.1861 0 0.0424 1.2502 1.2502 0.4574

–0.0915

0.8872 0.0096

–0.1175

3.5558 3.4423 0.0424 1.2502 1.2502

–0.2529 –0.0368

1.8198

–0.7841

4 0.1293 1.9835 1.9643 0.0424 1.2502 1.2502 0.2798 0.1254 2.0211

–1.0080

–0.1175

2.3332 1.9643 0.0424 1.2502 1.2502 0.8986

–0.2488

1.5784

–0.8115

–0.1175

6.2186 6.2282 0.0424 1.2502 1.2502 0.0827

–0.0133

1.4412

–0.4550

7 0 6.2186 6.2282 0.0424 1.2502 1.2502

–0.6813

0.0502 1.6820

–0.5745

8 0 6.1161 6.2282 0.0424 1.2502 1.2502 0.2990 0.5435 0.8706 0.0532

9 0 5.9841 6.1161 0.0424 1.2502 1.2502

–1.2067

0.1298 2.1044

–0.9259

Figure 2: Pendulum angle versus time of TSK fuzzy

model 1 and of real-world process for validation data.

The TSK fuzzy model 2 has evolved to



rules. The parameter values of the TSK fuzzy model

2, computed by the OIA for

2n

, are presented in

Table 2.

The time responses of

y of the TSK fuzzy model

2 and of the real-world process are presented in

Figure 3. Figure 3 shows a slightly improved

behaviour compared to Figure 2.

The TSK fuzzy model 3 has evolved to



rules.

The parameter values of the TSK fuzzy model 3,

computed by the OIA for

3n

, are presented in

Table 3.

The time responses of

y versus time of the TSK

fuzzy model 3 and of the real-world process are

illustrated in Figure 4. Figure 4 shows an improved

behaviour with respect to Figure 3.

As pointed out in Section 1, the OIA and the

TSK fuzzy model performance (as the result of the

OIA) have been compared with the following three

OIAs that lead to evolving TSK fuzzy models:

ANFIS, DENFIS and FLEXFIS. Since Figure 2

illustrates the poor performance of the TSK fuzzy

model 1, the comparison has been focused on the

TSK fuzzy models 2 and 3. Two TSK fuzzy models

have been obtained for each OIA. The fair

comparison of all fuzzy models has been conducted

in terms of using the same inputs, numbers and

shapes of m.f.s as those of the TSK fuzzy models 2

and 3, and the numbers of rules

have been set

such that to be very close.

The comparison of the models is carried out in

terms of the root mean square error (RMSE)

between the pendulum angles of the TSK fuzzy

models and of the real-world process. The

expression of this global performance index is

,)()/1(







xyDRMSE

(23)

where

is the output (the pendulum angle) of the

TSK fuzzy models and

is the output (the

pendulum angle) of the laboratory setup at the

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

discrete time moment k. The RMSE has been

computed and measured for the training data and for

the testing (validation) data.

Figure 3: Pendulum angle versus time of TSK fuzzy

model 2 and of real-world process for validation data.

The results obtained for the eight TSK fuzzy

models on the testing data are summarized in Table

4. Table 4 includes the numbers of parameters

the final evolved TSK fuzzy models.

Table 4 and Figures 2, 3 and 4 prove that the best

performance on the testing data is exhibited by the

TSK fuzzy model 3 obtained by the OIA presented

in Section 2. Table 4 illustrates the performance

improvement achieved by the evolving TSK fuzzy

models obtained by proposed OIA compared to

other three OIAs. In addition, the performance

improvement with respect to another implementation

of the OIA given in (Precup et al., 2012c) is ensured.

The results presented in Table 5 and in Figures 3

and 4 also show that the performance of the

proposed TSK fuzzy models are consistent with the

testing data. However, a different scaling used, for

example, in Figures 3 and 4, could show in a more

illustrative way the differences.

As expected, Table 4 confirms that more inputs

lead to improved model performance. But the

selection of the input variables is carried out

systematically in the step 1 of the OIA by that input

selection algorithm that guides the modelling.

The models and the performance depend on the

values of the parameters



and



. Different models

and results for these models are obtained for other

values of these two parameters.

Based on these experimental results, presented

only for the testing data and not for the validation

data, the proposed evolving TSK fuzzy models can

be accepted as very close to the real-world nonlinear

Figure 4: Pendulum angle versus time of TSK fuzzy

model 3 and of real-world process for validation data.

Table 4: Results for eight TSK fuzzy models on testing

data.

TSK

fuzzy

model

OIA

RMSE

2 Section 2 7 49 0.1672

2 ANFIS 8 56 0.2537

2 DENFIS 8 56 0.4094

2 FLEXFIS 7 49 0.3011

3 Section 2 9 90 0.1505

3 ANFIS 12 120 0.1814

3 DENFIS 10 90 0.3392

3 FLEXFIS 10 90 0.2506

process. However, different conclusions can be

drawn if other nonlinear processes are considered

(Precup et al., 2004; Deliparaschos et al., 2006;

Gusikhin et al., 2007; Precup and Preitl, 2007;

Ferreira and Ruano, 2009; Filip and Leiviskä, 2009;

Bošnak et al., 2012; Precup et al., 2012b; Guerra et

al., 2012; Lam and Lauber, 2013) if they are viewed

such that to belong to control systems. The OIA

should be reorganized such that to enable the cost-

effective implementation of the control solutions

(Precup et al., 2011, 2012a, 2012d;

4 CONCLUSIONS

This paper has given implementation details on an

OIA, which continuously evolves the rule bases and

the parameters of TSK fuzzy models by adding new

rules with more summarization power and

modifying the existing rules and parameters. The

OIA consists of seven steps, and the step 1 includes

an input selection algorithm that guides the

ImplementationofEvolvingFuzzyModelsofaNonlinearProcess

modelling in terms of ranking the inputs according

to their importance factors.

The main advantages of the new results given in

this paper are the simplicity and transparency of the

OIA, the simplicity of the evolving TSK fuzzy

models and their consistency with both the testing

data. These advantages have been proved by real-

time experimental results related to the fuzzy

modelling of a representative nonlinear process, i.e.,

the pendulum dynamics in the framework of

pendulum-crane systems.

The OIA has been implemented by the extension

of the OIAs given in (Angelov and Filev, 2004;

Precup et al., 2014) using the core of eFS Lab

reported in (Ramos and Dourado, 2004; Aires et al.,

2009). The comparison of the experimental results

shows the performance improvement exhibited by

two proposed TSK fuzzy models with respect to

other fuzzy models obtained by similar OIAs.

Future research will concern the further

performance improvement of the TSK fuzzy models.

Several optimization algorithms including nature-

inspired optimization algorithms (Duleba and

Sasiadek, 2003; Haber et al., 2009; Valdez et al.,

2011; Johanyák and Papp, 2012; Vaščák and Paľa,

2012; David et al., 2013; El Amraoui and

Mesghouni, 2014; Osaba et al., 2014; Tang et al.,

2014; Savio et al., 2014; Zhang et al., 2014) will be

incorporated to replace the RLS algorithm in the

step 6 of the OIA. The OIA will be applied to other

representative nonlinear processes as well. Since the

goal of the development of these TSK fuzzy models

is the model-based design of fuzzy control systems,

the models will be included in such control system

structures.

ACKNOWLEDGEMENTS

This work was supported by a grant from the

Romanian National Authority for Scientific

Research, CNCS – UEFISCDI, project number PN-

II-ID-PCE-2011-3-0109, by a grant from the

Partnerships in priority areas – PN II program of the

Romanian National Authority for Scientific

Research ANCS, CNDI – UEFISCDI, project

number PN-II-PT-PCCA-2011-3.2-0732, by grants

from the Partnerships in priority areas – PN II

program of the Romanian Ministry of Education and

Research (MEdC) – the Executive Agency for

Higher Education, Research, Development and

Innovation Funding (UEFISCDI), project numbers

PN-II-PT-PCCA-2013-4-0544 and PN-II-PT-PCCA-

2013-4-0070, and by a grant from the NSERC of

Canada.

REFERENCES

Aires, L., Araújo, J., Dourado, A., 2009. Industrial

monitoring by evolving fuzzy systems. In

Proceedings

of Joint 2009 IFSA World Congress and 2009

EUSFLAT Conference

. Lisbon, Portugal, 1358-1363.

Al-Hadithi, B. M., Jiménez, A., Matía, F., 2012. A new

approach to fuzzy estimation of Takagi-Sugeno model

and its applications to optimal control for nonlinear

systems.

Applied Soft Computing. 12, 280-290.

Allouche, B., Vermeiren, L., Dequidt, A., Dambrine, M.,

2014. Step-crossing feasibility of two-wheeled

transporter: Analysis based on Takagi-Sugeno

descriptor approach. In

Proceedings of IEEE 17

International Conference on Intelligent

Transportation Systems

. Qingdao, China, 2675-2680.

Angelov, P., 2002.

Evolving Rule based Models: A Tool

for Design of Flexible Adaptive Systems

. Berlin,

Heidelberg: Springer-Verlag.

Angelov, P., Filev, D., 2004. An approach to online

identification of Takagi-Sugeno fuzzy models.

IEEE

Transactions on Systems, Man, and Cybernetics, Part

B: Cybernetic

s. 34, 484-498.

Angelov, P., Filev, D., 2005. Simpl_eTS: A simplified

method for learning evolving Takagi-Sugeno fuzzy

models. In

Proceedings of 14

IEEE International

Conference on Fuzzy Systems

. Reno, NV, USA, 1068-

1073.

Bošnak, M., Matko, D., Blažič, S., 2012. Quadrocopter

control using an on-board video system with off-board

processing.

Robotics and Autonomous Systems. 60,

657-667.

Chang, W.-J., Huang, B.-J., 2014. Robust fuzzy control

subject to state variance and passivity constraints for

perturbed nonlinear systems with multiplicative

noises.

ISA Transactions. 53, 1787-1795.

Chiu, C.-S., 2014. A dynamic decoupling approach to

robust T-S fuzzy model-based control.

IEEE

Transactions on Fuzzy Systems

. 22, 1088-1100.

Chiu, S. L., 1994. Fuzzy model identification based on

cluster estimation.

Journal of Intelligent and Fuzzy

Systems.

2, 267-278.

David, R.-C., Precup, R.-E., Petriu, E. M., Radac, M.-B.,

Preitl, S., 2013. Gravitational search algorithm-based

design of fuzzy control systems with a reduced

parametric sensitivity.

Information Sciences. 247, 154-

1733.

Deliparaschos, K. M., Nenedakis, F. I., Tzafestas, S. G.,

2006. Design and implementation of a fast digital

fuzzy logic controller using FPGA technology.

Journal of Intelligent and Robotic Systems. 45, 77-96.

Dovžan, D., Logar, V., Škrjanc, I., 2014. Implementation

of an evolving Fuzzy Model (eFuMo) in a monitoring

system for a waste-water treatment process.

IEEE

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

Transactions on Fuzzy Systems. DOI

10.1109/TFUZZ.2014.2379252.

Duleba, I., Sasiadek, J. Z., 2003. Nonholonomic motion

planning based on Newton algorithm with energy

optimization.

IEEE Transactions on Control Systems

Technology

. 11, 355-363.

El Amraoui, A., Mesghouni, K., 2014. Optimization of a

train traffic management problem under uncertainties

and disruptions.

Studies in Informatics and Control.

23, 313-323.

Ferreira, P. M., Ruano, A. E., 2009. On-line sliding-

window methods for process model adaptation.

IEEE

Transactions on Instrumentation and Measurement

58, 3012-3020.

Filip, F.-G., Leiviskä, K., 2009. Large-scale complex

systems. In

Springer Handbook of Automation, S. Y.

Nof, Ed. Berlin, Heidelberg: Springer-Verlag, 619-

638.

Gao, Q., Feng, G., Dong, D., Liu, L., 2015. Universal

fuzzy models and universal fuzzy controllers for

discrete-time nonlinear systems.

IEEE Transactions

on Cybernetics

. 54, 880-887.

Guerra, T.-M., Bernal, M., Guelton, K., Labiod, S., 2012.

Non-quadratic local stabilization for continuous-time

Takagi-Sugeno models.

Fuzzy Sets and Systems. 201,

40-54.

Gusikhin, O. Y., Rychtyckyj, N., Filev, D., 2007.

Intelligent systems in the automotive industry:

applications and trends.

Knowledge and Information

Systems

. 12, 147-168.

Haber, R. E., Haber-Haber, R., Jiménez, A., Galán, R.,

2009. An optimal fuzzy control system in a network

environment based on simulated annealing. An

application to a drilling process.

Applied Soft

Computing

. 9, 889-895.

Jang, J.-S. R., 1993. ANFIS: Adaptive-Network-based

Fuzzy Inference System.

IEEE Transactions on

Systems, Man, and Cybernetics

. 23, 665-685.

Johanyák, Z. C., Papp, O., 2012. A hybrid algorithm for

parameter tuning in fuzzy model identification.

Acta

Polytechnica Hungarica

. 9, 153-165.

Juang, C.-F., Lin, C.-T., 1998. An on-line self-

constructing neural fuzzy inference network and its

applications.

IEEE Transactions on Fuzzy Systems. 6,

12-32, 1998.

Kasabov, N. K., Song, Q., 2002. DENFIS: Dynamic

Evolving Neural-Fuzzy Inference System and its

application for time-series prediction.

IEEE

Transactions on Fuzzy Systems

. 10, 144-154.

Kolemishevska-Gugulovska, T., Stankovski, M., Rudas, I.

J., Jiang, N., Jing, J., 2012. A min-max control

synthesis for uncertain nonlinear systems based on

fuzzy T-S model. In

Proceedings of 6

IEEE

International Conference Intelligent Systems

. Sofia,

Bulgaria, 303-310.

Lam, H. K., Lauber, J., 2013. Membership-function-

dependent stability analysis of fuzzy-model-based

control systems using fuzzy Lyapunov functions.

Information Sciences. 232, 253-266.

Li, H., Sun, X., Shi, P., Lam, H.-K., 2015. Control design

of interval type-2 fuzzy systems with actuator fault:

Sampled-data control approach.

Information Sciences.

302, 1-13.

Li, Y.-M., Sun, Y.-Y., 2012. Type-2 T-S fuzzy impulsive

control of nonlinear systems.

Applied Mathematical

Modelling

. 36, 2710-2723.

Lin, F.-J., Lin, C.-H., Shen, P.-H., 2001. Self-constructing

fuzzy neural network speed controller for permanent-

magnet synchronous motor drive.

IEEE Transactions

on Fuzzy Systems

. 9, 751-759.

Lughofer, E., 2011.

Evolving Fuzzy Systems -

Methodologies, Advanced Concepts and Applications

Berlin, Heidelberg: Springer-Verlag.

Lughofer, E., 2013. On-line assurance of interpretability

criteria in evolving fuzzy systems - achievements, new

concepts and open issues.

Information Sciences. 251,

22-46.

Lughofer, E., Klement, E. P., 2005. FLEXFIS: A variant

for incremental learning of Takagi-Sugeno fuzzy

systems. In

Proceedings of 14

IEEE International

Conference on Fuzzy Systems

. Reno, NV, USA, 915-

920.

Osaba, E., Diaz, F., Onieva, E., Carballedo, R., Perallos,

A., 2014. AMCPA: A population metaheuristic with

adaptive crossover probability and multi-crossover

mechanism for solving combinatorial optimization

problems.

International Journal of Artificial

Intelligence

. 12, 1-23.

Platt, J., 1991. A resource allocating network for function

interpolation.

Neural Computation. 3, 213-225.

Pratama, M., Anavatti, S. G., Angelov, P., Lughofer, E.,

2014. PANFIS: A novel incremental learning

machine.

IEEE Transactions on Neural Networks and

Learning Systems

. 25, 55-68.

Precup, R.-E., Angelov, P., Costa, B. S. J., Sayed-

Mouchaweh, M., 2015. An overview on fault

diagnosis and nature-inspired optimal control of

industrial process applications.

Computers in Industry.

DOI: 10.1016/j.compind.2015.03.001.

Precup, R.-E., David, R.-C., Petriu, E. M., Preitl, S.,

Radac, M.-B., 2012a. Novel adaptive gravitational

search algorithm for fuzzy controlled servo systems.

IEEE Transactions on Industrial Informatics. 8, 791-

800.

Precup, R.-E., Dragos, C.-A., Preitl, S., Radac, M.-B.,

Petriu, E. M., 2012b. Novel tensor product models for

automatic transmission system control.

IEEE Systems

Journal

. 6, 488-498.

Precup, R.-E., Filip, H.-I., Radac, M.-B., Petriu, E. M.,

Preitl, S., Dragos, C.-A., 2014. Online identification of

evolving Takagi-Sugeno-Kang fuzzy models for crane

systems.

Applied Soft Computing. 24, 1155-1163.

Precup, R.-E., Filip, H.-I., Radac, M.-B., Pozna, C.,

Dragos, C.-A., Preitl, S., 2012c. Experimental results

of evolving Takagi-Sugeno fuzzy models for a

nonlinear benchmark. In

Proceedings of 2012 IEEE

International Conference on Cognitive

Infocommunications

. Kosice, Slovakia, 567-572.

ImplementationofEvolvingFuzzyModelsofaNonlinearProcess

Precup, R.-E., Preitl, S., 2007. PI-fuzzy controllers for

integral plants to ensure robust stability.

Information

Sciences

. 177, 4410-4429.

Precup, R.-E., Preitl, S., Balas, M., Balas, V., 2004. Fuzzy

controllers for tire slip control in anti-lock braking

systems. In

Proceedings of IEEE International

Conference on Fuzzy Systems

. Budapest, Hungary, 3,

1317-1322.

Precup, R.-E., Preitl, S., Radac, M.-B., Petriu, E. M.,

Dragos, C.-A., Tar, J. K., 2011. Experiment-based

teaching in advanced control engineering.

IEEE

Transactions on Education

. 54, 345-355.

Precup, R.-E., Tomescu, M. L., Radac, M.-B., Petriu, E.

M., Preitl, S., Dragos, C.-A., 2012d. Iterative

performance improvement of fuzzy control systems

for three tank systems.

Expert Systems with

Applications

. 39, 8288-8299.

Ramos, J. V., Dourado, A., 2004. On line interpretability

by rule base simplification and reduction. In

Proceedings of European Symposium on Intelligent

Technologies, Hybrid Systems and Their

Implementation on Smart Adaptive Systems

. Aachen,

Germany, 1-6.

Sayed Mouchaweh, M., Devillez, A., Villermain Lecolier,

G., Billaudel, P., 2002. Incremental learning in fuzzy

pattern matching.

Fuzzy Sets and Systems. 132, 49-62.

Savio, M. R. D., Sankar, A., Vijayarajan, N. R., 2014. A

novel enumeration strategy of maximal bicliques from

3-dimensional symmetric adjacency matrix.

International Journal of Artificial Intelligence. 12, 42-

56.

Takagi, T., Sugeno, M., 1985. Fuzzy identification of

systems and its application to modeling and control.

IEEE Transactions on Systems, Man, and Cybernetics.

15, 116-132.

Tang, L., Zhao, Y., Liu, J., 2014. An improved differential

evolution algorithm for practical dynamic scheduling

in steelmaking-continuous casting production.

IEEE

Transactions on Evolutionary Computation

. 18, 209-

225.

Tsai, P.-W., Chen, C.-W., 2014, Novel criterion for

nonlinear time-delay systems using LMI fuzzy

Lyapunov method.

Applied Soft Computing. 25, 461-

472.

Turnau, A., Pilat, A., Hajduk, K., Korytowski, A., Grega,

W., Gorczyca, P., Kolek, K., Rosól, M., 2008.

Pendulum-Cart System User’s Manual. Krakow:

INTECO Ltd.

Tzafestas, S. G., Zikidis, K. C., 2001. NeuroFAST: On-

line neuro-fuzzy ART-based structure and parameter

learning TSK model.

IEEE Transactions on Systems

Man and Cybernetics, Part B: Cybernetics

. 31, 797-

802.

Valdez, F., Melin, P., Castillo, O., 2011. An improved

evolutionary method with fuzzy logic for combining

particle swarm optimization and genetic algorithms.

Applied Soft Computing. 11, 2625-2632.

Vaščák, J., Paľa, M., 2012. Adaptation of fuzzy cognitive

maps for navigation purposes by migration algorithms.

International Journal of Artificial Intelligence. 8, 20-

37.

Zhang, N., Zhang, X., Liu, H., Zhang, D., 2014.

Optimization scheme of forming linear WSN for

safety monitoring in railway transportation.

International Journal of Computers Communications

& Control

. 9, 800-810.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics