
A Physics-based Optimization Approach for Path Planning on Rough
Terrains
Diogo Amorim and Rodrigo Ventura
Institute for Systems and Robotics, Instituto Superior Tcnico, Universidade de Lisboa, Lisbon, Portugal
Keywords:
Path Planning, Fast Marching Method (FMM), Rapidly-exploring Random Trees (RRT), Rough Terrain.
Abstract:
The following paper addresses the problem of applying existing path planning methods targeting rough ter-
rains. Most path planning methods for mobile robots divide the environment in two areas — free and occupied
— and restrict the path to lie within the free space. The presented solution addresses the problem of path plan-
ning on rough terrains, where the local shape of the environment are used to both constrain and optimize the
resulting path. Finding both the feasibility and the cost of the robot crossing the terrain at a given point is
cast as an optimization problem. Intuitively, this problem models dropping the robot at a given location (x,y)
and determining the minimal potential energy pose (attitude angles and the distance of the centre of mass to
the ground). We then applied two path planning methods for computing a feasible path to a given goal: Fast
Marching Method (FMM) and Rapidly exploring Random Tree (RRT). Processing the whole mapped area,
determining the cost of every cell in the map, we apply a FMM in order to obtain a potential field free of local
minima. This field can then be used to either pre-compute a complete trajectory to the goal point or to control,
in real time, the locomotion of the robot. Solving the previously stated problem using RRT we need not to
process the entire area, but only the coordinates of the nodes generated. This last approach does not require
as much computational power or time as the FMM but the resulting path might not be optimal. In the end, the
results obtained from the FMM may be used in controlling the vehicle and show optimal paths. The output
from the RRT method is a feasible path to the goal position. Finally, we validate the proposed approach on
four example environments.
1 INTRODUCTION
This paper proposes a method that efficiently plans a
path for a mobile robot on rough terrain. Although
there are already some path planning methods that
easily solve this type of problem in 2D, we intend
to apply these tools to the same sort of problem, but
with a different premise: a different type of map used
as input. A map that not only represents a rough sur-
face with information about the free space but also the
elevation of each coordinate. These elevation vari-
ations may imply new challenges and obstacles e.g.
if a slope is too steep the vehicle will not be able to
climb it.
In the end, the purpose of this paper is to show
how to obtain a feasible path plan from A to B, where
the traversability of each position is taken into ac-
count. This traversability (cost) value is based on the
vehicle’s attitude as if it were dropped on the floor at
the given pose. To determine the attitude of the ve-
hicle we compute the minimal energy configuration
at each location. The robot’s attitude is the solution
of an optimization problem that solves the scenario
of dropping the robot on the surface at each point of
the map. We can then apply a FMM (Garrido et al.,
2009; Sethian, 1999) to the newly created cost map
to obtain a potential field with no local minima. Ulti-
mately this field is then used to guide the robot to its
goal smoothly and safely away from obstacles or haz-
ardous situations. Another way to determine a fea-
sible path is through the use of RRTs which is not
so computationally expensive, but does not guarantee
path optimality.
2 RELATED WORK
Path planning is a widely studied problem that has
been approached in many different ways over the
years as literature demonstrates, see for example the
textbooks (Siciliano and Khatib, 2008) and (LaValle,
2006) for extensive reviews. However, most of these
259
Amorim D. and Ventura R..
A Physics-based Optimization Approach for Path Planning on Rough Terrains.
DOI: 10.5220/0005529302590266
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 259-266
ISBN: 978-989-758-123-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

methods assume a prior division of the environment
between free and occupied space, while robot move-
ment is constrained to the free space. Rough terrains,
for which such a binary division is not trivial, often
require an alternative approach. In (Tarokh et al.,
1999) two path planning methods are compared to
show their ability to solve the same problem in dif-
ferent ways with different degrees of satisfaction of
the final resulting path.
One relevant work is described in a paper from
S. Garrido and his team (Garrido et al., 2013) that
applies the fast marching method to outdoor motion
planning on rough terrain. Despite the similarity in
Garrido’s work, the terrain is locally approximated by
a plane, which may pose problems for discontinuous
terrains, e.g. stairs or other discontinuities like debris.
Our approach neither relies on any surface approxi-
mation nor makes any smoothness assumption of the
input elevation map.
3 PROPOSED APPROACH
The approach proposed is based on two phases:
(1) computing a cost map, and (2) computing the op-
timal path to the goal. Firstly, the cost is obtained by
computing the expense of moving at each point of a
2-D grid covering the environment. The characteris-
tics we have found relevant to estimate the cost map
are the robot’s pose at each point and whether or not
the pose is stable. In this paper we set the cost to a
function of the deviation of the plane vehicle with re-
spect to a horizontal plane. Take for instance a vehicle
on a ramp: the cost is zero if the ”ramp” is horizon-
tal, and it increases with the inclination of the ramp.
This cost is set to infinity if that point is infeasible for
the robot to cross. To compute this deviation we con-
sider the robot being dropped vertically at the given
position, and then determine the robot pose that mini-
mizes its potential energy i.e., the one that minimizes
the height of the centre of mass of the vehicle (see
Fig. 1). This problem is cast as an optimization prob-
lem which is numerically solved for each point of the
grid. By defining the problem as a constrained op-
timization problem with non-linear constraints, it is
possible to determine the pose of the mobile robot as
well as the number of contact points with the ground.
This is an important factor to determine whether or
not it is possible for it to maintain a stable pose on
those coordinates.
The second step generates a path to the goal po-
sition, by application of a FMM or using RRT. Us-
ing the FMM we generate a potential field based on
the previously created cost map, with two fundamen-
Figure 1: Conceptualization of the problem of determining
the resting pose of the UGV on the terrain surface by means
of virtually dropping it from a hight.
tal properties, as far as path planning is concerned:
(1) it shows no local minima, and (2) the gradient de-
scent over the field is the optimal path to the goal, on
a given cost map. RRT is faster and computationally
more efficient as it does not need the whole map to be
processed, instead, the cost is only computed for the
coordinates of the generated nodes.
3.1 Computing the Cost Map
The most direct use of elevation maps is to compute
traversability costs at each cell of the grid. The costs
are computed by comparing the local terrain shape
with a kinematic model of the robot. Let us assume
that, for every cell of the map, the cost value is di-
rectly proportional to the angle between the vertical
vector of the inertial frame and the plane of the robot’s
body. Defining the cost as a direct proportion was ar-
bitrarily decided and in this simple approach it yields
good results, as it encourages paths with lower incli-
nations. The cost could be set as a different combina-
tion of the θ and γ angles like C
1
θ +C
2
γ for example,
where C
1
and C
2
are coefficients that weigh the influ-
ence of each direction of inclination. This angle be-
tween the vertical vector of the inertial frame and the
plane of the robot’s body can be calculated through a
combination of the roll and pitch angles. First we cre-
ate a normalized vector v
1
in R
3
with the coordinate
x = 0 which makes a γ degree angle with the Y axis
and a normalized vector v
2
with the coordinate y = 0
which makes a β degree angle with the X axis. Sec-
ondly the vectors (v
1
,v
2
) are added and the resulting
vector’s angle with the Z
I
axis is stored in the equiv-
alent cell of the cost map. Yet, if we were to keep
the absolute value of the resulting angle, we would be
admitting the cost of moving uphill or downhill on a
slope with equal inclination is the same. It appears
intuitive to say it will be harder for the robot to move
uphill rather than moving downhill. This is the rea-
son why we keep the information about the sign of γ,
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
260

adding that information to each cell of the cost map.
v
i
= (x
i
,y
i
,z
i
)
v
1
=
0,
1
cos(γ)
,
1
sin(γ)
v
2
=
1
cos(β)
,0,
1
sin(β)
v
3
= v
1
+ v
2
c
x,y
= K arccos
z
3
|v
3
|
sign(γ) ,∀x, y ∈ map
(1)
where K is a positive constant penalizing the devia-
tion from the horizontal position. In the end, we are
able to obtain information about the terrain character-
istics regarding its inclination and possible obstacles
for the UGV. In order to obtain both γ and β angles
we have to determine the robot’s pose as previously
mentioned. The robot’s pose characterizes its frame
R with respect to the inertial frame I , being defined
as
(x
cm,I
,y
cm,I
,z
cm,I
,θ, β,γ) (2)
where (x
cm,I
,y
cm,I
,z
cm,I
) are the coordinates of the R
in relation to I , and (θ, β,γ) are Euler angles Z −Y −
X. The first, θ (yaw) is the angle of rotation of the r
around the Z
R
axis, β (roll) the Y
R
axis, and γ (pitch)
the X
R
axis, where X
R
, Y
R
, and Z
R
are the axis of the
robot frame R .
There are n − 1 contact points characterized
(p
1,R
, p
2,R
),..., (p
n−1,R
) and the last point (p
cm,R
)
represents the vehicle’s centre of mass, which, as pre-
viously mentioned, was described as the origin of the
frame R . To determine the coordinates of the points
defining the robot on the I frame their coordinates
in R are multiplied by a rotation matrix and then
added the position of the R relative to the I . The
robot’s world is described in a (x,y, z) configuration
and it is determined in relation to the inertial frame
of reference (I ). The robot is defined as an n points
p
j,R
= (x
j,R
,y
j,R
,z
j,R
) structure (see Fig. 3 for an
example), all fixed to its reference frame, the robot’s
reference frame (R ) where the origin is set at the cen-
tre of mass of the robot. All in all, the main point is
to determine the relative position of the robot to its
world for every point of the map. This relative po-
sition defines the robot’s pose, which contains infor-
mation about the γ and β angles used to compute the
traversability. In order to emulate the conceptualiza-
tion shown in Fig. 1 we have to minimize the z
cm,I
coordinate of the robot’s centre of mass, in relation to
the I with the restriction that none of the points that
define the robot can pass through the surface. Further-
more, the vehicle also has pose limitations such as:
neither being upside down nor climbing hills steeper
than γ
max
or rolling more than β
max
. When inserted in
an optimization problem these limitations are trans-
lated as constrains, and so, in order to solve this spe-
cific problem one can resort to a constrained (multi-
variate) problem solving routine. In order to introduce
constraints in the optimization function it is necessary
to formulate them as inequalities. These functions are
always positive and in this specific case this means
that the z coordinate of each point defining the robot
minus the z coordinate of the point of the map directly
below must be positive, and this condition is respected
by the algorithm, to a certain error value. There are
n +2 constraints to this simple problem, one per each
point that defines the robot, one for the roll and an-
other for pitch angle limitations. More constraints can
and will be added in order to better simulate the hull
of the vehicle more accurately depicting it. The task
of determining the robot’s pose can then be defined as
a constrained optimization problem in the following
way:
Minimize: z
cm,I
Variables: z
cm,I
, β, γ
Subject to: ∀
j
(z
j,I
− map
x
j,I
,y
j,I
≥ 0)
β
max
− |β| ≥ 0
γ
max
− |γ| ≥ 0
(3)
The computational performance of the numerical op-
timization can be improved by providing a warm start
obtained in the following way. First, we approximate
a plane to the n − 1 points that are the projection of
the points defining the vehicle, on the surface, obtain-
ing an approximation of the pose. Second, we need to
rotate the robot’s points to the approximated pose and
then translate them vertically to the hight where only
one point touches the surface. Usually, this point is
the one above the highest point of the surface below.
As previously mentioned, the constraints determine
that the robot’s absolute pitch (γ) and roll (β) angles
do not reach values greater than γ
max
and β
max
. An-
other limitation is that none of the z coordinates of the
points defining the robot (z
j,I
) can be lower than the
elevation of the map directly below (map
x
j,I
,y
j,I
) thus
z
j,I
− map
x
j,I
,y
j,I
must be greater than 0.
All valid positions are the ones where the robot
touches the ground with three or more of the n points,
depending on the surface roughness. On the other
hand, if the function returns that only two or less
points are touching the surface it means that it is not a
valid position because of the pose limitations intro-
duced as constraints and that same position on the
map is considered an obstacle. After verifying the
pose angles provided by the previous routine, where it
was determined the horizontal deviation of the robot’s
plane, we are finally able to build a cost map.
APhysics-basedOptimizationApproachforPathPlanningonRoughTerrains
261

3.2 Path Planning
3.2.1 Fast Marching Methods
The path planning determines the best path, in the
given conditions, between the position of the robot
and the goal point. Initially, rather than determining
an explicit path, we create a potential field which al-
lows us to draw a path to the goal from any position
on the map, simply by following the negative gradi-
ent of the field. The potential field cannot have local
minima and ensures the optimal path to the goal posi-
tion avoiding obstacles or difficult patches of terrain.
This field is obtained by considering, for each point
x within the free region Ω ⊂ R
2
of the map, the min-
imal time it takes a wave to propagate from the goal
location to the current position. The computation of
this time for each point x in the free region Ω results
in a field u(x). It is well known that the path result-
ing from solving the ODE ˙x = −∇u(x) from an ini-
tial x(0) = x
0
results in the optimal path from x
0
to
the initial wave front. The wave front Γ ⊂ Ω is set
around the goal point. The propagation of a wave,
given an initial wave front Γ ⊂ Ω, can be modelled by
the Eikonal equation
|∇u(x)| = F(x)
u(Γ) = 0
(4)
where x ∈ Ω is the free space of robot position,
Γ ⊂ Ω the initial level set, and F(x) is a cost func-
tion (Sethian, 1996). This cost function allows the
specification, in an anisotropic way, that is, in a di-
rectionally independent way, the speed of the wave
propagation. In particular, for a point x, the wave
propagation speed is
1
F(x)
. This cost allows the result-
ing path to maintain a certain clearance to the mapped
obstacles, since the optimal path tends to keep away
from areas with higher costs i.e. lower propagation
speeds. The equation (4) presented is numerically
solved by the FMM algorithm, introduced by J. A.
Sethian (Sethian, 1996). By giving a discretization
of the map in a grid,the region of free space Ω, the
cost function F(x), and the goal point, we obtain a nu-
merical approximation to the solution of the Eikonal
equation on the grid points. The cost function F(x) is
obtained as described in the previous subsection.
3.2.2 Rapidly-exploring Random Tree
We use the RRT method to compute a path to the goal
at a lower resource expense. A Rapidly-exploring
Random Tree (RRT) is a data structure and algorithm
that is designed for efficiently searching nonconvex
Figure 2: The mobile robot RAPOSA-NG.
high-dimensional spaces. RRTs are constructed in-
crementally in a way that quickly reduces the ex-
pected distance of a randomly-chosen point to the
tree. These trees are particularly suited for path plan-
ning problems that involve obstacles and differential
constraints. Usually, an RRT alone is insufficient to
solve a planning problem. Thus, it can be consid-
ered as a component that can be incorporated into the
development of a variety of different planning algo-
rithms. Using the RRT we do not need to pre-compute
the cost of every cell of the map. Instead, as the
branches or nodes of the tree are randomly created we
calculate the cost for that particular position and store
it for future reference. Furthermore, we can vary the θ
angle of the robot when calculating the cost. For this
particular application of the algorithm we adapted it
in order to, when creating a new position to test, ran-
domly pick a cell of the map and an orientation as
well. Then, we compute the cost (or pose of the robot)
on that position and orientation. If the cost does not
respect our criteria, the node is pruned. If it is admis-
sible the node is connected to the nearest node creat-
ing a new branch, that might be part of the path to the
goal.
4 SIMULATION RESULTS
Following the previously mentioned approach, we
computed the subsequent results for a simulated UGV
which is a raw approximation to the tracked wheel
robot RAPOSA-NG Fig.2 (Ventura, 2014).
The UGV simulated is defined by 6 contact
points with the ground, 3 per each simulated track
(one at its beginning another at the end and one
at the middle point), and one other point that de-
fines its centre of mass as seen in Fig.3. In or-
der to achieve better accuracy one can easily add
more contact points, though this yields a larger com-
putational burden. The task at hand is to com-
pute a path between a start position and a goal ran-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
262

(a) (b)
Figure 3: Representation of the mobile vehicle and its ref-
erence frame. Fig. 3 (a) illustrates the top view of the rep-
resentation of the robot and Fig. 3 (b) shows a perspective
of the representation. In this case an approximation of the
representation of the robot in Fig. 2 is shown.
domly defined using the RAPOSA-NG. This assign-
ment must take into consideration the traversability
of the terrain. To solve the optimization problem we
tested two well known numerical constrained opti-
mization algorithms: Constrained Optimization BY
Linear Approximation and Sequential Least SQuares
Programming. The COBYLA algorithm (Powell,
2007) is based on linear approximations to the objec-
tive function and each constraint, where the derivative
of the objective function is not known. The SLSQP
algorithm (Kraft, 1988) allows us to deal with con-
strained minimization problems by sequentially min-
imizing the quadratic error of the result. It is possible
to require a level of accuracy from both algorithms.
After testing both, the COBYLA and the SLSQP, we
determined the latter is the fastest and more reliable
when limiting the error to the set value. Regarding
the path planning problem itself, the FMM is avail-
able in an extension module (scikit-fmm), from the
python libraries. When creating a path using RRTs
we modified some lines of code written by LaValle
(LaValle, 2006), changing the criteria by which the
nodes are chosen or pruned as explained before.
5 TEST SCENARIOS
The proposed approach was tested /simulated, using
the process explained in section 3, considering three
possible scenarios which presented a variety of fea-
tures that we considered relevant for the purpose mis-
sion of the RAPOSA-NG. The four chosen test sce-
narios, itemized below, intend to verify the robot’s
capabilities to overcome obstacles and hurdles that
could be present on a real life search and rescue
(SAR) scenario:
1. A representation of a mountain, Fig.4, area syn-
thetically generated, the surface is rendered from
a grey scale image that represents an elevation
map. This is a mountain like scenario, exemplary
of the typical scenario were outdoor unmanned
vehicles operate;
2. An image of irregular polygons at different
heights emulating debris, Fig.6. The sharp edges
of the debris like bricks or concrete walls are sim-
ulated as irregular polygonal steps;
3. A RoboCup Robot Rescue arena
1
Fig. 8. This
scenario, although a physical simulation of an ac-
tual SAR environment, is where, typically, these
robots are tested through a series of task fulfil-
ment, and competitions;
4. A valley like scenario where the least effort path
is clearly somewhere between the two mounts.
The maps can be scaled up/down for our convenience,
so that the scale of the robot is not too small. The first
map is 248x248 in a total of 61504 of cells to be pro-
cessed, the second and forth are 491x491 in a total
of 241081 cells and the third has a total of 117572
cells. Processing the entire surface from Fig.4 we ob-
tain the equivalent to a energy potential information
that can be depicted as seen in Fig.5. Fig.4 shows
the surface as it exists, in shape, but it is scaled down
so that the highest peak is not bigger than the robot’s
length. Fig.5 shows the same physical space as the
later but it is already processed to allow path planning
to occur. Notice that, the surface is as if tilted to the
right, this is because the goal was set on the right side
of the map and it is the point with the lowest poten-
tial energy. The represented peaks are softer than the
Fig.4 and possibly not even in the same place because
they do not represent elevation but a higher difficulty
for the autonomous vehicle maintain a stable position
or traverse. The same reasoning applies to the maps
in Fig.6 and 8 and resulting energy potential in Fig.7
and 9 respectfully. The highest peaks seen in Fig.7
are representing obstacles, points in space where the
robot is incapable to travel trough. The cost at those
points is so high (the peaks are scaled down to bet-
ter visualize the results), the path will never include
them. Fig.8 represents a complex environment and
with a variety of obstacles as walls and steps. Tak-
ing the world’s representation as in Fig.5, 7 or 9 the
optimal path to the goal corresponds to the gradient
descent from a given initial position and a path can
be determined from anywhere on the map. From the
representation of the potential we obtain the optimal
path, for the given cost map Fig.10 and Fig.11. The
path represented in Fig.10 was obtained from the rep-
resentation of the world depicted in Fig.5 and Fig.11
from Fig.7. The maps show isochrone lines, which
1
This elevation map is derived from running octomap
in simulation (ROS/Gazebo) over the RoboCup Robot
Rescue arena, http://www.isd.mel.nist.gov/projects/USAR/
arenas.htm. It was obtained by an autonomous robot with
a depth camera and SLAM methods (Kohlbrecher et al.,
2013)
APhysics-basedOptimizationApproachforPathPlanningonRoughTerrains
263
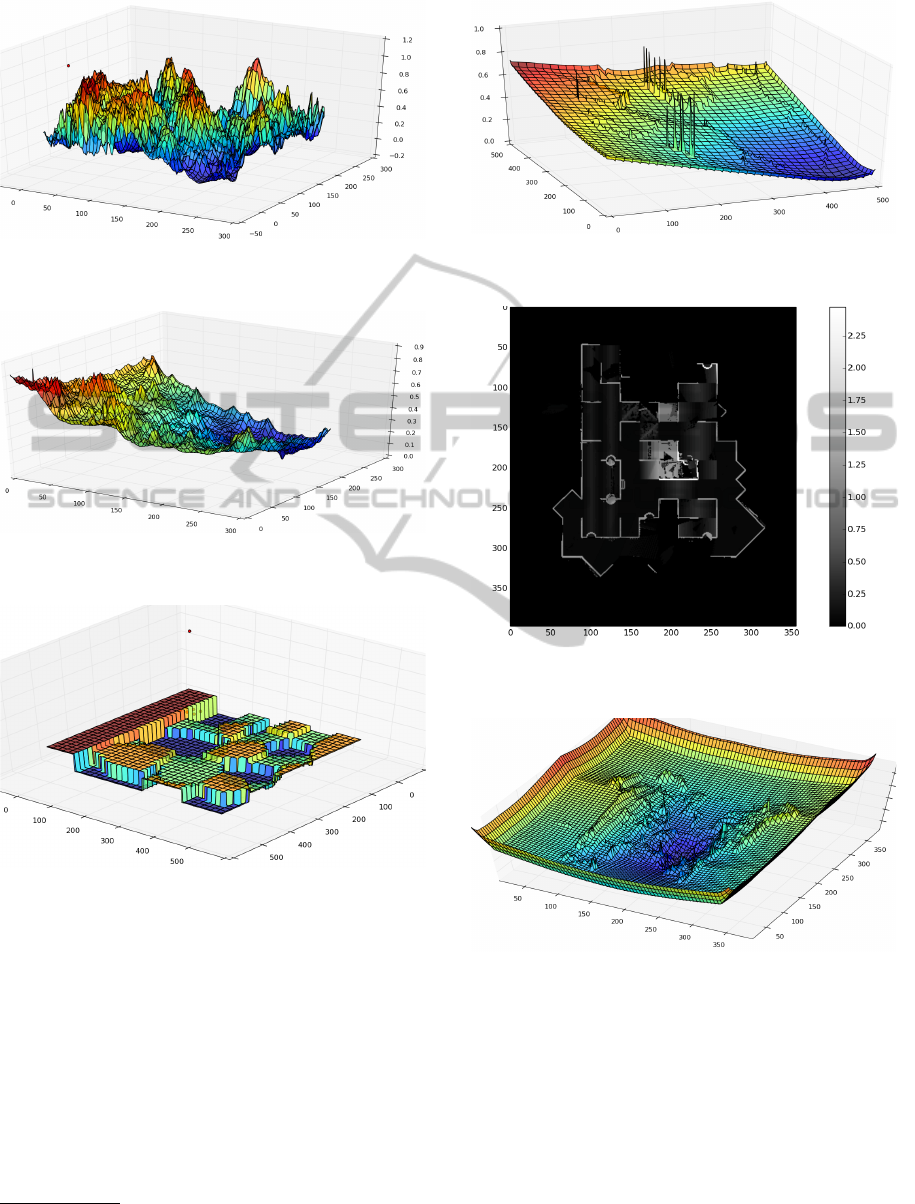
Figure 4: Scenario 1 - Rendering of the grey scale elevation
map.
Figure 5: Scenario 1 - Energy potential representation of
the processed Fig. 4 with the goal set at (220, 215).
Figure 6: Scenario 2 - Rendering of an environment simu-
lating debris, which includes discontinuities.
draw same travel time distances to the goal, that rep-
resent same travel cost to the goal from the lowest
cost in dark blue to the highest in red. The path plan-
ning algorithm chooses the minimal total cost route
based on the gradient of the lines. With this map rep-
resentation we can easily obtain the robot’s orienta-
tion and speed making it theoretically easy to develop
a controller for the vehicle. The map in Fig.4 takes
about ≈ 0.007 seconds/cell to be processed
2
(extract-
ing the world characteristics) but there is still room
for speed improvement as we are still developing con-
2
Intel Core i7-2630QM CPU @ 2.00 GHz personal
computer.
Figure 7: Scenario 2 - Energy potential representation of
the processed Fig. 6 with the goal set at (450, 50).
Figure 8: Scenario 3 - Grey scale image of an elevation map
of a real environment from NIST.
Figure 9: Scenario 3 - Energy potential representation of
the processed Fig. 8 with the goal set at (184,203) which is
the top of a simulated flight of stairs.
cepts. To compute the entire path shown in Fig.10 it
takes ≈ 0.0066 s, which means that after processing
the environment the vehicle can draw its own path in
real time. The other scenario, depicted in Fig.6 is pro-
cessed in ≈ 0.0045 seconds/cell and the computations
of the path planning represented in Fig.11 took a total
of ≈ 0.17 seconds.
The following results are the output of the RRT al-
gorithm we used to create a path. The surface used to
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
264
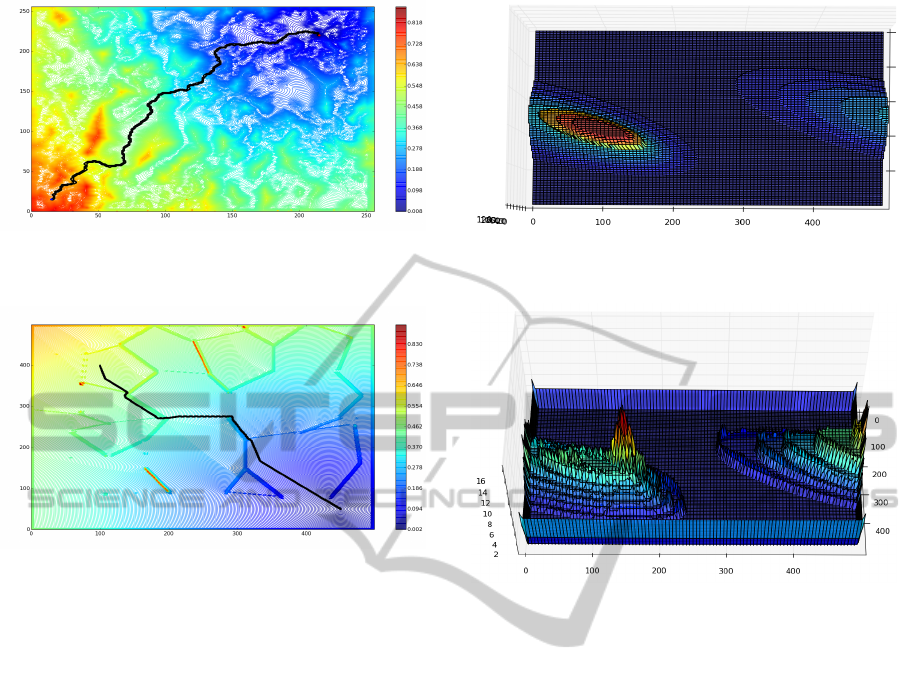
Figure 10: Scenario 1 - Path planning over the representa-
tion of the isochrone lines of the processed surface repre-
sented in Fig. 4.
Figure 11: Scenario 2 - Path planning over the representa-
tion of the isochrone lines of the processed surface repre-
sented in Fig. 6.
run some simulations is shown in Fig. 12 as seen from
above. It has conic shape to it and it is less steep at
the base, it represents a valley where the easiest path
would be to follow the lowland, but, if there is some
tolerance to an inclination, the robot can shorten its
path by climbing part of the mount. If we were to
compute the cost map for the whole surface, the out-
come would be as can be seen in Fig. 13. The result-
ing trees are shown in the Fig 14, for different pruning
thresholds. For a tree with approximately 1000 nodes,
enough to reach the goal, takes about 26 seconds to
grow.
Using the FMM, it seems that the horizontal devi-
ation threshold will not matter, since we will always
obtain the same path, as this method outputs the op-
timal path. The FMM yields a preference of follow-
ing the valley as the weight of the cost of the cell is
higher than the distance to goal, which means it will
only climb the mountain if the cost is of the same or-
der of the distance to the goal. The path is shown in
Fig. 15 and indicates that the path with the lowest
cost is always through the valley and it is not worth
it to climb the mount. The two methods generate dif-
ferent paths although being given the same map as
input and same start and goal points. The paths are
similar in the way that they pass mainly through the
Figure 12: Scenario 4 - Rendering of the grey scale eleva-
tion map.
Figure 13: Scenario 4 - Cost map representation of the pro-
cessed Fig. 12 for a fixed θ.
lowland and do not tend to climb over the mountain
but, as the robot is more tolerant to horizontal devi-
ations the RRT shows path possibilities which imply
climbing the mount. The FMM yields the same path
because the weight given to the travelled distance is
much smaller than the one given to the traversability
cost.
The FMM returns a smoother path because it re-
sults from a solution of a continuous equation (4), on
the other hand RRT output a broken path on the ac-
count of the discrete sample it makes of the terrain.
Also, RRT are much faster as it only analyses between
≈ 1000 and ≈ 2000 grid cells, a mere ≈ 0.4% to 0.8%
of the number of cells analysed to compute a path us-
ing FMM.
6 CONCLUSIONS AND FUTURE
WORK
This paper presents a path planning method for field
robots on a rough terrain. The method is based on
a novel method of determining the traversability, in
the form of a cost map, of the vehicle over the terrain.
This cost map is obtained by solving a constrained op-
APhysics-basedOptimizationApproachforPathPlanningonRoughTerrains
265
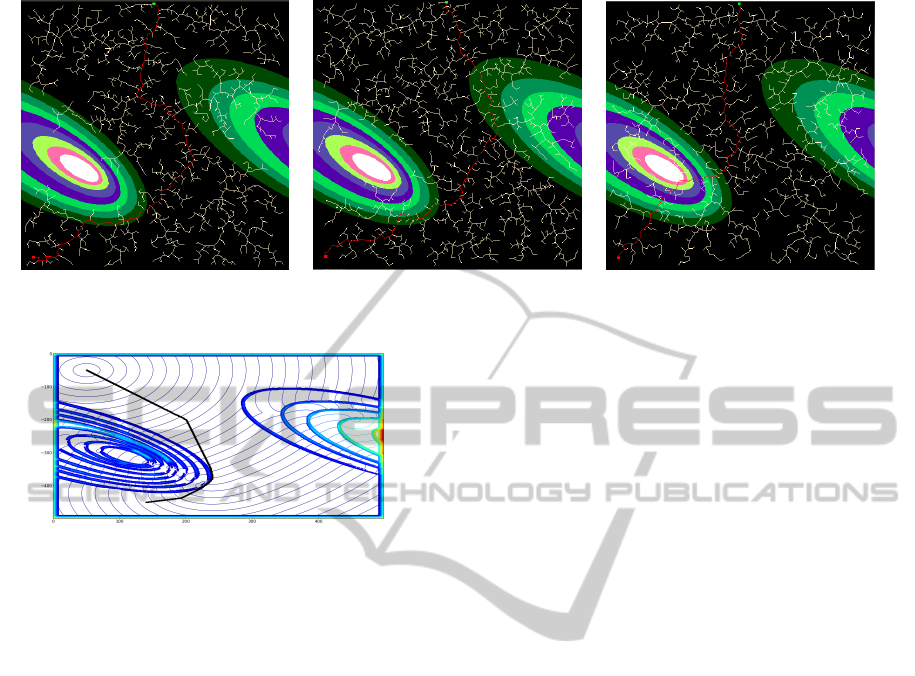
Figure 14: Scenario 4 - From left to right, resulting trees when pruning occurs for horizontal deviations higher than 6, 45, and
100 degrees.
Figure 15: Scenario 4 - Path planning over the representa-
tion of the isochrone lines of the processed surface repre-
sented in Fig. 12.
timization problem, which models the physical pose
of the robot over the terrain by the effect of the grav-
ity. The cost map is then used to compute optimal so-
lutions with standard path planning methods (FMM
and RTT). Simulation results illustrate the use of the
method over synthetic and real terrain data. However,
the main limitation with the current implementation
is the fixed θ (yaw) angle.
ACKNOWLEDGEMENTS
This work was supported by the FCT projects
[UID/EEA/50009/2013] and PT DC/EIA −
CCO/113257/2009.
REFERENCES
Garrido, S., Malfaz, M., and Blanco, D. (2013). Application
of the fast marching method for outdoor motion plan-
ning in robotics. Robotics and Autonomous Systems,
61(2):106–114.
Garrido, S., Moreno, L., Blanco, D., and Martin, F. (2009).
Smooth path planning for non-holonomic robots us-
ing fast marching. In Mechatronics, 2009. ICM 2009.
IEEE International Conference on, pages 1–6.
Kohlbrecher, S., Meyer, J., Graber, T., Petersen, K., von
Stryk, O., and Klingauf, U. (2013). Hector open
source modules for autonomous mapping and naviga-
tion with rescue robots. Proceedings of 17th RoboCup
international symposium.
Kraft, D. (1988). A software package for sequential
quadratic programming. DFVLR Obersfaffeuhofen,
Germany.
LaValle, S. (2006). Planning Algorithms. Cambridge Uni-
versity Press.
Powell, M. (2007). A view of algorithms for optimiza-
tion without derivatives. Mathematics Today-Bulletin
of the Institute of Mathematics and its Applications,
43(5):170–174.
Sethian, J. A. (1996). A fast marching level set method for
monotonically advancing fronts. Proceedings of the
National Academy of Sciences, 93(4):1591–1595.
Sethian, J. A. (1999). Fast marching methods. SIAM Re-
view, 41(2):199–235.
Siciliano, B. and Khatib, O. (2008). Springer Handbook of
Robotics. Springer.
Tarokh, M., Shiller, Z., and Hayati, S. (1999). A compari-
son of two traversability based path planners for plan-
etary rovers. Proc. i-SAIRAS99, pages 151–157.
Ventura, R. (2014). New Trends on Medical and Ser-
vice Robots: Challenges and Solutions, volume 20 of
MMS, chapter Two Faces of Human-robot Interaction:
Field and Service robots, pages 177–192. Springer.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
266
