
Study of Inheritance and Approximation Techniques for Adaptive
Multi-objective Particle Swarm Optimization
Ibtissem Bouoni
1
, Nadia Smairi
2
and Kamel Zidi
3
1
Faculty of Science Gafsa, Gafsa, Tunisia
2
Laboratory of Optimization Strategy and Intelligent Computer, ISG Tunis, Tunis, Tunisia
3
University of Tabuk, Tabuk, Saudi Arabia
Keywords: Multi-objective Optimization, Particle Swarm Optimization, MO-TRIBES, Inheritance Technique,
Approximation Technique, Fitness Evaluation, Time.
Abstract: In this paper, we propose to introduce inheritance and approximation techniques for the evaluation of the
objective function. The main idea of the approaches is to reduce MO-TRIBES complexity. Besides, in our
study, we incorporate at the beginning, an inheritance technique then an approximation technique
(Approximation 1: to consider the whole swarm, Approximation 2: to consider the tribe) at the evaluation of
the objective function. We conducted in our experiments eleven well-known multi-objective test functions.
The results showed a good behavior of our propositions on most tested functions. Moreover, TRIBES-
inheritance provided the best compared to MO-TRIBES, we concluded that MO-TRIBES with inheritance
give the best time than MO-TRIBES and MO-TRIBES with approximation. It also kept the same
performances with MO-TRIBES with a simple improvement for several functions.
1 INTRODUCTION
One of the problems of evolutionary algorithms is
that each one of them requires setting several control
parameters depending on the problem considered,
MO-TRIBES, an adaptive Particle Swarm
Optimization (PSO) technique, has the advantage
to be considered as a black box; the specialist
defines only the search space. The adaptability of
MO-TRIBES shows an increase in complexity
especially compared to a conventional MOPSO
algorithm.
We propose in this paper to minimize MO-
TRIBES complexity while keeping its performance.
In fact, the evaluation of the objective function is
often complicated especially in the multiobjective
case. We propose to introduce inheritance and
approximation techniques for the evaluation of the
objective function in order to reduce MO-TRIBES
complexity.
In section 2 of this paper, we introduce the
existing inheritance and approximation techniques.
In section 3, we define and discuss the state of art of
MO-TRIBES. In section 4, we present our proposed
approach and we use eleven well-known multi-
objective test functions in order to find the best one
from the proposed techniques. Then comparative
results are described in section 5, from which
conclusions are drawn in section 6.
2 STATE OF ART
2.1 Fitness Inheritance
Smith is the first who used Fitness Inheritance
technique to improve the Genetic algorithm
performance (Smith, Dike and Stegmann, 1995).
Authors proposed two probable ways of fitness
inheritance. The first consists in taking the average
fitness of the two parents while the second consists
of taking a weighted average of the fitness of the
two parents.
Sierra and Coello in (2005) proposed an
integration of inheritance techniques in a real code
multi-objective PSO (MOPSO). They concluded that
fitness inheritance reduces the cost without
decreasing the performance.
The purpose of this paper (Montes, Dávila and
Coello, 2007) is to find a trade-off between a lower
number of evaluations of each solution and a good
performance of the approach. A set of test problems
146
Bouoni I., Smairi N. and Zidi K..
Study of Inheritance and Approximation Techniques for Adaptive Multi-objective Particle Swarm Optimization.
DOI: 10.5220/0005529901460154
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 146-154
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
taken from the specialized literature was used to test
the capabilities of the proposed approach to save
evaluations and to preserve a competitive
performance.
This chapter (Becerra, Quintero and Coello,
2008), presents a review of techniques used to
integrate knowledge into evolutionary algorithms,
with particular emphasis on multi-objective
optimization.
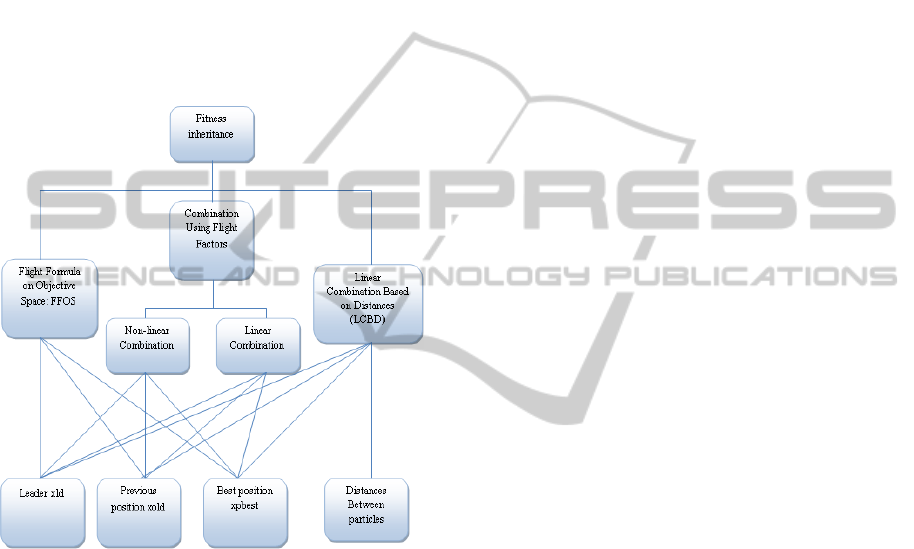
There are several techniques of inheritance that
we can divide into three broad families. For each
particle, we can apply different types of techniques
such as the inheritance shown in the following
figure:
Figure 1: Fitness Inheritance.
2.2 Fitness Approximation
Ratle presented a new approach based on a real code
genetic algorithm to accelerate convergence of
evolutionary optimization methods (Ratle, 1998).
In paper of (Jin, 2005), a comprehensive review
of the research on fitness approximation in
evolutionary calculation is presented. Main
problems like approximation levels, approximate
model management schemes, model construction
techniques are reviewed.
Lim presented (Lim, Jin, Ong, Bernhard and
Sendhoff, 2006) a Trusted Evolutionary Algorithm
TEA for solving optimization problems with
computationally expensive fitness functions. The
TEA is designed to maintain good worthiness of the
substitute models in predicting fitness improvements
or controlling approximation errors throughout the
evolutionary search.
(Bhattacharya, 2013) discusses some of the
key issues concerned with use of approximation
in evolutionary algorithm, possible best practices
and solutions.
3 MO-TRIBES
TRIBES is an adaptive Particle Swarm Optimization
(PSO) algorithm developed by Clerc (2006). This
algorithm is sufficient to delimit the space of
research and indicate how to evaluate the objective
function. Actually, it is enough to specify the
problem to be solved. This algorithm must
incorporate rules that define how, the structure of the
swarm must be modified and how a particle data
must behave while integrating information.
Multi-objective TRIBES was elaborated in the
beginning by Cooren (2008) and later by Smairi,
Bouamama, Ghedira and Siarry(2010). We consider
in the continuation the Smairi aproach. In fact, this
version takes the main mechanisms of TRIBES to
which are added to treat multi-objective problems.
In MO-TRIBES the swarm is divided into several
under-swarms (tribes), of different size and evolves
during the time. Every tribe is composed of a
variable number of particles.
At the beginning, we start with one particle
forming a tribe. After the first iteration a second
particle is generated, which will, in turn, form a new
tribe. In the next iteration, if the situation of both
particles does not improve, every tribe creates two
new particles: We form a new tribe containing four
particles. However, if we are close to an optimal
solution, the process is reversed and we begin to
eliminate particles, even tribes (only the good tribes
are capable of eliminating their worst elements).
4 OUR APPROACHES
The adaptability of MO-TRIBES shows an increase
in complexity especially compared to a conventional
MOPSO algorithm. Since the evaluation of the
objective function is often complex especially in
multi-objective case. We will propose, in this paper,
to incorporate inheritance and approximation
techniques for the objective function evaluation in
order to decrease MO-TRIBES complexity. In their
previous work, Sierra and Coello (Sierra and Coello,
2005) proposed to incorporate this technique into a
MOPSO.
StudyofInheritanceandApproximationTechniquesforAdaptiveMulti-objectiveParticleSwarmOptimization
147

4.1 Fitness Inheritance
From the previous work of Sierra and Coello, we
can conclude that the best inheritance technique is
Linear Combination Based on Distances (LCBD)
which gives better results and, at the same time, is
adaptable to MO-TRIBES. In fact, LBCD does not
consider the concept of speed that does not appear in
Mo-Tribes. In fact, this technique is not the best but
among the best ones that we have chosen because it
perfectly fits Mo-Tribes.
We have specifically chosen this technique that
takes into consideration the Euclidean distance d,
pbest which denotes its best position and the leader.
In this paper, we propose to simplify the calculation
of the objective function and minimize the time of
execution. We are going to integrate the technique
chosen inheritance while basing our work on:
1. The leader xld,
2. The old position of particle xold,
3. The best position xpbest,
4. The new particle xnew,
Here is the algorithm of MO-TRIBES after
modification:
Archive initialization
Swarm initialization
For each particle i, Determination of
the state of the particle
Évaluate Objectif function
Insert leader in archives
While criterion is not verified
Choice of the strategy of movement
Update of the position
While p
i
isn’t a leader,
For p% of particles applies
inheritance
i pbesti gbesti
1i 2 3
f(t) rf(t 1) rf rf
End For
End While
Update the archive
If n<NL
Determination of the quality of
the tribe
Adaptation of the swarm
Update archive Size
Calculate NL
End If
End While
Figure 2: Algorithm Mo-Tribes with Inheritance.
With:
r
1
=
1
123
d
;
ddd
(1)
r
2
=
2
123
d
;
ddd
(2)
r
3
=
3
123
d
;
ddd
(3)
And d1 =distance (xnew; xold); d2 =distance (xnew;
xpbest); d3 =distance (xnew; xld)
4.2 Fitness Approximation
A promising possibility when an evaluation is very
time-consuming or expensive is not to evaluate
every individual, but just estimate the quality of
some of the individuals based on an approximate
model of the fitness landscape.
Archive initialization
Swarm initialization
F
or each particle i, Determination of
the state of the particle
Évaluate Objectif function
Insert leader in archives
While criterion is not verified
Choice of the strategy of movement
Update of the position
While p
i
isn’t a leader,
F
or p% of particles applies
approximation
d(X
j
, X
k
) = min d(X
j
, X
i=1..n
)
jk
f (t) f (t)
j=j+1
End For
End While
Update the archive
If n<NL
D
etermination of the quality
of the tribe
Adaptation of the swarm
Update archive Size
Calculate NL
End If
End While
Figure 3: Algorithm Mo-Tribes with Approximation.
Approximations techniques approximate
individual fitness on the basis of the previously
observed objective function values of neighboring
individuals. There are many possible approximation
models. In this approach we propose the technique
in which the particle will take the objective value of
the nearest particle without considering the leader of
the swarm. Therefore, it is necessary to calculate the
distance between each particle and the other particle
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
148

members of the swarm, supposing that d is the
Euclidean distance between two particles. We will
test two versions of approximation:
- To take into consideration the totality of the
swarm in the calculation of distance.
- To take into consideration each tribe like a
separated swarm.
5 EXPERIMENTATIONS AND
RESULTS
5.1 Test Functions
In order to compare the proposed techniques, we
perform a study using eleven well-known test
functions taken from the specialized literature on
evolutionary algorithms (see table 6). These
functions present diverse difficulties such as
convexity, concavity, multimodality…etc.
Moreover, we fix the maximal number of
evaluations in the experimentations to 5e+4.
To study the fitness inheritance and
approximation, at each iteration, we vary the number
of particles on which we apply the inheritance and
approximation (p%): 20%, 40%, 60% and 80%,
knowing that these particles are not leaders. The
purpose is to see the effects of variation of particle
number inherited or approximated on convergence,
diversity and time.
It should be noted that these particles are not
introduced in the archive because their goals are
fictitious values (not actual values).
5.2 Metrics of Comparison
For assessing the performance of the algorithms,
there are many existent indicators measuring quality,
diversity and convergence. We choose the
combination of two binary indicators that was
proposed in (Knowles,Thiele and Zitler, 2006): R
indicator and hypervolume indicator. And time (The
unit time measurement used is the second) is used as
the metric of comparison to study the time variation.
5.3 Results
For both indicators, we present the summary of the
results obtained. In each case, we present the mean
of R indicator (table 4), hypervolume (table 3) and
time (table 2 and 5) measures over 20 independent
runs, the best results are shown in bold in the tables.
We observe that:
- MO-TRIBES with Inheritance generally give
better result than MO-TRIBES and MO-
TRIBES with approximation.
- For S-ZDT2 and S-ZDT4, MO-TRIBES have
the best values of the hypervolume and R-
indicator.
- Moreover for the rest of functions MO-
TRIBES with Inheritance has the better found
front.
- For the ZDT family, except S-ZDT1, WFG
family, R-DTLZ2 and SYMPART have the
best time obtained by MO-TRIBES with
Inheritance especially for percentages 40%
and 60% of inherited particle.
- For S-ZDT1, S-DTLZ2 and R-ZDT4 the best
time obtained with 20% to particles
inheritance.
In addition, we conclude that TRIBES-
Inheritance is very competitive as it supports both
convergence and diversity. In fact, it gives the best
time in comparison with MO-TRIBES and the two
types of approximation (We don’t show the result of
hypervolume and R indicator for approximation
because we conclude that the approximation does
not improve the time).
For 11 test functions we conclude that the
improvement is clear in terms of time, indicator R
and hypervolume especially for 40% and 60% of
inherited particles, the following table shows the
number of functions improved compared to MO-
TRIBES (see table 1).
We can conclude that this improvement results in
the guidance of the particle during inheritance.
However, approximation increases complexity
because of the calculation of the distance between
each current particle and the other particles of
swarm (or the distance between each current particle
and the other particles of swarm tribe of
approximation 2).
The approximation can be complex compared to
the actual calculation of the objective function,
especially when the size of the search space (ie when
the number of decision variables is limited the real
calculation of objective fitness is less complex than
approximation) is quite small and the number of
objectives too.
Table 1: The number of functions improved compared to
MO-TRIBES.
Nb of inherited particles H R Time
40% 6 6 8
60% 7 7 7
StudyofInheritanceandApproximationTechniquesforAdaptiveMulti-objectiveParticleSwarmOptimization
149

Table 2: Results for the time (Mo-Tribes with Inheritance).
Test functions
MO-TRIBES with Inheritance
MO-
TRIBES
20% 40% 60% 80%
S-ZDT1
Best 70,95 67,66 38,16 73,3 77,6
Mean 78,02 75,5
67,14
83,91 81,92
Worst 87,05 83,87 81,8 90,48 85,93
S-ZDT2
Best 8,68 9,09 10,76 11,47 40,59
Mean 16,34
14,16
15,35 16,86 51,71
Worst 28,2 21,62 25,32 21,61 63,63
S-ZDT4
Best 30,6 30,79 51,7 42,77 47,13
Mean 44,78
43,55
58,24 54,94 58,22
Worst 52,32 48,66 67,23 66,3 69,43
S-ZDT6
Best 20,74 13,59 32,68 32,24 26,18
Mean 25,69
18,62
35,08 39,12 30,23
Worst 28,34 23,32 36,99 47 36,52
DTLZ2
Best 215,32 212,07 211 220,07 210,35
Mean
218,8
224,99 223,19 228,21 219,11
Worst 225,57 232,27 230,67 240,11 224,44
R-DTLZ2
Best 43 48,72 47,81 17,2 33,41
Mean 50,13 54,76 51,52
20,98
38,78
Worst 58,34 64,73 54,34 28,69 44,84
R-ZDT4
Best 40,58 46,29 46,29 64,13 66,72
Mean
51,9
58,35 56,95 66,93 72,3
Worst 62,59 67,62 67,62 73,07 78,13
SYMPART
Best 74,25 72,25 70,83 51,83 85,73
Mean 81,29 79,79 79,22
71,39
88,91
Worst 85,87 85,86 88,37 86,55 93,08
OKA2
Best 92,07 94 94,73 96,57 89,86
Mean 95,92 96,96 102,3 101,38
95,11
Worst 99,15 100,5 119,16 105,72 100,83
WFG8
Best 7,29 11,3 10,48 14,69 22,12
Mean
11,24
12,6 14,406 16,26 31,23
Worst 16,37 14,62 16,51 17,61 47,86
WFG9
Best 144,89 137,1 167,77 152,33 168,66
Mean 170,15
159,41
180,15 174,68 181,28
Worst 191,25 187,5 204,58 205,13 189,39
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
150

Table 3: Result for Hypervolume(Mo-Tribes with Inheritance).
Test functions
MO-TRIBES with Inheritance
MO-
TRIBES
20% 40% 60% 80%
S-ZDT1
Best
6.65e-3 6.36e-3 6.29e-3 5.51e-3 2.28e-2
Mean
1.19e-2 1.75e-2 1.57e-2
1.03e-2
2.97e-2
Worst
2.66e-2 2.80e-2 5.75e-2 2.36e-2 4.01e-2
S-ZDT2
Best
2.16e-3 5.24e-3 1.19e-3 2.25e-3 4.36e-3
Mean
2.57e-2 2.98e-2 3.05e-2 3.13e-2
2.19e-2
Worst
5.59e-2 5.84e-2 5.21e-2 5.40e-2 4.86e-2
S-ZDT4
Best
3.07e-2 3.61e-2 2.19e-2 3.27e-2 1.86e-2
Mean
6.47e-2 5.49e-2 4.81e-2 4.94e-2
3.18e-2
Worst
9.70e-2 8.71e-2 6.31e-2 6.06e-2 3.96e-2
S-ZDT6
Best
5.81e-2 5.29e-2 3.16e-2 2.86e-2 3.65e-2
Mean
8.20e-2 8.71e-2
4.80e-2
6.03e-2 7.94e-2
Worst
1.09e-1 1.17e-1 7.95e-2 1.781e-1 1.79e-1
S-DTLZ2
Best
1.64e-4 3.75e-4 1.08e-4 2.58e-4 5.56e-4
Mean
7.63e-4
1.10e-3 1.11e-3 9.39e-4 1.49e-3
Worst
1.61e-3 2.50e-3 1.79e-3 1.01e-3 3.22e-3
R-DTLZ2
Best
2.15e-2 1.99e-2 2.03e-2 1.95e-2 2.10e-2
Mean
2.65e-2 2.55e-2 2.55e-2
2.34e-2
2.85e-2
Worst
3.76e-2 3.17e-2 3.02e-2 2.84e-2 4.20e-2
R-ZDT4
Best
4.81e-3 2.93e-2 1.62e-2 2.65e-2 2.50e-2
Mean
6.21e-3 3.12e-2
2.08e-2
3.87e-2 2.96e-2
Worst
8.23e-3 3.42e-2 2.58e-2 4.75e-2 3.29e-2
SYMPART
Best
-3.96e-4 -4.77e-4 3.77e-4 3.44e-4 3.25e-4
Mean
1.07e-4
-4.33e-4
5.32e-4 5.65e-4 5.59e-4
Worst
5.29e-4 -2.89e-4 6.90e-4 7.76e-4 7.02e-4
OKA2
Best
-8.47e-4 -1.23e-3 -1.23e-3 -1.23e-3 2.94e-5
Mean
-8.08e-4 -1.18e-3 -1.21e-3
-1.23e-3
2.0e-3
Worst
1.81e-3 -8.75e-4 -1.19e-3 -1.20e-3 1.11e-2
WFG8
Best
-1.89e-1 -1.96e-1 -1.89e-1 -2.03e-1 -1.93e-1
Mean
-1.86e-1 -1.89e-1 -1.88e-1
-1.94e-1
-1.90e-1
Worst
-1.82e-1 -1.86e-1 -1.87e-1 -1.85e-1 -1.84e-1
WFG9
Best
-1.45e-1 -1.44e-1 -1.46e-1 -1.41e-1 -1.46e-1
Mean
-1.42e-1 -1.41e-1
-1.44e-1
-1.40e-1 -1.44e-1
Worst
-1.42e-1 -1.35e-1 -1.40e-1 -1.38e-1 -1.41e-1
StudyofInheritanceandApproximationTechniquesforAdaptiveMulti-objectiveParticleSwarmOptimization
151

Table 4: Result for R-Indicator (Mo-Tribes with Inheritance).
Test functions
MO-TRIBES with Inheritance
MO-
TRIBES
20% 40% 60% 80%
S-ZDT1
Best
1.68e-3 2.08e-3 1.63e-2 1.47e-3 2.22e-2
Mean
3.08e-3 4.59e-3 4.13e-3
2.59e-3
7.77e-3
Worst
7.18e-3 8.66e-3 8.88e-3 6.42e-3 4.016e-2
S-ZDT2
Best
8.45e-4 2.45e-3 4.27e-4 8.17e-4 4.36e-3
Mean
1.89e-2 2.25e-2 2.47e-2 3.07e-2
1.52e-2
Worst
4.27e-2 4.35e-2 4.14e-2 4.21e-2 4.86e-2
S-ZDT4
Best
1.06e-2 1.24-2 7.55e-3 1.13e-2 1.86e-2
Mean
2.20e-2 1.87e-2
1.65e-2
1.69e-2 9.91e-2
Worst
3.28e-2 2.95e-2 2.15e-2 2.07e-2 3.96e-2
S-ZDT6
Best
2.55e-2 2.49e-2 1.42e-2 1.28e-2 3.65e-2
Mean
3.58e-2 3.84e-2
2.19e-2
2.63e-2 3.47e-2
Worst
4.73e-2 5.36e-2 3.63e-2 3.85e-2 1.79e-1
S-DTLZ2
Best
2.84e-5 7.43e-5 8.39e-5 6.63e-5 3.59e-4
Mean
1.55e-4
1.61e-4 2.11e-4 1.85e-4 2.20e-4
Worst
2.63e-4 2.32e-4 3.32e-4 2.78e-4 1.04e-4
R-DTLZ2
Best
3.56e-4 3.12e-4 3.54e-4 3.20e-4 3.82e-4
Mean
6.69e-4 4.23e-4 4.52e-4
3.79e-4
6.64e-4
Worst
2.46e-3 4.98e-4 5.97e-4 4.58e-4 2.44e-3
R-ZDT4
Best
2.40e-3 9.88e-3 5.41e-3 7.04e-3 2.50e-2
Mean
1.93e-3 1.05e-2
6.94e-3
1.29e-2 9.96e-3
Worst
2.60e-3 1.15e-2 8.66e-3 1.58e-2 3.29e-2
SYMPART
Best
8.46e-5 9.83e-5 1.27e-4 1.16e-4 1.1e-4
Mean
1.29e-4
1.47e-4 1.81e-4 1.92e-4 1.90e-4
Worst
1.8e-4 1.64e-4 2.35e-4 2.64e-4 2.38e-4
OKA2
Best
-1.06e-3 -1.06e-3 -1.06e-3 -1.06e-3 -1.06e-3
Mean
-1.06e-3
-1.05e-3 -1.05e-3 -1.05e-3
4.88e-4
Worst
-1.03e-3 -1.02e-3 -1.03e-3 -1.03e-3 6.70e-3
WFG8
Best
-2.33e-2 -2.46e-2 -2.32e-2 -2.58e-2 -2.41e-2
Mean
-2.28e-2 -2.33e-2 -2.31e-2
-2.41e-2
-2.35e-2
Worst
-2.21e-2 -2.27e-2 -2.31e-2 -2.27e-2 -2.24e-2
WFG9
Best
-1.88e-2 -1.88e-2 -1.91e-2 -1.83e-2 -1.92e-2
Mean
-1.86e-2 -1.83e-2
-1.89e-2
-1.82e-2 -1.88e-2
Worst
-1.85e-2 -1.73e-2 -1.81e-2 -1.78e-2 -1.84e-2
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
152

Table 5: Result for the Time (MO-TRIBES with Approximation 1 and Approximation 2).
Test functions
MO-TRIBES with Approximation 1 MO-TRIBES with Approximation 2
Mo-
TRIBES
20% 40% 60% 80% 20% 40% 60% 80%
S-ZDT1
Best
95,57 116,27 131,27 162,16 88.66 96.37 97.26 125.91 77,6
Mean
103,45 124,41 137,05 174,78 102,8 107,21 106,57 133,23
81,92
Worst
108,26 130,25 145,5 182,34 115.94 118.7 115.82 147.58 85,93
S-ZDT2
Best
43,22 56,95 73,51 109,84 70.5 51.68 70.32 100.08 40,59
Mean
48,73
60,74 82,38 125,32 83,41 64,19 76,04 131,59 51,71
Worst
58,25 68,94 91,34 148,61 94.88 84.22 90.08 149.25 63,63
S-ZDT4
Best
45,77 55,52 73,23 110,32 41.95 52.79 75.08 100.63 47,13
Mean
59 58,39 83,13 123,76
52,54
65,5 81,89 117,84 58,22
Worst
64,87 63,36 97,44 133,6 67.33 78.91 91.97 133.5 69,43
S-ZDT6
Best
44,95 56,91 76,05 103,37 44.77 56.47 73.34 94 26,18
Mean
53,01 61,68 80,45 114,45 51,68 59,4 78,6 104,5
30,23
Worst
58,83 66,3 83,44 121,13 56.5 62.52 87.33 109.45 36,52
R-ZDT4
Best
52,68 84,34 80,91 110,98 85.44 53.57 67.3 98.41 66,72
Mean
76,94 101,01 89,14 133,56 90,34
61,76
71,46 76,415 72,7
Worst
89,16 114,26 93,16 159,24 95.86 79.63 74.16 107.37 78,13
OKA2
Best
105,37 123,15 134,8 155,24 107.58 122.25 122.34 146.19 89,86
Mean
112,63 127,13 138,8 163,2 117,61 129,44 130,26 156,21
95,11
Worst
120,26 135,63 142,88 169,72 126.8 134.41 139.1 159.88 100,83
Sympart
Best
95,57 91,08 96,15 106,93 83.37 103.29 89.62 133.44 85,73
Mean
103,45 100,98 108,03 113,01 92,75 115,43 104,11 147,56
88,91
Worst
109,68 109,91 121,73 117,44 103.69 125.55 115.83 155.74 93,08
WFG8
Best
44,79 51,15 69,73 96,54 39.54 48.2 62.84 91.88 22,12
Mean
54,59 66,63 86,4 113,08 41,93 52,06 66,13 96,84
31,23
Worst
65,33 79,36 97,07 119,96 43.97 53.36 72.04 107.65 47,86
WFG9
Best
146,02 130,5 105,48 111,96 231.27 241.14 241.82 266.41 168,66
Mean
171,19 143,19
135,09
146,73 240,84 249,82 255,47 281,92 181,28
Worst
196,71 161,47 168,97 165,24 247.89 258.33 263 302.85 189,39
S-DTLZ2
Best
236,39 232,85 253,63 269,73 227.72 236.24 256.27 279.44 210,35
Mean
244,71 244,36 267,85 279,79 240,05 248,02 266,59 290,35
219,11
Worst
253,61 252,36 279,72 291,76 249.57 257.39 281.17 299.66 224,44
R-DTLZ2
Best
79,33 100,77 91,2 121,5 44.38 110.77 96.9 112.87 33,41
Mean
90 113,23 100,43 127,83 48,01 129,46 106,57 129,57
40,83
Worst
99,44 128,28 115,54 142,94 51.86 137.46 119.08 145.97 53,88
StudyofInheritanceandApproximationTechniquesforAdaptiveMulti-objectiveParticleSwarmOptimization
153

Table 6: Proprieties of the test functions.
Test
functions
number of
objective
function
Number of
parameter
Geometry
OKA2 2
3 Concave
SYMPART 2
30 Concave
S_ZDT1 2 30 Convex
S_ZDT2 2 30 Concave
S_ZDT4 2 30 Convex
R_ZDT4 2 10 Concave
S_ZDT6 2 30 Concave
S_DTLZ2 3 30 Concave
R_DTLZ2 3 30 Concave
WFG8 3 24 Concave
WFG9 3 24 Concave
Noting that the archive size for 2 objective functions
is 100, moreover 150 for 3 objective functions.
6 CONCLUSIONS
We have incorporated a fitness inheritance and
approximation techniques into MO-TRIBES
proposed previously by the authors. We studied the
proposed approaches using several well-known
multi-objective test functions.
We concluded that fitness inheritance give the
best time than MO-TRIBES and MO-TRIBES with
approximation. It also kept the same performances
with MO-TRIBES with a simple improvement for
several functions. As part of our ongoing work, we
are going to study another inheritance technique and
we try to improve time and performance in the same
code, indeed we can propose to test other functions
having a larger number of objectives to study the
effect of the size of the search space for uses these
techniques.
REFERENCES
Becerra, R, L., Quintero, L., V., S., Coello, C., A., C.,
2008. Knowledge Incorporation in Multi-objective
Evolutionary Algorithms, Multi-Objective
Evolutionary Algorithms for Knowledge Discovery
from Databases Studies in Computational
Intelligence, Volume 98, 23-46.
Bhattacharya, M., 2013. Evolutionary Approaches to
Expensive Optimisation. IJARAI International Journal
of Advanced Research in Artificial Intelligence,
Volume 2, No 3.
Clerc, M., 2006. Particle Swarm Optimization.
International Scientific and Technical Encyclopedia,
John Wiley & sons.
Cooren, Y., 2008. Perfectionnement d’un algorithme
adaptatif d’optimisation par essaim particulaire.
Applications en génie médicale et en électronique.
PhD thesis, Université Paris 12.
Jin, Y., 2005. A Comprehensive Survey of Fitness
Approximation in Evolutionary Computation, Soft
Computing-A Fusion of Foundations, Methodologies
and Applications, Volume 9, No 1, 3-12.
Knowles, J., Thiele, L., Zitler, L., 2006. A tutorial on the
Performance Assessement of Stochastic Multi-
objective Optimizers. Computer Engineering and
Networks Laboratory, ETH Zurich, Switzerland.
Lim, D., Ong, Y, S., Jin, Y., Bernhard, Sendhoff., 2006.
Trusted Evolutionary Algorithm. Congress on
Evolutionary Computation CEC’2006, Vancouver,
Canada, IEEE Service Center.
Montes, E,M., Dávila, L,M., Coello, C,A,C., 2007., A
Preliminary Study of Fitness Inheritance in
Evolutionary Constrained Optimization, Nature
Inspired Cooperative Strategies for Optimization
(NICSO 2007) Studies in Computational Intelligence,
Volume 129, 2008, 1-14.
Ratle, A., 1998. Accelerating the convergence of
Evolutionary Algorithms by Fitness Landscape
Approximation. International Conference on Parallel
Problem Solving from Nature (PPSN V), LNCS 3242,
786-793, Morgan Kaufmann Publishers.
Sierra, M, R., Coello, C., A., C., 2005. Fitness Inheritance
in Multi-Objective Particle Swarm Optimization. In
IEEE Swarm Intelligence Symposium, Pasadena,
California, USA, IEEE Service Center, 116-123.
Smairi, N., Bouamama, S., Ghedira,K., Siarry, P., 2010. A
new proposal for a multi-objective technique using
tribes and tabu search. ICINCO, Portugal, 86-91.
Smith, R, E., Dike, B, A., Stegmann, S, A., 1995. Fitness
Inheritance in Genetic Algorithms, In SAC ’95, 345-
350. ACM Press.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
154
