
Pitfalls When Solving Eigenproblems
With Applications in Control Engineering
Vasile Sima
1
and Peter Benner
2
1
National Institute for Research & Development in Informatics, Bd. Mares¸al Averescu, Nr. 8–10, Bucharest, Romania
2
Max Planck Institute for Dynamics of Complex Technical Systems, Sandtorstraße 1, 39106, Magdeburg, Germany
Keywords:
Deflating Subspaces, Eigenvalue Reordering, Generalized Eigenvalues, Generalized Schur Form, Numerical
Methods, Skew-Hamiltonian/Hamiltonian Matrix Pencil, Software, Structure-preservation.
Abstract:
There is a continuous research effort worldwide to improve the reliability, efficiency, and accuracy of numeri-
cal computations in various domains. One of the most promising research avenues is to exploit the structural
properties of the mathematical problems to be solved. This paper investigates some numerical algorithms for
the solution of common and structured eigenproblems, which have many applications in automatic control
(e.g., linear-quadratic optimization and H
∞
-optimization), but also in various areas of applied mathematics,
physics, and computational chemistry. Of much interest is to find the eigenvalues and certain deflating sub-
spaces, mainly those associated to the stable eigenvalues. Several simple examples are used to highlight the
pitfalls which may appear in such numerical computations, using state-of-the-art solvers. Balancing the ma-
trices and the use of condition numbers for eigenvalues are shown to be essential options in investigating the
behavior of the solvers and problem sensitivity.
1 INTRODUCTION
Many control system analysis and design numeri-
cal techniques and procedures require the compu-
tation of eigenvalues and bases of certain invari-
ant or deflating subspaces. Often, the correspond-
ing eigenproblems have special structure, which im-
plies structural properties of their spectra. Com-
mon structures are Hamiltonian and symplectic ma-
trices or matrix pencils. One relevant computational
problem in control theory and its applications is the
evaluation of the H
∞
- and L
∞
-norms of linear dy-
namic systems, which are used, e.g., to quantify the
trade-off between performance and robust stability.
State-of-the-art quadratically convergent algorithms
for the calculation of these norms use the purely
imaginary eigenvalues of a matrix or matrix pencil
at each iteration. This matrix (pencil) is Hamilto-
nian or symplectic, in the continuous- and discrete-
time case, respectively. (Actually, the pencils arising
in the continuous-time descriptor case can be put in
a skew-Hamiltonian/Hamiltonian form (Benner et al.,
2012a).) Another fundamental computation in con-
trol systems analysis and design is the solution of
continuous-time and discrete-time algebraic Riccati
equations (CAREs and DAREs). CAREs and DAREs
arise in many applications, such as factorization tech-
niques for transfer functions matrices, model reduc-
tion procedures based on stochastic bounded- or pos-
itive real balancing, stabilization and linear-quadratic
regulator problems, Kalman filtering, linear-quadratic
Gaussian (H
2
-)optimal control problems, computa-
tion of (sub)optimal H
∞
controllers, etc. Usually, the
stabilizing solution is required, which can be used
to stabilize the closed-loop system matrix or matrix
pencil. State-of-the-art CARE/DARE solvers (Laub,
1979; Mehrmann, 1991; Sima, 1996; Benner, 1999;
MathWorks, 2014) rely on computing stable invariant
or deflating subspaces of some Hamiltonian or sym-
plectic matrices or pencils. Finding such subspaces
involves eigenvalue reordering.
Recently, structure-exploiting techniques have
been investigated for solving (skew-)Hamiltonian and
skew-Hamiltonian/Hamiltonian eigenproblems, see,
e.g., (Benner et al., 2002; Benner and Kressner, 2006;
Benner et al., 2007), and the references therein. These
algorithms are more involved than those used in the
non-structured case. The initial reduction step is more
complicated, since the structure should be exploited.
Moreover, the standard QR or QZ algorithm (Golub
and Van Loan, 1996) for matrices or pencils is re-
placed by the periodic QR/QZ algorithm, see (Bo-
171
Sima V. and Benner P..
Pitfalls When Solving Eigenproblems - With Applications in Control Engineering.
DOI: 10.5220/0005533301710178
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 171-178
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

janczyk et al., 1992; Granat et al., 2007) and the refer-
ences inside. The periodic QR/QZ algorithm operates
on formal matrix products Π
p
i=1
A
s
i
i
, where s
i
= 1 or
s
i
= −1, with possibly singular factors in the pencil
case. The number of factors p to process (the “pe-
riod”) is two, four or six (Benner et al., 2002; Ben-
ner and Kressner, 2006; Benner et al., 2007). Eigen-
value reordering is also performed on these formal
matrix products. The main difference to the standard
reordering procedures implemented in the LAPACK
package (Anderson et al., 1999) is in the algorithm for
swapping two adjacent sequences of diagonal blocks,
involving the solution of periodic Sylvester-like equa-
tions. Details are given, e.g., in (Granat et al., 2007;
Sima, 2010) and the references therein.
Advanced structure-exploiting solvers have
been incorporated in the SLICOT Library
(www.slicot.org), see (Benner et al., 1999; Van Huf-
fel et al., 2004; Benner et al., 2010; Sima et al.,
2012; Benner et al., 2013a; Benner et al., 2013b).
Fortran and MATLAB software for eigenvalues and
invariant or deflating subspaces has been developed,
for both real and complex matrices. Versions with a
factored or not factored skew-Hamiltonian matrix S
in a pencil are covered. Some performance results
for computing the eigenvalues or eigenvalues and
stable deflating subspaces for real or complex matrix
pencils, with factored or not factored matrix S are
given in (Sima, 2011a; Sima, 2011b; Sima et al.,
2012; Benner et al., 2012b; Benner et al., 2013b).
The results have shown that these solvers provide
reliable and accurate solutions, and are often faster
than the state-of-the-art tools.
This paper addresses the numerical difficulties in
computations with structured solvers, mainly for the
periodic QR/QZ steps involved, e.g., difficulties as-
sociated to multiple or close eigenvalues. Small ex-
amples, including standard eigenproblems and stan-
dard products of 2-by-2 matrices, illustrating the nu-
merical behavior, are analyzed based on experimen-
tal evidence. Our examples show the need to use
specialized measures, such as (reciprocal) condition
numbers, and special techniques, like balancing, even
when solving or analyzing small eigenproblems.
2 ACCURACY OF COMPUTED
EIGENVALUES
Several kinds of n ×n matrix pencils A −λB are con-
sidered in this paper. The eigenvalues of A − λB
are the complex numbers λ
i
, i = 1 : n (multiplici-
ties counted), satisfying the relations Ax
i
= λBx
i
, with
x
i
6= 0, i = 1 : n. The vector x
i
is a right eigenvector
corresponding to the eigenvalue λ
i
; a vector y
i
6= 0 sat-
isfying y
H
i
A = λ
i
y
H
i
B is a left eigenvector correspond-
ing to λ
i
, where y
H
i
is the conjugate-transpose of y
i
.
Finding the eigenvalues and eigenvectors of A −λB
is the generalized eigenvalue problem. A standard
eigenvalue problem is obtained for B = I
n
, the iden-
tity matrix of order n. Simple eigenvalues (i.e., with
multiplicity 1) can be computed accurately, if well-
conditioned. Multiple eigenvalues are inherently ill-
conditioned, and so they cannot generally be found
with high accuracy, even for standard small order
eigenproblems. Briefly speaking, an eigenvalue λ
i
is
well-conditioned if small perturbations in the matrix
A or matrix pair (A, B) produce small changes in the
corresponding computed eigenvalue,
b
λ
i
. Eigenvalue
condition numbers are used to assess the condition-
ing, or, equivalently, the sensitivity to perturbations
in the data. Since condition numbers can be infinite,
their reciprocals are used in practical calculations.
LAPACK driver routines compute estimates of the
reciprocal condition numbers for individual or clus-
ters of eigenvalues and eigenvectors. We will denote
these estimates by rcond(λ
i
) and rcond(x
i
), respec-
tively. A balancing option allows to perform initial
row and column permutations (to isolate the eigen-
values available by inspection in the leading/trailing
parts of A and B), scale the matrices to make the 1-
norms of rows and corresponding columns as close as
possible, or to both permute and scale. Balancing of-
ten increases the accuracy of computed eigenvalues.
An approximate error bound on the chordal distance
between the computed generalized eigenvalue
b
λ
i
and
the corresponding exact eigenvalue λ
i
is
χ(
b
λ
i
,λ
i
) ≤ ε
M
k[kAk, kBk]k/rcond(λ
i
),
where ε
M
is the relative machine accuracy, and the
norms are for the matrices after balancing, if applied.
(The 1-norm is used in LAPACK routines for A and
B, but 2-norm for the vector of norms in square brack-
ets.) This means that perturbations in the elements of
A and B can be amplified by 1/rcond(λ
i
) in the com-
puted eigenvalue
b
λ
i
. The chordal distance between
two points (
b
α,
b
β) and (α,β) is defined by
χ([
b
α,
b
β],[α, β]) =
|
b
αβ −α
b
β|
q
|
b
α|
2
+ |
b
β|
2
p
|α|
2
+ |β|
2
.
An approximate error bound for the acute angle be-
tween the computed left or right eigenvectors
b
y
i
or
b
x
i
, and the true eigenvectors y
i
or x
i
, respectively, is
given by ε
M
k[ kAk, kBk] k/rcond(x
i
). See (Anderson
et al., 1999) for further details, where tighter bounds
are also given. A very simple example illustrates what
can be expected in eigenvalue computations using nu-
merical algorithms.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
172

Example 1. Consider a stable linear system with
transfer-function
H(s) =
1
(s + 1)
2
(s + 2)
,
hence with a double pole at −1, and another pole at
−2. A state-space matrix for this system is
A =
−4 −5 −2
1 0 0
0 1 0
.
Indeed, this is the companion matrix of the polyno-
mial z
3
+4z
2
+5z +2, which has exact roots −1, with
multiplicity 2, and −2. The eigenvalues of A should
coincide with the system poles. However, the eigen-
values corresponding to the double pole cannot gen-
erally be computed accurately. Indeed, the MATLAB
R2014b (MathWorks, 2014) function eig, based on
the state-of-the-art LAPACK routines, returns in dou-
ble precision arithmetic
−2
−0.9999999999999997 ±2.83263461777919·10
−8
ı
.
when using the command eig(A). The pole at −2 is
computed to full accuracy, but the double pole at −1
became a pair of complex conjugate values. The (ab-
solute and relative) errors of the eigenvalues of this
pair are about 2.83·10
−8
, slightly smaller than 2
√
ε
M
,
i.e., twice the square root of the relative machine ac-
curacy, hence more than half of the accuracy, has been
lost. Calling the function eig with no optional argu-
ment, as above, computes the eigenvalues after a pre-
liminary scaling of matrix A with a diagonal matrix D,
i.e., the iterative QR algorithm is applied to the ma-
trix D
−1
AD, with D = diag(2,1, 1) for this example.
Optionally, the LAPACK driver DGEESX also returns
the reciprocal condition numbers for eigenvalues and
eigenvectors, which in this case are
rcond(λ
1:3
) = [0.11111, 9.1602·10
−9
,9.1602·10
−9
],
rcond(x
1:3
) = [0.26087, 1.0950·10
−8
,1.0950·10
−8
],
respectively (rounded to 5 significant digits). The
transformed matrix A returned by DGEESX is block di-
agonal with diagonal blocks of order 1 and 2, and the
second block is
−0.9999999999999997 −2.833333333333334
2.831936074532138·10
−16
−0.9999999999999997
.
The small, but nonzero value of the subdiagonal ele-
ment is responsible for getting a pair of complex con-
jugate eigenvalues. Without balancing (e.g., using the
command eig(A,’nobalance’)), the last two eigen-
values are even less accurate,
−0.9999999999999986 ±3.817602171155931·10
−8
ı,
with errors of about 3.82·10
−8
, and the nonzero subdi-
agonal entry of the transformed matrix A is −4.7705·
10
−16
. The reciprocal condition numbers for eigen-
values and eigenvectors are
rcond(λ
1:3
) = [8.9087·10
−2
,1.1781·10
−8
,1.1781·10
−8
],
rcond(x
1:3
) = [0.24661,1.3038·10
−8
,1.3038·10
−8
].
Consider now a perturbation in the system poles.
Specifically, replacing the double pole by −1 −ε and
−1 + ε, the characteristic polynomial becomes
z
3
+ (4 +ε)z
2
+ (5 +2ε −ε
2
)z + 2 + ε −2ε
2
−ε
3
,
and the eigenvalues of the associated companion ma-
trix have been computed for values of ε set to
√
ε
M
,
10
√
ε
M
, and ε
1/4
M
. Three real eigenvalues have been
obtained for all tried parameter values, but just one
real eigenvalue for ε =
√
ε
M
when balancing was
used. The first eigenvalue was always accurately
computed, with errors of about 5.33·10
−15
or less,
with or without balancing. On the other hand, the
other two eigenvalues had errors of about 3.87·10
−8
or smaller. Specifically, for ε = 10ε
M
the errors were
about 5.45·10
−10
without balancing, and for ε =
√
ε
M
,
the errors were 6.75·10
−13
and 5.14·10
−12
, with and
without balancing, respectively. The reciprocal condi-
tion numbers have been comparable with their values
in the unperturbed case for ε set to
√
ε
M
or 10
√
ε
M
,
but increased to over 3.7·10
−5
for λ
2:3
and ε
1/4
M
. Note
that the error bounds given by the formulas above are
quite tight for all the investigated cases. The better ac-
curacy for the computed eigenvalues
b
λ
2:3
correspond-
ing to −1 −ε and −1 + ε when ε = ε
1/4
M
is due to the
bigger gap, 2ε
1/4
M
, between the true eigenvalues than
in the other cases. When this gap is zero, about half of
the accuracy is lost for this example. For a third order
system with a triple pole, about two thirds of accu-
racy (about 12 significant digits in double precision
computations) might be lost for each
b
λ
i
.
3 ACCURACY OF EIGENVALUES
FOR MATRIX PRODUCTS
Numerical difficulties appear also when computing
the periodic Schur decomposition of a matrix prod-
uct, Π
p
i=1
A
i
. This may happen even for 2 ×2 matrices
and p = 2. Such a decomposition is used, e.g., for
computing the eigenvalues and invariant subspaces of
Hamiltonian matrices (Benner and Kressner, 2006).
When A
i
are general matrices, the algorithm first re-
duces the matrix sequence to the periodic Hessenberg
PitfallsWhenSolvingEigenproblems-WithApplicationsinControlEngineering
173

form, using unitary transformations so that the eigen-
values of the product are preserved. In this form,
one matrix, usually the first one, is upper Hessen-
berg (i.e., all elements below the first subdiagonal are
zero), and all other factors are upper triangular. Then,
the sequence is further transformed similarly to one
in which the Hessenberg matrix is reduced to Schur
form, while the other matrices remain upper triangu-
lar. For complex matrices, the Schur form is also up-
per triangular, while in the real case, it is block up-
per triangular with diagonal blocks of order 1 or 2,
corresponding to real or complex conjugate eigenval-
ues, respectively. The real case only will be consid-
ered in the sequel, for convenience. As suggested by
the above presentation, the matrix product itself is not
evaluated, since forming it may yield large errors, de-
pending on its conditioning. However, the algorithm
computes some products of elements on the diagonals
(and uses sums with other products involving subdi-
agonal or superdiagonal elements), after the prelimi-
nary reduction to the Hessenberg-triangular form. If
some factors are ill-conditioned, it is possible that in-
accuracies in the intermediate results be strongly am-
plified in the computed decomposition. Nevertheless,
the returned eigenvalues are usually highly accurate.
The periodic Schur algorithm finds orthogonal
transformation matrices, Z
i
, i = 1 : p, such that the
transformed matrices,
e
A
i
= Z
T
i
A
i
Z
mod (i,p)+1
, i = 1 : p, (1)
have the required structure, i.e.,
e
A
1
is in upper real
Schur form, and
e
A
j
, j = 2 : p, are upper triangu-
lar. The eigenvalues are then readily obtained. Note
that (1) performs a similarity transformation, since
Π
p
i=1
e
A
i
= Z
T
1
(Π
p
i=1
A
i
)Z
1
, hence the eigenvalues are
theoretically preserved. The algorithm delivers the
eigenvalues and the matrices Z
i
and
e
A
i
, i = 1 : p.
Simple and well separated eigenvalues are accurately
computed; moreover, the formulas (1) are satisfied
with (high) precision for i > 1, but sometimes this is
not the case for i = 1, i.e., the obtained Schur form
may not be close to the true real Schur form. Also,
the eigenvalues of the matrix product Π
p
i=1
e
A
i
may dif-
fer from the computed eigenvalues, as shown by nu-
merical experiments. In some applications it is im-
portant to have accurate matrices
e
A
i
, i = 1 : p. Let
R
i
= Z
T
i
A
i
Z
mod (i,p)+1
−
e
A
i
, i = 1 : p, be the residuals
of the computed transformed matrices. Large norms
of some of these residuals indicate an inaccurate pe-
riodic Schur decomposition. The accuracy can be in-
creased by an iterative refinement process. Specif-
ically, another algorithm iteration (called sweep be-
low) is applied to the sequence
e
A
i
+ R
i
, i = 1 : p, and
the process continues similarly till the residual norms
Table 1: Absolute difference between the returned (2,1) el-
ement of
e
A
1
and its value computed using (1) for various
number of factors, p.
p (2,1)-element error p (2,1)-element error
10 7.78·10
−11
26 3.65·10
−2
11 7.43·10
−10
28 0.7068
16 8.66·10
−7
29 0.7743
19 1.52·10
−4
30 0.7163
22 1.85·10
−3
31 0.7205
25 4.98·10
−2
32 0.5688
are smaller than a given tolerance, or a specified num-
ber of iterations is exhausted. Often, one additional
sweep ensures acceptable accuracy, and sometimes it
is enough to update the matrix
e
A
1
only. If the transfor-
mations used in the additional sweep(s) are denoted
by Y
i
, then Z
i
Y
i
, i = 1 : p, usually transform the orig-
inal problem to one having the right structure and ac-
curate eigenvalues.
In a series of tests, the periodic Schur solver im-
plementation in the SLICOT Library has been applied
to several products of 2 ×2 real matrices. All values
of p from 2 to 32 have been tried. Since the inves-
tigated examples had real eigenvalues only, all fac-
tors
e
A
i
, i ≥ 1, are upper triangular. The computed
eigenvalues have been compared to those obtained
using the MATLAB functions eig and its symbolic
counterpart, symbolic/eig, applied to the product
of factors, Π
p
i=1
A
i
, the symbolic product of symbolic
factors, Π
p
i=1
A
i
, the product of transformed factors,
Π
p
i=1
e
A
i
, and the symbolic product of symbolic trans-
formed factors, Π
p
i=1
e
A
i
. The eigenvalues of all these
products agreed well. The difference between the
computed periodic matrix and the transformed orig-
inal periodic matrix, obtained using (1), has also been
computed. For several values of p, the (2,1) element
of the factor
e
A
1
from (1) differed significantly from its
zero value returned by the solver. All other elements
for all factors agreed very well to the returned values.
Table 1 gives the absolute value of the difference for
various p and one series of factor matrices.
The reciprocal condition numbers of the eigenval-
ues and eigenvectors of the matrix product have also
been computed, and their values have usually been
quite close to 1, agreeing with the eigenvalues’ good
observed accuracy. However, the conditioning for the
product of the transformed factors has been several
orders of magnitude worse. The computed eigen-
values most often correspond accurately to those of
Π
p
i=1
A
i
, but not to those of Π
p
i=1
e
A
i
. Using one ad-
ditional sweep, after updating the factor
e
A
1
only, the
absolute difference was of the order 10
−15
or less, for
the values p in Table 1. Moreover, the eigenvalues
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
174

have usually been more accurate.
The results for several other series of tests with
some mildly ill-conditioned factors have been similar,
but with different values of p and of the absolute dif-
ference. Actually, the numerical difficulties described
above can be encountered even for a product of two
2 ×2 matrices, as illustrated by the example below.
Example 2. Let
A
1
=
1.237 2.058
2.058 3.425
, A
2
=
16.825 13.890
13.890 11.467
,
be exact representations of the two matrices. Note
that the condition numbers for A
1
, A
2
, and A
1
A
2
are
about 1.5967·10
4
, 4.5739·10
6
, and 6.4931·10
10
, re-
spectively. There is an absolute error (in the (2,1)
element only) of order 10
−14
between the product
A
1
A
2
computed in double precision arithmetic and
that computed using symbolic calculations, via the
MATLAB command double(sym(A
1)*sym(A 2)).
The eigenvalues obtained using symbolic calculations
and conversion to double precision numbers, are
λ = [2.031200536560380·10
−9
;1.172582399979688·10
2
];
the SLICOT periodic Schur eigensolver returned
b
λ = [2.031200097007968·10
−9
;1.172582399979688·10
2
],
and the transformed matrices
e
A
1
and
e
A
2
−3.096329932867903·10
−4
1.552701519915428
0 −4.395524985047830
−6.560024032069280·10
−6
−9.422786660123904
0 −26.67673153813540
respectively. Therefore, the eigenvalues of the prod-
uct of the transformed matrices, computed as products
of the corresponding diagonal elements are
e
λ = [2.031199877082891·10
−9
;1.172582399952876·10
2
].
The element-wise absolute and relative errors be-
tween
b
λ and λ are about 4.40·10
−16
and 4.26·10
−14
,
and 2.16·10
−7
and 3.64·10
−16
, respectively. The last
value is also the approximate global relative error, i.e.,
k
b
λ −λk/kλk, using Euclidean norm. On the other
hand, the element-wise absolute and relative errors
between
e
λ and λ are about 6.59·10
−16
and 2.68·10
−9
,
and 3.25·10
−7
and 2.29·10
−11
; the last value is the
approximate global relative error of
e
λ compared to λ.
Clearly, although obtained using orthogonal trans-
formations only, the transformed matrices
e
A
i
, i = 1,2,
are inaccurate, and therefore
e
λ
i
are less accurate than
b
λ
i
. The inaccuracy of
e
A
i
is due to the ill-conditioning
of the matrix product A
1
A
2
, and the way the periodic
Schur algorithm works. The residual matrices of
e
A
i
,
i = 1, 2, have the following approximate values
R
1
=
0 4.44·10
−16
2.85·10
−10
0
,
R
2
=
5.26·10
−16
1.78·10
−15
1.78·10
−15
0
.
The largest residual appears in the (2,1) element of
R
1
. While this element should be zero, and numeri-
cally its magnitude should be of the order of ε
M
, in
the best case, the ill-conditioning of the matrix prod-
uct has determined its increase by six orders of mag-
nitude.
After updating the computed matrix
e
A
1
only and
using an additional sweep on the matrix sequence,
which is now in periodic Hessenberg-triangular form,
the new residuals have all elements equal to 0, except
for the (2,1) element of the new residual R
2
, which has
a value about 4.25·10
−16
. Moreover, the global resid-
uals, given by the difference between the matrices re-
turned by the additional sweep and those obtained us-
ing (1) with Z
i
replaced by Z
i
Y
i
, have all values with
magnitude comparable to ε
M
. The largest residual el-
ement is now the (1,2) element in the second residual
matrix, whose value is about 3.55·10
−15
. Also, the
eigenvalues of the matrix sequence returned after the
additional sweep coincide to those of
e
A
1
1
e
A
1
2
and are
b
λ
1
= [2.031200536459228·10
−9
;1.172582399979688·10
2
].
The second eigenvalue,
b
λ
1
2
, practically coincides to
λ
2
and
b
λ
2
, and the first 10 digits of
b
λ
1
1
coincide to
those of λ
1
, hence it has three additional correct dig-
its compared to
b
λ
1
. The element-wise absolute and
relative errors between
b
λ
1
and λ are about 1.01·10
−19
and 4.42·10
−14
, and 4.98·10
−11
and 1.21·10
−16
, re-
spectively, hence there is an improvement of 4 and 5
orders of magnitude compared to
e
λ. If
e
A
2
is also up-
dated as
e
A
1
, there is no noticeable improvement.
Many other 2 ×2 examples with a similar or even
worse behaviour have been found. In one case, the
(2,1) entry of R
1
had a value of order 10
−6
, but one ad-
ditional sweep reduced its magnitude to about 10
−22
.
Larger order examples have also been tried, and be-
haved better than the 2 ×2 case. For instance, for an
example with four 10 ×10 factors, the relative error
between
b
λ and λ (obtained with symbolic computa-
tions) has been 6.46·10
−16
, and the Frobenius norm
of the stacked residuals was 5.56·10
−12
.
The experiments have also shown that the eigen-
values conditioning does not depend on the condition-
ing of the matrix product.
PitfallsWhenSolvingEigenproblems-WithApplicationsinControlEngineering
175

4 ACCURACY OF EIGENVALUES
FOR SKEW-HAMILTONIAN/
HAMILTONIAN PROBLEMS
Often, badly scaled matrices or matrix pencils have
eigenvalues with magnitudes covering a large inter-
val. A structured matrix pencil example will be
discussed below. Consider a real 2m × 2m skew-
Hamiltonian/ Hamiltonian pencil αS −βH , with
S =
A D
E A
T
, H =
C V
W −C
T
, (2)
where D and E are skew-symmetric (D = −D
T
, E =
−E
T
), V and W are symmetric, and define J as
J =
0 I
m
−I
m
0
.
The eigenvalues for the real pencil αS −βH in (2)
are symmetric with respect to both real and imaginary
axes of the complex plane. Real or purely imaginary
eigenvalues appear in pairs λ, −λ (or λ,
¯
λ, in the sec-
ond case), while complex conjugate eigenvalues ap-
pear in quadruples, λ, −λ,
¯
λ, and −
¯
λ. Using two
orthogonal transformations, Q
1
and Q
2
, the structure-
exploiting algorithm computes the transformed matri-
ces
e
S,
e
T , and
e
H , so that
Q
T
1
SJ Q
1
J
T
=
e
A
e
D
0
e
A
T
:=
e
S,
J
T
Q
T
2
J SQ
2
=
e
B
e
F
0
e
B
T
:=
e
T ,
Q
T
1
H Q
2
=
e
C
1
e
V
0
e
C
T
2
:=
e
H , (3)
where
e
A,
e
B,
e
C
1
are upper triangular,
e
C
2
is upper
quasi-triangular (i.e., block upper triangular with 1 ×
1 or 2 × 2 diagonal blocks) and
e
D,
e
F are skew-
symmetric. Specifically, the first step reduces S to
skew-Hamiltonian triangular form, using Givens rota-
tions and Householder reflections, and updates A and
D in S, as well as C, V , and W in H correspond-
ingly, producing A
1
, ..., W
1
, respectively. Let S
1
and
H
1
be the obtained matrices, where the two diago-
nal blocks of H
1
are C
1
= C
1
and C
2
= −C
1
. A
skew-Hamiltonian block upper triangular matrix T
1
is built using B
1
= A
1
and F
1
= D
1
. Then, addi-
tional transformations are used to reduce the matrix
H
1
to a block upper triangular form, while updating
A
1
, D
1
, B
1
and F
1
to preserve their form or struc-
ture. Let
b
A,
b
D,
b
B,
b
F,
b
C
1
,
b
V , and
b
C
2
be the obtained
matrices, and
b
S,
b
T , and
b
H the block matrices built
from them, where
b
A,
b
B, and
b
C
1
are upper triangular,
b
D and
b
F are skew-symmetric, and
b
C
2
is upper Hes-
senberg. Finally, the periodic QZ algorithm is applied
to transform
b
C
2
to upper quasi-triangular form, while
preserving the upper triangular form of
b
A,
b
B, and
b
C
1
.
Specifically, the formal matrix product
b
C
2
b
A
−1
b
C
1
b
B
−1
is transformed without using matrix products and in-
verses. (Actually,
b
A and
b
B may be singular.) The
eigenvalues of the pencil αS −βH are the positive
and negative square roots of the eigenvalues of the
formal matrix product −
b
C
2
b
A
−1
b
C
1
b
B
−1
.
Example 3. In the computation of the H
∞
-norm
of a linear control system, an 18 × 18 skew-
Hamiltonian/Hamiltonian pencil was found for which
changes in scaling led to one small imaginary eigen-
value becoming real. The case with changes in scal-
ing will be referred to as Test 1 below, while the case
without changes will be referred to as Test 2. Specif-
ically, the two smallest eigenvalues were about 2.52·
10
−5
ı and 8.66·10
−4
ı for Test 2 data, but 2.30·10
−3
ı
and 1.83·10
−5
for Test 1 data. The final effect was
obtaining a wrong H
∞
-norm in the Test 1 case. A de-
tailed investigation of the associated numerical issue
has been performed.
Our specific example has m = 9 and a simple
structure. Specifically, A is diagonal with a
ii
= a
11
,
i = 2 : 7, a
j j
= 0, j = 8 : 9, C is almost upper triangu-
lar, with c
:,9
= 0, but c
i,i−1
, i = 3 : 7, c
8,1:2
and c
9,2:7
are nonzero; moreover, D = E = 0 and V and W are
diagonal, with v
ii
= w
ii
= 0, i = 1 : 7, v
j j
= −1 and
w
j j
= 1, j = 8 : 9; all other elements are 0. There
are four infinite eigenvalues. The only differences be-
tween Test 1 and Test 2 data are in the nonzero ele-
ments of A and C.
The first idea was to suspect an error in the SLI-
COT Library (Benner et al., 1999; Van Huffel et al.,
2004; Benner et al., 2013a; Benner et al., 2013b) rou-
tines used, i.e., in subroutine MB04BD or in one of the
routines it calls, e.g., a wrong decision test. But a step
by step analysis of the intermediate results proved
their correctness. Indeed, the transformed matrices
computed from the Test 1 data, including
b
A,
b
D,
b
B,
b
F,
b
C
1
,
b
V , and
b
C
2
(obtained in MB04BD just before call-
ing the periodic QZ algorithm), satisfy the required
structure and the needed relationships with the ini-
tial skew-Hamiltonian/Hamiltonian pencil. The max-
imum relative error is 2.42·10
−16
. The finite and
“positive” eigenvalues of the reduced problem, com-
puted using symbolic calculations, immediately after
the infinite part has been deflated, agree in position,
and within a relative error of about ε
1/2
M
, to those re-
turned by MB04BD.
The deflation which separated the finite and infi-
nite spectra has been produced at the end of the sec-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
176
ond iteration of the periodic QZ algorithm, hence few
more operations were applied on copies of
b
C
1
,
b
A,
b
C
2
,
and
b
B; moreover, the orthogonal matrices used, Z
1
,
..., Z
4
, have a very simple structure (slightly modified
identity matrices). Also, the transformed matrices,
denoted with check accent, satisfy the needed trans-
formation rules, i.e.,
ˇ
C
2
= Z
T
1
b
C
2
Z
2
,
ˇ
A = Z
T
3
b
AZ
2
,
ˇ
C
1
=
Z
T
3
b
C
1
Z
4
,
ˇ
B = Z
T
1
b
BZ
4
, so that the resulting formal
matrix product is
ˇ
C
2
ˇ
A
−1
ˇ
C
1
ˇ
B
−1
= Z
T
1
b
C
2
b
A
−1
b
C
1
b
B
−1
Z
1
.
The maximum relative error is about 2.25 ·10
−15
.
Moreover, the 7 ×7 trailing submatrices of
b
A and
b
B,
used as coefficient matrices in the two linear systems
corresponding to the finite spectrum, solved for ob-
taining the true matrix product using symbolic cal-
culations, have quite small condition numbers, about
9.36·10
3
and 3.39, respectively.
In addition to the analysis above, the reciprocal
condition numbers for eigenvalues and eigenvectors
for both Test 1 and Test 2 eigenproblems, with or
without balancing, have been computed. It was found
that the small eigenvalues for the Test 1 data are more
ill-conditioned than those for the Test 2 data. Omit-
ting the eigenvalues larger than 10
5
, including the in-
finite ones, the LAPACK driver DGGEVX without bal-
ancing returned the “small” eigenvalues and associ-
ated approximate condition information shown in Ta-
ble 2 for the Test 1 data. Note that there is just one
pair of complex conjugate eigenvalues instead of two.
Pairing is not as needed, and the eigenvalues which
should be paired do not agree well. The last eigen-
value should be paired to the third one above it (i.e.,
to 9.0169···73·10
−6
). There are at most eight iden-
tical significant digits in the paired eigenvalues. The
complex pair and the real pair of eigenvalues men-
tioned above have the smallest reciprocal condition
numbers (of order 10
−15
), hence they are very sensi-
tive. The one-norms of the matrices S and H were
about 2.3842·10
−7
and 7.3736, respectively.
Using instead DGGEVX with balancing (permuta-
tions and scaling), returned good results, as shown
in Table 3. Note that the pairing is much better than
in Table 2, and the eigenvalues are closer to their re-
quired position. The accuracy increased to at most
12 identical significant digits in the paired eigenval-
ues. Also, the conditioning has been significantly
improved for all eigenvalues. The one-norms of the
balanced skew-Hamiltonian and Hamiltonian matri-
ces were about 2.3842 and 4287.7. With scaling only,
the results are similar, so we omit them.
Using the scaling factors returned by DGGEVX
to scale the input matrices for a MEX-file based
on SLICOT subroutine MB04BD, the following finite
eigenvalues (including the “large” ones) have been
obtained:
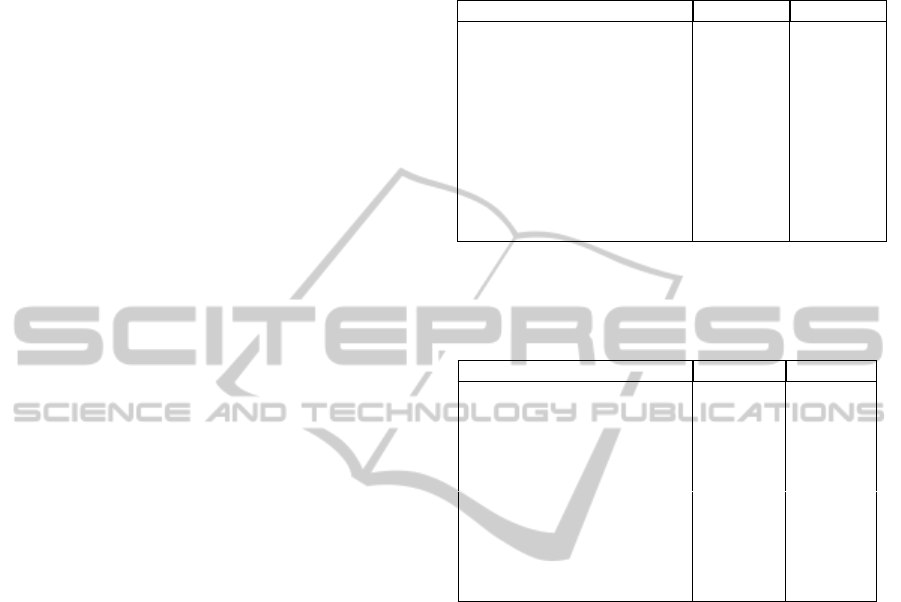
Table 2: The small eigenvalues and associated approxi-
mate condition numbers for eigenvalues, rcond(λ
i
), and for
eigenvectors, rcond(x
i
), computed using DGGEVX without
balancing for the Test 1 data.
λ
i
rcond(λ
i
) rcond(x
i
)
7.982789077728958·10
2
4.5·10
−9
1.4·10
−11
−7.982789039705131·10
2
4.5·10
−9
4.6·10
−11
−2.258073833805364·10
1
5.1·10
−12
5.9·10
−11
2.258073628829316·10
1
5.1·10
−12
2.8·10
−11
6.345831704138784·10
−6
±1.654595668192905·10
−3
ı 3.4·10
−15
8.4·10
−14
9.016920132336973·10
−6
2.0·10
−15
1.8·10
−18
−5.180515230574346 1.0·10
−13
1.7·10
−11
5.180514112635106 1.0·10
−13
1.5·10
−11
−2.180898342048099·10
−5
3.0·10
−15
1.8·10
−18
Table 3: The small eigenvalues and associated approxi-
mate condition numbers for eigenvalues, rcond(λ
i
), and for
eigenvectors, rcond(x
i
), computed using DGGEVX with bal-
ancing for the Test 1 data.
λ
i
rcond(λ
i
) rcond(x
i
)
7.982789076557393·10
2
4.1·10
−3
3.1·10
−5
−7.982789076562744·10
2
4.1·10
−3
5.5·10
−5
−2.258073819582842·10
1
2.3·10
−2
2.7·10
−4
2.258073819581395·10
1
2.3·10
−2
1.5·10
−4
−5.180514839367283 5.6·10
−3
9.9·10
−5
5.180514839369767 5.6·10
−3
1.0·10
−4
2.631383527274714·10
−9
±8.649722516061533·10
−4
ı 2.3·10
−8
1.6·10
−7
−2.631570224527866·10
−9
±2.522221870167959·10
−5
ı 1.0·10
−7
1.6·10
−5
λ =
8.860295592973415·10
6
ı
1.009148542240609·10
5
ı
7.982789076561136·10
2
2.258073819582885·10
1
5.180514839373116
2.521340745136690·10
−5
ı
8.652245367690063·10
−4
ı
.
This is the expected result for this data, but it was not
returned as such by MB04BD with no scaling. Note that
only the eigenvalues with positive real parts and, for
purely imaginary eigenvalues, only those with posi-
tive imaginary parts are listed. The other half of the
spectrum is obtained by symmetry.
All calculations above have been repeated for the
Test 2 data, and similar results have been obtained.
This problem is less sensitive. Better conditioning
than for the Test 1 data has been obtained for all bal-
ancing options. Indeed, the reciprocal condition num-
bers for the small eigenvalues are about one order of
magnitude larger than for the Test 1 data eigenprob-
lem, hence the condition numbers are smaller.
The analysis in Example 3 suggests that it would
be useful to include in the computational solver an op-
PitfallsWhenSolvingEigenproblems-WithApplicationsinControlEngineering
177

tion for balancing the skew-Hamiltonian/Hamiltonian
eigenproblem data, preserving the structure.
5 CONCLUSIONS
Numerical algorithms for the solution of common and
structured eigenproblems, encountered in many con-
trol theory applications and in other domains, have
been investigated. Eigenvalue computations for stan-
dard as well as formal matrix products have been
considered, and their accuracy and conditioning has
been discussed. Simple examples highlight the pit-
falls which may appear in such numerical computa-
tions, using state-of-the-art solvers. An iterative re-
finement process for the periodic Schur decomposi-
tion (not yet offered by software packages) is pro-
posed, and the improvement of the results is illus-
trated. Balancing the matrices or matrix pencils and
the use of condition number estimates for eigenvalues
are shown to be essential options in investigating the
behavior of the solvers and problem sensitivity.
REFERENCES
Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel,
J., Dongarra, J., Du Croz, J., Greenbaum, A., Ham-
marling, S., McKenney, A., and Sorensen, D. (1999).
LAPACK Users’ Guide. SIAM, Philadelphia, third
edition.
Benner, P. (1999). Computational methods for linear-
quadratic optimization. Supplemento ai Rendiconti
del Circolo Matematico di Palermo, II, (58):21–56.
Benner, P., Byers, R., Losse, P., Mehrmann, V., and
Xu, H. (2007). Numerical solution of real skew-
Hamiltonian/Hamiltonian eigenproblems. Technical
report, Technische Universit
¨
at Chemnitz, Chemnitz.
Benner, P., Byers, R., Mehrmann, V., and Xu, H. (2002).
Numerical computation of deflating subspaces of
skew Hamiltonian/Hamiltonian pencils. SIAM J. Ma-
trix Anal. Appl., 24(1):165–190.
Benner, P. and Kressner, D. (2006). Fortran 77 subroutines
for computing the eigenvalues of Hamiltonian matri-
ces II. ACM Trans. Math. Softw., 32(2):352–373.
Benner, P., Kressner, D., Sima, V., and Varga, A.
(2010). Die SLICOT-Toolboxen f
¨
ur Matlab. at—
Automatisierungstechnik, 58(1):15–25.
Benner, P., Mehrmann, V., Sima, V., Van Huffel, S., and
Varga, A. (1999). SLICOT — A subroutine library
in systems and control theory. In Applied and Com-
putational Control, Signals, and Circuits, 1, ch. 10,
pp. 499–539. Birkh
¨
auser, Boston.
Benner, P., Sima, V., and Voigt, M. (2012a). L
∞
-norm com-
putation for continuous-time descriptor systems us-
ing structured matrix pencils. IEEE Trans. Automat.
Contr., AC-57(1):233–238.
Benner, P., Sima, V., and Voigt, M. (2012b). Robust and
efficient algorithms for L
∞
-norm computations for de-
scriptor systems. In 7th IFAC Symposium on Robust
Control Design, pp. 189–194.
Benner, P., Sima, V., and Voigt, M. (2013a). FOR-
TRAN 77 subroutines for the solution of skew-
Hamiltonian/Hamiltonian eigenproblems. Part I: Al-
gorithms and applications. www.slicot.org.
Benner, P., Sima, V., and Voigt, M. (2013b). FOR-
TRAN 77 subroutines for the solution of skew-
Hamiltonian/Hamiltonian eigenproblems. Part II: Im-
plementation and numerical results. www.slicot.
org.
Bojanczyk, A. W., Golub, G., and Van Dooren, P. (1992).
The periodic Schur decomposition: algorithms and
applications. In SPIE Conference Advanced Signal
Processing Algorithms, Architectures, and Implemen-
tations III, 1770, pp. 31–42.
Golub, G. H. and Van Loan, C. F. (1996). Matrix Computa-
tions. The Johns Hopkins University Press, Baltimore,
Maryland, third edition.
Granat, R., K
˚
agstr
¨
om, B., and Kressner, D. (2007). Com-
puting periodic deflating subspaces associated with a
specified set of eigenvalues. BIT Numerical Mathe-
matics, 47(4):763–791.
Laub, A. J. (1979). A Schur method for solving algebraic
Riccati equations. IEEE Trans. Automat. Contr., AC–
24(6):913–921.
MathWorks (2014). MATLAB
R
: The Language of Techni-
cal Computing. R2014b. The MathWorks, Inc.
Mehrmann, V. (1991). The Autonomous Linear Quadratic
Control Problem. Theory and Numerical Solution.
Springer-Verlag, Berlin.
Sima, V. (1996). Algorithms for Linear-Quadratic Opti-
mization. Marcel Dekker, Inc., New York.
Sima, V. (2010). Structure-preserving computation of stable
deflating subspaces. In 10th IFAC Workshop “Adapta-
tion and Learning in Control and Signal Processing”.
Sima, V. (2011a). Computational experience with structure-
preserving Hamiltonian solvers in optimal control. In
8th International Conference on Informatics in Con-
trol, Automation and Robotics, vol. 1, pp. 91–96.
SCITEPRESS.
Sima, V. (2011b). Computational experience with structure-
preserving Hamiltonian solvers in complex spaces. In
5th International Scientific Conference on Physics and
Control.
Sima, V., Benner, P., and Kressner, D. (2012). New SLI-
COT routines based on structured eigensolvers. In
2012 IEEE International Conference on Control Ap-
plications, pp. 640–645. Omnipress.
Van Huffel, S., Sima, V., Varga, A., Hammarling, S., and
Delebecque, F. (2004). High-performance numeri-
cal software for control. IEEE Control Syst. Mag.,
24(1):60–76.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
178
