
Statistical Linearization and Consistent Measures of Dependence:
A Unified Approach
Kirill Chernyshov
V. A. Trapeznikov Institute of Control Sciences, 65 Profsoyuznaya Street, Moscow, Russia
Keywords: Cauchy-Schwarz Divergence, Input/Output Model, Maximal Correlation, Measures of Dependence, Mutual
Information, Rényi Entropy, Statistical Linearization, System Identification.
Abstract: The paper presents a unified approach to the statistical linearization of input/output mapping of non-linear
discrete-time stochastic systems driven with white-noise Gaussian process. The approach is concerned with
a possibility of applying any consistent measures of dependence (that is those measures of dependence of a
pair of random values, which vanish if and only if these random values are stochastically independent) in
statistical linearization problems and oriented to the elimination of drawbacks concerned with applying cor-
relation and dispersion (based on the correlation ratio) measures of dependence, based on linearized repre-
sentations of their input/output models.
1 PRELIMINARIES
Solving an identification problem of stochastic sys-
tems is always based on applying measures of de-
pendence of random values, both within representa-
tion of a system under study either by use of an in-
put/output mapping, or within state-space tech-
niques. Most frequently, conventional linear correla-
tion is used as such measures. Its application directly
follows from the identification problem statement
itself, when it is based on applying conventional
least squares approaches. The main advantage of the
measure is convenience of its application, involving
both a possibility of deriving explicit analytical rela-
tionships to determine required system characteris-
tics, and constructing estimation procedures via
sampled data, including those of based on applying
dependent observations.
However, the linear correlation as a measure of
dependence is known to be able to vanish even un-
der existence of a deterministic dependence between
random values. In particular, this is valid for the
quadratic dependence,
2
X
Y
, when X is the La-
placian random value (Rajbman, 1981), and for an
odd transformation of the form
XXY 35
3
,
where the random value X has the uniform distribu-
tion over the interval
1,1
(Rényi, 1959).
Just to overcome such a disadvantage, use of
more complicated, non-linear measures of depend-
ence has been involved into the system identifica-
tion. A key issue of the present paper is applying
consistent measures of dependence. In accordance to
the A.N. Kolmogorov terminology, a measure of
dependence
),( YX
between two random values X
and Y is referred as consistent, if
0),( YX if and
only if the random values X and Y are stochastically
independent.
The statistical linearization of input/output map-
pings relates to those identification problems, whose
solution is most considerably determined by charac-
teristics of dependence of input and output processes
of the system subject to identification. Meanwhile,
known approaches to the statistical linearization are
based either applying conventional correlations, or
dispersion (based on the correlation ratio) functions,
what, due to the reasons pointed out above, may give
rise constructing models, whose output is identically
equal to zero. A majority of literature references on
correlation based statistical linearization may be
found in the books of Roberts and Spanos (2003)
and Socha (2008).
The approach presented in the present paper is
concerned with a possibility of applying any con-
sistent measures of dependence in statistical lineari-
zation problems and is directed to elimination of the
drawbacks concerned with applying correlation and
dispersion measures of dependence under system
identification based on linearized representations of
input/output models.
524
Chernyshov K..
Statistical Linearization and Consistent Measures of Dependence: A Unified Approach.
DOI: 10.5220/0005534805240532
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 524-532
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 PROBLEM STATEMENT
Let in a non-linear dynamic stochastic system )(tz
be the output random process assumed to be station-
ary in the strict sense and ergodic,
)(su
be the out-
put random input process assumed within the present
problem statement to be the white-noise Gaussian
process. Processes z(t) and u(s) are also assumed to
be joint stationary in the strict sense, while the de-
pendence of the input and output processes of the
system is characterized by the probability distribu-
tion densities
),,(
uzp
zu
,
,2,1
. (1)
(being of course not known to the user). For sake of
simplicity but without loss of the generality, the pro-
cesses z(t) and u(s) are assumed to be zero-mean and
unit-variance, that is
0)()( sutz EE ,
1)()(
sutz varvar (2)
In (2),
E stands for the mathematical expectation,
and
var , for the variance.
A model of the system described by the densities
(1) and condition (2) is searched in the form
1
)()();(
ˆ
tuwWtz ,
,2,1t
, (3)
where
);(
ˆ
Wtz is the model output process,
,1),(
wW , ,2,1),( kkw are coeffi-
cients of the weight function of the linearized model,
subject to identification in accordance to a criterion
of the statistical linearization. Such a criterion is the
condition of coincidence of the mathematical expec-
tations of the system output process, described by
densities (1), and model output process (3), and the
condition of coincidence of a given measure of de-
pendence of the input and output processes of the
system described by densities (1) and input and out-
put processes of model (3), or mathematically,
0);(
ˆ
)( Wtztz EE ,
(4)
)()(
)(
ˆ
uWzzu
,
,2,1
,
(5)
where
)(
is some measure of dependence.
Again, in accordance to normalization conditions
(2), model (3) is implied to meet the condition
1);(
ˆ
Wtzvar ,
Accordingly, the weight coefficients of the model
meet the condition
1)(
1
2
w . (6)
Thus, expressions (4) and (5) represent a criterion of
the statistical linearization of a system described by
densities (1).
3 CONSTRUCTING THE
UNIVERSAL APPROACH
Let
out
t
x
1
1
1
)()()()(
jj
jtujwjtujw ,
,2,1
be a sequence of random values that are, obviously,
Gaussian, zero-mean, and having the variance
out
t
x
var
)(1)()(
2
1
2
1
1
2
kwjwjw
jj
,
,2,1
.
Then within the notations introduced and by virtue
of model (3) description, one may write the fallow-
ing matrix equalities
)(
10
)(1
)(
);(
ˆ
tu
x
w
tu
Wtz
out
t
, (7)
)(
);(
ˆ
10
)(1
)(
tu
Wtzw
tu
x
out
t
. (8)
As well known, if two n-dimensional random vec-
tors
z and x, having marginal probability distribution
densities
)(Y
Y
p and )(V
V
p correspondingly, are
connected with a one-to-one mapping
)(VY
,
then
)(
)(
)()(
1
1
Y
Y
YY
D
D
pp
VY
,
where
)(
)(
1
Y
Y
D
D
is the Jacobian of the inverse
transformation
)(
1
YV
.
In accordance to this relationship, the joint prob-
ability distribution density
),),(
ˆ
(
)(
ˆ
uWzp
uWz
of the
random values
);(
ˆ
Wtz and )(
tu may be ex-
StatisticalLinearizationandConsistentMeasuresofDependence:AUnifiedApproach
525

pressed via the joint probability distribution density
,,uxp
out
t
ux
out
t
of the random values
out
t
x
and )(
tu . In turn, the density
,,uxp
out
t
ux
out
t
is, evidently, of the form
)(,, upxpuxp
u
out
t
x
out
t
ux
out
t
out
t
,
where
out
t
x
xp
out
t
, )(up
u
are the marginal
probability distribution densities of the random val-
ues
out
t
x
and
)( ktu
correspondingly. Hence,
due to relationships (7) and (8), and by virtue of re-
lationship (6), one may write for the density
),),(
ˆ
(
)(
ˆ
uWzp
uWz
:
),),(
ˆ
(
)(
ˆ
uWzp
uWz
)())()(
ˆ
( upuwWzp
u
x
out
t
=
2
)(
ˆ
1)(
)(1)(
ˆ
2
1
)(12
1
u
Wz
w
w
u
Wz
T
e
w
,
(9)
that is this density is Gaussian.
Thus, calculating the measure of dependence
)(
)(
ˆ
k
uWz
for density (9) enables one to express
the measure as a transformation of
)(kw
:
)()(
)(
ˆ
)(
ˆ
w
uWz
uWz
.
(10)
Here the lower script “
” is used to underline the
dependence of the transformation of
)(kw
on a
given specific measure of dependence in criterion
(5).
Hence, virtue of criterion (5), formula (10) di-
rectly implies the relationship for the weight coeffi-
cients of linearized model (3)
)()(
1
w
zu
zu
,
,2,1
.
(11)
To “open” the sign of modulo in (11), one should
apply the sign of the regression of the output process
of the system onto the input one, that is
0)(,1
0)(,1
)(sign
zu
zu
zu
reg
reg
reg
,
where
)(
)(
)(
tu
tz
reg
zu
E
,
and
E
stands for the conditional mathematical
expectation. Thus, finally,
)()(sign)(
1
zuzu
zu
regw
,2,1
.
(12)
Accordingly, relationship (12) just determines the
weight function coefficients of linearized model (3).
4 TOWARDS CONSISTENT
MEASURES OF DEPENDENCE
As pointed out in Section 1, consistent measures of
dependence play a special role in the system identi-
fication, first of all, with regard to non-linear sys-
tems. A. Rényi (1989) has formulated axioms that
were recognized to be the most natural to define a
measure of dependence
YX ,
between two ran-
dom values X and Y, which is to characterize ex-
haustively such a dependence. These axioms are as
follows:
A)
YX ,
is defined for any pair of random val-
ues X and Y, if none of them is a constant with
probability 1.
B)
YX ,
=
XY ,
.
C)
1,0
YX
.
D)
0,
YX
if and only if X and Y are inde-
pendent.
E)
1,
YX
if there exists a deterministic de-
pendence between X and Y, that is either
)(XY
, or )(YX
, where
and
are
some Borel-measurable functions.
F)
If
and
are some one-to-one Borel-
measurable functions, then
)(),( YX
YX ,
.
G)
If the joint probability distribution of X and Y is
Gaussian, then
YXrYX ,,
, where
YXr , is the conventional correlation coeffi-
cient between X and Y.
Measures of dependence meeting the Rényi axi-
oms, with the exception, may be Axiom F, will be
hereinafter refereed as consistent in the Rényi sense.
The conventional correlation coefficient
YXr ,
is, of course, most widely known among different
measures of dependence. More delicate approach to
characterize the dependence of random values is
concerned with applying the correlation ratio
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
526

0)(,
)(
),(
Y
Y
X
Y
YX var
var
Evar
,
and the maximal correlation coefficient
YXS , ,
originally introduced by H. Gebelein (1941), and
investigated in papers of O.V. Sarmanov (1963a,b),
Sarmanov and Zakharov (1960), A. Rényi, and oth-
ers
)()(
)(),(
,
sup
,
XCYB
XCYB
YXS
CB
varvar
cov
,
0)(,0)( XCYB varvar
.
In the formula, the supremum is taken over the sets
of Borel-measurable functions {
B} and {C}, and
BB ,
CC , while
,cov stands for the co-
variance.
Meanwhile, it was shown in the paper of Rényi
(1959) that the maximal correlation coefficient
YXS , meets the above axioms only, while the
conventional correlation coefficient
YXr , and the
correlation ratio
YX ,
do not. In particular, Axi-
oms D, E, F are not met for the correlation coeffi-
cient, and Axioms D, F are not met for the correla-
tion ratio.
Here one should underline, that consistent in the
Kolmogorov sense measures of dependence are not
mandatory consistent in the Rényi sense. In the first
turn, this is concerned with meeting Rényi Axioms
C and G. And, at the same time, the approach to the
statistical linearization, presented in the preceding
Section, just directs the method of constructing
measures of dependence meeting Rényi Axioms C
and G. Namely, the approach is as follows:
1) For any measure of dependence
XY
be-
tween random values X and Y one should calculated
this measure for the two-dimensional Gaussian den-
sity depending on the correlation coefficient
),YXr .
2) Represent the expression obtained as a func-
tion in modulo of the correlation coefficient
),YXr
XY
,
(13)
and invert this function.
3) The expression obtained
XY
XY
1
(14)
(as a function of the initial measure of dependence
XY
) defines the measure of dependence between
two random values X and Y, meeting Rényi Axioms
C and G.
In particular, for the maximal correlation coeffi-
cient
YXS , the corresponding function
),),
),(
YXrYXr
YXS
XY
is the identi-
cal transformation. Meanwhile, one should be noted
that calculation of the maximal correlation coeffi-
cient is concerned with the necessity of applying a
complex iterative procedure of determining the first
eigenvalue and the pair of the first eigenfunctions
(corresponding to this eigenvalue) of the stochastic
kernel
)()(),( xpypyxp
xyxy
.
Along with the maximal correlation coefficient
based, in entity, on the comparison of moment char-
acteristics of the joint and marginal probability dis-
tributions of the pair of considered random values, a
broad class of measures of dependence is construct-
ed by use of the direct comparison of the joint and
marginal probability distributions of random values.
Such a class is known is the measure of divergence
of probability distributions. Most known among
them involves (Sarmanov and Zakharov, 1960):
Contingency coefficient
)()(),(
))()(),((
),(
2
2
ypxpyxp
ypxpyxp
YX
yxxy
yxxy
E
,
(15)
Shannon mutual information
)()(
),(
ln),(
ypxp
yxp
YXI
yx
xy
E ,
(16)
Measures of dependence (15), (16) meet all Rényi
Axioms with the exception of Axioms C and G.
Correspondingly, the methodology of formulae
(13), (14) implies the following transforms:
for the contingency coefficient (15),
),(
2
YX
=
)),((
1
),(
YX
YX
=
1),(
),(
2
2
YX
YX
,
(17)
for the Shannon mutual information (16)
),(21
),(
1)),((),(
YXI
YXI
eYXIYX
(18)
Formulae (17), (18) are known in the literature and
in the present paper are presented as illustrative ex-
amples confirming the applicability of formulae
(13), (14). Measures of dependence (17), (18) meet
all the Rényi Axioms and determine solution (12) of
the problem of the statistical linearization for the
StatisticalLinearizationandConsistentMeasuresofDependence:AUnifiedApproach
527

linearization criteria based on a corresponding
measure of dependence ((15), (16)).
5 MEASURES OF DEPENDENCE
BASED ON THE RÉNYI
ENTROPY
Besides the Shannon definition of the entropy,
which, in turn, leads to the definition of the Shannon
mutual information (16), other ways to define the
entropy are known. For a random value
X having the
probability distribution density
)(xp
x
, the Rényi
entropy of the order
α (Rényi, 1961, 1976a,b) is de-
fined as
1
)(ln
1
1
)(
xpXR
x
E
,
1,0
.
Meanwhile, as
α tends to 1, )( XR
tends to the
expression determining the Shannon entropy that,
thus, may be considered as the Rényi entropy of the
order 1.
From a computational point of view, especially
under the necessity of estimating by use of sample
data, the Rényi entropy was recognized as more
preferable than that of Shannon, since the Rényi
entropy is a ''logarithm of integral'', what is compu-
tationally simpler than an ''integral of logarithm'' as
in the case of the Shannon entropy. Meanwhile, the
selection of a specific value of the order
α, is of a
special importance, since the larger the order is, the
more complicated the computational procedure be-
comes.
Also one may be noted that the Rényi entropy for
continuous random values takes its magnitude at the
whole interval
;
as well as the Shannon
entropy; and for some probability distributions the
entropies of Rényi and Shannon may coincide. In
that case, of course, the Rényi entropy does not de-
pend on the order
α. Indeed, this is valid, for in-
stance, for the uniform distribution at the interval
ba; , when both the Shannon and Rényi entropy
have the form
ab ln . Analytical expressions for a
broad class of univariate and multivariate probability
distributions are presented in the papers of (Nadara-
jah and Zografos, 2003, Zografos and Nadarajah,
2005a,b).
As specific values of the order
1,0
any
one may be selected, but the problem complexity,
meanwhile, grows exponentially with the growth of
α; at the same time the value of 2
was recog-
nized in the literature as providing good results
(Principe et al., 2000). For
2
the expression
)(ln)(
2
xpXR
x
E
is known as the quadratic entropy.
So far, the consideration was concerned with the
Rényi entropy of one (possibly, multivariate) proba-
bility distribution density. Along with such (margin-
al) entropy, one may in a corresponding manner de-
fine the mutual Rényi entropy of the order
),(
21
for a pair of random values
X and Y with a joint and
marginal probability distribution densities. Within
such an approach, the first probability measure is
defined by the joint probability distribution density
),( yxp
xy
of the random values X and Y, the second
probability measure is defined by the multiplication
of the marginal probability distribution densities,
correspondingly
p
x
(x) and p
y
(y) of the random values
X and Y. Then the mutual Rényi entropy
),(
21
,
YXR
of the order ),(
21
may be defined
in this case as follows:
),(
21
,
YXR
=
21
)()(),(ln
1
1
1
ypxpyxp
yxxyp
xy
E
,
1,0
21
2
2
2
1
,
where the mathematical expectation is taken over
),( yxp
xy
. The marginal Rényi entropy is, thus, a
partial case of the mutual one, when either
0
1
,
or
0
2
. In the first case (
21
,0 ) the
mutual Rényi entropy takes the form
),(
,0
YXR
),(
)()(
ln
1
1
yxp
ypxp
xy
yx
p
xy
E
,
in the second case (
0,
21
),
1
0,
),(ln
1
1
),(
yxpYXR
xyp
xy
E
.
In the both cases, the mathematical expectation is
taken (formally) over
p
xy
(x,y). At the same time,
),(
,0
YXR
does not depend on
),( yxp
xy
, while
),(
0,
YXR
does not explicitly depend on p
x
(y) and
p
y
(y). So,
),(
0,
YXR
and
),(
,0
YXR
should be
considered as marginal entropies of the probability
distribution densities
)()( ypxp
yx
and
),( yxp
xy
correspondingly. These marginal entropies will be
designated as
)(
yx
ppR
and
)(
xy
pR
, that is
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
528

),()()(ln
1
1
)(
,0
1
YXRypxp
ppR
yxpp
yx
yx
E
,
where the mathematical expectation is taken over
)()( ypxp
yx
; and
1
),(ln
1
1
)(
yxppR
xypxy
xy
E
),(
0,
YXR
,
where the mathematical expectation is taken over
),( yxp
xy
.
Of course, one should be noted that
)()()(
yxxy
pRpRpR
, when the random
values X and Y are stochastically independent.
Also, within the consideration of non-zero cases,
when
0,0
21
, the ''symmetric'' case is em-
phasized, when
2
21
. It will serve as a
basis for constructing the mutual Rényi information
of the order
α for random values.
Again, since the Shannon mutual information
I(X,Y) for the pair of random values X and Y has the
representation via corresponding entropies of these
random values
),()()(),( YXHYHXHYXI
,
it would be natural to search for the mutual Rényi
information
),( YXI
R
of the order α in a similar
form, that is
)()(),(
),(
32
2
,
2
1 yxxy
R
ppRcpRcYXRc
YXI
, (19)
where
321
,, ccc are normalizing coefficients select-
ed in the manner to provide meeting the condition:
0),( YXI
R
, meanwhile
0),( YXI
R
if and only if the random values X and Y
are stochastically independent.
(20)
Condition (20) implies infinitely many solutions that
in a unified form may be written as
1,
2
,
1,
2
,
321
321
IFccc
IFccc
,
(21)
where
0
. Hence, one may just set 1
, and
taking into account all above considerations, the
mutual Rényi information of the order
α is written in
the form
11
2
1
2
)()(),(
)()(),(
ln
)(
1
),(
ypxpyxp
ypxpyxp
YXI
yxppxyp
yxxyp
R
yxxy
xy
EE
E
, where
1,1
1,1
)(
IF
IF
.
As well as the Shannon mutual information, thus
obtained
),( YXI
R
takes its values at the interval
,0 . Meanwhile, the fraction, standing inside the
sign of logarithm, has an evident interpretation as
the cosine of the angle between vectors of corre-
sponding Hilbert space formed by
α times integrated
functions mapping
2
R into
1
R , where the inner
product of its vectors
),(),,(
21
yxyx
is defined by
the natural expression
dxdyyxyxyxyx ),(),(),(),,(
2121
,
as well as the Euclidean norm of the vector
),( yx
has the form
dxdyyxyx
2
2
),(),(
.
Thus following to the notations introduced, the mu-
tual Rényi information may be written as
2
2
2
2
22
)()(),(
)()(,),(
ln
)(
1
),(
ypxpyxp
ypxpyxp
YXI
yxxy
yxxy
R
=
22
)()(,),(cosln
)(
1
ypxpyxp
yxxy
.
For a partial case, when
2
, the preceding ex-
pression directly implies the sol called Cauchy-
Schwartz divergence
),( YXD
CS
dxdyypxpdxdyyxp
dxdyypxpyxp
yxxy
yxxy
22
)()(),(
)()(),(
ln
,
(22)
StatisticalLinearizationandConsistentMeasuresofDependence:AUnifiedApproach
529

proposed declaratively in the fullness of time in a
number of papers (for instance, (Principe et al.,
2000) and subsequent papers), that is by involving
the Cauchy-Schwartz inequality, but disregarding
condition (19)-(21) imposed on the relationship be-
tween the mutual Rényi information and correspond-
ing Rényi entropies. Thus the Cauchy-Schwartz di-
vergence
),( YXD
CS
is a partial case of the mutual
Rényi information
),( YXI
R
as 2
.
The Cauchy-Schwartz divergence
),( YXD
CS
meets Rényi Axioms A, B, D, E and does not meet
Axioms C, F, G. At the same time,
),( YXD
CS
meets Axiom F in the case of affine transformations.
In accordance to formulae (13), (14), for
),( YXD
CS
in (22) one may construct the following transfor-
mation:
),( YXd
CS
),(4
),(4
342
12
YXD
YXD
CS
CS
e
e
.
(23)
One may show that the measure of dependence
),( YXd
CS
in (23) meets all Rényi Axioms with the
exception of Axiom F, but the property of invariance
to one-to-one transformations is preserved for any
affine transformations of random values. The behav-
ior of the measure (23) in dependence of values of
the Cauchy-Schwartz divergence is displayed in
Figure 1.
Measure of dependence (23) determines solution
(12) of the problem of the statistical linearization for
the linearization criteria based on the Cauchy-
Schwartz divergence (22).
0 0.2 0.4 0. 6 0.8
0
0.2
0.4
0.6
0.8
x
x
Figure 1: The dependence of the measure ),( YXd
CS
in
(23) of values of the Cauchy-Schwartz divergence (22).
6 EXAMPLE: SYSTEMS WITH
ZERO INPUT/OUTPUT
CORRELATION
As it was pointed out in Section 1, there exist nu-
merous examples, when applying conventional cor-
relation techniques under model deriving does not
provide suitable results. Among such systems, one
may emphasize those ones, for which the depend-
ence between input and output variables is described
by probability distribution densities belonging to the
O.V. Sarmanov class of distributions (Sarmanov,
1967, Kotz et al., 2000). In particular, these involve
the following one
12121
2
),(
22
22
2
3
2
3
2 yx
yx
ee
e
yxp
,
11
(24)
For density (24), the correlation coefficient
YXr ,
and correlation ratio
YX ,
are equal to zero,
while the maximal correlation coefficient is of the
form:
1
7
4
),( YXS
.
Magnitudes of the parameter λ considerably influ-
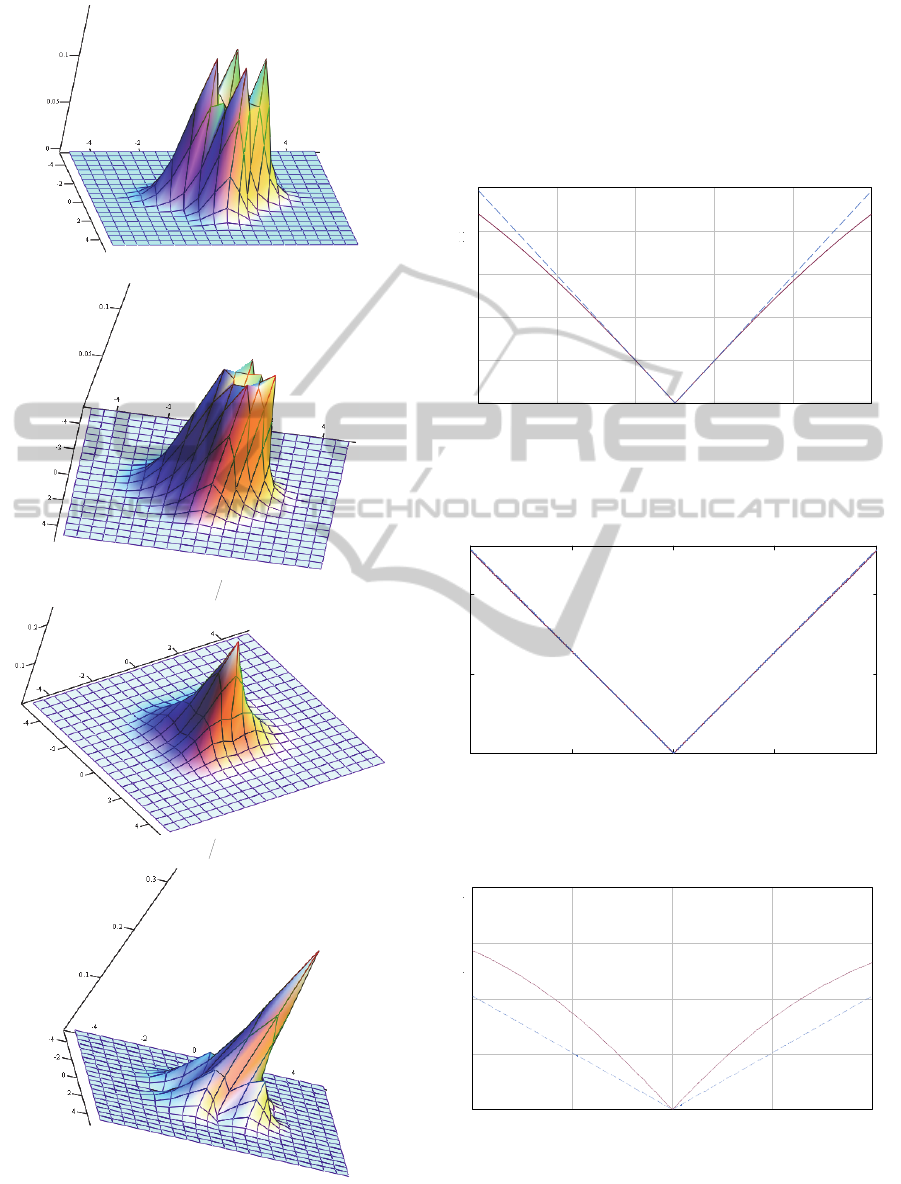
ence the shape of density (24). In Figure 2, the form
of probability distribution density (24) under some
magnitudes of the parameter λ is presented.
Thus, for instance, stochastic dependence (1) be-
tween the output process,
)(tz , and the input pro-
cess,
)(su
, of a non-linear system is defined by a
probability distribution density (of course, being not
known to the researcher) of form (24) with the pa-
rameter
)(
,
s
t
, then applying both
conventional correlation and dispersion techniques
of the statistical linearization would lead, under con-
structing model (3), to the representation to the out-
put system process as the identical zero, what is ex-
cluded under applying the approach presented,
which is based on consistent measures of depend-
ence.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
530
1
21
21
1
Figure 2: The shape of density (24) under various magni-
tudes of the parameter λ.
In Figure 3 (a, b, c), the dependence of the mag-
nitudes of
),(
2
XY
(17), ),( XY
(18), and
),( YXd
CS
(23) in the parameter λ is presented cor-
respondingly in the comparison with the magnitudes
of the maximal correlation coefficient
YXS , (the
dotted line).
1 0.6 0.2 0.2 0.6 1
0
0.104
0.208
0.312
0.416
0.52
y
),(
2
YX
),( YXS
Figure 3a: The comparison of magnitudes of
),(
2
YX
and
YXS , under various values of the parameter λ in
density (24).
1 0. 5 0 0.5
1
0
0. 2
0. 4
),( YX
),( YXS
Figure 3b: The comparison of magnitudes of
YX ,
and
YXS , under various values of the parameter λ in densi-
ty (24).
1 0.5 0 0.5 1
0
0.25
0.5
0.75
1
4
ab
),( YXd
CS
),( YXS
Figure 3c: The comparison of magnitudes of ),( YXd
CS
and
YXS , under various values of the parameter λ in
density (24).
StatisticalLinearizationandConsistentMeasuresofDependence:AUnifiedApproach
531

7 CONCLUSIONS
An approach to the statistical linearization of in-
put/output mappings of stochastic discrete-time sys-
tems driven with a white-noise Gaussian input pro-
cess has been considered. The approach is based on
applying consistent measures of dependence of ran-
dom values. Within the approach, the statistical line-
arization criterion is the condition of coincidence of
the mathematical expectations of output processes of
the system and model, and the condition of coinci-
dence of a consistent, in the Kolmogorov sense,
measure of dependence of output and input process-
es of the system and the same measure of depend-
ence of the model output and input processes. Ex-
plicit analytical expressions for the coefficients of
the weight function of the linearized input/output
model were derived as a function of this (forming
the statistical linearization criterion) consistent
measure of dependence of output and input process-
es of the system. Meanwhile, such a function defines
the form of a transformation that enables one to con-
struct corresponding consistent in the Rényi sense
measure of dependence from a consistent in the
Kolmogorov sense measure of dependence. In the
paper, a consistent in the Kolmogorov sense meas-
ure of dependence was referred as consistent in the
Rényi sense, if such a measure meets all Rényi Axi-
oms (Rényi, 1959) with the exception, may be, the
axiom of invariance with respect to one-to-one trans-
formations of random values under study. In particu-
lar, such a consistent in the Rényi sense measure of
dependence has been constructed from the Cauchy-
Schwartz divergence, being a consistent measure of
dependence in the Kolmogorov sense.
REFERENCES
Gebelein, H., 1941. “Das statistische Problem der
Korrelation als Variations- und Eigenwertproblem und
sein Zusammenhang mit der Ausgleichungsrechnung”,
Zeitschrift für Angewandte Mathematik und Mechanik,
vol. 21, no. 6, pp. 364-379.
Kotz, S., Balakrishnan, N., and N.L. Johnson, 2000. Con-
tinuous Multivariate Distributions. Volume 1. Models
and Applications / Second Edition, Wiley, New York,
752 p.
Nadarajah, S. and K. Zografos, 2003. “Formulas for Rényi
information and related measures for univariate distri-
butions”, Information Sciences, vol. 155, no. 1, pp.
119-138.
Nadarajah, S. and K. Zografos, 2005a. “Expressions for
Rényi and Shannon entropies for bivariate distribu-
tions”, Information Sciences, vol. 170, no. 2-4,
pp. 173-189..
Principe, J., Xu, D., and J. Fisher, 2000. “Information
Theoretic Learning”, In: Unsupervised Adaptive Fil-
tering / Haykin (Ed.). Wiley, New York, vol. 1, pp.
265-319.
Rajbman, N.S., 1981. “Extensions to nonlinear and mini-
max approaches”, Trends and Progress in System
Identification, ed. P. Eykhoff, Pergamon Press, Ox-
ford, pp. 185-237.
Rényi, A., 1959. “On measures of dependence”, Acta
Math. Hung., vol. 10, no 3-4, pp. 441-451.
Rényi, A., 1961. “On measures of information and entro-
py”, in: Proceedings of the 4th Berkeley Symposium
on Mathematics, Statistics and Probability (June 20-
July 30, 1960). University of California Press, Berke-
ley, California, vol. 1, pp. 547-561.
Rényi, A., 1976a. “Some Fundamental Questions of In-
formation Theory”, Selected Papers of Alfred Rényi,
Akademiai Kiado, Budapest, vol. 2, pp. 526-552.
Rényi, A., 1976b. “On Measures of Entropy and Infor-
mation”, Selected Papers of Alfréd Renyi, Akademiai
Kiado, Budapest, vol. 2, pp. 565-580.
Roberts, J.B. and P.D. Spanos, 2003. Random Vibration
and Statistical Linearization, Dover, New York,
464 p.
Sarmanov, O.V and E.K. Zakharov, 1960. “Measures of
dependence between random variables and spectra of
stochastic kernels and matrices”, Matematicheskiy
Sbornik, vol. 52(94), pp. 953-990. (in Russian).
Sarmanov, O.V., 1963a. “Investigation of stationary Mar-
kov processes by the method of eigenfunction expan-
sion”, Sel. Trans. Math. Statist. Probability, vol. 4, pp.
245-269.
Sarmanov, O.V., 1963b. “The maximum correlation coef-
ficient (nonsymmetric case)”, Sel. Trans. Math. Statist.
Probability, vol. 4, pp. 207-210.
Sarmanov, O.V., 1967. “Remarks on uncorrelated Gaussi-
an dependent random variables”, Theory Probab.
Appl., vol. 12, issue 1, pp. 124-126.
Socha. L., 2008. Linearization Methods for Stochastic
Dynamic Systems, Lect. Notes Phys. 730, Springer,
Berlin, Heidelberg, 383 p.
Zografos, K. and S. Nadarajah, 2005b. “Expressions for
Rényi and Shannon entropies for multivariate distribu-
tions”, Statistics & Probability Letters, vol. 71, no. 1,
pp. 71-84.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
532
